|
||||
|
|
звонок бесплатный
Наши сотрудники:
[email protected]
Екатерина - специалист по продаже а/м КАМАЗ
 [email protected]
[email protected]






Техника в наличии

Тягач КАМАЗ 44108-6030-24
2014г, 6х6, Евро3, дв.КАМАЗ 300 л.с., КПП ZF9, бак 210л+350л, МКБ,МОБ,рестайлинг.
цена 2 220 000 руб.,

КАМАЗ 4308-6063-28(R4)
4х2,дв. Cummins ISB6.7e4 245л.с. (Е-4),КПП ZF6S1000, V кузова=39,7куб.м., спальное место, бак 210л, шк-пет,МКБ, ТНВД BOSCH, система нейтрализ. ОГ(AdBlue), тент, каркас, рестайлинг, внутр. размеры платформы 6112х2470х730 мм
цена 1 950 000 руб.,

Самосвал КАМАЗ 6520-057
2014г, 6х4,Евро3, дв.КАМАЗ 320 л.с., КПП ZF16, ТНВД ЯЗДА, бак 350л, г/п 20 тонн, V кузова =20 куб.м.,МКБ,МОБ, со спальным местом.
цена 2 700 000 руб.,

Самосвал 6522-027
2014, 6х6, дв.КАМАЗ 740.51,320 л.с., КПП ZF16,бак 350л, г/п 19 тонн,V кузова 12куб.м.,МКБ,МОБ,задняя разгрузка,обогрев платформы.
цена 3 190 000 руб.,
СУПЕР ЦЕНА
на АВТОМОБИЛИ КАМАЗ
| 43118-010-10 (дв.740.30-260 л.с.) | 2 220 000 |
| 43118-6033-24 (дв.740.55-300 л.с.) | 2 300 000 |
| 65117-029 (дв.740.30-260 л.с.) | 2 200 000 |
| 65117-6010-62 (дв.740.62-280 л.с.) | 2 350 000 |
| 44108 (дв.740.30-260 л.с.) | 2 160 000 |
| 44108-6030-24 (дв.740.55,рест.) | 2 200 000 |
| 65116-010-62 (дв.740.62-280 л.с.) | 1 880 000 |
| 6460 (дв.740.50-360 л.с.) | 2 180 000 |
| 45143-011-15 (дв.740.13-260л.с) | 2 180 000 |
| 65115 (дв.740.62-280 л.с.,рест.) | 2 190 000 |
| 65115 (дв.740.62-280 л.с.,3-х стор) | 2 295 000 |
| 6520 (дв.740.51-320 л.с.) | 2 610 000 |
| 6520 (дв.740.51-320 л.с.,сп.место) | 2 700 000 |
| 6522-027 (дв.740.51-320 л.с.,6х6) | 3 190 000 |

подробнее про услугу перегона можно прочесть здесь.

|
Нужны самосвалы? Обратите внимание на Ford-65513-02. |
КАМАЗы в лизинг
ООО «Старт Импэкс» имеет возможность поставки грузовой автотехники КАМАЗ, а так же спецтехники на шасси КАМАЗ в лизинг. Продажа грузовой техники по лизинговым схемам имеет определенные выгоды для покупателя грузовика. Рассрочка платежа, а так же то обстоятельство, что грузовики до полной выплаты лизинговых платежей находятся на балансе лизингодателя, и соответственно покупатель автомобиля не платит налогов на имущество. Мы готовы предложить любые модели бортовых автомобилей, тягачей и самосвалов по самым выгодным лизинговым схемам.Контактная информация.
г. Набережные Челны, Промкомзона-2, Автодорога №3, база «Партнер плюс».
тел/факс (8552) 388373.
Схема проезда
Неподвижный блок. Сила натяжения троса формула
Неподвижный блок, все формулы и примеры задач
Общие сведения о неподвижном блоке
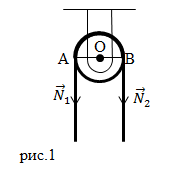
Неподвижный блок относят к простым механизмам (рис.1). Будем считать, что блок вращается без трения. Если веревка натянута и не скользит по блоку, то на блок действуют две силы натяжения веревки (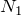 и
и 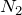 ). Точки приложения этих сил на рис. 1 обозначены как A и B, которые расположены на окружности блока.
). Точки приложения этих сил на рис. 1 обозначены как A и B, которые расположены на окружности блока.
Условия равновесия блока определяют из условия равновесия моментов сил, которые к нему приложены. Блок на рис.1 будет находиться в равновесии, если силы 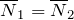 , так как плечи этих сил одинаковы (ОА=ОВ). Блок – это рычаг, который имеет равные плечи. Блок, который представлен на рис.1 не дает выигрыша в силе, однако он позволяет изменять направление действия силы. Тянуть за веревку, которая идет сверху обычно удобнее, чем за веревку, которая идет снизу.
, так как плечи этих сил одинаковы (ОА=ОВ). Блок – это рычаг, который имеет равные плечи. Блок, который представлен на рис.1 не дает выигрыша в силе, однако он позволяет изменять направление действия силы. Тянуть за веревку, которая идет сверху обычно удобнее, чем за веревку, которая идет снизу.
Вместо блока можно использовать гладкую неподвижную опору. При этом через нее перекидывают веревку или канат, скользящие по опоре, однако при этом существенно увеличивается сила трения.
Неподвижный блок выигрыша в работе не дает. Пути, которые проходят точки приложения сил, одинаковы, равны силы, значит, равны работы.
Комбинация блоков
Для получения выигрыша в силе используют комбинации блоков, например, двойной блок. При этом используют блоки разного радиуса, которые соединяют неподвижно между собой и насаживают на единую ось. К каждому блоку крепится веревка таким образом, что она может наматываться на блок или сматываться с него без скольжения. Плечи сил в данном случае неодинаковы. Двойной блок работает как неравноплечный рычаг. На рис.2 представлена схема двойного блока.
Условием равновесия такого рычага является выражение:
![Rendered by QuickLaTeX.com \[N_1r_1=N_2r_2 \qquad (1) \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-3746fbad72ff1dce294aee46f949d2dd_l3.png)
Двойной блок можно считать преобразователем силы. Прикладывая меньшую силу к веревке, приложенной к блоку большего радиуса, получают силу, которая действует со стороны веревки, навитой на блок меньшего радиуса.
Золотое правило механики
Формулировка «Золотого правила»: Отношение перемещений точек, к которым приложены силы в блоке всегда обратно отношению сил, которые приложены к этим точкам.
Для двойного блока, если для равновесия блока сила 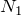 должна быть в n раз больше по величине, чем сила
должна быть в n раз больше по величине, чем сила 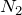 , то при вращении блока путь, который пройдет точка приложения силы
, то при вращении блока путь, который пройдет точка приложения силы 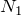 будет в n раз меньше, чем путь
будет в n раз меньше, чем путь 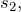 который проходит точка приложения силы
который проходит точка приложения силы 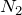 .
.
Золотое правило было сформулировано в древности как: «То, что выиграно в силе, проиграно в пути». В математическом виде это правило представим как:
![Rendered by QuickLaTeX.com \[\frac{N_2}{N_1}=\frac{s_1}{s_2} \qquad (2) \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-63de04daf47c36fd131422ce97b4ce96_l3.png)
Золотое правило стало первой самой простой формулировкой закона сохранения энергии. Золотое правило механики выполняется для случаев, когда движения простых механизмов равномерно или почти равномерно. Так, при вращении двойного блока концы веревок переместятся на расстояния, которые связаны с радиусами блоков как:
![Rendered by QuickLaTeX.com \[\frac{s_1}{s_2}=\frac{r_1}{r_2} \qquad (3) \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-df55e8c48112957f414c5781d77118ab_l3.png)
Следовательно, для того чтобы выполнялось золотое правило для двойного блока должно выполняться условие:
![Rendered by QuickLaTeX.com \[\frac{N_1}{N_2}=\frac{r_2}{r_1} \qquad (4) \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-c747c75589b70149dc1cceff9283d236_l3.png)
Когда силы 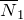 и
и 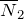 будут уравновешены, то блок должен покоиться или двигаться равномерно.
будут уравновешены, то блок должен покоиться или двигаться равномерно.
Примеры решения задач на неподвижный блок
ru.solverbook.com
Kvant. Формула Эйлера — PhysBook
Буздин А. И. О швартовке, трении и формуле Эйлера //Квант. — 1988. — № 5. — С. 49-50.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
Наверное, всем хорошо известно, что при швартовке судна с него бросают на пристань канат (швартов) с петлей на конце, которую надевают на причальную тумбу. Затем, когда судно подходит совсем близко к пристани, матрос быстро наматывает другой конец каната «восьмеркой» на специальную опору на палубе — кнехт (чугунная парная тумба). Таким способом удается надежно удерживать громадное судно рядом с причалом. В чем же здесь дело? В необычайной силе матроса?
По-видимому, многие, в том числе и прославленный писатель-фантаст Жюль Берн, склонны именно к такому заключению. Обратимся, вслед за Перельманом[1], к эпизоду из книги Жюля Верна «Матиас Шандор», где описывается подвиг силача-атлета Матифу. Этот герой при спуске на воду судна «Трабоколо» предотвратил его столкновение с маленькой прогулочной яхтой, что грозило яхте гибелью.
«...«Трабоколо» быстро скользило вниз по наклону. Белый дымок, появившийся вследствие трения, закрутился перед его носом, тогда как корма погрузилась уже в воду бухты (судно спускалось на воду кормой вперед — А. Б.).
Вдруг появляется человек, схватывает швартов, висящий у передней части «Трабоколо», и старается удержать его, пригнувшись к земле. В одно мгновение он наматывает швартов на вбитую в землю металлическую трубу и, рискуя быть раздавленным, держит с нечеловеческой силой в руках канат в продолжение 10 секунд.»
Жюль Берн правильно отметил роль, которую играет трение во время скольжения корабля,— нагрев его корпуса и возникновение из-за этого дыма. Однако он недооценил роль трения (и переоценил, тем самым, роль Матифу) при описании подвига атлета.
Давайте попробуем разобраться, какая сила нужна, чтобы удержать канат, уже намотанный на опору — трубу или кнехт.
Вначале трением пренебрежем и рассмотрим неподвижный участок каната, изогнутый опорой на малый угол Δα (см. рисунок). Пусть канат натянут силой T и со стороны опоры на рассматриваемый участок каната действует сила реакции N. Найдем ее из условия равновесия каната: сумма всех сил, действующих на участок каната, равна нулю. Отсюда
\(~N = T \Delta \alpha\)(здесь мы учли, что для малых углов sin Δα = Δα).
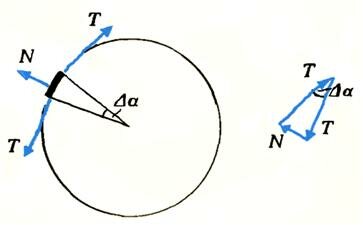
При наличии трения канат может быть неподвижным и в том случае, когда силы натяжения слева и справа от рассматриваемого участка немного отличаются друг от друга. Проскальзывание каната начнется тогда, когда разность этих сил достигнет максимальной величины силы трения покоя:
\(~\Delta T = F_{TP} = \mu N = \mu T \Delta \alpha\),где μ — коэффициент трения между канатом и опорой. Из последнего равенства следует, что скорость изменения силы натяжения каната с ростом угла охвата пропорциональна величине силы натяжения:
\(~\frac{\Delta T}{\Delta \alpha} \sim T \), или \(~\frac{\Delta T}{\Delta \alpha} =-\mu T \) .Знак минус здесь означает, что при увеличении угла охвата натяжение каната уменьшается.
В физике часто встречаются ситуации, когда скорость изменения какой- либо величины пропорциональна самой этой величине. Напомним, например, явление естественного радиоактивного распада («Физика 10», § 92): уменьшение числа нераспавшихся радиоактивных ядер в единицу времени пропорционально их же числу. Другим примером может служить разряд заряженного конденсатора через резистор: уменьшение заряда на конденсаторе пропорционально току через резистор, который, в свою очередь, пропорционален заряду конденсатора. Во всех этих случаях происходит очень быстрое изменение соответствующей величины. Действительно, если, например, скорость изменения скорости (ускорение) движения тела постоянна, то величина скорости линейно растет со временем. Если же ускорение пропорционально скорости, то оно все время увеличивается и скорость растет намного быстрее — по так называемому экспоненциальному закону.
Такая же зависимость получается и в нашем случае для изменения силы натяжения каната. (Подчеркнем еще раз, что речь идет о минимально возможной разности сил натяжения каната — когда вот-вот начнется его скольжение по опоре.) Впервые этот вопрос был рассмотрен великим математиком, механиком, физиком и астрономом Леонардом Эйлером (1707—1783). Он показал, что натяжение каната Т в зависимости от угла охвата опоры канатом (угол навития) а изменяется по закону
\(~T = T_0 e^{-\mu \alpha}\) ,где е = 2,72... — основание натурального логарифма, T0 — начальное натяжение каната (еще не навитого на опору).
Угол α (измеряемый в радианах) связан с числом оборотов n каната вокруг кнехта простым соотношением: α = 2 πn. Тогда, если при одном обороте натяжение каната уменьшается в k раз, т. е.
\(~\frac{T_0}{T_1} = e^{2 \mu \pi} = k\) ,после n оборотов натяжение ослабевает в kn раз:
\(~\frac{T_0}{T_n} = \frac{T_0}{T_1} \cdot \frac{T_1}{T_2} \cdot \ldots \cdot \frac{T_{n-1}}{T_n} = k^n = e^{2 \pi \mu n}\) .При коэффициенте трения μ = 0,3, например, один оборот каната вокруг кнехта уменьшает силу его натяжения почти в 7 раз, а если сделать два оборота — натяжение ослабевает примерно в 40 раз! С ростом числа оборотов натяжение каната (благодаря трению) становится все меньше и меньше и постепенно сходит на нет.
Возвращаясь к герою Жюля Верна Матифу, мы теперь можем сказать, что, намотав канат на железную трубу, он сильно облегчил себе задачу. Я. И. Перельман, используя содержащиеся в романе данные о «Трабоколо» и сделав соответствующие расчеты, обнаружил, что если силач Матифу успел обернуть канат вокруг трубы три раза, то на его месте мог бы быть и ребенок. Точно так же и при швартовке судов от матросов не требуется большой силы — нужно лишь проявить внимательность и ловкость и вовремя успеть быстро намотать канат на кнехт.
Заметим, что с рассмотренным явлением каждый из вас сталкивается практически ежедневно, что-нибудь завязывая — будь то шнурки, шарф или веревка. Ведь любой узел по существу представляет собой веревку, навитую на «опору» (ту же самую веревку).
Примечания
- ↑ Я. И. Перелыяан. «Занимательная физика».— М.: Наука, 1986. Книга 2. с. 35.
www.physbook.ru
Сила - натяжение - канат
Сила - натяжение - канат
Cтраница 2
Следовательно, если тело опускается равноускоренно, то сила натяжения каната, удерживающего это тело, будет меньше его веса. [16]
Следовательно, если тело опускается равноускоренно, то сила натяжения каната, удерживающего это тело, меньше его веса. [17]
Следовательно, если тело опускается равноускоренно, то сила натяжения каната, удерживающего это тело, меньше его веса. [18]
Спуск и подъем гидробура производится без талевой оснастки, а потому сила натяжения каната Р будет равна весу поднимаемого груза Q, а скорость навивки каната - скорости подъема гидробура. [20]
На балку действуют четыре силы: сила тяжести FT Mg, сила натяжения каната Т, силы реакции опоры Гд и FB - Так как груз находится в покое, то Т Т тд. [21]
Из формулы (6.4) очевидно, что, чем больше провисание, тем меньше сила натяжения каната. [22]
Уравнение движения бревна при выполнении условия задачи будет иметь вид maTcosa, где т-масса бревна, Т - сила натяжения каната, a - угол между бревном и поверхностью земли. [23]
Уравнение движения бревна при выполнении условия задачи будет иметь вид: maTcosa, где т-масса бревна, Г - сила натяжения каната, а - угол между бревном и поверхностью земли. [24]
В последних конструкциях лифтов вместо муфты 4 канат жестко крепят к рычагу 6, а для предотвращения обрыва каната зажимное устройство 3 выполняют с ограниченной силой натяжения каната или зажимное устройство не устанавливают. В последнем случае натяжение каната создается силами трения каната по канато-ведущему шкиву, а для получения нужной силы трения требуется правильно рассчитать вес груза натяжного устройства. [25]
Если бы канат был нерастяжимым и опоры абсолютно жесткими, то тогда, действительно, канат можно было бы разорвать сколь угодно малой силой; однако наличие даже небольших растяжений каната и деформаций опоры существенно ограничивает величину вызываемых малой силой натяжений каната. [26]
Направление ветра перпендикулярно) направлению течения реки. Найти силу натяжения каната, если лодка находится в покое. На каком расстоянии г от берега находится лодка. [27]
Тело массой 500 кг подвесили на канате, и оно движется равнопеременно вниз. Чему равна сила натяжения каната. С каким ускорением тело должно двигаться вниз, чтобы натяжение каната было равно нулю. [28]
Тяжелая однородная доска массой М упирается одним концом в угол между стенкой и полом, к другому концу привязан канат. Как меняется сила натяжения каната с увеличением угла а между доской и полом, если угол р остается постоянным. Как меняется направление силы, действующей со стороны стенки и пола, на стержень. [29]
Ускорение вагонетки во время торможения а v0 / t и направлено вверх вдоль уклона дороги. В этом направлении на вагонетку действуют сила натяжения каната Т и сила трения / kN kmg cos a. Составляющая силы тяжести mg sin а направлена вдоль уклона дороги вниз. [30]
Страницы: 1 2 3
www.ngpedia.ru
Динамика
Задача №1. Под действием силы тяги F, направленной вдоль горизонтальной плоскости, по ее поверхности начинает скользить без начальной скорости тело массой 4 кг и через 3 с после начала движения приобретает скорость 0,6 м/с. Найти силу F, если коэффициент трения между телом и плоскостью 0,2.
| v0 = 0; m = 4 кг; t = 3 c; v = 0,6 м/с; k = 0,2. | |
| F – ? |
Решение: на движущееся тело действует четыре силы: сила тяги , сила трения , сила тяжести и сила нормальной реакции плоскости. Вектор направлен параллельно плоскости вправо. Запишем для данного тела уравнение второго закона Ньютона в векторной форме:
(1)
За положительное направление оси Х примем направление движения тела, ось У направим вертикально вверх. Спроецировав все силы на ось Х, составим уравнение движения тела:
Отсюда
Найдя проекции сил на ось У, запишем уравнение (1) в проекции на эту ось:
;
Учитывая, что ,
получим (2)
Так как тело двигалось равноускоренно без начальной скорости, то в момент времени t скорость тела:
.
Отсюда находим: (3)
Подставив значения Fтр и а из формул (2) и (3) в формулу (1), найдем:
.
Проверим размерность:
Ответ: сила тяги равна F = 8,6 Н.
Задача №2. Груз массой 45 кг перемещается по горизонтальной плоскости под действием силы 294 Н, направленной под углом 30о к горизонту. Коэффициент трения груза о плоскость 0,1. Определить величину ускорения груза.
| F = 294 H; m = 45 кг; k = 0,1; α = 30о. | |
| а – ? |
Решение: на груз действуют: – сила тяжести; – сила нормальной реакции плоскости; – сила тяги; – сила трения. Вектор направлен параллельно плоскости направо. Запишем для данного тела уравнение второго закона Ньютона в векторной форме:
(1)
Выбрав за положительное направление оси Х направление движения тела, а ось У направив вертикально вверх, и, найдя проекции сил на оси, запишем уравнение (1) в проекциях на эти оси:
(2)
(3)
Из уравнения (3) находим, что
.
Тогда .
Подставим это выражение в (2) получим:
,
откуда
Ответ: груз перемещается с ускорением
Задача №3. На гладком столе лежат два связанных нитью груза массами 0,2 кг и 0,3 кг. К ним приложены силы 0,6 Н и 1 Н соответственно, линии действия которых совпадают с нитью. С каким ускорением движутся грузы? Чему равно натяжение нити? Трение не учитывать.
| F1 = 0,6 H; F2 = 1,0 H; m1 = 0,2 кг; m2 = 0,3 кг. | |
| а, Т – ? |
Решение: рассмотрим силы, действующие на каждый груз.
На первый груз действуют: – сила тяжести, – сила нормальной реакции; – сила натяжения нити, – приложенная сила. Уравнение движения для первого груза:
Проецируя векторное уравнение второго закона Ньютона для первого груза на оси 0Х и 0У, получаем:
(1)
На второй груз действуют силы: – сила тяжести, – сила нормальной реакции; – сила натяжения нити, – приложенная сила.
Запишем второй закон Ньютона для второго груза в проекциях на те же оси:
(2)
Складывая уравнения (1) и (2) и учитывая, что для невесомой и нерастяжимой нити:
Т1 = Т2 = Т,
а1 = а2 = а
получим
отсюда
м/с2.
Из уравнения (1):
Н.
Ответ: ускорение, с которым движется система грузов равно а = 0,8 м/с2; сила натяжения нити Т = 0,76 Н
Задача №4. Брусок массой 2 кг скользит по горизонтальной поверхности под действием груза массой 0,5 кг, прикрепленного к концу нерастяжимой нити, перекинутой через неподвижный блок. Коэффициент трения бруска о поверхность 0,1. Найти ускорение движения тела и силу натяжения нити. Массами блока и нити, а также трением в блоке пренебречь.
| m1 = 2 кг; m2 = 0,5 кг; k = 0,1. | |
| а1, Т – ? |
Решение: рассмотрим движение каждого груза отдельно. На брусок действуют: – сила тяжести; – сила нормальной реакции плоскости; – сила натяжения нити; – сила трения.
Запишем для бруска уравнение второго закона Ньютона в векторной форме:
Спроецировав полученное уравнение на выбранные направления осей 0Х и 0У, получим: (1)
(2)
Поскольку из уравнения (2) следует, что , то
Тогда уравнение примет вид:
(3)
На груз действуют: – сила тяжести; – сила натяжения нити. Запишем для груза уравнение второго закона Ньютона в векторной форме:
(4)
Спроецировав уравнение (4) на ось 0У, получим:
(5)
Решая совместно систему уравнений (3) и (5) методом почленного сложения уравнений и учитывая, что Т1 = Т2 = Т и а1 = а2 = а, получаем:
откуда
Силу натяжения нити находим из уравнения (5):
Ответ: ускорение блока а = 1,2 м/с2; сила натяжения нити Т ≈ 4,3 Н.
Задача №5. По наклонной плоскости с углом наклона 300 скользит вниз брусок. Найти его ускорение, если коэффициент трения бруска о плоскость равен 0,8.
| α = 300; k = 0,4. |
| а1 – ? |
Решение: на тело при его скольжении по наклонной плоскости действуют: – сила тяжести; – сила нормальной реакции плоскости; – сила трения.
Запишем для тела уравнение второго закона Ньютона в векторной форме:
Направим ось Х вдоль наклонной плоскости вниз, а ось У перпендикулярно плоскости вверх.
Найдем проекции сил на выбранные направления осей Х и У и запишем скалярные уравнения движения относительно этих осей:
; (1)
(2)
Из уравнения (2) находим, что
.
Учитывая, что , запишем уравнение (1) в виде:
,
откуда
м/с2≈1,6 м/с2
В частности, при отсутствии трения (k = 0):
a = gsinα;
а = 9,8·0,5 = 4,9 м/с2.
Ответ: брусок скользит вниз с ускорением а = 1,6 м/с2.
Задача №6. Груз массой 5 кг движется вверх по наклонной плоскости под действием связанного с ним невесомой и нерастяжимой нитью груза массой 2 кг. Начальные скорости тела и груза равны нулю, коэффициент трения тела о плоскость 0,1, угол наклона плоскости 360. Определить ускорение, с которым движется тело, и силу натяжения нити. Массами нитей, блока, а также трением в блоке пренебречь.
| m1 = 5 кг; m2 = 2 кг; k = 0,1; α = 360. | |
| а, Т – ? |
Решение. Рассмотрим движение каждого груза отдельно. На первый груз действуют: – сила тяжести; – сила нормальной реакции наклонной плоскости; – сила натяжения нити; – сила трения.
По условию задачи вектор ускорения для первого груза направлен вверх по наклонной плоскости. Запишем для первого груза уравнение второго закона Ньютона в векторной форме:
(1)
Направим ось Х вверх по наклонной плоскости, ось У1 – перпендикулярно к ней. Проецируя уравнение (1) на выбранные направления осей Х и У1, получаем:
(2)
(3)
Из уравнения (3) находим, что , поэтому
(4)
Подставляя выражение (4) в уравнение (2), получаем:
(5)
На второй груз действуют: – сила тяжести; – сила натяжения нити. Ускорение второго груза направлено вертикально вниз. Запишем уравнение второго закона Ньютона в векторной форме для второго груза:
(6)
Ось У2 направим вертикально вниз. Спроецировав уравнение (6) на ось У2, получим:
(7)
Сложив почленно уравнения (5) и (7), получим:
Учитывая, что Т1 = Т2 = Т и а1 = а2 = а, находим:
;
Силу натяжения нити определим из уравнения (7):
;
Ответ: ускорение движения тела а = –1,93 м/с2; сила натяжения нити Т = 15,74 Н. Полученные ответы справедливы только в том случае, если тело m1 двигалось вверх по наклонной плоскости. Если же в начальный момент тела были неподвижны или двигались в противоположном направлении, задачу следует переделать, так как направление силы трения при таком движении изменяется на противоположное.
Задача №7. Груз массой 100 г, привязанный на невесомой нити длиной 50 см, движется в вертикальной плоскости с постоянной скоростью 5 м/с. Определить натяжение нити при прохождении грузом нижней и верхней точек траектории. Чему равна разность сил натяжения в этих точках? Как она зависит от скорости движения груза?
| m = 100 г = 0,1 кг; ℓ = 50 см = 0,5 м; v = 5 м/с; g = 9,8 м/с2. | |
| Т1, Т2, ∆Т = Т1 – Т2 – ? |
Решение: на груз действуют две силы: сила тяжести и сила натяжения нити. Величина и направление силы тяжести не зависят от положения груза, а величина и направление силы натяжения изменяются при движении. Рассмотрим каждый случай отдельно.
1-ый случай (рис. а): тело находится в нижней точки траектории. Сила тяжести направлена вертикально вниз, сила натяжения вертикально вверх, и обе направлены перпендикулярно к скорости, следовательно и результирующая сила также перпендикулярна скорости и создаёт только нормальное ускорений . Запишем уравнение второго закона Ньютона в векторной форме:
Направим ось У по радиусу к центру окружности и запишем второй закон Ньютона в проекции на это направление:
где
тогда
откуда
2-ой случай (рис. б): тело находится в верхней точке траектории. В этом случае обе силы и сила тяжести и сила натяжения , направлены вниз и обе, как и в 1 случае, перпендикулярны к скорости. Запишем второй закон Ньютона в векторной форме:
.
Направим ось У опять по радиусу к центру окружности и запишем второй закон Ньютона в проекции на эту ось:
,
где
откуда
определим
Ответ: Т1 = 6 Н; Т2 = 4 Н; Т = 2 Н.
Задача №8. С каким ускорением надо поднимать груз на веревке, чтобы сила натяжения веревки была в 2 раза больше силы тяжести груза?
Решение: на груз действуют две силы: сила тяжести груза и сила реакции каната , численно равная по третьему закону Ньютона силе его натяжения (Тнат = Т). Эти силы направлены в противоположные стороны, причем Т > Р (груз движется вверх). Силы и , действуя на тело, сообщают ему ускорение, поэтому их равнодействующая определится по второму закону. Запишем векторное уравнение:
Абсолютное значение ускорения найдем из соотношения, записанного в проекциях на координатную ось ОХ
или
По условию данной задачи сила натяжения веревки Т = 2Р, следовательно:
phys-portal.ru
423800, Набережные Челны , база Партнер Плюс, тел. 8 800 100-58-94 (звонок бесплатный)