|
||||
|
|
звонок бесплатный
Наши сотрудники:
[email protected]
Екатерина - специалист по продаже а/м КАМАЗ
 [email protected]
[email protected]






Техника в наличии

Тягач КАМАЗ 44108-6030-24
2014г, 6х6, Евро3, дв.КАМАЗ 300 л.с., КПП ZF9, бак 210л+350л, МКБ,МОБ,рестайлинг.
цена 2 220 000 руб.,

КАМАЗ 4308-6063-28(R4)
4х2,дв. Cummins ISB6.7e4 245л.с. (Е-4),КПП ZF6S1000, V кузова=39,7куб.м., спальное место, бак 210л, шк-пет,МКБ, ТНВД BOSCH, система нейтрализ. ОГ(AdBlue), тент, каркас, рестайлинг, внутр. размеры платформы 6112х2470х730 мм
цена 1 950 000 руб.,

Самосвал КАМАЗ 6520-057
2014г, 6х4,Евро3, дв.КАМАЗ 320 л.с., КПП ZF16, ТНВД ЯЗДА, бак 350л, г/п 20 тонн, V кузова =20 куб.м.,МКБ,МОБ, со спальным местом.
цена 2 700 000 руб.,

Самосвал 6522-027
2014, 6х6, дв.КАМАЗ 740.51,320 л.с., КПП ZF16,бак 350л, г/п 19 тонн,V кузова 12куб.м.,МКБ,МОБ,задняя разгрузка,обогрев платформы.
цена 3 190 000 руб.,
СУПЕР ЦЕНА
на АВТОМОБИЛИ КАМАЗ
| 43118-010-10 (дв.740.30-260 л.с.) | 2 220 000 |
| 43118-6033-24 (дв.740.55-300 л.с.) | 2 300 000 |
| 65117-029 (дв.740.30-260 л.с.) | 2 200 000 |
| 65117-6010-62 (дв.740.62-280 л.с.) | 2 350 000 |
| 44108 (дв.740.30-260 л.с.) | 2 160 000 |
| 44108-6030-24 (дв.740.55,рест.) | 2 200 000 |
| 65116-010-62 (дв.740.62-280 л.с.) | 1 880 000 |
| 6460 (дв.740.50-360 л.с.) | 2 180 000 |
| 45143-011-15 (дв.740.13-260л.с) | 2 180 000 |
| 65115 (дв.740.62-280 л.с.,рест.) | 2 190 000 |
| 65115 (дв.740.62-280 л.с.,3-х стор) | 2 295 000 |
| 6520 (дв.740.51-320 л.с.) | 2 610 000 |
| 6520 (дв.740.51-320 л.с.,сп.место) | 2 700 000 |
| 6522-027 (дв.740.51-320 л.с.,6х6) | 3 190 000 |

подробнее про услугу перегона можно прочесть здесь.

|
Нужны самосвалы? Обратите внимание на Ford-65513-02. |
КАМАЗы в лизинг
ООО «Старт Импэкс» имеет возможность поставки грузовой автотехники КАМАЗ, а так же спецтехники на шасси КАМАЗ в лизинг. Продажа грузовой техники по лизинговым схемам имеет определенные выгоды для покупателя грузовика. Рассрочка платежа, а так же то обстоятельство, что грузовики до полной выплаты лизинговых платежей находятся на балансе лизингодателя, и соответственно покупатель автомобиля не платит налогов на имущество. Мы готовы предложить любые модели бортовых автомобилей, тягачей и самосвалов по самым выгодным лизинговым схемам.Контактная информация.
г. Набережные Челны, Промкомзона-2, Автодорога №3, база «Партнер плюс».
тел/факс (8552) 388373.
Схема проезда
Простые механизмы. КПД простых механизмов. Простейшие механизмы
Простые механизмы
т. е. ту же самую, что и при вертикальном поднятии груза.
Данные факты служат проявлениями так называемого золотого правила механики.
Золотое правило механики. Ни один из простых механизмов не даёт выигрыша в работе. Во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии, и наоборот.
Золотое правило механики есть не что иное, как простой вариант закона сохранения энергии.
17.6КПД механизма
На практике приходится различать полезную работу Aполезн, которую нужно совершить при помощи механизма в идеальных условиях отсутствиякаких-либопотерь, и полную работу Aполн, которая совершается для тех же целей в реальной ситуации.
Полная работа равна сумме:
полезной работы;
работы, совершённой против сил трения в различных частях механизма;
работы, совершённой по перемещению составных элементов механизма.
Так, при подъёме груза рычагом приходится вдобавок совершать работу по преодолению силы трения в оси рычага и по перемещению самого рычага, имеющего некоторый вес.
Полная работа всегда больше полезной. Отношение полезной работы к полной называется
коэффициентом полезного действия (КПД) механизма:
= Aполезн:
Aполн
КПД принято выражать в процентах. КПД реальных механизмов всегда меньше 100%. Вычислим КПД наклонной плоскости с углом при наличии трения. Коэффициент трения
между поверхностью наклонной плоскости и грузом равен .
Пусть груз массы m равномерно поднимается вдоль наклонной плоскости под действием
силы ~ из точки в точку на высоту (рис.55). В направлении, противоположном пере-
F P Q h
мещению, на груз действует сила трения скольжения ~. f
~
f
h
m~g
P
Рис. 55. Наклонная плоскость с трением
Ускорения нет, поэтому силы, действующие на груз, уравновешены:
studfiles.net
Простые механизмы. Подъемный механизм. Простые механизмы в быту
С самой древности человек пытается облегчить свой труд. Для этого он применяет различные приспособления. Что собой представляют простейшие механизмы? Какие существуют разновидности этих приспособлений? Чем отличаются простые и сложные механизмы? Об этом и многом другом – далее в статье. 
Общая информация
Простые механизмы (от греч. "машина, орудие") – устройства, дающие выигрыш в силе. Некоторые из этих приспособлений появились в самой древности. Простые механизмы могут являться самостоятельными устройствами либо быть элементами более сложных агрегатов. В зависимости от типа конструкции определяется и сфера применения того или иного приспособления. Использование простых механизмов существенно облегчает человеческую деятельность. Такие устройства дают выигрыш в силе. К примеру, клин, который вбивается в полено, обладает большей силой, чем сам удар по приспособлению. Поэтому дерево быстро распирает в разные стороны. Вместе с этим, удар на клин приходится сверху вниз, а части полена раздвигаются в стороны. То есть в данном случае происходит еще и преобразование в направлении движения.
Простые механизмы. Примеры
Существует несколько видов приспособлений:
Наклонная плоскость
а) винт применяется в шурупах, как сверло в отбойных молотках, дрелях; может служить и как подъемный механизм (Архимедов винт);
б) клин способствует увеличению давления за счет концентрирования массы на небольшой площади. Применяется в пуле, лопате, копье.
Рычаг – приспособление, описанное Архимедом. Может выступать как спусковой крючок, выключатель.
а) ворот применяется для ременной передачи и поднятия воды из колодца.
Колесо (изобретено в 3 тыс. до н. э. шумерами) является составной частью системы зубчатой передачи, применяется в транспорте.
Поршень способствует использованию энергии нагретых расширяющихся газов либо пара. Применяется данное приспособление в паровых машинах и огнестрельном оружии.
Ворот
Это приспособление представляет собой барабан (цилиндр), к которому прикрепляется рукоятка. Как правило, его применяли как подъемный механизм для поднятия воды из колодца. Тот выигрыш в силе, какой получается при использовании ворота, определяется отношением радиуса той окружности, по которой совершается движение рукоятки, к радиусу цилиндра (барабана), на который наматывается веревка. К современному типу ворота относится лебедка. Это приспособление представляет собой систему, включающую цилиндр и два зубчатых колеса разного радиуса. Выигрыш в силе, который в общем дает лебедка, определяют совокупным действием двух воротов. Современные устройства дают выигрыш в сорок-сто раз. 
Наклонная плоскость
Этот простой механизм также часто применяют при подъеме тяжелых тел. Выигрыш в силе определяют отношением длины самого приспособления к его высоте при условии малого трения. Зачастую, для создания большой силы (например, для работы ледокола или для колки дров) используют вид наклонной плоскости – клин. Его действие основывается на том, что при большом усилии в направлении обуха формируются большие силы, перпендикулярные боковым поверхностям устройства. Еще одной разновидностью наклонной плоскости является винт. Так же как и клин, это устройство способно менять направление либо числовое значение прилагаемой силы.
Простые механизмы. Рычаг
Это твердое тело, способное вращаться вокруг опоры (неподвижной). Наименьшее расстояние, которое разделяет точку опоры и прямую, вдоль которой воздействует сила на рычаг, называется плечом силы. Чтобы его найти, следует опустить перпендикуляр из точки опоры на линию действия усилия. Длина данного перпендикуляра и будет являться плечом. F1 и F2 – действующие на рычаг силы. Плечи, действующие на устройство – L1 и L2. Рычаг тогда находится в равновесии, когда действующие на него силы обратно пропорциональны плечам. Данное правило можно представить в виде формулы: F1 / F2 = L1 / L2. Этот принцип был установлен Архимедом. Данное правило показывает, что большую силу при помощи рычага можно уравновесить меньшей. Сила, приложенная к одному плечу, во столько раз больше той, что приложена к другому, во сколько одно плечо больше второго.
Как применяет приспособления человек сегодня?
Весьма распространены простые механизмы в быту. Так, достаточно сложно было бы открыть водопроводный кран, если бы не было у него небольшой ручки, которая представляет собой достаточно эффективный рычаг. То же можно сказать и о гаечном ключе, при помощи которого осуществляется откручивание или закручивание гаек или болтов. Чем длиннее рукоятка, тем легче будет осуществляться действие. Так, при работе с тяжелыми либо крупными гайками и болтами при ремонте сложных механизмов, станков, автомобилей, применяют ключи с рукоятками до одного метра в длину. Самая обычная дверь также является одним из видов рассматриваемых приспособлений. Если пробовать открывать дверь возле ее крепления, то это будет весьма затруднительно. Однако чем дальше от петель располагается ручка, тем легче открыть дверь. Достаточно наглядным примером является прыжок с шестом. Его длина порядка пяти метров. При помощи этого рычага и правильно приложенного усилия спортсмену удается взлететь на высоту до шести метров. Длинное плечо составляет при этом примерно три метра. Рычаги встречаются и в разных частях человеческого тела и тела животного. Это, в частности, челюсти, конечности. Бытовыми примерами рычага являются кусачки, ножницы для резки металла или бумаги. Машины различного вида имеют в своей конструкции также приспособления, позволяющие получить выигрыш в силе. Например, педали либо ручной тормоз на велосипеде, ручки швейных машин, клавиши в пианино.
Комплексное применение приспособлений
Простые механизмы встречаются в самых разных сочетаниях. Комбинированные устройства включают в себя две и более детали. Не обязательно это будет сложным механизмом – многие простые приспособления можно считать комплексными. Так, в мясорубке присутствует ручка (ворот), проталкивающий мясо винт и нож-резак (клин). В наручных часах стрелки поворачиваются при помощи системы зубчатых колес, имеющих разный диаметр и находящихся друг с другом в сцеплении. Одним из известных комбинированных несложных механизмов является домкрат. В нем использовано сочетание ворота и винта.
Заключение
Как стало ясно, простые механизмы существенно облегчают труд человека. Они могут состоять из одной или нескольких деталей. При этом даже при наличии двух и более элементов могут оставаться простыми, но могут являться и достаточно сложными. Различные агрегаты, печатные прессы, двигатели включают в себя несколько деталей. Среди элементов есть и рычаги, блоки, винты, колеса на осях, наклонные плоскости, клин. Все эти приспособления работают в комплексе. Благодаря им человек существенно облегчает труд. Передача механической энергии от одной части устройства к другой может осуществляться по-разному. Цепи, ремни, шестерни или зубчатые колеса считаются наиболее распространенными устройствами, способствующими передаче усилия и заставляющими отдельные элементы двигаться медленнее или быстрее, в том или ином направлении. Сложными и высокоскоростными устройствами управляют, как правило, электронные приборы. Электрические датчики благодаря особой настройке показывают, когда необходимо включать тот или иной механизм, следят также за корректной и стабильной работой системы. Многие устройства пришли в современную жизнь человека из самой древности. Люди постоянно совершенствуют сложные механизмы, расширяя таким образом сферу их применения. Несомненно, в повседневной жизни человека различные устройства занимают очень важное место. Многое невозможно представить без использования простых и сложных механизмов. Приспособления широко применяются в строительстве, сельском хозяйстве, при добыче полезных ископаемых и в прочих областях деятельности человека.
fb.ru
Т. Простые механизмы — PhysBook
Простейшие механизмы
Для облегчения совершения механической работы издавна используются различные приспособления — простые механизмы.
Простые механизмы — это устройства, в которых работа совершается только за счет механической энергии. Простые механизмы (рычаг, наклонная плоскость, блок и др.) служат для преобразования силы, их применяют при совершении работы в тех случаях, когда надо действием одной силы уравновесить другую силу.
Наклонная плоскость
Ее используют в тех случаях, когда надо поднять тяжелый груз на некоторую высоту.
Рассмотрим гладкую наклонную плоскость (рис. 1). Рассчитаем силу F, которую надо приложить к телу массой m, чтобы поднять его равномерно на высоту h.
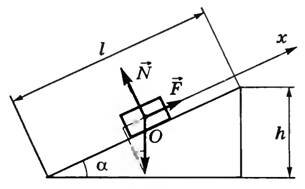
Рис. 1
Запишем основное уравнение динамики\[~\vec F + \vec N + m \vec g = 0\]. Спроецируем это равенство на ось Ox\[~F - mg \sin \alpha = 0\]. Отсюда искомая сила
\(~F = mg \sin \alpha = mg \frac hl \Rightarrow \frac{mg}{F} = \frac lh,\)т.е для равномерного поднятия груза с помощью наклонной плоскости необходимо приложить силу, во столько раз меньшую силы тяжести груза, во сколько раз длина наклонной плоскости больше ее высоты.
Рычаг
Рычагом называют имеющее неподвижную ось вращения твердое тело, на которое действуют силы, стремящиеся повернуть его вокруг этой оси. Различают рычаги первого и второго рода.
Рычагом первого рода называют рычаг, ось вращения О которого расположена между точками А и В приложения сил, а сами силы направлены в одну сторону (рис. 2, а). Это коромысло равноплечих весов, железнодорожный шлагбаум, ножницы и др.
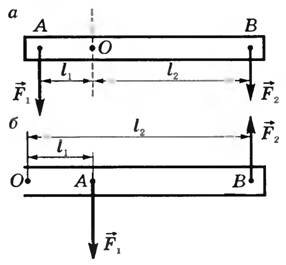
Рис. 2
Рычаг второго рода — рычаг, ось вращения О которого расположена по одну сторону от точек приложения сил, а сами силы направлены противоположно друг другу (рис. 2, б). Это гаечные ключи, щипцы для раскалывания орехов, двери и др.
Условие равновесия рычага вытекает из правила моментов M1 = M2.
Так как M1 = F1l1 и M2 = F2l2, где l1 и l2 — плечи сил, действующих на рычаг, то \(~\frac{F_1}{F_2} = \frac{l_2}{l_1}\) — условие равновесия рычага.
При равновесии рычага под действием двух сил модули этих сил обратно пропорциональны их плечам.
С помощью рычага можно получить выигрыш в силе, т.е. меньшей силой можно уравновесить большую силу.
Блок
Блоки используют для поднятия грузов. Блок представляет собой колесо с желобом, укрепленное в обойме. По желобу блока пропускают веревку, трос или цепь. Неподвижным называют такой блок, ось которого закреплена и при подъеме грузов она не поднимается и не опускается (рис. 3, а, б).
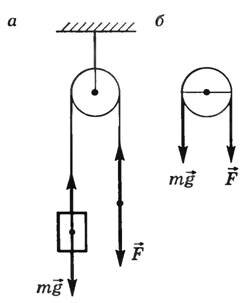
Рис. 3
Неподвижный блок можно рассматривать как равноплечий рычаг, у которого плечи приложенных сил равны радиусу колеса. Следовательно, из правила моментов mgr = Fr вытекает, что неподвижный блок выигрыша в силе не дает (F = mg). Он позволяет менять направление действия силы.
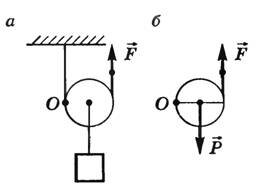
Рис. 4
На рисунке 4, а, б изображен подвижный блок (ось блока поднимается и опускается вместе с грузом). Такой блок поворачивается около мгновенной оси О. Правило моментов для него будет иметь вид
\(~mgr = F \cdot 2r \Rightarrow F = \frac{mg}{2}.\)Таким образом, подвижный блок дает выигрыш в силе в два раза.
Обычно на практике применяют комбинацию неподвижного блока с подвижным (рис. 5). Неподвижный блок применяется только для удобства. Он, изменяя направление действия силы, позволяет, например, поднимать груз, стоя на земле.
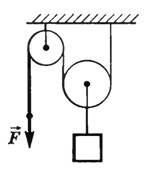
Рис. 5
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 73-75.
www.physbook.ru
Простые механизмы - СПИШИ У АНТОШКИ
С древности простые механизмы часто использовались комплексно, в самых различных сочетаниях.
Комбинированный механизм состоит из двух или большего числа простых. Это не обязательно сложное устройство; многие довольно простые механизмы тоже можно считать комбинированными.
Видов простых механизмов очень много. Это и рычаг, и блок, и клин, и наклонная плоскость и многие другие.
Простыми механизмами в физике называют приспособления, служащие для преобразования силы.
Например, в мясорубке имеются ворот (ручка), винт (проталкивающий мясо) и клин (нож-резак).
Наклонная плоскость, которая помогает вкатывать или втаскивать тяжелые предметы наверх – это тоже простой механизм
Стрелки наручных часов поворачиваются системой зубчатых колес разного диаметра, находящихся в зацеплении друг с другом. Один из наиболее известных несложных комбинированных механизмов – домкрат. Домкрат представляет собой комбинацию винта и ворота.
Чаще всего простые механизмы применяют для того, чтобы получить выигрыш в силе, то есть увеличить в несколько раз силу, действующую на тело.
Рычаг в физике - простой механизм
Рычагом в физике называют твердое тело, способное вращаться вокруг неподвижной опоры.
В качестве рычага могут быть использованы лом, доска и тому подобные предметы.

Различают два вида рычагов. У рычага первого рода точка опоры О находится между линиями действия приложенных сил. У рычага второго рода точка опоры расположена по одну сторону от них. То есть, если мы пытаемся при помощи лома сдвинуть с места тяжелый предмет, то рычаг первого рода – это ситуация, когда мы подкладываем брусок под лом, надавливая на свободный конец лома вниз. Неподвижной опорой у нас в данном случае будет являться брусок, а приложенные силы располагаются по обе стороны от него. А рычаг второго рода – это когда мы, подсунув край лома под тяжесть, тянем лом вверх, пытаясь таким образом перевернуть предмет. Здесь точка опоры О находится в месте упора лома о землю, а приложенные силы расположены по одну сторону от точки опоры.
Использование рычага позволяет получить выигрыш в силе. Так, например, рабочий, изображенный на левом рисунке , прикладывая к рычагу силу 400 Н, сможет приподнять груз весом 800 Н. Разделив 800 Н на 400 Н, мы получим выигрыш в силе, равный 2.
Закон равновесия сил на рычаге
Используя рычаг, мы можем получить выигрыш в силе и поднять неподъемный голыми руками груз. Расстояние от точки опоры до точки приложения силы называют плечом силы. Причем, можно рассчитать равновесие сил на рычаге по следующей формуле:
F1 / F2 = l2 / l1 ,
где F1 , F2 – силы, действующие на рычаг,
а l2 , l1 – плечи этих сил. (На рисунке выше ОВ и ОА - плечи рычага)
Это и есть закон равновесия рычага, который гласит: рычаг находится в равновесии тогда, когда действующие на него силы обратно пропорциональны плечам этих сил.
Этот закон был установлен Архимедом еще в третьем веке до нашей эры. Из него следует, что меньшей силой можно уравновесить большую. Для этого необходимо, чтобы плечо меньшей силы было больше плеча большей силы. А выигрыш в силе, получаемый с помощью рычага, определяется отношением плеч приложенных сил.
В наше время рычаги находят широкое применение как на производстве (например, подъемные краны, коробка передач в автомобиле), так и в быту (ножницы, кусачки, весы, гаечные ключи и т. д.).
Блок - это колесо с желобом по окружности для каната или цепи, ось которого жестко прикреплена к стене или потолочной балке. Грузоподъемные устройства обычно используют не один, а несколько блоков. Система блоков и тросов, предназначенная для повышения грузоподъемности, называется полиспаст.
Ворот - это два колеса, соединенные вместе и вращающиеся вокруг одной оси, например, колодезный ворот с ручкой.
Лебедка - конструкция , состоящая из двух воротов с промежуточными передачами в механизме привода.
Наклонная плоскость применяется для перемещения тяжелых предметов на более высокий уровень без их непосредственного поднятия.
К таким устройствам относятся пандусы, эскалаторы, обычные лестницы и конвейеры.
Клин - одна из разновидностей простого механизма под названием "наклонная плоскость". Клин состоит из двух наклонных плоскостей, основания которых соприкасаются. Его применяют, чтобы получить выигрыш в силе, то есть при помощи меньшей силы противодействовать большей силе.При рубке дров, чтобы облегчить работу, в трещину полена вставляют металлический клин и бьют по нему обухом топора.
Винт - наклонная плоскость, навитая на ось. Резьба винта – это наклонная плоскость, многократно обернутая вокруг цилиндра. Идеальный выигрыш в силе, даваемый клином, равен отношению его длины к толщине на тупом конце. Реальный выигрыш клина определить трудно.Из-за большого трения его КПД столь мал, что идеальный выигрыш не имеет особого значения. В зависимости от направления подъема наклонной плоскости винтовая резьба может быть левой или правой.
Примеры простых устройств с винтовой резьбой – домкрат, болт с гайкой, микрометр, тиски.
spishy-u-antoshki.ru
Простые механизмы - материалы для подготовки к ЕГЭ по Физике
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: простые механизмы, КПД механизма.
Механизм - это приспособление для преобразования силы (её увеличения или уменьшения).Простые механизмы - это рычаг и наклонная плоскость.
Рычаг.
Рычаг - это твёрдое тело, которое может вращаться вокруг неподвижной оси. На рис. 1) изображён рычаг с осью вращения . К концам рычага (точкам и ) приложены силы и . Плечи этих сил равны соответственно и
.
Условие равновесия рычага даётся правилом моментов: , откуда
.
 |
| Рис. 1. Рычаг |
Из этого соотношения следует, что рычаг даёт выигрыш в силе или в расстоянии (смотря по тому, с какой целью он используется) во столько раз, во сколько большее плечо длиннее меньшего.
Например, чтобы усилием 100 Н поднять груз весом 700 Н, нужно взять рычаг с отношением плеч 7 : 1 и положить груз на короткое плечо. Мы выиграем в силе в 7 раз, но во столько же раз проиграем в расстоянии: конец длинного плеча опишет в 7 раз большую дугу, чем конец короткого плеча (то есть груз).
Примерами рычага, дающего выигрыш в силе, являются лопата, ножницы, плоскогубцы. Весло гребца - это рычаг, дающий выигрыш в расстоянии. А обычные рычажные весы являются равноплечим рычагом, не дающим выигрыша ни в расстоянии, ни в силе (в противном случае их можно использовать для обвешивания покупателей).
Неподвижный блок.
Важной разновидностью рычага является блок - укреплённое в обойме колесо с жёлобом, по которому пропущена верёвка. В большинстве задач верёвка считается невесомой нерастяжимой нитью.
На рис. 2 изображён неподвижный блок, т. е. блок с неподвижной осью вращения (проходящей перпендикулярно плоскости рисунка через точку ).
 |
На правом конце нити в точке закреплён груз весом . Напомним, что вес тела - это сила, с которой тело давит на опору или растягивает подвес. В данном случае вес прило жен к точке
, в которой груз крепится к нити.
К левому концу нити в точке приложена сила .
Плечо силы равно , где
- радиус блока. Плечо веса равно
. Значит, неподвижный блок является равноплечим рычагом и потому не даёт выигрыша ни в силе, ни в расстоянии: во-первых, имеем равенство
, а во-вторых, в процессе движении груза и нити перемещение точки
равно перемещению груза.
Зачем же тогда вообще нужен неподвижный блок? Он полезен тем, что позволяет изменить направление усилия. Обычно неподвижный блок используется как часть более сложных механизмов.
Подвижный блок.
На рис. 3 изображён подвижный блок, ось которого перемещается вместе с грузом. Мы тянем за нить с силой , которая приложена в точке и направлена вверх. Блок вращается и при этом также движется вверх, поднимая груз, подвешенный на нити
.
 |
В данный момент времени неподвижной точкой является точка , и именно вокруг неё поворачивается блок (он бы "перекатывается" через точку ). Говорят ещё, что через точку проходит мгновенная ось вращения блока (эта ось направлена перпендикулярно плоскости рисунка).
Вес груза приложен в точке крепления груза к нити. Плечо силы равно
.
А вот плечо силы , с которой мы тянем за нить, оказывается в два раза больше: оно равно . Соответственно, условием равновесия груза является равенство
(что мы и видим на рис. 3: вектор в два раза короче вектора ).
Следовательно, подвижный блок даёт выигрыш в силе в два раза. При этом, однако, мы в те же два раза проигрываем в расстоянии: чтобы поднять груз на один метр, точку придётся переместить на два метра (то есть вытянуть два метра нити).
У блока на рис. 3 есть один недостаток: тянуть нить вверх (за точку ) - не самая лучшая идея. Согласитесь, что гораздо удобнее тянуть за нить вниз! Вот тут-то нас и выручает неподвижный блок.
 |
На рис. 4 изображён подъёмный механизм, который представляет собой комбинацию подвижного блока с неподвижным. К подвижному блоку подвешен груз, а трос дополнительно перекинут через неподвижный блок, что даёт возможность тянуть за трос вниз для подъёма груза вверх. Внешнее усилие на тросе снова обозначено вектором .
Принципиально данное устройство ничем не отличается от подвижного блока: с его помощью мы также получаем двукратный выигрыш в силе.
Наклонная плоскость.
Как мы знаем, тяжёлую бочку проще вкатить по наклонным мосткам, чем поднимать вертикально. Мостки, таким образом, являются механизмом, который даёт выигрыш в силе.
В механике подобный механизм называется наклонной плоскостью. Наклонная плоскость - это ровная плоская поверхность, расположенная под некоторым углом к горизонту. В таком случае коротко говорят: "наклонная плоскость с углом ".
Найдём силу, которую надо приложить к грузу массы , чтобы равномерно поднять его по гладкой наклонной плоскости с углом . Эта сила , разумеется, направлена вдоль наклонной плоскости (рис. 5).
 |
Выберем ось так, как показано на рисунке. Поскольку груз движется без ускорения, действующие на него силы уравновешены:
.
Проектируем на ось :
,
откуда
.
Именно такую силу нужно приложить, что двигать груз вверх по наклонной плоскости.
Чтобы равномерно поднимать тот же груз по вертикали, к нему нужно приложить силу, равную . Видно, что
, поскольку
. Наклонная плоскость действительно даёт выигрыш в силе, и тем больший, чем меньше угол .
Широко применяемыми разновидностями наклонной плоскости являются клин и винт.
Золотое правило механики.
Простой механизм может дать выигрыш в силе или в расстоянии, но не может дать выигрыша в работе.
Например, рычаг с отношением плеч 2 : 1 даёт выигрыш в силе в два раза. Чтобы на меньшем плече поднять груз весом , нужно к большему плечу приложить силу
. Но для поднятия груза на высоту
большее плечо придётся опустить на
, и совершённая работа будет равна:
т. е. той же величине, что и без использования рычага.
В случае наклонной плоскости мы выигрываем в силе, так как прикладываем к грузу силу , меньшую силы тяжести. Однако, чтобы поднять груз на высоту
над начальным положением, нам нужно пройти путь
вдоль наклонной плоскости. При этом мы совершаем работу
т. е. ту же самую, что и при вертикальном поднятии груза.
Данные факты служат проявлениями так называемого золотого правила механики.
Золотое правило механики. Ни один из простых механизмов не даёт выигрыша в работе. Во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии, и наоборот.
Золотое правило механики есть не что иное, как простой вариант закона сохранения энергии.
КПД механизма.
На практике приходится различать полезную работу A полезн, которую нужно совершить при помощи механизма в идеальных условиях отсутствия каких-либо потерь, и полную работу Aполн,которая совершается для тех же целей в реальной ситуации.
Полная работа равна сумме:-полезной работы;-работы, совершённой против сил трения в различных частях механизма;-работы, совершённой по перемещению составных элементов механизма.
Так, при подъёме груза рычагом приходится вдобавок совершать работу по преодолению силы трения в оси рычага и по перемещению самого рычага, имеющего некоторый вес.
Полная работа всегда больше полезной. Отношение полезной работы к полной называется коэффициентом полезного действия (КПД) механизма:
=Aполезн/Аполн.
КПД принято выражать в процентах. КПД реальных механизмов всегда меньше 100%.
Вычислим КПД наклонной плоскости с углом при наличии трения. Коэффициент трения между поверхностью наклонной плоскости и грузом равен .
Пусть груз массы равномерно поднимается вдоль наклонной плоскости под действием силы из точки
в точку
на высоту
(рис. 6). В направлении, противоположном перемещению, на груз действует сила трения скольжения .
 |
Ускорения нет, поэтому силы, действующие на груз, уравновешены:
.
Проектируем на ось X:
. (1)
Проектируем на ось Y:
. (2)
Кроме того,
, (3)
Из (2) имеем:
.
Тогда из (3):
.
Подставляя это в (1), получаем:
.
Полная работа равна произведению силы F на путь, пройденный телом вдоль поверхности наклонной плоскости:
Aполн=.
Полезная работа, очевидно, равна:
Аполезн=.
Для искомого КПД получаем:
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
Простые механизмы
Физика > Простые механизмы
Простой механизм – устройство, изменяющее направление силы или увеличивающее ее. Выделяют 6 категорий.
Задача обучения
- Разобраться в том, как механизм использует силу для выполнения работы против силы нагрузки.
Основные пункты
- Разделение на 6 категорий появилось в эпоху Возрождения: рычаг, колесо и ось, ролик, наклонная плоскость, клин и винт.
- Простые механизмы могут объединяться с другими устройствами для создания более сложной конструкции. С их помощью объясняют процесс работы.
- Сила, вырабатываемая простым механизмом, способна превзойти изначальную.
Термины
- Механизм – механическое или электрическое устройство, выполняющее человеческие задачи.
- Система рычагов – увеличение силы при помощи рычага, совершающего обороты вокруг стержня.
- Механическое преимущество – соотношение полученной силы и изначальной.
Простые механизмы
Простой механизм – устройство, изменяющее направление или показатель силы. Это базовые приспособления, использующие рычаги для увеличения силы. Чаще всего этот термин употребляют для одной из 6 категорий, придуманных в эпоху Возрождения. Среди них:
- рычаг
- колесо и ось
- ролик
- наклонная плоскость
- клин
- винт.
Когда простой механизм соединяется с другим, формируется больший механизм, который можно разбить на детали и проследить элементарные движения в нем. Например, велосипед представлен колесами, рычагами и роликами.
Таблица простых механизмов из энциклопедии 1728 года. Простые механизмы играют роль словаря, при помощи которого можно освоить более сложные модели
Механика
Простой механизм обладает приложенной силой, функционирующей против силы нагрузки. Если не наблюдается траты на трение, то работа над нагрузкой приравнивается к работе прилагаемой силы. За счет пропорционального сокращения дистанции можно увеличить исходную силу. Если механизм не впитывает энергию, то механическое преимущество можно рассчитать из геометрии механизма. К примеру, механическое преимущество рычага = отношению всех рычагов.
Если простой механизм не расходует энергию на трение, то это идеальный механизм. В таком случае мощность подачи энергии приравнивается к мощности выхода энергии: Pin = Pout.
Количество создаваемой механизмом силы не может превосходить введенную
Другие примеры
Среди простых механизмов можно встретить лопаты и тачки. В них заметны три силы: входящая, исходящая и сила на оси вращения. В примере с тачками исходящая сила расположена между осью колеса и входной силой. В лопате – между осью поворота и нагрузкой.
Оба механизма применяют концепцию рычагов
v-kosmose.com
Простые механизмы. КПД простых механизмов – FIZI4KA

1. Простые механизмы — приспособления, которые сконструировал и использовал человек, чтобы облегчить работу по перемещению тяжёлых предметов. К ним относят: рычаг, блок, наклонную плоскость. Разновидностями этих механизмов являются: клин, ворот и винт.
Все простые механизмы позволяют преобразовать силу, действующую на тело: либо уменьшить её, либо изменить её направление.
2. Рычаг — это стержень, вращающийся вокруг неподвижной опоры или оси (рис. 51). На рисунке показан рычаг, который может вращаться вокруг точки О, расположенный между концами рычага. К одному концу рычага подвешен груз, действующий на рычаг с силой \( F_1 \), равной весу груза. Действуя на длинный конец рычага с силой \( F_2 \), человек поднимает груз. При этом сила \( F_1 \) стремится повернуть рычаг по часовой стрелке, а груз \( F_2 \) — против часовой стрелки.
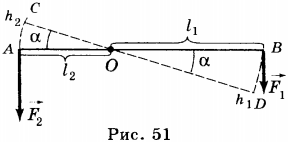
Плечом силы называют кратчайшее расстояние (перпендикуляр) от точки опоры до линии действия силы. Так, плечом силы \( F_1 \) является расстояние ОА \( (l_1) \), плечом силы \( F_2 \) — расстояние ОВ \( (l_2) \).
Из эксперимента следует, что рычаг находится в равновесии, если произведение силы, вращающей рычаг по часовой стрелке, и её плеча равно произведению силы, вращающей рычаг против часовой стрелки, и её плеча, т.е. \( F_1l_1=F_2l_2 \). Произведение силы, действующей на рычаг, и её плеча называют моментом силы: \( Fl=M \). Соответственно, если рычаг находится в равновесии, то \( M_1=M_2 \).
Условие равновесия рычага можно записать по-другому:\( \frac{F_1}{F_2}=\frac{l_2}{l_1} \). Это равенство означает, что рычаг находится в равновесии, если силы, действующие на него, обратно пропорциональны их плечам. Оно называется условием равновесия рычага.
Рычаг другого типа вращается вокруг точки, находящейся на конце рычага. Примером такого рычага может служить тачка. Когда используется такой рычаг, то вес груза направлен вниз, а человек действует на свободный конец рычага с силой, направленной вверх. Для такого рычага также справедливо условие равновесия, приведенное выше.
3. При подъеме груза работа силы, действующей на груз, равна \( A_1=F_1h_1 \), работа силы, приложенной к другому концу рычага, равна \( A_2=F_2h_2 \). Рассмотрение треугольников AOC и BOD позволяет сделать вывод о том, что они подобны и \( \frac{AO}{BO}=\frac{AC}{BD} \) или \( \frac{l_1}{l_2}=\frac{h_1}{h_2} \). Поскольку \( F_1l_1=F_2l_2 \), то \( F_1h_1=F_2h_2 \), т.е. \( A_1=2 \). Таким образом, рычаг, позволяя выиграть в силе, не даёт выигрыша в работе.
4. Ещё одним простым механизмом является блок. Блок — это колесо с желобом, по которому пропускается трос и которое может вращаться относительно оси О (см. рис. ниже).

Если ось блока закреплена, то блок не перемещается, и он называется неподвижным.
Неподвижный блок можно рассматривать как рычаг, вращающийся вокруг точки, лежащей посередине рычага. Плечи такого рычага равны друг другу: OA = OB. В соответствии с условием равновесия рычага приложенные к блоку силы тоже равны: \( P=F \). Следовательно, неподвижный блок не даёт выигрыша в силе, но он позволяет поднимать груз, прикладывая силу, направленную не вверх, а вниз, что облегчает перемещение груза.
Чтобы получить выигрыш в силе используют подвижный блок (рис. 53). К нему непосредственно прикрепляется груз, один конец троса закрепляется, а к другому прикладывают силу и, таким образом, перебирая трос, поднимают блок с грузом.

В этом случае точкой вращения блока является точка А (см. рис. 52).
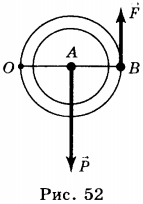
Плечи действующих сил равны соответственно: AO и AB, при этом AB = 2AO. В соответствии с условием равновесия рычага: \( P=2F \). Таким образом, подвижный блок даёт выигрыш в силе в 2 раза: \( F=P/2 \).
Измерив расстояние \( h_1 \), которое проходит груз, и расстояние \( h_2 \), на которое перемещается конец троса, можно обнаружить, что расстояние \( h_2=2h_1 \). Таким образом, подвижный блок даёт выигрыш в силе в 2 раза и в 2 раза проигрыш в пути. Соответственно, работа \( Ph_1=Fh_2 \), т.е. \( A_1=2 \). Подвижный блок, так же как и рычаг, не даёт выигрыша в работе.
5. Наклонная плоскость используется в том случае, если нужно поднять объемный тяжёлый груз на какую-либо высоту (рис. 54).
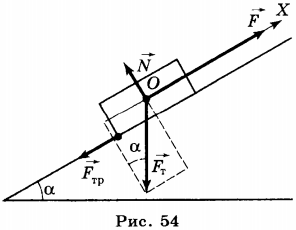
Например, нужно погрузить ящик с металлическими деталями в кузов грузовика. В этом случае кладут массивную доску так, что она образует наклонную плоскость, один конец которой находится на земле, а другой на грузовике, и по этой плоскости втаскивают ящик. Чтобы поднять ящик вертикально вверх нужно приложить к нему силу, равную его весу \( P \). Перемещая равномерно ящик по наклонной плоскости, в отсутствие трения прикладывают силу, равную \( F=P\sin\alpha \), т.е. меньшую веса ящика, но при этом, выигрывая в силе, проигрывают в расстоянии. Работа по подъёму ящика по вертикали равна работе, совершаемой при его перемещении вдоль наклонной плоскости. Это справедливо, если сила сопротивления движению пренебрежимо мала. При наличии трения перемещение ящика вдоль наклонной плоскости требует совершения большей работы, чем при его движении вертикально вверх. В этом случае говорят о коэффициенте полезного действия (КПД) наклонной плоскости. Он равен отношению полезной работы ко всей совершённой работе: \( \mathbf{КПД}=A_п/A_с\cdot 100 \% \), где \( A_п \) — полезная работа, \( A_п=mgh \); \( A_с \) — совершённая работа при перемещении ящика вдоль наклонной плоскости, \( A_c=Fl \), где \( F \) — приложенная сила, \( l \) — длина наклонной плоскости.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Исследуя условия равновесия рычага, ученик выполнил соответствующую лабораторную работу. В таблице представлены значения сил и их плеч для рычага, находящегося в равновесии. Определите, чему равно плечо \( l_1 \)?

1) 12,8 м2) 2,5 м3) 0,8 м4) 0,25 м
2. Ученик выполнял лабораторную работу по исследованию условий равновесия рычага. Результаты для сил и их плеч, которые он получил, представлены в таблице.

Чему равна сила \( F_1 \), если рычаг находится в равновесии?
1) 100 Н2) 50 Н3) 25 Н4) 9 Н
3. Рычаг находится в равновесии под действием двух сил. Сила \( F_1 \) = 6 Н. Чему равна сила \( F_2 \), если длина рычага 50 см, а плечо силы \( F_1 \) равно 30 см?
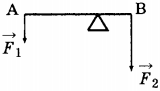
1) 0,1 Н2) 3,6 Н3) 9 Н4) 12 Н
4. Выигрыш в силе, приложенной к грузу, нельзя получить с помощью
1) подвижного блока2) неподвижного блока3) рычага4) наклонной плоскости
5. С помощью неподвижного блока в отсутствие трения силе
1) выигрывают в 2 раза2) не выигрывают, но и не проигрывают3) проигрывают в 2 раза4) возможен и выигрыш, и проигрыш
6. С помощью подвижного блока в отсутствие трения
1) выигрывают в работе в 2 раза2) проигрывают в силе в 2 раза3) не выигрывают в силе4) выигрывают в силе в 2 раза
7. На рисунке изображён неподвижный блок, с помощью которого, прикладывая к свободному концу нити силу 20 Н, равномерно поднимают груз. Если трением пренебречь, то масса поднимаемого груза равна
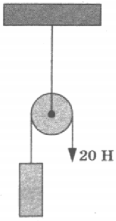
1) 4 кг2) 2 кг3) 0,5 кг4) 1 кг
8. Наклонная плоскость даёт выигрыш в силе в 2 раза. В работе при отсутствии силы трения эта плоскость
1) даёт выигрыш в 2 раза2) даёт выигрыш в 4 раза3) не даёт ни выигрыша, ни проигрыша4) даёт проигрыш в 2 раза
9. Вдоль наклонной плоскости длиной 5 м поднимают груз массой 40 кг, прикладывая силу 160 Н. Чему равна высота наклонной плоскости, если трение при движении груза пренебрежимо мало?
1) 1,25 м2) 2 м3) 12,5 м4) 20 м
10. Груз массой 10 кг поднимают по наклонной плоскости длиной 2 м и высотой 0,5 м, прикладывая силу 40 Н. Чему равен КПД наклонной плоскости?
1) 160%2) 62,5%3) 16%4) 6,25%
11. Груз поднимают с помощью подвижного блока радиусом \( R \) (см. рисунок). Установите соответствие между физическими величинами (левый столбец) и формулами, по которым они определяются (правый столбец).
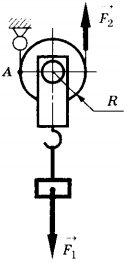
Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫA) плечо силы \( \vec{F}_1 \) относительно точки AБ) плечо силы \( \vec{F}_2 \) относительно точки AB) момент силы \( \vec{F}_1 \) относительно точки A
ФОРМУЛЫ1) \( F_1R \)2) \( 2F_1R \)3) \( \frac{F_1}{R} \)4) \( R \)5) \( 2R \)
12. Из перечня приведённых ниже высказываний выберите два правильных и запишите их номера в таблицу.
1) Любой простой механизм даёт выигрыш в силе.2) Ни один простой механизм не даёт выигрыша в работе.3) Наклонная плоскость выигрыша в силе не даёт.4) Коэффициент полезного действия показывает, какая часть совершенной работы является полезной.5) Неподвижный блок даёт выигрыш в силе в 2 раза.
Часть 2
13. Чему равна сила, с которой действуют на брусок массой 0,2 кг, перемещая его по наклонной плоскости длиной 1,6 м и высотой 0,4 м, если КПД наклонной плоскости 80%.
Ответы
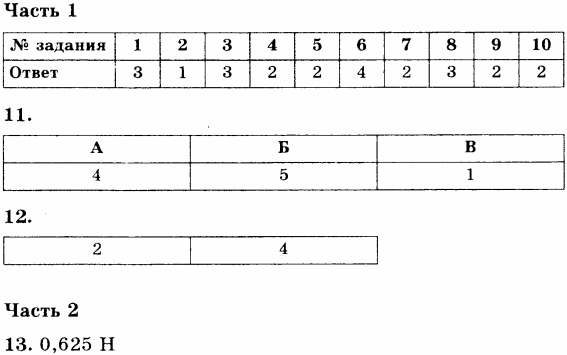
Простые механизмы. КПД простых механизмов
Оценкаfizi4ka.ru
423800, Набережные Челны , база Партнер Плюс, тел. 8 800 100-58-94 (звонок бесплатный)