|
||||
|
|
звонок бесплатный
Наши сотрудники:
[email protected]
Екатерина - специалист по продаже а/м КАМАЗ
 [email protected]
[email protected]






Техника в наличии

Тягач КАМАЗ 44108-6030-24
2014г, 6х6, Евро3, дв.КАМАЗ 300 л.с., КПП ZF9, бак 210л+350л, МКБ,МОБ,рестайлинг.
цена 2 220 000 руб.,

КАМАЗ 4308-6063-28(R4)
4х2,дв. Cummins ISB6.7e4 245л.с. (Е-4),КПП ZF6S1000, V кузова=39,7куб.м., спальное место, бак 210л, шк-пет,МКБ, ТНВД BOSCH, система нейтрализ. ОГ(AdBlue), тент, каркас, рестайлинг, внутр. размеры платформы 6112х2470х730 мм
цена 1 950 000 руб.,

Самосвал КАМАЗ 6520-057
2014г, 6х4,Евро3, дв.КАМАЗ 320 л.с., КПП ZF16, ТНВД ЯЗДА, бак 350л, г/п 20 тонн, V кузова =20 куб.м.,МКБ,МОБ, со спальным местом.
цена 2 700 000 руб.,

Самосвал 6522-027
2014, 6х6, дв.КАМАЗ 740.51,320 л.с., КПП ZF16,бак 350л, г/п 19 тонн,V кузова 12куб.м.,МКБ,МОБ,задняя разгрузка,обогрев платформы.
цена 3 190 000 руб.,
СУПЕР ЦЕНА
на АВТОМОБИЛИ КАМАЗ
| 43118-010-10 (дв.740.30-260 л.с.) | 2 220 000 |
| 43118-6033-24 (дв.740.55-300 л.с.) | 2 300 000 |
| 65117-029 (дв.740.30-260 л.с.) | 2 200 000 |
| 65117-6010-62 (дв.740.62-280 л.с.) | 2 350 000 |
| 44108 (дв.740.30-260 л.с.) | 2 160 000 |
| 44108-6030-24 (дв.740.55,рест.) | 2 200 000 |
| 65116-010-62 (дв.740.62-280 л.с.) | 1 880 000 |
| 6460 (дв.740.50-360 л.с.) | 2 180 000 |
| 45143-011-15 (дв.740.13-260л.с) | 2 180 000 |
| 65115 (дв.740.62-280 л.с.,рест.) | 2 190 000 |
| 65115 (дв.740.62-280 л.с.,3-х стор) | 2 295 000 |
| 6520 (дв.740.51-320 л.с.) | 2 610 000 |
| 6520 (дв.740.51-320 л.с.,сп.место) | 2 700 000 |
| 6522-027 (дв.740.51-320 л.с.,6х6) | 3 190 000 |

подробнее про услугу перегона можно прочесть здесь.

|
Нужны самосвалы? Обратите внимание на Ford-65513-02. |
КАМАЗы в лизинг
ООО «Старт Импэкс» имеет возможность поставки грузовой автотехники КАМАЗ, а так же спецтехники на шасси КАМАЗ в лизинг. Продажа грузовой техники по лизинговым схемам имеет определенные выгоды для покупателя грузовика. Рассрочка платежа, а так же то обстоятельство, что грузовики до полной выплаты лизинговых платежей находятся на балансе лизингодателя, и соответственно покупатель автомобиля не платит налогов на имущество. Мы готовы предложить любые модели бортовых автомобилей, тягачей и самосвалов по самым выгодным лизинговым схемам.Контактная информация.
г. Набережные Челны, Промкомзона-2, Автодорога №3, база «Партнер плюс».
тел/факс (8552) 388373.
Схема проезда
Как определить центр тяжести сечения. Как определить центр тяжести
Как найти центр тяжести фигуры? Расчет в Excel!
Опубликовано 21 Окт 2013Рубрика: Механика | 3 комментария
 В инженерной практике случается, что возникает необходимость вычислить координаты центра тяжести сложной плоской фигуры, состоящей из простых элементов, для которых расположение центра тяжести известно. Такая задача является частью задачи определения...
В инженерной практике случается, что возникает необходимость вычислить координаты центра тяжести сложной плоской фигуры, состоящей из простых элементов, для которых расположение центра тяжести известно. Такая задача является частью задачи определения...
...геометрических характеристик составных поперечных сечений балок и стержней. Часто с подобными вопросами приходится сталкиваться инженерам-конструкторам вырубных штампов при определении координат центра давления, разработчикам схем погрузки различного транспорта при размещении грузов, проектировщикам строительных металлических конструкций при подборе сечений элементов и, конечно, студентам при изучении дисциплин «Теоретическая механика» и «Сопротивление материалов».
Библиотека элементарных фигур.

Для симметричных плоских фигур центр тяжести совпадает с центром симметрии. К симметричной группе элементарных объектов относятся: круг, прямоугольник (в том числе квадрат), параллелограмм (в том числе ромб), правильный многоугольник.
Из десяти фигур, представленных на рисунке выше, только две являются базовыми. То есть, используя треугольники и сектора кругов, можно скомбинировать почти любую фигуру, имеющую практический интерес. Любые произвольные кривые можно, разбив на участки, заменить дугами окружностей.
Оставшиеся восемь фигур являются самыми распространенными, поэтому они и были включены в эту своеобразную библиотеку. В нашей классификации эти элементы не являются базовыми. Прямоугольник, параллелограмм и трапецию можно составить из двух треугольников. Шестиугольник – это сумма из четырех треугольников. Сегмент круга — это разность сектора круга и треугольника. Кольцевой сектор круга — разность двух секторов. Круг – это сектор круга с углом α=2*π=360˚. Полукруг – это, соответственно, сектор круга с углом α=π=180˚.
Расчет в Excel координат центра тяжести составной фигуры.
Передавать и воспринимать информацию, рассматривая пример, всегда легче, чем изучать вопрос на чисто теоретических выкладках. Рассмотрим решение задачи «Как найти центр тяжести?» на примере составной фигуры, изображенной на рисунке, расположенном ниже этого текста.

Составное сечение представляет собой прямоугольник (с размерами a1=80 мм, b1=40 мм), к которому слева сверху добавили равнобедренный треугольник (с размером основания a2=24 мм и высотой h3=42 мм) и из которого справа сверху вырезали полукруг (с центром в точке с координатами x03=50 мм и y03=40 мм, радиусом r3=26 мм).
В помощь для выполнения расчета привлечем программу MS Excel или программу OOo Calc. Любая из них легко справится с нашей задачей!
В ячейках с желтой заливкой выполним вспомогательные предварительныерасчеты.
В ячейках со светло-желтой заливкой считаем результаты.
Синий шрифт – это исходные данные.
Черный шрифт – это промежуточные результаты расчетов.
Красный шрифт – это окончательные результаты расчетов.
Начинаем решение задачи – начинаем поиск координат центра тяжести сечения.
Исходные данные:
1. Названия элементарных фигур, образующих составное сечение впишем соответственно
в ячейку D3: Прямоугольник
в ячейку E3: Треугольник
в ячейку F3: Полукруг
2. Пользуясь представленной в этой статье «Библиотекой элементарных фигур», определим координаты центров тяжести элементов составного сечения xci и yci в мм относительно произвольно выбранных осей 0x и 0y и запишем
в ячейку D4: =80/2=40,000
xc1=a1/2
в ячейку D5: =40/2=20,000
yc1= b1/2
в ячейку E4: =24/2=12,000
xc2=a2/2
в ячейку E5: =40+42/3=54,000
yc2= b1+h3/3
в ячейку F4: =50=50,000
xc3=x03
в ячейку F5: =40-4*26/3/ПИ()=28,965
yc3= y03-4*r3/3/π
3. Рассчитаем площади элементов F1, F2, F3 в мм2, воспользовавшись вновь формулами из раздела «Библиотека элементарных фигур»
в ячейке D6: =40*80=3200
F1=a1*b1
в ячейке E6: =24*42/2=504
F2=a2*h3/2
в ячейке F6: =-ПИ()/2*26^2=-1062
F3= -π/2*r3^2
Площадь третьего элемента – полукруга – отрицательная потому, что это вырез – пустое место!

Расчет координат центра тяжести:
4. Определим общую площадь итоговой фигуры F0 в мм2
в объединенной ячейке D8E8F8: =D6+E6+F6=2642
F0=F1+F2+F3
5. Вычислим статические моменты составной фигуры Sx и Sy в мм3 относительно выбранных осей 0x и 0y
в объединенной ячейке D9E9F9: =D5*D6+E5*E6+F5*F6=60459
Sx=yc1*F1+ yc2*F2+ yc3*F3
в объединенной ячейке D10E10F10: =D4*D6+E4*E6+F4*F6=80955
Sy=xc1*F1+ xc2*F2+ xc3*F3
6. И в завершение рассчитаем координаты центра тяжести составного сечения Xc и Yc в мм в выбранной системе координат 0x — 0y
в объединенной ячейке D11E11F11: =D10/D8=30,640
Xc=Sy/F0
в объединенной ячейке D12E12F12: =D9/D8=22,883
Yc=Sx/F0
Задача решена, расчет в Excel выполнен — найдены координаты центра тяжести сечения, составленного при использовании трех простых элементов!
Заключение.
Пример в статье был выбран очень простым для того, чтобы легче было разобраться в методологии расчетов центра тяжести сложного сечения. Метод заключается в том, что любую сложную фигуру следует разбить на простые элементы с известными местами расположения центров тяжести и произвести итоговые вычисления для всего сечения.
Если сечение составлено из прокатных профилей – уголков и швеллеров, то их нет необходимости разбивать на прямоугольники и квадраты с вырезанными круговыми «π/2»- секторами. Координаты центров тяжести этих профилей приведены в таблицах ГОСТов, то есть и уголок и швеллер будут в ваших расчетах составных сечений базовыми элементарными элементами (о двутаврах, трубах, прутках и шестигранниках говорить нет смысла – это центрально симметричные сечения).
Расположение осей координат на положение центра тяжести фигуры, конечно, не влияет! Поэтому выбирайте систему координат, упрощающую вам расчеты. Если, например, я развернул бы в нашем примере систему координат на 45˚ по часовой стрелке, то вычисление координат центров тяжести прямоугольника, треугольника и полукруга превратилось бы в еще один отдельный и громоздкий этап расчетов, который «в уме» не выполнишь.
Представленный ниже расчетный файл Excel в данном случае программой не является. Скорее – это набросок калькулятора, алгоритм, шаблон по которому следует в каждом конкретном случае составлять свою последовательность формул для ячеек с яркой желтой заливкой.
Итак, как найти центр тяжести любого сечения вы теперь знаете! Полный расчет всех геометрических характеристик произвольных сложных составных сечений будет рассмотрен в одной из ближайших статей в рубрике «Механика». Следите за новостями на блоге.
Для получения информации о выходе новых статей и для скачивания рабочих файлов программ прошу вас подписаться на анонсы в окне, расположенном в конце статьи или в окне вверху страницы.
После ввода адреса своей электронной почты и нажатия на кнопку «Получать анонсы статей» НЕ ЗАБЫВАЙТЕ ПОДТВЕРЖДАТЬ ПОДПИСКУ кликом по ссылке в письме, которое тут же придет к вам на указанную почту (иногда — в папку «Спам»)!
Несколько слов о бокале, монете и двух вилках, которые изображены на «значке-иллюстрации» в самом начале статьи. Многим из вас, безусловно, знаком этот «трюк», вызывающий восхищенные взгляды детей и непосвященных взрослых. Тема этой статьи – центр тяжести. Именно он и точка опоры, играя с нашим сознанием и опытом, попросту дурачат наш разум!
Центр тяжести системы «вилки+монета» всегда располагается на фиксированном расстоянии по вертикали вниз от края монеты, который в свою очередь является точкой опоры. Это положение устойчивого равновесия! Если покачать вилки, то сразу становится очевидным, что система стремится занять свое прежнее устойчивое положение! Представьте маятник – точка закрепления (=точка опоры монеты на кромку бокала), стержень-ось маятника (=в нашем случае ось виртуальная, так как масса двух вилок разведена в разные стороны пространства) и груз внизу оси (=центр тяжести всей системы «вилки+монета»). Если начать отклонять маятник от вертикали в любую сторону (вперед, назад, налево, направо), то он неизбежно под действием силы тяжести будет возвращаться в исходное устойчивое состояние равновесия (это же самое происходит и с нашими вилками и монетой)!
Кто не понял, но хочет понять – разберитесь самостоятельно. Это ведь очень интересно «доходить» самому! Добавлю, что этот же принцип использования устойчивого равновесия реализован и в игрушке ванька–встань-ка. Только центр тяжести у этой игрушки расположен выше точки опоры, но ниже центра полусферы опорной поверхности.
Всегда рад вашим комментариям, уважаемые читатели!!!
Прошу, УВАЖАЯ труд автора, скачивать файл ПОСЛЕ ПОДПИСКИ на анонсы статей.
Ссылка на скачивание файла: raschet-tsentra-tyazhesti (xls 17,0KB).
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
al-vo.ru
Содержание
Инструкция
|
completerepair.ru
Центр тяжести и его определение.
Центр тяжести
Центр параллельных сил
Центром параллельных сил называется такая точка на линии действия равнодействующей системы параллельных сил, через которую проходит равнодействующая и в том случае, если все силы системы повернуть вокруг их точек приложения на один и тот же угол, сохраняя параллельность сил.
Покажем существование центра параллельных сил на системе двух сил F1 и F2 (см. рисунок 1). На основании теоремы о сложении двух параллельных сил, направленных в одну сторону, определим равнодействующую этих сил и положение линии ее действия по формулам:
FΣ = F1 + F2; F1/F2 = BC/AC.
Нетрудно увидеть, что точка С, лежащая на линии АВ, соединяющей точки приложения данных сил, является центром двух параллельных сил F1 и F2, так как при повороте их на один и тот же угол α отношение плеч ВС и СА не изменится, и равнодействующая также пройдет через точку С.
Если дана система параллельных сил, то равнодействующую этой системы можно найти, последовательно попарно складывая все силы. На линии действия равнодействующей системы параллельных сил также будет существовать точка, обладающая свойствами центра параллельных сил, т. е. если все силы системы вращать вокруг этой точки, равнодействующая этих сил все равно останется приложенной к этой точке.
Выведем формулы для определения координат центра системы n параллельных сил.
Пусть даны пространственная система n параллельных сил и равнодействующая этой системы. Выберем систему осей координат и обозначим координаты точки приложения сил данной системы и координаты точки приложения равнодействующей (см. рисунок 2).
Запишем моменты сил данной системы относительно оси y. Для того, чтобы легче представить, чему равен момент силы относительно оси, следует мысленно перенести силу вдоль линии ее действия до положения, когда точка приложения силы окажется в плоскости координатных осей (см. рисунок 2, сила F1’):
Мy(F1) = F1x1, My(F2) = F2x2, ................ ................ My(Fn) = Fnxn, My(FΣ) = FΣxC.
Применим теорему о моменте равнодействующей относительно оси. Тогда:
FΣxC = F1x1 + F2x2 + .... + Fnxn, откуда
xC = (F1x1 + F2x2 + .... +Fnxn)/FΣ.
Записав моменты сил относительно оси x и вновь применив теорему о моменте равнодействующей, получим:
yC = (F1y1 + F2y2 + .... +Fnyn)/FΣ.
Для определения координаты zC повернем все силы системы вокруг их точек приложения в одну сторону так, чтобы силы стали параллельны оси y. При этом точка С не изменит своего положения, так как она является центром параллельных сил данной системы.
Запишем моменты всех сил относительно оси x и применим теорему о моменте равнодействующей, в результате получим:
zC = (F1z1 + F2z2 +....+Fnzn)/FΣ.
Равнодействующая системы параллельных сил равна их алгебраической сумме, т. е. FΣ = ΣFi. Применив сокращенную формулу записи, получим формулы для определения координат центра параллельных сил в следующем виде:
xC = Σ(Fixi)/ΣFi; yC = Σ(Fiyi)/ΣFi; zC = Σ(Fizi)/ΣFi.
Заметим, что в полученных формулах силы и моменты сил берут со знаком согласно ранее установленным правилам (если вектор силы направлен по направлению координатной оси, сила считается положительной, и наоборот, а момент силы считается положительным, если его вращающее действие относительно точки направлено против часовой стрелки).
***
Определение положения центра тяжести
Уникальность центра системы параллельных сил заключается в том, что равнодействующая сил системы, приложенная в этом центре, не создает относительно него вращающего момента, поскольку плечо равнодействующей равно нулю. Полученные выше формулы для определения координат центра системы параллельных сил на практике чаще всего используют для нахождения центра тяжести различных тел и фигур.
Сила, с которой тело притягивается к Земле, называется силой тяжести. Элементарной частицей тела называется такая малая частица, положение которой в пространстве определяется координатами одной точки.
Рассмотрим тело, состоящее из большого количества элементарных частиц. Силы тяжести каждой частицы, направленные к центру Земли, образуют систему сходящихся сил, но для тел, размеры которых ничтожно малы по сравнению с размерами нашей планеты, с достаточной степенью точности можно считать эти силы системой параллельных сил.
Центром тяжести тела называется центр параллельных сил тяжести всех элементарных частиц этого тела. Очевидно, что силы тяжести частиц тела образуют относительно центра тяжести систему параллельных сил, равнодействующая которой не имеет вращающего действия. Это свойство равнодействующей, проходящей через центр тяжести тела, используют, например, для балансировки колес, валов, при расчетах конструкций на устойчивость и т. п.
Центр тяжести является геометрической точкой, которая может лежать вне тела (например, кольцо, изогнутое тело и т. п.). Центр тяжести будем обозначать точкой С.
Координаты центра тяжести тела находят по тем же формулам, что и координаты центра параллельных сил:
xC = Σ(Gixi)/ΣFi; yC = Σ(Giyi)/ΣFi; zC = Σ(Gizi)/ΣGi,
где Gi - сила тяжести каждой элементарной частицы тела; xi, yi, zi – координаты частицы; ΣGi – сила тяжести всего тела.
В случае однородных тел по таким же формулам можно определять координаты центра тяжести объемов, площадей и линий, представив Gi, как произведение удельной массы (удельной силы тяжести) тела на его объем:
Gi = γVi, где γ – удельная сила тяжести (для однородного тела γ – величина постоянная). Если подставить эти зависимости в выведенные ранее формулы, и сократить на постоянный множитель γ, получим координаты центра тяжести для объема однородного тела:
xC = Σ(Vixi)/ΣVi; yC = Σ(Viyi)/ΣVi; zC = Σ(Vizi)/ΣVi.
При помощи аналогичных преобразований можно вывести формулы для нахождения координат центра тяжести плоской фигуры (пластины), имеющей одинаковую толщину h по всей площади: если Gi = γhAi, (здесь Аi – площадь элементарной площадки пластины), то
xC = Σ(Aixi)/ΣAi; yC = Σ(Aiyi)/ΣAi; zC = Σ(Aizi)/ΣAi.
Если тело, например, представляет собой однородную проволоку, постоянного поперечного сечения А (т. е. линию), то сила тяжести элементарной частицы, выраженная через длину li (после аналогичных математических преобразований) равна:
xC = Σ(lixi)/Σli; yC = Σ(liyi)/Σli; zC = Σ(lizi)/Σli.
***
Методы нахождения центра тяжести
k-a-t.ru
Как найти центр тяжести?
Перед тем, как найти центр тяжести простых фигур, таких которые обладают прямоугольной, круглой, шарообразной или цилиндрической, а также квадратной формой, необходимо знать, в какой точке находится центр симметрии конкретной фигуру. Поскольку в данных случаях, центр тяжести будет совпадать с центром симметрии.
Центр тяжести однородного стержня располагается в его геометрическом центре. Если необходимо определить центр тяжести круглого диска однородной структуры, то для начала найдите точку пересечения диаметров круга. Она и будет центром тяжести данного тела. Рассматривая такие фигуры, как шар, обруч и однородный прямоугольный параллелепипед, можно с уверенностью сказать, что центр тяжести обруча будет находиться в центре фигуры, но вне ее точек, центр тяжести шара - геометрический центр сферы, и в последнем случае, центром тяжестью считается пересечение диагоналей прямоугольного параллелепипеда.
Центр тяжести неоднородных тел
Чтобы найти координаты центра тяжести, как и сам центр тяжести неоднородного тела, необходимо разобраться, на каком отрезке данного тела располагается точка, в которой пересекаются все силы тяжести, действующие на фигуру, если ее переворачивать. На практике для нахождения такой точки подвешивают тело на нить, постепенно меняя точки прикрепления нити к телу. В том случае, когда тело находится в равновесии, то центр тяжести тела будет лежать на линии, которая совпадает с линией нити. В противном случае сила тяжести приводит тело в движение.
Возьмите карандаш и линейку, начертите вертикальные прямые, которые визуально будут совпадать с нитевыми направлениями (нити, закрепляемые в различных точках тела). Если форма тела достаточно сложная, то проведите несколько линий, которые будут пересекаться в одной точке. Она и станет центром тяжести для тела, над которым вы производили опыт.
Центр тяжести треугольника
Для нахождения центра тяжести треугольника, н
elhow.ru
Определение положения центра тяжести — Мегаобучалка
Сила, с которой тело притягивается к Земле, называется силой тяжести.
Элементарной частицей тела называется такая малая частица, положение которой в пространстве определяется координатами одной точки. Рассмотрим тело, состоящее из большого количества элементарных частиц. Силы тяжести каждой частицы, направленные к центру Земли, образуют систему сходящихся сил, но для тел размеры которых малы по сравнению с размерами Земли, с достаточной степенью точности можно считать эти силы системой параллельных сил.
Центром тяжести тела называется центр параллельных сил тяжести всех элементарных чистки тела.
Центр тяжести есть геометрическая точка, которая может лежать вне тела (например, кольцо, цилиндр с отверстием).
Координаты центра тяжести тела находят по тем же формулам, что и координаты центра параллельных сил, а именно:
где (Gi,—сила тяжести каждой элементарной частицы тела; xi, yi, zi,— координаты частицы; Σ Gi -сила тяжести всего тела.
В случае однородных тел по таким же формулам можно определять координаты центра тяжести объемов, площадей и линий. Например, для абсциссы хсполучим следующие формулы:
1) сила тяжести элементарной частицы, выраженная через ее объем Viравна
2) если тело представляет собой однородную пластинку
где γ удельная сила тяжести (для однородного тела — величина постоянная). Тогда
следовательно, для объема
толщиной h, то сила тяжести элементарной частицы, выраженная
через площадь Аiравна
тогда
следовательно, для площади
3) если тело представляет собой однородную проволоку постоянного поперечного сечения А. то сила тяжести элементарной частицы, выраженная через длину li, равна
тогда
следовательно, для линии
- Устойчивость равновесия. Момент опрокидывающий и момент удерживающий. Коэффициент устойчивости. Условие устойчивости.
Наряду с выполнением условий прочности и жесткости, необходимо обеспечить и устойчивость конструкций.
При неизменной схеме нагружения, под устойчивостью понимается свойство способности системы сохранять свое первоначальное равновесное состояние. Если рассматриваемая система таким свойством не обладает, то она называется неустойчивой, а ее равновесное состояние - неустойчивым состоянием.
При неизменной схеме нагружения, в процессе роста интенсивности нагрузок, явление перехода системы от одного равновесного состояния к другому равновесному состоянию, называется потерей устойчивости системы. Значения внешних сил, при которых происходит потеря устойчивости, называются критическими.
В некоторых случаях при потере устойчивости, система, переходя в новое устойчивое равновесное состояние, продолжает выполнять свои функции. Однако в подавляющем большинстве случаев, потеря устойчивости системы сопровождается возникновением больших перемещений, пластических деформаций или ее полным разрушением. Поэтому сохранение исходного (расчетного) равновесного состояния системы является важной задачей и одной из основных проблем сопротивления материалов.
- Геометрические характеристики плоских сечений.
При выборе расчетной схемы вводятся упрощения и в геометрию реального объекта. Основным упрощающим приемом в сопротивлении материалов является приведение геометрической формы тела к схемам бруса (стержня) или оболочки. Как известно, любое тело в пространстве характеризуется тремя измерениями. Брусом называется геометрический объект, одно из измерений которого (длина) много больше двух других. Геометрически брус может быть образован путем перемещения плоской фигуры вдоль некоторой кривой, как это показано на рис. 1.1.
| Рис. 1.1 |
Эта кривая называется осью бруса, а плоская замкнутая фигура, располагающая свой центр тяжести на оси бруса и нормальная к ней, называется его поперечным сечением. Брус может иметь как постоянное, так и переменное поперечное сечение. Многие сложные конструкции на практике рассматриваются как комбинации элементов, имеющих форму бруса, поэтому в настоящей книге преимущественно рассматриваются методы расчета бруса как основного геометрического объекта изучения науки сопротивления материалов. Второй основной геометрической формой, рассматриваемой в сопротивлении материалов, является оболочка, под которой подразумевается тело, у которого одно из измерений (толщина) намного меньше, чем два других.
Для соединения отдельных частей конструкции между собой и передачи внешней нагрузки на основание на нее накладываются связи, ограничивающие перемещения тех точек сооружения, к которым они приложены. Связи могут ограничивать либо повороты точек сооружения, либо их линейные смещения, либо и то и другое.
- Понятие прочности, жесткости, устойчивости, пластичности и упругости.
В заключение отметим наиболее важные свойства материалов которые обнаруживаются при их испытаниях. Эти свойства имеют фундаментальное значение при построении физических уравнений механики твердого деформируемого тела.
Упругость - это способность твердого деформируемого тела восстанавливать свою форму и объем после прекращения действия внешних нагрузок.
Пластичность - это свойство твердого деформируемого тела до разрушения необратимо изменять свою форму и объем от действия внешних сил.
Вязкость - это свойство оказывать сопротивление за счет трения происходящего при перемещении элементарных частиц тела относительно друг друга в процессе деформирования. Отметим, что при этом, как показывают результаты экспериментов, сила сопротивления, возникающая за счет внутреннего трения материалов, прямым образом зависит от величины скорости перемещения элементарных частиц относительно друг друга.
Упругость, пластичность и вязкость являются главными физическими свойствами твердого деформируемого тела.
Ползучесть - это явление характеризующееся изменения во времени величин деформаций и напряжений в теле при действии статических нагрузок.
Выносливость - при действии периодически изменяющихся по времени нагрузок, это явление, которое характеризуется чувствительностью и изменениями прочностных свойств материалов в зависимости от числа циклов нагружения.
- Внешние силы. Деформация и ее виды.
Силы являются мерилом механического взаимодействия тел. Если конструкция рассматривается изолированно от окружающих тел, то действие последних на нее заменяется силами, которые называются внешними. Внешние силы, действующие на тело, можно разделить на активные (независимые) и реактивные. Реактивные усилия возникают в связях, наложенных на тело, и определяются действующими на тело активными усилиями.
По способу приложения внешние силы делятся на объемные и поверхностные.
Объемные силы распределены по всему объему рассматриваемого тела и приложены к каждой его частице. В частности, к объемным силам относятся собственный вес сооружения, магнитное притяжение или силы инерции. Единицей измерения объемных
сил является сила, отнесенная к единице объема - кН/м3 .
Поверхностные силы приложены к участкам поверхности и являются результатом непосредственного контактного взаимодействия рассматриваемого объекта с окружающими телами. В зависимости от соотношения площади приложения нагрузки и общей площади поверхности рассматриваемого тела, поверхностные нагрузки подразделяются на сосредоточенные и распределенные. К первым относятся нагрузки, реальная площадь приложения которых несоизмеримо меньше полной площади поверхности тела (например, воздействие колонн на фундаментную плиту достаточно больших размеров можно рассматривать как действие на нее сосредоточенных усилий). Если же площадь приложения нагрузки сопоставима с площадью поверхности тела, то такая нагрузка рассматривается как распределенная. Сосредоточенные усилия измеряются в кН, а распределенные - кН/м2.
Взаимодействие между частями рассматриваемого тела характеризуется внутренними силами, которые возникают внутри тела под действием внешних нагрузок и определяются силами межмолекулярного воздействия.
Величины внутренних усилий определяются с применением метода сечений, суть которого заключается в следующем. Если при действии внешних сил тело находится в состоянии равновесия, то любая отсеченная часть тела вместе с приходящимися на нее внешними и внутренними усилиями также находится в равновесии, следовательно, к ней применимы уравнения равновесия.
- Метод сечений для определения внутренних усилий. Виды внутренних усилий, частные случаи.
Рассмотрим тело, имеющее форму бруса (рис. 1.2, а).
Рис. 1.2
Пусть к нему приложена некоторая система внешних сил Р1, Р2, Р3,..., Рn , удовлетворяющая условиям равновесия, т.е. при действии указанных внешних сил тело находится в состоянии равновесия.
Если рассечь брус сечением А на две части и правую отбросить, то, т.к. связи между частями тела устранены, необходимо действие правой (отброшенной) части на левую заменить некоей системой внутренних сил (PА ), действующей в сечении А (рис. 1.2, б).
Обозначая через Pлев и Рправ суммы внешних сил, приложенных соответственно, к левой и правой частям бруса (относительно сечения А), и учитывая, что
Pлев + Рправ = 0 (1.1)
для отсеченных частей бруса получим следующие очевидные соотношения:
Рлев + PA = 0; Рправ - PA = 0. (1.2)
Последние соотношения показывают, что равнодействующая внутренних сил РА в сечении А может определяться с равным успехом из условий равновесия либо левой, либо правой частей рассеченного тела. В этом суть метода сечений.
- Понятие о напряжении. Составляющие полного напряжения.
В окрестности произвольной точки К, принадлежащей сечению А некоторого нагруженного тела, выделим элементарную площадку DF, в пределах которой действует внутреннее усилие D (рис. 1.4, а). Векторная величина
(1.5)
называется полным напряжением в точке К. Проекция вектора полного напряжения на нормаль к данной площадке обозначается через s и называется нормальным напряжением.
Рис. 1.4
Проекции вектора на перпендикулярные оси в плоскости площадки (рис. 1.4, б) называются касательными напряжениями по направлению соответствующих осей и обозначаются t´ и t´´. Если через ту же самую точку К провести другую площадку, то, в общем случае будем иметь другое полное напряжение. Совокупность напряжений для множества площадок, проходящих через данную точку, образует напряженное состояние в этой точке.
- Растяжение и сжатие. Закон Гука.
Многочисленные экспериментальные наблюдения за поведением деформируемых тел показывают, что в определенных диапазонах перемещения точек тела пропорциональны действующим на него нагрузкам. Впервые указанная закономерность была высказана в 1776 году английским ученым Гуком и носит название закона Гука.
В соответствии с этим законом перемещение произвольно взятой точки А (рис. 1.5, а) нагруженного тела по некоторому направлению, например, по оси x, а может быть выражено следующим образом:
u = dx P, (1.8)
где Р - сила, под действием которой происходит перемещение u; dx×- коэффициент пропорциональности между силой и перемещением.
Очевидно, что коэффициент dx зависит от физико-механических свойств материала, взаимного расположения точки А и точки приложения и направления силы Р, а также от геометрических особенностей системы. Таким образом, последнее выражение следует рассматривать как закон Гука для данной системы.
В современной трактовке закон Гука определяет линейную зависимость между напряжениями и деформациями, а не между силой и перемещением. Коэффициенты пропорциональности в этом случае представляют собой физико-механические характеристики материала и уже не связаны с геометрическими особенностями си-
стемы в целом.
Системы, для которых соблюдается условие пропорциональности между перемещениями и внешними силами, подчиняются принципу суперпозиции, или принципу независимости действия сил.
- Три расчета на прочность при растяжении и сжатии.
Наиболее распространенным методом расчета деталей машин и элементов сооружений на прочность является расчет по напряжениям. В основу этого метода положено предположение, что определяющим параметром надежности конструкции является напряжение или, точнее говоря, напряженное состояние в точке. Расчет выполняется в следующем порядке.
На основании анализа напряженного состояния конструкции выявляется та точка сооружения, где возникают наибольшие напряжения. Расчетная величина напряжений сопоставляется с предельно допустимой величиной напряжений для данного материала, полученной на основе предварительных лабораторных испытаний. Из сопоставления найденных расчетных напряжений и предельных напряжений делается заключение о прочности конструкции.
Указанный метод является не единственным. Например, на практике в некоторых случаях используется метод расчета конструкций по разрушающим нагрузкам. В этом методе путем расчета определяется предельная нагрузка, которую может выдержать конструкция, не разрушаясь и не изменяя существенно свою форму. Предельная (разрушающая) нагрузка сопоставляется с проектной нагрузкой, и на этом основании делается вывод о несущей способности конструкции в эксплуатационных условиях.
Методы расчета конструкций выбираются в зависимости от условий работы конструкций и требований, которые к ней предъявляются. Если необходимо добиться наименьших изменений формы конструкции, то производится расчет по допускаемым перемещениям. Это не исключает и одновременной проверки системы на прочность по напряжениям.
При расчете конструкций по напряжениям условие прочности записывается в виде:
smax £ [s] , (2.24)
где smax - расчетное значение напряжения в точке, где возникают наибольшие напряжения, [s] - допускаемое напряжение.
Величина [s] определяется по формуле:
. (2.25)
Здесь n - число, большее единицы, называемое коэффициентом запаса по прочности. Для особо ответственных конструкций, для которых требуется не допускать возникновения пластических деформаций, за величину sa принимается sa= sУ . В тех случаях, когда допустимо возникновение пластических деформаций, как правило, принимается sa = sТ. Для хрупких материалов, а в некоторых случаях и умеренно пластических материалов, принимается sa = sВ . Здесь sВ - временное сопротивление материала.
Критерий прочности, принятый в методе допускаемых напряжений, а именно, напряжения в точке, не всегда и не полностью характеризует условие наступления разрушения конструкции. В ряде случаев за такой критерий целесообразнее принимать предельную нагрузку, которую может выдержать заданная система, не разрушаясь и несущественно изменяя свою форму.
При определении разрушающей нагрузки для конструкций из пластичного материала применяется схематизированная диаграмма напряжений - диаграмма Прандтля (рис. 2.10). Схематизация диаграммы заключается в предположении, что материал на начальном этапе деформирования находится в упругой стадии вплоть до предела текучести, а затем материал обладает неограниченной площадкой текучести. Материал, работающий по такой диаграмме, называется идеально упруго-пластическим. Такая схематизированная диаграмма деформирования в большей степени соответствует действительной диаграмме деформирования материала, имеющего ярко выраженную площадку текучести, т.е. пластичным материалам (см. п. 2.7).
Если расчет конструкций ведется по предельной нагрузке, то определяющим является выполнение условия
Рmax £ [P ], (2.26)
где [P ] - допускаемая сила, которая определяется по формуле:
, (2.27)
Здесь Рa - значение внешних нагрузок, при которых происходит разрушение конструкции; n1 - коэффициент запаса.
В случае расчета конструкции на жесткость необходимо удовлетворять условию
u £ [u], (2.28)
где u и [u] - расчетное и предельно допустимое значения перемещения.
- Продольные силы. Построение эпюр продольных сил и нормальных напряжений. Абсолютное удлинение и укорочение.
3. Построение эпюр Nz и sz По причине линейной зависимости нормальной силы и напряжений от координаты z для построения их эпюр достаточно значений Nz иsz в граничных сечениях каждого из участков. Необходимым условием правильности построения этих графиков является выполнение следующих требований:
- скачок в эпюре Nz должен находиться в точке приложения сосредоточенного усилия и быть равным по величине значению этой силы;
- скачки в эпюре sz должны совпадать с точками приложения внешней силы Р и изменения площади поперечного сечения колонны.
После анализа полученных эпюр легко можно убедиться, что построения выполнены правильно.
Вычисление перемещения верхнего конца колонны от действия всех сил. Полное перемещение согласно закону Гука может быть вычислено по формуле
.
- Продольная и поперечная деформации при растяжении и сжатии.
Под действием внешних сил твердые тела изменяют свою геометрическую форму, а точки тела неодинаково перемещаются в пространстве. Вектор , имеющий свое начало в точке А недеформированного состояния, а конец в т. деформированного состояния, называется вектором полного перемещения т. А (рис. 1.5, а). Его проекции на оси xyz называются осевыми перемещениями и обозначаются u, v и w, соответственно.
Для того, чтобы охарактеризовать интенсивность изменения формы и размеров тела, рассмотрим точки А и В его недеформированного состояния, расположенные на расстоянии S друг от друга (рис. 1.5, б).
Рис. 1.5
Пусть в результате изменения формы тела эти точки переместились в положение А¢ и В¢, соответственно, а расстояние между ними увеличилось на величину DS и составило S + DS. Величина
(1.6)
называется линейной деформацией в точке А по направлению АВ. Если рассматривать деформации по направлениям координатных осей xyz, то в обозначения соответствующих проекций линейной деформации вводятся индексы ex , ey , ez .
Линейные деформации ex , ey , ez характеризуют изменения объема тела в процессе деформирования, а формоизменения тела - угловыми деформациями. Для их определения рассмотрим прямой угол, образованный в недеформированном состоянии двумя отрезками ОD и ОС (рис. 1.5, б). При действии внешних сил указанный угол DOC изменится и примет новое значение D¢O¢C¢. Величина
(Ð DOC - Ð D¢O¢C¢) = g (1.7)
называется угловой деформацией, или сдвигом в точке О в плоскости СОD. Относительно координатных осей деформации сдвига обозначаются gxy , gxz , gyz .
Совокупность линейных и угловых деформаций по различным направлениям и плоскостям в данной точке образует деформированное состояние в точке.
- Испытание материалов при растяжении и сжатии.
Для количественной оценки основных свойств материалов, как
| Рис. 2.9 |
правило, экспериментально определяют диаграмму растяжения в координатах s и e (рис. 2.9), На диаграмме отмечены характерные точки. Дадим их определение.
Наибольшее напряжение, до которого материал следует закону Гука, называется пределом пропорциональности sП . В пределах закона Гука тангенс угла наклона прямой s = f (e) к оси e определяется величиной Е.
Упругие свойства материала сохраняются до напряжения sУ , называемого пределом упругости. Под пределом упругости sУ понимается такое наибольшее напряжение, до которого материал не получает остаточных деформаций, т.е. после полной разгрузки последняя точка диаграммы совпадает с начальной точкой 0.
Величина sТ называется пределом текучести материала. Под пределом текучести понимается то напряжение, при котором происходит рост деформаций без заметного увеличения нагрузки. Если необходимо различать предел текучести при растяжении и сжатии sТ соответственно заменяется на sТР и sТС . При напряжениях больших sТ в теле конструкции развиваются пластические деформации eП , которые не исчезают при снятии нагрузки.
Отношение максимальной силы, которую способен выдержать образец, к его начальной площади поперечного сечения носит название предела прочности, или временного сопротивления, и обозначается через, sВР (при сжатии sВС ).
- Диаграмма растяжения малоуглеродистой стали.
Для испытаний на растяжение применяют разрывные машины, позволяющие в процессе испытания определять усилия и соответствующие им деформации образца. По этим данным строят первичную диаграмму растяжения, в которой по оси ординат откладывают усилия, по оси абсцисс — соответствующие им удлинения. Диаграмма растяжения может быть получена и автоматически при помощи специальных диаграммных аппаратов. Характер диаграммы растяжения зависит от свойств испытуемого материала. Типичный вид такой диаграммы для малоуглеродистой стали изображен на рис.4.2.
Рассмотрим характерные участки и точки этой диаграммы, а также соответствующие им стадии деформирования образца.
От начала нагружения до определенного значения растягивающей силы имеет место прямая пропорциональная зависимость между удлинением образца и силой. Эта зависимость на диаграмме выражается прямой ОА. На этой стадии растяжения справедлив закон Гука.
Обозначим силу, при которой нарушается закон пропорциональности, через . На диаграмме этому значению силы на диаграмме соответствует точка А. Напряжение, вызванное силой , называется пределом пропорциональности и вычисляется по формуле
.
- Диаграмма растяжения и сжатия хрупких материалов.
Способность материалов получать остаточные деформации носит название пластичности. На рис. 2.9 была представлена характерная диаграмма для пластических материалов.
Рис. 2.10 Рис. 2.11
Противоположным свойству пластичности является свойство хрупкости, т.е. способность материала разрушаться без образования заметных остаточных деформаций. Материал, обладающий этим свойством, называется хрупким. К хрупким материалам относятся чугун, высокоуглеродистая сталь, стекло, кирпич, бетон, природные камни. Характерная диаграмма деформации хрупких материалов изображена на рис. 2.11.
- Диаграмма сжатия пластичных материалов
При выполнении практических расчетов реальную диаграмму (рис. 2.9) упрощают, и с этой целью применяются различные аппроксимирующие диаграммы. Для решения задач с учетом упруго-пластических свойств материалов конструкций чаще всего применяется диаграмма Прандтля. По этой диаграмме напряжение изменяется от нуля до предела текучести по закону Гука s = Е e, а далее при росте e, s = sТ (рис. 2.10).
- Понятие о наклепе. Явление ползучести. Релаксация.
Если дислокация подходит к границе двух зерен и не может выйти на поверхность, она застревает. Следующие дислокации, подходят к застрявшей дислокации, образуя скопление дислокаций вблизи границ зерен. Чем мельче зерна, тем больше поверхность их раздела, и тем выше уровень напряжений, необходимый для смещения дислокаций. Напряжения скапливаются у границ зерен, все больше заполняя решетку. Для дальнейшей деформации кристалла необходимо повысить внешнее усилие. При этом происходит прорыв дислокаций через препятствие, раздробление блоков, увеличение их границ, и тем самым больше мест скопления дислокаций. Упрочнение металла в результате скопления дислокаций на границах зерен и невозможности их перемещения называется наклепом металла при холодной деформации. В результате наклепа возрастает упругое искажение кристаллической решетки, увеличивается сопротивление деформации и уменьшается пластичность. Увеличение прочности особенно интенсивно происходит на начальных стадиях деформации (до 25%).
Для упрочнения металла в него вводят атомы другого металла (легируют), т.е. повышают количество дефектов кристаллической решетки.
Таким образом, с одной стороны дефекты ослабляют металл, а с другой – затрудняют движение дислокаций, что упрочняет металл.
Кроме увеличения количества дислокаций при холодной деформации происходит и изменение формы кристаллов. Зерна, имевшие до деформации произвольную ориентацию, после деформации вытягиваются в определенном направлении. Механические свойства металла становятся неодинаковыми в различных направлениях, т.е. материал становится анизотропным. Ориентация кристаллических решеток зерен в определенном направлении с появлением анизотропии свойств называется текстурой. Таким образом, наклеп сопровождается текстурой кристаллов.
Кроме увеличения прочностных свойств при наклепе увеличивается электрическое сопротивление (до 50%), уменьшается электропроводность, коррозионная стойкость и магнитная проницаемость металлов.
Явление непрерывной деформации под действием постоянного напряжения называется ползучестью. Характеристикой ползучести является предел ползучести, характеризующий условное растягивающее напряжение, при котором скорость и деформация ползучести за определённое время достигают заданной величины. Если допуск даётся по скорости ползучести, то предел ползучести обозначается σ(сигма) с двумя индексами: нижний соответствует заданной скорости ползучести в %/ч (проценты в час), а верхний - температуре испытания. Если задаётся относительное удлинение, то в обозначение предела ползучести вводят три индекса: один верхний соответствует температуре испытания, два нижних — деформации и времени. Для деталей, работающих длительный срок (годы), предел ползучести должен характеризоваться малой деформацией, возникающей при значительной длительности приложения нагрузки. Для паровых турбин, лопаток паровых турбин, работающих под давлением, допускается суммарная деформация не более 1 % за 100000 часов, в отдельных случаях допускается 5 %. У лопаток газовых турбин деформация может быть 1-2 % на 100—500 часов.
РЕЛАКСАЦИЯ (от лат. relaxatio-ослабление), процесс установления в системе термодинамического равновесия. Состояние макроскопич. системы определяется мн. параметрами, и процессы достижения равновесия по разным параметрам могут протекать с разл. скоростями. Выделяют период линейной релаксации, когда нек-рый параметр состояния xi лишь незначительно отличается от своего равновесного значения. В этот период скорость изменения параметра dxi/dt пропорциональна величине отклонения хi от:
где тi-время релаксации. Отсюда следует, что в момент времени t отклонениеехр (—t/тi). За время тi малое отклонение параметра хi от равновесного значения уменьшается в е раз. Величины vi = 1/тi, обратные временам релаксации, наз. частотами релаксации.
- Расчеты на прочность. Допускаемое напряжение и коэффициент запаса прочности по пределу текучести и по пределу прочности.
Традиционные инженерные расчеты на прочность деталей машин основываются на статическом анализе нагрузок, обосновании выбора расчетных нагрузок и их сочетаний, механических свойств материалов и методологии выбора коэффициента запаса.
При действии ударных нагрузок развитие и распространение пластических деформаций в образце затруднено, поэтому происходит повышение пределов текучести и прочности материала (по величине практически совпадают) при резком уменьшении относительного удлинения.
Фактические нагрузки, действующие на деталь, и свойства материалов, из которых она изготовлена, могут значительно отличаться от тех, которые принимаются для расчета.
При этом факторы, снижающие прочность детали (перегрузки, неоднородность материалов и т. д.), носят чаще всего случайный характер и предварительно не могут быть учтены.
Так как детали и сооружения в целом должны безопасно работать и при этих неблагоприятных условиях, то необходимо принять определенные меры предосторожности. С этой целью напряжения, обеспечивающие безотказную работу (эксплуатации) машины или любого другого сооружения, должны быть ниже тех предельных напряжений, при которых может произойти разрушение или возникнуть пластические деформации.
Таким образом, принимают
где [σ]- допускаемое напряжение; [n] - нормативный (т. е. предписываемый нормами проектирования конструкций) коэффициент запаса прочности, называемый также коэффициентом безопасности, σn - предельное напряжение материала.
При статических нагрузках за предельное напряжение для хрупких материалов принимают предел прочности, для пластичных - предел текучести, так как при напряжениях, равных пределу текучести, возникают значительные пластические деформации, которые недопустимы.
Таким образом, коэффициент запаса прочности вводится для того, чтобы обеспечить безопасную, надежную работу сооружения и отдельных его частей, несмотря на возможные неблагоприятные отклонения действительных условий их работы от расчетных.
Вопрос о нормативном коэффициенте запаса прочности [n] решается с учетом имеющегося опыта эксплуатации сооружений и машин.
В последнее время один общий коэффициент запаса расчленяют на ряд составляющих частных коэффициентов запаса, каждый из которых отражает влияние на прочность элемента конструкции какого-либо определенного фактора или группы факторов. Например, один из коэффициентов отражает возможные отклонения механических характеристик материала от принимаемых в качестве расчетных, другой - отклонения действующих нагрузок от их расчетных значений и т. д.
Такое разделение общего коэффициента запаса позволяет лучше учесть многообразные конкретные условия работы деталей машин и сооружений и проектировать их с большей надежностью и экономичностью.
Коэффициент запаса прочности представляют в виде произведения
В вопросе о частных коэффициентах и их значениях до сих пор нет единообразия. Значения коэффициентов запаса прочности обычно принимают на основании опыта конструирования и эксплуатации машин определенного типа. В настоящее время в машиностроении имеются рекомендации пользоваться одним, тремя, пятью и даже десятью частными коэффициентами запаса прочности. В «Справочнике машиностроителя» рекомендуется пользоваться тремя частными коэффициентами:
n1 - коэффициент, учитывающий неточность в определении нагрузок и напряжений. Значение этого коэффициента при повышенной точности определения действующих напряжений может приниматься равным 1,2-1,5, при меньшей точности расчета – 2-3;
n2 - коэффициент, учитывающий неоднородность материала, повышенную его чувствительность к недостаткам механической обработки. Коэффициент n2 в расчетах по пределу текучести при действии статических нагрузок можно принимать по Табл. 4.3 (без учета влияния абсолютных размеров) в зависимости от отношения предела текучести к пределу прочности.
- Метод расчета по предельным состояниям. Предельные состояния и надежность строительных конструкций. Три вида расчета на прочность.
В соответствии с методом расчёта по предельным состояниям вместо ранее применявшегося единого коэффициента запаса прочности (по методу допускаемых напряжений) используется несколько, учитывающих особенности работы сооружения, независимых коэффициентов, каждый из которых имеет определённый вклад в обеспечение надёжности конструкции и гарантии от возникновения предельного состояния.
Метод предельных состояний, разработанный в СССР и основанный на исследованиях под руководством профессора Н. С. Стрелецкого[4], введён строительными нормами и правилами в 1955 году[8] и в Российской Федерации является основным методом при расчёте строительных конструкций[1].
Этот метод характеризуется полнотой оценки несущей способности и надёжности конструкций благодаря учёту: вероятностных свойств действующих на конструкции нагрузок и сопротивлений этим нагрузкам; особенностей работы отдельных видов конструкций; пластических свойств материалов.
Расчёт конструкции по методу предельных состояний должен гарантировать ненаступление предельного состояния
Метод расчета по предельным состояниям
megaobuchalka.ru
Тема 1.6. Центр тяжести тела
⇐ ПредыдущаяСтр 3 из 7Следующая ⇒Тема относительно проста для усвоения, однако крайне важна при изучении курса сопротивления материалов. Главное внимание здесь необходимо обратить на решение задач как с плоскими и геометрическими фигурами, так и со стандартными прокатными профилями.
Вопросы для самоконтроля
1. Что такое центр параллельных сил?
Центр параллельных сил есть точка, через которую проходит линия равнодействующей системы параллельных сил, приложенных в заданных точках, при любом изменении направления этих сил в пространстве.
2. Как найти координаты центра параллельных сил?
Для определения координат центра параллельных сил воспользуемся теоремой Вариньона.
Относительно оси x
Mx(R) = ΣMx(Fk), -yCR = ΣykFk и yC = ΣykFk /ΣFk.
Относительно оси y
My(R) = ΣMy(Fk), -xCR = ΣxkFk и xC = ΣxkFk /ΣFk.
Чтобы определить координату zC, повернем все силы на 90° так, чтобы они стали параллельны оси y (рисунок 1.5, б). Тогда
Mz(R) = ΣMz(Fk), -zCR = ΣzkFk и zC = ΣzkFk /ΣFk.
Следовательно, формула для определения радиус-вектора центра параллельных сил принимает вид
rC = ΣrkFk /ΣFk.
3. Что такое центр тяжести тела?
Центр Тяжести-неизменно связанная с твердым телом точка, через которую проходит равнодействующая сил тяжести, действующих на частицы этого тела при любом положении тела в пространстве. У однородного тела, имеющего центр симметрии (круг, шар, куб и т. д.), центр тяжести находится в центре симметрии тела. Положение центра тяжести твердого тела совпадает с положением его центра масс.
4. Как найти центр тяжести прямоугольника, треугольника, круга?
Для нахождения центра тяжести треугольника, необходимо нарисовать треугольник – фигуру, состоящую из трех отрезков, соединенных между собой в трех точках. Перед тем, как найти центр тяжести фигуры, необходимо, используя линейку, измерить длину одной стороны треугольника. В середине стороны поставьте отметку, после чего противоположную вершину и середину отрезка соедините линией, которая называется медианой. Тот же самый алгоритм повторите со второй стороной треугольника, а затем и с третьей. Результатом вашей работы станут три медианы, которые пересекаются в одной точке, которая будет являться центром тяжести треугольника. Если необходимо определить центр тяжести круглого диска однородной структуры, то для начала найдите точку пересечения диаметров круга. Она и будет центром тяжести данного тела. Рассматривая такие фигуры, как шар, обруч и однородный прямоугольный параллелепипед, можно с уверенностью сказать, что центр тяжести обруча будет находиться в центре фигуры, но вне ее точек, центр тяжести шара - геометрический центр сферы, и в последнем случае, центром тяжестью считается пересечение диагоналей прямоугольногопараллелепипеда.
5. Как найти координаты центра тяжести плоского составного сечения?
Метод разбиения: если плоскую фигуру можно разбить на конечное число таких частей, для каждой из которых положение центра тяжести известно, то координаты центра тяжести всей фигуры опредляются по формулам:
ХC = ( 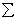 sk xk ) / S; YC = (
sk xk ) / S; YC = ( 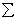 sk yk ) / S,
sk yk ) / S,
где xk, yk - координаты центров тяжести частей фигуры;
sk - их площади;
S = 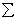 sk - площадь всей фигуры.
sk - площадь всей фигуры.
6. Центр тяжести

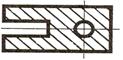
1. В каком случае для определения центра тяжести достаточно определить одну координату расчетным путем?
В первом случае для определения центра тяжести достаточно определить одну координату Тело разбивается на конечное число частей, для каждой из которых положение центра тяжести C и площадь S известны. Например, проекцию тела на плоскость xOy (рисунок 1.) можно представить в виде двух плоских фигур с площадями S1 и S2 (S = S1 + S2). Центры тяжести этих фигур находятся в точках C1(x1, y1) и C2(x2, y2). Тогда координаты центра тяжести тела равны
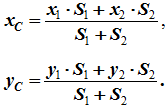
Так как центры фигур лежат на оси ординат (х = 0), то находим только координату Ус.
2 Как учитывается площадь отверстия в фигуре 4 в формуле для определения центра тяжести фигуры?
Метод отрицательных масс
Этот метод заключается в том, что тело, имеющее свободные полости, считают сплошным, а массу свободных полостей – отрицательной. Вид формул для определения координат центра тяжести тела при этом не меняется.
Таким образом, при определении центра тяжести тела, имеющего свободные полости, следует применять метод разбиения, но считать массу полостей отрицательной.
В результате изучения темы студент должен:
иметь представление о центре параллельных сил и его свойствах;
знатьформулы для определения координат центра тяжести плоских фигур;
уметьопределять координаты центра тяжести плоских фигур простых геометрических фигур и стандартных прокатных профилей.
ЭЛЕМЕНТЫ КИНЕМАТИКИ И ДИНАМИКИИзучив кинематику точки, обратите внимание на то, что прямолинейное движение точки как неравномерное, так и равномерное всегда характеризуется наличием нормального (центростремительного) ускорения. При поступательном движении тела (характеризуемом движением любой его точки) применимы все формулы кинематики точки. Формулы для определения угловых величин тела, вращающегося вокруг неподвижной оси, имеют полную смысловую аналогию с формулами для определения соответствующих линейных величин поступательно движущегося тела.
Тема 1.7. Кинематика точкиПри изучении темы обратите внимание на основные понятия кинематики: ускорение, скорость, путь, расстояние.
Вопросы для самоконтроля
1. В чем заключается относительность понятий покоя и движения?
Механическое движение -это изменение движения тела, или (его частей) в пространстве относительно др. тел с течением времени. Полет брошенного камня, вращение колеса- примеры механического движения.
2. Дайте определение основных понятий кинематики: траектории, расстоянию, пути, скорости, ускорению, времени.
Скорость – это кинематическая мера движения точки, характеризующая быстроту изменения ее положения в пространстве. Скорость является векторной величиной, т. е. она характеризуется не только модулем (скалярной составляющей), но и направлением в пространстве.
Как известно из физики, при равномерном движении скорость может быть определена длиной пути, пройденного за единицу времени: v = s/t = const (предполагается, что начало отсчета пути и времени совпадают). При прямолинейном движении скорость постоянна и по модулю, и по направлению, а ее вектор совпадает с траекторией.
Единица скорости в системе СИ определяется соотношением длина/время, т. е. м/с.
Ускорение есть кинематическая мера изменения скорости точки во времени. Другими словами - ускорение - это скорость изменения скорости. Как и скорость, ускорение является величиной векторной, т. е. характеризуется не только модулем, но и направлением в пространстве.
При прямолинейном движении вектор скорости всегда совпадает с траекторией и поэтому вектор изменения скорости тоже совпадает с траекторией.
Из курса физики известно, что ускорение представляет собой изменение скорости в единицу времени. Если за небольшой промежуток времени Δt скорость точки изменилась на Δv, то среднее ускорение за данный промежуток времени составило: аср = Δv/Δt.
Среднее ускорение не дает представление об истинной величине изменения скорости в каждый момент времени. При этом очевидно, что чем меньше рассматриваемый промежуток времени, во время которого произошло изменение скорости, тем ближе значение ускорения будет к истинному (мгновенному). Отсюда определение: истинное (мгновенное) ускорение есть предел, к которому стремится среднее ускорение при Δt, стремящемся к нулю:
а = lim аср при t→0 или lim Δv/Δt = dv/dt.
Учитывая, что v = ds/dt, получим: а = dv/dt = d2s/dt2.
Истинное ускорение в прямолинейном движении равно первой производной скорости или второй производной координаты (расстояния от начала отсчета перемещения) по времени. Единица ускорения - метр, деленный на секунду в квадрате (м/с2).
Траектория — линия в пространстве, вдоль которой движется материальная точка.Путь — это длина траектории. Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t. Путь – скалярная величина.
Расстояние определяет положение точки на ее траектории и отсчитывается от некоторого начала отсчета. Расстояние является алгебраической величиной, так как в зависимости от положения точки относительно начала отсчета и от принятого направления оси расстояний оно может быть и положительным, и отрицательным. В отличие от расстояния путь, пройденный точкой, всегда определяется положительным числом. Путь совпадает с абсолютным значением расстояния только в том случае, когда движение точки начинается от начала отсчета и совершается по траектории в одном направлении.
В общем случае движения точки путь равен сумме абсолютных значений пройденных точкой расстояний за данный промежуток времени:
3. Какими способами может быть задан закон движения точки?
1.Естественный способ задания движения точки.
При естественном способе задания движения предполагается определение параметров движения точки в подвижной системе отсчета, начало которой совпадает с движущейся точкой, а осями служат касательная, нормаль и бинормаль к траектории движения точки в каждом ее положении. Чтобы задать закон движения точки естественным способом необходимо:
1) знать траекторию движения;
2) установить начало отсчета на этой кривой;
3) установить положительное направление движения;
4) дать закон движения точки по этой кривой, т.е. выразить расстояние от начала отсчета до положения точки на кривой в данный момент времени ∪OM=S(t) .
2.Векторный способ задания движения точки
В этом случае положение точки на плоскости или в пространстве определяется вектором-функцией. Этот вектор откладывается от неподвижной точки, выбранной за начало отсчета, его конец определяет положение движущейся точки.
3.Координатный способ задания движения точки
В выбранной системе координат задаются координаты движущейся точки как функции от времени. В прямоугольной декартовой системе координат это будут уравнения:
4. Как направлен вектор истинной скорости точки при криволинейном движении?
При неравномерном движении точки модуль ее скорости с течением времени меняется. Представим себе точку, движение которой задано естественным способом уравнением s = f(t).
Если за небольшой промежуток времени Δt точка прошла путь Δs, то ее средняя скорость равна:
vср = Δs/Δt.
Средняя скорость не дает представления об истинной скорости в каждый данный момент времени (истинную скорость иначе называют мгновенной). Очевидно, что чем меньше промежуток времени, за который определяется средняя скорость, тем ближе ее значение будет к мгновенной скорости.
Истинная (мгновенная) скорость есть предел, к которому стремится средняя скорость при Δt, стремящемся к нулю:
v = lim vср при t→0 или v = lim (Δs/Δt) = ds/dt.
Таким образом, числовое значение истинной скорости равно v = ds/dt. Истинная (мгновенная) скорость при любом движении точки равна первой производной координаты (т. е. расстояния от начала отсчета перемещения) по времени.
При Δt стремящемся к нулю, Δs тоже стремится к нулю, и, как мы уже выяснили, вектор скорости будет направлен по касательной (т. е. совпадает с вектором истинной скорости v). Из этого следует, что предел вектора условной скорости vп, равный пределу отношения вектора перемещения точки к бесконечно малому промежутку времени, равен вектору истинной скорости точки.
5. Как направлены касательное и нормальное ускорения точки?
Направление вектора ускорения совпадает с направлением изменения скорости Δ 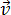 =
= 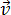 -
- 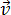 0
0
Касательное ускорение в данной точке направлено по касательной к траектории движения точки; если движение ускоренное, то направление вектора касательного ускорения совпадает с направлением вектора скорости; если движение замедленное – то направление вектора касательного ускорения противоположно направлению вектора скорости.
6. Какое движение совершает точка, если касательное ускорение равно нулю, а нормальное не изменяется с течением времени?
Равномерное криволинейное движение характеризуется тем, что численное значение скорости постоянно (v = const), скорость меняется лишь по направлению. В этом случае касательное ускорение равно нулю, так как v = const (рис.б),
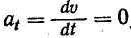
а нормальное ускорение не равно нулю, так как r — конечная величина.
7. Как выглядят кинематические графики при равномерном и равнопеременном движении?
При равномерном движении тело за любые равные промежутки времени проходит равные пути. Для кинематического описания равномерного прямолинейного движения координатную ось OX удобно расположить по линии движения. Положение тела при равномерном движении определяется заданием одной координаты x. Вектор перемещения и вектор скорости всегда направлены параллельно координатной оси OX. Поэтому перемещение и скорость при прямолинейном движении можно спроецировать на ось OX и рассматривать их проекции как алгебраические величины.
При равномерном движении путь изменяется, согласно линейной зависимости 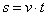 . В координатах
. В координатах 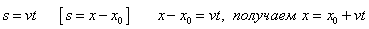 . Графиком является наклонная линия.
. Графиком является наклонная линия.

В результате изучения темы студент должен:
иметь представлениео пространстве, времени, траектории; средней и истиной скорости;
знатьспособы задания движения точки; параметры движения точки по заданной траектории.
Читайте также:
- D-технология построения чертежа. Типовые объемные тела: призма, цилиндр, конус, сфера, тор, клин. Построение тел выдавливанием и вращением. Разрезы, сечения.
- I. ПОЧЕМУ СИСТЕМА МАКАРЕНКО НЕ РЕАЛИЗУЕТСЯ
- I. Теоретические основы использования палочек Кюизенера как средство математического развития дошкольников.
- II. Система обязательств позднейшего права
- II. Соотношение — вначале самопроизвольное, затем систематическое — между положительным мышлением и всеобщим здравым смыслом
- II.2.6. Методы математической статистики
- IV. Тематика и перечень курсовых работ и рефератов.
- IV. Фитнес-центры в Санкт-петербурге
- IX. СТРОИТЕЛЬСТВО, БОДИБИЛДИНГ ТЕЛА, ХАРАКТЕРА, УМА, ПАМЯТИ.
- MS Word. Работа с математическими формулами
- VI. ОБСЛЕДОВАНИЕ БОЛЬНОГО ПО ОРГАНАМ И СИСТЕМАМ
- VI. СЕКСУАЛЬНАЯ ЭНЕРГИЯ. ЦЕНТРЫ НАСЫЩЕНИЯ. ЧТО ЖЕ ЭТО ТАКОЕ, «СЕКСУАЛЬНАЯ РЕВОЛЮЦИЯ»
lektsia.com
Как определить центр тяжести
Еще в школе на уроках физики мы впервые знакомимся с таким понятием, как центр тяжести. Задача не из легких, но хорошо объяснима и понятна. Не только юному физику понадобится знать определение центра тяжести. И если вы столкнулись с данной задачей, стоит прибегнуть к подсказкам и напоминаниям, дабы обновить свою память.Инструкция
- Проштудировав учебники физики, механики, словари или энциклопедии, вы наткнетесь на определение центра тяжести или как по другому называют центр масс.В разных науках немного разные определения, но суть, фактически, не теряется. Центр тяжести всегда находится в центре симметрии тела. Для более наглядного понятия «центр тяжести (или по другому называют центр масс) - это точка, что неизменно связанна с твердым телом. Через неё проходит равнодействующая сил тяжести, действующие на частицу данного тела при любом его положение».
- Если центр тяжести твердого тела - это точка, значит она должна иметь свои координаты.Для определения важно знать координаты по x, y, z, i-той части тела и вес, обозначающийся буквой - p.
- Рассмотрим пример задачи.Даны два тела различных масс m1 и m2,на которые действуют разные весовые силы (как изображено на рисунке). Записав формулы веса:P1= m1*g, Р2= m2*g;Центр тяжести находится между двумя массами. И если все тело подвесить в т.О, наступит значение равновесие, то есть эти предметы перестанут перевешивать друг друга.
- Разнообразные геометрические фигуры имеют физические и математические расчеты по поводу центра тяжести. К каждому свой подход и свой метод.Рассматривая диск, уточняем, что центр тяжести находится внутри него, точнее в точке пересечения диаметров (как показано на рисунке в т.С - точка пересечение диаметров). Таким же способом находят центры параллелепипеда или однородного шара.
- Представленный диск и два тела с массами m1 и m2 - однородной массы и правильной формы. Здесь можно отметить, что искомый нами центр тяжести находится внутри этих предметов. Однако, в телах с неоднородной массой и неправильной формы центр может находится за пределами предмета. Чувствуете сами, что задача уже становится сложнее.
completerepair.ru
423800, Набережные Челны , база Партнер Плюс, тел. 8 800 100-58-94 (звонок бесплатный)












