|
||||
|
|
звонок бесплатный
Наши сотрудники:
[email protected]
Екатерина - специалист по продаже а/м КАМАЗ
 [email protected]
[email protected]






Техника в наличии

Тягач КАМАЗ 44108-6030-24
2014г, 6х6, Евро3, дв.КАМАЗ 300 л.с., КПП ZF9, бак 210л+350л, МКБ,МОБ,рестайлинг.
цена 2 220 000 руб.,

КАМАЗ 4308-6063-28(R4)
4х2,дв. Cummins ISB6.7e4 245л.с. (Е-4),КПП ZF6S1000, V кузова=39,7куб.м., спальное место, бак 210л, шк-пет,МКБ, ТНВД BOSCH, система нейтрализ. ОГ(AdBlue), тент, каркас, рестайлинг, внутр. размеры платформы 6112х2470х730 мм
цена 1 950 000 руб.,

Самосвал КАМАЗ 6520-057
2014г, 6х4,Евро3, дв.КАМАЗ 320 л.с., КПП ZF16, ТНВД ЯЗДА, бак 350л, г/п 20 тонн, V кузова =20 куб.м.,МКБ,МОБ, со спальным местом.
цена 2 700 000 руб.,

Самосвал 6522-027
2014, 6х6, дв.КАМАЗ 740.51,320 л.с., КПП ZF16,бак 350л, г/п 19 тонн,V кузова 12куб.м.,МКБ,МОБ,задняя разгрузка,обогрев платформы.
цена 3 190 000 руб.,
СУПЕР ЦЕНА
на АВТОМОБИЛИ КАМАЗ
| 43118-010-10 (дв.740.30-260 л.с.) | 2 220 000 |
| 43118-6033-24 (дв.740.55-300 л.с.) | 2 300 000 |
| 65117-029 (дв.740.30-260 л.с.) | 2 200 000 |
| 65117-6010-62 (дв.740.62-280 л.с.) | 2 350 000 |
| 44108 (дв.740.30-260 л.с.) | 2 160 000 |
| 44108-6030-24 (дв.740.55,рест.) | 2 200 000 |
| 65116-010-62 (дв.740.62-280 л.с.) | 1 880 000 |
| 6460 (дв.740.50-360 л.с.) | 2 180 000 |
| 45143-011-15 (дв.740.13-260л.с) | 2 180 000 |
| 65115 (дв.740.62-280 л.с.,рест.) | 2 190 000 |
| 65115 (дв.740.62-280 л.с.,3-х стор) | 2 295 000 |
| 6520 (дв.740.51-320 л.с.) | 2 610 000 |
| 6520 (дв.740.51-320 л.с.,сп.место) | 2 700 000 |
| 6522-027 (дв.740.51-320 л.с.,6х6) | 3 190 000 |

подробнее про услугу перегона можно прочесть здесь.

|
Нужны самосвалы? Обратите внимание на Ford-65513-02. |
КАМАЗы в лизинг
ООО «Старт Импэкс» имеет возможность поставки грузовой автотехники КАМАЗ, а так же спецтехники на шасси КАМАЗ в лизинг. Продажа грузовой техники по лизинговым схемам имеет определенные выгоды для покупателя грузовика. Рассрочка платежа, а так же то обстоятельство, что грузовики до полной выплаты лизинговых платежей находятся на балансе лизингодателя, и соответственно покупатель автомобиля не платит налогов на имущество. Мы готовы предложить любые модели бортовых автомобилей, тягачей и самосвалов по самым выгодным лизинговым схемам.Контактная информация.
г. Набережные Челны, Промкомзона-2, Автодорога №3, база «Партнер плюс».
тел/факс (8552) 388373.
Схема проезда
Описание схемы железобетонного моста. Схема моста
4.4 Конструктивная схема моста
Длина моста составит:
Lм = Вм +2·(⋅ m=55,9+2·1,5·(7,7-5,15)=65,25м
Значит, принимаем схему моста18+21+18, что в сумме составляет 57 метров.
Опору выбираем массивную, так как разница между проектной отметкой моста и отметкой дна русла составило 7,38 м
4.5 Расчет глубины заложения фундамента опор!!!!!
Отметку заложения подошвы фундамента опор определяем по формуле
м, где
hрм.мах – глубина потока с учётом общего размыва,
Δhм – глубина воронки местного размыва,
,
Δε – гарантийный запас на неточность определения элементов размытого русла,
Δhк – конструктивная глубина заделки фундамента в грунт.
Расчёт глубины воронки местного размыва
Глубина воронки размыва вычисляется по формуле И.А. Ярославцева.
В случае несвязных грунтов (песок среднезернистый)–
м
где
k – коэффициент, зависящий от относительной глубины потока;
kф – коэффициент, учитывающий форму опоры;
Bо – средняя ширина опоры, м;
g – ускорение свободного падения;
d – диаметр частиц несвязных грунтов, м;
Скорость набегания потока на опору принимается равной vрм в главном русле, vлпм или vппм – в пойменных частях отверстия.
Гарантийный запас Δ складывается из погрешности определения элементов размытого русла Δε и конструктивной глубины заделки фундамента в грунт Δhк. Считается, что
.
Для фундамента мелкого заложения Δhк должна быть не менее 1м. В соответствии со СНиП 2.02.01–83* «Основания зданий и сооружений», фундаменты должны быть заглублены не менее чем на 2,5 м от наинизшей отметки дна водотока в месте расположения опоры после его общего и местного размыва расчетным паводком. Данные требования могут быть выражены условием
Δ=max(2,5; Δε+Δhк)=0,29+1,0=1,29, принимаем Δ=2,5м
Проектирование регуляционных сооружений
Струенаправляющие дамбы нам не нужны, так как расход воды на левой и правой пойме не превышает 15% от расчетного максимального расхода.
4.7 Определение минимальных отметок подходных насыпей
Назначение минимальной отметки проезда по мосту связано с определением необходимого возвышения низа пролетных строений моста над уровнем воды. Для мостов через несудоходные реки минимальная отметка проезда находится по формуле
Нм min=РУВВ+Гн+hконстр=156,95+1,0+1,23=159,18 м ,
где Гн – подмостовой габарит, равный 0,5 м, при наличии на реке заторов льда – 0,75 м, при карчеходе – 1 м; hконстр – конструктивная высота пролетного строения.
Минимальная отметка проезда является контрольной точкой, ограничивающей положение проектной линии продольного профиля снизу.
Бровка пойменных насыпей должна возвышаться над уровнем воды так, чтобы он не достигал отметки низа дорожной одежды. В силу этого минимальная отметка бровки насыпи на подходах к мосту определяется по формуле
Н н min=РУВВ+ΔZн+hнаб+Δ =156,95+0,26+0,74+0,5=158,45
где ΔZн – подпор воды у насыпи; hнаб – высота подъема набегающей волны; Δ - толщина дорожной одежды, принимаемая равной 0,5 м.
Сужение живого сечения потока, вызванное строительством мостового перехода, приводит к образованию подпора воды перед ним. Подпор воды у подходной насыпи можно определить по эмпирической формуле
где Вр – ширина разлива реки при РУВВ; Lм – ширина мостового отверстия; i – бытовой уклон реки; β – степень стеснения потока мостом; – относительная длина верховых струенаправляющих дамб;lв – длина верховых струенаправляющих дамб; θ - количество пойм; k и kр – поправочные коэффициенты, определяемые по формулам
;
где ρ – коэффициент размыва.
Высота подъема набегающей волны hнаб вычисляется по зависимости
,
где kw – коэффициент, характеризующий шероховатость откоса; m – коэффициент заложения откосов пойменной насыпи на подтопляемых участках, m = 2; hп – средняя глубина потока на пойме при РУВВ.
studfiles.net
Схема балочного железобетонного моста
Основные части и некоторые особенности балочных железобетонных мостов рассмотрим на примере небольшого моста под железную дорогу (рис. 6.1). Нагрузка от веса подвижного состава передается шпалами мостового полотна через балласт на пролетные строения (1). Пролетные строения, работая на изгиб, передают нагрузку в виде опорных давлений через опорные части (2) на опоры и далее на грунт основания. Мост имеет промежуточную опору, или бык, (4) и концевые опоры, или устои, (3). Устои, кроме передачи давлений от пролетных строений на грунт, сопрягают мост с насыпями подходов.
Пролетное строение расчленено на два монтажных блока (10) и (15), соединенных с помощью диафрагм (12). Половины каждой диафрагмы входят в состав разных блоков и после установки блоков на опоры объединяются монтажными швами.
Каждый блок представляет собой балку таврового сечения, имеющего плиту (16), ребро, состоящее из стенки (14) и нижнего пояса (13), а также внутренние (11) и наружные (7) бортики и тротуары (6). Наружные бортики поддерживают балласт (17). Продолжением их служат плиты тротуаров, заканчивающиеся выступом вниз для прикрепления перил (5). В бортиках предусмотрены углубления для заводки гидроизоляции.
Гидроизоляция (9) исключает просачивание воды в бетон, которое может привести к быстрому снижению его прочности. Гидроизоляция состоит из цементной подготовки, с уклонами к трубкам (8), водонепроницаемого эластичного слоя, наклеиваемого на подготовку, и защитного слоя из цементного раствора, армированного стальной сеткой, назначение которого – предохранение изолирующего слоя от повреждений.

Рис. 6.1 – Схема балочного моста
Основные размеры, характеризующие конструкцию моста: полная длина моста L, расчетные пролеты пролетных строений l, полная длина пролетных строений lп, отверстие моста l01 + l02, высота сечения – h и строительная высота hc пролетного строения. Положение конструкции по высоте отражается отметками уровня меженных вод (УМВ), уровня высоких вод (УВВ), подошвы рельса (ПР) или для мостов под автомобильную дорогу уровня проезда (УП), подошв фундаментов опор (ПФ).
На практике применяют конструкции различных типов, однако основные части моста при всем многообразии их форм остаются по своему назначению теми же. Формы отдельных элементов сооружения зависят от местных условий, нагрузки, длины пролетов, условий изготовления и монтажа.
Основные задачи, которые приходится решать при проектировании железобетонного балочного пролетного строения после выбора системы (простая балка) и длины пролета:
- назначение типа поперечного сечения пролетного строения, а также способа его членения на монтажные элементы;
- установление способа соединения монтажных блоков между собой, в частности необходимости применения поперечных диафрагм;
- назначение первоначальных размеров поперечных сечений и частей конструкции, уточняемых затем в процессе расчета;
- рассмотрение одного из вариантов армирования главных балок с определением типа рабочей арматуры, схемы ее расположения в бетоне, а также целесообразности предварительного напряжения;
- выбор типа деталей конструкции (тротуаров, опорных частей, перил, гидроизоляции и водоотвода, деформационных швов).
Эти задачи должны решаться во взаимосвязи и с учетом условий изготовления монтажных блоков, их перевозки, установки и соединения, а также с учетом эксплуатационных качеств пролетных строений. Следует обеспечивать наименьшие стоимость, трудоемкость изготовления и монтажа и наибольшую долговечность конструкции. Ниже анализируется накопленный опыт и приводятся рекомендации по решению указанных задач при проектировании новых пролетных строений.
vse-lekcii.ru
Мостовые схемы постоянного тока
Мостовые схемы постоянного тока
Никакую книгу по электрическим измерениям нельзя было бы назвать полной без раздела о мостовых схемах. Эти гениальные схемы используют индикатор баланса для сравнения двух напряжений, точно так же как и лабораторные весы сравнивают две массы и указывают на то, что они равны. В отличие от "потенциометрических" схем, используемых для простого измерения неизвестного напряжения, мостовые схемы могут использоваться для измерения всех видов электрических величин, в том числе и сопротивлений.
Стандартная мостовая схема, часто называемая мостом Уитстона (Wheatstone bridge), изображена на рисунке 1.
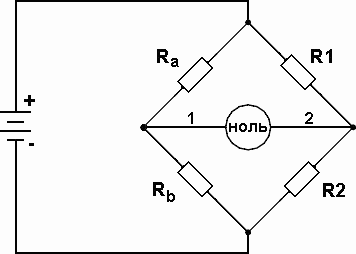
Рис. 1.
Когда напряжение между точкой 1 и минусом батареи равно напряжению между точкой 2 и отрицательным выводом батареи, то индикатор баланса будет показывать ноль, и про такой мост говорят что он "сбалансирован". Состояние баланса моста полностью зависит от отношений Ra/Rb и R1/R2, и оно не зависит от напряжения питания. Для измерения сопротивлений с помощью моста Уитстона на место резисторов Ra или Rb устанавливается неизвестное сопротивление, в то время как остальные три резистора являются прецизионными и их номинал известен. Каждый из этих трёх резисторов может быть заменён сопротивлением другой величины или их номиналы могут быть скорректированы, что бы мост сбалансировался, и когда это произойдёт то величина сопротивления неизвестного резистора может быть определена из соотношения величин известных сопротивлений.
Для этого необходимо, что бы измерительная система имела набор переменных резисторов с точно известными значениями, которые могут служить эталонными стандартами. Например, если мост настроен на измерение сопротивления Rx (рисунок 2), то мы должны знать точное значение остальных трёх сопротивлений при сбалансированном мосте, что бы определить величину сопротивления Rx:
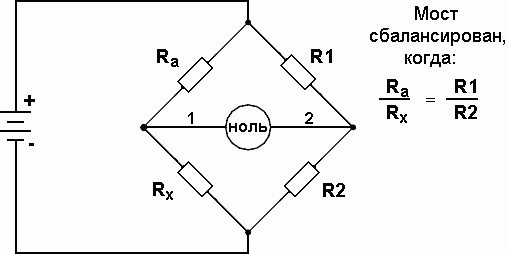
Рис. 2.
Каждое из четырёх сопротивлений в мостовой схеме называют плечом. Резистор, последовательно соединённый с неизвестным сопротивлением, Rx обычно называют реостатом моста (это будет сопротивление Ra на рисунке 2), а другие два сопротивления называют плечами отношений моста.
Точные и стабильные образцовые сопротивления к счастью, не сложно изготовить. В действительности они были одними из первых электрических "Стандартных" устройств, изготовленных в научных целях. На рисунке 3 приведена фотография старинного блока стандартных сопротивлений:

Рис. 3. Магазин образцовых сопротивлений
Стандарт сопротивлений, изображённый на рисунке 3, является переменным с дискретным шагом изменения сопротивления: величина сопротивления между клеммами может изменяться в зависимости от количества и положения медных вставок, вставленных в разъёмы.
Мосты Уитстона считаются превосходным средством измерения сопротивления среди схем различных омметров. Но в отличие от всех этих схем, являющихся нелинейными (и имеющих нелинейные шкалы), и связанные с этим погрешности измерений, мостовая схема является линейной (математика описания её работы основана на простых отношениях и пропорциях) и довольно точной.
Имея стандартные сопротивления достаточной точности и нуль-детектор с необходимой чувствительностью, достижимая точность измерения сопротивления может быть не хуже +-0,05% при использовании моста Уитстона. Это метод измерения сопротивления предпочитают использовать в калибровочных лабораториях из-за его высокой точности.
Существует много вариаций основной схемы моста Уитстона. Большинство мостов постоянного тока используются для измерения сопротивления, в то время как мосты переменного тока могут быть использованы для измерения различных электрических величин, таких как индуктивность, ёмкость и частота.
Интересным вариантом моста Уитстона является двойной мост Кельвина, используемый для измерения очень малых сопротивлений (обычно менее 1/10 Ома), его схема изображена на рисунке 4:

Рис. 4. Двойной мост Кельвина.Ra и Rx являются низкоомными сопротивлениями.
Низкоомные резисторы на рисунке изображены толстой линией, так же как и проводники, соединяющие их с источником напряжения, обеспечивающим сильный ток. Принцип работы этого измерительного моста причудливой конфигурации, пожалуй, лучше всего понять, если начать объяснение принципа его работы со стандартного моста Уитстона, настроенного для измерения низкого сопротивления, этот мост развивался шаг за шагом до его нынешнего состояния в попытке преодолеть некоторые проблемы, возникшие в мосте Уитстона стандартной конфигурации.
Если бы мы использовали стандартный мост Уитстона для измерения небольших сопротивлений, то его схема бы выглядела примерно так (рисунок 5):

Рис. 5.
Когда нуль-детектор указывает нулевое напряжение, мы знаем, что мост сбалансирован и что соотношение Ra/Rx и RM/RN математически равны друг другу. Зная значения Ra, RM, and RN поэтому мы имеем все необходимые данные, чтобы найти величину Rx. Почти.
Имеется проблема в том, что соединения и соединительные провода между Ra и Rx обладают неким сопротивлением, и эти паразитные сопротивления могут быть существенными по сравнению с низким сопротивлением Ra и Rx. Эти паразитные сопротивления понизят реальное напряжение, учитывая большой ток, протекающий через них, и таким образом будут влиять на показания детектора нуля и на баланс моста (Рисунок 6):

Рис. 6.Паразитное напряжение Eпров. ухудшает точность измерения Rx.
Так как мы не хотим измерять сопротивление этих паразитных проводников и сопротивление соединений, а нас интересует только измерение сопротивления Rx, то надо найти такой способ включения нуль-детектора, что бы на его показания не влияли падения напряжений, протекающего через эти сопротивления. Если мы присоединим нуль-детектор и плечи отношений RM/RN напрямую к выводам Ra и Rx, то это приведёт нас к такой реализации измерительного моста (Рисунок 7):

Рис. 7.Теперь только два паразитных падения напряжения Eпров. являются частями цепи нуль-детектора.
Теперь два крайних падения напряжения Eпров. не оказывают воздействия на нуль-детектор и не влияют на точность измерений сопротивления Rx. Но два оставшихся падения напряжений Eпров. являются проблемой, так как проводник, соединяющий нижний по схеме вывод Ra и верхний по схеме вывод Rx теперь шунтирует оба падения напряжения и по нему будет течь существенный ток, который создаст на этом проводнике своё падение напряжения.
Зная, что левая часть нуль-детектора должна быть подключена к двум крайним выводам сопротивлений Ra и Rx, что бы не вносить ошибки, связанные с паразитными падениями напряжения Eпров. в цепи нуль-детектора, и что любой прямой провод, соединяющий выводы этих сопротивлений Ra и Rx будет сам нести значительный ток и создавать ещё большее паразитное падение напряжения, то единственным способом преодолеть эту проблему является создание соединения, имеющее существенное сопротивление, между нижнем по схеме выводом Ra и верхнем по схеме выводом Rx (Рисунок 8):

Рис. 8.
Справится с паразитными падениями напряжений между выводами сопротивлений Ra Rx можно путём изменения сопротивления двух новых резисторов таким образом, что бы отношение их величин было бы таким же, как и отношение величин сопротивлений в плече отношений, находящихся по схеме с правой стороны от нуль-детектора. Вот почему эти резисторы были помечены Rm и Rn в оригинальной схеме двойного моста Кельвина: для обозначения их соразмерности с сопротивлениями RM и RN (Рисунок 9):

Рис. 9. Двойной мост КельвинаRa и Rx являются низкоомными сопротивлениями.
При отношении Rm/Rn равном отношению RM/RN, резистор в плече реостата Ra регулируется до тех пор, пока нуль-индикатор не покажет, что мост сбалансирован, и тогда можно будет сказать, что отношение Ra/Rx равно отношению RM/RN, или просто найти Rx из следующего уравнения:

Полное уравнение баланса двойного моста Кельвина выглядит следующим образом (Rпров. - это сопротивление толстых соединительных проводов между низкоомным образцовым сопротивлением Ra и испытуемым сопротивлением Rx):

До тех пор пока соотношение между RM и RN равно отношению между Rm и Rn, уравнение баланса будет не сложнее чем у обычного моста Уитстона, при Rx/Ra равном RN/RM, так как последнее выражение в уравнении будет равно нулю, так что будет отсутствовать влияние всех сопротивлений, кроме Rx, Ra, RM, и RN.
Во многих двойных мостовых схемах Кельвина RM=Rm и RN=Rn. Однако чем меньше значения сопротивлений Rm и Rn, тем более чувствительным должен быть нуль-детектор, потому что там будет меньше последовательное сопротивление. Увеличение чувствительности детектора является полезным, так как оно позволит обнаруживать слабые дисбалансы, и таким образом мост можно будет сбалансировать с большой точностью. Таким образом некоторые высокоточные двойные мосты Кельвина используют сопротивления Rm и Rn со значениями в 100 раз меньше, чем значения сопротивлений RM и RN в другом плече. К сожалению, однако, чем ниже значения сопротивлений Rm и Rn, тем больший ток по ним будет течь, что увеличит влияние любого сопротивления в точке подключения Rm и Rn к Ra и Rx. Как вы можете видеть, высокая точность инструмента требует, чтобы учитывались все ошибки различных факторов, и часто лучшее, что может быть достигнуто является компромиссом минимизации двух или более различных видов ошибок.
- ИТОГ:
- Мостовые схемы используют чувствительный индикатор нуля для сравнения двух напряжений на их равенство.
- Мост Уитстона (Wheatstone bridge) может быть использован для измерения сопротивлений путём сравнения сопротивления неизвестного номинала и образцового сопротивления с известной величиной, так же как с помощью лабораторных весов измеряют неизвестный вес путём сравнения его со стандартными грузами.
- Двойной мост Кельвина является вариантом моста Уитстона для измерения очень малых сопротивлений. Его усложнение по сравнению с базовой схемой моста Уитстона является необходимым для избежания ошибок, вносимых паразитными сопротивлениями на пути тока между низкоомным образцовым сопротивлением и сопротивлением, величина которого измеряется.
BACK
zpostbox.ru
Описание схемы железобетонного моста
Комплекс сооружений, возводимых при пересечении дорогой реки, называют мостовым переходом. В его состав входят мост, подходы к нему, регуляционные сооружения и берегоукрепительные устройства.
Зная указанные в задании класс реки, поперечный профиль русла и требуемое отверстие моста, проектируем схему мостового перехода. Схема мостового перехода представлена в приложении А.
Мосты состоят из пролетных строений и опор. Проектируемый мост состоит из шести пролетов: два пролета по 15 м (1,6), три по 24 м (2,3,5) и один пролет длиной 33 м (4), перекрывающий судоходный переход (т.к. река по заданию является судоходной). При таком составе пролетов обеспечивается требуемое отверстие моста, равное 110 м, а также соблюдается размер подмостового судоходного габарита (30х7 м) (см. приложение А). Схема моста 15+24+24+33+24+15.
Определяем основные отметки для составления схемы моста.
Отметка низа пролетного строения
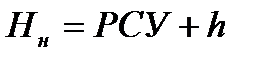 ,
,
где 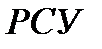 - отметка расчетного судоходного уровня;
- отметка расчетного судоходного уровня;
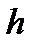 - высота подмостового габарита.
- высота подмостового габарита.
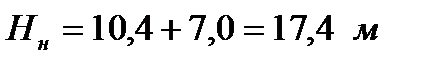 .
.
Отметка проезжей части моста
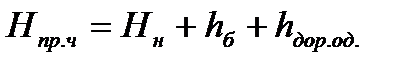 ,
где ,
где 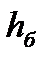 - высота балки пролетного строения; - высота балки пролетного строения;
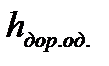 - толщина дорожной одежды. - толщина дорожной одежды.
|
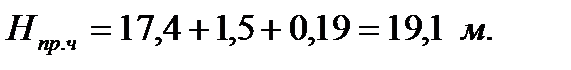
После выбора величины и размещения судоходного пролета проектируем остальные пролеты, которыми перекрываем оставшуюся часть заданного отверстия моста.
При этом следует помнить, что с точки зрения архитектуры длины пролетов средней части моста должны быть больше береговых. Число пролетов должно быть таким, чтобы получить требуемое отверстие моста. При составлении схемы моста рекомендуется использовать не более трех типов пролетных строений.
Важное место при проектировании моста отводится правильному выбору конструкций опор. В конструкции промежуточной опоры обычно различают следующие части: подферменную плиту или оголовок, тело опоры и фундамент. На подферменную плиту непосредственно передается опорное давление от пролетного строения. Определим параметры опор, необходимые для составления схемы моста:
Отметку низа опоры для промежуточных опор в русле реки при применении свайных фундаментах в виде низкого ростверка назначаем на 0,5 м ниже уровня меженных вод
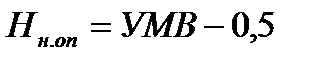
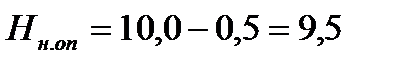 м.
м.
1) отметку верха опоры принимаем
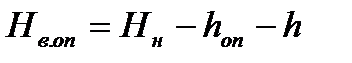
где 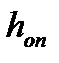 - высота опорной части:
- высота опорной части:
h – превышение краев пролета за счет поперечного уклона.
 м.
м.
В качестве промежуточных опор применяем массивные сборно-монолитные опоры, так как наблюдается наличие значительных ледоходов. Береговые устои применяем обсыпного типа, так как насыпь более 8 м. При обсыпных устоях откос конуса выступает за переднюю стенку устоя, поэтому подвергается непосредственному воздействию течения воды, что предъявляет повышенные требования к конструкции его укрепления.
Пролетные строения моста включают следующие основные части: главные несущие конструкции, проезжую часть с ездовым полотном, системы связи и опорные части.
В соответствии с заданием габарит моста – Г11,5, ездовое полотно состоит из двух полос движения: ширина проезжей части – 7,5 м, с полосами безопасности шириной – 1,5 м. Ширина моста, включающая в себя габарит проезжей части, тротуары и ограждения, равна:
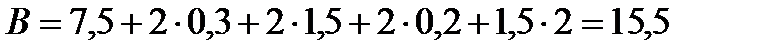 м.
м.
Ширина тротуара, согласно заданию, 1,5 м. С наружной стороны тротуары ограждаются перилами 1,2 м, а с внутренней стороны жестким барьерным ограждением высотой 0,75 м.
Для обеспечения быстрого отвода воды поверхностям ездового полотна и тротуарам придаем продольный уклон 10 ‰ и поперечные уклоны 20 ‰. Необходимость обеспечить плавность перехода от насыпи к мосту достигается путем создания в местах сопряжения моста с насыпью специальных переходных участков в виде переходных плит.
Несущие элементы проезжей части – железобетонные плиты проезжей части (принимаем толщиной 18 см) воспринимают нагрузку от транспортных средств с ездового полотна, от пешеходов с тротуаров и передают их на основные несущие конструкции пролетного строения.Несущая частьпролетного строения воспринимает действие веса пролетного строения и временной подвижной нагрузки и передает его на опоры.
Для определения количества балок делим ширину моста на расстояние между осями балок:
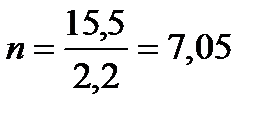 принимаем 7 балок.
принимаем 7 балок.
Опорные части– это элементы, с помощью которых реакции от несущей конструкции передаются на опоры в заданном месте. Опоры моста воспринимают нагрузки и передают их на грунт через фундаменты.
Конструкция дорожной одежды представлена на рис. 2.1.
infopedia.su
схема, принцип действия и т.д.
Мост Уитстона — это одна из наиболее часто используемых мостовых схем в контрольно-измерительных приборах.
Схема моста Уитстона часто используется в системах измерения температуры. В этих системах устройство, называемое термометр сопротивления или терморезистор, обычно помещается в одной из ветвей схемы мостика.
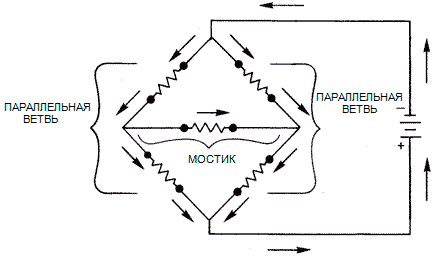 Принципиальная схема мостика УитстонаОбратите внимание на основы электричества и на приборы электроники.
Принципиальная схема мостика УитстонаОбратите внимание на основы электричества и на приборы электроники. Величина тока в мосте Уитстона определяется величиной разности сопротивлений: чем больше разность, тем больше будет течь ток; а если разность сопротивлений меняется, количество протекающего тока будет тоже меняться. Именно это свойство делает схему мосте Уитстона очень полезной в контрольно-измерительных устройствах и системах управления. Точные измерения переменных величин процессов достигаются тем, что переменные параметры процессов изменяют сопротивление в схеме мостика. Даже очень малые изменения величины сопротивления могут быть обнаружены при измерении тока, протекающего через мостик.
Принцип работы моста Уитстона
Схема моста Уитстона имеет два плеча сопротивления, каждое из которых содержит два резистора. Третья ветвь схемы — это соединение между двумя параллельными ветвями. Эта третья ветвь называется мостиком. Ток течет от отрицательной клеммы батарейки к верхней точке мостовой схемы. Затем, ток делится между двумя параллельными ветвями, причем количество тока, протекающее по каждой из ветвей, зависит от величины сопротивления в ветви. Наконец, ток возвращается к положительной клемме батарейки.
При равных величинах сопротивлений равное количество тока течет в каждой из ветвей. По мостику ток не течет, на что указывает нулевое положение измерителя. При этом условии о мостике говорят, что он уравновешен.
 Уравновешенная схема мостика Уитстона
Уравновешенная схема мостика УитстонаПри неравных величинах сопротивления в ветвях, ток течет в схеме от ветви с большим сопротивлением к ветви с меньшим сопротивлением. Это будет верно, пока два верхних резистора фиксированы и равны по величине, как это имеет место в схемах мостика Уитстона, используемых в контрольно-измерительных системах. Измеритель на рисунке показывает, что ток в мостике течет слева направо.
 Неуравновешенная схема мостика Уитстона
Неуравновешенная схема мостика Уитстонаkipiavp.ru
Схемы железобетонных вантовых мостов
Вантовыми называют мосты, в которых основные элементы растянуты и образуют геометрически неизменяемую систему, в состав которой часто включают балку жесткости с расположенной на ней проезжей частью. Балку жесткости поддерживают растянутые наклонные элементы – ванты, прикрепленные к сжатым стойкам–пилонам.
Ванты можно изготовлять из стальных тросов, пучков или кабелей высокой прочности, поэтому вантовые мосты получаются легкими и экономичными. Расход железобетона на 1 м2 полезной площади при пролетах 100–300 м. существенно меньше, чем для других видов железобетонных мостов; дополнительные расходы на ванты относительно уменьшаются с увеличением пролета. Вантовая система может быть выполнена из сборного железобетона с использованием современных методов, монтажа и в общем имеет перспективу широкого применения.
С 1962 г. построено около 20 железобетонных вантовых мостов, в том числе шесть с пролетами более 200 м. Наибольший пролет (320 м) имеет мост Бротон во Франции. Вантовые мосты строили в основном под автомобильную дорогу, но имеются примеры и железнодорожных вантовых мостов.
Вантовые мосты (рис. 9.1) могут иметь балку жесткости (1), поддержанную наклонными вантами (2) и (4) с помощью пилонов (3). Особую роль играют крайние ванты (2), прикрепленные к балке жесткости над опорами. Они препятствуют горизонтальным перемещениям головы пилона при действии вертикальных нагрузок и придают всей системе жесткость. Усилия в этих вантах значительны; как правило, на крайних опорах появляются отрицательные опорные реакции, которые должны быть восприняты.
Благодаря передаче горизонтальных составляющих усилий в вантах на балку жесткости в ней на большей части длины, кроме изгибающих моментов, возникают и сжимающие усилия. Это весьма благоприятно для железобетонной балки жесткости: создается как бы предварительное напряжение бетона балки, что позволяет уменьшить количество арматуры и в ряде случаев исключить преднапряженную арматуру.
В двухпилонной схеме вантового моста (рис. 9.1, а, в, г) балка жесткости поддерживается вантами в большем числе точек, расположенных равномерно по длине. Углы наклона вантов, как правило, получаются более благоприятными, а система в целом – более экономичной. Однопилонная схема (рис. 9.1, б) может оказаться приемлемой лишь в особых местных условиях или по архитектурным соображениям, если она лучше вписывается в ансамбль зданий и сооружений города.

Рис. 9.1 – Схемы вантовых мостов
Ванты сходятся в одной точке на голове пилона (рис. 9.1, а, б) – система «пучок» или прикрепляются к пилону рассредоточение (см. рис. 9.1, в, г) – система «арфа». В первом случае пилон при наличии крайних вантов (2) почти не работает на изгиб от вертикальных нагрузок; кроме того, средние ванты имеют больший наклон к горизонту, что уменьшает действующие на них усилия. В системе «арфа» при ее одностороннем загружении пилон интенсивно работает на изгиб, однако узлы прикрепления вантов к пилону проще, а к балке жесткости однотипны, так как углы наклона всех вантов одинаковы.
Особенно упрощается конструкция вантов и их креплений в многовантовой системе (см. рис. 9.1, г). Кроме того, в этой системе нет мест приложения к балке жесткости значительных усилий и, следовательно, не возникает проблема борьбы с местными напряжениями в этих местах.
К недостаткам многовантовой системы можно отнести трудность регулирования усилий в вантах, а также не очень привлекательный внешний вид.
При выборе схемы вантового моста необходимо учитывать приведенные выше, а также следующие соображения. Опирание балки жесткости только на подвижные опорные части (см. рис. 9.1) имеет свои преимущества, так как при постановке одной неподвижной опорной части изменение температуры вызывает несимметричные искажения геометрической системы, что нежелательно. Однако продольные горизонтальные силы (торможение) передаются через ванты на верх пилонов, вызывая появление в пилонах значительных изгибающих моментов. Практика проектирования показывает, что в мостах под автодорогу эти силы могут быть восприняты без существенного развития поперечного сечения пилонов.
Крайние ванты закреплены на концах балки жесткости (см. рис. 9.1). Возможен вариант анкеровки крайних вантов и в опорах. Этот вариант предпочтительнее с точки зрения облегчения монтажа, так как верх пилона закреплен крайним вантом независимо от того, смонтирована ли балка жесткости. Горизонтальные составляющие усилий в вантах передают на опору с помощью специальных опорных частей, а в середине пролета устраивают разрыв балки жесткости (рис. 9.2, а) либо применяют измененную систему с соединением средних вантов в середине пролета (рис. 9.2, б). Работу железобетонной балки жесткости на растяжение допускать не следует. Для уменьшения панелей балки жесткости и сокращения веса монтажных элементов, по длине равных панели, применяют более сложные вантовые системы (рис. 9.2, в).

Рис. 9.2 – Вантовые системы с закреплением крайних вантов на устоях
Ванты на всех стадиях монтажа при любом положении временной нагрузки на мосту должны оставаться растянутыми, что обеспечивают выбором надлежащего соотношения между пролетами вантовой системы, правильной последовательности монтажа и при необходимости регулированием усилий в вантах. Необходимый запас против появления сжимающих усилий в вантах проверяют расчетом.
Большинство вантовых систем (см. рис. 9.1) имеет три пролета: главный и два боковых с закреплением крайних вантов в балке жесткости над крайними опорами. Узлы прикрепления крайних вантов к балке жесткости занимают значительную длину по фасаду. Если здесь балка жесткости опирается не на устои, а на промежуточные опоры, конструирование узла опирания балки жесткости вантовой системы и соседнего пролетного строения становится затруднительным. Для преодоления этих затруднений целесообразно включить в состав балки жесткости соседние пролеты, сделав ее неразрезной. При этом длину соседних пролетов подбирают так, чтобы в них можно было сохранить поперечное сечение балки жесткости, принятое по условиям ее работы в составе вантовой системы (рис. 9.3, а).

Рис. 9.3 – Схемы многопролетных вантовых мостов
Особенность систем с закреплением крайних вантов над опорой (см. рис. 9.1) – геометрическая неизменяемость даже при включении в балку шарниров в местах прикрепления вантов, что соответствует минимальной изгибной жесткости балки. Эти системы обладают поэтому большой жесткостью, а изгибающие моменты в балке сравнительно невелики.
При необходимости устройства в мосту двух смежных судоходных пролетов, поддерживаемых вантами (рис. 9.3, б), средний треугольник может поворачиваться относительно верха пилона. Неизменяемость системы обеспечивается только за счет изгибной жесткости балки, что приводит к появлению больших прогибов и изгибающих моментов в балке при несимметричном загружении временной нагрузкой, особенно в сечениях, где прикреплены крайние ванты треугольника. Поэтому такую систему можно рекомендовать лишь при сравнительно небольших пролетах.
Для улучшения работы системы можно закрепить балку жесткости на опоре от горизонтальных смещений, а поскольку при этом сильно возрастут изгибающие моменты в пилоне, сделать его жестким и А–образной формы. Такое решение принято в ряде крупнейших вантовых мостов за рубежом (рис. 9.3, в). Горизонтальные силы передают на опору с помощью наклонных подкосов. Пилон выполнен жестким, балка жесткости у середины пролета прерывается подвесной балкой.
При выборе схемы вантового моста важно правильно назначить ее размеры – расстояния между точками прикрепления вантов к балке жесткости, высоту пилона, и следовательно, углы наклона вантов к горизонту, а также соотношение жесткостей балки и вантов. Эти вопросы необходимо решать с учетом принятого способа монтажа пролетного строения.
Для стандартизации элементов конструкции, как правило, оказывается полезным разбить балку жесткости на равные панели или сделать среднюю панель несколько меньше остальных, чтобы избежать большой разницы в изгибающих моментах по длине балки. Изгибающие моменты в балке жесткости уменьшаются при сокращении расстояния между точками подвеса и при увеличении жесткости вантов.
На основании имеющегося опыта проектирования можно дать некоторые рекомендации по назначению основных размеров вантовых систем при пролетах до 200–250 м. Оптимальные соотношения размеров следует уточнять с помощью составления и сравнения вариантов. Расстояние между точками опирания балки на ванты и опоры желательно назначать не очень большим, как правило, не более 30–40 м, а в многовантовых системах – до 10–15 м. Наклон вантов к горизонту не должен быть меньше 1:3 (лучше до 1:2,5), так как при слишком пологих вантах усилия в них возрастают, жесткость системы уменьшается и узлы прикрепления вантов к балке усложняются.
Высоту сечения балки жесткости можно предварительно назначить на основании общих соображений о ее работе, высказанных выше. Рациональная высота находится в пределах 1/15–1/25d и 1/40–1/70L, где d – расстояние между точками опирания на ванты или опоры, L – длина наибольшего пролета системы, причем меньшие значения соответствуют большей длине панелей и пролетов. Иногда высоту принимают еще меньшей – до 1/100L. Назначая меньшие значения высоты сечения, можно несколько снизить изгибающие моменты в балке жесткости.
Для увеличения жесткости вантов и дальнейшего уменьшения изгибающих моментов в балке применяют жесткие железобетонные ванты с предварительным напряжением.
Способ монтажа существенно влияет на схему моста и еще более на конструктивные формы балки жесткости, поэтому основные характеристики должны быть установлены перед выбором системы.
В поперечном сечении ванты располагают в одной плоскости или в двух плоскостях. Пилон и ванты, находящиеся в одной плоскости (рис. 9.4, а), обычно размещают в пределах ширины разделительной полосы между проезжими частями обоих направлений движения. При загружении одной проезжей части временной нагрузкой в балке жесткости, кроме изгибающих, возникают крутящие моменты и одна сторона поперечного сечения балки перегружается. Для восприятия крутящих моментов и уменьшения перегрузки одной стороны балки необходимо применять коробчатое сечение, обладающее большей жесткостью на кручение. Достоинством этого решения является сравнительная простота прикрепления вантов к балке жесткости, которая для этого должна иметь среднюю стенку, а также сокращение объема опор, особенно значительное при использовании коробки с наклонными боковыми стенками.

Рис. 9.4 – Поперечные разрезы при расположении вантов в одной плоскости
При расположении вантов в одной плоскости пилоны могут быть одиночными или А–образными (рис. 9.4, б). Одиночные пилоны экономичнее, однако труднее конструировать узел пересечения пилона с балкой жесткости, который может быть выполнен с пропуском пилона сквозь балку жесткости с усилением ее для компенсации ослабления. Возможно решение этого узла с установкой пилона на балку жесткости при жестком или шарнирном его опирании; балку жесткости в месте опирания также усиливают.
При расположении вантов в двух плоскостях проезжую часть обычно размещают между ними, а тротуары выносят на консоли за плоскости вантов (рис. 9.5, а). Пилон обычно выполняют в виде рамы с двумя стойками, соединенными поверху распоркой. Для сопряжения ног пилона и балки жесткости при расположении вантов в вертикальных плоскостях можно придать ногам пилона небольшой наклон и избавить распорку от работы на изгиб. Ванты располагают иногда в наклонных плоскостях с закреплением в верхней части А–образного пилона (рис. 9.5, б).

Рис. 9.5 – Поперечные разрезы при расположении вантов в двух плоскостях
При проектировании вантовых мостов с железобетонными балками жесткости под железную дорогу необходимо иметь в виду, что нагрузка здесь значительно больше автомобильной, а нормативные прогибы ниже. Поэтому рациональная длина пролетов для вантовых железнодорожных мостов меньше и, как показали предварительные исследования, может находиться в пределах до 60–80 м.
Необходимо обеспечивать достаточную жесткость железнодорожных мостов, применяя, например, жесткие железобетонные ванты. Для этих мостов сравнительно большее значение имеют тормозные силы, которые должны надежно восприниматься конструкцией моста. Для этого предусматривают неподвижную опорную часть в балке жесткости или жесткие пилоны, способные воспринимать тормозную силу при передаче ее через ванты на верх пилонов.
vse-lekcii.ru
Проектирование схемы моста
Схема моста влияет на его технико-экономические показатели, надежность и долговечность сооружения (пропуск ледохода и паводковых вод, условия эксплуатации и содержания), технологию строительства сооружения.
Мост имеет береговые опоры без заборных стенок, длина моста складывается из отверстия моста (L0=24м) и суммарной толщины промежуточных и береговых опор :
(1.1)
.
Конструирование и расчет пролетного строения со сближенными прогонами
Конструирование пролетного строения
Конструирование пролетного строения заключается в назначении числа прогонов (n) и расстояний между ними (d). Количество прогонов определяют, исходя из ширины моста.
Количество прогонов вычисляют по формуле:
; (2.1)
Округлив количество прогонов (n) до ближайшего целого числа, уточняем расстояние между прогонами (d):
(2.2)
Расчет элементов проезжей части моста
Доски верхнего настила распределяют сосредоточенную нагрузку от давления колеса автомобиля на доски нижнего настила и защищают их от истирания. Размеры досок продольного верхнего настила назначаются конструктивно. Толщину досок верхнего настила принимают в = 7см, ширина досок 17см.
Учитывая упругое распределение нагрузки досками верхнего настила, усилие на одну доску принимаем равным половине усилия от давления колеса тележки нагрузки А11 или НК-80, т. е.
; (2.3)
кН - усилие от давления колеса тележки нагрузки А11;
Нкг - усилие от давления 1 колеса тележки нагрузки НК-80.
Расчетный изгибающий момент в доске нижнего настила от воздействия колеса автомобильной нагрузки, пренебрегая собственным весом настила, будет:
, (2.4)
где - коэффициент надёжности по нагрузке для тележки равный 1,5.
Расчетный изгибающий момент в доске нижнего настила от воздействия колеса нагрузки НК-80, пренебрегая собственным весом настила, будет:
, (2.5)
где коэффициент надёжности по нагрузке для нагрузки НК-80 равный 1.
Необходимый момент сопротивления доски вычисляют по формуле:
; (2.6)
где - изгибающий момент от временной нагрузки;𝑅𝑑𝑏- расчетное сопротивление доски на изгиб.
3
Задавая ширину доски нижнего настила bH=20см, определяют ее толщину δН:
(2.7)
На скалывание доски не рассчитываю, т.к. скалывающие напряжения незначительны.
Расчет сближенных прогонов
Так как сближенные прогоны укладываются на небольших расстояниях друг от друга (0,6-1,0м), то при расчете пролетных строений учитывают упругое распределение нагрузки досками нижнего настила на прогоны, которое зависит от вида нагрузки (сосредоточенная или распределенная) и соотношения жесткостей нижнего настила и прогонов.
Нагрузка А11 состоит из равномерно распределенной нагрузки интенсивностью υ=10,8кН/м (1,1т/м) и двухосной тележки с давлением на каждую ось Ртел = 108кН (11,0т).
Коэффициент упругого распределения вычисляют по формуле:
; (2.8)
.
где Jпр= (0,0485+0,0479)d4=0,0964354=144660,25см4- момент инерции сечения прогона; Jн - момент инерции двух досок нижнего настила; lr=700см - расчетный пролет прогона.
В упругом распределении нагрузки участвуют две доски нижнего настила, и момент инерции вычисляют по формуле:
. (2.9)
см4.
Если , то нагрузка распределяется на 5 прогона.
Упругое распределение нагрузки учитывается коэффициентом αi, и в общем виде усилие, действующее на прогон:
(2.10)
(2.11)
(2.12)
Полное давление от колес тележки нагрузки А11 с учетом упругого распределения нагрузки будет равно:
(2.13)
.
Вычисляем момент от действия тележки по формуле:
; (2.14)
где - коэффициент надежности по нагрузке; Y1 и Y2 - ординаты линии влияния момента и вычисляются они по формуле:
(2.15)
(2.16)
.
Так как равномерно распределенная полосовая составляющая нагрузки А11 распределяется по всей длине прогона, то в упругом распределении этой нагрузки участвуют все доски нижнего настила, и коэффициент упругого распределения необходимо вычислить заново, учитывая изменение момента инерции нижнего настила:
; (2.17)
см4;
Изгибающий момент от равномерно распределенной полосовой нагрузки ν вычисляется по формуле:
; (2.18)
где – коэффициент надёжности нагрузке, ν = 10,8 кН/м (1,1 т/м) - равномерно распределенная полосовая нагрузка от А11.
кНсм.
Полный изгибающий момент от нагрузки А11 равен:
; (2.19)
кНсм
При продольной установке тележки нагрузки НК-80 в середине пролета изгибающий момент определяется по формуле:
; (2.20)
(2.21)
.
(2.22)
(2.23)
м=145 см,
м=85см,
Изгибающий момент от постоянной нагрузки вычисляют по формуле:
; (2.24)
где ;- коэффициенты надежности по нагрузке для верхнего настила и для остальной части постоянной нагрузки;
- нагрузка от массы досок верхнего настила;
=/м- нагрузка от массы нижнего настила;
кН/м - нагрузка от массы прогона.
где Апр=(0,7827+0,7801)352 =0,191433=1914,43- площадь поперечного сечения прогона; д - удельная плотность древесины;
Расчетный изгибающий момент в сечении вычисляется по формуле:
; (2.25)
где Мвр = max.
м
По принятым размерам поперечного сечения прогона вычисляют момент сопротивления (Wпр=) и выполняют проверку прочности прогона на изгиб:
σ =≤Rdb; Rdb=15,7МПа,
σ ==2489,79кН/м2=2,49МПа.
Разница между значениями превышает 4%, это допустимо в связи с погрешностями в проектировании. Условие прочности выполняется. Из этого следует, что в заданном сечении перенапряжение.
Если прогоны одноярусные, то вычисляем диаметр бревна прогона в отрубе:
dот = dпр – 0.01; (2.26)
dот =26-0,01см.
studfiles.net
423800, Набережные Челны , база Партнер Плюс, тел. 8 800 100-58-94 (звонок бесплатный)