|
||||
|
|
звонок бесплатный
Наши сотрудники:
[email protected]
Екатерина - специалист по продаже а/м КАМАЗ
 [email protected]
[email protected]






Техника в наличии

Тягач КАМАЗ 44108-6030-24
2014г, 6х6, Евро3, дв.КАМАЗ 300 л.с., КПП ZF9, бак 210л+350л, МКБ,МОБ,рестайлинг.
цена 2 220 000 руб.,

КАМАЗ 4308-6063-28(R4)
4х2,дв. Cummins ISB6.7e4 245л.с. (Е-4),КПП ZF6S1000, V кузова=39,7куб.м., спальное место, бак 210л, шк-пет,МКБ, ТНВД BOSCH, система нейтрализ. ОГ(AdBlue), тент, каркас, рестайлинг, внутр. размеры платформы 6112х2470х730 мм
цена 1 950 000 руб.,

Самосвал КАМАЗ 6520-057
2014г, 6х4,Евро3, дв.КАМАЗ 320 л.с., КПП ZF16, ТНВД ЯЗДА, бак 350л, г/п 20 тонн, V кузова =20 куб.м.,МКБ,МОБ, со спальным местом.
цена 2 700 000 руб.,

Самосвал 6522-027
2014, 6х6, дв.КАМАЗ 740.51,320 л.с., КПП ZF16,бак 350л, г/п 19 тонн,V кузова 12куб.м.,МКБ,МОБ,задняя разгрузка,обогрев платформы.
цена 3 190 000 руб.,
СУПЕР ЦЕНА
на АВТОМОБИЛИ КАМАЗ
| 43118-010-10 (дв.740.30-260 л.с.) | 2 220 000 |
| 43118-6033-24 (дв.740.55-300 л.с.) | 2 300 000 |
| 65117-029 (дв.740.30-260 л.с.) | 2 200 000 |
| 65117-6010-62 (дв.740.62-280 л.с.) | 2 350 000 |
| 44108 (дв.740.30-260 л.с.) | 2 160 000 |
| 44108-6030-24 (дв.740.55,рест.) | 2 200 000 |
| 65116-010-62 (дв.740.62-280 л.с.) | 1 880 000 |
| 6460 (дв.740.50-360 л.с.) | 2 180 000 |
| 45143-011-15 (дв.740.13-260л.с) | 2 180 000 |
| 65115 (дв.740.62-280 л.с.,рест.) | 2 190 000 |
| 65115 (дв.740.62-280 л.с.,3-х стор) | 2 295 000 |
| 6520 (дв.740.51-320 л.с.) | 2 610 000 |
| 6520 (дв.740.51-320 л.с.,сп.место) | 2 700 000 |
| 6522-027 (дв.740.51-320 л.с.,6х6) | 3 190 000 |

подробнее про услугу перегона можно прочесть здесь.

|
Нужны самосвалы? Обратите внимание на Ford-65513-02. |
КАМАЗы в лизинг
ООО «Старт Импэкс» имеет возможность поставки грузовой автотехники КАМАЗ, а так же спецтехники на шасси КАМАЗ в лизинг. Продажа грузовой техники по лизинговым схемам имеет определенные выгоды для покупателя грузовика. Рассрочка платежа, а так же то обстоятельство, что грузовики до полной выплаты лизинговых платежей находятся на балансе лизингодателя, и соответственно покупатель автомобиля не платит налогов на имущество. Мы готовы предложить любые модели бортовых автомобилей, тягачей и самосвалов по самым выгодным лизинговым схемам.Контактная информация.
г. Набережные Челны, Промкомзона-2, Автодорога №3, база «Партнер плюс».
тел/факс (8552) 388373.
Схема проезда
3.11 Естественные механическая и электромеханическая характеристика асинхронного двигателя (ад). Механическая характеристика асинхронного двигателя
Механическая характеристика асинхронного двигателя. Формула Клосса.
|
| Механической характеристикой двигателя называется зависимость частоты вращения ротора от момента на валуn = f (M2). Так как при нагрузке момент холостого хода мал, то M2 ≈ M и механическая характеристика представляется зависимостью n = f (M). Если учесть взаимосвязь s = (n1 - n) / n1, то механическую характеристику можно получить, представив ее графическую зависимость в координатах n и М (рис. 1). Рис. 1. Механическая характеристика асинхронного двигателя Естественная механическая характеристика асинхронного двигателя соответствует основной (паспортной) схеме его включения и номинальным параметрам питающего напряжения. Искусственные характеристикиполучаются, если включены какие-либо дополнительные элементы: резисторы, реакторы, конденсаторы. При питании двигателя не номинальным напряжением характеристики также отличаются от естественной механической характеристики. Механические характеристики являются очень удобным и полезным инструментом при анализе статических и динамических режимов электропривода. |
Выражение для электромагнитного момента (*) справедливо для любого режима работы и может быть использовано для построения зависимости момента от скольжения при изменении последнего от +∞ до −∞ (рис. 2.14).
Рассмотрим часть этой характеристики, соответствующая режиму двигателя, т.е. при скольжении, изменяющемся от 1 до 0. Обозначим момент, развиваемый двигателем при пуске в ход (S=1) как Mпуск. Скольжение, при котором момент достигает наибольшего значения, называют критическим скольжением Sкр, а наибольшее значение момента – критическим моментом Mкр. Отношение критического момента к номинальному называют перегрузочной способностью двигателя
Mкр/Mн=λ=2÷3.
Из анализа формулы (*) на максимум можно получить соотношения для Mкр и Sкр
| Mкр=Cм | U12 | ; Sкр≈ | R2 | . |
| 2X2 | X2 |
Критический момент не зависит от активного сопротивления ротора, но зависит от подведенного напряжения. При уменьшении U1 снижается перегрузочная способность асинхронного двигателя.
Из выражения (*), разделив M на Mкр, можно получить формулу, известную под названием «формула Клосса», удобную для построенияM=f(S).
|
| M | = | 2 |
| Mкр | S/Sкр+Sкр/S |
Если в эту формулу подставить вместо M и S номинальные значения момента и скольжения (Mн и Sн), то можно получить соотношение для расчета критического скольжения.
.
Участок характеристики (рис. 2.14), на котором скольжение изменяется от 0 до Sкр, соответствует устойчивой работе двигателя. На этом участке располагается точка номинального режима (Mн, Sн). В пределах изменения скольжения от 0 до Sкр изменение нагрузки на валу двигателя будет приводить к изменению частоты вращения ротора, изменению скольжения и вращающего момента. С увеличением момента нагрузки на валу частота вращения ротора станет меньше, что приведет к увеличению скольжения и электромагнитного (вращающего) момента. Если момент нагрузки превысит критический момент, то двигатель остановится.
Участок характеристики, на котором скольжение изменяется отSкрдо 1, соответствует неустойчивой работе двигателя. Этот участок характеристики двигатель проходит при пуске в ход и при торможении.
Энергетическая диаграмма АД
Преобразование активной мощности в двигателе связано с потерями. Они делятся на электрические, магнитные и механические.
Отобразим энергетическую диаграмму двигателя, описывая энергетические процессы, протекающие в двигателе.
–активная мощность, потребляемая двигателем из сети.
Часть мощности теряется на нагрев обмотки статора. Другая часть мощности рассеивается на магнитные потери в сердечнике статора.
Остальная мощность с помощью основного магнитного потока передается из статора в ротор и является электромагнитной мощностью двигателя.
Часть электромагнитной мощности расходуется на нагрев обмотки ротора. Магнитные потери в сердечнике ротора малы и , а частота. Поэтому магнитные потери в сердечнике ротора не указываются.
–механическая мощность двигателя. Механические потери обусловлены трением вала ротора в подшипниках и сопротивлением воздуха.
Уравнение баланса активной мощности имеет вид:
При проектировании и эксплуатации АД представляет интерес соотношение между активной и реактивной мощностями, называемое коэффициентом мощности:
Q1=const, не зависит от нагрузки
Р1 повышается с повышением нагрузки, а, следовательно, повышается cosφ
studfiles.net
3.11 Естественные механическая и электромеханическая характеристика асинхронного двигателя (ад)
Основным методом анализа установившихся режимов асинхронного двигателя является использование схем замещения. При этом обычно рассматриваются явления, относящиеся к одной фазе двигателя при соединении обмоток статора и ротора в звезду. Одной из таких схем является Т-образная схема замещения, изображенная на рис. 3.11.1 (в ней не учитываются потери в стали машины).
В соответствии с этой схемой для основных величин, характеризующих работу АД, в курсе электрических машин получены такие выражения:
Приведенный ток ротора
;
Электромагнитная мощность:
;
Электромагнитный момент:
Критический момент:
;
Номинальное и критическое скольжения:
; ;
Т.к в АД при отсутствии в цепи ротора добавочного сопротивления r1r'2, то можно найти соотношение
и
Здесь – перегрузочная способность двигателя по М. Поделив М на МКР, после преобразований получим уравнение механической характеристики АД, называемое уравнением Клосса.
Задаваясь различными значениями скольжения, можно построить естественную механическую характеристику двигателя во всем возможном диапазоне изменения скольжения. На рис. 3.11.2 приведены естественные характеристики АД для прямого и обратного действия электромагнитного момента.
Если пренебречь активным сопротивлением r1 обмотки статора, что вполне допустимо для АД большой мощности, то =0 и уравнение механической характеристики принимает вид (это тоже формула Клосса):
.
В значительном числе случаев работа АД нормально протекает при S от 0 до (1,21,5)SH, т.е. при S<(0,350,4)SKP. Это обстоятельство позволяет в упрощенном выражении механической характеристики пренебречь отношением , которое в 8÷10 раз меньше. В этом случае механическая характеристика АД может быть представлена прямой, описываемой уравнением (в пределах до МН):
.
Следует иметь в виду, что формулы Клосса достаточно точно описывают механические характеристики АД с фазным ротором. В к.з. АД, выпускаемых обычно с относительно глубокими пазами в роторе, либо с двойной беличьей клеткой, имеется в той или иной степени явление вытеснения тока в стержнях ротора. Поэтому их параметры непостоянны и механические характеристики значительно отличаются от характеристик, рассчитанных по формулам Клосса. Однако, эти формулы благодаря своей простоте позволяют выполнять многие расчеты и делать общие заключения о свойствах и работе АД. В тех же случаях, когда необходима большая точность, должны использоваться экспериментально снятые механические характеристики. У некоторых к.з. АД при малых скоростях механическая характеристика имеет провал, (см. рис.3.11.3), вызванный влиянием высших гармоник поля, с чем следует считаться при пуске двигателя под нагрузкой.
Электромеханические характеристики АД представляют собой зависимости и. Т.к. ток ротора является основной величиной для оценки режима работы двигателя, рассмотрим зависимость.
При использовании формулы
это не всегда удается сделать ввиду отсутствия данных о сопротивлениях обмоток двигателя. В связи с этим для получения зависимости воспользуемся формулой Клосса и выражением электромагнитного момента.
,
Отсюда
При номинальном режиме:
: отсюда
Подставляя 3r2’ в выражение для I2’, получим уравнение электромеханической характеристики:
т.к. при отсутствии в цепи ротора добавочного сопротивления и.
Задаваясь величиной S, получим графическую зависимость . Она изображена на рис. 3.11.4.
studfiles.net
МЕХАНИЧЕСКАЯ ХАРАКТЕРИСТИКА АСИНХРОННОГО ДВИГАТЕЛЯ
Количество просмотров публикации МЕХАНИЧЕСКАЯ ХАРАКТЕРИСТИКА АСИНХРОННОГО ДВИГАТЕЛЯ - 380
Механической характеристикой принято называть зависимость частоты вращения ротора двигателя или скольжения от момента͵ развиваемого двигателем при установившемся режиме работы. n= f(М) или s = f(M).
Механическая характеристика является одной из важнейших характеристик двигателя. При выборе двигателя к производственному механизму из множества двигателей с различными механическими характеристиками выбирают тот, механическая характеристика которого удовлетворяет требованиям механизма.
Уравнение механической характеристики асинхронного двигателя должна быть получено на основании формулы (10.41) и схемы замещения.
С помощью схемы замещения (см. рис. 10.17) определяют приведенный ток фазы ротора:
| I'2 = | U1ф | , | |
| √ | (r1 + | r'2 | ) + (x1 + x'2)2 |
| s |
(10.49)
где
| r'2 | = r'2 + | r'2(1 - s) | . |
| s | s |
Полученное значение тока I'2 nподставляют в уравнение момента (10.41), в котором предварительно I2 и r2 заменяют через их приведенные значения:
| M = | 3I22r2 | = | 3I'22r'2 | . |
| ω0s | ω0s |
(10.50)
После подстановки получим
| M = | 3U1ф2r'2 | = |
| ω0s [(r1 + | r' | )2+ (x1 + x'2)2] |
| s |
(10.51)
Выражение (10.51) представляет собой уравнение механической характеристики, поскольку оно связывает момент и скольжение двигателя. Остальные входящие в уравнение величины: напряжение сети и параметры двигателя — постоянны 1 и не зависят от sи М.Располагая параметрами двигателя, можно рассчитать и построить его механическую характеристику, которая будет иметь вид, изображенный на рис. 10.18.
Рис. 10.18. Механическая характеристика асинхронного двигателя
1 Сопротивление r2 зависит от частоты f2 и, следовательно, от s, но для двигателей общего назначения изменение r2 незначительно.
При этом крайне важно отметить, что после включения двигателя в нем происходят сложные переходные электромагнитные процессы. В тех случаях, когда время разбега оказывается соизмеримым с временем электромагнитных процессов, механическая характеристика двигателя в период разбега может существенно отличаться от статической.
Одной из важных точек характеристики, представляющей интерес при анализе работы и выборе двигателя, является точка, где момент, развиваемый двигателем, достигает наибольшего значения. Эта точка имеет координаты nкр , sкр , Mmax . Значение критического скольжения sкр , при котором двигатель развивает максимальный (критический) момент Мmax, легко определить, в случае если взять производную dM/ds выражения (10.51) и приравнять ее нулю.
После дифференцирования и последующих преобразований выражение sкр будет иметь следующий вид:
| sкр = ± | r'2 | . |
| √r12+ xк2 |
(10.52)
где хк = x1 + х'2.
Подставив sкр вместо s в уравнение (10.51), получим выражение максимального момента
| Мmax = | 3U1ф2 | . |
| 2ω0(r1 ± √r12+ xк2) |
(10.53)
Необходимо отметить, что из выражений (10.51) — (10.53) вытекает следующее. Момент, развиваемый двигателем, при любом скольжении пропорционален квадрату напряжения. Максимальный момент пропорционален квадрату напряжения и не зависит от сопротивления цепи ротора. Критическое скольжение пропорционально сопротивлению цепи ротора и не зависит от напряжения сети.
Полученные выражения удобны для анализа, однако из-за отсутствия в каталогах параметровr1, х1, х2 их использование для расчетов и построения характеристик затруднено.
В практике обычно пользуются уравнением механической характеристики, с помощью которого можно произвести необходимые расчёты и построения, используя только каталожные данные.
Активное сопротивление обмотки статора r1 значительно меньше остальных сопротивлений цепи статора и ротора, и им обычно пренебрегают. Тогда выражения (10.51) — (10.53) будут иметь вид
| M = | 3U1ф2r'2 | ; |
| ω0s [(r'2/s)2 + хк2] |
(10.54)
sкр = ± r'2/хк; (10.55)
(10.56)
Упрощенное уравнение механической характеристики получается из совместного решения уравнений (10.54) — (10.56):
| M = | 2M max | ; |
| s/sк + sк/s |
(10.57)
Значение Мmax определяется из отношения Мmax/Мном = λ, указываемого в каталогах, a sкр — из уравнения (10.57), в случае если решить его относительно sкр и вместо текущих значений s и М подставить их номинальные значения, которые легко определить по паспортным данным:
sкр = sном (λ ± √λ2 - 1), (10.58)
где sном = (n0 - nном)/n0; λ = Мmax/Мном.
Следует отметить, что в зоне от М = 0 до М ≈ 0,9Мmax механическая характеристика близка к прямой линии. По этой причине, к примеру, при расчетах пусковых и регулировочных резисторов эту часть механической характеристики принимают за прямую линию, проходящую через точки М = 0, n = n0 и Мном , nном . Уравнение механической характеристики в этой части будет иметь вид
referatwork.ru
Механические характеристики асинхронного электродвигателя
Анализ работы асинхронного электродвигателя удобно проводить на основе его механических характеристик, представляющих собой графически выраженную зависимость вида п = f(М). Скоростными характеристиками в этих случаях пользуются весьма редко, так как для асинхронного электродвигателя скоростная характеристика представляет собой зависимость числа оборотов от тока ротора, при определении которого встречается ряд трудностей, особенно, в случае асинхронных электродвигателей с короткозамкнутым ротором.
Для асинхронных электродвигателей, так же как и для электродвигателей постоянного тока, различают естественные и искусственные механические характеристики. Асинхронный электродвигатель работает на естественной механической характеристике в том случае, если его статорная обмотка подключена к сети трехфазного тока, напряжение и частота тока которой соответствует номинальным значениям, и если в цепь ротора не включены какие-либо дополнительные сопротивления.
На рис. 42 была приведена зависимость М = f(s), которая позволяет легко перейти к механической характеристике n = f(M), так как, согласно выражению (82), от величины скольжения зависит скорость вращения ротора.
Подставив формулу (81) в выражение (91) и решив полученное уравнение относительно п2 получим следующее уравнение механических характеристик асинхронного электродвигателя
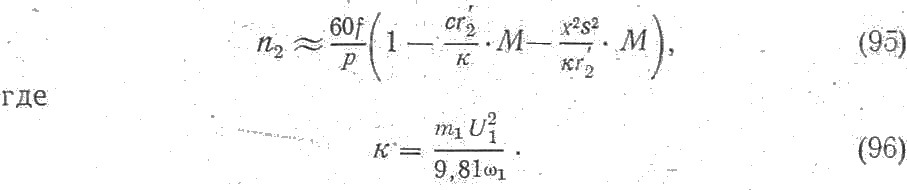
Член r1s опущен, ввиду его малости. Механические характеристики, соответствующие этому уравнению, приведены на рис. 44.
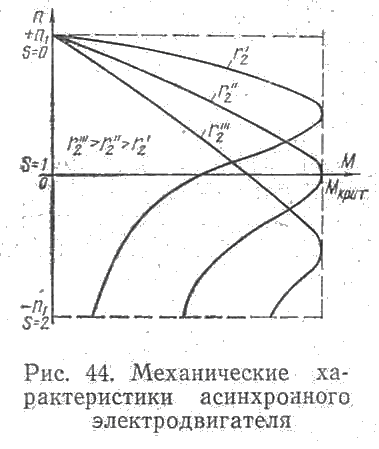
Для практических построений уравнение (95) неудобно, поэтому на практике обычно пользуются упрощенными уравнениями. Так, в случае работы электродвигателя на естественной характеристике при вращающем моменте, не превышающем 1,5 его номинального значения, скольжение обычно не превышает 0,1. Поэтому для указанного случая в уравнении (95) можно пренебречь членом x2 s2 /kr’2·M , в результате чего получим следующее упрощенное уравнение естественной характеристики:
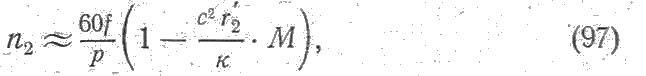
являющееся уравнением прямой линии, наклоненной к оси абсцисс.
Хотя уравнение (97) является приближенным, опыт показывает, что при изменениях момента в пределах от М = 0 до М=1,5Мн характеристики асинхронных электродвигателей действительно прямолинейны и уравнение (97) дает результаты, хорошо согласующиеся с опытными данными.
При введении в цепь ротора дополнительных сопротивлений характеристику п = f(М) с достаточной для практических целей точностью также можно считать прямолинейной в указанных пределах для вращающего момента и производить ее построение по уравнению (97).
Таким образом, механические характеристики асинхронного электродвигателя в диапазоне от М = 0 до М = 1,5 Мн при различных сопротивлениях роторной цепи представляют семейство прямых, пересекающихся в одной точке, соответствующей синхронному числу оборотов (рис. 45). Как показывает уравнение (97), наклон каждой характеристики к оси абсцисс определяется величиной активного сопротивления роторной цепи r’2. Очевидно, чем больше сопротивление, введенное в каждую фазу ротора, тем больше наклонена к оси абсцисс характеристика.

Как указывалось, обычно на практике скоростными характеристиками асинхронных электродвигателей не пользуются. Расчет же пусковых и регулировочных сопротивлений производят с помощью уравнения (97). Построение естественной характеристики можно выполнить по двум точкам — по синхронной скорости n1= 60f /р при нулевом моменте и по номинальной скорости при номинальном моменте.
Следует иметь в виду, что для асинхронных электродвигателей зависимость момента от тока ротора I2 носит более сложный характер, чем зависимость момента от тока якоря для
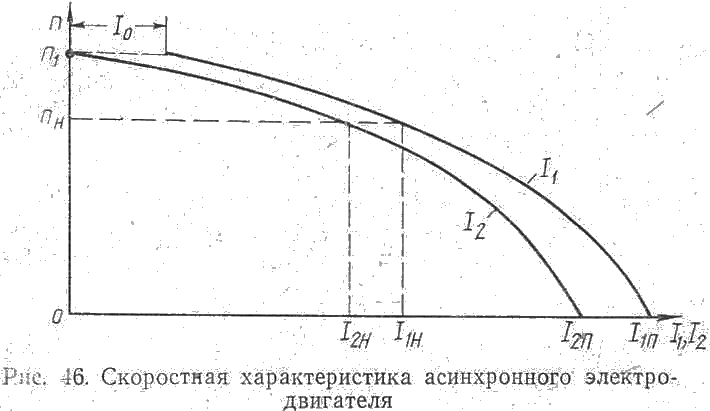
электродвигателей постоянного тока. Поэтому скоростная характеристика асинхронного двигателя неидентична механической характеристике. Характеристика п = f(I2) имеет вид, показанный на рис. 46. Там же дана характеристика n = f (I1).
vdvizhke.ru
Характеристики асинхронного двигателя ~ Электропривод
К энергетическим характеристикам асинхронного двигателя относятся КПД двигателя(η) коэффициент мощности (cosφ) и скольжение S.коэффициент полезного действия (η) вычисляется как отношение полезной мощности на валу двигателя Р2 кВт, к активной мощности, потребляемой двигателем из сети Р1 кВт;η = Р2/ Р1 коэффициент мощности (cos(φ)вычисляется как отношение потребляемой активной мощности Р1 кВт, к полной мощности, потребляемой из сети S1 кВА;

По ГОСТ Р. 51677-2000 асинхронные двигатели общепромышленного назначения делятся на двигатели с нормальным КПД и двигатели с повышенным КПД. У асинхронных двигателей с повышенным КПД, суммарные потери не меньше, чем на 20%, чем у двигателей с нормальным КПД такой же мощности и частоты вращения. Коэффициенты мощностей (cosφ) асинхронных двигателей определены в ГОСТ.Р 51677. Значения КПД и cosφ конкретного асинхронного двигателя можно узнать по каталогу или по шильдику.
Причем КПД и cosφ асинхронного двигателя определяются и нагрузкой машины. В справочниках по электрическим машинам можно увидеть эти зависимости.
Линейный ток двигателя можно определить исходя из номинальной полезной мощность (Р2, кВт), номинального напряжения (UH, В ), КПД (η) и cosφ.

Мощность, потребляемая из сети можно определить из формулы:

Скольжение вычисляется как разницу между номинальной n1 и синхронной nc частотой вращения двигателя, приведенной к номинальной скорости двигателя n1:

Номинальную частоту вращения ротора n1 или скольжение (S, %)можно определить по каталогу двигателя или прочесть на его шильдике.
Механические и пусковые характеристики асинхронного двигателя
Одной из основных характеристик асинхронного двигателя, является механическая характеристика. Механической характеристикой называют зависимость скорости вращения или скольжения от вращающего момента на валу двигателя. Она позволяет сравнить и согласовать механические свойства двигателя и рабочего механизма. Соответственно, зависимость скорости вращения или скольжения от тока статора называют электромеханической характеристикой.

Механическая характеристика асинхронного двигателя определяет зависимость момента на валу двигателя от скольжения, при сохранении неизменного напряжении и частоты питающей сети
Пусковые характеристики определяют величину пускового моментаMп, минимального момента Мmin, максимального или критического момента Мкр., пускового тока Iп или пусковой мощности Sп или их отношениями. Диаграмма момента, приведенного к номинальному моменту, от скольжения получила название относительной механической характеристики.
Номинальный вращающий момент можно определить по формуле:

P2н- номинальная мощность , кВт,N1н- номинальная частота вращенияю, об/мин.
Пусковые характеристики асинхронного двигателя

Пусковые характеристики асинхронного двигателя регламентирует ГОСТ 28327 ( МЭК 60034 — 12), а их значения приводятся в каталогах. Стандартные асинхронные двигатели могут иметь два исполнения по механическим характеристикам, которые определены в ГОСТ 28327 и МЭК 60034-12:N – двигатели с нормальный моментом;Н –двигатели с повышенным моментом.
Двигатели , изготовленные в исполнении N, рассчитывают на два последовательных пуска с остановкой между пусками из холодного состояния или на один пуск из нагретого состояния, после работы при номинальной нагрузке.
Момент сопротивления нагрузки при запуске прямо пропорционален квадрату частоты вращения и равняется номинальному моменту при номинальной частоте вращения, а значение внешнего момента инерции, γ , кг*м2, не должно превышать рассчитанного по формуле

где Р-номинальная мощность двигателя, кВт;р — число пар полюсов;
При построении характеристики предполагается, что момент сопротивления нагрузки остается постоянным и равен номинальному моменту. Кроме того он не зависит от частоты вращения. Значение же внешнего момента инерции не превышаетт 50% величины, полученной по приведенной выше формуле.
Механические характеристики асинхронных мшин зависят в том числе и от типа ротора, его номинальной мощности, и от числа пар полюсов.
Ввиду того, что разность в значениях момента при соответствующих скольжениях у двигателей с различным числом пар полюсов невелика, и не превышает значения поля допуска на моменты. Различные механические характеристики для разных исполнений асинхронных двигателей показаны на рис

1 — исполнение N; 2 — исполнение Н; 3 — с повышенным скольжением. Механические характеристики группы двигателей, одной серии, или ее части обычно укладываются в некоторую зону. По средней линии этой зоны можно составить групповую механическую характеристику. Величина зоны групповой характеристики меньше поля допуска двигателей на моменты.
eprivod.com
Механическая характеристика асинхронного двигателя
Асинхронный двигатель преобразовывает электрическую энергию в механическую. Механическая характеристика асинхронного двигателя, электромеханическая и другие содержат информацию, без которой невозможна его правильная эксплуатация.
Эта конструкция достаточно широко применяется в различных сферах человеческой жизнедеятельности. Без них немыслима работа станков, транспортеров, подъемно-транспортных машин. Двигатели, обладающие небольшой мощностью, широко используются в автоматике.
ОГЛАВЛЕНИЕ
- Устройство асинхронной машины
- Принцип работы асинхронной машины
- Механическая характеристика
- Электромеханическая характеристика
- Рабочие характеристики
Устройство асинхронной машины
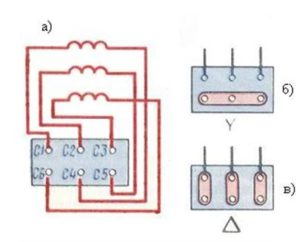
Схематичное устройство асинхронной машины
Классическая асинхронная машина состоит из 2 основных частей: ротора (подвижной) и статора (неподвижной). Три отдельные фазы составляют обмотку статора. С1, С2 и С3 — обозначения начала фаз. С3, С4 и С5 — соответственно концы фаз. Все они подсоединены к клеммному разъему по схеме звезда или треугольник, что показано на рисунках а, б, в. Схему выбирают учитывая паспортные данные двигателя и сетевое напряжение.
Статор создает внутри электродвигателя магнитное поле, которое постоянно вращается.
Ротор различают короткозамкнутый и фазный.
В короткозамкнутом скорость вращения не регулируется. Конструкция с ним проще и дешевле. Однако пусковой момент у него слишком мал по сравнению с машинами, у которых фазный ротор. Здесь скорость вращения регулируется за счет возможности ввода дополнительного сопротивления.
Принцип работы асинхронной машины
Подавая напряжение на обмотку статора, по каждой фазе можно наблюдать изменяющиеся магнитные потоки, которые по отношению друг к другу смещены на 120 градусов. Общий результирующий поток получается вращающимся и создает ЭДС внутри проводников ротора.
Там появляется ток, который во взаимодействии с результирующим потоком создает пусковой момент. Это приводит к вращению ротора.
Возникает скольжение S, т. е. разность между частотой вращения самого ротора n2 и частотой магнитного поля статора n1. Первоначально оно равно 1. Впоследствии частота возрастает, разность n1 – n2 уменьшается. Это ведет к уменьшению вращающего момента.
На холостом ходу скольжение минимально. Оно достигает критического значения Sкр, когда увеличивается статический момент. Превышение Sкр ведет к нестабильной работе машины.
Механическая характеристика
Как основная, помогает проводить детальный анализ работы электродвигателя. Она выражает непосредственную зависимость частоты вращения самого ротора от электромагнитного момента n=f (M).
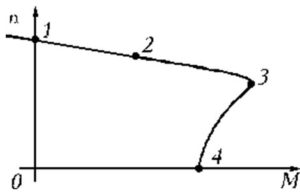 Из графика видно, что на участке 1-3 машина работает устойчиво. 3-4 — непосредственный отрезок неустойчивой работы. Идеальный холостой ход соответствует точке 1.
Из графика видно, что на участке 1-3 машина работает устойчиво. 3-4 — непосредственный отрезок неустойчивой работы. Идеальный холостой ход соответствует точке 1.
Точка 2 — номинальный режим работы. Точка 3 — частота вращения достигла критического значения. Пусковой момент Мпуск — точка 4.
Наши читатели рекомендуют! Для экономии на платежах за электроэнергию наши читатели советуют "Экономитель энергии Electricity Saving Box". Ежемесячные платежи станут на 30-50% меньше, чем были до использования экономителя. Он убирает реактивную составляющую из сети, в результате чего снижается нагрузка и, как следствие, ток потребления. Электроприборы потребляют меньше электроэнергии, снижаются затраты на ее оплату.загрузка...
Существуют технические способы расчетов и построения механической характеристики с учетом данных паспорта.
В первоначальной точке 1 n0=60f/p (p – количество пар полюсов). Поскольку nн и Mн непосредственно координаты точки 2, расчет номинального момента производится по формуле Mн=9,55*Рн/ nн, где Рн — номинальная мощность. Значение nн указано в паспорте двигателя. В точке 3 Mкр=Mнλ. Пусковой момент в точке 4 Mпуск=Mн*λпуск (значения λ, λпуск — из паспорта).
Механическая характеристика, построенная таким образом, называется естественной. Изменяя другие параметры можно получить искусственную механическую характеристику.
Полученные результаты дают возможность проанализировать и согласовать механические свойства самого двигателя и рабочего механизма.
Электромеханическая характеристика
Она являет собой зависимость угловой скорости вращения от тока статора. Используя несколько опорных точек можно построить электромеханическую характеристику. Номинальный ток рассчитывается по формуле:
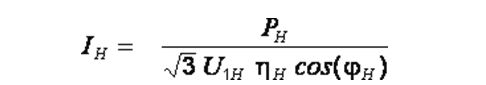
Ток холостого хода составляет 30—40% от номинального.
Формула расчета при критическом скольжении:
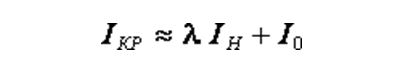
Ток в начальный момент пуска:
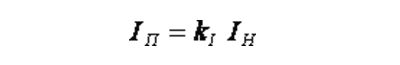
Все значения отражают электромеханическую характеристику.
Рабочие характеристики
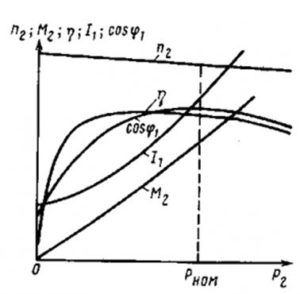 Рабочие характеристики асинхронного электродвигателя — это взаимосвязь нескольких параметров от полезной мощности P2. В их число входят: частота вращения самого ротора n2, момент на валу М, скольжение S, ток статора I1, расходуемая мощность P, коэффициент мощности СОSφ и КПД.
Рабочие характеристики асинхронного электродвигателя — это взаимосвязь нескольких параметров от полезной мощности P2. В их число входят: частота вращения самого ротора n2, момент на валу М, скольжение S, ток статора I1, расходуемая мощность P, коэффициент мощности СОSφ и КПД.
Причем частота электрического тока и напряжение неизменны, в отличие от нагрузки.
Как правило, рабочие характеристики асинхронного двигателя строятся в диапазоне значений скольжения от 0 до значения, превышающего номинальное на 10%. Это зона, где машина работает устойчиво.
Частота вращения ротора n2 уменьшается при возрастании нагрузки на валу. Но эти изменения не превышают 5%. Ток I1 растет, поскольку при последующем увеличении нагрузки его активная составляющая превышает реактивную.
СОSφ при холостом ходе мал. Но затем он возрастает. При повышенных нагрузках СОSφ уменьшается из-за возрастающего внутри обмотки ротора реактивного сопротивления.
КПД холостого хода равен 0. С увеличением нагрузки наблюдается его резкий рост, а впоследствии, снижение.
electricvdele.ru
МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЭЛЕКТРОДВИГАТЕЛЕЙ ПЕРЕМЕННОГО ТОКА Механическая характеристика трехфазного асинхронного двигателя с короткозамкнутым ротор
стоимость монтажа металлочерепицы. жми сюдаСхема включения асинхронного электродвигателя с короткозамкнутым ротором показана на рис. 7.1, а. Механическая характеристика двигателя выражает зависимость между вращающим моментом и частотой вращения п, угловой скоростью или скольжением s.
Упрощенное уравнение механической характеристики асинхронного двигателя (формула Клосса) имеет вид


Зная величину Мн и si; и задаваясь значениями s, можно построить механическую характеристику асинхронного двигателя (рис. 7.1, б).
Участок 1, 2 представляет собой рабочую, устойчивую часть характеристики, на которой двигатель работает устойчиво. Потеря скорости при изменении нагрузки составляет 3—6% номинальной, поэтому эту часть характеристики относят к разряду жестких.
Участок характеристики 2, 3 — нерабочий. Двигатель работать под нагрузкой на этой части характеристики не может, поэтому эту часть характеристики называют неустойчивой.
Отношение критического момента Mti к номинальному /Ином называется перегрузочной способностью двигателя Л:
Отношение пускового момента Ма к номинальному Меом называется кратностью пускового момента


Такой частоты вращения ротор двигателя не может достичь самостоятельно, так как для этого необходимо, чтобы момент сопротивления был равен нулю.
Величина пускового тока в 3—8 раз больше номинального, поэтому недопустимо держать включенным двигатель, если он не развернулся после включения или если он опрокинулся (остановился) в результате перегрузки.
Трехфазный асинхронный электродвигатель с коротко- замкнутым ротором имеет следующие положительные качества: простота конструкции; отсутствие нормально искрящих частей; большая перегрузочная способность и жесткость характеристики; надежность в работе и дешевизна в изготовлении.
Наряду с положительными качествами электродвигатель с короткозамкнутым ротором имеет следующие недостатки: высокая чувствительность двигателя к колебаниям напряжения; большой пусковой ток; малый пусковой момент.
Учитывая особенности механической характеристики асинхронных электродвигателей с короткозамкутым ротором, применять их рекомендуется для установок с жесткой характеристикой, перегружаемых в процессе работы и запускаемых без нагрузки.
Трехфазные асинхронные двигатели с короткозамкнутым ротором общего назначения из-за малых пусковых моментов и больших пусковых токов мало пригодны для привода горных машин. Для них созданы специальные короткозамкнутые электродвигатели с уменьшенным пусковым током и увеличенным пусковым моментом, v В основу улучшения пусковых свойств короткозамкнутых двигателей положен принцип автоматического включения дополнительного активного сопротивления в обмотку ротора на период пуска при сохранении принципиального устройства короткозамкнутого ротора. Осуществление этого принципа достигается за счет специальной конструкции обмоток ротора, активное сопротивление которых автоматически изменяется по мере изменения скольжения в двигателе. Для этого обмотки ротора выполняются либо с глубоким пазом (рис. 7.2, б), либо с двойной «беличьей клеткой» (рис. 7.2, а).

Механические характеристики двигателя с глубоким пазом 1 и двигателя с двойной «беличьей клеткой» 2 приведены на рис. 7.2 в.
Как видно из характеристик, пусковой момент двигателя с двойной «беличьей клеткой» больше критического, поэтому опрокидывание этого двигателя в результате перегрузки менее вероятно. Даже при вынужденной остановке двигатель сохранит большой пусковой момент п легко разгонится, как только будет устранена причина перегрузки.
alyos.ru
423800, Набережные Челны , база Партнер Плюс, тел. 8 800 100-58-94 (звонок бесплатный)











