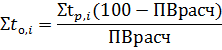|
||||
|
|
звонок бесплатный
Наши сотрудники:
[email protected]
Екатерина - специалист по продаже а/м КАМАЗ
 [email protected]
[email protected]






Техника в наличии

Тягач КАМАЗ 44108-6030-24
2014г, 6х6, Евро3, дв.КАМАЗ 300 л.с., КПП ZF9, бак 210л+350л, МКБ,МОБ,рестайлинг.
цена 2 220 000 руб.,

КАМАЗ 4308-6063-28(R4)
4х2,дв. Cummins ISB6.7e4 245л.с. (Е-4),КПП ZF6S1000, V кузова=39,7куб.м., спальное место, бак 210л, шк-пет,МКБ, ТНВД BOSCH, система нейтрализ. ОГ(AdBlue), тент, каркас, рестайлинг, внутр. размеры платформы 6112х2470х730 мм
цена 1 950 000 руб.,

Самосвал КАМАЗ 6520-057
2014г, 6х4,Евро3, дв.КАМАЗ 320 л.с., КПП ZF16, ТНВД ЯЗДА, бак 350л, г/п 20 тонн, V кузова =20 куб.м.,МКБ,МОБ, со спальным местом.
цена 2 700 000 руб.,

Самосвал 6522-027
2014, 6х6, дв.КАМАЗ 740.51,320 л.с., КПП ZF16,бак 350л, г/п 19 тонн,V кузова 12куб.м.,МКБ,МОБ,задняя разгрузка,обогрев платформы.
цена 3 190 000 руб.,
СУПЕР ЦЕНА
на АВТОМОБИЛИ КАМАЗ
| 43118-010-10 (дв.740.30-260 л.с.) | 2 220 000 |
| 43118-6033-24 (дв.740.55-300 л.с.) | 2 300 000 |
| 65117-029 (дв.740.30-260 л.с.) | 2 200 000 |
| 65117-6010-62 (дв.740.62-280 л.с.) | 2 350 000 |
| 44108 (дв.740.30-260 л.с.) | 2 160 000 |
| 44108-6030-24 (дв.740.55,рест.) | 2 200 000 |
| 65116-010-62 (дв.740.62-280 л.с.) | 1 880 000 |
| 6460 (дв.740.50-360 л.с.) | 2 180 000 |
| 45143-011-15 (дв.740.13-260л.с) | 2 180 000 |
| 65115 (дв.740.62-280 л.с.,рест.) | 2 190 000 |
| 65115 (дв.740.62-280 л.с.,3-х стор) | 2 295 000 |
| 6520 (дв.740.51-320 л.с.) | 2 610 000 |
| 6520 (дв.740.51-320 л.с.,сп.место) | 2 700 000 |
| 6522-027 (дв.740.51-320 л.с.,6х6) | 3 190 000 |

подробнее про услугу перегона можно прочесть здесь.

|
Нужны самосвалы? Обратите внимание на Ford-65513-02. |
КАМАЗы в лизинг
ООО «Старт Импэкс» имеет возможность поставки грузовой автотехники КАМАЗ, а так же спецтехники на шасси КАМАЗ в лизинг. Продажа грузовой техники по лизинговым схемам имеет определенные выгоды для покупателя грузовика. Рассрочка платежа, а так же то обстоятельство, что грузовики до полной выплаты лизинговых платежей находятся на балансе лизингодателя, и соответственно покупатель автомобиля не платит налогов на имущество. Мы готовы предложить любые модели бортовых автомобилей, тягачей и самосвалов по самым выгодным лизинговым схемам.Контактная информация.
г. Набережные Челны, Промкомзона-2, Автодорога №3, база «Партнер плюс».
тел/факс (8552) 388373.
Схема проезда
Физические величины. Точность и погрешность измерений. Точность измерения линейки
1. Однократные измерения размера линейкой.
Линейка является простейшим измерительным устройством. Цена деления линейки может быть различной. Для измерения с помощью линейки необходимо нулевую отметку ш
Рис. 1.1. Линейка
калы совместить с краем измеряемого отрезка.Результат измерения считывается по шкале линейки по другому краю измеряемого отрезка.
Погрешность измерения с помощью линейки составляет не более ½ цены ее наименьшего деления. Доли наименьшего деления считываются на глаз с точностью, не превышающей погрешность измерения, то есть 0,5 цены деления.
Пример 1.По линейке с ценой деления 1 мм произведен отсчет. Результат измерения записывается так:
Пример 2.Той же линейкой измерен размер. Результат измерения записывается следующим образом:При выполнении этого задания проводятся однократные измерения размера любого предмета линейкой, например, размер грани параллелепипеда или стороны треугольника из набора принадлежностей, оцениваются погрешности измерения и результат представляется в виде:, (см. примеры 1 и 2).
2. Однократные измерения штангенциркулем.
Штангенциркуль представляет собой металлическую линейку 1, на конце которой имеется поперечный выступ 2. Другой такой же выступ имеется на обойме 3. Они движутся по линейке. Обойма имеет окно 4, позволяющее видеть основную шкалу линейки. Внутренние поверхности выступов строго перпендикулярны линейке. Когда они прилегают друг к другу, указатель «нуль» на обойме находится против нулевого деления шкалы линейки. Измеряемый предмет зажимается между выступами.
Д
Рис. 1.2. Штангенциркуль
ля измерения внутренних размеров отверстий наружные стороны концов выступов обычно делаются строго перпендикулярными линейке и слегка закругляются. Расстояние между ними при установке обоймы на нуль шкалы (обычно 8 или 10 мм) указывается на штангенциркуле 6. Иногда для измерения внутренних размеров делаются специальные ножи на тыльной стороне выступов, концы выступов заостряются. Такое устройство позволяет измерять отверстия малых размеров, но точность измерения при этом меньше.Достаточно высокая точность измерения штангенциркулем достигается с помощью нониуса. Нониус – это дополнительная линейка со шкалой 5, нанесенной по краю подвижной 3.
Нулевой штрих шкалы нониуса служит одновременно указателем для считывания числа целых делений по основной шкале и началом отсчета долей миллиметра по шкале нониуса. Обычно число делений нониуса n= 10 илиn=20.При 10 делениях нониуса всей длине его шкалы соответствует 19мм основной шкалы, то есть 10 делений нониуса имеют длину, на 1 мм меньшую, чем 20 делений основной шкалы. Цену деления нониуса штангенциркуля можно найти по формуле . При 10 делениях нониусаи. При 20 делениях нониуса. Погрешность градуировки штангенциркуля приn= 10 равна 0,1 мм, а приn= 20 равна 0,05 мм.
Пример 3. Нониус штангенциркуля имеет цену деления 0,1 мм. Число целых делений шкалы до нуля нониуса – 12. Штрих основной шкалы совпадает со штрихом шкалы нониуса, которому предшествует 4 деления его шкалы. Результат отсчетаРезультат измерения записывается в виде:
При выполнении этого задания проводятся однократные измерения размера любого предмета штангенциркулем, оцениваются погрешности измерения и результат представляется в виде (см. пример 3).
3. Однократные измерения размера микрометром.
Для измерения внешних размеров предметов с большой точностью, чем штангенциркулем, служит микрометр. Он состоит из скобы 1, жестко соединенной с измерительным упором 2, цилиндра 3, барабана 4, который соединен с микрометрическим винтом и подвижным измерительным упором 5. На цилиндре 3 нанесено 2 миллиметровых шкалы: нижняя – основная, верхняя – дополнительная, смещенные относительно друг друга на 0,5 мм. Левый конусный конец барабана имеет круговую шкалу 6, состоящую из 50 делений. Шаг микрометрического винта равен 0,5 мм, поэтому один оборот барабана соответствует изменению линейного размера 0,5 мм.
Рис. 1.3. Микрометр
Измеряемый предмет помещают между винтом 5 и противоположным ему упором 2 так, как показано на рисунке 1.3. Винт вращают и доводят до соприкосновения с предметом. При измерении микрометром существенно постоянство вращательного момента, приложенного к барабану при соприкосновении упоров с измеряемым предметом. Поэтому барабан 4 следует вращать, прикладывая усилие не к нему самому, а к головке 7. Она соединяется с винтом с помощью «трещотки», которая передает усилие только до тех пор, пока она не достигнет определенной величины. Когда же эта величина достигнута, дальнейшее вращение головки происходит в «холостую» и не изменяет показания микрометра.Результат измерения получают в следующем порядке. Сначала производят отсчет размера по основной и дополнительным шкалам с точностью до 0,5 мм, после этого осуществляется отсчет сотых долей миллиметра по шкале барабана и результаты суммируются.
Погрешность градуировки микрометров составляет 0,004 мм.
Пример 4.На основной шкале видно 5 целых миллиметровых делений. Следующая справа за меткой 5 основной шкалы отметка дополнительной шкалы не видна. Отсчет по шкале барабана – 24.
Результат отсчета . Результат измерения:.
При выполнении этого задания проводятся однократные измерения размера любого предмета микрометром, оценивается погрешность и результат представляется в виде: (см. пример 4).
4. Повторное измерение размеров
Повторные измерения предметов являются прямыми наблюдениями. Процедура их осуществляется очень просто: одним и тем же измерительным инструментом – линейкой, штангенциркулем или микрометром измеряют один и тот же размер несколько раз через определенный интервал времени, и результаты заносятся в таблицу.
Обработка результатов эксперимента.
Погрешность величины l в каждом измерении отдельным измерительным инструментом находится по методике расчета погрешностей прямых измерений, задавая доверительную вероятностьи коэффициент Стьюдента.
, (1.17)
где
, (1.18)
. (1.19)
2. Погрешность смешанных измерений вычисляется аналогично:
(1.20)
Сравниваются погрешности и объясняются расхождения.
Задание 2. Измерение объема параллелепипеда.
Такие измерения являются косвенными и их можно осуществить двумя способами.
Способ 1. Однократные измерения
Одним из измерительных инструментов один раз определяется длина одной грани параллелепипеда и результат записывается в виде:
(1.21)
Обработка результатов эксперимента.
1. Погрешность однократных косвенных измерений различными инструментами рассчитывается по формуле (1.10). Так как объем , то
,,,
и, следовательно,
,
то есть:
,
. (1.22)
Результат измерения представляется в виде
2. В том случае, если длина всех граней измерена одним и тем же инструментом с одинаковой погрешностью ,то
Способ 2. Повторные измерения
Осуществляются повторные измерения любым измерительным инструментом одной грани несколько раз, и результаты заносятся в таблицу.
Обработка результатов эксперимента.
Вычисляется среднее значение объема и погрешность
его определения по формуле (1.22):
, (1.23)
где ,,вычисляют по методике расчета погрешностей прямых измерений.
Любопытно провести эти измерения, используя для получения результата различные измерительные инструменты, вычислить погрешность и сравнить значения объема и погрешности, полученные при измерении линейкой, штангенциркулем и микрометром, а также при смешанных измерениях.
Задание 3. Измерение плоских углов транспортиром.
Для простейших измерений углов применяется транспортир, который представляет собой полукруг, дуга которого разделена на через. Чтобы измерить уголу,накладывают транспортир (рис. 1.4) так, чтобы вершина угла совпала с центром полукруга, а стороны – с радиусами ОА и ОВ. Тогда число градусов, содержащихся в дуге, заключенной между сторонами угла АОВ, дает числовое значение его величины. Погрешность измерения углов по транспортиру составляет половину деления шкалы – 0,5.
Рис. 1.4. Транспортир
Пример 5. Результат отсчета по шкале транспортира. Результат измерения
Более сложные и более точные приборы для измерения углов мы не рассматриваем.
1. Однократное измерение углов.
При выполнении этого задания проводятся однократные измерения углов треугольника из набора принадлежностей, оцениваются погрешности измерения и результат представляется в виде: , причем очевидно, что.
2. Многократные измерения углов.
Погрешности величин у, b, а находятся по формуле расчета погрешностей прямых измерений:
. (1.26)
И в первом, и во втором случае можно проверить результат, используя формулу . При этом погрешность суммы углов отличается от погрешности измерения отдельного угла и вычисляется по формуле
(1.27)
Задание 4. Измерение времени секундомером.
Для измерения времени применяются секундомеры. Механические секундомеры имеют цену деления 0,1 и 0,2 с.
Основная погрешность этих секундомеров равна цене деления, а погрешность отсчета зависит от быстроты реакции на включение и остановку секундомера. Установлено, что неточности пуска и остановки дают погрешность порядка 0,3 с. Таким образом, при работе с секундомером с ценой деления 0,2 с погрешность может достигать 0,5 с.
Применяются электронные секундомеры с ценой деления 0,01 и 0,001 с. Их целесообразно использовать вместе с устройствами, обеспечивающими совпадение пуска и остановки с началом и концом процесса, длительность которого определяется.
Пример 6.По индикатору электронного секундомера с ценой деления 0,01 с зарегистрировано некоторое время. Результат измеренияМетодика измерения интервалов времени и обработки результатов при однократных и повторных измерениях та же, что и в предыдущих заданиях по измерению линейных размеров и углов.
Задание 5. Измерение температуры термометром.
Термометр представляет собой капиллярную трубку из стекла, которая заполнена жидкостью, обычно ртутью или подкрашенным спиртом. Капиллярная трубка помещена в корпус из стекла, в котором также закреплена измерительная шкала. Погрешность измерения температуры термометрами различных типов регламентируется ГОСТ 400-80 и имеет, в большинстве случаев, величину, равную цене деления.
Методика измерения температуры и обработки результатов при однократных и многократных измерениях та же, что и в предыдущих заданиях.
Лабораторная работа 2
studfiles.net
1. Измерительные металлические линейки
Теоретические сведения
Измерительная линейка представляет собой металлическую полосу, на плоскости которой нанесены деления
Очень часто измерительные линейки называют штриховыми мерами. Это название указывает, что линейка является мерой и эта мера многозначная, а размер по ней определяют между штрихами.
Номенклатура измерительных линеек в принципе включает большую разновидность - от простейших ученических деревянных линеек до высокоточных металлических линеек, на которых имеется лупа для отсчета по шкале, и далее до линеек с точностью до долей микрометра, устанавливаемых в станках.
Металлические измерительные линейки изготавливают общей длиной от 150 до 1000 мм. Обычно промежуточные размеры имеют 300 и 500 мм.
Конструкции линеек в принципе однотипны, т.е. представляют собой металлическую полосу, на широкой поверхности которой нанесены деления, в подавляющем большинстве случаев через І мм между осями штрихов (рис. І, а). Иногда линейки делают с расстоянием 0,5 мм между штрихами, но практически пользоваться линейками с отсчитыванием 0,5 мм трудно, так же как и изготавливать такие линейки.
Нулевой штрих, т.е. начало отсчета в линейках, обычно находится с левой стороны, совпадая с концом линейки. и это дает основание считать, что линейка со стороны нулевого штриха является концевой мерой.
Линейки изготавливают либо с одной, либо с двумя шкалами.
Иногда изготавливают линейки, у которых нулевые деления имеются и с левой, и с правой стороны. Ширина линейки обычно в среднем бывает 20-40 мм, а толщина - 0,5-1,0 мм. Поверхность линейки подвергают хромированию для предохранения от коррозии.
Измерение линейкой производится так называемым непосредственным методом, т.е. прикладыванием ее к измеряемому объекту и сопоставлением его длины со значением меры. Чаще всего эти измерения осуществляют совмещением нулевого штриха линейки с краем детали. Непосредственным называется метод измерения, в котором значение величины определяют непосредственно по отсчетному устройству измерительного средства.
Погрешность измерения линейкой складывается из погрешности нанесения делений, погрешности совмещения штрихов с краями измеряемой детали и погрешности отсчета значения. Если погрешность нанесения штрихов на линейках обычно находится в пределах 0.1-0.2 мм (в зависимости от длины), то погрешность отсчета доходит до 0.2-0.3 мм и более. В общем случае можно принять, что погрешность измерения находится в пределах 0.5 мм при условии острых краев измеряемой детали и тщательности измерения, но в большинстве случаев при измерении линейкой удовлетворяются погрешностью измерения в пределах 1 мм.
Поверку линеек, т.е. определение погрешности нанесения штрихов, производят по образцовым измерительным линейкам, которые называют штриховыми метрами. Штриховой метр (рис.1,б) представляет собой более жесткую конструкцию, чем обычные линейки. На скосах этого метра нанесены деления через 0.2 мм с погрешностью в пределах 0.05 мм. На специальных направляющих метра помещают две каретки с кронштейнами, на которых находятся лупы с 7-кратным увеличением. При проверке измерительной линейки штриховой метр устанавливают на проверяемую линейку и сравнивают шкалы обеих линеек. Погрешность такого сравнения не превышает 0.01 мм.
studfiles.net
Измерительная металлическая линейка - Большая Энциклопедия Нефти и Газа, статья, страница 1
Измерительная металлическая линейка
Cтраница 1
Измерительные металлические линейки изготовляются из стальной пружинной термообработанной ленты со светлополпровашшй поверхностью длиной до 1 м и с ценой деления 1 мм. Складные металлические метры изготовляются длиной 1 м и состоят из 10 стальных упругих пластин, соединенных шарнирно. Измерительные металлические рулетки выпускаются 2-го и 3-го классов точности. Допускаемые отклонения действительной длины миллиметровых делений рулеток должны быть не более 0.15 и 0 20 мм, сантиметровых - не более 0 20 и 0 30 мм, дециметровых и метровых - не более 0 30 и 0 40 мм для 2-го и 3-го классов точности соответственно. Металлические измерительные линейки должны иметь отклонения между любыми штрихами не более 0 10 мм для линеек длиной до 300 мм, 0 15 мм для линеек длиной от 300 до 500 мм и 0 20 мм для линеек длиной от 500 до 1000 мм. [1]
Измерительные металлические линейки применяются для грубых измерений при ремонтных работах и изготовляются по ГОСТ 427 - 56 с одной или двумя шкалами с верхними пределами измерений 150, 300, 500 и 1000 мм. [2]
Измерительные металлические линейки предназначаются для линейных измерений непосредственным сравнением измеряемых размеров со шкалой меры. Они изготавливаются длиной 150; 300; 500 и 1000 мм из стальной пружинной термообработанной ленты с наименьшим интервалом между делениями 1 мм. Допускаемые отклонения миллиметровых делений составляют 0 05 мм, сантиметровых 0 10 мм. [4]
Измерительные металлические линейки применяются для грубых измерений при ремонтных работах и изготовляются по ГОСТ 427 - 56 с одной или двумя шкалами с верхними пределами измерений 150, 300, 500 и 1000 мм. [5]
Измерительные металлические линейки предназначены для непосредственных измерений длин. [6]
Измерительные металлические линейки имеют длину 150, 300, 500 и 1000 мм. Цена деления составляет 0 5 или 1 мм. Точность намерения равна 0 25 мм. [7]
Измерительные металлические линейки изготовляют длиной 150 - 1000 мм с ценой деления 0 5 или 1 мм. Складные металлические метры имеют развернутую длину 1000 мм, цена деления 1 мм. Измерительные металлические рулетки выпускают длиной 1 - 50 м, цена деления шкалы 1 мм. [8]
Измерительные металлические линейки изготовляют с одной или двумя шкалами длиной 150, 300, 500 и 1000 мм с ценой деления 0 5 или 1 мм. Для линеек длиной до 300 мм погрешность по длине не должна превышать 0 1 мм, до 1 м 0 2 мм. Линейки должны быть защищены антикоррозионным хромовым покрытием. [9]
Измерительные металлические линейки изготовляют с одной или двумя шкалами длиной 150, 300, 500 и 1000 мм. [10]
Простейшим штриховым инструментом является измерительная металлическая линейка. [11]
Для пространственной разметки применяют следующие инструменты: измерительную металлическую линейку, вертикальную измерительную линейку с подставкой, проверочные и разметочные угольники, чертилку, рейсмас, штангенрейсмас, циркуль, кернеры и молоток. Эти инструменты описаны в гл. [13]
Прямолинейность тяг тензометра, применяемых для передачи деформации образца на измерительное устройство, проверяют измерительной металлической линейкой, прикладываемой ребром. Зазор не должен превышать 0 3 мм. [14]
Точность установки монтируемого оборудования выверяют измерительными инструментами и приспособлениями. Измерительные металлические линейки ( рис. 96, а, б) изготовляют с одной или двумя шкалами длиной 150, 300, 500 и 1000 мм с ценой деления 0 5 или 1 мм. Для линеек длиной до 300 мм погрешность по длине не должна превышать 0 1 мм, длиной до 1 м - 0 2 мм. Линейки должны быть защищены антикоррозионным хромовым покрытием. [15]
Страницы: 1 2
www.ngpedia.ru
Физические величины. Точность и погрешность измерений
Физические величины. Точность и погрешность измерений
Измерять – значит, познавать
Данная тема посвящена физическим величина и их измерениям. В физике часто приходится измерять те или иные величины. Измерить можно высоту дома или длину улицы.
Можно измерить объём воды в колбе или массу воды в стакане.
Но что означают эти измерения? Измерить какую-либо величину – значит сравнить её с однородной величиной, принятой за единицу. Из приведённых выше примеров, можно заметить, что, например, единицей объёма является литр, а единицей массы является грамм. Для удобства была введена международная система единиц, которая называется СИ.
В этой системе длина измеряется в метрах, масса в килограммах, объём - в кубических метрах, время – в секундах и так далее. В процессе изучения физики будут вводиться новые величины и соответствующие им единицы измерения. Иногда физические величины можно не измерять, а вычислять по формуле. Например, для того, чтобы вычислить среднюю скорость нужно пройденное расстояние разделить на время. То есть, данная формула помогает вычислить такую физическую величину, как средняя скорость.
Известно что, иногда применяются единицы измерения, которые в десятки, сотни, тысячи и так далее раз больше принятых единиц измерения. Такие единицы измерения называются кратными.
Каждая приставка соответствует тому или иному множителю. Например, «Дека» означает в 10 раз больше, «гекто» - в сто раз больше, «кило» - в тысячу раз больше, «мега» - в миллион раз больше и так далее. Необходимо отметить, что в физике принято записывать такие множители в виде степени числа 10. Например, вместо миллиона записывается 106. Также, могут быть использованы единицы, которые в десятки, сотни, тысячи и так далее раз меньше принятых единиц измерения. Такие единицы измерения называются дольными.
Каждая приставка соответствует тому или иному множителю. Например, «Деци» означает в 10 раз меньше, «санти» - в сто раз меньше, «милли» - в тысячу раз меньше, «микро» - в миллион раз меньше и так далее. Эти приставки также записываются в виде степени числа 10. Например, вместо записи числа 0,000001 записывается 10–6.
У каждого ученика имеется линейка, длина которой измеряется в сантиметрах, то есть в единицах, которые в сто раз меньше метра. Поэтому, если длина линейки составляет 15 сантиметров, мы можем сказать, что её длина 0,15 метра.
Линейка – это прибор для измерения длины. Конечно, линейка относится к самым простым измерительным приборам. Существуют значительно более сложные приборы: например, термометр, который применяется для измерения температуры, гигрометр, который используется для измерения влажности или амперметр, который используется для измерения силы электрического тока.
Важно знать, как пользоваться измерительными приборами и насколько могут быть точны те или иные измерения. У каждого ученика есть линейка и карандаш. Можно попытаться измерить длину карандаша. В первую очередь нужно определить, какова цена деления измерительного прибора. Для этого необходимо найти два ближайших штриха шкалы, возле которых указаны значения величины (например, 1 см и 2 см). Далее нужно сосчитать число делений, заключенных между цифрами 1 и 2. При подсчёте получается, что количество этих делений равно 10. Таким образом, между отметками 1 см и 2 см заключено десять делений. Вычитаем из большего числа меньшее и делим на количество делений между ними. В результате вычислений получаем, что цена деления линейки составляет 0,1 см или 1 мм. Данный пример объясняет, как определить цену деления любого измерительного прибора.
Как видно из рисунка, длина карандаша чуть меньше десяти сантиметров. Если бы на этой линейке не было миллиметровых делений, то можно было сказать, что длина карандаша равна десяти сантиметрам. Но это было бы не совсем точное измерение. Такую неточность называют погрешностью измерения. В представленном случае, на линейке есть миллиметровые деления, поэтому можно измерить длину карандаша с более высокой точностью – 9,8 см. Это говорит о том, что чем меньше цена деления, тем больше точность измерения. Ну а большая точность измерения означает меньшую погрешность. Однако абсолютно точных измерений не существует. Если дать один и тот же карандаш каждому ученику из класса и попросить измерить длину карандаша, не у всех получится одинаковый результат. Тем не менее, погрешность измерения не может быть больше цены деления. Например, если видно, что длина карандаша не точно 9,8 см, а чуточку больше, то понятно, что длина карандаша находится в промежутке от 9,8 см до 9,9 см.
Погрешность измерений принято считать равной половине цены деления измерительного прибора. То есть, в рассмотренном случае, погрешность измерений составляет 0,5 мм. Поэтому, после того, как измерили карандаш и записали, что его длина равна 9,8 см, следует записать погрешность.
Знак «±» означает, что указанная длина может быть на полмиллиметра больше или на полмиллиметра меньше. Таким образом, истинное значение длины карандаша находится в промежутке от 9,75 см до 9,85 см.
В общем случае запись измеряемых величин с учетом погрешности имеет следующий вид:
где А – измеряемая величина;
а – результат измерения;
Da – погрешность измерений.
Необходимо отметить, что при сложении или вычитании величин с погрешностью, погрешность результата равна сумме погрешностей каждой величины. В этом легко убедиться на примере. На рисунке показаны два отрезка AB и CD, длины которых измерены с определенной погрешностью.
Рассчитаем сумму длин этих отрезков. Из рисунка видно, что отрезок AB равен 1 м ± 1 см. Истинная длина этого отрезка находится в промежутке 99 см ≤ АВ ≤ 101 см. Отрезок CD равен 12 см ± 0,5 см. Истинная длина этого отрезка находится в промежутке от 11,5 см ≤ CD ≤ 12,5 см. Поэтому, сумма длин этих отрезков будет иметь еще большую погрешность. Прежде чем производить вычисления, необходимо перевести обе длины в одинаковые единицы измерения.
Таким образом, получаем, что сумма длин отрезков AB и CD равна
Важно отметить, что этот же промежуток мы бы получили, если бы сложили наименьшие и наибольшие длины отрезков AB и CD. Следовательно, при сложении или вычитании величин, измеренных с погрешностями, погрешность результата равна сумме погрешностей каждой из величин.
Упражнения.
Упражнение 1. Заполните таблицу, указав, что из перечисленных слов является физическим телом, единицей измерения, физической величиной или физическим явлением: ветер, Луна, килограмм, дерево, длина, скорость, испарение.
Решение:
Упражнение 2. Родители измерили рост братьев Димы и Васи с помощью рулетки, цена деления которой 1 см. Подсчитайте, насколько см Дима выше, чем Вася.
Решение:
Упражнение 3. Найдите суммарную массу животных с погрешностью.
Решение:
Основные выводы:
– Для описания физических тел или физических явлений вводится физическая величина, которую можно измерить с помощью измерительных приборов или вычислить по формуле.
– Измерение величины – это сравнение её с однородной величиной, принятой за единицу.
– Кратные приставки – это приставки означающие увеличение в десятки, сотни, тысячи и так далее раз.
– Дольные приставки – это приставки, означающие уменьшение в десятки, сотни, тысячи и так далее раз.
– Погрешность измерений – неточность допускаемая при измерении. За погрешность измерений данного прибора принимают половину цены деления этого прибора.
– При сложении или вычитании величин с погрешностями, погрешность результата вычислений равна сумме погрешностей каждой величины.
videouroki.net
Точность и погрешность измерений — урок. Физика, 7 класс.
Измерить какую-нибудь величину — это значит сравнить её с однородной величиной, принятой за единицу.
Всякое измерение может быть выполнено с большей или меньшей точностью.В качестве примера рассмотрим измерение длины бруска линейкой с сантиметровыми делениями.

Вначале определим цену деления линейки. Она будет равна \(1\) см. Если левый конец бруска совместить с нулевым штрихом, то правый будет находиться между \(9\) и \(10\) штрихами, но ближе к \(10\). Какое же из этих двух значений следует принять за длину бруска? Очевидно, то, которое ближе к истинному значению, т.е. \(10\) см. Считая, что длина бруска \(10\) см, мы допустим неточность, так как брусок чуть короче \(10\) см.
В физике допускаемую при измерении неточность называют погрешностью измерений.
Погрешность измерения не может быть больше цены деления измерительного прибора. В нашем случае погрешность измерения бруска не превышает \(1\) см. Если такая точность измерений нас не устраивает, то можно произвести измерения с большей точностью. Но тогда придётся взять масштабную линейку с миллиметровыми делениями, т.е. с ценой деления \(1\) мм. В этом случае длина бруска окажется равной \(9,8\) см.

Для более точных измерений можно воспользоваться штангенциркулем с ценой деления \(0,1\) мм или \(0,05\) мм.

Из этого примера видно, что точность измерений зависит от цены деления шкалы прибора.
Чем меньше цена деления, тем больше точность измерения.
Точность измерения зависит от правильного применения измерительного прибора, расположения глаз при отсчёте по прибору.Вследствие несовершенства измерительных приборов и несовершенства в развитии наших органов чувств, при любом измерении получаются лишь приближённые значения, несколько бóльшие или меньшие истинного значения измеряемой величины.
Во время выполнения лабораторных работ или просто измерений следует считать, что:
Погрешность измерений равна половине цены деления шкалы измерительного прибора.
При записи величин (с учётом погрешности) следует пользоваться формулой: A=a±Δa, где \(A\) — измеряемая величина, \(a\) — результат измерений, Δa — погрешность измерений (Δ — греческая буква «дельта»).
Источники:
Пёрышкин А.В. Физика. 7 кл. – 14-е изд., стереотип. – М.: Дрофа, 2010.
www.yaklass.ru
Как пользоваться штангенциркулем, микрометром, линейкой
С измерением длины, ширины и высоты домашнему мастеру приходится сталкиваться постоянно. Угол в 90° или 45° тоже не редко приходится выдерживать. Иначе качественно ремонт квартиры или изготовление самоделок не выполнить. Точности при выполнении линейных измерений 1 мм в подавляющем большинстве случаев достаточно, и для них подойдет рулетка или простая линейка.

Зачастую рулетки имеют дополнительно пузырьковый уровень, который позволяет выставить горизонтально мебель, холодильник и другие предметы. Но точность такого уровня не высокая из-за маленькой длины опорной плоскости рулетки. В дополнение колбочка с пузырьком воздуха в рулетках часто установлена не точно, что не обеспечивает горизонтальность и выполненной работы.
В продаже, для измерения линейных размеров представлен широкий ряд лазерных измерительных приборов, но, к сожалению, из-за высокой цены они не доступны для непрофессионалов.
Инструкцияпо применению штангенциркуля (колумбуса)
Штангенциркуль – это линейный измерительный инструмент служащий для измерения наружных и внутренних размеров деталей включая глубину, с точностью 0,1 мм.
Измерить диаметр сверла, самореза и размеры других небольших деталей с достаточной точностью линейкой не получится. В таких случаях нужно использовать штангенциркуль, который позволяет измерять линейные размеры с точностью до 0,1 мм. С помощью штангенциркуля можно выполнить измерение толщины листового материала, внутреннего и внешнего диаметров трубы, диаметр высверленного отверстия, его глубину и другие измерения.
Штангенциркули бывают с отсчетом измеряемой величины по линейке и нониусу, циферблату часового типа и цифровому индикатору. Разновидность штангенциркуля с линейкой для измерения глубины отверстий профессионалы еще называют «Колумбус».

Доступным по цене, высоконадежным является штангенциркуль с нониусом типа ШЦ-1 с диапазоном измерений от 0 до 125 мм, что для большинства случаев вполне достаточно. Штангенциркуль ШЦ-1 дополнительно позволяет измерять диаметр отверстий и глубину.
В настоящее время в продаже появился цифровой пластиковый штангенциркуль китайского производства ценой менее $4, фотография которого представлена ниже.

Штангенциркуль из пластмассы, хотя его губки сделаны из карбона, назвать измерительным инструментом сложно, так как он не сертифицирован и поэтому точность показаний 0,1 мм заявленная производителем не гарантирована. В дополнение при частом использовании пластик быстро износится, и погрешность показаний увеличится.
Штангенциркуль из пластмассы, если его показания точны для домашних редких измерений вполне подойдет. Для проверки штангенциркуля можно измерять хвостовик сверла, на котором выбит размер или диаметр штыря электрической вилки.
Устройство и принцип работы нониуса штангенциркуля
Устроен классический штангенциркуль следующим образом. На измерительной штанге с помощью пазов установлена подвижная рамка. Для того, чтобы рамка плотно сидела, внутри установлена плоская пружина и предусмотрен винт, для жесткой ее фиксации. Фиксация необходима при проведении разметочных работ.
На штанге нанесена метрическая шкала с шагом 1 мм и цифрами обозначены сантиметровые деления. На рамке нанесена дополнительная шкала с 10 делениями, но с шагом 1,9 мм. Шкала на рамке называется нониусом в честь ее изобретателя португальского математика П.Нуниша. Штанга и рамка имеют измерительные губки для наружных и внутренних измерений. К рамке дополнительно закреплена линейка глубиномера.

Измерения выполняются зажимом между губками детали. После зажима рамка фиксируется винтом для того, чтобы она не сместилась. Количество миллиметров отсчитывается по шкале на штанге до первой риски нониуса. Десятые доли миллиметров отсчитываются по нониусу. Какой штрих по счету слева на право на нониусе совпадет с любой из рисок шкалы на штанге, столько и будет десятых долей миллиметра.

Как видно на фото, измеренный размер составляет 3,5 мм, так как от нулевой отметки шкалы на штанге до первой риски нониуса получилось 3 полных деления (3 мм) и на нониусе совпала с риской шкалы штанги риска пятого деления нониуса (одно деление на нониусе соответствует 0,1 мм измерений).
Примеры измерения штангенциркулем
Для измерения толщины или диаметра детали нужно развести губки штангенциркуля, вставить в них деталь и свести губки до соприкосновения с поверхностью детали. Надо проследить, чтобы плоскости губок при смыкании были параллельны плоскости измеряемой детали. Внешний диаметр трубы измеряется точно так же, как и размер плоской детали, только нужно, чтобы губки прикасались к диаметрально противоположным сторонам трубы.

Для того, чтобы измерять внутренний размер в детали или внутренний диаметр трубы, у штангенциркуля есть дополнительные губки для внутренних измерений. Их заводят в отверстие и раздвигают до упора в стенки детали. При измерении внутренних диаметров отверстий добиваются максимального показания, а при измерении в отверстии параллельных сторон, добиваются минимальных показаний.

В некоторых типах штангенциркулей губки не смыкаются до нуля и имеют собственную толщину, которая обычно на них выбита, например, число «10», хотя первая риска нониуса стоит на нулевой отметке. В случае измерения внутренних отверстий таким штангенциркулем к считанным показаниям по шкале нониуса добавляется 10 мм.
С помощью штангенциркуля типа колумбус, имеющего подвижную линейку глубиномера можно измерять глубину отверстий в деталях.

Для этого нужно полностью выдвинуть линейку глубиномера из штанги, вставить ее до упора в отверстие. Подвести до упора в поверхность детали торца штанги штангенциркуля, при этом не допуская выхода линейки глубиномера из отверстия.

На фотографии, для наглядности, я продемонстрировал измерение глубины отверстия, приложив линейку глубиномера штангенциркуля с внешней стороны отрезка трубы.
Примеры выполнения разметки деталей штангенциркулем
Штангенциркуль не предназначен для нанесения разметочных линий на материалах и деталях. Но если губки штангенциркуля для наружных измерений заточить на мелкозернистом наждачном круге, придав им острую форму, как показано на фотографии, то разметку штангенциркулем производить будет довольно удобно.
Снимать лишний металл с губок нужно очень аккуратно и медленно, не допуская цветов побежалости металла губок от сильного разогрева, иначе можно их испортить. Чтобы ускорить работу, для охлаждения губок, можно периодически окунать их на непродолжительное время в емкость с холодной водой.

Для того, чтобы отмерять полоску листового материала с параллельными сторонами, нужно раздвинуть губки штангенциркуля ориентируясь по шкале на заданный размер, одной губкой вести по торцу листа, а второй процарапать линию. Так как губки штангенциркуля закалены, они не истираются. Можно размечать как мягкие материалы, так и твердые (медь, латунь, сталь). Остаются хорошо видные риски.

С помощью заточенных остро губок штангенциркуля можно легко наметить линию окружности. Для этого в центре делается неглубокое отверстие диаметром около 1 мм, в него упираясь одной из губок, второй прочерчивают линию окружности.

Благодаря доработке формы губок штангенциркуля для наружных измерений, появилась возможность точно, удобно и быстро выполнять разметку деталей для их последующей механической обработки.
Как измерять микрометром на практике
Получить размер изделий с точностью 0,01 мм можно выполнив измерения микрометром. Их много модификаций, но самый распространенный это гладкий микрометр типа МК-25, обеспечивающий диапазон измерений от 0 до 25 мм с точностью 0,01 мм. Микрометром удобно измерять диаметр сверла, толщину листового материала, диаметр провода.

Микрометр представляет собой скобу, с одной стороны которой находится опорная пятка, а с другой имеется стебель и высокоточная резьба, в которую закручивается микровинт. На стебле нанесена метрическая шкала, по которой выполняется отсчет миллиметров. На микровинте имеется вторая шкала с 50 делениями, по которой отсчитываются сотые доли мм. Сумма этих двух величин является измеренным размером.
Для того, чтобы выполнить измерение микрометром, деталь размещают между пяткой и торцом микрометрического винта и вращают по часовой стрелке за ручку трещотки (находится на торце барабана микрометрического винта) до тех пор, пока трещотка не издаст три щелчка.

На стебле нанесено две шкалы с шагом 1 мм – основная оцифрованная через каждых 5 мм и дополнительная, сдвинутая относительно основной на 0,5 мм. Наличие двух шкал позволяет повысить тонность измерений.
Отсчет показаний выполняется следующим образом. Сначала считывают, сколько целых, не закрытых барабаном, миллиметров получилось по оцифрованной, нижней шкале на стебле. Далее проверяют по верхней шкале наличие риски, расположенной правее от риски нижней шкалы. Если риски не видно, то переходят к снятию показаний со шкалы на барабане. Если риска просматривается, значит, к целому числу полученных миллиметров добавляется еще 0,5 мм. Показания на барабане отсчитывают относительно прямой линии, нанесенной вдоль стебля между шкалами.
Например, размер измеренной детали составляет: 13 мм по нижней шкале, на верхней шкале открытой метки, правее открытой на нижней шкале нет, значить 0,5 мм добавлять не нужно, плюс 0,23 мм по шкале барабана, в результате сложения получаем: 13 мм+0 мм+0,23 мм=13,23 мм.
Микрометр с цифровым отсчетом результатов измерений применять удобнее и позволяет измерять с точностью до 0,001 мм.

Если, например, села батарейка, то цифровым микрометром можно выполнять измерения точно так же, как и гладким МК-25, так как имеется и система отсчета по делениям с точностью 0,01 мм. Цена микрометров с цифровым отсчетом результатов измерений высока и для домашнего мастера неподъемна.
Как измерять трубу большого диаметра
Губки штангенциркуля с диапазоном измерений от 0 до 125 мм имеют длину 40 мм и поэтому позволяют измерять трубы с внешним диаметром до 80 мм. В случае необходимости измерять трубу большего диаметра или при отсутствии под рукой штангенциркуля можно воспользоваться народным способом. Обвить трубу по окружности одним витком не растягивающейся нитки или проволоки, измерять длину этого витка с помощью простой линейки, а затем разделить полученный результат на число Π=3,14.
Не смотря на простоту, такой способ измерения диаметра трубы позволяет обеспечить точность 0,5 мм, что для домашнего мастера вполне достаточно. Для более точного измерения нужно намотать больше витков.
Как измерять угол
Для получения заданного угла при разметке можно воспользоваться транспортиром, с которым все познакомились еще в школе на уроках геометрии. Для измерения в быту точности его вполне достаточно.

На фотографии представлена пластмассовая линейка в виде треугольника, имеющего углы 45º и 90º, с встроенным транспортиром. С помощью него можно выполнить разметку и проверить точность полученного угла.

При выполнении разметки металлических деталей используют слесарный металлический угольник, обеспечивающие более высокую точность измерений.
Как пользоваться стуслом
Для получения прямого или угла 45º без разметки, удобно использовать приспособление, которое называется стусло. С помощью стусла удобно пилить в размер под углом наличники для дверей, багет, плинтуса и многое другое. Распил получается с требуемым углом автоматически.

Достаточно отмерять длину, вложить полоску материала между вертикальными стенками стусла и удерживая рукой выполнить распил. Для получения качественного торца доски следует использовать пилу с мелкими зубцами. Хорошо подходит ножовка по металлу. Удается распиливать даже лакированные доски без сколов лака.

Угол 450 при пилении с использования стусла, получается также легко, как и прямой. Благодаря высоким направляющим стенок стусла можно распиливать доски разной толщины.

Стусло можно купить готовое, но его не сложно сделать самостоятельно из подручного материала. Достаточно взять три доски из дерева или фанеры подходящего размера, и к боковым торцам одной из них саморезами прикрутить две другие. Сделать направляющие пропилы под требуемыми углами и приспособление стусло готово.
ydoma.info
Измерение линейных размеров,
ОПРЕДЕЛЕНИЕ ПЛОЩАДЕЙ, ОБЪЕМОВ
И ПЛОТНОСТИ ТВЕРДЫХ ТЕЛ
Цель работы: ознакомиться с работой нониуса, научиться проводить измерения линейных размеров тел c помощью штангенциркуля и микрометра и определять погрешности при измерениях и расчетах.
Принадлежности: штангенциркуль, микрометр, набор измеряемых тел.
Вопросы, знание которых обязательно для допуска к выполнению работы
Что называется нониусом?
Что такое цена деления? Как определить цену деления нониуса?
Что называется приборной погрешностью?
В каких случаях следует пользоваться штангенциркулем, в каких – микрометром?
Как определяется среднее арифметическое значение измерений?
Что называется абсолютной погрешностью (средней абсолютной погрешностью) измерений?
Что называется относительной погрешностью измерений?
Как рассчитать погрешность прямых измерений?
Как рассчитывается погрешность косвенных измерений в вашей работе?
Какие цифры называются значащими?
Как записывают окончательный результат физических измерений?
Расскажите порядок выполнения работы.
Введение
В науке, технике, повседневной жизни для измерения линейных величин пользуются различными приборами и инструментами.
Измерения длины производят масштабными линейками. Величина наименьшего деления такой линейки называется ценой одного деления. Обычно цена одного деления линейки равна 1 мм. Если измерения производят с точностью до долей миллиметра, то пользуются вспомогательной шкалой измерительного инструмента – нониусом. Для измерения линейных величин применяют линейный нониус.
Линейным нониусом называется специальная шкала, дополняющая обычный масштаб и позволяющая повысить точность измерений в 10…20 раз. Нониус служит для отсчета десятых долей меньшего деления масштабной линейки. Величина деления нониуса обычно меньше наименьшего деления масштабной линейки, а вся шкала нониуса равна 1 мм. Соответственно, определив количество делений на шкале нониуса, мы сможем определить и цену деления данной шкалы, поделив 1 мм на количество делений шкалы нониуса. Измерение с помощью нониуса производится следующим образом: измеряемый объект устанавливается так, чтобы один конец его совпадал с нулем масштабной линейки, а сам объект располагался вдоль нее; нуль нониуса совмещается с другим концом измеряемого объекта. Для измерения длины нужно измерить по шкале масштабной линейки расстояние между нулем масштабной линейки и нулем нониуса. Таким образом, число целых делений отсчитывается по масштабной линейке. Число десятых и сотых делений определяется по значению деления нониуса. На шкале нониуса выбирается деление, точно совпадающее с делением масштабной линейки. Затем величина данного деления умножается на цену деления нониуса.
Нониусами снабжают штангенциркули (рис. 2) и микрометры (рис. 3).
Рис. 1 Рис. 3
В микрометре используются микрометрические винты – винты с малым и очень точно выдержанным шагом. Один поворот винта микрометра передвигает его стержень на 0,5 мм. Барабан, связанный со стержнем, разбит на 50 делений. Поворот на одно деление соответствует смещению стержня на 0,01 мм. С этой точностью обычно и производятся измерения с помощью микрометра.
studfiles.net
423800, Набережные Челны , база Партнер Плюс, тел. 8 800 100-58-94 (звонок бесплатный)