|
||||
|
|
звонок бесплатный
Наши сотрудники:
[email protected]
Екатерина - специалист по продаже а/м КАМАЗ
 [email protected]
[email protected]






Техника в наличии

Тягач КАМАЗ 44108-6030-24
2014г, 6х6, Евро3, дв.КАМАЗ 300 л.с., КПП ZF9, бак 210л+350л, МКБ,МОБ,рестайлинг.
цена 2 220 000 руб.,

КАМАЗ 4308-6063-28(R4)
4х2,дв. Cummins ISB6.7e4 245л.с. (Е-4),КПП ZF6S1000, V кузова=39,7куб.м., спальное место, бак 210л, шк-пет,МКБ, ТНВД BOSCH, система нейтрализ. ОГ(AdBlue), тент, каркас, рестайлинг, внутр. размеры платформы 6112х2470х730 мм
цена 1 950 000 руб.,

Самосвал КАМАЗ 6520-057
2014г, 6х4,Евро3, дв.КАМАЗ 320 л.с., КПП ZF16, ТНВД ЯЗДА, бак 350л, г/п 20 тонн, V кузова =20 куб.м.,МКБ,МОБ, со спальным местом.
цена 2 700 000 руб.,

Самосвал 6522-027
2014, 6х6, дв.КАМАЗ 740.51,320 л.с., КПП ZF16,бак 350л, г/п 19 тонн,V кузова 12куб.м.,МКБ,МОБ,задняя разгрузка,обогрев платформы.
цена 3 190 000 руб.,
СУПЕР ЦЕНА
на АВТОМОБИЛИ КАМАЗ
| 43118-010-10 (дв.740.30-260 л.с.) | 2 220 000 |
| 43118-6033-24 (дв.740.55-300 л.с.) | 2 300 000 |
| 65117-029 (дв.740.30-260 л.с.) | 2 200 000 |
| 65117-6010-62 (дв.740.62-280 л.с.) | 2 350 000 |
| 44108 (дв.740.30-260 л.с.) | 2 160 000 |
| 44108-6030-24 (дв.740.55,рест.) | 2 200 000 |
| 65116-010-62 (дв.740.62-280 л.с.) | 1 880 000 |
| 6460 (дв.740.50-360 л.с.) | 2 180 000 |
| 45143-011-15 (дв.740.13-260л.с) | 2 180 000 |
| 65115 (дв.740.62-280 л.с.,рест.) | 2 190 000 |
| 65115 (дв.740.62-280 л.с.,3-х стор) | 2 295 000 |
| 6520 (дв.740.51-320 л.с.) | 2 610 000 |
| 6520 (дв.740.51-320 л.с.,сп.место) | 2 700 000 |
| 6522-027 (дв.740.51-320 л.с.,6х6) | 3 190 000 |

подробнее про услугу перегона можно прочесть здесь.

|
Нужны самосвалы? Обратите внимание на Ford-65513-02. |
КАМАЗы в лизинг
ООО «Старт Импэкс» имеет возможность поставки грузовой автотехники КАМАЗ, а так же спецтехники на шасси КАМАЗ в лизинг. Продажа грузовой техники по лизинговым схемам имеет определенные выгоды для покупателя грузовика. Рассрочка платежа, а так же то обстоятельство, что грузовики до полной выплаты лизинговых платежей находятся на балансе лизингодателя, и соответственно покупатель автомобиля не платит налогов на имущество. Мы готовы предложить любые модели бортовых автомобилей, тягачей и самосвалов по самым выгодным лизинговым схемам.Контактная информация.
г. Набережные Челны, Промкомзона-2, Автодорога №3, база «Партнер плюс».
тел/факс (8552) 388373.
Схема проезда
Вес тела. Сила реакции опоры. Сила натяжения нити. Формула сила натяжения троса
Формула силы натяжения нити
ОПРЕДЕЛЕНИЕСила натяжения нити равна сумме сил, действующих на нить, и противоположна им по направлению.
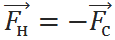
Здесь 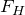 – сила натяжения нити,
– сила натяжения нити, 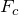 – векторная сумма сил, действующих на нить.
– векторная сумма сил, действующих на нить.
Единица измерения силы – Н (ньютон).
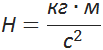
Эта формула – следствие третьего закона Ньютона применительно к нити. Если на нити подвешен какой-то груз, который находится в покое, то сила натяжения нити по модулю равна весу этого груза. Обычно в задачах участвует невесомая нерастяжимая нить, которая просто проводит через себя силу, однако встречаются задачи, где нить под воздействием силы растягивается. При этом она ведёт себя как пружина, подчиняясь закону Гука:
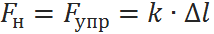
Где  – жёсткость нити,
– жёсткость нити,  — удлинение нити.
— удлинение нити.
Примеры решения задач по теме «Сила натяжения нити»

| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Вес тела. Сила реакции опоры. Сила натяжения нити | LAMPA
Многие из вас пользуются или пользовались обычной проводной компьютерной мышкой. Если такая проводная мышка рядом с вами, то посмотрите на нее (а если ее нет рядом — то представьте). Мы знаем, что, как и на все тела на Земле, на нее действует сила тяжести Fтяготения=m⋅gF_{тяготения}=m\cdot gFтяготения=m⋅g.


- на тело действует сила тяжести m⋅g⃗m\cdot\vec{g}m⋅g⃗
- из-за действия силы тяжести на мышку мышка давит на стол с силой P⃗\vec{P}P⃗ (вес тела)
- и уже стол "отвечает" мышке на ее давление силой реакции опоры N⃗\vec{N}N⃗.
Важно помнить, что хотя силы N⃗\vec{N}N⃗ и P⃗\vec{P}P⃗ связаны друг с другом и равны по модулю, но приложены они к разным телам. Еще раз:
- вес тела P⃗\vec{P}P⃗ приложен к опоре (столу) со стороны мышки
- сила реакции опоры N⃗\vec{N}N⃗ приложена к мышке со стороны стола как "ответ" стола на действие мышки.
Давайте посмотрим, насколько хорошо вы усвоили разницу между весом P⃗\vec{P}P⃗ и силой реакции опоры N⃗\vec{N}N⃗. Попробуйте решить классическую задачу.
lampa.io
Формулы нахождения силы натяжения нити и всё, что с этим связано
Силой натяжения называют ту, что действует на объект, сравнимый с проволокой, шнуром, кабелем, ниткой и так далее. Это могут быть несколько объектов сразу, в таком случае сила натяжения будет действовать на них и необязательно равномерно. Объектом натяжения называют любой предмет, подвешенный на все вышеперечисленное. Но кому это нужно знать? Несмотря на специфичность информации, она может пригодиться даже в бытовых ситуациях.
Например, при ремонте дома или квартиры. Ну и, конечно же, всем людям, чья профессия связана с расчетами:
- инженерам;
- архитекторам;
- проектировщикам и пр.
Натяжения нити и подобных объектов
А зачем им это знать и какая от этого практическая польза? В случае с инженерами и конструкторами знания о мощи натяжения позволят создавать устойчивые конструкции. Это означает, что сооружения, техника и прочие конструкции смогут дольше сохранять свою целостность и прочность. Условно, эти расчеты и знания можно разделить на 5 основных пунктов, чтобы в полной мере понять, о чем идет речь.
1 Этап
Задача: определить силу натяжения на каждом из концов нити. Эту ситуацию можно рассматривать как результат воздействия сил на каждый конец нити. Она равняется массе, помноженной на ускорение свободного падения. Предположим, что нить натянута туго. Тогда любые воздействия на объект приведет к изменению натяжения (в самой нити). Но даже при отсутствии активных действий, по умолчанию будет действовать сила притяжения. Итак, подставим формулу: Т=м*g+м*а, где g – ускорение падения (в данном случае подвешенного объекта), а – любое иное ускорение, действующее извне.
Есть множество сторонних факторов, влияющих на расчеты – вес нити, ее кривизна и так далее. Для простых расчетов это мы не будем пока что учитывать. Иными словами – пусть нить будет идеальна с математической точки зрения и «без изъянов».
Возьмем «живой» пример. На балке подвешена прочная нить с грузом в 2 кг. При этом отсутствует ветер, покачивания и прочие факторы, так или иначе влияющие на наши расчеты. Тогда мощь натяжения равна силе тяжести. В формуле это можно выразить так: Fн=Fт=м*g, в нашем случае это 9,8*2=19,6 ньютона.
2 Этап
Заключается он в вопросе об ускорении. К уже имеющейся ситуации давайте добавим условие. Суть его в том, чтобы на нить действовало еще и ускорение. Возьмем пример попроще. Представим, что нашу балку теперь поднимают вверх со скоростью 3 м/с. Тогда, к натяжению прибавится ускорение груза и формула примет следующий вид: Fн=Fт+уск*м. Ориентируясь на прошлые расчеты получаем: Fн=19,6+3*2=25,6 ньютона.
3 Этап
Тут уже посложнее, так как речь идет об угловом вращении. Следует понимать, что при вращении объекта вертикально, сила, воздействующая на нить, будет намного больше в нижней точке. Но давайте возьмем пример с несколько меньшей амплитудой качания (по типу маятника). В этом случае для расчетов нужна формула: Fц=м* v²/r. Тут искомое значение обозначает дополнительную мощь натяжения, v – скорость вращения подвешенного груза, а r – радиус окружности, по которому вращается груз. Последнее значение фактически равняется длине нити, пускай она составляет 1,7 метра.
Итак, подставляя значения, находим центробежные данные: Fц=2*9/1,7=10,59 ньютона. А теперь, чтобы узнать полную силу натяжения нити, надо к имеющимся данным о состоянии покоя прибавить центробежную силу: 19,6+10,59=30,19 ньютона.
4 Этап
Следует учитывать меняющуюся силу натяжения по мере прохождения груза через дугу. Иными словами – независимо от постоянной величины притяжения, центробежная (результирующая) сила меняется по мере того, как качается подвешенный груз.
Чтобы лучше понять этот аспект, достаточно представить себе привязанный груз к веревке, которую можно свободно вращать вокруг балки, к которой она закреплена (как качели). Если веревку раскачать достаточно сильно, то в момент нахождения в верхнем положении сила притяжения будет действовать в «обратную» сторону относительно силы натяжения веревки. Иными словами – груз станет «легче», из-за чего ослабнет и натяжение на веревку.
Предположим, что маятник отклоняется на угол, равный двадцати градусам от вертикали и движется со скоростью 1,7 м/с. Сила притяжения (Fп) при этих параметрах будет равна 19,6*cos(20)=19,6*0,94=18,424 Н; центробежная сила (F ц=mv²/r)=2*1,7²/1,7=3,4 Н; ну а полное натяжение (Fпн) будет равняться Fп+ Fц=3,4+18,424=21,824 Н.
5 Этап
Его суть заключается в силе трения между грузом и другим объектом, что в совокупности косвенно влияет на натяжение веревки. Иначе говоря – сила трения способствует увеличению силы натяжения. Это хорошо видно на примере перемещения объектов по шершавой и гладкой поверхностях. В первом случае трение будет большим, поэтому и сдвигать предмет становится тяжелее.
Общее натяжение в данном случае вычисляется по формуле: Fн=Fтр+Fу, где Fтр – трение, а Fу – ускорение. Fтр=мкР, где мк – трение между объектами, а Р – сила взаимодействия между ними.
Чтобы лучше понять данный аспект, рассмотрим задачу. Допустим, у нас груз 2 кг и коэффициент трения равен 0,7 с ускорением движения 4м/с постоянной скорости. Теперь задействуем все формулы и получаем:
- Сила взаимодействия — Р=2*9,8=19,6 ньютона.
- Трение — Fтр=0,7*19,6=13,72 Н.
- Ускорение — Fу=2*4=8 Н.
- Общая сила натяжения — Fн=Fтр+Fу=13,72+8=21,72 ньютона.
Теперь вы знаете больше и можете сами находить и рассчитывать нужные значения. Конечно, для более точных расчетов нужно учитывать больше факторов, но для сдачи курсовой и реферата этих данных вполне достаточно.
Видео
Это видео поможет вам лучше разобраться в данной теме и запомнить ее.
liveposts.ru
Расчет натяжения троса и реакции опоры
Задача
Однородная балка AB весом P закреплена в точке A шарнирно-неподвижной опорой; трос BC, удерживающий балку, составляет с ней угол α. Определить натяжение троса и реакцию опоры A (рисунок 2.2, а).
Решение
Силы, действующие на балку, приложены к разным ее точкам, поэтому в данной задаче нужно рассмотреть равновесие балки. Балка однородная, поэтому сила P (вес балки) приложена к ее середине (рисунок 2.2, б).
Реакция троса – сила T – направлена вдоль троса. Направление реакции опоры A можно определить, воспользовавшись теоремой о трех силах. По этой теореме линии действия трех непараллельных сил P, T и RA должны пересекаться в одной точке. То есть угол β должен быть равен углу α.
Далее возможно геометрическое или аналитическое решение.
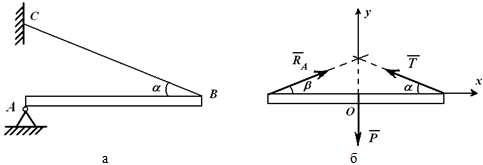
Рисунок 2.2
Так как система находится в равновесии, то
P + T + RA=0. (2.7)
Строим это геометрическое равенство (рисунок 2.3), начиная с известной силы P; под углом α к горизонтали через конец векторa P проводим линию MN, вдоль которой направлена сила T. Так как сумма всех сил должна быть равна нулю, то вектор RA должен заканчиваться в начале вектора P под углом β к горизонту (линия KL).
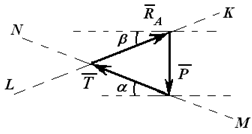
Рисунок 2.3
Точка пересечения линий MN и KL – это конец вектора T и начало вектора RA. Далее можно определить величины T и RA, умножив длины отрезков на выбранный масштаб или воспользовавшись теоремой синусов:
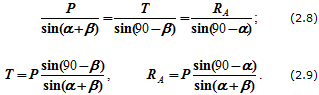
Аналитическое решение предполагает составление двух уравнений. Проецируем векторное равенство (2.7) на выбранные оси координат (рисунок 2.2,б) и получаем два уравнения равновесия с двумя неизвестными:
∑xi=0, -Tcosα+RAcosβ=0;∑yi=0, -P+Tsinα+RAsinβ. (2.10)
Из этих уравнений определяются величины T и RA:
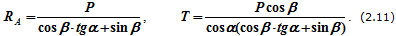
Другие примеры решения задач >>
isopromat.ru
Силы упругости: пружины, канаты и нити
В задачах в этой статьи рассмотрены случаи, когда тело поднимают или опускают с ускорением. При этом натяжение нити, на которой подвешен груз, разное. Даны примеры составления уравнений по второму закону Ньютона в проекциях на оси.
Задача 1. Грузовик взял на буксир легковой автомобиль массой  т и, двигаясь равноускоренно, за
т и, двигаясь равноускоренно, за  с проехал
с проехал  м. На сколько при этом удлиняется трос, соединяющий автомобили, если его жесткость
м. На сколько при этом удлиняется трос, соединяющий автомобили, если его жесткость  Н/м? Трение не учитывать.
Н/м? Трение не учитывать.
Удлинение троса можно найти, зная силу упругости:


Так как трение учитывать не нужно, то по второму закону Ньютона

Следовательно,

Определим ускорение грузовика:


Окончательно для удлинения троса получаем:

Ответ получен в метрах, можно записать его в мм: 0,64 мм.
Задача 2. На нити, выдерживающей натяжение  Н, поднимают груз массой
Н, поднимают груз массой  кг из состояния покоя вертикально вверх. Считая движение равноускоренным, найти предельную высоту
кг из состояния покоя вертикально вверх. Считая движение равноускоренным, найти предельную высоту  , на которую можно поднять груз за
, на которую можно поднять груз за  с так, чтобы нить не оборвалась.
с так, чтобы нить не оборвалась.

К задаче 2
Запишем второй закон Ньютона в проекция на вертикальную ось:

Тогда ускорение равно:

Высота, на которую тело можно поднять с таким ускорением, равна

Ответ: 5 м
Задача 3. Веревка выдерживает груз массой  кг при вертикальном подъеме его с некоторым ускорением и груз массой
кг при вертикальном подъеме его с некоторым ускорением и груз массой  кг при опускании его с таким же по модулю ускорением. Какова максимальная масса груза
кг при опускании его с таким же по модулю ускорением. Какова максимальная масса груза  , который можно поднимать или опускать на этой веревке с постоянной скоростью?
, который можно поднимать или опускать на этой веревке с постоянной скоростью?

К задаче 3
Запишем уравнения по второму закону как для подъема, так и для спуска тела. Направим ось вверх, тогда при подъеме:

При спуске:

Ускорение по условию одно и то же, тогда:

Или

Приравняв, можем найти силу натяжения веревки, которую она выдерживает:




Если бы груз массой  просто висел на такой веревке, то мы бы записали
просто висел на такой веревке, то мы бы записали

Следовательно,


Ответ: 190 кг
Задача 4. Груз массой  кг подвешен к пружине жесткостью
кг подвешен к пружине жесткостью  Н/м. Длина пружины в нерастянутом состоянии
Н/м. Длина пружины в нерастянутом состоянии  м. Найти длину пружины
м. Найти длину пружины  , когда на ней висит груз. Какой будет длина пружины, если пружина с грузом будет находиться в лифте, движущемся с ускорением
, когда на ней висит груз. Какой будет длина пружины, если пружина с грузом будет находиться в лифте, движущемся с ускорением  м/с
м/с , направленным а) вверх; б) вниз?
, направленным а) вверх; б) вниз?

К задаче 4
Если груз повешен на пружину, ее длина увеличивается:

При движении лифта вверх запишем второй закон (ось направлена вверх):


Тогда длина пружины в этом случае:

При движении лифта вниз запишем второй закон (ось направлена вверх):


Тогда длина пружины в этом случае:

Ответ:  ,
,  ,
,  .
.
Задача 5. Четырьмя натянутыми нитями груз закреплен на тележке. Силы натяжения горизонтальных нитей соответственно  и
и  , а вертикальных –
, а вертикальных –  и
и  . С каким ускорением движется тележка по горизонтальной плоскости?
. С каким ускорением движется тележка по горизонтальной плоскости?

К задаче 5
Запишем уравнения по второму закону в проекциях на оси, которые расположим традиционно: ось  вправо, ось
вправо, ось  – вверх. Тогда, если тележка движется вправо, по оси, имеем:
– вверх. Тогда, если тележка движется вправо, по оси, имеем:


Из второго уравнения найдем массу груза:


Тогда ускорение тележки (и груза) равно:


Если же тележка движется влево (против оси), то изменится только первое уравнение:


Тогда ускорение тележки (и груза) равно:

easy-physic.ru
Расчет натяжения каната.
Стр 1 из 5Следующая ⇒Исходные данные
Рис 1. Расчетная схема механизма.
1-Грузоподьемность Q=2 тонны
2-Высота подъема груза H=3,5 м
3-Скорость подъема Vп=18 м/мин
4-Кратность полиспаты =1
5-Количество ветвей набегающих на барабан а=1
6-Режим работы- средний
Выбор типа подъемного органа.
В качестве подъемного органа выбираем стальной проволочный канат двойной свивки.
Рис.2 Поперечное сечение каната.
Расчет натяжения каната.
Максимальное натяжение на ветке каната.
Fmax=Qg=2000*9.81=19620 H
Расчетное разрывное усилие каната.
Fрасч=k* Fmax=19620*5=98100 H
k-для среднего режима работы коэффициент запаса равен 5.
По ГОСТ 2688-80 выбираем канат двойной свивки по Fрасч.
Канат 14-Г-I-1578 где,
· Первая цифра 14- диаметр каната, мм.
· Вторая Г- канат грузовой.
· Третья I- марка проволоки.
· Четвертая 1578- максимальное разрывное усилие, Н
Конструкция каната
Канат ЛК-Р-6х19(1+6+6/6)+1.о.с ГОСТ 2588-80 ,где
ЛК-Р- с линейным касанием проволок разных диаметров в верхнем слое пряди.
· 6х19- канат шестипрядный по 19 проволок в пряди.
· (1+6+6/6)- навивка проволок по слоям.
· 1.о.с.- органический сердечник.
Расчет барабана.
Рис.3 Профиль канавок на барабане
mykonspekts.ru
Работа равнодействующей силы, тяжести, трения, упругости. Мощность, коэффициент полезного действия. Примеры, формулы
Тестирование онлайн
Работа
Работа - это скалярная величина, которая определяется по формуле
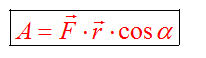
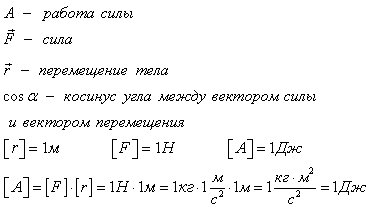
Работу выполняет не тело, а сила! Под действием этой силы тело совершает перемещение.
Обратите внимание, что у работы и энергии одинаковые единицы измерения. Это означает, что работа может переходить в энергию. Например, для того, чтобы тело поднять на некоторую высоту, тогда оно будет обладать потенциальной энергией, необходима сила, которая совершит эту работу. Работа силы по поднятию перейдет в потенциальную энергию.
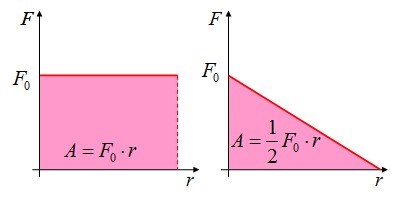
Правило определения работы по графику зависимости F(r): работа численно равна площади фигуры под графиком зависимости силы от перемещения.
Угол между вектором силы и перемещением
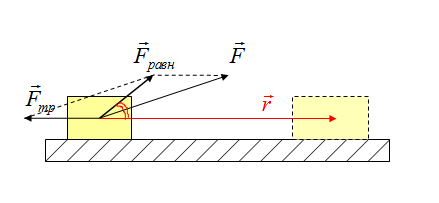
1) Верно определяем направление силы, которая выполняет работу; 2) Изображаем вектор перемещения; 3) Переносим вектора в одну точку, получаем искомый угол.
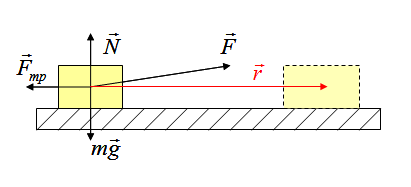
На рисунке на тело действуют сила тяжести (mg), реакция опоры (N), сила трения (Fтр) и сила натяжения веревки F, под воздействием которой тело совершает перемещение r.
Работа силы тяжести
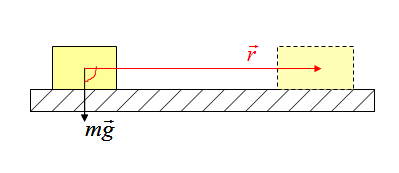
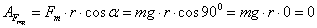
Работа реакции опоры
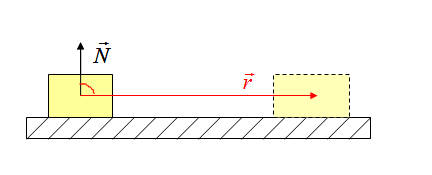
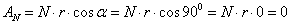
Работа силы трения
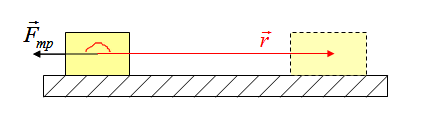
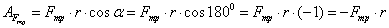
Работа силы натяжения веревки
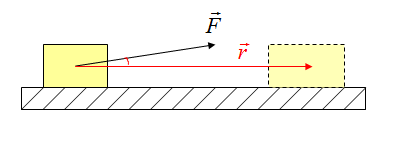
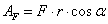
Работа равнодействующей силы
Работу равнодействующей силы можно найти двумя способами: 1 способ - как сумму работ (с учетом знаков "+" или "-") всех действующих на тело сил, в нашем примере 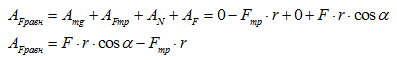 2 способ - в первую очередь найти равнодействующую силу, затем непосредственно ее работу, см. рисунок
2 способ - в первую очередь найти равнодействующую силу, затем непосредственно ее работу, см. рисунок
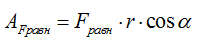
Работа силы упругости
Для нахождения работы, совершенной силой упругости, необходимо учесть, что эта сила изменяется, так как зависит от удлинения пружины. Из закона Гука следует, что при увеличении абсолютного удлинения, сила увеличивается.
Для расчета работы силы упругости при переходе пружины (тела) из недеформированного состояния в деформированное используют формулу
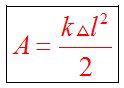
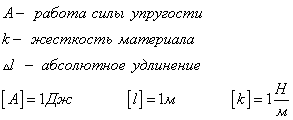
Мощность
Скалярная величина, которая характеризует быстроту выполнения работы (можно провести аналогию с ускорением, которое характеризует быстроту изменения скорости). Определяется по формуле
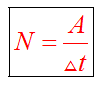

Коэффициент полезного действия
КПД - это отношение полезной работы, совершенной машиной, ко всей затраченной работе (подведенной энергии) за то же время
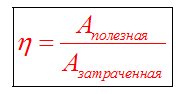
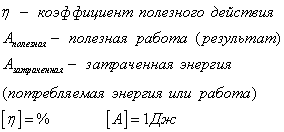
Коэффициент полезного действия выражается в процентах. Чем ближе это число к 100%, тем выше производительность машины. Не может быть КПД больше 100, так как невозможно выполнить больше работы, затратив меньше энергии.
КПД наклонной плоскости - это отношение работы силы тяжести, к затраченной работе по перемещению вдоль наклонной плоскости.
Главное запомнить
1) Формулы и единицы измерения;2) Работу выполняет сила; 3) Уметь определять угол между векторами силы и перемещения
Если работа силы при перемещении тела по замкнутому пути равна нулю, то такие силы называют консервативными или потенциальными. Работа силы трения при перемещении тела по замкнутому пути никогда не равна нулю. Сила трения в отличие от силы тяжести или силы упругости является неконсервативной или непотенциальной.
Есть условия, при которых нельзя использовать формулу 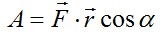 Если сила является переменной, если траектория движения является кривой линией. В этом случае путь разбивается на малые участки, для которых эти условия выполняются, и подсчитать элементарные работы на каждом из этих участков. Полная работа в этом случае равна алгебраической сумме элементарных работ:
Если сила является переменной, если траектория движения является кривой линией. В этом случае путь разбивается на малые участки, для которых эти условия выполняются, и подсчитать элементарные работы на каждом из этих участков. Полная работа в этом случае равна алгебраической сумме элементарных работ: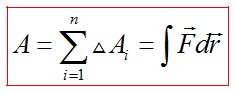
Значение работы некоторой силы зависит от выбора системы отсчета.
fizmat.by
423800, Набережные Челны , база Партнер Плюс, тел. 8 800 100-58-94 (звонок бесплатный)












