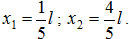|
||||
|
|
звонок бесплатный
Наши сотрудники:
[email protected]
Екатерина - специалист по продаже а/м КАМАЗ
 [email protected]
[email protected]






Техника в наличии

Тягач КАМАЗ 44108-6030-24
2014г, 6х6, Евро3, дв.КАМАЗ 300 л.с., КПП ZF9, бак 210л+350л, МКБ,МОБ,рестайлинг.
цена 2 220 000 руб.,

КАМАЗ 4308-6063-28(R4)
4х2,дв. Cummins ISB6.7e4 245л.с. (Е-4),КПП ZF6S1000, V кузова=39,7куб.м., спальное место, бак 210л, шк-пет,МКБ, ТНВД BOSCH, система нейтрализ. ОГ(AdBlue), тент, каркас, рестайлинг, внутр. размеры платформы 6112х2470х730 мм
цена 1 950 000 руб.,

Самосвал КАМАЗ 6520-057
2014г, 6х4,Евро3, дв.КАМАЗ 320 л.с., КПП ZF16, ТНВД ЯЗДА, бак 350л, г/п 20 тонн, V кузова =20 куб.м.,МКБ,МОБ, со спальным местом.
цена 2 700 000 руб.,

Самосвал 6522-027
2014, 6х6, дв.КАМАЗ 740.51,320 л.с., КПП ZF16,бак 350л, г/п 19 тонн,V кузова 12куб.м.,МКБ,МОБ,задняя разгрузка,обогрев платформы.
цена 3 190 000 руб.,
СУПЕР ЦЕНА
на АВТОМОБИЛИ КАМАЗ
| 43118-010-10 (дв.740.30-260 л.с.) | 2 220 000 |
| 43118-6033-24 (дв.740.55-300 л.с.) | 2 300 000 |
| 65117-029 (дв.740.30-260 л.с.) | 2 200 000 |
| 65117-6010-62 (дв.740.62-280 л.с.) | 2 350 000 |
| 44108 (дв.740.30-260 л.с.) | 2 160 000 |
| 44108-6030-24 (дв.740.55,рест.) | 2 200 000 |
| 65116-010-62 (дв.740.62-280 л.с.) | 1 880 000 |
| 6460 (дв.740.50-360 л.с.) | 2 180 000 |
| 45143-011-15 (дв.740.13-260л.с) | 2 180 000 |
| 65115 (дв.740.62-280 л.с.,рест.) | 2 190 000 |
| 65115 (дв.740.62-280 л.с.,3-х стор) | 2 295 000 |
| 6520 (дв.740.51-320 л.с.) | 2 610 000 |
| 6520 (дв.740.51-320 л.с.,сп.место) | 2 700 000 |
| 6522-027 (дв.740.51-320 л.с.,6х6) | 3 190 000 |

подробнее про услугу перегона можно прочесть здесь.

|
Нужны самосвалы? Обратите внимание на Ford-65513-02. |
КАМАЗы в лизинг
ООО «Старт Импэкс» имеет возможность поставки грузовой автотехники КАМАЗ, а так же спецтехники на шасси КАМАЗ в лизинг. Продажа грузовой техники по лизинговым схемам имеет определенные выгоды для покупателя грузовика. Рассрочка платежа, а так же то обстоятельство, что грузовики до полной выплаты лизинговых платежей находятся на балансе лизингодателя, и соответственно покупатель автомобиля не платит налогов на имущество. Мы готовы предложить любые модели бортовых автомобилей, тягачей и самосвалов по самым выгодным лизинговым схемам.Контактная информация.
г. Набережные Челны, Промкомзона-2, Автодорога №3, база «Партнер плюс».
тел/факс (8552) 388373.
Схема проезда
48) Центр тяжести тела. Методы нахождения центра тяжести. Определение центра тяжести
13. Центр тяжести твердого тела; центр тяжести объема, площади и линии. Способы определения положения центров тяжести тел.
Центром тяжести твердого тела называется геометрическая точка, жестко связанная с этим телом, и являющаяся центром параллельных сил тяжести, приложенных к отдельным элементарным частицам тела (рисунок 1.6).
Радиус-вектор этой точки
Рисунок 1.6
Для однородного тела положение центра тяжести тела не зависит от материала, а определяется геометрической формой тела.
Если удельный вес однородного тела γ, вес элементарной частицы тела
Pk = γΔVk (P = γV) подставить в формулу для определения rC, имеем
Откуда, проецируя на оси и переходя к пределу, получаем координаты центра тяжести однородного объема
Аналогично для координат центра тяжести однородной поверхности площадью S (рисунок 1.7, а)
Рисунок 1.7
Для координат центра тяжести однородной линии длиной L (рисунок 1.7, б)
Способы определения координат центра тяжести
Исходя из полученных ранее общих формул, можно указать способы определения координат центров тяжести твердых тел:
1 Аналитический (путем интегрирования).
2 Метод симметрии. Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
3 Экспериментальный (метод подвешивания тела).
4 Разбиение. Тело разбивается на конечное число частей, для каждой из которых положение центра тяжести C и площадь S известны. Например, проекцию тела на плоскость xOy (рисунок 1.8) можно представить в виде двух плоских фигур с площадями S1 и S2 (S = S1 + S2). Центры тяжести этих фигур находятся в точках C1(x1, y1) и C2(x2, y2). Тогда координаты центра тяжести тела равны
Рисунок 1.8
5 Дополнение (метод отрицательных площадей или объемов). Частный случай способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9):
Рисунок 1.9
Центры тяжести простейших фигур
Рисунок 1.10
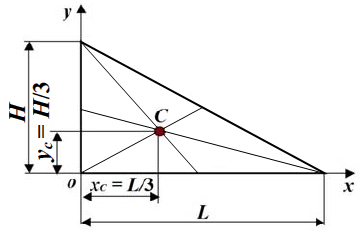
1 Треугольник
Центр тяжести площади треугольник совпадает с точкой пересечения его медиан (рисунок 1.10, а).
DM = MB, CM = (1/3)AM.
2 Дуга окружности
Дуга имеет ось симметрии (рисунок 1.10, б). Центр тяжести лежит на этой оси, т.е. yC = 0.
dl – элемент дуги, dl = Rdφ, R – радиус окружности, x = Rcosφ, L = 2αR,
Следовательно:
xC = R(sinα/α).
3 Круговой сектор
Сектор радиуса R с центральным углом 2α имеет ось симметрии Ox, на которой находится центр тяжести (рисунок 1.10, в).
Разбиваем сектор на элементарные секторы, которые можно считать треугольниками. Центры тяжести элементарных секторов располагаются на дуге окружности радиуса (2/3)R.
Центр тяжести сектора совпадает с центром тяжести дуги AB:
14. Способы задания движения точки.
При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета.
При координатном способе задания движения задаются координаты точки как функции времени:
Это параметрические уравнения траектории движущейся точки, в которых роль параметра играет время t. Чтобы записать ее уравнение в явной форме, надо исключить из них t.
При естественном способе задания движения задаются траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты: s=s(t) . Этим способом удобно пользоваться, если траектория точки заранее известна.
15. 1.2 Скорость точки
Рассмотрим перемещение точки за малый промежуток времени Δt:
тогда
средняя скорость точки за промежуток времени Dt . Скорость точки в данный момент времени
Скорость точки – это кинематическая мера ее движения, равная производной по времени от радиус-вектора этой точки в рассматриваемой системе отсчета. Вектор скорости направлен по касательной к траектории точки в сторону движения.
studfiles.net
6. Центр тяжести тел
6.1. Общие сведения
Центр параллельных силРассмотрим две параллельные, направленные в одну сторону силы  , и
, и  , приложенные к телу в точках А1 и А2 (рис.6.1). Эта система сил имеет равнодействующую
, приложенные к телу в точках А1 и А2 (рис.6.1). Эта система сил имеет равнодействующую 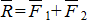 , линия действия которой проходит через некоторую точку С. Положение точки С можно найти с помощью теоремы Вариньона:
, линия действия которой проходит через некоторую точку С. Положение точки С можно найти с помощью теоремы Вариньона:
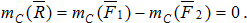
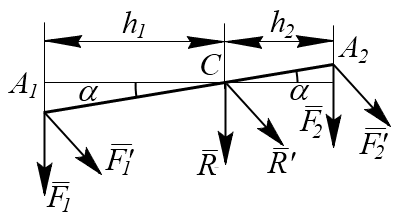 Рис.6.1
Рис.6.1
Если повернуть силы  и
и  около точек А1 и А2 в одну сторону и на один и тот же угол, то получим новую систему параллельных сал, имеющих те же модули. При этом их равнодействующая будет также проходить через точку С. Такая точка называется центром параллельных сил.Рассмотрим систему параллельных и одинаково направленных сил
около точек А1 и А2 в одну сторону и на один и тот же угол, то получим новую систему параллельных сал, имеющих те же модули. При этом их равнодействующая будет также проходить через точку С. Такая точка называется центром параллельных сил.Рассмотрим систему параллельных и одинаково направленных сил 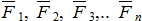 , приложенных к твердому телу в точках
, приложенных к твердому телу в точках  . Эта система имеет равнодействующую
. Эта система имеет равнодействующую 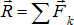 .Если каждую силу системы повернуть около точек их приложения в одну и ту же сторону и на один и тот же угол, то получатся новые системы одинаково направленных параллельных сил с теми же модулями и точками приложения. Равнодействующая таких систем будет иметь тот же модуль R, но всякий раз другое направление. Сложив силы F1 и F2 найдем что их равнодействующая R1, которая всегда будет проходить через точку С1, положение которой определяется равенством
.Если каждую силу системы повернуть около точек их приложения в одну и ту же сторону и на один и тот же угол, то получатся новые системы одинаково направленных параллельных сил с теми же модулями и точками приложения. Равнодействующая таких систем будет иметь тот же модуль R, но всякий раз другое направление. Сложив силы F1 и F2 найдем что их равнодействующая R1, которая всегда будет проходить через точку С1, положение которой определяется равенством 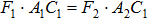 . Сложив далее R1 и F3, найдем их равнодействующую, которая всегда будет проходить через точку С2, лежащую на прямой А3С2. Доведя процесс сложения сил до конца придем к выводу, что равнодействующая всех сил действительно всегда будет проходить через одну и ту же точку С, положение которой по отношению к точкам
. Сложив далее R1 и F3, найдем их равнодействующую, которая всегда будет проходить через точку С2, лежащую на прямой А3С2. Доведя процесс сложения сил до конца придем к выводу, что равнодействующая всех сил действительно всегда будет проходить через одну и ту же точку С, положение которой по отношению к точкам  будет неизменным. Точка С, через которую проходит линия действия равнодействующей системы параллельных сил при любых поворотах этих сил около точек их приложения в одну и ту же сторону на один и тот же угол называется центром параллельных сил (рис. 6.2).
будет неизменным. Точка С, через которую проходит линия действия равнодействующей системы параллельных сил при любых поворотах этих сил около точек их приложения в одну и ту же сторону на один и тот же угол называется центром параллельных сил (рис. 6.2).
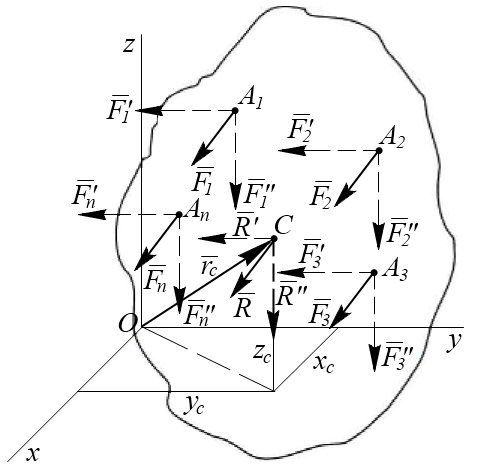 Рис.6.2
Рис.6.2
Определим координаты центра параллельных сил. Поскольку положение точки С по отношению к телу является неизменным, то ее координаты от выбора системы координат не зависят. Повернем все силы около их приложения так, чтобы они стали параллельны оси Оу и применим к повернутым силам теорему Вариньона. Так как R' является равнодействующей этих сил, то, согласно теореме Вариньона, имеем 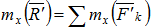 , т.к.
, т.к. 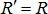 ,
, 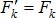 , получим
, получим
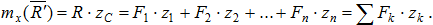
Отсюда находим координату центра параллельных сил zc:
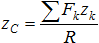
Для определения координаты xc составим выражение момента сил относительно оси Oz.
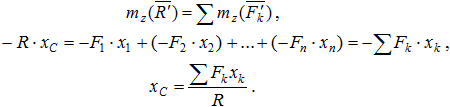
Для определения координаты yc повернем все силы, чтобы они стали параллельны оси Oz.
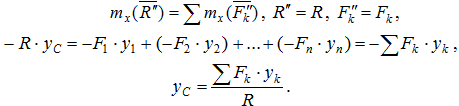
Положение центра параллельных сил относительно начала координат (рис. 6.2) можно определить его радиусом-вектором:
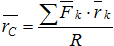
6.2. Центр тяжести твердого тела
Центром тяжести твердого тела называется неизменно связанная с этим телом точка С, через которую проходит линия действия равнодействующей сил тяжести данного тела, при любом положении тела в пространстве.Центр тяжести применяется при исследовании устойчивости положений равновесия тел и сплошных сред, находящихся под действием сил тяжести и в некоторых других случаях, а именно: в сопротивлении материалов и в строительной механике – при использовании правила Верещагина.Существуют два способа определения центра тяжести тела: аналитический и экспериментальный. Аналитический способ определения центра тяжести непосредственно вытекает из понятия центра параллельных сил.Координаты центра тяжести, как центра параллельных сил, определяются формулами:
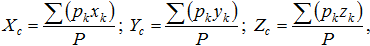
где Р - вес всего тела; pk - вес частиц тела; xk, yk, zk - координаты частиц тела.Для однородного тела вес всего тела и любой её части пропорционален объёму P=Vγ, pk=vkγ , где γ - вес единицы объёма, V - объем тела. Подставляя выражения P, pk в формулы определения координат центра тяжести и, сокращая на общий множитель γ, получим:
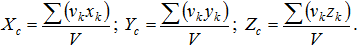
Точка С, координаты которой определяются полученными формулами, называется центром тяжести объема.Если тело представляет собой тонкую однородную пластину, то центр тяжести определяется формулами:
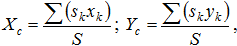
где S – площадь всей пластины; sk - площадь её части; xk, yk - координаты центра тяжести частей пластины.Точка С в данном случае носит название центра тяжести площади.Числители выражений, определяющих координаты центра тяжести плоских фигур, называются статическими моментами площади относительно осей у и х:
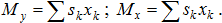
Тогда центр тяжести площади можно определить по формулам:
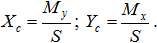
Для тел, длина которых во много раз превышает размеры поперечного сечения, определяют центр тяжести линии. Координаты центра тяжести линии определяют формулами:
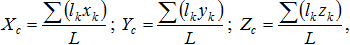
где L - длина линии; lk - длина ее частей; xk, yk, zk - координата центра тяжести частей линии.
6.3. Способы определения координат центров тяжести тел
Основываясь на полученных формулах, можно предложить практические способы определения центров тяжести тел.1. Симметрия. Если тело имеет центр симметрии, то центр тяжести находится в центре симметрии.Если тело имеет плоскость симметрии. Например, плоскость ХОУ, то центр тяжести лежит в этой плоскости.2. Разбиение. Для тел, состоящих из простых по форме тел, используется способ разбиения. Тело разбивается на части, центр тяжести которых находится методом симметрии. Центр тяжести всего тела определяется по формулам центра тяжести объема (площади).
Пример. Определить центр тяжести пластины, изображенной на помещенном ниже рисунке (рис. 6.3). Пластину можно разбить на прямоугольники различным способом и определить координаты центра тяжести каждого прямоугольника и их площади.
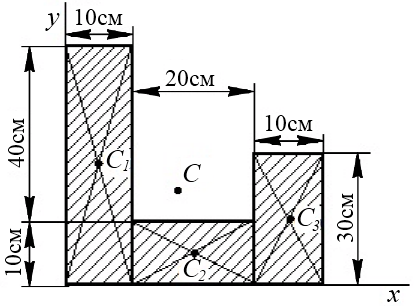 Рис.6.3
Рис.6.3
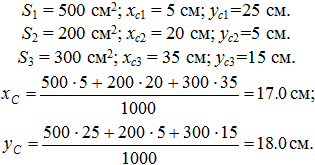
Ответ: xc=17.0см; yc=18.0см.
3. Дополнение. Этот способ является частным случаем способа разбиения. Он используется, когда тело имеет вырезы, срезы и др., если координаты центра тяжести тела без выреза известны.
Пример. Определить центр тяжести круглой пластины имеющий вырез радиусом r = 0,6 R (рис. 6.4).
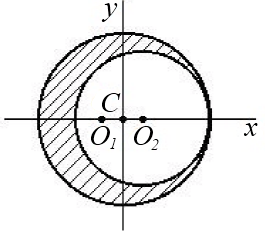 Рис.6.4
Рис.6.4
Круглая пластина имеет центр симметрии. Поместим начало координат в центре пластины. Площадь пластины без выреза 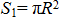 , площадь выреза
, площадь выреза 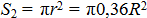 . Площадь пластины с вырезом
. Площадь пластины с вырезом 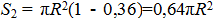 ;
; 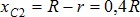 .Пластина с вырезом имеет ось симметрии О1x, следовательно, yc=0.
.Пластина с вырезом имеет ось симметрии О1x, следовательно, yc=0.
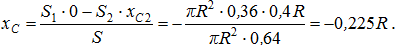
4. Интегрирование. Если тело нельзя разбить на конечное число частей, положение центров тяжести которых известны, тело разбивают на произвольные малые объемы 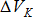 , для которых формула с использованием метода разбиения принимает вид:
, для которых формула с использованием метода разбиения принимает вид: 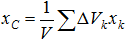 .Далее переходят к пределу, устремляя элементарные объемы к нулю, т.е. стягивая объемы в точки. Суммы заменяют интегралами, распространенными на весь объем тела, тогда формулы определения координат центра тяжести объема принимают вид:
.Далее переходят к пределу, устремляя элементарные объемы к нулю, т.е. стягивая объемы в точки. Суммы заменяют интегралами, распространенными на весь объем тела, тогда формулы определения координат центра тяжести объема принимают вид:
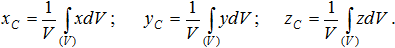
Формулы для определения координат центра тяжести площади:

Координаты центра тяжести площади необходимо определять при изучении равновесия пластинок, при вычислении интеграла Мора в строительной механике.
Пример. Определить центр тяжести дуги окружности радиуса R с центральным углом АОВ = 2α (рис. 6.5).
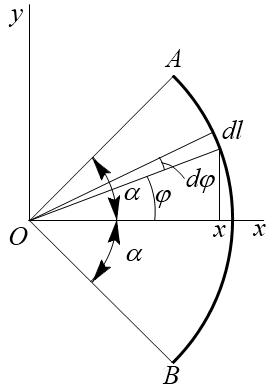 Рис. 6.5
Рис. 6.5
Дуга окружности симметрична оси Ох, следовательно, центр тяжести дуги лежит на оси Ох, yс = 0.Согласно формуле для центра тяжести линии:
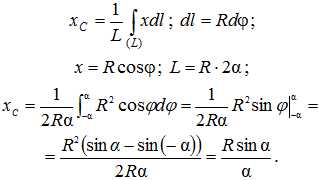
6. Экспериментальный способ. Центры тяжести неоднородных тел сложной конфигурации можно определять экспериментально: методом подвешивания и взвешивания. Первый способ состоит в том, что тело подвешивается на тросе за различные точки. Направление троса на котором подвешено тело, будет давать направление силы тяжести. Точка пересечения этих направлений определяет центр тяжести тела.Метод взвешивания состоит в том, что сначала определяется вес тела, например автомобиля. Затем на весах определяется давление заднего моста автомобиля на опору. Составив уравнение равновесия относительно какой- либо точки, например оси передних колес, можно вычислить расстояние от этой оси до центра тяжести автомобиля (рис. 6.6).
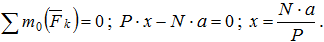
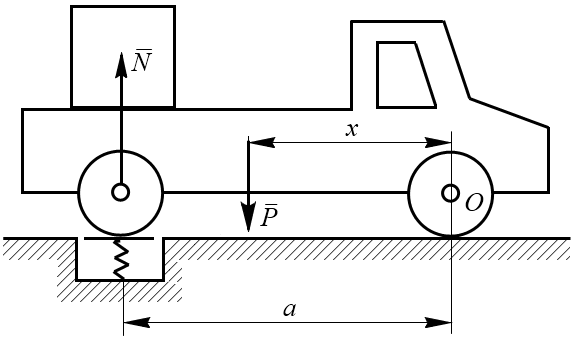 Рис.6.6
Рис.6.6
Иногда при решении задач следует применять одновременно разные методы определения координат центра тяжести.
6.4. Центры тяжести некоторых простейших геометрических фигур
Для определения центров тяжести тел часто встречающейся формы (треуголника, дуги окружности, сектора, сегмента) удобно использовать справочные данные (табл. 6.1).
Таблица 6.1
Координаты центра тяжести некоторых однородных тел
| № | Наименование фигуры | Рисунок |
| 1 | Дуга окружности: центр тяжести дуги однородной окружности находится на оси симметрии (координата уc=0).
где α – половина центрального угла; R – радиус окружности. |
|
| 2 | Однородный круговой сектор: центр тяжести расположен на оси симметрии (координата уc=0).
где α – половина центрального угла; R – радиус окружности. |
|
| 3 | Сегмент: центр тяжести расположен на оси симметрии (координата уc=0).
где α – половина центрального угла; R – радиус окружности. |
|
| 4 | Полукруг:
|
|
| 5 | Треугольник: центр тяжести однородного треугольника находится в точке пересечения его медиан.
где x1, y1, x2, y2, x3, y3 – координаты вершин треугольника | |
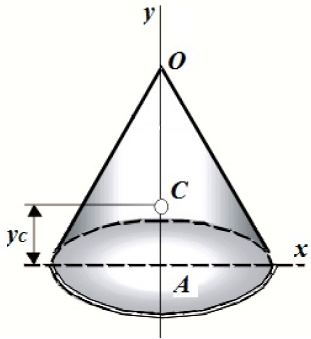
| 6 | Конус: центр тяжести однородного кругового конуса лежит на его высоте и отстоит на расстояние 1/4 высоты от основания конуса.
|
|
| 7 | Полусфера: центр тяжести лежит на оси симметрии.
|
|
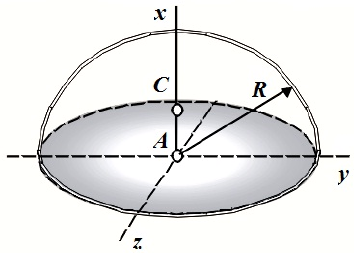
| 8 | Трапеция:
|
|
| 9 |
|
|
| 10 |
|
|
6.5. Методические указания к решению задач по определению положения центров тяжести однородных тел
При решении задач на определение центра тяжести однородных тел сложной формы следует придерживаться следующего порядка:1. Выбрать метод, который наиболее применим к данной задаче (метод разбиения или метод дополнения).2. Разбить сложное тело на простые элементы, для которых центры тяжести известны.3. Выбрать оси координат. При этом необходимо помнить, что: если тело имеет плоскость симметрии, то его центр тяжести лежит в этой плоскости; если тело имеет ось симметрии, то его центр тяжести лежит на этой оси; если тело имеет центр симметрии, то его центр тяжести совпадает с центром симметрии.4. Определить координаты центров тяжести отдельных простых тел относительно выбранных осей.5. Используя формулы, соответствующие выбранному методу, определить искомые координаты центра тяжести заданного тела.
teormech.ru
Определение центра тяжести тел
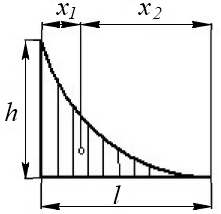
Определение центра тяжести произвольного тела путем последовательного сложения сил, действующих на отдельные его части,— трудная задача; она облегчается только для тел сравнительно простой формы.
Пусть тело состоит только из двух грузов массы  и
и  , соединенных стрежнем (рис. 125). Если масса стержня мала по сравнению с массами
, соединенных стрежнем (рис. 125). Если масса стержня мала по сравнению с массами  и
и  , то ею можно пренебречь. На каждую из масс действуют силы тяжести, равные соответственно
, то ею можно пренебречь. На каждую из масс действуют силы тяжести, равные соответственно 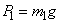 и
и 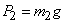 ; обе они направлены вертикально вниз, т. е. параллельно друг другу. Как мы знаем, равнодействующая двух параллельных сил приложена в точке
; обе они направлены вертикально вниз, т. е. параллельно друг другу. Как мы знаем, равнодействующая двух параллельных сил приложена в точке  , которая определяется из условия
, которая определяется из условия
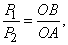 или
или 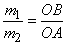 .
.

Рис. 125. Определение центра тяжести тела, состоящего из двух грузов
Следовательно, центр тяжести делит расстояние между двумя грузами в отношении, обратном отношению их масс. Если это тело подвесить в точке  , оно останется в равновесии.
, оно останется в равновесии.
Так как две равные массы имеют общий центр тяжести в точке, делящей пополам расстояние между этими массами, то сразу ясно, что, например, центр тяжести однородного стержня лежит в середине стержня (рис. 126).
Поскольку любой диаметр однородного круглого диска делит его на две совершенно одинаковые симметричные части (рис. 127), то центр тяжести должен лежать на каждом диаметре диска, т. е. в точке пересечения диаметров — в геометрическом центре диска  . Рассуждая сходным образом, можно найти, что центр тяжести однородного шара лежит в его геометрическом центре, центр тяжести однородного прямоугольного параллелепипеда лежит на пересечении его диагоналей и т. д. Центр тяжести обруча или кольца лежит в его центре. Последний пример показывает, что центр тяжести тела может лежать вне тела.
. Рассуждая сходным образом, можно найти, что центр тяжести однородного шара лежит в его геометрическом центре, центр тяжести однородного прямоугольного параллелепипеда лежит на пересечении его диагоналей и т. д. Центр тяжести обруча или кольца лежит в его центре. Последний пример показывает, что центр тяжести тела может лежать вне тела.

Рис. 126. Центр тяжести однородного стержня лежит в его середине
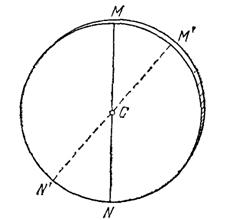
Рис. 127. Центр однородного диска лежит в его геометрическом центре
Если тело имеет неправильную форму или если оно неоднородно (например, в нем есть пустоты), то расчет положения центра тяжести часто затруднителен и это положение удобнее найти посредством опыта. Пусть, например, требуется найти центр тяжести куска фанеры. Подвесим его на нити (рис. 128). Очевидно, в положении равновесия центр тяжести тела  должен лежать на продолжении нити, иначе сила тяжести будет иметь момент относительно точки подвеса, который начал бы вращать тело. Поэтому, проведя на нашем куске фанеры прямую, представляющую продолжение нити, можем утверждать, что центр тяжести лежит на этой прямой.
должен лежать на продолжении нити, иначе сила тяжести будет иметь момент относительно точки подвеса, который начал бы вращать тело. Поэтому, проведя на нашем куске фанеры прямую, представляющую продолжение нити, можем утверждать, что центр тяжести лежит на этой прямой.
Действительно, подвешивая тело в разных точках и проводя вертикальные прямые, мы убедимся, что все они пересекутся в одной точке. Эта точка и есть центр тяжести тела (так как он должен лежать одновременно на всех таких прямых). Подобным образом можно определить положение центра тяжести не только плоской фигуры, но и более сложного тела. Положение центра тяжести самолета определяют, вкатывая его колесами на платформы весов. Равнодействующая сил веса, приходящихся на каждое колесо, будет направлена по вертикали, и найти линию, по которой она действует, можно по закону сложения параллельных сил.
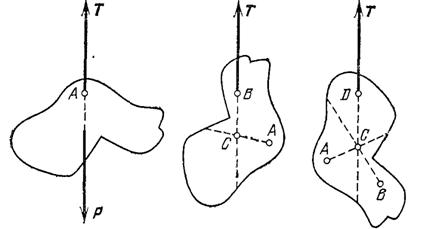
Рис. 128. Точка  пересечения вертикальных линий, проведенных через точки подвеса
пересечения вертикальных линий, проведенных через точки подвеса 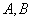 и
и 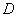 есть центр тяжести тела
есть центр тяжести тела
При изменении масс отдельных частей тела или при изменении формы тела положение центра тяжести меняется. Так, центр тяжести самолета перемещается при расходовании горючего из баков, при загрузке багажа и т. п. Для наглядного опыта, иллюстрирующего перемещение центра тяжести при изменении формы тела, удобно взять два одинаковых бруска, соединенных шарниром (рис. 129). В том случае, когда бруски образуют продолжение один другого, центр тяжести лежит на оси брусков. Если бруски согнуть в шарнире, то центр тяжести оказывается вне брусков, на биссектрисе угла, который они образуют. Если на один из брусков надеть дополнительный груз, то центр тяжести переместится в сторону этого груза.
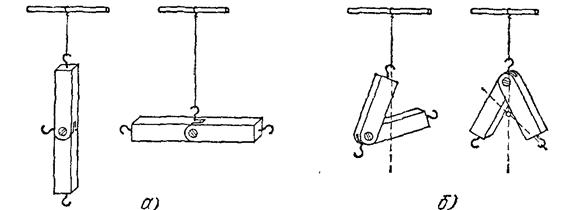
Рис. 129. а) Центр тяжести соединенных шарниром брусков, расположенных на одной прямой, лежит на оси брусков, б) Центр тяжести согнутой системы брусков лежит вне брусков
81.1. Где находится центр тяжести двух одинаковых тонких стержней, имеющих длину 12 см и скрепленных в виде буквы Т?
81.2. Докажите, что центр тяжести однородной треугольной пластины лежит на пересечении медиан.
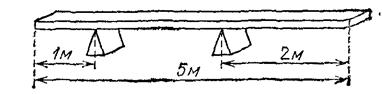
Рис. 130. К упражнению 81.3
81.3. Однородная доска массы 60 кг лежит на двух опорах, как показано на рис. 130. Определите силы, действующие на опоры.
sfiz.ru
48) Центр тяжести тела. Методы нахождения центра тяжести.
На каждую частицу тела, находящегося вблизи поверхности Земли, действует направленная вертикально вниз сила, которая называется силой тяжести. Силы тяжести каждой частицы тела, строго говоря, направлены по радиусам к центру Земли и не являются параллельными. Но для тел, размеры которых малы по сравнению с размерами Земли, непараллельность настолько незначительна, что в расчетах с большой точностью силы тяжести их частиц можно считать параллельными, сохраняющими свои значения, точки приложения и параллельность при любых поворотах тела. Поэтому, обозначив силу тяжести частицы через Рк , можно, согласно формулам и , найти точку С, которая неизменно связана с телом и называется центром системы параллельных сил тяжести. Таким образом, центром тяжести твердого тела называется центр системы параллельных сил тяжести частиц данного тела. Точка С — это геометрическая точка, она может и не принадлежать телу, но она всегда с ним связана, например центр тяжести баскетбольного мяча, кольца и др. Выразим силу тяжести (вес) частицы тела через ее объем V. Тогда величина называется удельным весом, а величина - плотностью тела в данной точке. ("гамма"-Н/м3) ("ро"-Н*с2/м4)
Методы нахождения центра тяжести.
1) Метод симметрии.
Покажем, что если однородное тело имеет плоскость, ось или центр материальной симметрии, то его центр тяжести находится соответственно в плоскости, на оси или в центре симметрии.
а. Пусть тело симметрично относительно плоскости Оху
Тогда вследствие симметрии каждому элементу К тела объемом (, , ) будет соответствовать элемент К' того же объема с координатами (, ,-). Поэтому статический момент объема и координата . Следовательно, центр тяжести тела будет лежать в плоскости симметрии Оху.
б. Пусть тело симметрично относительно оси Oz.
Тогда всякому элементу К тела объемом с координатами (, , ) будет соответствовать такой же по объему элемент К', расположенный симметрично относительно оси Oz и имеющий координаты (-,- , ). Поэтому статические моменты и, следовательно, координаты . Таким образом, центр тяжести будет находится на оси симметрии.
в. Пусть тело имеет центр симметрии, который примем за начало координат. Тогда всякой частице тела объемом , определяемой радиус-вектором rк, будет соответствовать частица такого же объема с радиус-вектором (-rк), симметричная ей относительно центра О. Поэтому . Следовательно, центр тяжести будет находиться в центре симметрии. Например, центры тяжести однородных куба, сферы, кольца, прямоугольной или круглой пластины лежат в геометрическом центре этих тел.
2) Метод разбиения.
Этот метод основан на применении формул и . Его используют, когда тело можно разбить на ряд частей, центры тяжести которых известны из условий симметрии. Метод разбиения можно наглядно проиллюстрировать с помощью рисунка.
Расположив тело в системе координат, разделив его мысленно на отдельные части, веса которых Р1, Р2, Р3, Р4, а центры тяжести известны, вычислим вес тела и, согласно формулам, координаты центра тяжести С всего тела. Если тело имеет вырез, причем известны центр тяжести тела без выреза и центр тяжести вырезанного тела, то для определения координат центра тяжести используют метод отрицательных масс (частный случай метода разбиения).
На рисунке изображена квадратная пластина, сторона которой а. В пластине выполнено круглое отверстие с радиусом r=0,2а и координатами центра x2=-0,3а; у2=0. Координаты центра тяжести С, пластины без отверстия x1=0, у1=0. Рассмотрим два тела: пластину без отверстия и диск, соответствующий вырезанному отверстию. При использовании формул вес диска будем считать отрицательным. Тогда, где р — вес единицы площади пластины.
studfiles.net
Определение положения центра тяжести тела
Найти координаты центра тяжести плоской однородной фигуры (варианты 1-75).
Все размеры даны в миллиметрах.
Вопросы для самоконтроля
Что такое трение скольжения? Как определяется коэффициент трения скольжения?
Что такое трение качения и верчения? Как определяется коэффициенты трения качения и верчения?
Что такое центр тяжести тела?
Способы определения плоской фигуры?
Задачи, рекомендуемые для самостоятельного решения: 9.1 – 9.28 [2].
Литература: [1], [3], [4].
Кинематика
Лекция 7
Кинематика точки
Кинематикой называется раздел механики, в котором изучаются геометрические свойства движения тел без учета их инертности (массы) и действующих на них сил.
Для определения положения движущегося тела (или точки) с тем телом, по отношению к которому изучается движение, жестко связывают какую-нибудь систему координат, которая вместе с телом образует систему отсчета. Если координаты всех точек тела в выбранной системе отсчета остаются все время постоянными, то тело по отношению к этой системе отсчета находится в покое. Если координаты каких-нибудь точек тела с течением времени изменяются, то тело по отношению к данной системе координат находится в движении.
Движение тел совершается в пространстве с течением времени. В механике рассматривается трехмерное евклидовое пространство. Время является скалярной величиной, непрерывно изменяющейся величиной. Отсчет времени ведется от некоторого начального (), о выборе которого в каждом случае уславливаются. Разность между двумя последовательными моментами времени называется промежутком времени.
Кинематически задавать движение или закон движения тела (точки) – значит, задать положение этого тела (точки) относительно данной системы отсчета в любой момент времени.
Основная задача кинематики состоит в том, чтобы, зная закон движения данного тела (или точки), определить все кинематические величины, характеризующие тела в целом, так и движение каждой из его точек в отдельности (траектории, скорости, ускорения и т.п.).
Вначале изучим движения точки, а затем перейдем к изучению кинематики твердого тела.
Способы задания движения точки. Траектория
Чтобы задать движение точки, надо задать ее в любом положении по отношению к выбранной системе отсчета в любой момент времени. Для задания движения точки можно применять один из следующих трех способов:
Естественный;
Координатный;
Векторный.
Естественный способ задания движения
Непрерывная линия, которую описывает движущаяся точка относительно данной системы отсчета, называется траекторией точки. Если траектория – прямая линия, то движение точки называется прямолинейным; а если кривая – то движение точки называется криволинейным.
Пусть кривая является траекторией движения точкиотносительно системы отсчета,,,, (рис. 1.1.).
Рис. 7.1.
Выберем на этой траектории какую-нибудь неподвижную точку , которую примем за начало отсчета; затем, рассматривая траекторию как криволинейную координатную ось, установим на ней положительное и отрицательное направление. Тогда положение точкибудет однозначно определяться криволинейной координатой, которая равна расстоянию от точкидо точки. Чтобы знать положение точкина траектории, в любой момент времени надо знать зависимость:
(7.1.)
Уравнение (7.1.) выражает закон движения точки вдоль траектории. Таким образом, чтобы задать движения точки естественным способом, надо знать:
Траекторию точки;
Начало отсчета на траектории;
Законы движения точки вдоль траектории в виде .
studfiles.net
Положения центра тяжести некоторых фигур
Прямоугольник. Так как прямоугольник имеет две оси симметрии , то его центр тяжести находится на пересечении осей симметрии, т.е. в точке пересечения диагоналей прямоугольника.
Треугольник. Центр тяжести лежит в точке пересечения его медиан. Из геометрии известно, что медианы треугольника пересекаются в одной точке и делятся в отношении 1:2 от основания.
Круг. Так как круг имеет две оси симметрии, то его центр тяжести находится на пересечении осей симметрии.
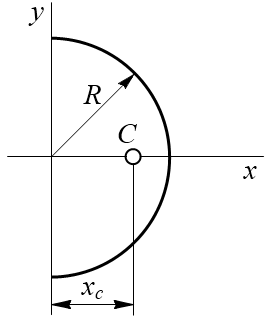
Полукруг. Полукруг имеет одну ось симметрии, то центр тяжести лежит на этой оси. Другая координата центра тяжести вычисляется по формуле: .
Многие конструктивные элементы изготавливают из стандартного проката – уголков, двутавров, швеллеров и других. Все размеры, а так же геометрические характеристики прокатных профилей это табличные данные, которые можно найти в справочной литературе в таблицах нормального сортамента (ГОСТ 8239-89, ГОСТ 8240-89).
Пример 1. Определить положение центра тяжести фигуры, представленной на рисунке.
Решение:
Выбираем оси координат, так чтобы ось Ох прошла по крайнему нижнему габаритному размеру, а ось Оу – по крайнему левому габаритному размеру.
Разбиваем сложную фигуру на минимальное количество простых фигур:
прямоугольник 20х10;
треугольник 15х10;
круг R=3 см.
Вычисляем площадь каждой простой фигуры, её координаты центра тяжести. Результаты вычислений заносим в таблицу
| № фигуры | Площадь фигуры А, | Координаты центра тяжести | |
| Х, см | У, см | ||
| 1 | =20·10=200 | 20:2=10 | 10:2=5 |
| 2 | |||
| 3 | 10 | 5 | |
Вычисляем координаты центра тяжести фигуры по формулам:
Ответ: С(14,5; 4,5)
Пример 2. Определить координаты центра тяжести составного сечения, состоящего из листа и прокатных профилей.
Решение.
Выбираем оси координат, так как показано на рисунке.
Обозначим фигуры номерами и выпишем из таблицы необходимые данные:
– швеллер №10; высота h=100 мм; ширина b=46 мм; площадь сечения ;
- двутавр №16; высота h=160 мм; ширина b=81 мм; площадь сечения ;
– лист 5х100; толщина 5 мм; ширина 100 мм.
Вычисляем координаты центра тяжести каждой фигуры. Составное сечение симметрично, поэтому центр тяжести находится на оси симметрии и координата . Результаты вычислений заносим в таблицу
| № фигуры | Площадь фигуры А, | Координаты центра тяжести | |
| Х, см | У, см | ||
| 1 | =10,9 | 0 | |
| 2 | 0 | ||
| 3 | 0 | ||
Вычисляем координаты центра тяжести фигуры по формулам:
Ответ: С(0; 10)
Лабораторная работа №1 «Определение центра тяжести составных плоских фигур»
Цель: Определить центр тяжести заданной плоской сложной фигуры опытным и аналитическим способами и сравнить их результаты.
Порядок выполнения работы
Начертить в тетрадях свою плоскую фигуру по размерам, с указанием осей координат.
Определить центр тяжести аналитическим способом.
Разбить фигуру на минимальное количество фигур, центры тяжести которых, мы знаем, как определить.
Указать номера площадей и координаты центра тяжести каждой фигуры.
Вычислить координаты центра тяжести каждой фигуры.
Вычислить площадь каждой фигуры.
Вычислить координаты центра тяжести всей фигуры по формулам (положение центра тяжести нанести на чертеж фигуры):
;
Записать координаты центра тяжести.
Определить центр тяжести опытным путем на установке для определения координат центра тяжести.
Вырезать данную фигуру из тонкого картона.
Определить центр тяжести своей фигуры на установке.
Установка для опытного определения координат центра тяжести способом подвешивания состоит из вертикальной стойки 1 (см. рис.), к которой прикреплена игла 2. Плоская фигура 3 изготовлена из картона, в котором легко проколоть отверстие. Отверстия А и В прокалываются в произвольно расположенных точках (лучше на наиболее удаленном расстоянии друг от друга). Плоская фигура подвешивается на иглу сначала в точке А, а потом в точке В. При помощи отвеса 4, закрепленного на той же игле, на фигуре прочерчивают карандашом вертикальную линию, соответствующую нити отвеса. Центр тяжести С фигуры будет находиться в точке пересечения вертикальных линий, нанесенных при подвешивании фигуры в точках А и В.
Приклеить фигуру с определенным центром тяжести в тетрадь.
Записать значения координат центра тяжести, найденных при подвешивании фигур:
Сравнить результаты: ;
Сделать вывод:
Задание для лабораторной работы. Номер схемы соответствует Вашему порядковому номеру в журнале.
studfiles.net
Центр тяжести - методы нахождения.
Методы нахождения центра тяжести
Наиболее часто для нахождения центра тяжести тела или фигуры применяют следующие методы:
- метод симметрии;
- метод разбиения;
- метод отрицательных масс.
Рассмотрим приемы, применяемые в каждом из перечисленных методов.
***
Метод симметрии
Представим себе однородное тело, которое имеет плоскость симметрии. Выберем такую систему координат, чтобы оси x и z лежали в плоскости симметрии (см. рисунок 1).
В этом случае каждой элементарной частице силой тяжести Gi с абсциссой yi = +a соответствует такая же элементарная частица с абсциссой yi = -a, тогда:
yC = Σ(Gixi)/ΣGi = 0.
Отсюда вывод: если однородное тело имеет плоскость симметрии, то центр тяжести тела лежит в этой плоскости.
Аналогично можно доказать и следующие положения:
- Если однородное тело имеет ось симметрии, то центр тяжести тела лежит на этой оси;
- Если однородное тело имеет две оси симметрии, то центр тяжести тела находится в точке их пересечения;
- Центр тяжести однородного тела вращения лежит на оси вращения.
***
Метод разбиения
Этот метод заключается в том, что тело разбивают на наименьшее число частей, силы тяжести и положение центров тяжести которых известны, после чего применяют приведенные ранее формулы для определения общего центра тяжести тела.
Допустим, что мы разбили тело силой тяжести G на три части G', G'', G''', абсциссы центров тяжести этих частей x'C, x''C, x'''C известны. Формула для определения абсциссы центра тяжести всего тела:
xC = Σ(Gixi)/ΣGi.
Перепишем ее в следующем виде:
xCΣGi = Σ(Gixi) или GxC = Σ(Gixi).
Последнее равенство запишем для каждой из трех частей тела отдельно:
G'x'C = Σ(G'x'i), G''x''C = Σ(G''ix''i), G'''x'''C = Σ(G'''ix'''i).
Сложив левые и правые части этих трех равенств, получим:
G'x'C + G''x''C + G'''x'''C = Σ(G'ix'i) + Σ(G''x''i) + Σ(G'''ix'''i) = Σ(Gixi).
Но правая часть последнего равенства представляет собой произведение GxC, так как
GxC = Σ(Gixi),
Следовательно, xC = (G'x'C + G''x''C + G'''x'''C)/G, что и требовалось доказать. Аналогично определяются координаты центра тяжести на координатных осях y и z:
yC = (G'y'C + G''y''C + G'''y'''C)/G, zC = (G'z'C + G''z''C + G'''z'''C)/G.
Полученные формулы аналогичны формулам для определения координат цента тяжести, выведенные выше. Поэтому в исходные формулы можно подставлять не силы тяжести элементарных частиц Gi, а силы тяжести конечных частей; под координатами xi, yi, zi понимают координаты центров тяжести частей, на которые разбито тело.
***
Метод отрицательных масс
Этот метод заключается в том, что тело, имеющее свободные полости, считают сплошным, а массу свободных полостей – отрицательной. Вид формул для определения координат центра тяжести тела при этом не меняется.
Таким образом, при определении центра тяжести тела, имеющего свободные полости, следует применять метод разбиения, но считать массу полостей отрицательной.
***
Практические методы определения центра тяжести тел
На практике для определения центра тяжести плоских тел сложной формы часто применяют метод подвешивания, который заключается в том, что плоское тело подвешивают на нити за какую-нибудь точку. Прочерчивают вдоль нити линию, и тело подвешивают за другую точку, не находящуюся на полученной линии. Затем вновь проводят линию вдоль нити. Точка пересечения двух линий и будет являться центром тяжести плоского тела.
Еще один способ определения центра тяжести, применяемый на практике, называется метод взвешивания. Этот метод часто применяется для определения центра тяжести крупных машин и изделий – автомобилей, самолетов, колесных тракторов и т. п., которые имеют сложную объемную форму и точечную опору на грунт. Метод заключается в применении условий равновесия, исходя из того, что сумма моментов всех сил, действующих на неподвижное тело равна нулю. Практически это осуществляется взвешиванием одной из опор машины (задние или передние колеса устанавливаются на весы), при этом показания весов, по сути, являются реакцией опоры, которая учитывается при составлении уравнения равновесия относительно второй точки опоры (находящейся вне весов). По известной массе (соответственно – весу) тела, показанию весов в одной из точек опоры, и расстоянию между точками опоры можно определить расстояние от одной из точек опоры до плоскости, в которой расположен центр тяжести. Чтобы найти подобным образом линию (ось), на которой расположен центр тяжести машины, необходимо произвести два взвешивания по принципу, изложенному выше для метода подвешивания (см. рис. 1а).
***
Положение центра тяжести некоторых фигур
Прямоугольник. Так как прямоугольник имеет две оси симметрии, то центр тяжести его площади находится в точке пересечения этих осей, иначе говоря, в точке пересечения диагоналей прямоугольника.
Треугольник. Пусть дан треугольник АBD (см. рисунок 2). Разобьем его на элементарные (бесконечно узкие) полоски, параллельные стороне AD. Центр тяжести каждой полоски будет лежать на медиане Bd (т. е. в середине каждой полоски), следовательно, на этой медиане будет лежать и центр тяжести всей площади треугольника. Разбив треугольник на элементарные полоски, параллельные стороне AB, увидим, что искомый центр тяжести лежит и на медиане aD. Проделав аналогичное действие с треугольником относительно стороны ВD, получим тот же результат – центр тяжести находится на соответствующей медиане. Следовательно, центр тяжести всей площади треугольника лежит на точке пересечения его медиан, поскольку эта точка является единственной общей точкой для всех трех медиан данной геометрической фигуры.
Из геометрии известно, что медианы треугольника пересекаются в одной точке и делятся в соотношении 1:2 от основания. Следовательно, центр тяжести треугольника расположен на расстоянии одной трети высоты от каждого основания.
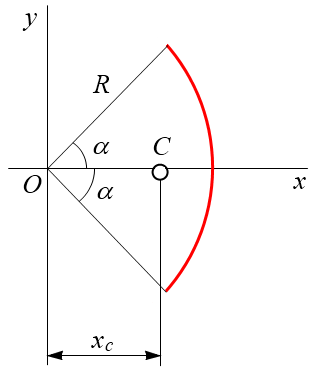
Дуга окружности. Возьмем дугу окружности АВ радиусом R с центральным углом 2α (см. рисунок 3). Систему координат выберем так, чтобы начало координат было в центре окружности, а ось x делила дугу пополам, тогда yC = 0 вследствие симметрии дуги относительно оси x. Определим координату центра тяжести xC.
Разобьем дугу АВ на элементарные части li, одна из которых изображена на рисунке. Тогда, согласно сделанным выше выводам,
xC =Σ(lixCi)/Σli.
Дугу li вследствие малости примем за отрезок прямой. Из подобия треугольника ODiCi и элементарного треугольника S (на рисунке заштрихован) получим:
Li/Δyi = R/xCi или lixi = RΔyi.
Тогда:
xC =Σ(lixCi)/Σli = Σ(RΔyi)/l = RΣΔyi/l = R×AB/l,
поскольку RΣΔyi = AB, а Σli = l – длина дуги АВ. Но АВ = 2R sinα, а l = 2Rα, следовательно,
xC = (R sinα)/α.
При α = π/2 рад (полуокружность), xC = 2R/π.
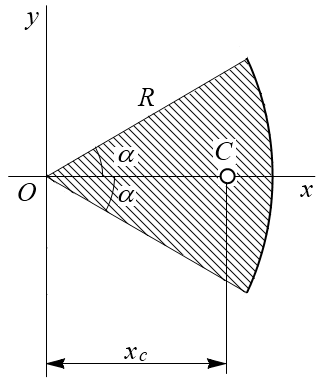
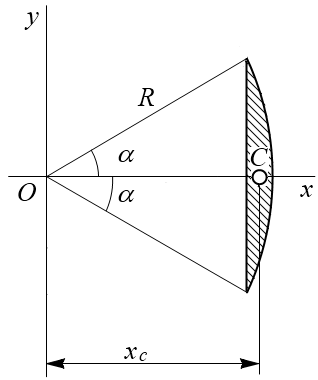
Круговой сектор. Возьмем сектор радиусом R с центральным углом 2α (см. рисунок 3а). Проведем оси координат, как показано на рисунке (ось x направлена вдоль оси симметрии сектора), тогда yC = 0.
Определим xC, для чего разобьем сектор на ряд элементарных секторов, каждый из которых из-за малости дуги li можно принять за равнобедренный треугольник с высотой R. Тогда центр тяжести каждого элементарного сектора будет находиться на дуге радиуса 2R/3 и задача определения центра тяжести сектора сводится к определению центра тяжести этой дуги. Очевидно, что
xC = 2 R sinα/(3α).
При α = π/2 рад (полукруг): xC = 4R/(3π).
***
Пример решения задачи на определение центра тяжести
Задача: Определить положение центра тяжести сечения, составленного из двутавра № 22 и швеллера № 20, как показано на рисунке 4.
Решение. Из курса инженерной графики известно, что номер проката соответствует наибольшему габаритному размеру его сечения, выраженного в сантиметрах.
Так как сечение, составленное из двутавра и швеллера, представляет собой фигуру, симметричную относительно оси y, то центр тяжести такого сечения лежит на этой оси, т. е. xC = 0. По справочнику определим площади и координаты центров тяжести двутавра 1 и швеллера 2.
Для двутаврового сечения: А1 = 15,2 см2; y1= 22/2 = 11 см. Для швеллерного сечения: А2 = 12 см2; y2 = 22 + d – z0= 22 + 0,32 – 1,25 = 21,07 см, где d – толщина стенки швеллера; z0 – размер, определяющий положение центра тяжести швеллера.
Применим формулу для определения координаты центра тяжести всего сечения:
yC = Σ(Aiyi)/ΣAi,
тогда:
yC = (A1y1 +A2y2)/(A1 +A2) = (15,2×11 + 12×21,07)/(15,2 + 12) = 15,4 см.
Задача решена.
***
Кинематика точки
k-a-t.ru
423800, Набережные Челны , база Партнер Плюс, тел. 8 800 100-58-94 (звонок бесплатный)


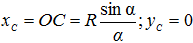
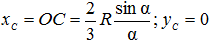
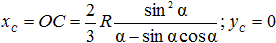
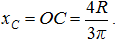
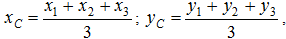
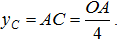
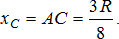
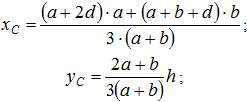
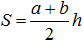 - площадь фигуры.
- площадь фигуры.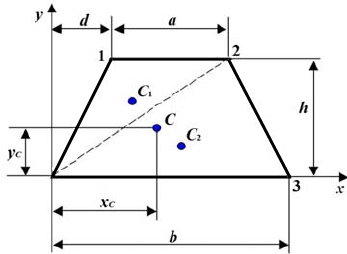
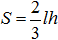 – площадь фигуры;
– площадь фигуры;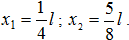
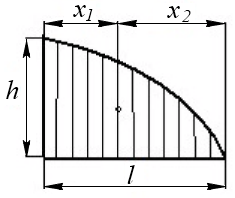
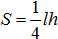 – площадь фигуры;
– площадь фигуры;