|
||||
|
|
звонок бесплатный
Наши сотрудники:
[email protected]
Екатерина - специалист по продаже а/м КАМАЗ
 [email protected]
[email protected]






Техника в наличии

Тягач КАМАЗ 44108-6030-24
2014г, 6х6, Евро3, дв.КАМАЗ 300 л.с., КПП ZF9, бак 210л+350л, МКБ,МОБ,рестайлинг.
цена 2 220 000 руб.,

КАМАЗ 4308-6063-28(R4)
4х2,дв. Cummins ISB6.7e4 245л.с. (Е-4),КПП ZF6S1000, V кузова=39,7куб.м., спальное место, бак 210л, шк-пет,МКБ, ТНВД BOSCH, система нейтрализ. ОГ(AdBlue), тент, каркас, рестайлинг, внутр. размеры платформы 6112х2470х730 мм
цена 1 950 000 руб.,

Самосвал КАМАЗ 6520-057
2014г, 6х4,Евро3, дв.КАМАЗ 320 л.с., КПП ZF16, ТНВД ЯЗДА, бак 350л, г/п 20 тонн, V кузова =20 куб.м.,МКБ,МОБ, со спальным местом.
цена 2 700 000 руб.,

Самосвал 6522-027
2014, 6х6, дв.КАМАЗ 740.51,320 л.с., КПП ZF16,бак 350л, г/п 19 тонн,V кузова 12куб.м.,МКБ,МОБ,задняя разгрузка,обогрев платформы.
цена 3 190 000 руб.,
СУПЕР ЦЕНА
на АВТОМОБИЛИ КАМАЗ
| 43118-010-10 (дв.740.30-260 л.с.) | 2 220 000 |
| 43118-6033-24 (дв.740.55-300 л.с.) | 2 300 000 |
| 65117-029 (дв.740.30-260 л.с.) | 2 200 000 |
| 65117-6010-62 (дв.740.62-280 л.с.) | 2 350 000 |
| 44108 (дв.740.30-260 л.с.) | 2 160 000 |
| 44108-6030-24 (дв.740.55,рест.) | 2 200 000 |
| 65116-010-62 (дв.740.62-280 л.с.) | 1 880 000 |
| 6460 (дв.740.50-360 л.с.) | 2 180 000 |
| 45143-011-15 (дв.740.13-260л.с) | 2 180 000 |
| 65115 (дв.740.62-280 л.с.,рест.) | 2 190 000 |
| 65115 (дв.740.62-280 л.с.,3-х стор) | 2 295 000 |
| 6520 (дв.740.51-320 л.с.) | 2 610 000 |
| 6520 (дв.740.51-320 л.с.,сп.место) | 2 700 000 |
| 6522-027 (дв.740.51-320 л.с.,6х6) | 3 190 000 |

подробнее про услугу перегона можно прочесть здесь.

|
Нужны самосвалы? Обратите внимание на Ford-65513-02. |
КАМАЗы в лизинг
ООО «Старт Импэкс» имеет возможность поставки грузовой автотехники КАМАЗ, а так же спецтехники на шасси КАМАЗ в лизинг. Продажа грузовой техники по лизинговым схемам имеет определенные выгоды для покупателя грузовика. Рассрочка платежа, а так же то обстоятельство, что грузовики до полной выплаты лизинговых платежей находятся на балансе лизингодателя, и соответственно покупатель автомобиля не платит налогов на имущество. Мы готовы предложить любые модели бортовых автомобилей, тягачей и самосвалов по самым выгодным лизинговым схемам.Контактная информация.
г. Набережные Челны, Промкомзона-2, Автодорога №3, база «Партнер плюс».
тел/факс (8552) 388373.
Схема проезда
Как узнать модуль зубчатого колеса? Онлайн расчет шестеренок
Расчёт диаметра шестерни с прямым и косым зубом.

Сегодня рассмотрим как рассчитать диаметр шестерни. Сразу скажу что диаметр прямозубой шестерни имеет одну формулу, а диаметр косозубой шестерни имеет другую формулу. Хотя многие считают по одной формуле, это ошибочно. Данные расчёты нужны для других расчётах при изготовлении зубчатых колёс. Итак перейдём непосредственно к формулам (без коррекции):
Для начала значения которые надо знать при расчётах в данных формулах:
- De — диаметр окружности выступов.
- Dd — диаметр делительной окружности (непосредственно от шага которой считается модуль шестерни).
- Di — диаметр окружности впадин.
- Z — число зубьев шестерни.
- Z1 — число зубьев шестерни малого колеса.
- Z2 — число зубьев шестерни большого колеса.
- M (Mn) — модуль (модуль нормальный, по делительному диаметру).
- Ms — модуль торцевой.
- β (βd) — угол наклона шестерни (иметься ввиду угол наклона по делительному диаметру).
- Cos βd — косинус угла на делительном диаметре.
- A — межцентровое расстояние.
Формула расчёта диаметров прямозубого зубчатого колеса (шестерни):
De=(Z×M)+2M=Dd+2M=(Z+2)×M
Dd=Z×M
Формула расчёта диаметров косозубого зубчатого колеса (шестерни с косым зубом):
De=Dd+2Mn
Вроде как и на прямозубых колёсах, но на косозубых мы имеем другой делительный диаметр, следовательно диаметр окружности выступов будет другим!
Dd=Z×Mn/Cos βd=Z×Ms
То есть количество зубьев умножаем на модуль и делим на косинус угла зуба по делительному диаметру или количество зубьев умножаем на модуль торцевой.
Определяем торцевой модуль:
Ms=Mn/Cos βd =2A/Z1+Z2
То есть модуль торцевой равен — модуль нормальный делить на косинус угла зуба шестерни по делительному диаметру или два умножить на межцентровое расстояние и делить на число зубьев малого колеса плюс число зубьев большого колеса.
Для этого нам уже необходимо знать межцентровое расстояние, которое можно посчитать по формуле:
A=(Z1+Z2/2Cos βd)×Mn=0,5Ms(Z1+Z2)
То есть число зубьев малого колеса плюс число зубьев большого колеса разделить на 2 умножить на косинус угла зуба шестерни по делительному диаметру и всё это умножить на модуль или число зубьев малого колеса плюс число зубьев большого колеса умножить (0,5 умножить на модуль торцевой).
Как видите посчитать диаметр прямозубого колеса очень просто, а вот посчитать диаметр колеса с косым зубом тут уже посложнее, так как требуется много различных составляющих. Данные составляющие не всегда есть, что усложняет расчёт. Так что для некоторых расчётов понадобится знание некоторых точных параметров, таких как точный (подчеркну точный) угол наклона зубьев шестерни на делительном диаметре или точное межцентровое расстояние! Все расчёты взаимосвязаны, всё это надо для других расчётов зубчатых передач при проектировании и в ремонтном деле.
Поделится, добавить в закладки!zuborez.info
Geargenerator - онлайн конструктор зубчатого зацепления
Если вы попали на эту страницу, то наверняка знаете программу Gear Template Generator(подробнее о программе). Эта программа позволяет делать расчет параметров зубчатого зацепления. Gear Template Generator устанавливается локально на компьютер и позволяет создавать чертеж пары шестеренок с необходимыми параметрами. (Скачать Gear Template Generator можно тут)
Сейчас я расскажу о аналоге Gear Template Generator – онлайн конструкторе зубчатого зацепления Geargenerator. Собственно если вы введете в адресную строку браузера Geargenerator.com, то попадете на страницу конструктора.
Вот так выглядит начальное окно программы
Окно поделено на две части. Левая часть – панель настроек программы и шестеренок. На правой части будет отображаться результат.
Рассмотрим левую часть
Она условно разделена на несколько блоков с набором параметров. Рассмотрим эти блоки.
Самый верхний блок Animation – анимация движения шестеренок. Старт/стоп, сброс. Можно задать скорость вращения.
Далее идет блок Gears – это список шестеренок и работа с их количеством. По умолчанию там их четыре. Можно добавить, удалить или очистить. Причем новая шестеренка будет добавляться к той, которая выделена в данный момент.
Следующий блок настроек Connection properties – он отвечает за варианты стыковки шестеренок
Поле Parent gear #: - тут можно для текущей шестеренке указать номер родительской шестеренки(из списка Gears). По умолчанию самая первая шестеренка – нулевая. Таким образом можно быстро пере стыковать шестеренки.
Поле Axle connection: - определяет способ стыковки шестеренок. Если установить тут галочку – шестеренки будут стыковаться на одной оси.
Поле Connection angle: - указывает угол на центр шестеренки относительно родительской шестеренки.
Пояснение
Положение шестеренки #1 при значении Connection angle: – 60
Положение шестеренки #1 при значении Connection angle: – 85
Далее Gear properties – параметры самих шестеренок(количество зубьев, параметры зуба и т.д.) В этом же блоке есть самая главная кнопка - Download SVG – клик по ней начинает загрузку файла с шестеренками в формате SVG
Последний блок Display – настройки отображения самого конструктора. Можно поменять цветовую схему, включить/выключить сетку и метки на шестеренках.
Теперь небольшой пример работы
Уменьшим количество зубьев шестеренки #3 до 42
Добавим шестеренку #4 к шестеренке #3 (для этого в блоке Gears нужно кликнуть по #3, а затем по кнопке Add New)
Укажем для #4, что она должна располагаться на одной оси с #3
Добавим к #3 и #4 еще по одному зубчатому колесу с указанием параметра Connection angle (разведем их в стороны)
Нажмем кнопку Start/Stop – и посмотрим на анимацию. Таким образом можно не только собрать нужную последовательность передач, но и подобрать расположение осей шестеренок для дальнейшего размещения в корпусе изделия.
Резюме.
В этом онлайн конструкторе зубчатого зацепления можно выстроить почти весь механизм часов(то, что касается шестеренок). Можно строить достаточно сложные схемы соединения зубчатых колес. В отличие от Gear Template Generator, где можно строить только одну пару шестеренок. Но Gear Template Generator дает большую свободу в настройке параметров шетеренок.
GearGenerator позволяет экспортировать только в SVG.
GearGenerator работает онлайн, не требует установки и бесплатен.
Еще один плюс - все параметры созданного вами зубчатого зацепления добавляются в адресную строку. Сохранить или поделиться результатом своего конструирования можно скопировав текст адресной строки. Пример, который я описывал выше - результат можно увидеть по этой ссылке.
Обе программы обладают своими плюсами. Какую из них выбрать – выбор за вами.
Перейти на сайт GearGenerator можно по этой ссылке.
mebel-sam.net.ua
Модуль зубьев зубчатого колеса: расчет, стандартные, определение
Зубчатая передача впервые была освоена человеком в глубокой древности. Имя изобретателя осталось скрыто во тьме веков. Первоначально зубчатые передачи имели по шесть зубьев — отсюда и пошло название «шестерня». За многие тысячелетия технического прогресса передача многократно усовершенствовалась, и сегодня они применяются практически в любом транспортном средстве от велосипеда до космического корабля и подводной лодки. Используются они также в любом станке и механизме, больше всего шестеренок используется в механических часах.

Зубчатое колесо
Что такое модуль зубчатого колеса
Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров
- диаметр;
- число зубьев;
- шаг;
- высота зубца;
- и некоторые другие.
Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.
Скачать ГОСТ 9563-60
В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.
Для расчета этого параметра применяют следующие формулы:
m=t/π,
где t — шаг.

Параметры зубчатых колес
Модуль зубчатого колеса можно рассчитать и следующим образом:
m=h/2,25,
где h — высота зубца.
И, наконец,
m=De/(z+2),
где De — диаметр окружности выступов,а z — число зубьев.
Что же такое модуль шестерни?
это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.
Формула расчета параметров прямозубой передачи
Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

Расчет модуля зубчатого колеса
Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:
π×D=t×z,
проведя преобразование, получим:
D=(t /π)×z
Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.
t/π=m,
размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:
В=m×z;
выполнив преобразование, находим:
m=D / z.
Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов De получается равным
De=d+2× h’,
где h’- высота головки.
Высоту головки приравнивают к m:
h’=m.
Проведя математические преобразования с подстановкой, получим:
De=m×z+2m = m(z+2),
откуда вытекает:
m=De/(z+2).
Диаметр окружности впадин Di соответствует De за вычетом двух высот основания зубца:
Di=D-2h“,
где h“- высота ножки зубца.
Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:
h’ = 1,25m.

Устройство зубчатого колеса
Выполнив подстановку в правой части равенства, имеем:
Di = m×z-2×1,25m = m×z-2,5m;
что соответствует формуле:
Di = m(z-2,5m).
Полная высота:
h = h’+h“,
и если выполнить подстановку, то получим:
h = 1m+1,25m=2,25m.
Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.
Следующий важный размер, толщину зубца s принимают приблизительно равной:
- для отлитых зубцов: 1,53m:
- для выполненных путем фрезерования-1,57m, или 0,5×t
Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины sв, получаем формулы для ширины впадины
- для отлитых зубцов: sв=πm-1,53m=1,61m:
- для выполненных путем фрезерования- sв= πm-1,57m = 1,57m
Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:
- усилия, прикладываемые к детали при эксплуатации;
- конфигурация деталей, взаимодействующих с ней.
Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.
Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.
Исходные данные и замеры
На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.
Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.
Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.
Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.
Результаты расчетов
Для более крупных потребуются измерения и вычисления.
Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:
m=De/(z+2)
Последовательность действий следующая:
- измерить диаметр штангенциркулем;
- сосчитать зубцы;
- разделить диаметр на z+2;
- округлить результат до ближайшего целого числа.

Зубец колеса и его параметры
Данный метод подходит как для прямозубых колес, так и для косозубых.
Расчет параметров колеса и шестерни косозубой передачи
Расчетные формулы для важнейших характеристик шестерни косозубой передачи совпадают с формулами для прямозубой. Существенные различия возникают лишь при прочностных расчетах.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
stankiexpert.ru
Расчет зубчатой передачи в Excel
Опубликовано 22 Июн 2013Рубрика: Механика | 90 комментариев
 Для полного и точного проектировочного расчета зубчатой цилиндрической эвольвентной передачи необходимо знать: передаточное число передачи, крутящий момент на одном из валов, частоту вращения одного из валов, суммарное машинное время работы передачи,...
Для полного и точного проектировочного расчета зубчатой цилиндрической эвольвентной передачи необходимо знать: передаточное число передачи, крутящий момент на одном из валов, частоту вращения одного из валов, суммарное машинное время работы передачи,...
...тип передачи (прямозубая, косозубая или шевронная), вид передачи (с внешним зацеплением или внутренним), график нагрузки (режим работы – доля времени действия максимальных нагрузок), материал и термообработку шестерни и колеса, схему расположения передачи в редукторе и в общей схеме привода.
На основании вышеперечисленных исходных данных при помощи многочисленных таблиц, разнообразных диаграмм, коэффициентов, формул определяются основные параметры зубчатой передачи: межосевое расстояние, модуль, угол наклона зубьев, число зубьев шестерни и колеса, ширины зубчатых венцов шестерни и колеса.
В детальном алгоритме расчетов — около пятидесяти смысловых программных шагов! При этом часто при работе приходится возвращаться на несколько шагов назад, отменять принятые ранее решения и вновь двигаться вперед, понимая, что, возможно, придется вновь вернуться. Найденные в результате такой кропотливой работы расчетные значения межосевого расстояния и модуля необходимо в конце расчетов округлить до ближайшего большего значения из стандартизованного ряда…
То есть, считали-считали, а в конце — «бац» — и просто на 15…20% результаты увеличили…
Студентам в курсовом проекте по «Деталям машин» такой расчет делать нужно! В реальной жизни инженера, я думаю, это не всегда целесообразно.
В предлагаемой вашему вниманию статье я расскажу как быстро и с приемлемой для практики точностью выполнить проектировочный расчет зубчатой передачи. Работая инженером-конструктором, я довольно часто применял изложенный ниже алгоритм в своей работе, когда не требовалась высокая точность прочностных расчетов. Так бывает при единичном изготовлении передачи, когда проще, быстрее и дешевле спроектировать и изготовить зубчатую пару с некоторым излишним запасом прочности. Используя предлагаемую программу расчета, можно легко и достаточно быстро проверить результаты, полученные, например, с помощью другой аналогичной программы или убедиться в правильности «ручных» расчетов.
По сути, данная статья является в какой-то мере продолжением темы, начатой в посте «Расчет привода тележки». Там результатами расчета были: передаточное число привода, статический момент сопротивления движению, приведенный к валу колеса и статическая мощность двигателя. Для нашего расчета они будут частью исходных данных.
Проектировочный расчет цилиндрической зубчатой передачи будем выполнять в программе MS Excel.
Начинаем. Обращаю ваше внимание, что материалом для всех зубчатых колес выбираем Сталь40Х или Сталь45 с твердостью HRC 30…36 (для шестерни – «потверже», для колеса – «помягче», но в этом диапазоне) и допустимыми контактными напряжениями [σH]=600МПа. В практике – это наиболее распространенный и доступный материал и термообработка.
Расчет в примере будет выполнен для косозубой передачи. Общая схема зубчатой передачи изображена на представленном далее рисунке.

Запускаем Excel. В ячейках со светло-зеленой и бирюзовой заливкой пишем исходные данные и уточненные пользователем (принятые) расчетные данные. В ячейках со светло-желтой заливкой считываем результаты расчетов. В ячейках со светло-зеленой заливкой помещены мало подверженные изменениям исходные данные.
Заполняем ячейки исходными данными:
1. Коэффициент полезного действия передачи КПД (это КПД эвольвентного зубчатого зацепления и КПД двух пар подшипников качения) пишем
в ячейку D3: 0,931
2. Значение интегрального коэффициента K, зависящего от типа передачи (смотри примечание к ячейке D4), записываем
в ячейку D4: 11,5
3. Угол наклона зубьев (предварительный) bп в градусах выбираем из рекомендованного диапазона в примечании к ячейке D5 и вводим
в ячейку D5: 15,000
4. Передаточное число uп, определенное в предварительных расчетах, записываем
в ячейку D6: 4,020
5. Записываем мощность на быстроходном валу передачи P1 в Ваттах
в ячейку D7: 250
6. Частоту вращения быстроходного вала n1 в оборотах в минуту вводим
в ячейку D8: 1320

Программа расчета зубчатой передачи выдает первый блок расчетных параметров:
7. Вращательный момент на быстроходном валу T1 в Ньютонах умноженных на метр
в ячейке D9: =30*D7/(ПИ()*D8)=1,809
T1=30*P1/(3,14*n1)
8. Мощность на тихоходном валу передачи P2 в Ваттах
в ячейке D10: =D7*D3=233
P2=P1*КПД
9. Частота вращения тихоходного вала n2 в оборотах в минуту
в ячейке D11: =D8/D6=328
n2=n1/uп
10. Вращательный момент на тихоходном валу T2 в Ньютонах умноженных на метр
в ячейке D12: =30*D10/(ПИ()*D11)=6,770
T2=30*P2/(3,14*n2)
11. Расчетный диаметр делительной окружности шестерни d1р в миллиметрах
в ячейке D13: =D4*(D12*(D6+1)/D6)^0,33333333=23,427
d1р=K*(T2*(uп+1)/uп )^0,33333333
12. Расчетный диаметр делительной окружности колеса d2р в миллиметрах
в ячейке D14: =D13*D6=94,175
d2р= d1р*uп
13. Максимальный расчетный модуль зацепления m(max)р в миллиметрах
в ячейке D15: =D13/17*COS (D5/180*ПИ())=1,331
m(max)р=d1р/17*cos(bп)
14. Минимальный расчетный модуль зацепления m(min)р в миллиметрах
в ячейке D16: =D15/2 =0,666
m(min)р=m(max)р/2
15. Выбираем модуль зацепления m в миллиметрах из диапазона рассчитанных выше значений и из стандартизованного ряда, приведенного в примечании к ячейке В17 и записываем
в ячейку D17: 1,250
Далее в диалоговом режиме пользователя и программы определяем следующие основные параметры зубчатой передачи:
16. Расчетная ширина зубчатого венца колеса b2р в миллиметрах
в ячейке D18: =D13*0,6=14,056
b2р= d1р*0,6
17. Округляем ширину зубчатого венца колеса b2 в миллиметрах и вводим
в ячейку D19: 14,000
18. Программа определяет ширину зубчатого венца шестерни b1 в миллиметрах
в ячейке D20: =D19+4=18,000
b1=b2+4
19. Далее находится расчетное число зубьев шестерни z1р
в ячейке D21: =D13*COS (D5/180*ПИ())/D17 =18,1
z1р=d1р*cos(bп)/m
20. Округляем полученное выше значение числа зубьев шестерни z1 и записываем
в ячейку D22: 19
21. Далее по аналогии — расчетное число зубьев колеса z2р
в ячейке D23: =D22*D6 =76,4
z2р=z1*uп
22. Округленное число зубьев колеса z2 записываем
в ячейку D24: 77
23. Уточняем расчетом передаточное число (окончательное) u
в ячейке D25: =D24/D22=4,053
u=z2/z1
24. Рассчитываем отклонение передаточного числа окончательного от предварительного delta в процентах и сравниваем с допустимыми значениями, приведенными в примечании к ячейке D26
в ячейке D26: =(D25/D6-1)*100=0,81
delta=u/uп-1
25. Далее программа находит расчетное межосевое расстояние зубчатой передачи awр в миллиметрах
в ячейке D27: =D17*(D22+D24)/(2*COS (D5/180*ПИ())=62,117
awр=m*(z1+z2)/(2*cos(bп))
26. Округляем в большую сторону расчетное значение межосевого расстояния зубчатой передачи по стандартизованному ряду, приведенному в примечании к ячейке D28, и вводим окончательное межосевое расстояние aw в миллиметрах
в ячейку D28: 63,000
27. В завершение программа уточняет угол наклона зубьев зубчатой передачи b в градусах
в ячейке D27: =ЕСЛИ(D5=0;0;ACOS (D17*(D22+D24)/(2*D28))/ПИ()*180)=17,753
b=arccos(m*(z1+z2)/(2*aw))
Итак, мы выполнили по упрощенной схеме проектировочный расчет зубчатой цилиндрической передачи, целью которого было определение основных габаритных параметров на основе заданных силовых.
Далее конструктору для выполнения чертежей элементов передачи необходимо выполнить геометрический расчет зацепления. Но это, возможно, тема другого поста.
Прошу УВАЖАЮЩИХ труд автора скачать файл ПОСЛЕ ПОДПИСКИ на анонсы статей.
ОСТАЛЬНЫМ можно скачать просто так... — никаких паролей нет!
Буду рад увидеть ваши комментарии, уважаемые читатели.
Ссылка на скачивание файла: raschet-zubchatoi-peredachi (xls 38,5KB).
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
al-vo.ru
Расчёт диаметров шкивов ремённой передачи для поликлиновидного ремня. Онлайн калькулятор. :: АвтоМотоГараж
Работы по переборке электродвигателя подходят к завершению. Приступаем к расчёту шкивов ремённой передачи станка. Немного терминологии по ремённой передаче.
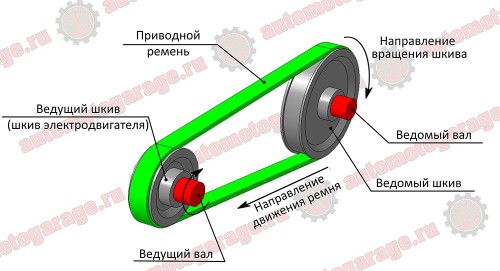
Главными исходными данными у нас будут три значения. Первое значение это скорость вращения ротора (вала) электродвигателя 2790 оборотов в секунду. Второе и третье это скорости, которые необходимо получить на вторичном валу. Нас интересует два номинала 1800 и 3500 оборотов в минуту. Следовательно, будем делать шкив двухступенчатый.
Заметка! Для пуска трёхфазного электродвигателя мы будем использовать частотный преобразователь поэтому расчётные скорости вращения будут достоверными. В случае если пуск двигателя осуществляется при помощи конденсаторов, то значения скорости вращения ротора будут отличаться от номинального в меньшую сторону. И на этом этапе есть возможность свести погрешность к минимуму, внеся поправки. Но для этого придётся запустить двигатель, воспользоваться тахометром и замерить текущую скорость вращения вала.
Наши цели определены, переходим выбору типа ремня и к основному расчёту. Для каждого из выпускаемых ремней, не зависимо от типа (клиноременный, поликлиновидный или другой) есть ряд ключевых характеристик. Которые определяют рациональность применения в той или иной конструкции. Идеальным вариантом для большинства проектов будет использование поликлиновидного ремня. Название поликлиновидный получил за счет своей конфигурации, она типа длинных замкнутых борозд, расположенных по всей длине. Названия ремня происходит от греческого слова «поли», что означает множество. Эти борозды ещё называют по другому – рёбра или ручьи. Количество их может быть от трёх до двадцати.
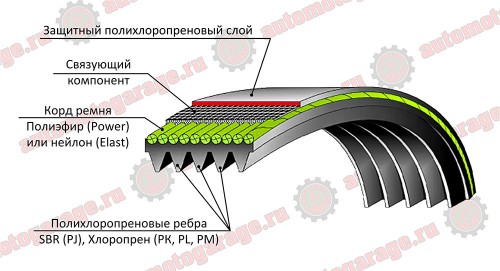
Поликлиновидный ремень перед клиноременным имеет массу достоинств, таких как:
- благодаря хорошей гибкости возможна работа на малоразмерных шкивах. В зависимости от ремня минимальный диаметр может начинаться от десяти – двенадцати миллиметров;
- высокая тяговая способность ремня, следовательно рабочая скорость может достигать до 60 метров в секунду, против 20, максимум 35 метров в секунду у клиноременного;
- сила сцепления поликлинового ремня с плоским шкивом при угле обхвата свыше 133° приблизительно равна силе сцепления со шкивом с канавками, а с увеличением угла обхвата сила сцепления становится выше. Поэтому для приводов с передаточным отношением свыше трёх и углом обхвата малого шкива от 120° до 150° можно применять плоский (без канавок) больший шкив;
- благодаря легкому весу ремня уровни вибрации намного меньше.
Принимая во внимание все достоинства поликлиновидных ремней, мы будем использовать именно этот тип в наших конструкциях. Ниже приведена таблица пяти основных сечений самых распространённых поликлиновидных ремней (PH, PJ, PK, PL, PM).
| Обозначение | PH | PJ | PK | PL | PM |
| Шаг ребер, S, мм | 1.6 | 2.34 | 3.56 | 4.7 | 9.4 |
| Высота ремня, H, мм | 2.7 | 4.0 | 5.4 | 9.0 | 14.2 |
| Нейтральный слой, h0, мм | 0.8 | 1.2 | 1.5 | 3.0 | 4.0 |
| Расстояние до нейтрального слоя, h, мм | 1.0 | 1.1 | 1.5 | 1.5 | 2.0 |
| Минимальный диаметр шкива, db, мм | 13 | 20 | 45 | 75 | 180 |
| Максимальная скорость, Vmax, м/с | 60 | 60 | 50 | 40 | 35 |
| Диапазон длины, L, мм | 1140…2404 | 356…2489 | 527…2550 | 991…2235 | 2286…16764 |
Рисунок схематичного обозначения элементов поликлиновидного ремня в разрезе.
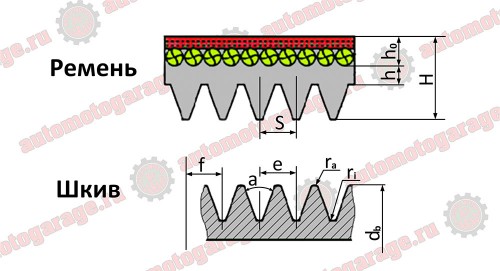
Как для ремня, так и для ответного шкива имеется соответствующая таблица с характеристиками для изготовления шкивов.
| Сечение | PH | PJ | PK | PL | PM |
| Расстояние между канавками, e, мм | 1,60±0,03 | 2,34±0,03 | 3,56±0,05 | 4,70±0,05 | 9,40±0,08 |
| Суммарная погрешность размера e, мм | ±0,3 | ±0,3 | ±0,3 | ±0,3 | ±0,3 |
| Расстояние от края шкива fmin, мм | 1.3 | 1.8 | 2.5 | 3.3 | 6.4 |
| Угол клина α, ° | 40±0,5° | 40±0,5° | 40±0,5° | 40±0,5° | 40±0,5° |
| Радиус ra, мм | 0.15 | 0.2 | 0.25 | 0.4 | 0.75 |
| Радиус ri, мм | 0.3 | 0.4 | 0.5 | 0.4 | 0.75 |
| Минимальный диаметр шкива, db, мм | 13 | 12 | 45 | 75 | 180 |
Минимальный радиус шкива задаётся не спроста, этот параметр регулирует срок службы ремня. Лучше всего будет если немного отступить от минимального диаметра в большую сторону. Для конкретной задачи мы выбрали самый распространённый ремень типа «РК». Минимальный радиус для данного типа ремней составляет 45 миллиметров. Учтя это, мы будем отталкиваться ещё и от диаметров имеющихся заготовок. В нашем случае имеются заготовки диаметром 100 и 80 миллиметров. Под них и будем подгонять диаметры шкивов.

Начинаем расчёт. Приведём ещё раз наши исходные данные и обозначим цели. Скорость вращения вала электродвигателя 2790 оборотов в минуту. Ремень поликлиновидный типа «РК». Минимальный диаметр шкива, который регламентируется для него, составляет 45 миллиметров, высота нейтрального слоя 1,5 миллиметра. Нам нужно определить оптимальные диаметры шкивов с учётом необходимых скоростей. Первая скорость вторичного вала 1800 оборотов в минуту, вторая скорость 3500 оборотов в минуту. Следовательно, у нас получается две пары шкивов: первая 2790 на 1800 оборотов в минуту, и вторая 2790 на 3500. Первым делом найдём передаточное отношение каждой из пар.
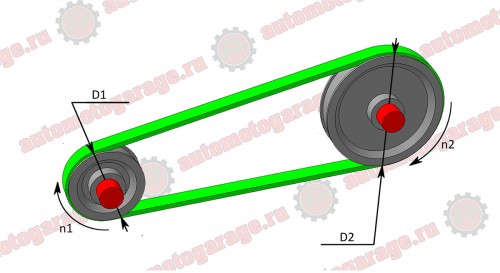
Формула для определения передаточного отношения:
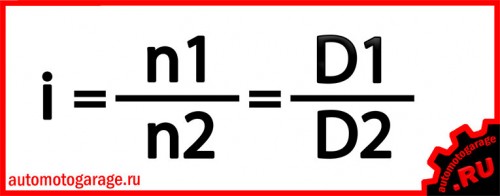 , где n1 и n2 – скорости вращения валов, D1 и D2 – диаметры шкивов.
, где n1 и n2 – скорости вращения валов, D1 и D2 – диаметры шкивов.
Первая пара 2790 / 1800 = 1.55Вторая пара 2790 / 3500 = 0.797
Далее по следующей формуле определяем диаметр большего шкива:
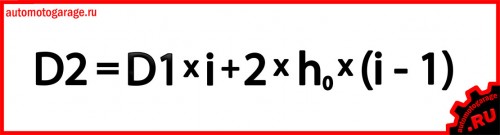 , где h0 нейтральный слой ремня, параметр из таблицы выше.
, где h0 нейтральный слой ремня, параметр из таблицы выше.
D2 = 45x1.55 + 2x1.5x(1.55 – 1) = 71.4 мм
Для удобства расчётов и подбора оптимальных диаметров шкивов можно использовать онлайн калькулятор.
Инструкция как пользоваться калькулятором. Для начала определимся с единицами измерений. Все параметры кроме скорости указываем в милиметрах, скорость указываем в оборотах в минуту. В поле «Нейтральный слой ремня» вводим параметр из таблицы выше столбец «PК». Вводим значение h0 равным 1,5 миллиметра. В следующем поле задаём скорость вращения валя электродвигателя 2790 оборотов в минуту. В поле диаметр шкива электродвигателя вводим значение минимально регламентируемое для конкретного типа ремня, в нашем случае это 45 миллиметров. Далее вводим параметр скорости, с которым мы хотим, чтобы вращался ведомый вал. В нашем случае это значение 1800 оборотов в минуту. Теперь остаётся нажать кнопку «Рассчитать». Диаметр ответного шкива мы получим соответствующем в поле, и оно составляет 71.4 миллиметра.
Примечание: Если необходимо выполнить оценочный расчёт для плоского ремня или клиновидного, то значением нейтрального слоя ремня можно пренебречь, выставив в поле «ho» значение «0».
Теперь мы можем (если это нужно или требуется) увеличить диаметры шкивов. К примеру, это может понадобится для увеличения срока службы приводного ремня или увеличить коэффициент сцепления пара ремень-шкив. Также большие шкивы иногда делают намеренно для выполнения функции маховика. Но мы сейчас хотим максимально вписаться в заготовки (у нас имеются заготовки диаметром 100 и 80 миллиметров) и соответственно подберём для себя оптимальные размеры шкивов. После нескольких переборов значений мы остановились на следующих диаметрах D1 – 60 миллиметров и D2 – 94,5 миллиметров для первой пары.
D2 = 60x1.55 + 2x1.5x(1.55 – 1) = 94.65 мм
Для второй пары D1 – 75 миллиметров и D2 – 60 миллиметров.
D2 = 75x0.797 + 2x1.5x(0.797 – 1) = 59.18 мм
Далее мы приступаем к изготовлению шкивов. Всем удачной работы!
Дополнительная информация по шкивам:
Мы начали первые экспиременты и уже подготовили первую часть материала: Тест ремённого привода. Поликлиновидный ремень. Так же выпустили обучающий короткометражный видеофильм.
Расчёт диаметров шкивов ремённой передачи для поликлиновидного ремня. Онлайн калькулятор.
Расчёт диаметров шкивов ремённой передачи с использованием клиновидного ремня. Онлайн калькулятор.
Расчёт диаметров шкивов ремённой передачи с применение плоского ведомого шкива. Онлайн калькулятор.
Расчёт длинны приводного поликлиновидного ремня. Онлайн калькулятор.
Расчёт длинны приводного клиновидного ремня. Онлайн калькулятор.
Расчёт и подбор натяжного ролика для поликлиновидного ремня
Расчёт и подбор натяжного ролика для клиновидного ремня
Точим шкив для поликлиновидного ремня
Тест ремённого привода. Поликлиновидный ремень. Первая передача.
Онлайн калькуляторы на все случаи жизни, рекомендуем ознакомиться:
Расчёт количества масла для бензина,
Расчёт масла для топливной смеси - ёмкость без маркировки объёма,
Расчёт шунтирующего сопротивления амперметра,
Онлайн калькулятор - закон Ома (ток, напряжение, сопротивление) + Мощность,
Расчет трансформатора с тороидальным магнитопроводом,
Расчет трансформатора с броневым магнитопроводом.
automotogarage.ru
Программа для расчета и черчения шестерни. GEAR TEMPLATE GENERATOR
Если Вы интересуетесь изготовлением различных изделий из фанеры, то наверняка на просторах интернета встречали/видели различные движущиеся механизмы(состоящие из разнообразных шестерен). Например, марбл машины или вот такой сейф из фанеры:
более подробно о этом сейфе можно посмотреть на этом видео:
Зубчатые зубчатые колеса являются наиболее легко визуализированными общими передачами, которые передают движение между двумя параллельными валами. Из-за их формы они классифицируются как тип цилиндрических шестерен. Так как поверхности зубьев шестеренок параллельны осям установленных валов, в осевом направлении не создается осевое усилие. Кроме того, из-за простоты производства эти механизмы могут быть выполнены с высокой степенью точности. С другой стороны, шпоры имеют недостаток, поскольку они легко создают шум.
Вообще говоря, когда две зубчатые шестерни находятся в сетке, шестерня с большим количеством зубьев называется «шестерней», а другая с меньшим количеством зубьев называется «шестерня». В последние годы обычно устанавливается угол давления до 20 градусов. В коммерческом оборудовании наиболее часто используется часть эвольвентной кривой в качестве профиля зуба.
Наверняка, вам бы хотелось найти чертежи такого сейфа. Изготовить его или использовать идеи его механизмов в своих проектах. Поскольку автор этого сейфа продает свои изделия, вряд ли он будет выкладывать чертежи.
Но это не повод расстраиваться. Подобные механизмы можно спроектировать самому. И для этого не нужно особых знаний в программах 3д моделирования. Достаточно общих знаний о том, как работают шестерни и программы GEAR TEMPLATE GENERATOR
Несмотря на то, что они не ограничены цилиндрическими зубчатыми передачами, используются переключаемые передачи с переключением передач, когда необходимо слегка отрегулировать расстояние по центру или усилить зубцы шестерни. Они изготавливаются путем регулировки расстояния между зубчатым режущим инструментом, называемым хобовым инструментом, и шестерней на стадии производства. Когда сдвиг положительный, прочность на изгиб шестерни увеличивается, а отрицательный сдвиг слегка уменьшает центральное расстояние.
Зазор - это игра между зубами, когда две зубчатые передачи являются сетчатыми и необходимы для плавного вращения зубчатых колес. Когда зазор слишком велик, он приводит к повышенной вибрации и шуму, а слишком низкий люфт приводит к отказу зуба из-за отсутствия смазки.
Я расскажу, как это делать. Но для начала немного о авторских правах. Данную программу я нашел в свободном доступе в интернете. На сайте автора есть более новая версия программы, которая стоит денег. У нее более расширенный функционал. Предполагаю, что та версия программы, которую я нашел, распространялась бесплатно. Если это не так – прошу сообщить мне об этом и я удалю программу со своего сайта.
Другими словами, они являются эвольвентными зубчатыми колесами, используя часть эвольвентной кривой в качестве формы их зубов. В общем, эвольвентная форма представляет собой наиболее распространенную зубчатую форму зубчатого ремня благодаря, среди прочего, способности поглощать небольшие ошибки центрального расстояния, легко сделанные производственные инструменты упрощают изготовление, толстые корни зубов делают его сильным и т.д. зуб форма часто описывается как спецификация на чертеже цилиндрического зубчатого колеса, как указано высотой зубов.
Итак, после того как запустите GEAR TEMPLATE GENERATOR, вы увидите вот такое окно
Интерфейс программы имеет стандартное верхнее меню, поле визуального отображения результатов, внизу вкладки и поля для указания различных опций и параметров.
В дополнение к стандартным зубам полной глубины существуют расширенные дополнения и профили зубов. Эта статья воспроизводится с разрешения. Масао Кубота, Хагурума Нюмон, Токио: Омша, ООО. Зубная форма зубчатых колес обычно показана как плоская кривая на поперечном сечении, перпендикулярном валу. Поэтому вместо шагового цилиндра используется окружность шага. Контактная точка двух кругов питча называется точкой основного тона. Точка тангажа - это точка, в которой два направления кругов касаются катящегося контакта, так что это пятно, которое не имеет относительного движения между шестернями или, другими словами, мгновенный центр относительного движения.
GEAR TEMPLATE GENERATOR строит чертежи одновременно только двух «элементов». Это может быть шестерня-шестерня(различные варианты), шестерня-прямая деталь с зубцами, или звездочка-цепь.
westix.ru
Как узнать модуль зубчатого колеса? Расчет в Excel.
Опубликовано 20 Янв 2014Рубрика: Механика | 21 комментарий
 При поломке зубчатого колеса или шестерни в редукторе какого-либо механизма или машины возникает необходимость по «старой» детали, а иногда по фрагментам обломков создать чертеж для изготовления нового колеса и/или шестерни. Эта статья будет полезна тем,...
При поломке зубчатого колеса или шестерни в редукторе какого-либо механизма или машины возникает необходимость по «старой» детали, а иногда по фрагментам обломков создать чертеж для изготовления нового колеса и/или шестерни. Эта статья будет полезна тем,...
...кому приходится восстанавливать зубчатые передачи при отсутствии рабочих чертежей на вышедшие из строя детали.
Обычно для токаря и фрезеровщика все необходимые размеры можно получить с помощью замеров штангенциркулем. Требующие более пристального внимания, так называемые, сопрягаемые размеры – размеры, определяющие соединение с другими деталями узла - можно уточнить по диаметру вала, на который насаживается колесо и по размеру шпонки или шпоночного паза вала. Сложнее обстоит дело с параметрами для зубофрезеровщика. В этой статье мы будем определять не только модуль зубчатого колеса, я попытаюсь изложить общий порядок определения всех основных параметров зубчатых венцов по результатам замеров изношенных образцов шестерни и колеса.
«Вооружаемся» штангенциркулем, угломером или хотя бы транспортиром, линейкой и программой MS Excel, которая поможет быстро выполнять рутинные и порой непростые расчеты, и начинаем работу.
Как обычно раскрывать тему я буду на примерах, в качестве которых рассмотрим сначала цилиндрическую прямозубую передачу с наружным зацеплением, а затем косозубую.
Расчетам зубчатых передач на этом сайте посвящено несколько статей: «Расчет зубчатой передачи», «Расчет геометрии зубчатой передачи», «Расчет длины общей нормали зубчатого колеса». В них приведены рисунки с обозначениями параметров, используемых в данной статье. Эта статья продолжает тему и призвана раскрыть алгоритм действий при ремонтно-восстановительных работах, то есть работах, обратных проектировочным.
Расчеты можно выполнить в программе MS Excel или в программе OOo Calc из пакета Open Office.
О правилах форматирования ячеек листа Excel, которые применены в статьях этого блога, можно прочитать на странице «О блоге».
Расчет параметров колеса и шестерни прямозубой передачи.
Изначально полагаем, что зубчатое колесо и шестерня имеют эвольвентные профили зубьев и изготавливались с параметрами исходного контура по ГОСТ 13755-81. Этот ГОСТ регламентирует три главных (для нашей задачи) параметра исходного контура для модулей больше 1 мм. (Для модулей меньше 1 мм исходный контур задается в ГОСТ 9587-81; модули меньше 1 мм рекомендуется применять только в кинематических, то есть не силовых передачах.)
Для правильного расчета параметров зубчатой передачи необходимы замеры и шестерни и колеса!
Исходные данные и замеры:
Начинаем заполнение таблицы в Excel с параметров исходного контура.

1. Угол профиля исходного контура α в градусах записываем
в ячейку D3: 20
2. Коэффициент высоты головки зуба ha* вводим
в ячейку D4: 1
3. Коэффициент радиального зазора передачи c* заносим
в ячейку D5: 0,25
В СССР и в России 90% зубчатых передач в общем машиностроении изготавливались именно с такими параметрами, что позволяло применять унифицированный зубонарезной инструмент. Конечно, изготавливались передачи с зацеплением Новикова и в автомобилестроении применялись специальные исходные контуры, но все же большинство передач проектировалось и изготавливалось именно с контуром по ГОСТ13755-81.
4. Тип зубьев колеса (тип зацепления) T записываем
в ячейку D6: 1
T=1 – при наружных зубьях у колеса
T=-1 – при внутренних зубьях у колеса (передача с внутренним зацеплением)
5. Межосевое расстояние передачи aw в мм измеряем по корпусу редуктора и заносим значение
в ячейку D7: 80,0
Ряд межосевых расстояний зубчатых передач стандартизован. Можно сравнить измеренное значение со значениями из ряда, который приведен в примечании к ячейке C7. Совпадение не обязательно, но высоковероятно.
6-9. Параметры шестерни: число зубьев z1, диаметры вершин и впадин зубьев da1 и df1 в мм, угол наклона зубьев на поверхности вершин βa1 в градусах подсчитываем и измеряем штангенциркулем и угломером на исходном образце и записываем соответственно
в ячейку D8: 16
в ячейку D9: 37,6
в ячейку D10: 28,7
в ячейку D11: 0,0
10-13. Параметры колеса: число зубьев z2, диаметры вершин и впадин зубьев da2 и df2 в мм, угол наклона зубьев на цилиндре вершин βa2 в градусах определяем аналогично — по исходному образцу колеса — и записываем соответственно
в ячейку D12: 63
в ячейку D13: 130,3
в ячейку D14: 121,4
в ячейку D11: 0,0
Обращаю внимание: углы наклона зубьев βa1 и βa2 – это углы, измеренные на цилиндрических поверхностях вершин зубьев!!!
Измеряем диаметры, по возможности, максимально точно! Для колес с четным числом зубьев сделать это проще, если вершины не замяты. Для колес с нечетным числом зубьев при замере помним, что размеры, которые показывает штангенциркуль несколько меньше реальных диаметров выступов!!! Делаем несколько замеров и наиболее с нашей точки зрения достоверные значения записываем в таблицу.

Результаты расчетов:
14. Предварительные значения модуля зацепления определяем по результатам замеров шестерни m1 и зубчатого колеса m2 в мм соответственно
в ячейке D17: =D9/(D8/COS (D20/180*ПИ())+2*D4)=2,089
m1=da1/(z1/cos (β1)+2*(ha*))
и в ячейке D18: =D13/(D12/COS (D21/180*ПИ())+2*D4)=2,005
m2=da2/(z2/cos (β2)+2*(ha*))
Модуль зубчатого колеса играет роль универсального масштабного коэффициента, определяющего как габариты зубьев, так и общие габариты колеса и шестерни.
Сравниваем полученные значения со значениями из стандартного ряда модулей, фрагмент которого приведен в примечании к ячейке C19.
Полученные расчетные значения, как правило, очень близки к одному из значений стандартного ряда. Делаем предположение, что искомый модуль зубчатого колеса и шестерни m в мм равен одному из этих значений и вписываем его
в ячейку D19: 2,000
15. Предварительные значения угла наклона зубьев определяем по результатам замеров шестерни β1 и зубчатого колеса β2 в градусах соответственно
в ячейке D20: =ASIN (D8*D19/D9*TAN (D11/180*ПИ()))=0,0000
β1=arcsin (z1*m*tg (βa1)/da1)
и в ячейке D21: =ASIN (D12*D19/D13*TAN (D15/180*ПИ()))=0,0000
β2=arcsin (z2*m*tg (βa2)/da2)
Делаем предположение, что искомый угол наклона зубьев β в градусах равен измеренным и пересчитанным значениям и записываем
в ячейку D22: 0,0000
16. Предварительные значения коэффициента уравнительного смещения вычисляем по результатам замеров шестерни Δy1 и зубчатого колеса Δy2 соответственно
в ячейке D23: =2*D4+D5- (D9-D10)/(2*D19)=0,025
Δy1=2*(ha*)+(c*) — (da1-df1)/(2*m)
и в ячейке D24: =2*D4+D5- (D13-D14)/(2*D19)= 0,025
Δy2=2*(ha*)+(c*) - (da2— df2)/(2*m)
Анализируем полученные расчетные значения, и принятое решение о значении коэффициента уравнительного смещения Δy записываем
в ячейку D25: 0,025
17,18. Делительные диаметры шестерни d1 и зубчатого колеса d2 в мм рассчитываем соответственно
в ячейке D26: =D19*D8/COS (D22/180*ПИ())=32,000
d1=m*z1/cos(β)
и в ячейке D27: =D19*D12/COS (D22/180*ПИ())=126,000
d2=m*z2/cos(β)
19. Делительное межосевое расстояние a в мм вычисляем
в ячейке D28: =(D27+D6*D26)/2=79,000
a=(d2+T*d1)/2
20. Угол профиля αt в градусах рассчитываем
в ячейке D29: =ATAN (TAN (D3/180*ПИ())/COS (D22/180*ПИ()))/ПИ()*180=20,0000
αt=arctg(tg (α)/cos(β))
21. Угол зацепления αtw в градусах вычисляем
в ячейке D30: =ACOS (D28*COS (D29/180*ПИ())/D7)/ПИ()*180=21,8831
αtw=arccos(a*cos (αt)/aw)

22,23. Коэффициенты смещения шестерни x1 и колеса x2 определяем соответственно
в ячейке D31: =(D9-D26)/(2*D19) -D4+D25=0,425
x1=(da1— d1)/(2*m) — (ha*)+Δy
и в ячейке D32: =(D13-D27)/(2*D19) -D4+D25 =0,100
x2=(da2— d1)/(2*m) — (ha*)+Δy
24,25. Коэффициент суммы (разности) смещений xΣ(d)вычисляем для проверки правильности предыдущих расчетов по двум формулам соответственно
в ячейке D33: =D31+D6*D32=0,525
xΣ(d)=x1+T*x2
и в ячейке D34: =(D12+D6*D8)*((TAN (D30/180*ПИ()) — (D30/180*ПИ())) — (TAN (D29/180*ПИ()) — (D29/180*ПИ())))/(2*TAN (D3/180*ПИ()))=0,523
xΣ(d)=(z2+T*z1)*(inv(αtw) — inv(αt))/(2*tg(α))
Значения, рассчитанные по разным формулам, отличаются очень незначительно! Полагаем, что найденные значения модуля зубчатого колеса и шестерни, а также коэффициентов смещения определены верно!
Расчет параметров колеса и шестерни косозубой передачи.
Переходим к примеру с косозубой передачей и повторяем все действия, которые мы делали в предыдущем разделе.
Измерить угол наклона зубьев с необходимой точностью при помощи угломера или транспортира практически очень сложно. Я обычно прокатывал колесо и шестерню по листу бумаги и затем по отпечаткам транспортиром делительной головки кульмана производил предварительные измерения с точностью в градус или больше... В представленном ниже примере я намерил: βa1=19° и βa2=17,5°.
Еще раз обращаю внимание, что углы наклона зубьев на цилиндре вершин βa1 и βa2 – это не угол β, участвующий во всех основных расчетах передачи!!! Угол β – это угол наклона зубьев на цилиндре делительного диаметра (для передачи без смещения).

Ввиду малости значений рассчитанных коэффициентов смещения уместно предположить, что передача была выполнена без смещения производящих контуров шестерни и зубчатого колеса.
Воспользуемся сервисом Excel «Подбор параметра». Подробно и с картинками об этом сервисе я в свое время написал здесь.
Выбираем в главном меню Excel «Сервис» — «Подбор параметра» и в выпавшем окне заполняем:
Установить в ячейке: $D$33
Значение: 0
Изменяя значение ячейки: $D$22
И нажимаем OK.
Получаем результат β=17,1462°, xΣ(d)=0, x1=0,003≈0, x2=-0,003≈0!

Передача, скорее всего, была выполнена без смещения, модуль зубчатого колеса и шестерни, а также угол наклона зубьев мы определили, можно делать чертежи!
Важные замечания.
Смещение исходного контура при нарезке зубьев применяют для восстановления изношенных поверхностей зубьев колеса, уменьшения глубины врезания на валах-шестернях, для увеличения нагрузочной способности зубчатой передачи, для выполнения передачи с заданным межосевым расстоянием не равным делительному расстоянию, для устранения подрезания ножек зубьев шестерни и головок зубьев колеса с внутренними зубьями.
Различают высотную коррекцию (xΣ(d)=0) и угловую (xΣ(d)≠0).
Смещение производящего контура на практике применяют обычно при изготовлении прямозубых колес и очень редко косозубых. Это обусловлено тем, что по изгибной прочности косой зуб прочнее прямого, а необходимое межосевое расстояние можно обеспечить соответствующим углом наклона зубьев. Если высотную коррекцию изредка применяют для косозубых передач, то угловую практически никогда.
Косозубая передача работает более плавно и бесшумно, чем прямозубая. Как уже было сказано, косые зубья имеют более высокую прочность на изгиб и заданное межосевое расстояние можно обеспечить углом наклона зубьев и не прибегать к смещению производящего контура. Однако в передачах с косыми зубьями появляются дополнительные осевые нагрузки на подшипники валов, а диаметры колес имеют больший размер, чем прямозубые при том же числе зубьев и модуле. Косозубые колеса менее технологичны в изготовлении, особенно колеса с внутренними зубьями.
Подписывайтесь на анонсы статей в окнах, расположенных в конце каждой статьи или вверху каждой страницы.
Не забывайте подтверждать подписку кликом по ссылке в письме, которое тут же придет к вам на указанную почту (может прийти в папку «Спам»)!!!
Уважаемые читатели! Ваш опыт и мнение, «оставленные» ниже в комментариях к статье, будут интересны и полезны коллегам и автору!!!
Прошу уважающих труд автора скачивать файл после подписки на анонсы статей!
Ссылка на скачивание файла: modul-zubchatogo-kolesa (xls 41,0KB).
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
al-vo.ru
423800, Набережные Челны , база Партнер Плюс, тел. 8 800 100-58-94 (звонок бесплатный)