|
||||
|
|
звонок бесплатный
Наши сотрудники:
[email protected]
Екатерина - специалист по продаже а/м КАМАЗ
 [email protected]
[email protected]






Техника в наличии

Тягач КАМАЗ 44108-6030-24
2014г, 6х6, Евро3, дв.КАМАЗ 300 л.с., КПП ZF9, бак 210л+350л, МКБ,МОБ,рестайлинг.
цена 2 220 000 руб.,

КАМАЗ 4308-6063-28(R4)
4х2,дв. Cummins ISB6.7e4 245л.с. (Е-4),КПП ZF6S1000, V кузова=39,7куб.м., спальное место, бак 210л, шк-пет,МКБ, ТНВД BOSCH, система нейтрализ. ОГ(AdBlue), тент, каркас, рестайлинг, внутр. размеры платформы 6112х2470х730 мм
цена 1 950 000 руб.,

Самосвал КАМАЗ 6520-057
2014г, 6х4,Евро3, дв.КАМАЗ 320 л.с., КПП ZF16, ТНВД ЯЗДА, бак 350л, г/п 20 тонн, V кузова =20 куб.м.,МКБ,МОБ, со спальным местом.
цена 2 700 000 руб.,

Самосвал 6522-027
2014, 6х6, дв.КАМАЗ 740.51,320 л.с., КПП ZF16,бак 350л, г/п 19 тонн,V кузова 12куб.м.,МКБ,МОБ,задняя разгрузка,обогрев платформы.
цена 3 190 000 руб.,
СУПЕР ЦЕНА
на АВТОМОБИЛИ КАМАЗ
| 43118-010-10 (дв.740.30-260 л.с.) | 2 220 000 |
| 43118-6033-24 (дв.740.55-300 л.с.) | 2 300 000 |
| 65117-029 (дв.740.30-260 л.с.) | 2 200 000 |
| 65117-6010-62 (дв.740.62-280 л.с.) | 2 350 000 |
| 44108 (дв.740.30-260 л.с.) | 2 160 000 |
| 44108-6030-24 (дв.740.55,рест.) | 2 200 000 |
| 65116-010-62 (дв.740.62-280 л.с.) | 1 880 000 |
| 6460 (дв.740.50-360 л.с.) | 2 180 000 |
| 45143-011-15 (дв.740.13-260л.с) | 2 180 000 |
| 65115 (дв.740.62-280 л.с.,рест.) | 2 190 000 |
| 65115 (дв.740.62-280 л.с.,3-х стор) | 2 295 000 |
| 6520 (дв.740.51-320 л.с.) | 2 610 000 |
| 6520 (дв.740.51-320 л.с.,сп.место) | 2 700 000 |
| 6522-027 (дв.740.51-320 л.с.,6х6) | 3 190 000 |

подробнее про услугу перегона можно прочесть здесь.

|
Нужны самосвалы? Обратите внимание на Ford-65513-02. |
КАМАЗы в лизинг
ООО «Старт Импэкс» имеет возможность поставки грузовой автотехники КАМАЗ, а так же спецтехники на шасси КАМАЗ в лизинг. Продажа грузовой техники по лизинговым схемам имеет определенные выгоды для покупателя грузовика. Рассрочка платежа, а так же то обстоятельство, что грузовики до полной выплаты лизинговых платежей находятся на балансе лизингодателя, и соответственно покупатель автомобиля не платит налогов на имущество. Мы готовы предложить любые модели бортовых автомобилей, тягачей и самосвалов по самым выгодным лизинговым схемам.Контактная информация.
г. Набережные Челны, Промкомзона-2, Автодорога №3, база «Партнер плюс».
тел/факс (8552) 388373.
Схема проезда
§26. Термодинамические параметры. Термодинамический процесс. Термодинамические процессы
Основные термодинамические процессы.
Термодинамические процессы
Как упоминалось в предыдущей статье, термодинамическим процессом называют изменение состояния системы, в результате которого хотя бы один из ее параметров (температура, объем или давление) изменяет свое значение. Впрочем, если учесть, что все параметры термодинамической системы неразрывно взаимосвязаны, то изменение любого из них неизбежно влечет изменение хотя бы одного (в идеале) или нескольких (в реальности) параметров. В общем случае можно сказать, что термодинамический процесс связан с нарушением равновесия системы, и если система находится в равновесном состоянии, то никаких термодинамических процессов в ней протекать не может.
Равновесное состояние системы - понятие абстрактное, поскольку невозможно изолировать что-либо материальное от окружающего мира, поэтому в любой реальной системе неизбежно протекают разнообразные термодинамические процессы. При этом в некоторых системах могут иметь место настолько медленные, почти незаметные изменения, что связанные с ними процессы можно условно считать состоящими из последовательности равновесных состояний системы. Такие процессы называют равновесными или квазистатическими. Еще один возможный сценарий последовательных изменений в системе, после которых она возвращается к исходному состоянию, называют круговым процессом или циклом. Понятия равновесного и кругового процесса лежат в основе многих теоретических выводов и прикладных приемов термодинамики.
Изучение термодинамического процесса заключается в определении работы, совершенной в данном процессе, изменения внутренней энергии, количества теплоты, а также в установлении связи между отдельными величинами, характеризующими состояние газа.
Из всех возможных термодинамических процессов наибольший интерес представляют изохорный, изобарный, изотермический, адиабатный и политропный процессы.
***
Изохорный процесс
Изохорным называют термодинамический процесс, протекающий при постоянном объеме. Такой процесс может совершаться при нагревании газа, помещенного в закрытый сосуд. Газ в результате подвода теплоты нагревается, и его давление возрастает. Изменение параметров газа в изохорном процессе описывает закон Шарля: p1/T1 = p2/T2, или в общем случае:
p/T = const.
Давление газа на стенки сосуда прямо пропорционально абсолютной температуре газа.
Так как в изохорном процессе изменение объема dV равно нулю, то можно сделать вывод, что вся подведенная к газу теплота расходуется на изменение внутренней энергии газа (никакая работа не совершается).
***
Изобарный процесс
Изобарным называют термодинамический процесс, протекающий при постоянном давлении. Такой процесс можно осуществить, поместив газ в плотный цилиндр с подвижным поршнем, на который действует постоянная внешняя сила при отводе и подводе теплоты. При изменении температуры газа поршень перемещается в ту или иную сторону; при этом объем газа изменяется в соответствии с законом Гей-Люссака:
V/T = const.
Это означает, что в изобарном процессе объем занимаемый газом, прямо пропорционален температуре. Можно сделать вывод, что изменение температуры в этом процессе неизбежно приведет к изменению внутренней энергии газа, а изменение объема связано с выполнением работы, т. е. при изобарном процессе часть тепловой энергии тратится на изменение внутренней энергии газа, а другая часть – на выполнение газом работы по преодолению действия внешних сил. При этом соотношение между затратами теплоты на увеличение внутренней энергии и на выполнение работы зависит от теплоемкости газа.
***
Изотермический процесс
Изотермическим называют термодинамический процесс, протекающий при неизменной температуре. Практически осуществить изотермический процесс с газом очень трудно. Ведь необходимо соблюсти условие, чтобы в процессе сжатия или расширения газ успевал обмениваться температурой с окружающей средой, поддерживая собственную температуру постоянной. Изотермический процесс описывается законом Бойля-Мариотта: pV = const, т. е. при постоянной температуре величина давления газа обратно пропорциональна его объему.
Очевидно, что при изотермическом процессе внутренняя энергия газа не изменяется, поскольку его температура постоянна. Чтобы выполнялось условие постоянства температуры газа, от него необходимо отводить теплоту, эквивалентную работе, затраченной на сжатие:
dq = dA = pdv.
Используя уравнение состояния газа, проделав ряд преобразований и подстановок, можно сделать вывод, что работа газа при изотермическом процессе определяется выражением:
A = RT ln(p1/p2).
***
Адиабатный процесс
Адиабатным называют термодинамический процесс, протекающий без теплообмена рабочего тела с окружающей средой. Подобно изотермическому, осуществить на практике адиабатный процесс очень сложно. Такой процесс может протекать с рабочим телом, помещенным в сосуд, например, цилиндр с поршнем, окруженный высококачественным теплоизолирующим материалом. Но какой бы качественный теплоизолятор мы не применяли в данном случае, некоторым, пусть даже ничтожно малым, количеством теплоты рабочее тело и окружающая среда неизбежно будут обмениваться. Поэтому на практике можно создать лишь приближенную модель адиабатного процесса. Тем не менее, многие термодинамические процессы, осуществляемые в теплотехнике, протекают настолько быстро, что рабочее тело и среда не успевают обмениваться теплотой, поэтому с некоторой степенью погрешности такие процессы можно рассматривать как адиабатные.
Для вывода уравнения, связывающего давление и объем 1 кг газа в адиабатном процессе, запишем уравнение первого закона термодинамики:
dq = du + pdv.
Поскольку для адиабатного процесса теплопередача dq равна нулю, а изменение внутренней энергии есть функция теплопроводности от температуры: du = cvdT, то можно записать:
cvdT + pdv = 0 (3).
Продифференцировав уравнение Клапейрона pv = RT, получим:
pdv + vdp = RdT.
Выразим отсюда dT и подставим в уравнение (3). После перегруппировки и преобразований получим:
pdvcv/(R + 1) + cvvdp/R = 0.
С учетом уравнения Майера R = cp – cv последнее выражение можно переписать в виде:
pdv(cv + cp - cv)/(cp – cv) + cvvdp/(cp – cv) = 0,
или
cppdv + cvvdp = 0 (4).
Разделив полученное выражение на cv и обозначив отношение cp/cv буквой k, после интегрирования уравнения (4) получим (при k = const):
ln vk + ln p = const или ln pvk = const или pvk = const.
Полученное уравнение является уравнением адиабатного процесса, в котором k – показатель адиабаты. Если предположить, что объемная теплоемкость cv является величиной постоянной, т. е. cv = const, то работу адиабатного процесса можно представить в виде формулы (приводится без вывода):
l = cv(T1 – T2) или l = (p1v1 – p2v2)/(k-1).
***
Политропный процесс
В отличие от рассмотренных выше термодинамических процессов, когда какой-либо из параметров газа оставался неизменным, политропный процесс характеризуется возможностью изменения любого из основных параметров газа. Все рассмотренные выше термодинамические процессы являются частными случаями политропных процессов. Общее уравнение политропного процесса имеет вид pvn = const, где n – показатель политропы - постоянная для данного процесса величина, которая может принимать значения от - ∞ до + ∞.
Очевидно, что придавая показателю политропы определенные значения, можно получить тот или иной термодинамический процесс – изохорный, изобарный, изотермический или адиабатный. Так, если принять n = 0, получим p = const – изобарный процесс, если принять n = 1, получим изотермический процесс, описываемый зависимостью pv = const; при n = k процесс является адиабатным, а при n равном - ∞ или + ∞. мы получим изохорный процесс.
Так как уравнение политропы по своему содержанию аналогично уравнению адиабатного процесса, то формулы, устанавливающие связь между параметрами политропного процесса будут аналогичны таковым для адиабатного процесса с той лишь разницей, что показатель адиабаты k нужно заменить на показатель политропы n. Тогда:
p2/p1 = (v1/v2)n; Tnp(n-1) = const; Tnv(n-1) = const.
Работа газа при политропном процессе может быть определена по формуле:
l = (p1v1 – p2v2)/(k-1).
Теплоемкость при политропном процессе (приводится без вывода):
cn = cv(n – k)/(n – 1).
***
Понятие энтальпии и энтропии
Скачать теоретические вопросы к экзаменационным билетам по учебной дисциплине "Основы гидравлики и теплотехники" (в формате Word, размер файла 68 кБ)
Скачать рабочую программу по учебной дисциплине "Основы гидравлики и теплотехники" (в формате Word):
Скачать календарно-тематический план по учебной дисциплине "Основы гидравлики и теплотехники" (в формате Word):
k-a-t.ru
19 Термодинамические процессы
При изучении равновесных и обратимых термодинамических процессов идеальных газов должны быть выявлены: во-первых, закономерность изменения основных параметров, характеризующих состояние рабочего тела; во-вторых, особенности реализации условий первого закона термодинамики.
В общем случае два любых параметра рабочего тела могут изменяться произвольно. Однако наибольший интерес представляют частные случаи. К числу частных термодинамических процессов относятся: изохорный, изобарный, изотермический, адиабатный, и политропный, который при определенных условиях может рассматриваться в качестве обобщенного по отношению ко всем выше перечисленным процессам.
Политропный процесс
Политропным процессом называется такой термодинамический процесс изменения состояния физической системы, при котором в течение всего процесса сохраняется постоянство теплоемкости.
Пусть С – теплоемкость политропного процесса, тогда используя выражения или ; и , получим уравнение первого закона термодинамики в виде:
. (92)
С учетом выражения после ряда преобразований имеем:
, (93)
откуда получим уравнение политропы:
, (94)
где – показатель политропы.
Согласно определению политропного процесса n может быть любым, но постоянным в некотором интервале числом, которое достаточно близко воспроизводило бы разнообразные встречающиеся в практике линии индикаторных диаграмм.
Очевидно, что при некоторых частных значениях n уравнение (94) должно превращаться в уравнения простейших термодинамических процессов.
20 Действительно, если в уравнении (94) n = 0, получим уравнение изобары:
.
В этом случае (для изобарного процесса) уравнение первого закона термодинамики для изолированных систем будет совпадать с формулой (49).
При получим уравнение изохоры:
,
поскольку величина будет бесконечно мала по сравнению с объемом (), ею можно пренебречь, тогда:
.
22 Из определения изохорного процесса очевидно, что работа в этом процессе не совершается, поскольку работа есть произведение (работа всегда связана с изменением объема). Тогдауравнение первого закона термодинамики для изолированных систем (49) при изохорном процессе примет вид:
. (95)
Таким образом, подведенная к изолированной системе теплота в изохорном процессе расходуется только на изменение внутренней энергии системы.
При получим уравнение изотермы:
,
но поскольку, согласно закону Бойля – Мариотта, если произведение давления и объема есть величина постоянная, то процесс – изотермический, тогда:
.
21 В изотермическом процессе не происходит изменения внутренней энергии системы, поскольку температура постоянна. Тогда уравнение первого закона термодинамики для изолированных систем (49) при изотермическом процессе примет вид:
. (96)
Таким образом, подведенная к изолированной системе теплота в изотермическом процессе расходуется только на совершение системой внешней работы.
При получим уравнение адиабаты:
.
23 Показатель адиабаты еще называют коэффициентом Пуассона. Величина этого показателя зависит от числа атомов в молекуле газа. При этом может принимать следующие значения:
для одноатомных газов (на самом деле состояние одноатомного газа не существует, оно введено для идеальных газов) ;
для двухатомных газов (CO; О2; N2; Н2; F2; Cl2; воздух и др.) ;
для трехатомных газов (CO2; N2O; NO2 и др.) .
По определению, адиабатный процесс – это процесс, протекающий без теплообмена с окружающей средой, т.е. . Тогдауравнение первого закона термодинамики для изолированных систем (49) при адиабатном процессе примет вид:
(97)
Таким образом, в адиабатном процессе работа может совершать за счет изменения (уменьшения) внутренней энергии системы в течение некоторого времени.
Таким образом политропный процесс является обобщающим по отношению к простейшим процессам. Для политропы справедливы соотношения:
; ; . (98)
Работу политропного процесса можно определить по следующим формулам:
; ; ;
; . (99)
В PV-координатах работа l характеризуется площадью под процессом. Если то иверно и обратное.
Теплоемкость политропного процесса можно определить по формуле:
. (100)
Таким образом, еще раз подтверждается, что теплоемкость идеального газа зависит от характера термодинамического процесса, что наглядно подтверждается на рисунке 7.
Рисунок 7 – Зависимость теплоемкости С процесса от показателя п политропы
На рисунке 8 представлены совмещенные диаграммы различнох термодинамических процессов.
Рисунок 8 - Совмещенные диаграммы различных термодинамических
процессов в PV- и TS – координатах
Если в РV- и ТS – координатах выбрать некоторую произвольную точку 1 и провести из нее все рассмотренные выше термодинамические процессы, то все поле построенной таким образом диаграммы делится на 8 областей, характеризующихся определенными признаками. Так, все процессы слева от точки 1 на РV – диаграмме сопровождаются отрицательной работой. Все процессы справа от точки 1 на TS – диаграмме происходят с подводом теплоты, слева – с отводом теплоты, вверх от изотермы – с увеличением внутренней энергии и энтальпии; вниз – с уменьшением. Области, выделенные на PV – диаграмме, соответствуют процессам с подводом теплоты, а на ТS – диаграмме – процессам с положительной теплоемкостью и т.д.
Для определения изменения энтропии в политропном процессе достаточно уравнение (100) подставить в выражение , и с учетом того, чтополучим:
. (101)
После интегрирования:
. (102)
С учетом выражений (98), можно записать:
. (103)
Изменения внутренней энергии и энтропии в политропном процессе определяются в ТS – координатах площадями соответственно под изохорным и изобарным процессами, происходящими в том же интервале температур .
studfiles.net
Термодинамические процессы. Анализ термодинамических процессов. Термодинамические процессы идеальных газов
В этой статье мы рассмотрим термодинамические процессы. Ознакомимся с их разновидностями и качественными характеристиками, а также изучим явление круговых процессов, обладающих в начальной и конечной точках одинаковыми параметрами.
Введение

Термодинамическими процессами называют явления, при которых происходит макроскопическое изменение термодинамики всей системе. Наличие разницы между исходным и конечным состоянием носит название элементарного процесса, но при этом необходимо, чтобы это различие было бесконечно малым. Область пространства, в границах которого протекает это явление, именуется рабочим телом.
По типу устойчивость можно различать равновесную и неравновесную. Равновесный механизм представляет собой процесс, в ходе которого все типы состояния, сквозь которые протекает система, относятся к равновесному состоянию. Реализация таких процессов происходит в случае, когда изменение протекает довольно медленно, или, другими словами, явление носит квазистатический характер.
Явление теплового типа можно разделить на обратимый и необратимый термодинамический процессы. К обратимым причисляют механизмы, при которых реализуется возможность проводить процесс в противоположное направление, при помощи одних и тех же промежуточных состояний.
Адиабатическая теплопередача
Адиабатическим путем теплообмена, является термодинамический процесс, происходящий в масштабах макромира. Еще одной характеристикой является отсутствие обмена теплом с пространством вокруг.
Широкомасштабные исследования в области данного процесса уходят стартом развития в начало восемнадцатого века.
Адиабатические типы процессов представляю собой частный случай политропной формы. Это обусловлено тем, что в таком виде газовая теплоемкость равняется нулю, а значит, постоянная величина. Обратить подобный процесс можно лишь при наличии точки равновесия всех моментов во времени. Изменения в показателе энтропии не наблюдаются в таком случае либо протекают слишком медленно. Существует ряд авторов, признающих адиабатические процессы только в обратимых.
Термодинамический процесс газа идеального типа в форме адиабатического явления описывает уравнение Пуассона.
Изохорная система

Механизм изохорического типа – это термодинамический процесс, основанный на постоянной величине объема. Его можно наблюдать в газах или жидкостях, которые достаточно нагревали в сосуде, с неизменным объемом.
Термодинамический процесс идеального газа в изохорической форме, позволяет молекулам сохранять соответствие пропорций по отношению к температуре. Это обуславливается законом Шарля. Для реальных газов данная догма науки не применима.
Изобарная система
Изобарная система представлена в виде термодинамического процесса, который происходит при наличии постоянного давления снаружи. Протекание И.п. в достаточно медленном темпе, позволяющем давлению в пределах системы считаться постоянной и соответствующему показателю внешнего давления может считаться обратимым. Также к таким явлениям можно отнести случай, в котором изменение в выше упомянутом процессе, протекают с маленькой скоростью, позволяющей считать давление постоянным.
Осуществить И.п. можно в системе, подведенной (или отведенной) к теплоте dQ. Для этого необходимо произвести расширение работы Pdv и изменение внутреннего типа энергии dU, T.
Изменения в уровне энтропии – dS, T – абсолютное значение температуры.
Термодинамические процессы идеальных газов в изобарной системе обуславливают наличие пропорциональности объема с температурой. Реальные газы определенное количество теплоты израсходует для внесения изменений в средний тип энергии. Работа такого явление равна показателю произведения давления извне, на изменения в объеме.
Изотермическое явление
Одним из основных термодинамических процессов является его изотермическая форма. Он происходит в физических системах, с постоянным показателем температуры.
Для реализации данного явления систему, как правило, переносят в термостат, с огромным показателем теплопроводности. Взаимный обмен тепла протекает с достаточной скоростью, чтобы обогнать скорость протекания самого процесса. Уровень температуры системы почти не имеет отличий от показателей термостата.
Осуществить процесс изотермической природы также можно с использованием тепловых стоков и (или) источников, проводя контроль постоянства температуры, используя термометры. Одним из самых распространенных примеров такого явления служит кипение жидкостей в условиях постоянного давления.

Изоэнтропийное явление
Изоэнтропийная форма тепловых процессов протекает в условиях постоянной величины энтропии. Механизмы тепловой природы можно получить, используя равенство Клаузиуса для обратимых процессов.
Только обратимые адиабатические процессы можно называть изоэнтропийными. Неравенство Клаузиуса утверждает, что необратимые типы тепловых явлений сюда относиться не могут. Однако постоянство энтропии можно наблюдать и при необратимом тепловом явлении, если работа в термодинамическом процессе над энтропией производится так, что она незамедлительно удаляется. Глядя на термодинамические диаграммы, линии, отображающие изоэнтропийные процессы, можно именовать как адиабаты или изоэнтропы. Чаще прибегают к первому названию, что вызвано отсутствием возможности корректно изображать линии на диаграмме, характеризующейпроцесс необратимого характера. Объяснение и дальнейшая эксплуатация изоэнтропийных процессов имеют огромное значение, так как часто применяется в достижении целей, практическом и теоретическом знании.
Изоэнтальпийный тип процесса

Изоэнтальпийный процесс – тепловое явление, наблюдаемое при наличии энтальпии в постоянной величине. Расчеты ее показателя делаются благодаря формуле: dH = dU + d(pV).
Энтальпией называют параметр, при помощи которого можно охарактеризовать систему, в которой изменения при возврате в обратное состояние самой системы не наблюдаются и, соответственно, равняются нулю.
Изоэнтальпийное явление теплообмена может на примере проявлять себя в термодинамическом процессе газов. Когда молекулы, например этана или бутана, «протискиваются» сквозь перегородку с пористым строением, а теплообмен газа с теплом вокруг не наблюдается. Такое можно наблюдать в эффекте Джоуля-Томсона, применяемого в процессе получения сверхнизких показателей температуры. Изоэнтальпийные процессы являются ценными, в силу того, что дают возможность понижать температуру в рамках среды, не тратя для этого энергию.
Политропная форма
Характеристикой политропного процесса является его возможность изменять физические параметры системы, но оставлять показатель теплоемкости (C) в постоянной величине. Диаграммы, отображающие термодинамические процессы в такой форме, именуются политропными. Один из самых простых примеров обратимости отражается в идеальных газах и определяется при помощи уравнения: pVn= const. P – показатели давления, V – объемная величина газа.
«Кольцо» процесса

Термодинамические системы и процессы могут образовывать циклы, которые имеют круговую форму. Они всегда имеют идентичные показатели в начальном и конечном параметре, оценивающем состояние тела. К таким качественным характеристикам можно отнести наблюдение за показателями давления, энтропии, температуры и объема.
Термодинамический цикл находит себя в выражении модели процесса, протекающего в настоящих тепловых механизмах, превращающих тепло в работу механического типа.
Рабочее тело входит в состав компонентов каждой такой машины.
Обратимый термодинамический процесс представлен в виде цикла, который имеет пути проведения как в направлении прямо, так и обратно. Его положение залегает в системе замкнутого типа. Суммарный коэффициент системной энтропии при повторе каждого цикла не изменяется. У механизма, в котором теплопередача происходит только между нагревательным или холодильным аппаратом и рабочим телом, обратимость возможно только при цикле Карно.
Существует ряд других циклических явлений, которые могут обращаться лишь при достижении введения дополнительного резервуара с теплом. Такие источники называют регенераторами.

Анализ термодинамических процессов, в ходе которых происходит регенерация, показывает нам, что все они общие по циклу Рейтлингера. Доказано на ряде расчетов и экспериментов, что обратимый цикл обладает наибольшей степенью эффективности.
fb.ru
Термодинамические процессы реальных газов
В качестве реального газа рассмотрим водяной пар, который широко используется во многих отраслях техники, и прежде всего в теплоэнергетике, где он является основным рабочим телом. Поэтому исследование термодинамических свойств воды и водяного пара имеет большое практическое значение.
Процесс парообразования. Основные понятия и определения. Рассмотрим процесс получения пара. Для этого 1 кг воды при температуре 0 °С поместим в цилиндр с подвижным поршнем. Приложим к поршню извне некоторую постоянную силу Р. Тогда при площади поршня F давление будет постоянным и равным p=P/F. Изобразим процесс парообразования, т. е. превращения вещества из жидкого состояния в газообразное, в р,v-диаграмме
Начальное состояние воды, находящейся под давлением р и имеющей температуру 0°С, изобразится на диаграмме точкой a0. При подводе теплоты к воде ее температура постепенно повышается до тех пор, пока не достигнет температуры кипения ts, соответствующей данному давлению. При этом удельный объем жидкости сначала уменьшается, достигает минимального значения при t=4°С, а затем начинает возрастать. (Такой аномалией — увеличением плотности при нагревании в некотором диапазоне температур — обладают немногие жидкости. У большинства жидкостей удельный объем при нагревании увеличивается монотонно). Состояние жидкости, доведенной до температуры кипения, изображается на диаграмме точкой а'.
При дальнейшем подводе теплоты начинается кипение воды с сильным увеличением объема. В цилиндре теперь находится двухфазная среда — смесь воды и пара, называемая влажным насыщенным паром. По мере подвода теплоты количество жидкой фазы уменьшается, а паровой — растет. Температура смеси при этом остается неизменной и равной ts, так как вся теплота расходуется на испарение жидкой фазы. Следовательно — процесс парообразования на этой стадии является изобарно-изотермическим. Наконец, последняя капля воды превращается в пар, и цилиндр оказывается заполненным только паром, который называется сухим насыщенным. Состояние его изображается точкой а".
Рис. 6. р,v-диаграмма водяного пара
Насыщенным называется пар, находящийся в термическом и динамическом равновесии с жидкостью, из которой он образуется. Динамическое равновесие заключается в том, что количество молекул, вылетающих из воды в паровое пространство, равно количеству молекул, конденсирующихся на ее поверхности. В паровом пространстве при этом равновесном состоянии находится максимально возможное при данной температуре число молекул. При увеличении температуры количество молекул, обладающих энергией, достаточной для вылета в паровое пространство, увеличивается. Равновесие восстанавливается за счет возрастания давления пара, которое ведет к увеличению его плотности и, следовательно, количества молекул, в единицу времени конденсирующихся на поверхности воды. Отсюда следует, что давление насыщенного пара является монотонно возрастающей функцией его температуры, или, что тоже самое, температура насыщенного пара есть монотонно возрастающая функция его давления.
При увеличении объема над поверхностью жидкости, имеющей температуру насыщения, некоторое количество жидкости переходит в пар, при уменьшении объема «излишний» пар снова переходит в жидкость, но в обоих случаях давление пара остается постоянным.
Насыщенный пар, в котором отсутствуют взвешенные частицы жидкой фазы, называется сухим насыщенным паром. Его удельный объем и температура являются функциями давления. Поэтому состояние сухого пара можно задать любым из параметров — давлением, удельным объемом или температурой.
Двухфазная смесь, представляющая собой пар со взвешенными в нем капельками жидкости, называется влажным насыщенным паром. Массовая доля сухого насыщенного пара во влажном называется степенью сухости пара и обозначается буквой х. Массовая доля кипящей воды во влажном паре, равная 1-х, называется степенью влажности. Для кипящей жидкости х=0, а для сухого насыщенного пара х=1. Состояние влажного пара характеризуется двумя параметрами: давлением (или температурой насыщения ts, определяющей это давление) и степенью сухости пара.
При сообщении сухому пару теплоты при том же давлении его температура будет увеличиваться, пар будет перегреваться. Точка а изображает состояние перегретого пара и в зависимости от температуры пара может лежать на разных расстояниях от точки а". Таким образом, перегретым называется пар, температура которого превышает температуру насыщенного пара того же давления.
Так как удельный объем перегретого пара при том же давлении больше, чем насыщенного, то в единице объема перегретого пара содержится меньшее коли-чество молекул, значит, он обладает меньшей плотностью. Состояние перегретого пара, как и любого газа, определяется двумя любыми независимыми параметрами.
Если рассмотреть процесс парообразования при более высоком давлении, то можно заметить следующие изменения. Точка a0, соответствующая состоянию 1 кг воды при О °С и новом давлении, остается почти на той же вертикали, так как вода практически несжимаема. Точка а' смещается вправо, ибо с ростом давления увеличивается температура кипения, а жидкость при повышении температуры расширяется. Что же касается пара (точка а"), то, несмотря на увеличение температуры кипения, удельный объем пара все-таки падает из-за более сильного влияния растущего давления.
Поскольку удельный объем жидкости растет, а пара падает, то при постоянном увеличении давления мы достигнем такой точки, в которой удельные объемы жидкости и пара сравняются. Эта точка называется критической. В критической точке различия между жидкостью и паром исчезают. Для воды параметры критической точки К составляют: ркр=221,29·105 Па; tкр= 374,15°С; vкр= 0,00326 м3/кг.
Критическая температура — это максимально возможная температура сосуществования двух фаз: жидкости и насыщенного пара. При температурах, больших критической, возможно существование только одной фазы. Название этой фазы (жидкость или перегретый пар) в какой-то степени условно и определяется обычно ее температурой. Все газы являются сильно перегретыми сверх Tкр парами. Чем выше температура перегрева (при данном давлении), тем ближе пар по своим свойствам к идеальному газу.
Наименьшим давлением, при котором еще возможно равновесие воды и насыщенного пара, является давление, соответствующее тройной точке. Под последней понимается то единственное состояние, в котором могут одновременно находиться в равновесии пар, вода и лед (точка А' на рис. 6.). Параметры тройной точки для воды: р0 = 611 Па; t0 = 0,01 °С; v0 = 0,00100 м3/кг. Процесс парообразования, происходящий при абсолютном давлении р0 = 611 Па, показан на диаграмме изобарой А'А", которая практически совпадает с осью абсцисс. При более низких давлениях пар может сосуществовать лишь в равновесии со льдом. Процесс образования пара непосредственно изо льда называется сублимацией.
Если теперь соединить одноименные точки плавными кривыми, то получим нулевую изотерму I, каждая точка которой соответствует состоянию 1 кг воды при 0°С и давлении р, нижнюю пограничную кривую II, представляющую зависимость от давления удельного объема жидкости при температуре кипения, и верхнюю пограничную кривую III, дающую зависимость удельного объема сухого насыщенного пара от давления.
Все точки горизонталей между кривыми II и III соответствуют состояниям влажного насыщенного пара, точки кривой II определяют состояние кипящей воды, точки кривой III — состояния сухого насыщенного пара. Влево от кривой II до нулевой изотермы лежит область не кипящей однофазной жидкости, вправо от кривой III — область перегретого пара. Таким образом, кривые II и III определяют область насыщенного пара, отделяя ее от области воды и перегретого пара, и поэтому называются пограничными. Выше точки К, где пограничных кривых нет, находится область однофазных состояний, в которой нельзя провести четкой границы между жидкостью и паром.
Определение параметров воды и пара. Термодинамические параметры кипящей воды и сухого насыщенного пара берутся из таблиц теплофизических свойств воды и водяного пара. В этих таблицах термодинамические величины со штрихом относятся к воде, нагретой до температуры кипения, а величины с двумя штрихами — к сухому насыщенному пару.
Поскольку для изобарного процесса подведенная к жидкости теплота , то, применив это соотношение к процессу а'а", получим
.
Величина r называется теплотой парообразования и определяет количество теплоты, необходимое для превращения одного килограмма воды в сухой насыщенный пар той же температуры.
Приращение энтропии в процессе парообразования определяется формулой
.
За нулевое состояние, от которого отсчитываются величины s', принято состояние воды в тройной точке. Так как состояние кипящей воды и сухого насыщенного пара определяется только одним параметром, то по известному давлению или температуре из таблиц воды и водяного пара берутся значения v', v" , h', h" ,s', s", r.
Удельный объем vx, энтропия sx и энтальпия hx влажного насыщенного пара определяются по правилу аддитивности. Поскольку в 1 кг влажного пара содержится x кг сухого и кг кипящейводы, то
.
Аналогично
;
;
Непосредственно из таблиц взять параметры влажного пара нельзя. Их определяют по приведенным выше формулам по заданному давлению (или температуре) и степени сухости.
Однофазные состояния не кипящей воды и перегретого пара задаются двумя параметрами. По заданным давлению и температуре из таблиц воды и перегретого пара находят значения v, h, s.
Т,s-диаграмма водяного пара. Для исследования различных процессов с водяным паром кроме таблиц используется Т, s-диаграмма. Она строится путем переноса числовых данных таблиц водяного пара в Т, s-координаты.
Рис. 7. T,s - диаграмма водяного пара
Состояние воды в тройной точке (s0 = 0; T0 = 273,16 К) изображается в диаграмме точкой А'. Откладывая на диаграмме для разных температур значения s' и s", получим нижнюю и верхнюю пограничные кривые. Влево от нижней пограничной кривой располагается область жидкости, между пограничными кривыми — двухфазная область влажного насыщенного пара, вправо и вверх от верхней пограничной кривой — область перегретого пара.
На диаграмму наносят изобары, изохоры и линии постоянной степени сухости, для чего каждую изобару а'а" делят на одинаковое число частей и соединяют соответствующие точки линиями x = const. Область диаграммы, лежащая ниже нулевой изотермы, отвечает различным состояниям смеси пар+лед.
h,s - диаграмма водяного пара. Если за независимые параметры, определяющие состояние рабочего тела, принять энтропию s и энтальпию h, то каждое состояние можно изобразить точкой на h,s-диаграмме.
На рис. 8 изображена h, s-диаграмма для водяного пара, которая строится путем переноса числовых данных таблиц водяного пара в h, s-координаты.
За начало координат принято состояние воды в тройной точке. Откладывая на диаграмме для различных давлений значения s' и h'' для воды при температуре, кипения, а также s" и h" для сухого насыщенного пара, получаем нижнюю и верхнюю пограничные кривые.
Рис 8. h,s - диаграмма водяного пара
Изобары в двухфазной области влажного пара представляют собой пучок расходящихся прямых. Действительно, в процессе р=const , или , т.е. тангенс угла наклона изобары в h,s-координатах численно равен абсолютной температуре данного состояния. Так как в области насыщения изобара совпадает с изотермой, тангенс угла наклона постоянен и изобара является прямой. Чем выше давление насыщения, тем выше температура, тем больше тангенс угла наклона изобары, поэтому в области насыщения прямые р = const расходятся. Чем больше давление, тем выше лежит изобара. Критическая точка К лежит не на верши-не, как это было в р,v- и Т,s-диаграммах, а на левом склоне пограничной кривой.
В области перегрева температура пара (при постоянном давлении) растет с увеличением s примерно по логарифмической кривой и крутизна изобары увеличивается. Аналогичный характер имеют изобары и в области воды, но они идут так близко от пограничной кривой, что практически сливаются с ней.
При низких давлениях и относительно высоких температурах перегретый пар по своим свойствам близок к идеальному газу. Так как в изотермическом процессе энтальпия идеального газа не изменяется, изотермы сильно перегретого пара идут горизонтально. При приближении к области насыщения, т. е. к верхней пограничной кривой, свойства перегретого пара значительно отклоняются от свойств идеального газа и изотермы искривляются.
В h,s-диаграмме водяного пара нанесены также линии v=const, идущие круче изобар.
Обычно всю диаграмму не выполняют, а строят только ее верхнюю часть, наиболее употребительную в практике расчетов. Это дает возможность изображать ее в более крупном масштабе. Для любой точки на этой диаграмме можно найти р, v, t, h, s, x. Большое достоинство диаграммы состоит в том, что количество теплоты в изобарном процессе равно разности ординат конечной и начальной точек процесса и изображается отрезком вертикальной прямой, а не площадью как в Т,s-диаграмме, поэтому h,s-диаграмма исключительно широко используется при проведении тепловых расчетов.
Основные термодинамические процессы водяного пара.
Для анализа работы паросиловых установок существенное значение имеют изохорный, изобарный, изотермический и адиабатный процессы. Расчет этих процессов можно выполнить либо с помощью таблицы воды и водяного пара, либо с помощью h,s-диаграммы. Первый способ более точен, но второй более прост и нагляден.
Общий метод расчета по h,s-диаграмме состоит в следующем. По известным параметрам наносится начальное состояние рабочего тела, затем проводится линия процесса и определяются его параметры в конечном состоянии. Далее вычисляется изменение внутренней энергии, определяются количества теплоты и работы в заданном процессе.
Изохорный процесс. Из диаграммы на рисунке видно, что нагреванием при постоянном объеме влажный пар можно перевести в сухой насыщенный и перегретый. Охлаждением его можно сконденсировать, но не до конца, так как при каком угодно низком давлении над жидкостью всегда находится некоторое количество насыщенного пара. Это означает, что изохора не пересекает нижнюю пограничную кривую.
Рис 9. Изохорный процесс водяного пара
Изменение внутренней энергии водного пара при v=const
.
Данная формула справедлива и для всех без исключения остальных термодинамических процессов.
В изохорном процессе работа 1=0, поэтому подведенная теплота расходуется (в соответствии с первым законом термодинамики) на увеличение внутренней энергии пара:
Изобарный процесс. При подводе теплоты к влажному насыщенному пару его степень сухости увеличивается и он (при постоянной температуре) переходит в сухой, а при дальнейшем подводе теплоты — в перегретый пар (температура пара при этом растет). При отводе теплоты влажный пар конденсируется при Ts= const.
Полученная в процессе теплота равна разности энтальпий:
.
Работа процесса подсчитывается по формуле:
.
Рис. 10. Изобарный процесс водяного пара
Изотермический процесс. Внутренняя энергия водяного пара в процессе T = const не остается постоянной (как у идеального газа), так как изменяется ее потенциальная составляющая. Величина находится по формуле .
Количество полученной в изотермическом процессе теплоты равно
.
Работа расширения определяется из первого закона термодинамики:
.
Рис. 11. Изотермический процесс водяного пара
Адиабатный процесс. При адиабатном расширении давление и температура пара уменьшаются, и перегретый пар становится сначала сухим, а затем влажным. Работа адиабатного процесса определяется выражением
.
Рис. 12. Адиабатный процесс водяного пара
studfiles.net
Лекция 6 Термодинамические процессы реальных газов
В качестве реального газа рассмотрим водяной пар, который широко используется во многих отраслях техники, и прежде всего в теплоэнергетике, где он является основным рабочим телом. Поэтому исследование термодинамических свойств воды и водяного пара имеет большое практическое значение.
Процесс парообразования. Основные понятия и определения. Рассмотрим процесс получения пара. Для этого 1 кг воды при температуре 0 °С поместим в цилиндр с подвижным поршнем. Приложим к поршню извне некоторую постоянную силу Р. Тогда при площади поршня F давление будет постоянным и равным p=P/F. Изобразим процесс парообразования, т. е. превращения вещества из жидкого состояния в газообразное, в р,v-диаграмме
Начальное состояние воды, находящейся под давлением р и имеющей температуру 0°С, изобразится на диаграмме точкой a0. При подводе теплоты к воде ее температура постепенно повышается до тех пор, пока не достигнет температуры кипения ts, соответствующей данному давлению. При этом удельный объем жидкости сначала уменьшается, достигает минимального значения при t=4°С, а затем начинает возрастать. (Такой аномалией — увеличением плотности при нагревании в некотором диапазоне температур — обладают немногие жидкости. У большинства жидкостей удельный объем при нагревании увеличивается монотонно). Состояние жидкости, доведенной до температуры кипения, изображается на диаграмме точкой а'.
При дальнейшем подводе теплоты начинается кипение воды с сильным увеличением объема. В цилиндре теперь находится двухфазная среда — смесь воды и пара, называемая влажным насыщенным паром. По мере подвода теплоты количество жидкой фазы уменьшается, а паровой — растет. Температура смеси при этом остается неизменной и равной ts, так как вся теплота расходуется на испарение жидкой фазы. Следовательно — процесс парообразования на этой стадии является изобарно-изотермическим. Наконец, последняя капля воды превращается в пар, и цилиндр оказывается заполненным только паром, который называется сухим насыщенным. Состояние его изображается точкой а".
Рисунок 6.1 - р,v-диаграмма водяного пара
Насыщенным называется пар, находящийся в термическом и динамическим равновесии с жидкостью, из которой он образуется. Динамическое равновесие заключается в том, что количество молекул, вылетающих из воды в паровое пространство, равно количеству молекул, конденсирующихся на ее поверхности. В паровом пространстве при этом равновесном состоянии находится максимально возможное при данной температуре число молекул. При увеличении температуры количество молекул, обладающих энергией, достаточной для вылета в паровое пространство, увеличивается. Равновесие восстанавливается за счет возрастания давления пара, которое ведет к увеличению его плотности и, следовательно, количества молекул, в единицу времени конденсирующихся на поверхности воды. Отсюда следует, что давление насыщенного пара является монотонно возрастающей функцией его температуры, или, что то же самое, температура насыщенного пара есть монотонно возрастающая функция его давления.
При увеличении объема над поверхностью жидкости, имеющей температуру насыщения, некоторое количество жидкости переходит в пар, при уменьшении объема «излишний» пар снова переходит в жидкость, но в обоих случаях давление пара остается постоянным.
Насыщенный пар, в котором отсутствуют взвешенные частицы жидкой фазы, называется сухим насыщенным паром. Его удельный объем и температура являются функциями давления. Поэтому состояние сухого пара можно задать любым из параметров — давлением, удельным объемом или температурой.
Двухфазная смесь, представляющая собой пар со взвешенными в нем капельками жидкости, называется влажным насыщенным паром. Массовая доля сухого насыщенного пара во влажном называется степенью сухости пара и обозначается буквой х. Массовая доля кипящей воды во влажном паре, равная 1-х, называется степенью влажности. Для кипящей жидкости х=0, а для сухого насыщенного пара х=1. Состояние влажного пара характеризуется двумя параметрами: давлением (или температурой насыщения ts, определяющей это давление) и степенью сухости пара.
При сообщении сухому пару теплоты при том же давлении его температура будет увеличиваться, пар будет перегреваться. Точка а изображает состояние перегретого пара ив зависимости от температуры пара может лежать на разных расстояниях от точки а". Таким образом, перегретым называется пар, температура которого превышает температуру насыщенного пара того же давления.
Так как удельный объем перегретого пара при том же давлении больше, чем насыщенного, то в единице объема перегретого пара содержится меньшее количество молекул, значит, он обладает меньшей плотностью. Состояние перегретого пара, как и любого газа, определяется двумя любыми независимыми параметрами.
Если рассмотреть процесс парообразования при более высоком давлении, то можно заметить следующие изменения. Точка a0, соответствующая состоянию 1 кг воды при О °С и новом давлении, остается почти на той же вертикали, так как вода практически несжимаема. Точка а' смещается вправо, ибо с ростом давления увеличивается температура кипения, а жидкость при повышении температуры расширяется. Что же касается пара (точка а"), то, несмотря на увеличение температуры кипения, удельный объем пара все-таки падает из-за более сильного влияния растущего давления.
Поскольку удельный объем жидкости растет, а пара падает, то при постоянном увеличении давления мы достигнем такой точки, в которой удельные объемы жидкости и пара сравняются. Эта точка называется критической. В критической точке различия между жидкостью и паром исчезают. Для воды параметры критической точки К составляют: ркр=221,29·105 Па; tкр = 374,15 °С; vкр = 0,00326 м3/кг.
Критическая температура — это максимально возможная температура сосуществования двух фаз: жидкости и насыщенного пара. При температурах, больших критической, возможно существование только одной фазы. Название этой фазы (жидкость или перегретый пар) в какой-то степени условно и определяется обычно ее температурой. Все газы являются сильно перегретыми сверх Tкр парами. Чем выше температура перегрева (при данном давлении), тем ближе пар по своим свойствам к идеальному газу.
Наименьшим давлением, при котором еще возможно равновесие воды и насыщенного пара, является давление, соответствующее тройной точке. Под последней понимается то единственное состояние, в котором могут одновременно находиться в равновесии пар, вода и лед (точка А' на рисунке). Параметры тройной точки для воды: р0 = 611 Па; t0 = 0,01 °С; v0=0,00100 м3/кг. Процесс парообразования, происходящий при абсолютном давлении р0=611 Па, показан на диаграмме изобарой А'А", которая практически совпадает с осью абсцисс. При более низких давлениях пар может сосуществовать лишь в равновесии со льдом. Процесс образования пара непосредственно из льда называется сублимацией.
Если теперь соединить одноименные точки плавными кривыми, то получим нулевую изотерму I, каждая точка которой соответствует состоянию 1 кг воды при 0°С и давлении р, нижнюю пограничную кривую II, представляющую зависимость от давления удельного объема жидкости при температуре кипения, и верхнюю пограничную кривую III, дающую зависимость удельного объема сухого насыщенного пара от давления.
Все точки горизонталей между кривыми II и III соответствуют состояниям влажного насыщенного пара, точки кривой II определяют состояние кипящей воды, точки кривой III — состояния сухого насыщенного пара. Влево от кривой II до нулевой изотермы лежит область некипящей однофазной жидкости, вправо от кривой III — область перегретого пара. Таким образом, кривые II и III определяют область насыщенного пара, отделяя ее от области воды и перегретого пара, и поэтому называются пограничными. Выше точки К, где пограничных кривых нет, находится область однофазных состояний, в которой нельзя провести четкой границы между жидкостью и паром.
Определение параметров воды и пара. Термодинамические параметры кипящей воды и сухого насыщенного пара берутся из таблиц теплофизических свойств воды и водяного пара. В этих таблицах термодинамические величины со штрихом относятся к воде, нагретой до температуры кипения, а величины с двумя штрихами — к сухому насыщенному пару.
Поскольку для изобарного процесса подведенная к жидкости теплота , то, применив это соотношение к процессу а'а", получим
.
Величина r называется теплотой парообразования и определяет количество теплоты, необходимое для превращения одного килограмма воды в сухой насыщенный пар той же температуры.
Приращение энтропии в процессе парообразования определяется формулой
.
За нулевое состояние, от которого отсчитываются величины s', принято состояние воды в тройной точке. Так как состояние кипящей воды и сухого насыщенного пара определяется только одним параметром, то по известному давлению или температуре из таблиц воды и водяного пара берутся значения v', v" , h', h" ,s', s", r.
Удельный объем vx, энтропия sx и энтальпия hx влажного насыщенного пара определяются по правилу аддитивности. Поскольку в 1 кг влажного пара содержится x кг сухого и кг кипящейводы, то
.
Аналогично
;
;
Непосредственно из таблиц взять параметры влажного пара нельзя. Их определяют по приведенным выше формулам по заданному давлению (или температуре) и степени сухости.
Однофазные состояния некипящей воды и перегретого пара задаются двумя параметрами. По заданным давлению и температуре из таблиц воды и перегретого пара находят значения v, h, s.
Т, s-диаграмма водяного пара. Для исследования различных процессов с водяным паром кроме таблиц используется Т, s-диаграмма. Она строится путем переноса числовых данных таблиц водяного пара в Т, s-координаты.
Рисунок 6.2 - T, s-диаграмма водяного пара
Состояние воды в тройной точке (s0 = 0; T0 = 273,16 К) изображается в диаграмме точкой А'. Откладывая на диаграмме для разных температур значения s' и s", получим нижнюю и верхнюю пограничные кривые. Влево от нижней пограничной кривой располагается область жидкости, между пограничными кривыми — двухфазная область влажного насыщенного пара, вправо и вверх от верхней пограничной кривой — область перегретого пара.
На диаграмму наносят изобары, изохоры и линии постоянной степени сухости, для чего каждую изобару а'а" делят на одинаковое число частей и соединяют соответствующие точки линиями x = const. Область диаграммы, лежащая ниже нулевой изотермы, отвечает различным состояниям смеси пар+лед.
h, s-диаграмма водяного пара. Если за независимые параметры, определяющие состояние рабочего тела, принять энтропию s и энтальпию h, то каждое состояние можно изобразить точкой на л, s-диаграмме.
На рисунке 6.3 изображена h, s-диаграмма для водяного пара, которая строится путем переноса числовых данных таблиц водяного пара в h, s-координаты.
За начало координат принято состояние воды в тройной точке. Откладывая на диаграмме для различных давлений значения s' и h'' для воды при температуре, кипения, а также s" и h" для сухого насыщенного пара, получаем нижнюю и верхнюю пограничные кривые.
Рисунок 6.3 - h, s-диаграмма водяного пара
Изобары в двухфазной области влажного пара представляют собой пучок расходящихся прямых. Действительно, в процессе р=const , или , т.е. тангенс угла наклона изобары в h, s-координатах численно равен абсолютной температуре данного состояния. Так как в области насыщения изобара совпадает с изотермой, тангенс угла наклона постоянен и изобара является прямой. Чем выше давление насыщения, тем выше температура, тем больше тангенс угла наклона изобары, поэтому в области насыщения прямые р = const расходятся. Чем больше давление, тем выше лежит изобара. Критическая точка К лежит не на вершине, как это было в р, v- и Т, s-диаграммах, а на левом склоне пограничной кривой.
В области перегрева температура пара (при постоянном давлении) растет с увеличением s примерно по логарифмической кривой и крутизна изобары увеличивается. Аналогичный характер имеют изобары и в области воды, но они идут так близко от пограничной кривой, что практически сливаются с ней.
При низких давлениях и относительно высоких температурах перегретый пар по своим свойствам близок к идеальному газу. Так как в изотермическом процессе энтальпия идеального газа не изменяется, изотермы сильно перегретого пара идут горизонтально. При приближение к области насыщения, т. е. к верхней пограничной кривой, свойства перегретого пара значительно отклоняются от свойств идеального газа и изотермы искривляются.
В h, s-диаграмме водяного пара нанесены также линии v=const, идущие круче изобар.
Обычно всю диаграмму не выполняют, а строят только ее верхнюю часть, наиболее употребительную в практике расчетов. Это дает возможность изображать ее в более крупном масштабе.
Для любой точки на этой диаграмме можно найти р, v, t, h, s, x. Большое достоинство диаграммы состоит в том, что количество теплоты в изобарном процессе равно разности ординат конечной и начальной точек процесса и изображается отрезком вертикальной прямой, а не площадью как в Т, s-диаграмме, поэтому h, s-диаграмма исключительно широко используется при проведении тепловых расчетов.
Основные термодинамические процессы водяного пара. Для анализа работы паросиловых установок существенное значение имеют изохорный, изобарный, изотермический и адиабатный процессы. Расчет этих процессов можно выполнить либо с помощью таблицы воды и водяного пара, либо с помощью h, s-диаграммы. Первый способ более точен, но второй более прост и нагляден.
Общий метод расчета по h, s-диаграмме состоит в следующем. По известным параметрам наносится начальное состояние рабочего тела, затем проводится линия процесса и определяются его параметры в конечном состоянии. Далее вычисляется изменение внутренней энергии, определяются количества теплоты и работы в заданном процессе.
Изохорный процесс. Из диаграммы на рисунке видно, что нагреванием при постоянном объеме влажный пар можно перевести в сухой насыщенный и перегретый. Охлаждением его можно сконденсировать, но не до конца, так как при каком угодно низком давлении над жидкостью всегда находится некоторое количество насыщенного пара. Это означает, что изохора не пересекает нижнюю пограничную кривую.
Рисунок 6.4 - Изохорный процесс водяного пара
Изменение внутренней энергии водного пара при v=const
.
Данная формула справедлива и для всех без исключения остальных термодинамических процессов.
В изохорном процессе работа 1=0, поэтому подведенная теплота расходуется (в соответствии с первым законом термодинамики) на увеличение внутренней энергии пара:
Изобарный процесс. При подводе теплоты к влажному насыщенному пару его степень сухости увеличивается и он (при постоянной температуре) переходит в сухой, а при дальнейшем подводе теплоты — в перегретый пар (температура пара при этом растет). При отводе теплоты влажный пар конденсируется при Ts= const.
Полученная в процессе теплота равна разности энтальпий:
.
Работа процесса подсчитывается по формуле:
.
Рисунок 6.5 - Изобарный процесс водяного пара
Изотермический процесс. Внутренняя энергия водяного пара в процессе T = const не остается постоянной (как у идеального газа), так как изменяется ее потенциальная составляющая. Величина находится по формуле .
Количество полученной в изотермическом процессе теплоты равно
.
Работа расширения определяется из первого закона термодинамики:
.
Рисунок 6.6 - Изотермический процесс водяного пара
Адиабатный процесс. При адиабатном расширении давление и температура пара уменьшаются, и перегретый пар становится сначала сухим, а затем влажным. Работа адиабатного процесса определяется выражением
.
Рисунок 6.7 - Адиабатный процесс водяного пара
studfiles.net
§26. Термодинамические параметры. Термодинамический процесс.
Определение:Термодинамической системой называется совокупность макроскопических объектов: тел и полей,
которые могут обмениваться энергией как друг с другом, так и с внешней средой, то есть телами и полями, которые являются внешними по отношению к данной системе.
Для описания состояния термодинамической системы вводятся термодинамические величины, которые называются термодинамическими параметрами состояния системы: p,V,t0, и т. д.
Определение:Равновесное состояние (состояние термодинамического равновесия) называется состояние системы, не изменяющееся с течением времени (стационарное состояние) и независящее от процессов, происходящих во внешней среде.
Равновесное состояние устанавливается в системе при постоянных внешних условиях и сохраняется в системе произвольно долгое время. Во всех частях термодинамической системы, находящейся в состоянии термодинамического равновесия, температура одинакова.
К понятию температуры подойдём следующим образом:
если при соприкосновении 2-х тел происходит теплообмен, то говорят, что у этих тел различные температуры, если теплового обмена нет, одинаковые температуры; то тело, которое передаёт энергию в форме тепла, имеет большую температуру, а тело, принимающее энергию в форме тепла, имеет меньшую температуру. При длительном контактетемпература соприкасающихся тел выравнивается.
Определение:Температура равновесной системы является мерой интенсивности теплового движения её молекул.
Для равновесной системы, частицы которой подчиняются законам классической статической физики, средняя кинетическая энергия теплового движения пропорциональна температуре системы. Температуру можно измерить только косвенным путём, основываясь на том факте, что целый ряд физических свойств тел, поддающихся прямому или косвенному измерению, зависят от температуры это длина, объём, сопротивление, удельное сопротивление, упругие и пластичные свойства и т. д. Измерения любых из этих свойств может быть основой измерения температуры. Для этого необходимо, чтобы для тела, названного термометрическим телом, была известна функциональная зависимость данного свойства от температуры. Температурные шкалы, устанавливаемые с помощью термометрического тела, называют эмпирическими.
Международная стоградусная шкала (шкала Цельсия), в которой в качестве двух основных точек выбраны температуры кипения и плавления дистиллированной воды приp =1,01325 10 5 Па: tплав. = 0о С,tкип. =100о С. Цена одного градуса равна одной сотой полученного интервалаодин Цельсий. На практике, для измерения температуры используются градусники, основанные на зависимости объёма жидких тел (например: ртути, спирта) от температуры. Вначале фиксируются на шкале две точки для моментов замерзания и закипания дистиллированной воды, а затем интервал между этими точками на шкале делится на равные сто долей.
Абсолютная шкала температур (шкала Кельвина). В подавляющем большинстве физических законов используется температура из данной шкалы. Это связано с тем, что математическая запись физических законов имеет более компактный вид именно при использовании температуры из шкалы Кельвина. Почему происходит именно так? Ответ находится за рамками общего курса физики. Здесь можно только отметить, что абсолютная шкала температуры имеет детерминированную связь с термодинамической шкалой температур, которая не зависит от свойств термометрических тел.
Связь между этими шкалами выражается соотношением: Т = 273,15 + t0, т.е. цена градуса в обоих шкалах одинакова. Температура по шкале КельвинаТ = 0 Кназывается абсолютным нулём.
Параметры системы разделяются на внешниеивнутренние.
Определение:Внешними параметрами системы называется физические величины, зависящие от положения в пространстве и различных свойств тел, являющихся внешними по отношению к данной системе.
Пример: газ в сосуде V(объём) внешний параметр.
Определение:Внутренними параметрами системы называется физические величины, зависящие как от положения в пространстве внешних по отношению к системе тел, так и от координат и скоростей частиц, образующих данную систему.
Пример: для газа p(давление) иU(внутренняя энергия).
Параметры состояния равновесной системы не являются независимыми, так как они зависят от внешних параметров и температуры.
Определение:Уравнением состояния простой системы называется функциональная зависимость равновесного давления в системе от объёма и температуры, то есть p = f(V,T).
В термодинамике уравнение состояния получают опытным путём, а в молекулярной физике теоретически. В этом состоит взаимосвязь между статистическими и термодинамическими методами.
Определение:Термодинамическим процессом называется процесс, при котором изменяется хотя бы один из внешних параметров системы.
Определение:Термодинамический процесс называется равновесным, если система бесконечно медленно проходит непрерывный ряд бесконечно близких равновесных состояний.
Остальные процессы не равновесны.
Пример равновесного процесса: крайне медленное изотермическое сжатие газа поршнем, находящемся в цилиндре.
Определение:Изопроцессами называются термодинамические процессы, происходящие в системе с постоянной массой при каком- либо одном постоянном параметре состояния.
Изотермический при T = const:p1 V1=p2 V2.
Изохорный при V = const:.
Изобарный при p = const:.
Определение:Адиабатическим называется термодинамический процесс, который происходит в системе без теплообмена с внешними телами.
Примерами адиабатических процессов являются все быстротекущие термодинамические процессы: детонация рабочей смеси во всех типах двигателей внутреннего сгорания, горение топлива в турбореактивных двигателях и т.д. Скорость протекания данных процессов настолько велика, что потерями на теплообмен можно пренебречь.
Определение:Функциями состояния называются физические величины, характеризующие состояние системы, независящие от вида процессов происходящих в системе, и определяемых значениями параметров начального и конечного состояний системы.
studfiles.net
Основные термодинамические процессы идеального газа
⇐ ПредыдущаяСтр 2 из 11Следующая ⇒Виды процессов. Основными процессами в технической термодинамике, весьма важными и в теоретическом, и в прикладном отношениях, являются:
изохорный – протекающий при постоянном объеме;
изобарный – протекающий при постоянном давлении;
изотермический – протекающий при постоянной температуре;
адиабатный – при котором отсутствует теплообмен с окружающей средой;
политропный – удовлетворяющий уравнению pvn = const.
Первые четыре процесса являются частными случаями политропного процесса.
При исследовании этих процессов определяют уравнение процесса в координатах p, v и T, s,связь между параметрами состояния газа, измерение внутренней энергии, величину внешней работы и количество отведенной теплоты.
Изохорный процесс.При изохорном процессе выполняется условие dv = 0 или v = const.Из уравнения идеального газа следует, что
p/T = R/v = const
т.е. давление газа прямо пропорционально его абсолютной температуре:
p2/p1 = T2/T1.
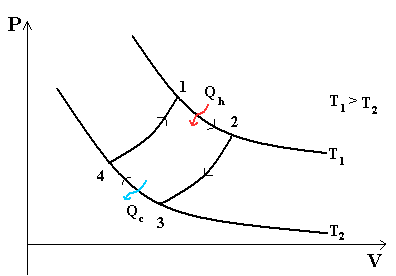
рис. 2.4 Изохорный процесс на p - v и T - s диаграммах (а, в) и схема энергобаланса (б)
Графики процесса на p – v и T – s – диаграммах, а также схема энергобаланса представлены на рисунке. Работа расширения в этом процессе равна нулю, так как dv = 0. Количество теплоты, подведенной к рабочему телу в процессе 1 – 2 при cv = const, определяется из соотношения

Так как l = 0, то в соответствии с первым законом термодинамики
Δu = q и Δu = cv(T2 – T1) при p = const.
Изобарный процесс. Изобарным называется процесс, происходящий при постоянном давлении. Из уравнения состояния идеального газа при p = const находим
v/T = R/p = const
или
v2/v1 = T2/T1
т.е. в изобарном процессе объем газа пропорционален его абсолютной температуре (закон Гей-Люссака). Графики процесса на p - v и T – s – диаграммах, а ттакже схема знергобалланса изображены на рис. 2.5.

рис.2.5. Изобарный процесс на p - v и T - s - диаграммах (а,в) и схема энергобаланса (б)
Из выражения

следует, что

так как pv1 = RT1 и pv2 = RT2.
Количество теплоты сообщаемое газу при нагревании (или отдаваемое им при охлаждении), находим из уравнения

Или
q = cp(T2 = T1).
Изотермический процесс. При изотермическом процессе температура постоянная, следовательно, pv = RT = const или p2/p1 = v1/v2, т.е. давление и объем обратно пропорциональны друг другу, так что при изотермическом сжатии давление газа возрастает, а при расширении – падает (закон Бойля – Мариотта).
Графиком изотермического процесса в координатах p, v (рис.2.6,а) является равнобокая гипербола, для которой координатные оси служат асимптомами.
Работа процесса

Так как энергия не меняется, то внутренняя энергия идеального газа в данном процессе остается постоянной (Δu = 0) и вся подводимая к газу теплота полностью превращается в работу расширения q = l.

рис. 2.6. Изотермический процесс на p - v и T - s - диаграммах (а,в) и схема энергобаланса (б)
При изотермическом сжатии от газа отводится теплота в количестве, равным затраченной на сжатие работе. Схема энергобаланса и и график изобарного процесса на T – s – диаграмме приведены на рис. 2.6, б,в.
Адиабатный процесс. Адиабатным называется процесс изменения состояния газа, который происходит без теплообмена с окружающей средой. Такой процесс соответствует случаю, когда сосуд или оболочка, вмещающие в себе газ, изолированы в тепловом отношении от окружающей среды. Для данного случая уравнение первого закона термодинамики, поскольку в нем по условию dq = 0, принимает вид
du + pdv = 0
или
Δu + l = 0
Откуда
Δu = -l.
Это означает, что в адиабатном процессе работа расширения совершается только за счет расходования внутренней энергии газа и что при сжатии, происходящем за счет действия внешних сил, вся совершаемая ими работа идет на увеличение внутренней энергии газа.
Обозначим теплоемкость в адиабатном процессе через сад и выразим условие du= 0 следующим образом:
du= садdT = 0
Это условие говорит о том, что теплоемкость в адиабатном процессе равна нулю, т.е. сад = 0. Известно, что
Cp/Cv = k
Уравнение кривой адиабатного процесса (адиабаты) в координатах p, v (рис.2.7 а) имеет вид
pvk = const,
где k – называется показателем адиабаты (эту величину называют также коэффициентом Пуассона).
Из выражений l = -Δu = cv(T1 – T2) и i1 – i2 = cp(T1 – T2) следует, что
i1 – i2 = lтехн,
т.е. техническая работа адиабатного процесса расширения равна разности энтальпий начала и конца процесса.

Рис.2.7 Адиабптный процесс на p - v и T - s lиаграммах (а, в) и схема энергобаланса (б)
Адиабатный процесс, происходящий без внутреннего трения в рабочем теле, называется изоэнтропийным. На T – s диаграмме (рис.2.7, в) он изображается вертикальной прямой.
Обычно реальные адиабатные процессы протекают при наличии внутреннего трения в рабочем теле, в результате которого всегда выделяется теплота, которая тут же сообщается самому рабочему телу. В этом случае ds > 0, процесс называется реальным адиабатным процессом.
Политропный процесс и его обобщающее значение. Политропным называется процесс, который происходит при постоянной теплоемкости и описывается уравнением
pvn = const.
Показатель политропы n может принимать любое численное значение в пределах от -∞ до +∞, но для данного процесса он является величиной постоянной.
Из уравнения (2.13) и уравнения Клайперона нетрудно получить выражения, устанавливающие связь между p v и T в любых двух точках на политропе:

Политропный процесс имеет обобщающее значение, ибо охватывает всю совокупность основных термодинамических процессов.
8 Реальные газы отличаются от идеальных газов тем, что молекулы этих газов имеют конечные собственные объемы и связаны между собой силами взаимодействия, имеющими электромагнитную и квантовую природу. Эти силы существуют между любыми молекулами при любых условиях и уменьшаются с увеличением расстояния между молекулами. При сближении молекул на малые расстояния силы притяжения резко уменьшаются и переходят в силы отталкивания, достигающие очень больших значений.
Из-за наличия сил взаимодействия между молекулами и конечности их объема законы идеальных газов ни при каких условиях не могут быть строго применимы к реальным газам.
При практических расчетах различных свойств реальных газов находит широкое применение отношение , которое по лучило название коэффициента сжимаемости. Так как для идеальных газов при любых условиях и , то коэффициент сжимаемости выражает отклонение свойств реального газа от свойств идеального. Значение для реальных газов в зависимости от давления и температуры может быть больше и меньше единицы, и только при очень малых давлениях и высоких температурах оно практически равно единице.
Рис. 1.23.1 Рис. 1.23.2
На рис. 1.24.1 показана зависимость от давления при температуре °С для некоторых газов. Повышение давления и понижение температуры, увеличение концентрации молекул газа и уменьшение расстояния между ними усиливает отклонения свойств реального от свойств идеального газа. Из уравнения Клапейрона – Менделеева следует, что при любой постоянной температуре зависимость от должна изображаться прямой, параллельной оси давления. В действительности изотермы всех газов представляют собой кривыё даже в области не очень высоких давлений, а при давлениях от 20 МПа и выше кривые довольно круто поднимаются вверх.
Читайте также:
lektsia.com
423800, Набережные Челны , база Партнер Плюс, тел. 8 800 100-58-94 (звонок бесплатный)