|
||||
|
|
звонок бесплатный
Наши сотрудники:
[email protected]
Екатерина - специалист по продаже а/м КАМАЗ
 [email protected]
[email protected]






Техника в наличии

Тягач КАМАЗ 44108-6030-24
2014г, 6х6, Евро3, дв.КАМАЗ 300 л.с., КПП ZF9, бак 210л+350л, МКБ,МОБ,рестайлинг.
цена 2 220 000 руб.,

КАМАЗ 4308-6063-28(R4)
4х2,дв. Cummins ISB6.7e4 245л.с. (Е-4),КПП ZF6S1000, V кузова=39,7куб.м., спальное место, бак 210л, шк-пет,МКБ, ТНВД BOSCH, система нейтрализ. ОГ(AdBlue), тент, каркас, рестайлинг, внутр. размеры платформы 6112х2470х730 мм
цена 1 950 000 руб.,

Самосвал КАМАЗ 6520-057
2014г, 6х4,Евро3, дв.КАМАЗ 320 л.с., КПП ZF16, ТНВД ЯЗДА, бак 350л, г/п 20 тонн, V кузова =20 куб.м.,МКБ,МОБ, со спальным местом.
цена 2 700 000 руб.,

Самосвал 6522-027
2014, 6х6, дв.КАМАЗ 740.51,320 л.с., КПП ZF16,бак 350л, г/п 19 тонн,V кузова 12куб.м.,МКБ,МОБ,задняя разгрузка,обогрев платформы.
цена 3 190 000 руб.,
СУПЕР ЦЕНА
на АВТОМОБИЛИ КАМАЗ
| 43118-010-10 (дв.740.30-260 л.с.) | 2 220 000 |
| 43118-6033-24 (дв.740.55-300 л.с.) | 2 300 000 |
| 65117-029 (дв.740.30-260 л.с.) | 2 200 000 |
| 65117-6010-62 (дв.740.62-280 л.с.) | 2 350 000 |
| 44108 (дв.740.30-260 л.с.) | 2 160 000 |
| 44108-6030-24 (дв.740.55,рест.) | 2 200 000 |
| 65116-010-62 (дв.740.62-280 л.с.) | 1 880 000 |
| 6460 (дв.740.50-360 л.с.) | 2 180 000 |
| 45143-011-15 (дв.740.13-260л.с) | 2 180 000 |
| 65115 (дв.740.62-280 л.с.,рест.) | 2 190 000 |
| 65115 (дв.740.62-280 л.с.,3-х стор) | 2 295 000 |
| 6520 (дв.740.51-320 л.с.) | 2 610 000 |
| 6520 (дв.740.51-320 л.с.,сп.место) | 2 700 000 |
| 6522-027 (дв.740.51-320 л.с.,6х6) | 3 190 000 |

подробнее про услугу перегона можно прочесть здесь.

|
Нужны самосвалы? Обратите внимание на Ford-65513-02. |
КАМАЗы в лизинг
ООО «Старт Импэкс» имеет возможность поставки грузовой автотехники КАМАЗ, а так же спецтехники на шасси КАМАЗ в лизинг. Продажа грузовой техники по лизинговым схемам имеет определенные выгоды для покупателя грузовика. Рассрочка платежа, а так же то обстоятельство, что грузовики до полной выплаты лизинговых платежей находятся на балансе лизингодателя, и соответственно покупатель автомобиля не платит налогов на имущество. Мы готовы предложить любые модели бортовых автомобилей, тягачей и самосвалов по самым выгодным лизинговым схемам.Контактная информация.
г. Набережные Челны, Промкомзона-2, Автодорога №3, база «Партнер плюс».
тел/факс (8552) 388373.
Схема проезда
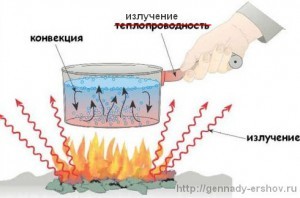
Как происходит теплопередача. Как происходит теплопроводность
Как происходит теплопередача
Теплопередача - это процесс передачи тепла из одной среды в другую, при этом обе среды должны являться жидкостями или газами. При теплопередаче происходит обмен энергией между средами без участия механического воздействия. Существует три вида теплопередачи.Инструкция
- Теплопроводность заключается в передаче тепла от более нагретых частей вещества к менее нагретым, приводящая к выравниванию температуры вещества. Молекулы вещества, обладающие большей энергией, передают ее молекулам, обладающим меньшей энергией. К теплопроводности относится закон Фурье, который заключается в связи между градиентом температуры в среде и плотности теплового потока. Градиент - это вектор, показывающий направление изменения скалярного поля. Отклонения от этого закона могут быть при очень сильных ударных волнах (большие значения градиента), при очень низких температурах и в разреженных газах, когда молекулы вещества чаще сталкиваются со стенками сосуда, чем между собой. В случает разреженных газов процесс теплопередачи рассматривается не как теплообмен, а как передача тепла между телами, находящимися в газовой среде.
- Конвекция - это перенос тепла в жидкостях, газах или сыпучих веществах, действующий согласно кинетической теории. Суть кинетической теории состоит в том, что все тела (материальные) состоят из атомов и молекул, которые находятся в непрерывном движении. На основе этой теории, конвекция представляет собой теплопередачу между веществами на молекулярном уровне, при условии что тела находятся под действием силы тяжести и неравномерно нагреты. Нагретое вещество, под действием силы тяжести, перемещается относительно менее нагретого вещества в сторону, обратную силе тяжести. Более нагретые вещества поднимаются, а более холодные - опускаются. Ослабление действия конвекции наблюдается в случаях высокой теплопроводности и вязкой среды, а также на конвекцию в ионизированных газах сильно влияет степень его ионизации и магнитное поле.
- Тепловое излучение. Вещество за счет внутренней энергии создает электромагнитное излучение со сплошным спектром, которое может передаваться между веществами. От того, насколько нагрето вещество, зависит положение максимума его спектра. Чем выше температура, тем больше энергии выделяет вещество и, следовательно, тем больше тепла можно передать.
- Теплопередача может происходить через тонкую перегородку или стенку между телами, от более теплого вещества к менее теплому. Более нагретое вещество передает часть тепла к стенке, после чего происходит процесс теплопередачи в стенке и от стенки идет теплоотдача к менее нагретому веществу. Интенсивность количества передаваемой теплоты напрямую зависит от коэффициента теплопередачи, который определяется как количество теплоты, передающееся через единицу площади поверхности перегородки в единицу времени при разнице температур между веществами в 1 Кельвин.
completerepair.ru
Теплопроводность - это... Что такое Теплопроводность?
Теплопрово́дность — это процесс переноса внутренней энергии от более нагретых частей тела (или тел) к менее нагретым частям (или телам), осуществляемый хаотически движущимися частицами тела ( атомами, молекулами, электронами и т.п.). Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества. Явление теплопроводности заключается в том, что кинетическая энергия атомов и молекул, которая определяет температуру тела, передаётся другому телу при их взаимодействии или передаётся из более нагретых областей тела к менее нагретым областям. Иногда теплопроводностью называется также количественная оценка способности конкретного вещества проводить тепло.
Численная характеристика теплопроводности материала равна количеству теплоты, проходящей через материал площадью 1 кв.м за единицу времени (секунду) при единичном температурном градиенте. Данная численная характеристика используется для расчета теплопроводности для калибрования и охлаждения профильных изделий.
Исторически считалось, что передача тепловой энергии связана с перетеканием теплорода от одного тела к другому. Однако более поздние опыты, в частности, нагрев пушечных стволов при сверлении, опровергли реальность существования теплорода как самостоятельного вида материи. Соответственно, в настоящее время считается, что явление теплопроводности обусловлено стремлением объектов занять состояние более близкое к термодинамическому равновесию, что выражается в выравнивании температуры.
Закон теплопроводности Фурье
В установившемся режиме плотность потока энергии, передающейся посредством теплопроводности, пропорциональна градиенту температуры:
где — вектор плотности теплового потока — количество энергии, проходящей в единицу времени через единицу площади, перпендикулярной каждой оси, — коэффициент теплопроводности (иногда называемый просто теплопроводностью), — температура. Минус в правой части показывает, что тепловой поток направлен противоположно вектору grad T (то есть в сторону скорейшего убывания температуры). Это выражение известно как закон теплопроводности Фурье.[1]
В интегральной форме это же выражение запишется так (если речь идёт о стационарном потоке тепла от одной грани параллелепипеда к другой):
где — полная мощность тепловых потерь, — площадь сечения параллелепипеда, — перепад температур граней, — длина параллелепипеда, то есть расстояние между гранями.
Коэффициент теплопроводности измеряется в Вт/(м·K).
Коэффициент теплопроводности вакуума
Коэффициент теплопроводности вакуума почти ноль (чем глубже вакуум, тем ближе к нулю). Это связано с низкой концентрацией в вакууме материальных частиц, способных переносить тепло. Тем не менее, тепло в вакууме передаётся с помощью излучения. Поэтому, например, для уменьшения теплопотери стенки термоса делают двойными, серебрят (такая поверхность лучше отражает излучение), а воздух между ними откачивают.
Связь с электропроводностью
Связь коэффициента теплопроводности с удельной электрической проводимостью в металлах устанавливает закон Видемана — Франца:
где — постоянная Больцмана, — заряд электрона.
Коэффициент теплопроводности газов
Коэффициент теплопроводности газов определяется формулой[2]
Где: i — сумма поступательных и вращательных степеней свободы молекул (для двухатомного газа i=5, для одноатомного i=3), k — постоянная Больцмана, M — молярная масса, T — абсолютная температура, d — эффективный диаметр молекул, R — универсальная газовая постоянная. Из формулы видно, что наименьшей теплопроводностью обладают тяжелые одноатомные (инертные) газы, наибольшей — легкие многоатомные (что подтверждается практикой, максимальная теплопроводность из всех газов — у водорода, минимальная — у радона, из не радиоактивных газов - у ксенона).
Обобщения закона Фурье
Следует отметить, что закон Фурье не учитывает инерционность процесса теплопроводности, то есть в данной модели изменение температуры в какой-то точке мгновенно распространяется на всё тело. Закон Фурье не применим для описания высокочастотных процессов (и, соответственно, процессов, чьё разложение в ряд Фурье имеет значительные высокочастотные гармоники). Примерами таких процессов являются распространение ультразвука, ударные волны и т.п. Инерционность в уравнения переноса первым ввел Максвелл[3], а в 1948 году Каттанео был предложен вариант закона Фурье с релаксационным членом:[4]
Если время релаксации пренебрежимо мало, то это уравнение переходит в закон Фурье.
Коэффициенты теплопроводности различных веществ
| Графен | (4840±440) — (5300±480) |
| Алмаз | 1001—2600 |
| Графит | 278,4—2435 |
| Карбид кремния | 490 |
| Серебро | 430 |
| Медь | 382—390 |
| Оксид бериллия | 370 |
| Золото | 320 |
| Алюминий | 202—236 |
| Нитрид алюминия | 200 |
| Нитрид бора | 180 |
| Кремний | 150 |
| Латунь | 97—111 |
| Хром | 93,7 |
| Железо | 92 |
| Платина | 70 |
| Олово | 67 |
| Оксид цинка | 54 |
| Сталь | 47 |
| Кварц | 8 |
| Стекло | 1-1,15 |
| КПТ-8 | 0,7 |
| Вода при нормальных условиях | 0,6 |
| Кирпич строительный | 0,2—0,7 |
| Силиконовое масло | 0,16 |
| Пенобетон | 0,14—0,3 |
| Древесина | 0,15 |
| Нефтяные масла | 0,12 |
| Свежий снег | 0,10—0,15 |
| Вата | 0,055 |
| Воздух (300 K, 100 кПа) | 0,026 |
| Вакуум (абсолютный) | 0 (строго) |
другие вещества
| Кальций | 201 |
| Бериллий | 201 |
| Вольфрам | 173 |
| Магний | 156 |
| Родий | 150 |
| Иридий | 147 |
| Молибден | 138 |
| Рутений | 117 |
| Хром | 93,9 |
| Осмий | 87,6 |
| Титан | 21,9 |
| Тефлон | 0,25 |
| Бумага | 0,14 |
| Полистирол | 0,082 |
| Шерсть | 0,05 |
| Минеральная вата | 0,045 |
| Пенополистирол | 0,04 |
| Стекловолокно | 0,036 |
| Пробковое дерево | 0,035 |
| Пеноизол | 0,035 |
| Каучук вспененный | 0,03 |
| Аргон | 0,0177 |
| Аэрогель | 0,017 |
| Ксенон | 0,0057 |
На практике нужно также учитывать проводимость тепла за счет конвекции молекул и проникаемости излучений. Например, при полной нетеплопроводности вакуума, тепло может передаваться за счет излучения (пример — Солнце, установки инфракрасного излучения). А газ или жидкость могут обмениваться нагретыми или охлажденными слоями самостоятельно или искусственно (пример — фен, греющие вентиляторы). Так же в конденсированных средах возможно «перепрыгивание» фононов из одного твердого тела в другое через субмикронные зазоры, что способствует распространению звуковых волн и тепла, даже если зазоры представляют собой идеальный вакуум.
Примечания
См. также
Ссылки
dic.academic.ru
Процесс - теплопроводность - Большая Энциклопедия Нефти и Газа, статья, страница 1
Процесс - теплопроводность
Cтраница 1
Процесс теплопроводности в области О ( х, у, г) имитируется путем прохождения электрического тока либо в геометрически подобной электропроводящей области Ga ( x, у, г), либо в эквивалентной электрической схеме с сосредоточенными параметрами. На границах области Ga ( x, у, г) организуется подвод электрического тока / или задаются электрические потенциалы и с соблюдением подобия в граничных и начальных условиях для модели и натурного образца. [1]
Процесс теплопроводности в материальных слоях конструкции подчиняется закону Фурье, уравнение которого в дифференциальной форме рассматривается в курсе теплопередачи. [2]
Процессы теплопроводности и возможное огибание теплоносителем кромок продольных перегородок в кожухах классов F и Q ( ТЕМА) также могут привести к уменьшению эффективной разности температур. [4]
Процессы теплопроводности и диффузии в неподвижной среде в чистом виде могут наблюдаться только в твердых телах, так как в жидкостях и газах на эти процессы неизбежно накладывается движение среды как целого - свободная и вынужденная конвекция. [5]
Процесс теплопроводности в твердых и жидких телах осуществляется путем взаимодействия колеблющихся частиц ( молекул, атомов, ионов), составляющих тело. Наиболее интенсивное колебание частиц, происходящее в области повышенной температуры, передается соседним частицам, постепенно распространяясь на все тело. В металлах, кроме того, теплопроводность значительно увеличивается благодаря свободным электронам, которые могут перемещаться внутри металла, непосредственно перенося свою кинетическую энергию из области повышенной температуры в область более низкой температуры. Важная роль свободных электронов в процессе теплопроводности подтверждается тем фактом, что коэффициент теплопроводности металлов приблизительно пропорционален их коэффициенту электропроводности. В жидкостях ( как и в газах) процесс передачи теплоты может усиливаться конвекцией, если нагретые части жидкости расположены ниже холодных. [6]
Процесс теплопроводности, описываемый полученными здесь формулами, обладает тем свойством, что влияние всякого теплового возмущения распространяется мгновенно на все пространство. Так, из формулы (51.5) видно, что тепло из точечного источника распространяется так, что уже в следующий момент времени температура среды обращается в нуль лишь асимптотически на бесконечности. Это свойство сохраняется и для среды с зависящей от температуры температуропроводностью х, если только эта зависимость не приводит к обращению х в нуль в какой-либо области пространства. [7]
Процесс теплопроводности заключается в переносе энергии, происходящем благодаря взаимодействию смежных элементов тела, находящихся при различной температуре. Чтобы вывести основной закон, который позволял бы в каждом отдельном случае найти эту функцию, необходимо воспользоваться обоими началами термодинамики. [8]
Процесс теплопроводности состоит в распространении тепла внутри тела путем непосредственного взаимного соприкосновения структурных частиц - молекул, атомов, свободных электронов, в результате чего кинетическая энергия передается от более нагретых частиц к менее нагретым. Теплопроводность имеет место в твердых телах и в весьма тонких неподвижных слоях жидкости или газа. [9]
Процесс теплопроводности при нестационарном режиме с давних пор интересовал инженеров, ибо различные технологические операции, например нагревание металла для ковки, штамповки, закалки и др., происходят при нестационарном режиме. [10]
Процесс теплопроводности, описываемый полученными здесь формулами, обладает тем свойством, что влияние всякого теплового возмущения распространяется мгновенно на все пространство. Так, из формулы ( 51 5) видно, что тепло из точечного источника распространяется так, что уже в следующий момент времени температура среды обращается в нуль лишь асимптотически на бесконечности. Это свойство сохраняется и для среды с зависящей от температуры температуропроводностью х если только эта зависимость не приводит к обращению х в нуль в какой-либо области пространства. [11]
Процесс теплопроводности при этом не происходит, так как нет разности температур. [12]
Процесс теплопроводности при постоянном во времени градиенте в каждой точке называется стационарным. [13]
Процесс теплопроводности при конечной разности температур нестатичен и потому необратим. [14]
Процесс теплопроводности, так же как и другие виды теплообмена, осуществляется только при условии, что в различных точках тела температура не одинакова. Как известно, температура является параметром состояния тела и характеризует степень его нагретости. Совокупность значений температуры во всех точках рассматриваемого пространства в данный момент времени называют температурным полем. [15]
Страницы: 1 2 3 4
www.ngpedia.ru
ГРАВИТАЦИЯТеплопередача
 Физика, как наука утверждает, что в природе существуют три вида теплопередачи: теплопроводность, конвекция и лучистый теплообмен. Практически во всех источниках просматривается данная иерархия – на первом месте теплопроводность, на втором – конвекция и на третьем – лучистый теплообмен.
Физика, как наука утверждает, что в природе существуют три вида теплопередачи: теплопроводность, конвекция и лучистый теплообмен. Практически во всех источниках просматривается данная иерархия – на первом месте теплопроводность, на втором – конвекция и на третьем – лучистый теплообмен.
Почему сложилась такая последовательность, очевидно, из истории открытия данных явлений. Если теплопроводность и конвекция были известны древним людям, то электромагнитные волны были предсказаны Максвеллом, а затем открыты Герцем только в конце 19 века (1888 году).
«Теплопередача - это процесс переноса теплоты внутри тела или от одного тела к другому, обусловленный разностью температур».
Теплопередачу в газах и жидкостях еще можно представить как взаимное проникновение молекул и атомов – горячих в более холодную, а холодных в горячую среду. Но как происходит теплопередача в твердых телах?
Я уже частично коснулся проблемы теплопередачи в предыдущей статье «Получение теплоты», когда речь шла о крафоне. Краснофотонное излучение и переизлучение – это и есть, теплопередача в твердых телах. Особенно хорошо это свойство выражено в металлах. Хорошую теплопроводность в металлах физики связывают с присутствием свободных электронов. Но есть один диэлектрик по имени «алмаз», у которого нет свободных, нет слабо связанных электронов, но его теплопроводность зашкаливает.
Теплопроводность алмаза

Какой минерал на Земле, описывая который мы как попугаи повторяем «самый», «самый». Нет, не золото и не платина – это алмаз. Самый твердый, самый дорогой, самый износостойкий, самый блестящий, самый редкий и т.д.
Есть еще одно свойство, связанное с алмазом и словом самый – его теплопроводность. Теплопроводность алмаза при комнатной температуре в 3 - 6 раз выше теплопроводности серебра и меди, самых теплопроводных металлов на Земле. Сколько бы вы не грели алмаз в сжатой ладони, он останется холодным. Если сделать из алмаза чайную ложечку, то вы каждый раз, опуская ее в горячий чай, будете обжигать пальцы.
Как и чем можно объяснить самую высокую теплопроводность алмаза? Чтобы разобраться с этим не простым вопросом, обратимся к теплопроводности металлов.
Металлы, как известно, являются проводниками, причем, чем лучше металл проводит электрический ток, тем он лучше и проводит тепло. Наука связывает данный эффект со свободными электронами, которые под действием разности потенциалов, выстраиваются в цепь и создают прохождение электрического тока.
Возьмем медный стержень длиной несколько сантиметров и будем нагревать один конец. Через некоторое, весьма короткое, время второй конец также будет нагреваться. Физики говорят – стержень обладает теплопроводностью, а свободные, не связанные или слабо связанные электроны, быстро перемещаются и переносят теплоту вдоль стержня.
Медь прекрасный проводник электрического тока. Тогда что происходит с алмазом – он диэлектрик и у него нет свободных электронов-зарядов, а теплопроводность в 5 раз выше, чем у меди.
На мой взгляд, высокая теплопроводность алмаза связана с тремя факторами:
- строением кристаллической решетки;
- малыми расстояниями между атомами;
- плотным электромагнитным эфиром.
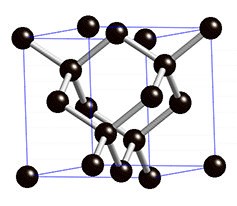 В кристаллической решётке алмаза каждый атом углерода жестко связан ковалентными связями с четырьмя другими атомами, размещёнными на одинаковом расстоянии. Эти связи по всем направлениям одинаково прочные. Лишним доказательством того, что у алмаза нет свободных электронов говорит о его очень малом коэффициенте теплового расширения (0,0000008), немного уступая кварцевому стеклу. Поскольку у алмаза не может быть конвекции, и нет свободных электронов, то очевидно, основным видом теплопередачи в алмазе является лучистый теплообмен. Структура кристаллической решетки усиливает этот процесс. Даже незначительная разность тепловых потенциалов с помощью излучения быстро выравнивает их.
В кристаллической решётке алмаза каждый атом углерода жестко связан ковалентными связями с четырьмя другими атомами, размещёнными на одинаковом расстоянии. Эти связи по всем направлениям одинаково прочные. Лишним доказательством того, что у алмаза нет свободных электронов говорит о его очень малом коэффициенте теплового расширения (0,0000008), немного уступая кварцевому стеклу. Поскольку у алмаза не может быть конвекции, и нет свободных электронов, то очевидно, основным видом теплопередачи в алмазе является лучистый теплообмен. Структура кристаллической решетки усиливает этот процесс. Даже незначительная разность тепловых потенциалов с помощью излучения быстро выравнивает их.
Снова вернемся к металлам и еще раз разберемся со словами теплопроводность, конвекция и лучистый теплообмен. Начнем с теплопроводности, что скрывается под этим словом?
Под данным словом кроется некий диффузионный перенос теплоты от одного атома к другому. Т.е. свободные электроны, нагретые на одном конце стержня, через некоторое время должны появиться на другом конце стержня и нагреть его. Но так ли это. Рассудим логически, какой колонии электронов нужно перебежать хотя бы на несколько миллиметров, не говоря уже от одного конца стержня к другому, чтобы выровнять температуру, если каждый из них может перенести 1 квант энергии. Получается, что практически все «горячие» электроны должны перебежать на данное расстояние или на противоположную сторону стержня, чтобы нагреть его до той же температуры. Но, в таком случае, они должны возвратиться обратно, иначе нарушится кристаллическая решетка горячего конца, и металл развалится. А как они вернутся обратно, если температурный градиент направлен в одну сторону?
У физиков есть еще одна версия по переносу тепла. Свободные электроны контактируют, иначе соударяются с другими себе подобными и таким образом, по цепочке переносят тепло с нагретого конца к холодному. Но как заставить контактировать эти электроны, они же свободные и летят куда хотят. Не путать с электрическим током, там электроны подчиняются внешнему электрическому полю, т.к. сами находятся под зарядом и по команде этого поля они выстраиваются в проводящую цепочку. А тепловое, нейтральное поле для свободных электронов не указ, да к тому же пространства вокруг, гораздо больше, чем для мячей футбольное поле. Представьте картину, каждому игроку противоборствующих команд дали по мячу и поставили задачу: попасть в такой же мяч противника. Удары выполняются по очереди с разных сторон поля. И сколько же ударов нужно нанести игрокам, чтобы попасть в заветную мишень. Даже у классных игроков процент попадания будет низкий, не говоря уже о дилетантах, свободных хаотичных игроках. Перенос тепла в этом случае будет ничтожным.
В любых телах и веществах существует только один перенос энергии от одного атома к другому – это электромагнитный или лучеиспускание, что и косвенно подтверждает нам замечательный минерал – алмаз.
Поэтому, теплопроводность есть не что иное, как тот самый лучистый теплообмен. Отсюда следует, что в природе существуют не три вида теплопередачи, а два: лучистый теплообмен и конвекция. По большому счету, конвективные потоки тоже связаны с лучистым теплообменом, но поскольку они идут только в разреженных субстанциях – жидкостях и газах, то конвекцию пока оставим в покое.
В большинстве случаев, в земных условиях, разности температур нет, но теплообмен, как мы знаем, не прекращается между ними ни на долю секунды.
Вот здесь я ловлю себя на слове. Если разности температур не было, то не было бы и теплопередачи. В любом веществе всегда существует разность температур и давлений, только эту разницу мы ничем измерить не можем. Еще не изобрело человечество таких чувствительных приборов, которыми можно было измерить разность температур между молекулами.
Поэтому, определение теплопередачи в общем виде должно быть записано следующим образом: теплопередача - это процесс переноса теплоты внутри тела или от одного тела к другому, обусловленный разностью температур, с помощью электромагнитного излучения.
В широком, всеобъемлющем, смысле формулировка теплопередачи сводится к весьма короткому словосочетанию:
Теплопередача – это выравнивание теплового потенциала.
Вывод из вышесказанного: стены наших зданий нужно делать из воздуха, а батареи отопления в домах следует изготавливать из алмаза!
Назад Вперед
gennady-ershov.ru
Теплопроводность — Википедия РУ
Теплопрово́дность — способность материальных тел проводить энергию (теплоту) от более нагретых частей тела к менее нагретым частям тела, осуществляемому хаотически движущимися частицами тела (атомами, молекулами, электронами и т. п.). Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества.
Теплопроводностью называется также количественная характеристика способности тела проводить тепло. В сравнении тепловых цепей с электрическими это аналог проводимости.
Количественно способность вещества проводить тепло характеризуется коэффициентом теплопроводности. Эта характеристика равна количеству теплоты, проходящему через однородный образец материала единичной длины и единичной площади за единицу времени при единичной разнице температур (1 К). В системе СИ единицей измерения коэффициента теплопроводности является Вт/(м·K).
Исторически считалось, что передача тепловой энергии связана с перетеканием гипотетического теплорода от одного тела к другому. Однако с развитием молекулярно-кинетической теории явление теплопроводности получило своё объяснение на основе взаимодействия частиц вещества. Молекулы в более нагретых частях тела движутся быстрее и передают энергию посредством столкновений медленным частицам в более холодных частях тела.
В установившемся режиме плотность потока энергии, передающейся посредством теплопроводности, пропорциональна градиенту температуры:
q→=−ϰgrad(T),{\displaystyle {\vec {q}}=-\varkappa \,\mathrm {grad} (T),}где q→{\displaystyle {\vec {q}}} — вектор плотности теплового потока — количество энергии, проходящей в единицу времени через единицу площади, перпендикулярной каждой оси, ϰ{\displaystyle \varkappa } — коэффициент теплопроводности (удельная теплопроводность), T{\displaystyle T} — температура. Минус в правой части показывает, что тепловой поток направлен противоположно вектору grad(T){\displaystyle \mathrm {grad} (T)} (то есть в сторону скорейшего убывания температуры). Это выражение известно как закон теплопроводности Фурье.[1]
В интегральной форме это же выражение запишется так (если речь идёт о стационарном потоке тепла от одной грани параллелепипеда к другой):
P=−ϰSΔTl,{\displaystyle P=-\varkappa {\frac {S\Delta T}{l}},} [Вт/(м·К) · (м2·К)/м = Вт/(м·К) · (м·К) = Вт]где P{\displaystyle P} — полная мощность тепловых потерь, S{\displaystyle S} — площадь сечения параллелепипеда, ΔT{\displaystyle \Delta T} — перепад температур граней, l{\displaystyle l} — длина параллелепипеда, то есть расстояние между гранями.
Связь с электропроводностью
Связь коэффициента теплопроводности ϰ{\displaystyle \varkappa } с удельной электрической проводимостью σ{\displaystyle \sigma } в металлах устанавливает закон Видемана — Франца:
ϰσ=π23(ke)2T,{\displaystyle {\frac {\varkappa }{\sigma }}={\frac {\pi ^{2}}{3}}\left({\frac {k}{e}}\right)^{2}T,} где k{\displaystyle k} — постоянная Больцмана; e{\displaystyle e} — заряд электрона; T{\displaystyle T} — абсолютная температура.Коэффициент теплопроводности газов
В газах коэффициент теплопроводности может быть найден по приближённой формуле[2]
ϰ∼13ρcvλv¯,{\displaystyle \varkappa \sim {\frac {1}{3}}\rho c_{v}\lambda {\bar {v}},}где ρ{\displaystyle \rho } — плотность газа, cv{\displaystyle c_{v}} — удельная теплоёмкость при постоянном объёме, λ{\displaystyle \lambda } — средняя длина свободного пробега молекул газа, v¯{\displaystyle {\bar {v}}} — средняя тепловая скорость. Эта же формула может быть записана как[3]
ϰ=ik3π3/2d2RTμ,{\displaystyle \varkappa ={\frac {ik}{3\pi ^{3/2}d^{2}}}{\sqrt {\frac {RT}{\mu }}},}где i{\displaystyle i} — сумма поступательных и вращательных степеней свободы молекул (для двухатомного газа i=5{\displaystyle i=5} , для одноатомного i=3{\displaystyle i=3} ), k{\displaystyle k} — постоянная Больцмана, μ{\displaystyle \mu } — молярная масса, T{\displaystyle T} — абсолютная температура, d{\displaystyle d} — эффективный (газокинетический) диаметр молекул, R{\displaystyle R} — универсальная газовая постоянная. Из формулы видно, что наименьшей теплопроводностью обладают тяжелые одноатомные (инертные) газы, наибольшей — легкие многоатомные (что подтверждается практикой, максимальная теплопроводность из всех газов — у водорода, минимальная — у радона, из нерадиоактивных газов — у ксенона).
Теплопроводность в сильно разреженных газах
Приведённое выше выражение для коэффициента теплопроводности в газах не зависит от давления. Однако если газ сильно разрежен, то длина свободного пробега определяется не столкновениями молекул друг с другом, а их столкновениями со стенками сосуда. Состояние газа, при котором длина свободного пробега молекул ограничивается размерами сосуда называют высоким вакуумом. При высоком вакууме теплопроводность убывает пропорционально плотности вещества (то есть пропорциональна давлению в системе): ϰ∼13ρcvlv¯∝P{\displaystyle \varkappa \sim {\frac {1}{3}}\rho c_{v}l{\bar {v}}\propto P} , где l{\displaystyle l} — размер сосуда, P{\displaystyle P} — давление.
Таким образом коэффициент теплопроводности вакуума тем ближе к нулю, чем глубже вакуум. Это связано с низкой концентрацией в вакууме материальных частиц, способных переносить тепло. Тем не менее, энергия в вакууме передаётся с помощью излучения. Поэтому, например, для уменьшения теплопотерь стенки термоса делают двойными, серебрят (такая поверхность лучше отражает излучение), а воздух между ними откачивают.
Следует отметить, что закон Фурье не учитывает инерционность процесса теплопроводности, то есть в данной модели изменение температуры в какой-то точке мгновенно распространяется на всё тело. Закон Фурье неприменим для описания высокочастотных процессов (и, соответственно, процессов, чьё разложение в ряд Фурье имеет значительные высокочастотные гармоники). Примерами таких процессов являются распространение ультразвука, ударные волны и т. п. Инерционность в уравнения переноса первым ввел Максвелл[4], а в 1948 году Каттанео был предложен вариант закона Фурье с релаксационным членом:[5]
τ∂q∂t=−(q+ϰ∇T).{\displaystyle \tau {\frac {\partial \mathbf {q} }{\partial t}}=-\left(\mathbf {q} +\varkappa \,\nabla T\right).}Если время релаксации τ{\displaystyle \tau } пренебрежимо мало, то это уравнение переходит в закон Фурье.
http-wikipediya.ru
Теплопроводность | Virtual Laboratory Wiki
Теплопрово́дность — это перенос теплоты структурными частицами вещества (молекулами, атомами, электронами) в процессе их теплового движения. Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества. Явление теплопроводности заключается в том, что кинетическая энергия атомов и молекул, которая определяет температуру тела, передаётся другому телу при их взаимодействии или передаётся из более нагретых областей тела к менее нагретым областям. Иногда теплопроводностью называется также количественная оценка способности конкретного вещества проводить тепло.
Исторически считалось, что передача тепловой энергии связана с перетеканием теплорода от одного тела к другому. Однако более поздние опыты, в частности, нагрев пушечных стволов при сверлении, опровергли реальность существования теплорода как самостоятельного вида материи. Соответственно, в настоящее время считается, что явление теплопроводности обусловлено стремлением занять состояние более близкое к термодинамическому равновесию, что выражается в выравнивании температуры.
В установившемся режиме поток энергии, передающейся посредством теплопроводности, пропорционален градиенту температуры:
$ \vec{q}=-\varkappa\,\mathrm{grad}(T), $где $ \vec{q} $ — вектор потока тепла — количество энергии, проходящей в единицу времени через единицу площади, перпендикулярной каждой оси, $ \varkappa $ — коэффициент теплопроводности (иногда называемый просто теплопроводностью), $ T $ — температура. Это выражение известно как закон теплопроводности Фурье.
В интегральной форме это же выражение запишется так (если речь идёт о стационарном потоке тепла от одной грани параллелепипеда к другой):
$ P=-\varkappa\frac{S\Delta T}{h}, $где $ P $ — полная мощность тепловых потерь, $ S $ — площадь сечения параллелепипеда, $ \Delta T $ — перепад температур граней, $ h $ — длина параллелепипеда, то есть расстояние между гранями.
Коэффициент теплопроводности измеряется в Вт/(м·K).
Коэффициенты теплопроводности различных веществ Править
| Алмаз | 1001—2600 |
| Серебро | 430 |
| Медь | 382—390 |
| Золото | 320 |
| Алюминий | 202—236 |
| Латунь | 97—111 |
| Железо | 92 |
| Платина | 70 |
| Олово | 67 |
| Сталь | 47 |
| Кварц | 8 |
| Стекло | 1 |
| Вода | 0,6 |
| Кирпич строительный | 0,2—0,7 |
| Пенобетон | 0,14—0,3 |
| Газобетон | 0,1—0,3 |
| Дерево | 0,15 |
| Шерсть | 0,05 |
| Минеральная вата | 0,045 |
| Пенополистирол | 0,04 |
| Пеноизол | 0,035 |
| Воздух (300 K, 100 кПа) | 0,026 |
| Воздух (сухой неподвижный) | 0,024—0,031 |
| Аргон | 0,0177 |
| Ксенон | 0,0057 |
| Вакуум (абсолютный) | 0 (строго) |
На практике нужно также учитывать проводимость тепла за счет конвекции молекул и проникаемости излучений. Например, при полной нетеплопроводности вакуума, тепло может передаваться за счет излучения (пример — Солнце, установки инфракрасного излучения). А газ или жидкость могут обмениваться нагретыми или охлажденными слоями самостоятельно или искусственно (пример — фен, греющие вентиляторы).
Паутина превзошла по теплопроводности медь
Представитель рода Nephila. Видно, что паутина имеет яркий, почти золотой отлив (фото Xinwei Wang research group).
Учёные из университета Айовы (Iowa State University) решили исследовать способность паутины передавать тепло. Для этого они «надоили» паутину восьми пауков вида Nephila clavipes. Результаты их измерений оказались удивительными: полученный показатель теплопроводности составил 416 ватт/(метр*Кельвин). Это означает, что так называемая каркасная нить паутины обеспечивает передачу тепла лучше, чем медь (353–401 Вт/(м*К)), и, практически, аналогична серебру (406–430 Вт/(м*К)). Получается, что паутина проводит тепло в тысячу раз лучше нити тутового шелкопряда и, в среднем, в 800 раз лучше, чем другие органические материалы.
Нить паутины имеет гибкую, но прочную структуру. Она в 15 раз тоньше человеческого волоса и имеет толщину всего 4 микрометра. Нить представляет собой белок, обогащённый глицином, аланином и серином, содержащий внутри нанокристаллы.
При всей своей кажущейся хрупкости паутина сравнима по прочности со сталью (для своего веса), но при этом обладает высокой упругостью. Эти уникальные свойства обещают широкое применение искусственной паутине во многих областях биотехнологии. Кстати, при растяжении нить паутины проявляет ещё более интересные свойства. Исследователи из США выяснили, что теплопроводность нити паутины растёт прямо пропорционально её растяжению. Например, если растянуть нить на 20% от нормальной длины, паутина станет на 20% лучше проводить тепло.
По мнению американцев, результат их открытия может быть использован в различных сферах. На основе паутины можно будет создавать новые теплоотводящие элементы для электроники или медицинские бинты, которые не будут приводить к перегреву.
Коэффициент теплопроводности вакуума Править
Коэффициент теплопроводности вакуума стремится к нулю. Это связано с низкой концентрацией в вакууме материальных частиц, способных переносить тепло. Тепло в вакууме передаётся только излучением. Поэтому для уменьшения теплопотери стенки термоса делают двойными, серебрят (такая поверхность хуже излучает и лучше отражает), а воздух между ними откачивают.
Связь с электропроводностью Править
Связь коэффициента теплопроводности $ K $ с удельной электрической проводимостью $ \sigma $ в металлах устанавливает закон Видемана — Франца:
$ \frac{K}{\sigma}=\frac{\pi^2}{3}\left(\frac{k}{e}\right)^2T, $где $ k $ — постоянная Больцмана, $ e $ — заряд электрона.
Обобщения закона Фурье Править
Следует отметить, что закон Фурье не учитывает инерционность процесса теплопроводности, то есть в данной модели изменение температуры в какой-то точке мгновенно распространяется на всё тело. Закон Фурье не применим для описания высокочастотных процессов (и, соответственно, процессов, чьё разложение в ряд Фурье имеет значительные высокочастотные гармоники). Примерами таких процессов являются распространение ультразвука, ударные волны и т. д. Инерционность в уравнения переноса первым ввел Максвелл[1], а в 1948 году Каттанео был предложен вариант закона Фурье с релаксационным членом:[2]
$ \tau\frac{\partial\mathbf{q}}{\partial t}=-\left(\mathbf{q}+\varkappa\,\nabla T\right). $Если время релаксации $ \tau $ пренебрежимо мало, то это уравнение переходит в закон Фурье.
- ↑ J. C. Maxwell, Philos. Trans. Roy. Soc. London 157 (1867) 49.
- ↑ C. Cattaneo, Atti Seminario Univ. Modena 3 (1948) 33.
Другие способы теплопередачи
Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Теплопроводность. Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .
ru.vlab.wikia.com
Теплопроводность — WiKi
Теплопрово́дность — способность материальных тел проводить энергию (теплоту) от более нагретых частей тела к менее нагретым частям тела, осуществляемому хаотически движущимися частицами тела (атомами, молекулами, электронами и т. п.). Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества.
Теплопроводностью называется также количественная характеристика способности тела проводить тепло. В сравнении тепловых цепей с электрическими это аналог проводимости.
Количественно способность вещества проводить тепло характеризуется коэффициентом теплопроводности. Эта характеристика равна количеству теплоты, проходящему через однородный образец материала единичной длины и единичной площади за единицу времени при единичной разнице температур (1 К). В системе СИ единицей измерения коэффициента теплопроводности является Вт/(м·K).
Исторически считалось, что передача тепловой энергии связана с перетеканием гипотетического теплорода от одного тела к другому. Однако с развитием молекулярно-кинетической теории явление теплопроводности получило своё объяснение на основе взаимодействия частиц вещества. Молекулы в более нагретых частях тела движутся быстрее и передают энергию посредством столкновений медленным частицам в более холодных частях тела.
В установившемся режиме плотность потока энергии, передающейся посредством теплопроводности, пропорциональна градиенту температуры:
q→=−ϰgrad(T),{\displaystyle {\vec {q}}=-\varkappa \,\mathrm {grad} (T),}где q→{\displaystyle {\vec {q}}} — вектор плотности теплового потока — количество энергии, проходящей в единицу времени через единицу площади, перпендикулярной каждой оси, ϰ{\displaystyle \varkappa } — коэффициент теплопроводности (удельная теплопроводность), T{\displaystyle T} — температура. Минус в правой части показывает, что тепловой поток направлен противоположно вектору grad(T){\displaystyle \mathrm {grad} (T)} (то есть в сторону скорейшего убывания температуры). Это выражение известно как закон теплопроводности Фурье.[1]
В интегральной форме это же выражение запишется так (если речь идёт о стационарном потоке тепла от одной грани параллелепипеда к другой):
P=−ϰSΔTl,{\displaystyle P=-\varkappa {\frac {S\Delta T}{l}},} [Вт/(м·К) · (м2·К)/м = Вт/(м·К) · (м·К) = Вт]где P{\displaystyle P} — полная мощность тепловых потерь, S{\displaystyle S} — площадь сечения параллелепипеда, ΔT{\displaystyle \Delta T} — перепад температур граней, l{\displaystyle l} — длина параллелепипеда, то есть расстояние между гранями.
Связь с электропроводностью
Связь коэффициента теплопроводности ϰ{\displaystyle \varkappa } с удельной электрической проводимостью σ{\displaystyle \sigma } в металлах устанавливает закон Видемана — Франца:
ϰσ=π23(ke)2T,{\displaystyle {\frac {\varkappa }{\sigma }}={\frac {\pi ^{2}}{3}}\left({\frac {k}{e}}\right)^{2}T,} где k{\displaystyle k} — постоянная Больцмана; e{\displaystyle e} — заряд электрона; T{\displaystyle T} — абсолютная температура.Коэффициент теплопроводности газов
В газах коэффициент теплопроводности может быть найден по приближённой формуле[2]
ϰ∼13ρcvλv¯,{\displaystyle \varkappa \sim {\frac {1}{3}}\rho c_{v}\lambda {\bar {v}},}где ρ{\displaystyle \rho } — плотность газа, cv{\displaystyle c_{v}} — удельная теплоёмкость при постоянном объёме, λ{\displaystyle \lambda } — средняя длина свободного пробега молекул газа, v¯{\displaystyle {\bar {v}}} — средняя тепловая скорость. Эта же формула может быть записана как[3]
ϰ=ik3π3/2d2RTμ,{\displaystyle \varkappa ={\frac {ik}{3\pi ^{3/2}d^{2}}}{\sqrt {\frac {RT}{\mu }}},}где i{\displaystyle i} — сумма поступательных и вращательных степеней свободы молекул (для двухатомного газа i=5{\displaystyle i=5} , для одноатомного i=3{\displaystyle i=3} ), k{\displaystyle k} — постоянная Больцмана, μ{\displaystyle \mu } — молярная масса, T{\displaystyle T} — абсолютная температура, d{\displaystyle d} — эффективный (газокинетический) диаметр молекул, R{\displaystyle R} — универсальная газовая постоянная. Из формулы видно, что наименьшей теплопроводностью обладают тяжелые одноатомные (инертные) газы, наибольшей — легкие многоатомные (что подтверждается практикой, максимальная теплопроводность из всех газов — у водорода, минимальная — у радона, из нерадиоактивных газов — у ксенона).
Теплопроводность в сильно разреженных газах
Приведённое выше выражение для коэффициента теплопроводности в газах не зависит от давления. Однако если газ сильно разрежен, то длина свободного пробега определяется не столкновениями молекул друг с другом, а их столкновениями со стенками сосуда. Состояние газа, при котором длина свободного пробега молекул ограничивается размерами сосуда называют высоким вакуумом. При высоком вакууме теплопроводность убывает пропорционально плотности вещества (то есть пропорциональна давлению в системе): ϰ∼13ρcvlv¯∝P{\displaystyle \varkappa \sim {\frac {1}{3}}\rho c_{v}l{\bar {v}}\propto P} , где l{\displaystyle l} — размер сосуда, P{\displaystyle P} — давление.
Таким образом коэффициент теплопроводности вакуума тем ближе к нулю, чем глубже вакуум. Это связано с низкой концентрацией в вакууме материальных частиц, способных переносить тепло. Тем не менее, энергия в вакууме передаётся с помощью излучения. Поэтому, например, для уменьшения теплопотерь стенки термоса делают двойными, серебрят (такая поверхность лучше отражает излучение), а воздух между ними откачивают.
Следует отметить, что закон Фурье не учитывает инерционность процесса теплопроводности, то есть в данной модели изменение температуры в какой-то точке мгновенно распространяется на всё тело. Закон Фурье неприменим для описания высокочастотных процессов (и, соответственно, процессов, чьё разложение в ряд Фурье имеет значительные высокочастотные гармоники). Примерами таких процессов являются распространение ультразвука, ударные волны и т. п. Инерционность в уравнения переноса первым ввел Максвелл[4], а в 1948 году Каттанео был предложен вариант закона Фурье с релаксационным членом:[5]
τ∂q∂t=−(q+ϰ∇T).{\displaystyle \tau {\frac {\partial \mathbf {q} }{\partial t}}=-\left(\mathbf {q} +\varkappa \,\nabla T\right).}Если время релаксации τ{\displaystyle \tau } пренебрежимо мало, то это уравнение переходит в закон Фурье.
ru-wiki.org
423800, Набережные Челны , база Партнер Плюс, тел. 8 800 100-58-94 (звонок бесплатный)











