|
||||
|
|
звонок бесплатный
Наши сотрудники:
[email protected]
Екатерина - специалист по продаже а/м КАМАЗ
 [email protected]
[email protected]






Техника в наличии

Тягач КАМАЗ 44108-6030-24
2014г, 6х6, Евро3, дв.КАМАЗ 300 л.с., КПП ZF9, бак 210л+350л, МКБ,МОБ,рестайлинг.
цена 2 220 000 руб.,

КАМАЗ 4308-6063-28(R4)
4х2,дв. Cummins ISB6.7e4 245л.с. (Е-4),КПП ZF6S1000, V кузова=39,7куб.м., спальное место, бак 210л, шк-пет,МКБ, ТНВД BOSCH, система нейтрализ. ОГ(AdBlue), тент, каркас, рестайлинг, внутр. размеры платформы 6112х2470х730 мм
цена 1 950 000 руб.,

Самосвал КАМАЗ 6520-057
2014г, 6х4,Евро3, дв.КАМАЗ 320 л.с., КПП ZF16, ТНВД ЯЗДА, бак 350л, г/п 20 тонн, V кузова =20 куб.м.,МКБ,МОБ, со спальным местом.
цена 2 700 000 руб.,

Самосвал 6522-027
2014, 6х6, дв.КАМАЗ 740.51,320 л.с., КПП ZF16,бак 350л, г/п 19 тонн,V кузова 12куб.м.,МКБ,МОБ,задняя разгрузка,обогрев платформы.
цена 3 190 000 руб.,
СУПЕР ЦЕНА
на АВТОМОБИЛИ КАМАЗ
| 43118-010-10 (дв.740.30-260 л.с.) | 2 220 000 |
| 43118-6033-24 (дв.740.55-300 л.с.) | 2 300 000 |
| 65117-029 (дв.740.30-260 л.с.) | 2 200 000 |
| 65117-6010-62 (дв.740.62-280 л.с.) | 2 350 000 |
| 44108 (дв.740.30-260 л.с.) | 2 160 000 |
| 44108-6030-24 (дв.740.55,рест.) | 2 200 000 |
| 65116-010-62 (дв.740.62-280 л.с.) | 1 880 000 |
| 6460 (дв.740.50-360 л.с.) | 2 180 000 |
| 45143-011-15 (дв.740.13-260л.с) | 2 180 000 |
| 65115 (дв.740.62-280 л.с.,рест.) | 2 190 000 |
| 65115 (дв.740.62-280 л.с.,3-х стор) | 2 295 000 |
| 6520 (дв.740.51-320 л.с.) | 2 610 000 |
| 6520 (дв.740.51-320 л.с.,сп.место) | 2 700 000 |
| 6522-027 (дв.740.51-320 л.с.,6х6) | 3 190 000 |

подробнее про услугу перегона можно прочесть здесь.

|
Нужны самосвалы? Обратите внимание на Ford-65513-02. |
КАМАЗы в лизинг
ООО «Старт Импэкс» имеет возможность поставки грузовой автотехники КАМАЗ, а так же спецтехники на шасси КАМАЗ в лизинг. Продажа грузовой техники по лизинговым схемам имеет определенные выгоды для покупателя грузовика. Рассрочка платежа, а так же то обстоятельство, что грузовики до полной выплаты лизинговых платежей находятся на балансе лизингодателя, и соответственно покупатель автомобиля не платит налогов на имущество. Мы готовы предложить любые модели бортовых автомобилей, тягачей и самосвалов по самым выгодным лизинговым схемам.Контактная информация.
г. Набережные Челны, Промкомзона-2, Автодорога №3, база «Партнер плюс».
тел/факс (8552) 388373.
Схема проезда
Описание работы механизма по кинематической схеме. Кинематическая схема механизма
Описание работы механизма по кинематической схеме
Геометрические параметры звеньев:
lOA=0.18м, lAB=0.37м, lBC=0.92м, x1=0.85м, x2=0.37м, y=0.22м Рис.1 Механизм стана холодной калибровки труб
В состав исполнительного механизма Стана холодной калибровки труб входят шесть звеньев: стойка 0, кривошип 1, шатун 2, кулиса 3, кулисный камень 4, ползун 5. Входным звеном является кривошип 1, выходным ползун 5. Механическая энергия от привода станка сообщается кривошипу 1, который вращается относительно стойки 0. Движение от кривошипа 1 через шатун 2 передается кулисе 3, которая движется возвратно-качательно относительно неподвижной оси С. Движение кулисы 3 через кулисный камень 4 сообщает ползуну 5, который движется возвратно-поступательно: сверху вниз – рабочий ход, в обратную сторону - холостой ход. Кулисный камень 4 совершает сложное движение: переносное вращательное - вместе с кулисой 3 и относительное поступательное - вдоль кулисы 3.
Структурный анализ механизма
Данный механизм состоит из шести звеньев: стойка 0, кривошип 1, шатун 2, кулиса 3, кулисный камень 4, ползун 5. Звенья механизма образуют семь кинематических пар: 0 – 1, 1 – 2, 2 – 3, 3 – 0, 4 – 5 – вращательные, одноподвижные, пятого класса; 3 – 4 – поступательные, одноподвижные, пятого класса; 5 – 0 – цилиндрическая, двухподвижная, четвертого класса. Все кинематические пары низшие, механизм – рычажный. Механизм также является плоским (звенья механизма движутся в плоскостях, параллельных неподвижной плоскости), содержит два замкнутых кинематических контура (0-1-2-3-0, 0-3-4-5-0). Число степеней свободы механизма определим, применяя универсальную формулу Чебышева
,
где n – число звеньев, pН – число низших кинематических пар. В рассматриваемом механизме n = 6, pН = 7, поэтому - механизм обладает одной степенью свободы.
Выявим избыточные связи: кинематическая пара стойка-ползун, как видно на структурной схеме, имеет ветвление: число избыточных связей типа Б определим по формуле
,
где i - индекс ветвления пары, Si – число независимых связей в i – той ветви, S – класс кинематической пары. Так как в данном случае ,(оба ветвления цилиндрические) и(класс цилиндрической пары – четвертый), то
Число избыточных связей, образованных при замыкании контуров (тип В), определим из формулы Малышева
,
где WЧ – число степеней свободы, найденное по формуле Чебышева, WСМ – число степеней свободы, найденное по формуле Сомова – Малышева: ,
где i – класс кинематических пар, pi – число кинематических пар класса i.
В данном случае
и .
Таким образом, в механизме имеется четыре избыточные связи типа Б и пять избыточных связей типа В.
В соответствии с принципом Ассура, выделим начальный механизм, обладающий числом степеней свободы всего исследуемого механизма. Этот механизм – кривошипный, состоит из стойки 0 и кривошипа 1. Остальные звенья образуют ведомую цепь, имеющую нулевую подвижность относительно звеньев начального механизма. Ведомая цепь состоит из двух структурных групп первого класса второго порядка: ВВВ и ПВП (2 – 3 и 4 – 5)
Рис. 2 Структура механизма
studfiles.net
Кафедра «Теоретическая механика»
Федеральное агентство по образованию
Государственное образовательное учреждение высшего
профессионального образования
НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
СОСТАВЛЕНИЕ КИНЕМАТИЧЕСКИХ СХЕМ И
СТРУКТУРНЫЙ АНАЛИЗ ПЛОСКИХ МЕХАНИЗМОВ
Методические указания к лабораторной работе № 2 по дисциплине
«Теория механизмов и машин»
Нижний Новгород 2005
Составитель: Л.К.Лобанова
УДК 621.01
Составление кинематических схем и структурный анализ плоских механизмов. Методические указания к лабораторной работе № 2 по дисциплине «Теория механизмов и машин» / НГТУ; Сост.: Л.К.Лобанова. – Н.Новгород, 2005. – 23 с.
Научный редактор З.Е.Васильева
Редактор
Подп. в печать . Формат 60х841/16. Бумага газетная. Печать офсетная.
Печ. л. Уч.-изд. л. Тираж экз. Заказ
Нижегородский государственный технический университет.
Типография НГТУ, 603600, ул. Минина, 24
© Нижегородский государственный
технический университет, 2005
ЦЕЛЬ РАБОТЫ
Целью работы является приобретение навыков в составлении кинематических схем механизмов и в структурном анализе их, усвоение и закрепление теоретических сведений по классификации механизмов.
ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ
Система тел, предназначенная для преобразования движения одного или нескольких твердых тел в требуемые движения других твердых тел, называется механизмом.
Любой механизм состоит из определенного количества твердых тел.
Звенья механизма
Одно или несколько твердых тел, неподвижно соединенных в единую жесткую систему, называется звеном.
Если эта система подвижна, она называется подвижным звеном. Например, шатун двигателя считается одним подвижным звеном (рис.1), хотя состоит из ряда деталей: тела шатуна1; крышки 2; вкладышей 3; болтов, шайб и гаек 4. Если система неподвижна – она называется неподвижным звеном или стойкой.
Любой механизм состоит из подвижных звеньев и стойки. Из подвижных звеньев выделяют входные и выходные звенья.
Звено, которому сообщается движение, преобразуемое механизмом в требуемые движения других звеньев, называется входным звеном.
Выходным звеном называется звено, совершающее движение, для выполнения которого предназначен механизм. Остальные подвижные звенья называются соединительными или промежуточными.
Обычно в механизме имеется одно входное и одно выходное звено. Входное звено получает движение от двигателя, а выходное соединяется с рабочим органом машины или указателем прибора. Но могут быть механизмы с несколькими входными и выходными звеньями.
2.2. Кинематические пары
Для образования механизма звенья (подвижные и неподвижные) должны быть определенным образом соединены между собой.
Соединение двух соприкасающихся звеньев, допускающее их относительное движение, называется кинематической парой.
Классифицируют кинематические пары по условиям связи, по характеру соприкосновения звеньев и по способу замыкания.
Свободное тело в пространстве имеет шесть возможных движений (рис.2) или шесть степеней свободы: три поступательных движения вдоль осей прямоугольной системы координат ХYZ и три вращательных движения вокруг этих осей. Ограничения, препятствующие свободному движению тела, называют условиями связи. Соединение двух звеньев в кинематическую пару накладывает на относительное движение этих звеньев определенные ограничения, число которых не может быть больше пяти, так как при шести ограничениях звенья теряют относительную подвижность, т.е. кинематическая пара переходит в жесткое соединение.
Класс кинематических паропределяется числом условий связи (числом отнятых степеней свободы). В табл.1 показаны наиболее распространенные кинематические пары. Необходимо помнить, что при подсчете числа условий связи, следовательно, и при определении класса кинематической пары, нужно учитывать только независимые между собой движения. Например, в винтовой кинематической паре одновременно происходит не только вращение гайки относительно винта, но и относительное ее перемещение вдоль оси винта. Эти движения взаимосвязаны, поэтому винтовую пару относят к пятому классу.
По характеру относительного движения различают вращательные или шарниры (В), поступательные (П), вращательно-поступательные (В + П) и с винтовым движением (ВП) кинематической пары.
Соединение в одном шарнире n звеньев осуществляется (n – 1) кинематическими парами.
В зависимости от характера соприкосновения звеньев пары делят на низшие и высшие.
Совокупность поверхностей, линий и точек звена, по которым оно может соприкасаться с другим звеном, образуя кинематическую пару, называют элементами кинематической пары.
Низшей кинематической парой (табл.1, в, г, д, е) называется пара, в которой требуемое относительное движение звеньев может быть получено постоянным соприкосновением ее элементов по поверхности.
Кинематическая пара, в которой требуемое относительное движение звеньев может быть получено только соприкосновением ее элементов по линиям и в точках, называется высшей (табл.1, а, б). Высшую пару можно схематически представить в виде криволинейного контура, соприкасающегося с другим криволинейным контуром. Подобные пары встречаются в зубчатых (рис.2), кулачковых (рис.3) и других механизмах.
Для того чтобы элементы кинематических пар находились в контакте, т.е. для обеспечения существования пар, применяется геометрическое или силовое замыкание.
При геометрическом замыкании (рис.3, а) непрерывность взаимодействия обусловлена геометрией звеньев (ролик толкателя располагается в пазу кулачка, профильный паз кулачка охватывает ролик толкателя). Низшие пары большей частью замкнуты геометрически. Силовое замыкание (рис.3, б) осуществляется при помощи внешних сил, приложенных к звеньям, образующим эту пару (сила тяжести, сила упругости пружины или давление жидкости в гидроцилиндре).
Рис.3. Кулачковые механизмы
Таблица 1
studfiles.net
Лекция 1. Параметры механической системы электропривода
Электроприводы как электромеханические объекты управления современных промышленных агрегатов характеризуются весьма сложной механической частью, которая представляет собой многомассовую систему с упругими связями и зазорами в них. Кроме того, рабочие органы отдельных механизмов сложных технологических комплексов могут быть связаны между собой через обрабатываемый материал или изделие. Электрическая часть электроприводов может быть многодвигательной и выполняться с питанием электродвигателей как от общего, так и от индивидуальных преобразователей, что определяет их взаимное влияние друг на друга. В целом, работа современных систем автоматизированного электропривода характеризуется взаимосвязью электромагнитных процессов, механических явлений и технологических факторов, действием внешних (изменение моментов нагрузки, сил и моментов трения, напряжения питающей сети и др.) и внутренних (изменение электромеханических параметров привода) возмущений. Указанные обстоятельства должны быть учтены при математическом описании электромеханических объектов управления в целом и механической системы привода в частности.
1.1. Примеры кинематических схем производственных механизмов
Механическая система электропривода включает в себя большое количество кинематически связанных элементов и узлов: двигатель, муфты, валы, шестерни, винтовые, ременные и другие передачи, поступательно движущиеся массы и т.п. Каждая связь состоит из одной или нескольких механических, гидравлических, пневматических, электрических цепей, через которые передаются требуемые исполнительные движения. Простейшие механические цепи представляют собой отдельные пары: зубчатые, винтовые, червячные, ременные и т.п. Изображение кинематической цепи производственного механизма посредством условных обозначений ее элементов называется кинематической схемой механизма.
Ниже приведены упрощенные кинематические схемы некоторых исполнительных механизмов производственных агрегатов, где, упуская конструктивные подробности их реализации, основное внимание уделено принципиальным особенностям механической части электропривода.
Кинематическая схема механизма подачи металлорежущего станка
Схема приведена на рис. 1.1. Механизм подачи осуществляет преобразование вращательного движения в поступательное. Основными передачами механизма подачи являются винт – гайка и зубчатая передача, которая может и отсутствовать. Характерные особенности механизма подачи: податливость винта и его соединений, возможность наличия кинематических зазоров в передаче винт – гайка и зубчатой передаче.
Рис. 1.1. Кинематическая схема механизма подачи металлорежущего станка: 1 – электродвигатель; 2 – зубчатая передача; 3 – винт; 4 – гайка; 5 – стол
Кинематическая схема механизма подъема
Схема приведена на рис. 1.2. Механизм подъема осуществляет преобразование вращательного движения в поступательное.
Рис. 1.2. Кинематическая схема механизма подъема: 1 – электродвигатель; 2 – редуктор; 3 – барабан лебедки; 4 – канат
Основными элементами механизма являются редуктор с несколькими зубчатыми передачами и подъемная лебедка, состоящая из барабана и канатов. Схема заправки канатов имеет варианты в зависимости от конкретного назначения механизма. Возможны варианты однодвигательного привода и двухдвигательного с общим и индивидуальными редукторами. Характерные особенности механизма подъема: податливость канатов, провисание канатов, наличие зазоров в зубчатых зацеплениях, возможность раскачивания груза. При жестком соединении валов приводные электродвигатели чаще всего включаются последовательно и питаются от общего преобразователя.
studfiles.net
Кинематическая схема механизма
План скоростей
2.2. Определение ускорений точек звеньев и угловых ускорений звеньев
2.2.1.Определение ускорения точки А:
Так как угловая скорость является постоянной, то .
. Вектор ускорения направлен параллельно кривошипу О1А от точки А к точке О1.
Выбираем масштаб плана ускорений . Найдём отрезок, изображающий вектор ускорения на плане: мм. Из полюса плана ускорений pa откладываем данный отрезок в направлении, параллельном АО1.
2.2.2. Определение ускорения точки В:
Запишем векторное уравнение: .
Вектор относительного ускорения раскладываем на нормальную и касательную составляющие: .
Нормальное относительное ускорение равно: м/с2.
Найдём отрезок, изображающий вектор ускорения на плане:
мм.
Продолжаем строить план ускорений. Вектор ускорения направлен параллельно АВ. Откладываем отрезок an из точки a плана ускорений в указанном направлении от точки В к точке А.
Вектор ускорения направлен перпендикулярно АВ. Проводим это направление из точки n плана ускорений.
Вектор ускорения раскладываем на нормальную и касательную составляющие:
.
Нормальное ускорение равно: м/с2.
Найдём отрезок, изображающий вектор ускорения на плане: мм.
Продолжаем строить план ускорений. Вектор ускорения направлен параллельно ВO2. Откладываем отрезок из точки плана ускорений в указанном направлении от точки В к точке O2. Вектор ускорения направлен перпендикулярно ВO2. Проводим это направление из точки m плана ускорений. Две прямые линии, проведённые из точек n и m в указанных направлениях, пересекаются в точке b.
Найдем величины ускорений. Измеряя длины полученных отрезков и умножая их на масштаб , получим:
м/с2;
м/с2;
м/с2;
м/с2.
2.2.3. Определение ускорения точки c:
Запишем векторное уравнение: .
Вектор относительного ускорения раскладываем на нормальную и касательную составляющие: .
Нормальное относительное ускорение равно:
м/с2.
Найдём отрезок, изображающий вектор ускорения на плане: мм. Продолжаем строить план ускорений. Так как отрезок bk мал, то его на плане ускорений не откладываем. Точки b и k совпадают.
Вектор ускорения направлен перпендикулярно ВС. Проводим это направление из точки k плана ускорений.
Вектор ускорения направлен параллельно оси X–X. Проводим это направление из полюса pa. Две прямые линии, проведённые из точек k и pa в указанных направлениях, пересекаются в точке c.
Найдем величины ускорений. Измеряя длины полученных отрезков и умножая их на масштаб , получим:
м/с2;
м/с2;
м/с2.
2.2.4. Определение ускорения точки s1:
м/с2. Вектор ускорения направлен параллельно кривошипу О1А от точки S1 к точке О1.
2.2.5. Определение ускорения точки S2:
Воспользуемся следствием из теоремы подобия. Составим пропорцию:
, мм.
Данный отрезок откладываем на прямой ab от точки a. Точку s2 соединяем с полюсом pa.
Величина ускорения: м/с2.
2.2.6. Определение ускорения точки S3:
Воспользуемся следствием из теоремы подобия. Составим пропорцию:
, мм.
Данный отрезок откладываем на прямой pab от точки b. Точку s3 соединяем с полюсом pa.
Величина ускорения: м/с2.
2.2.7. Определение ускорения точки S4:
Воспользуемся следствием из теоремы подобия. Составим пропорцию:
, мм.
Данный отрезок откладываем на прямой bc от точки b. Точку s4 соединяем с полюсом pa.
Величина ускорения: м/с2.
2.2.8. Определение углового ускорения шатуна АВ:
с-2.
Для определения направления переносим вектор в точку В шатуна АВ и смотрим, как она движется относительно точки А. Направление этого движения соответствует . В данном случае угловое ускорение направлено против часовой стрелки.
2.2.9. Определение углового ускорения коромысла ВO2:
с-2.
Для определения направления переносим вектор в точку В коромысла ВО2 и смотрим, как она движется относительно точки О2. Направление этого движения соответствует . В данном случае угловое ускорение направлено по часовой стрелке.
2.2.10. Определение углового ускорения шатуна ВС:
с-2.
Для определения направления переносим вектор в точку C шатуна ВС и смотрим, как она движется относительно точки B. Направление этого движения соответствует. В данном случае угловое ускорение направлено против часовой стрелки.
| Исследуемая величина | Отрезок на плане | Направление | Величина отрезка на плане, мм | Масштабный коэффициент | Значение величины, м/с2 |
| 118 | 5,9 | ||||
| 10 | 0,48 | ||||
| 21 | 1,05 | ||||
| 23 | 1,15 | ||||
| 91 | 4,57 | ||||
| 27 | 1,35 | ||||
|
| 95 | 4,75 | |||
| 1 | 0,058 | ||||
| 88 | 4,4 | ||||
|
| 88 | 4,4 | |||
| 65 | 3,25 | ||||
| 59 | 2,95 | ||||
|
| 107 | 5,35 | |||
|
| 48 | 2,4 | |||
|
| 69 | 3,45 | |||
| Против часовой стрелки | 5,25 с–2 | ||||
| По часовой стрелке | 25,68 с–2 | ||||
| Против часовой стрелки | 2,2 с–2 | ||||
studfiles.net
Кинематические и конструктивные схемы механизмов передвижения
Строительные машины и оборудование, справочник

Категория:
Мостовые перегружатели
 Кинематические и конструктивные схемы механизмов передвижения
Кинематические и конструктивные схемы механизмов передвиженияОсобенностью рассматриваемых перегружателей является выполнение ими подъемно-транспортных операций при неподвижном перегружателе. Перегружатель перемещается без груза при неподвижной тележке для занятия новой позиции. Перемещения перегружателей являются, таким образом, установочными, и механизм передвижения перегружателя включается сравнительно редко (4—8% от общего времени работы перегружателя).
Установочный характер передвижения и большая масса перегружателей определили относительно малые скорости их передвижения: 9—36 м/мин.
В современных конструкциях перегружателей применяется агрегатно-балансирная схема механизмов передвижения с индивидуальным приводом ходовых агрегатов.
Масса механизма передвижения современных перегружателей с индивидуальным приводом составляет 5—9% общей массы перегружателя, и только у перегружателей весьма большой массы она составляет 15—17%.
Каждый из ходовых балансирных агрегатов (тележек) механизма передвижения А, В, С и D представляет собой полностью унифицированный агрегат, включающий в себя ходовые колеса, систему балансирной подвески и приводную часть с электродвигателем.
Типичные схемы балансиров перегружателей с четырьмя колесами на одном рельсе показаны на рис. 1, а, б, в. Большая масса перегружателей предопределила применение четырех подкрановых рельсов.
У перегружателей значительной массы (2000—2400 т) применяется шестнадцатиколесная система балансиров при четырех или шести подкрановых рельсах (рис. 2, а, б). В последней схеме четырехрельсовая опора устанавливается на стороне большей консоли. Каждая приводная колесная пара имеет индивидуальный привод.
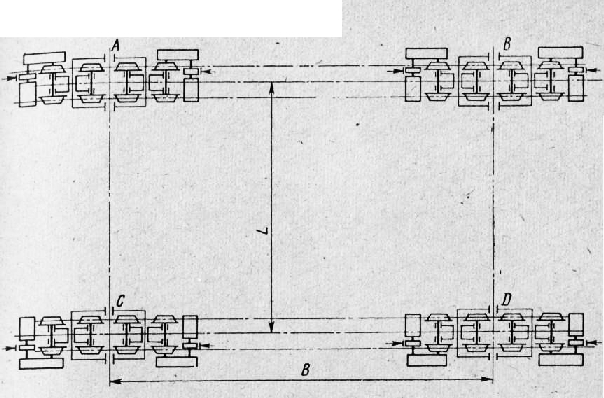
Рис. 1. Общая схема механизма передвижения перегружателя: А, В, С, D — ходовые балансирные агрегаты; I — гибкая опора; II — жесткая опора
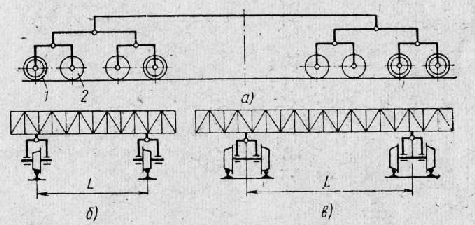
Рис. 2. Схема четырехколесных балансиров перегружателей:
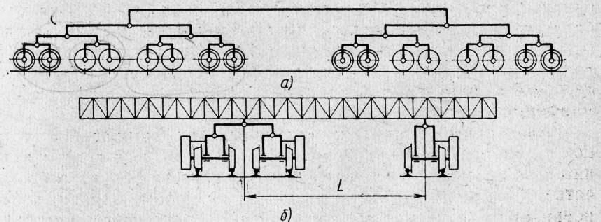
Рис. 3. Схема восьмиколесного балансира: а — вид сбоку; б — опирание на рельсы
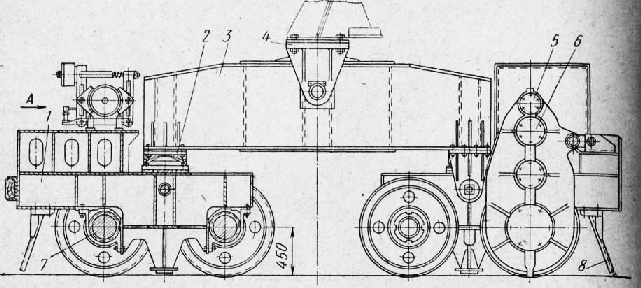
Рис. 4. Двухрельсовый балансирный агрегат перегружателя конструкции скмз
При 50%-ном числе приводных колес применяются две схемы привода колес: с установкой привода на каждом малом балансире и установкой на одном из малых балансиров двух двигателей, при этом второй малый балансир остается полностью неприводным. Первая схема позволяет получить более равномерное приложение тягового усилия, а конструкция балансиров получается более унифицированной.
Балансирный агрегат механизма передвижения перегружателя конструкции СКМЗ показан на рис. 4. Ходовые колеса приводятся во вращение от электродвигателя через редуктор с зубчатым колесом. Редуктор размещен на малом балансире. Установка привода на малом балансире позволяет передавать вращение на ходовые колеса независимо от положения балансира. У двухрельсовых балансирных агрегатов опоры балансиров делают сферическими, что позволяет балансиру занимать положение, соответствующее продольному и поперечному уклону рельсов. у однорельсовых агрегатов балансиры соединяются при помощи шарнира с цилиндрическим валиком. Таким же шарниром соединяется и главный балансир с опорой перегружателя. Расчистка подкрановых путей производится метельником.
Малые скорости и пути передвижения перегружателей позволяют применять в буксах валов и осей ходовых колес подшипники скольжения. Такая конструкция удобна при замене (выкатке) колесных пар, однако требует регулярного ухода за буксами. Поэтому в последних конструкциях перегружателей завода «Сибтяжмаш» в механизме передвижения применены подшипники качения (рис. 5), более удобные и надежные в эксплуатации.
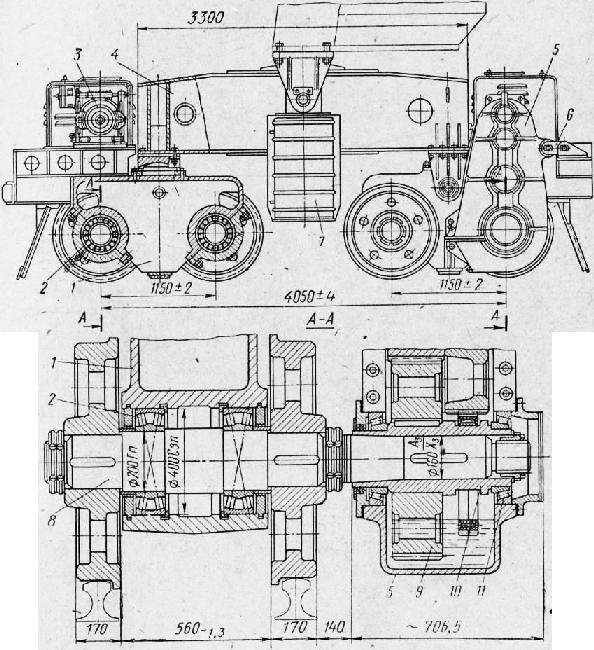
Рис. 5. Двухрельсовый балансирный агрегат перегружателя конструкции завода «Сибтяжмаш»: 1 — малый балансир; 2 — роликовый подшипник; 3 — двигатель; 4 — большой балансир; 5 — редуктор; 6 — серьга; 7 — установка для централизованной густой смазки; 8 — приводной вал; 9 — приводное колесо; 10 — втулка-гильза; 11 — конический роли
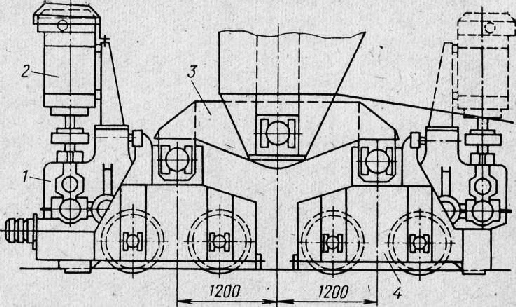
Рис. 6. Схема ходовых балансирных агрегатов механизма передвижения перегружателя конструкции фирмы МАН: 1 — редуктор; 2 — электродвигатель; 3 — главный балансир; 4 — малый балансир
Корпуса редукторов крепятся к малым балансирам с помощью шарнирных серег или лап, заходящих в направляющие балансира. Однако при соединении лапами в чугунных корпусах через 4—6 месяцев появляются трещины, и их приходится заменять стальными. При шарнирном соединении срок службы чугунных редукторов возрастает.
Двухрельсовый балансирный агрегат механизма передвижения перегружателя, изготовляемого фирмой МАН, показан на рис. 6. Агрегат имеет вертикальные электродвигатели, все колеса его приводные.
Ходовые колеса перегружателей делают цилиндрическими двухребордными или коническими одноребордными.
Колесно-рельсовый ход с коническими одноребордными колесами создает большую устойчивость передвижения в результате выравнивания перекоса перегружателя. Последнее достигается без участия или при незначительном участии реборд. Одноре-бордные колеса более просты в изготовлении и поэтому применяются более широко.
Читать далее: Ограничители перекоса перегружателей
Категория: - Мостовые перегружатели
Главная → Справочник → Статьи → Форум
stroy-technics.ru
Кинематическая схема механизма
План ускорений
3. Силовой расчет механизма
3.1. Силовой расчет последней группы Ассура вида ВВП
3.1.1. Определение сил тяжести звеньев:
Н, Н.
3.1.2. Определение сил инерции:
Н, Н.
Силы инерции направлены в противоположную сторону соответствующим ускорениям центров масс звеньев.
3.1.3. Определение момента инерции:
Нм;
Момент инерции направлен в противоположную сторону угловому ускорению .
Построим группу Ассура в масштабе .
Покажем все действующие на нее силы и неизвестные реакции , , .
3.1.4. Определим реакцию :
Составим уравнение моментов всех сил, действующих на звено 4, относительно точки С.
; .
Найдем реакцию .
Длины плеч h2 и h3 измерены на расчетной схеме и умножены на масштабный коэффициент м/мм.
м, м.
3.1.5. Определим реакции и :
Составим векторное уравнение равновесия всех сил, действующих на всю группу Ассура.
; .
Выберем масштаб плана сил м/мм.
Вычислим величины отрезков, соответствующих векторам сил. Данные занесем в табл. 1:
Таблица 1
| Обозначение силы | ||||||||||
| Величина силы, Н | 49 | 49 | 17,25 | 16,25 | 40 | 20,5 | 17 | 27 | 62 | 27 |
| Отрезок на плане, мм | 49 | 49 | 17 | 16 | 40 | 21 | 17 | 27 | 62 | 27 |
Строим план сил. В соответствии с векторным уравнением откладываем отрезки, соответствующие векторам . Векторы можно откладывать в любом порядке, но обязательно начать построение с вектора . Затем из начала вектора проводим направление вектора , а из конца последнего вектора проводим направление вектора . Пересекаясь, эти направления замыкают многоугольник сил.
Измеряя на плане сил отрезки, соответствующие векторам , , и умножая их на масштаб , получим значение этих реакций. Данные занесены в табл. 1.
3.1.6. Определим реакцию r54.
Составим векторное уравнение равновесия всех сил, действующих звено 4.
; .
Выберем масштаб плана сил м/мм.
Строим план сил. В соответствии с векторным уравнением откладываем отрезки, соответствующие векторам . Векторы можно откладывать в любом порядке. Соединяя начало первого вектора и конец последнего, получим многоугольник сил и отрезок, определяющий реакцию . Измеряя его длину и умножая на масштаб , получим величину реакции .
3.2. Силовой расчет предпоследней группы Ассура вида ВВВ.
3.2.1. Определение сил тяжести звеньев:
Н, Н.
3.2.2. Определение сил инерции:
Н, Н.
Силы инерции направлены в противоположную сторону соответствующим ускорениям центров масс звеньев.
3.2.3. Определение моментов инерции:
Нм; Нм.
Моменты инерции направлены в противоположные стороны соответствующим угловым ускорениям.
Построим группу Ассура в масштабе .
Покажем все действующие на нее силы (в том числе реакцию ) и неизвестные реакции .
3.2.4. Определим реакцию .
Составим уравнение моментов всех сил, действующих на звено 2, относительно точки В.
; .
Найдем реакцию :
Длины плеч h5 и h6 измерены на расчетной схеме и умножены на масштабный коэффициент м/мм.
м, м.
Последняя группа Ассура вида ВВП м/мм
| План сил для группы Ассура м/мм | План сил для звена 4 м/мм |
3.2.5. Определим реакцию .
Составим уравнение моментов всех сил, действующих на звено 3, относительно точки В.
; .
Найдем реакцию .
Длины плеч h4 и h5 измерены на расчетной схеме и умножены на масштабный коэффициент м/мм.
м, м.
3.2.6. Определим реакции и .
Составим векторное уравнение равновесия всех сил, действующих на всю группу Ассура.
; .
Выберем масштаб плана сил м/мм.
Вычислим величины отрезков, соответствующих векторам сил. Данные занесем в табл. 2.
Строим план сил. В соответствии с векторным уравнением откладываем отрезки, соответствующие векторам . Векторы можно откладывать в любом порядке, но обязательно начать построение с вектора , а закончить построение вектором . Затем из начала вектора проводим направление вектора , а из конца вектора проводим направление вектора . Пересекаясь, эти направления замыкают многоугольник сил. Измеряя на плане сил отрезки, соответствующие векторам , , , , , и умножая их на масштаб , получим значение этих реакций. Данные занесены в табл. 2.
Таблица 2
| Обозначение силы | |||||||||||
| Величина силы, Н | 19,6 | 19,6 | 10,7 | 4,8 | 27 | 12,5 | 2,66 | 12 | 46,5 | 5,56 | 46 |
| Отрезок на плане, мм | 39 | 39 | 21 | 10 | 54 | 25 | 5 | 24 | 93 | 11 | 92 |
| Предпоследняя группа Ассура вида ВВВ м/мм | План сил для группы Ассура м/мм |
studfiles.net
Кинематические пары. Схемы механизмов
⇐ ПредыдущаяСтр 3 из 5Следующая ⇒
Кинематическая пара – подвижное соединение двух звеньев. Из теоретической механики известно, что твердое тело (рис. 3) в трехмерном пространстве имеет шесть степеней свободы: три поступательных и три вращательных.
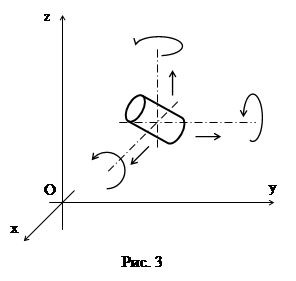 |
Если одно звено соприкасается с другим звеном, то, относительно этого звена оно лишается одной или нескольких степеней свободы. В подвижном соединении одно звено относительно другого может иметь максимум пять степеней свободы, минимум – одну степень свободы. В теории механизмов, вместо принятого в теоретической механике словосочетания «степень свободы», часто используют термин «подвижность» Можно сказать, что в соединении двух звеньев, каждое из этих звеньев накладывает на другое определенное число ограничений относительного перемещения – так называемых связей. Класс кинематической пары определяется числом независимых связей, накладываемых одним звеном на другое в их подвижном соединении. Таким образом, кинематические пары подразделяются на пять классов, а подвижность кинематической пары определяется формулой:
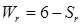 ,
, 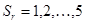 ,
,
где Sr – класс кинематической пары. Обозначение «r» в формуле указывает на то, что речь идет о связях и подвижностях одного звена относительно другого (лат. Relativus - относительный).
Кинематическая пара называется высшей, если контакт звеньев осуществляется по линии или в точке.
Кинематическая пара называется низшей, если звенья соприкасаются по поверхности.
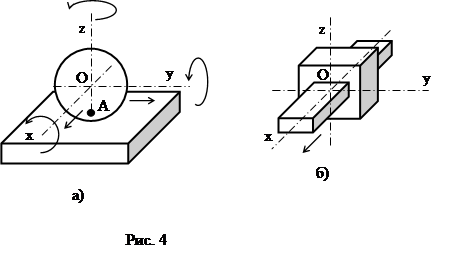 |
Пример 1
Кинематическая пара шар-плоскость (рис. 4,а) имеет первый класс, так как контакт шара и плоскости в точке A дает только одну связь (Sr = 1). Подвижность пары 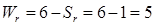 . Данная кинематическая пара является высшей.
. Данная кинематическая пара является высшей.
Пример 2
Поступательная кинематическая пара (рис. 4,б) имеет пятый класс ( 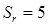 ) и является одноподвижной. Контакт звеньев в данной кинематической паре осуществляется по поверхностям, поэтому пара – низшая.
) и является одноподвижной. Контакт звеньев в данной кинематической паре осуществляется по поверхностям, поэтому пара – низшая.
В таблице 1 приведены графические и буквенные обозначения кинематических пар, которые используются при составлении схем механизмов.
Таблица 1
Структурная схема дает представление о структуре механизма (его звеньях и кинематических парах), на ней также указываются направления движений входных и выходных звеньев. Звенья на схеме нумеруются арабскими цифрами, причем стойка всегда обозначается цифрой «0». Проектирование механизма начинается с разработки его структурной схемы.
Кинематическая схема является более информативной: она содержит также сведения об основных геометрических размерах звеньев и выполняется в масштабе. Разработка кинематической схемы механизма осуществляется на основе его структурной схемы.
Классификация механизмов
Механизмы различаются по функциональному назначению, по конструктивному устройству, по расположению в пространстве, по наличию или отсутствию замкнутых кинематических контуров.
По функциональному назначению механизмы подразделяются на исполнительные, передаточные и программные.
· Исполнительные механизмы предназначены для приведения в движение рабочих органов машины в соответствии с выполняемым технологическим процессом.
· Передаточные механизмы служат для преобразования механической энергии двигателей в механическую энергию с параметрами, требуемыми для приведения в движение входных звеньев исполнительного механизма.
· Программные механизмы задают программу движения механической части машины.
Пример
Рассмотрим транспортную машину – автомобиль. Рабочими органами автомобиля являются колеса. Исполнительный механизм – шасси. Коробка передач – многоступенчатый передаточный механизм, необходимый для согласования работы двигателя и шасси в различных режимах движения машины. Двигатель автомобиля содержит газораспределительный механизм, который является программным (он управляет движением впускных и выпускных клапанов двигателя).
По конструктивному устройству различают рычажные, зубчатые, кулачковые и фрикционные механизмы.
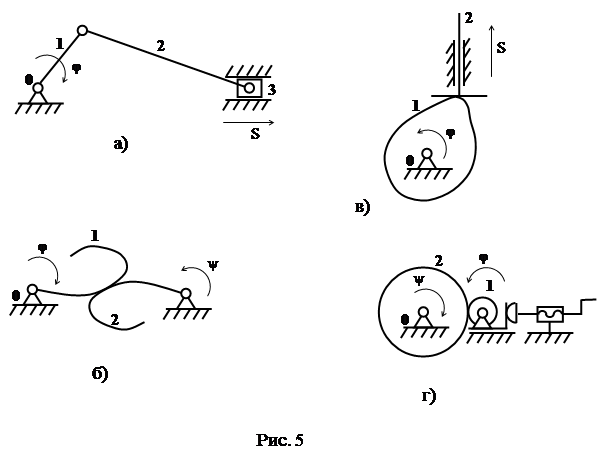
· Механизм, в котором все кинематические пары низшие, называется рычажным (рис. 5,а).
· В зубчатом механизме движение от одного звена к другому передается посредством зубчатого зацепления (рис. 5,б).
· Кулачковый механизм содержит звено со сложным профилем, называемое кулачком (рис 5,в).
· Во фрикционном механизме движение от одного звена к другому передается за счет сил трения (рис. 5,г; звенья вспомогательного винтового механизма, предназначенного для поджатия колеса 1, не пронумерованы).
Механизмы также могут быть комбинированными: например, зубчато-рычажный или зубчато-фрикционный механизмы.
 |
По расположению в пространстве механизмы подразделяются на плоские и пространственные.
· Механизм называется плоским, если траектории точек всех его подвижных звеньев находятся в плоскостях, параллельных неподвижной плоскости. На рис. 5 показаны структурные схемы плоских механизмов.
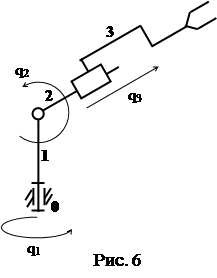
· Механизм называется пространственным, если траектории точек его подвижных звеньев лежат в непараллельных плоскостях. На рис. 6 приведена схема пространственного механизма – манипулятора, работающего в сферической системе координат.
 |
Механизм называется замкнутым, если каждое его звено образует, как минимум, две кинематические пары. Если есть хотя бы одно звено, образующее только одну кинематическую пару, механизм – разомкнутый.
Механизм называется одноконтурным, если он содержит один замкнутый кинематический контур. Если в механизме имеется более чем один замкнутый контур, то механизм – многоконтурный. На рис. 5 приведены схемы замкнутых одноконтурных механизмов; на рис. 6 – схема разомкнутого механизма, не имеющего замкнутых кинематических контуров.
Контрольные вопросы
1. Что называется кинематической парой?
2. Что называют подвижностями кинематической пары?
3. Как определяется класс кинематической пары?
4. Может ли кинематическая пара иметь класс выше пятого? Обоснуйте свой ответ.
5. Какие кинематические пары называются низшими? Высшими?
6. Чем отличается структурная схема механизма от его кинематической схемы?
7. Перечислите разновидности механизмов по функциональному назначению.
8. Какие механизмы называются рычажными?
9. Чем отличается плоский механизм от пространственного механизма?
10. Сформулируйте условие, в соответствии с которым механизм определяется как замкнутый.
11. Может ли разомкнутый механизм иметь замкнутые кинематические контуры? Обоснуйте свой ответ.
ЛЕКЦИЯ 3
Плоские четырехзвенные рычажные механизмы. Наименования звеньев рычажных механизмов. Степени свободы механизмов. Универсальные структурные формулы. Основные и местные подвижности в механизмах.
Читайте также:
lektsia.com
423800, Набережные Челны , база Партнер Плюс, тел. 8 800 100-58-94 (звонок бесплатный)






