Работа №1

ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ГРУЗОПОДЪЕМНОГО
УСТРОЙСТВА

1. Исходные данные

Принципиальная схема грузоподъемного
устройства.

Варианты заданий для расчета (приложение
1).

Данные для выбора каната, барабана,
электродвигателя и редуктора (приложения
2 …5).

2. Задание

2.1. Изобразить схему грузоподъемного
устройства.

2.2. Определить максимальное натяжение
каната F_max
и подобрать канат.

2.3. Определить размеры барабана.

2.4. Подобрать электродвигатель.

2.5. Подобрать редуктор.

3. Рекомендации по выполнению.

3.1. Схема грузоподъемного устройства.

Рис.1 – Схема лебедки (механизма подъема):
1– электродвигатель, 2 – соединительная
муфта с колодочным тормозом, 4 –
двухступенчатый редуктор, 5 – канатный
барабан, 6 – канат, 7 – направляющий
блок, 8 – неподвижные блоки, 9 – подвижные
блоки полиспаста, F_нб
– усилие в канате, набегающем на барабан,
Q – масса поднимаемого
груза.

Барабан 5 лебедки приводится в движение
электродвигателем 1 через муфты 2, 4 и
редуктор 3. Наружная поверхность одной
из полумуфт муфты 2 используется в
качестве тормозного шкива двухколодочного
тормоза.

Редуктор необходим для увеличения
крутящего момента электродвигателя

М_вм = М_дв i_рh_р,
(1)

где М_вм – крутящий момент на
ведомом валу редуктора, момент,
передаваемый на барабан лебедки, М_дв
– крутящий момент на валу электродвигателя;
i_p –
передаточное число редуктора; h_р
– КПД редуктора.

Полиспасты в грузоподъемных машинах
служат для выигрыша в силе, т.е. получения
минимально возможного натяжения каната,
набегающего на барабан лебедки. Это
позволяет уменьшить диаметры каната и
барабана.

Основной характеристикой полиспаста
является его кратность. Кратность
полиспаста (его передаточное отношение)
определяется отношением числа ветвей
каната, на которых подвешен груз, к числу
ветвей, подходящих к барабану или
отношением скоростей барабана и груза.

(2)

где v_бар – окружная
скорость барабана лебедки, v_гр
– скорость подъем груза.

Кратность
полиспаста назначается по грузоподъемности
машины.

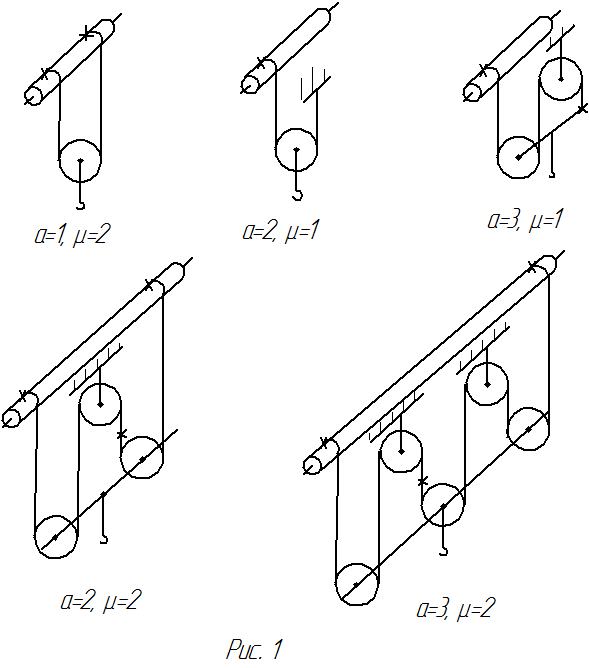
На рис.2 приведена схема одинарного
четырех кратного полиспаста.

На рис. 3 показаны схемы сдвоенных
полиспастов с различной кратностью.

Максимальное
разрывное усилие каната, по которому в
стандартах на канаты выбирается его
диаметр (см. приложение 2),

(3)

где
F_нб
– статическое усилие в набегающей на
барабан ветви каната;

k
– запас прочности каната (см. табл. 2).

Статическое
усилие (без учета динамических нагрузок)
в набе­гающей на барабан ветви каната
полиспаста

(4)

где
Q – грузоподъемность крана;

G_п
– масса крюковой подвески с навешиваемыми
приспособлениями, G_п
=0,02Q;

n_гр
– число ветвей полиспаста, на которых
подвешен груз;

– к.
п. д. полиспаста.

Величина
к.п.д. полиспаста зависит от к.п.д. блоков
и их числа n_бл

в полиспасте.

К.п.д.
полиспастов
с блоками на подшипниках качения, для
которых к.п.д. блока h
_бл
=
0,98, приведены в табл.1:

Таблица
1

Кратность — полиспаст — Большая Энциклопедия Нефти и Газа, статья, страница 2

Cтраница 2

По окончательно принятой кратности полиспаста определяются пределы изменения усилий Si в замыкающих канатах ( фиг.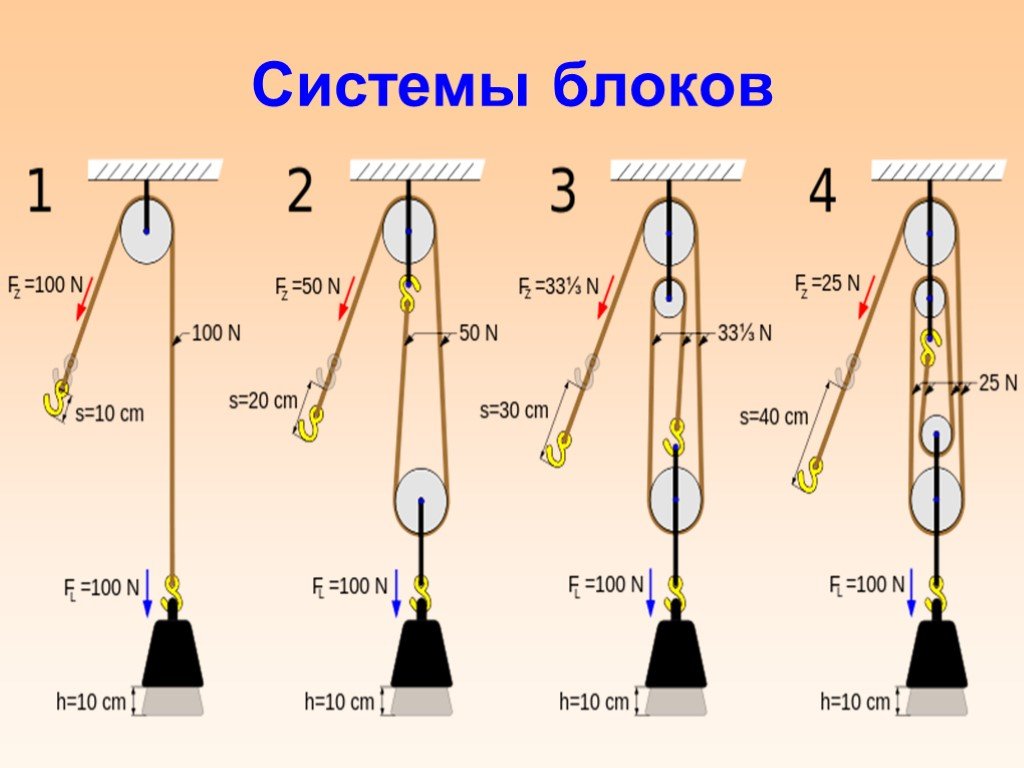
 [16]

Что такое кратность полиспаста и как она определяется. Как определяется КПД полиспаста.
 [17]

ПОл — кратность полиспаста; ц — КПД полиспаста.
 [18]

Что такое кратность полиспаста и как она определяется.
 [19]

Чем отличается кратность полиспаста в зависимости от того, сбегает канат с подвижного или неподвижного блока.
 [20]

С увеличением кратности полиспаста улучшается зачерпывающая способность грейфера, но увеличивается время зачерпывания. Установка вибраторов на челюстях содействует внедрению челюстей в материал. Зубья на челюстях могут быть полезными только для сильно слежавшихся — и смерзшихся материалов.
 [21]

При выборе кратности полиспаста необходимо учитывать, что скорость подъема груза также обратно пропорциональна этой кратности. Высота подъема груза полиспастом зависит от длины запасованного каната.
 [22]

Что называется кратностью полиспаста.
 [23]

Тип каната и кратность полиспаста взаимосвязаны с общей компоновкой механизма и его параметрами; увеличение кратности полиспаста дает возможность использовать канаты, барабаны и блоки меньшею диаметра, что позволяет уменьшить передаточное число редуктора и снизить массу и габариты машины, но одновременно требует увеличения длины каната и канатоемкости барабана. Увеличение числа блоков при повышении кратности полиспаста вызывает также возрастание потерь энергии и необходимость некоторого увеличения мощности, затрачиваемой на подъем груза вследствие уменьшения КПД полиспаста.
 [24]

По мере увеличения кратности полиспаста и, следовательно, большего выигрыша в силе сопротивление сжатию охваченного челюстями материала преодолевается меньшим усилием в замыкающем канате, которое направлено вверх.
 [25]

Пу тем изменения кратности полиспаста с целью получения примерно одинаковых крутящих моментов от груза и потребной мощности двигателя достигается унификация механизмов подъема машин различной грузоподъемности.
 [27]

Следовательно, выражение кратности полиспаста ап есть частное от деления числа ветвей, на которых висит груз, на число ветвей каната, наматываемых на барабан.
 [29]

Что понимают под кратностью полиспаста.
 [30]

Страницы:  

   1

   2

   3

   4

   5

римановых поверхностей — Слои в алгебраической геометрии: кратность

На самом деле я не алгебраический геометр, поэтому в своем ответе я буду придерживаться простой ситуации, когда $f\colon X\to Y$ является конечным сюръективным морфизмом между гладкими неприводимые многообразия над $k$. Оба ваших примера попадают в эту категорию.

Если $x\in X$ — точка (не обязательно замкнутая) и $y = f(x)$, то кратность, которую вы, вероятно, ищете, — это целое число, которое я обозначу как $m_f(x)$, что равно $$m_f(x):= \dim_{\kappa(y)}\mathcal{O}_{X,x}/\mathfrak{m}_y\mathcal{O}_{X,x} = \ dim_{\kappa(y)}\mathcal{O}_{X,x}\otimes_{\mathcal{O}_{Y,y}}\kappa(y),$$, где здесь вы используете $f$ для превратить $\mathcal{O}_{X,x}$ в $\mathcal{O}_{Y,y}$-модуль.

Другой способ вычисления этого числа заключается в следующем. Определенное ранее пространство $X_y$ является схемой, и его общие точки соответствуют прообразам пространства $y$. Если $x$ — точка общего положения $X_y$, то $\mathcal{O}_{X_y,x}$ — артиново кольцо, и можно взять его длину, которую я буду обозначать $v_f(x):= длина\,\mathcal{O}_{X_y,x}$. Тогда можно вывести $m_f(x) = v_f(x)\times [\kappa(x):\kappa(y)]$. В обоих ваших примерах $x$ и $y$ были замкнутыми точками, поэтому $\kappa(x) = \kappa(y) = k$, а множитель $[\kappa(x):\kappa(y) ]$ равно $1$. Таким образом, $m_f(x) = v_f(x)$. 92)$, длина которого составляет $2$. Таким образом, $v_f(x) = m_f(x) = 2$.

Второй пример устроен аналогично. Тот факт, что $x$ и $y$ являются или не являются делителями, не имеет никакого значения.

Можно показать, что в конкретной ситуации, которую я рассматриваю (конечный морфизм между гладкими многообразиями), каждая (не обязательно замкнутая) точка $y\in Y$ имеет одинаковое количество прообразов при подсчете с кратностью $m_f$, и это целое число является степенью $d$ отображения $f$. Набросок доказательства этого факта таков: конечные морфизмы между гладкими неприводимыми многообразиями над любым алгебраически замкнутым полем плоские, поэтому $f_*\mathcal{O}_X$ является локально свободным $\mathcal{O}_Y$ -модуль ранга $d$. Слой $f_*\mathcal{O}_X$ в $y\in Y$ в точности равен $\bigoplus_{f(x) = y} \mathcal{O}_{X,x}/\mathfrak{m} _y\mathcal{O}_{X,x}$, так что $$d = \sum_{f(x) = y} \dim\mathcal{O}_{X,x}/\mathfrak{m}_y \mathcal{O}_{X,x} = \sum_{f(x) = y} m_f(x).$$ 9{-1}(D)$ и $n_i = v_f(x_i)$. Конечно, если и $X$, и $Y$ являются кривыми, то дивизоры являются замкнутыми точками, а $m_f = v_f$ в замкнутых точках, поэтому в частном случае кривых $n_i$ должно задаваться как $m_f$.

Взаимосвязи диаграмм классов UML с примерами

Диаграммы классов являются основными строительными блоками объектно-ориентированного моделирования, поэтому важно понимать различные взаимосвязи диаграмм классов и то, как они влияют на ваше решение. Мы перечислили их ниже с примерами.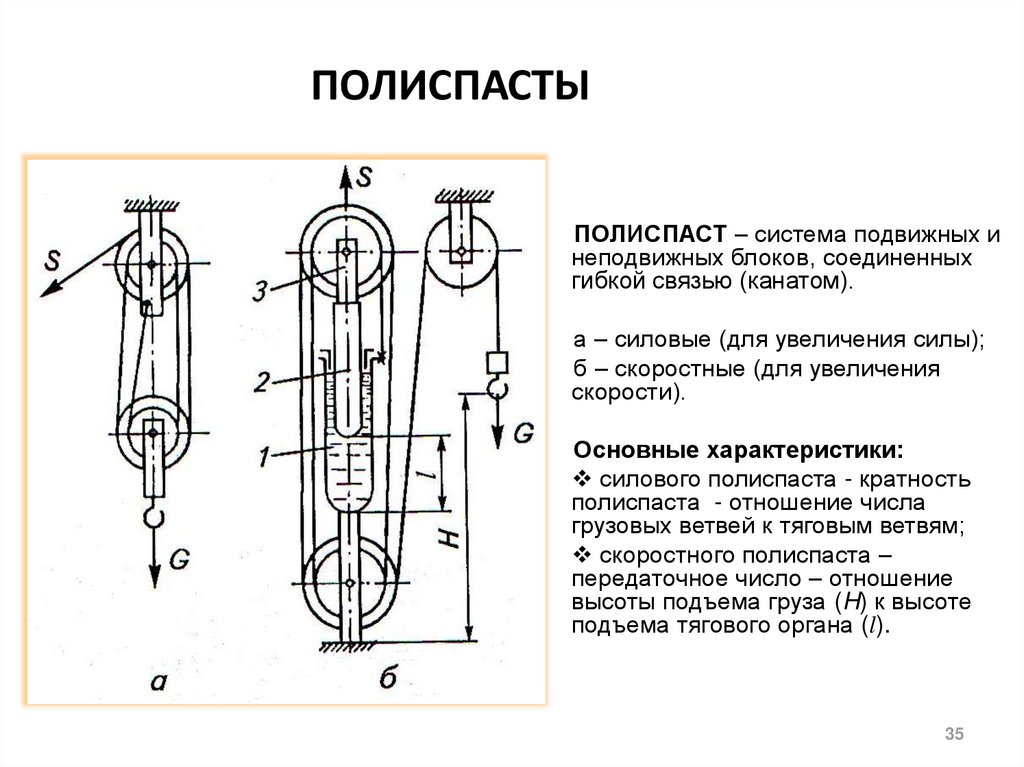

Creately упрощает создание диаграмм классов, показывая логическую связь на основе контекста.

Создайте диаграмму классов >>

Диаграмма классов Отношения

Классы определенным образом связаны друг с другом. В частности, отношения на диаграммах классов включают различные типы логических связей. Возможны следующие типы логических соединений в UML:

• Ассоциация
• Направленная ассоциация
• Рефлексивная ассоциация
• Кратность
• Агрегация
• Состав
• Наследование/Обобщение
• Реализация

Отношения в диаграммах классов UML

Ассоциация

Ассоциация

— это широкий термин, охватывающий почти любую логическую связь или связь между классами. Например, пассажиры и авиакомпания могут быть связаны, как указано выше.

Направленная ассоциация

Направленная ассоциация

относится к направленной связи, представленной линией со стрелкой.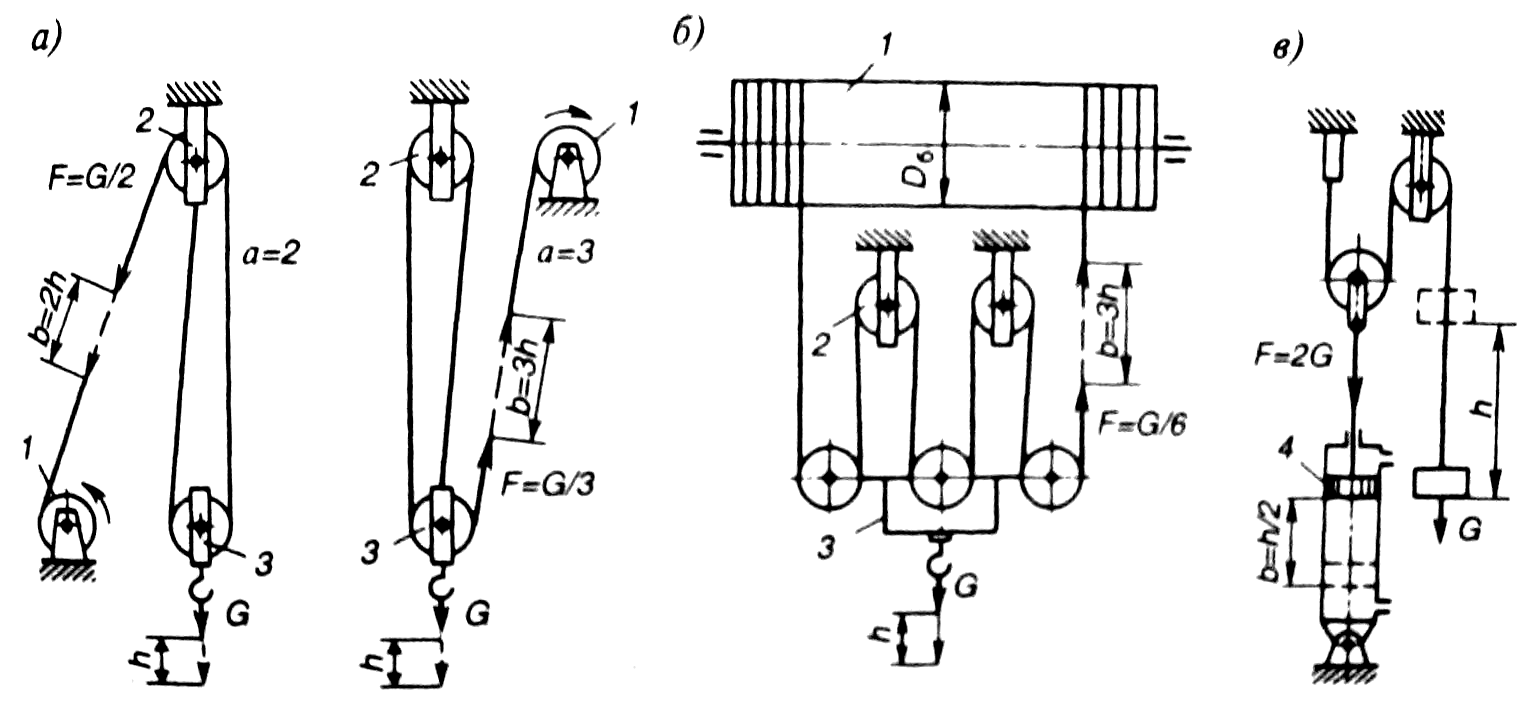 Стрелка изображает направленный поток, содержащий контейнер.

Рефлексивная ассоциация

Рефлексивная ассоциация

Это происходит, когда класс может иметь несколько функций или обязанностей. Например, сотрудник, работающий в аэропорту, может быть пилотом, авиационным инженером, билетным диспетчером, охранником или членом ремонтной бригады. Если член ремонтной бригады управляется авиационным инженером, в двух экземплярах одного и того же класса может существовать взаимосвязь «управление по».

Множественность

Множественность

является активной логической ассоциацией, когда изображается кардинальность класса по отношению к другому. Например, один парк может включать несколько самолетов, в то время как один коммерческий самолет может содержать от нуля до многих пассажиров. Обозначение 0..* на диаграмме означает «ноль ко многим».

Агрегация

Агрегация

относится к формированию определенного класса в результате агрегирования одного класса или создания коллекции. Например, класс «библиотека» состоит из одной или нескольких книг, среди прочих материалов. В совокупности содержащиеся классы не сильно зависят от жизненного цикла контейнера. В том же примере книги останутся таковыми даже при расформировании библиотеки. Чтобы показать агрегацию на диаграмме, нарисуйте линию от родительского класса к дочернему классу с ромбом рядом с родительским классом.

Чтобы показать агрегацию на диаграмме, проведите линию от родительского класса к дочернему классу с ромбом рядом с родительским классом.

Состав

Состав

Отношение композиции очень похоже на отношение агрегации. с той лишь разницей, что его основная цель состоит в том, чтобы подчеркнуть зависимость содержащегося класса от жизненного цикла класса-контейнера. То есть содержащийся класс будет уничтожен при уничтожении класса-контейнера. Например, боковой карман наплечной сумки также перестанет существовать после уничтожения наплечной сумки.

Чтобы показать связь композиции на диаграмме UML, используйте линию направления, соединяющую два класса, с закрашенным ромбом, примыкающим к классу-контейнеру, и стрелкой направления к содержащемуся классу.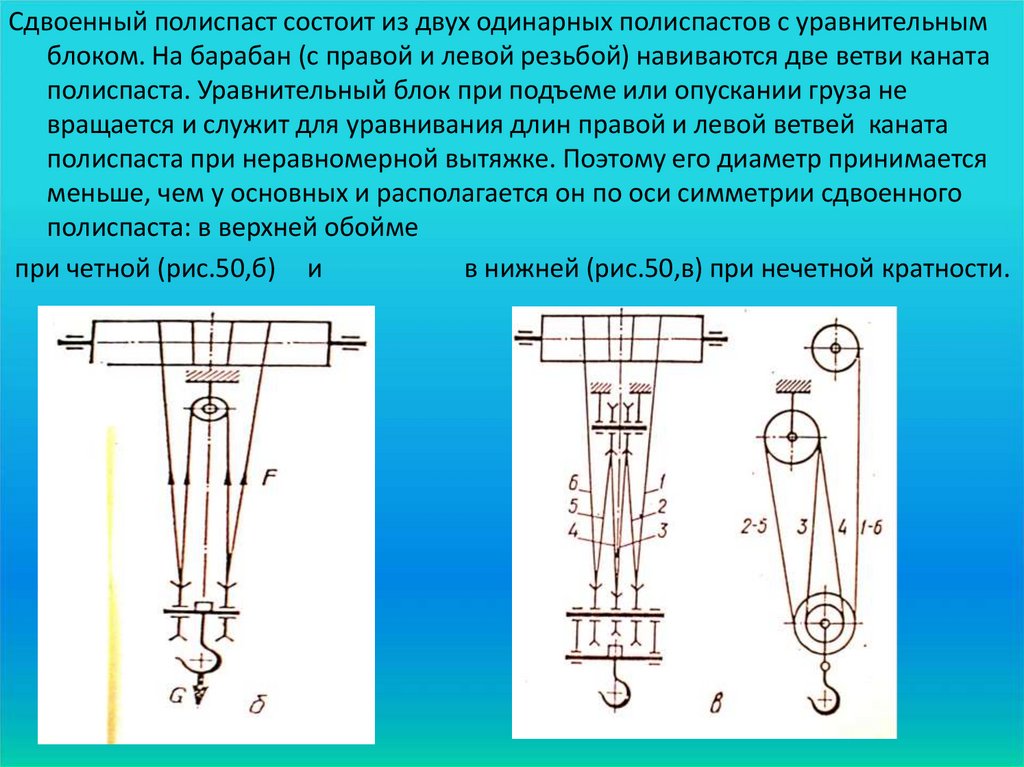

Наследование/обобщение

Наследование

относится к типу отношений, в которых один связанный класс является дочерним по отношению к другому в силу принятия тех же функций родительского класса. Другими словами, дочерний класс — это особый тип родительского класса. Чтобы показать на диаграмме UML наследование, сплошная линия от дочернего класса к родительскому классу рисуется с помощью незакрашенной стрелки.

Реализация

Реализация

обозначает реализацию функциональности, определенной в одном классе, другим классом. Чтобы показать взаимосвязь в UML, прерывистая линия с незакрашенной сплошной стрелкой рисуется из класса, определяющего функциональность класса, реализующего функцию. В этом примере настройки печати, заданные с помощью интерфейса настройки принтера, реализуются принтером.

Рисование диаграмм классов с помощью Creately

Мы много думали об отношениях, когда создавали инструменты для построения диаграмм классов. Наши коннекторы подстраиваются под контекст и показывают только самые логичные отношения при соединении классов. Это значительно уменьшило ваши шансы на ошибку.

Создать диаграмму классов

Рисование с нуля может быть громоздким. Вы можете сразу приступить к работе, используя наши профессионально разработанные диаграммы классов. Просмотрите наши примеры диаграмм классов и выберите тот, который тесно связан с вашей системой.

Что такое диаграммы классов?

Диаграммы классов являются основным строительным блоком в объектно-ориентированном моделировании. Они используются для отображения различных объектов в системе, их атрибутов, операций и взаимосвязей между ними.

На следующем рисунке показан пример простого класса:

Простая диаграмма классов с атрибутами и операциями (Нажмите на шаблон, чтобы редактировать его онлайн)

В примере изображен класс под названием «кредитный счет». Классы на диаграммах классов представлены прямоугольниками, разделенными на три части:

1. Верхний раздел содержит имя класса.
2. Средняя часть содержит атрибуты класса.
3. В нижнем разделе показаны возможные операции, связанные с классом.

Пример показывает, как класс может очень систематически и четко инкапсулировать все важные данные конкретного объекта. Диаграмма классов — это набор классов, подобных приведенному выше.

Есть еще вопросы о взаимосвязях диаграмм классов?

Надеюсь, я ясно объяснил различные отношения между диаграммами классов. Они не так сложны, как вы думаете, и их можно освоить после некоторой практики. А с помощью нашего инструмента у вас не должно возникнуть проблем с диаграммами классов. Если у вас есть еще вопросы, не стесняйтесь задавать их в разделе комментариев. Кроме того, ознакомьтесь с этим руководством по типам диаграмм UML с примерами для дальнейшего чтения.

Ссылки:

1. Основы UML: диаграмма классов Введение в структурные диаграммы в UML 2 Дональда Белла

2. Диаграмма классов, опубликованная на веб-сайте Википедии

3. Часть 1 диаграммы классов UML, опубликованная на веб-сайте developer.com

4. Диаграмма классов из Visual Case Tool — UML Tutorial, опубликованная на веб-сайте Visual Case

5.  Ассоциации, опубликованные на веб-сайте Sybase

Как визуализировать отношения диаграммы классов UML?

Отношения диаграммы классов UML можно визуализировать с помощью различных типов стрелок и символов, в зависимости от типа отношения. Например, отношения наследования представлены сплошной линией со стрелкой, указывающей на родительский класс, а отношения ассоциации представлены сплошной линией без стрелки.

Может ли класс UML иметь несколько отношений с другими классами?

Да, класс UML может иметь несколько отношений с другими классами, включая наследование, ассоциацию, агрегацию и композицию.

Какова цель использования отношений диаграммы классов UML?

Целью использования отношений диаграммы классов UML является моделирование взаимодействия между различными классами в системе, помогающее гарантировать, что система спроектирована логичным и эффективным образом.