|
КГТУ им. А.Н.Туполева каф. АиАХ
| |
|---|---|
|
|
ТЕМА 7
Карданная передача предназначена для передачи
Карданная передача чаще всего соединяет ведомый
Коробка передач крепится на раме (кузове), а ведущий
Примеры расположения карданных передач показаны на
Карданные шарниры это устройства, обеспечивающие
Жесткий карданный шарнир неравных угловых
При повороте вала 1 вокруг своей оси на угол
Соотношение между углами определяется выражением tg
Чтобы избежать неравномерного вращения ведущих колес
γ1
Углы γ
Упругие карданные шарниры устанавливают при
Одновременно эти элементы выполняют функции
Типовая конструкция карданного вала показана на
Карданные шарниры равных угловых скоростей
На рис 7.5 изображен шариковый карданный
При этом, в передаче момента участвуют только два
º.
На рис 7.6 показана другая конструкция
На рис 7.6а показаны детали шарнира, а на рис 7.6б
º.
На рис 7.7 показан третий тип карданного
Здесь изображен шарнир привода ведущего управляемого
Можно привести еще много конструктивных решений
|
|
| |
|
| |
|
| |
|
| |
|
| |
|
Рис. 7.8. Привод переднего колеса автомобиля «ВАЗ»–2121, «Нива»:
| |
|
|
|
ИНСТРУКЦИЯ К ЛАБОРАТОРНО-ПРАКТИЧЕСКОЙ РАБОТЕ «Промежуточные соединения и карданные передачи » | Учебно-методический материал:
ИНСТРУКЦИЯ К ЛАБОРАТОРНОПРАКТИЧЕСКОЙ РАБОТЕ
по МДК 01. 02 Эксплуатация и техническое обслуживание сельскохозяйственных машин и оборудования.
02 Эксплуатация и техническое обслуживание сельскохозяйственных машин и оборудования.
1.Тема: Промежуточные соединения и карданные передачи
2.Цель работы: Познакомиться с конструкцией и принципом действия промежуточных соединений и карданных передач.
3. Порядок выполнения
3.1 Прочитать общие сведения
3.2 На формате А4, оформленном рамкой и основной надписью, записать тему, цель работы, задание с исходным данными (по указанному варианту)
3.3 Дать описание принципа работы промежуточных соединений (карданных передач).
3.4 Выполнить схему промежуточных соединений (карданных передач)и указать их основные элементы.
3.5 По представленному ниже описанию произвести разборку и сборку промежуточных соединений (карданных передач) по указанному варианту.
4. Время выполнения работы: 6 часов
5.Общие сведения
Промежуточные соединения
Предназначены для передачи вращательного движения от одного вала к другому, оси которых совпадают.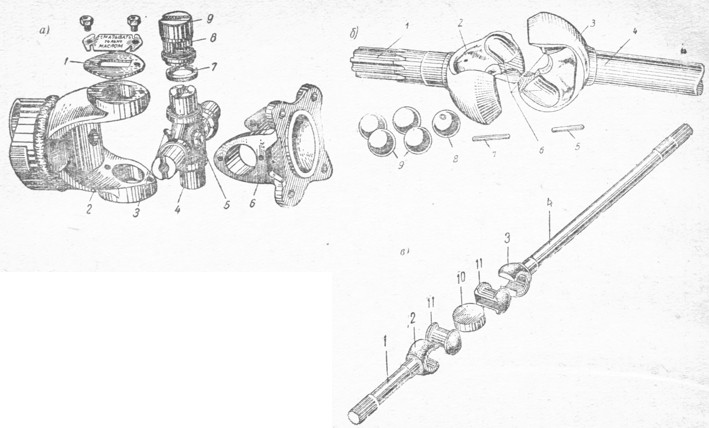 Однако несоосность валов может возникнуть при неточностях изготовления, погрешностях сборки, деформации рам и корпусов, а также изменении взаимного расположения сборочных единиц в процессе эксплуатации.
Однако несоосность валов может возникнуть при неточностях изготовления, погрешностях сборки, деформации рам и корпусов, а также изменении взаимного расположения сборочных единиц в процессе эксплуатации.
Соединяя валы не жестко, а специальными шарнирами, уменьшают вредные нагрузки на детали, возникающие от несоосности валов, и этим повышают их долговечность.
В гусеничных тракторах коробка передач и задний мост обычно расположены в одном корпусе или их корпуса жестко соединены один с другим, а двигатель же с муфтой сцепления установлен на раме отдельно. Поэтому необходимо промежуточное соединение между валами муфты сцепления и коробки передач, так как их несоосность может возникнуть от перекоса при установке двигателя с муфтой сцепления на раму.
В полурамных колесных трактоpax корпуса муфты сцепления, коробки передач и заднего моста жестко соединены между собой и образуют остов. Возможная несоосность валов муфты сцепления и коробки передач здесь значительно меньше.
Поэтому требования к промежуточным соединениям, а соответственно и конструкция последних различные.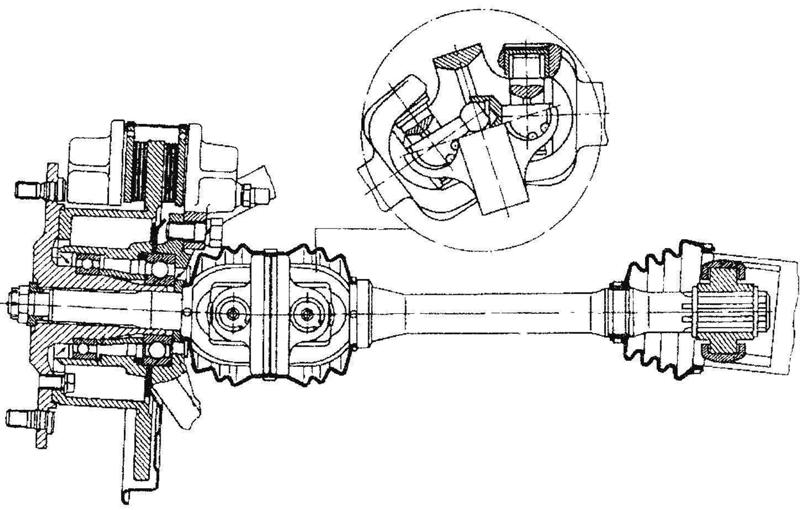 Длина этих соединений постоянна.
Длина этих соединений постоянна.
По числу шарниров промежуточные соединения делят на одинарные и двойные, т. е. с одним или двумя шарнирами.
По конструкции шарниров соединения могут быть Жесткие, Мягкие (упругие) и Комбинированные. Жесткие шарниры состоят только из металлических деталей, а мягкие имеют упругие неметаллические элементы.
Одинарное упругое промежуточное соединение с резиновыми элементами, работающими на сжатие, применяют на тракторах ЮМЗ-6Л и ЮМЗ-6М для соединения вала муфты сцепления с первичным валом коробки передач. Передняя вилка этого соединения выполнена как единое целое с валом 1 (рис. 1) муфты сцепления, а задняя — аналогично с первичным валом 2 коробки передач. Вилки расположены крестообразно. В четыре свободных промежутка между ними (по окружности) вложены резиновые элементы 3, удерживаемые от выпадения прижимами 4 с болтами 5.
Двойное упругое промежуточное соединение устанавливают на тракторах ДТ-75МВ и ДТ-175С. Основная часть такого соединения — две головки, каждая из которых
представляет собой два соединенных заклепками и сваркой штампованных диска 2 (рис. 2), в цилиндрические гнезда которых предварительно вставлены металлические втулки 4 с упругими элементами 1. Упругие элементы изготовлены из резины и для большей прочности снаружи покрыты несколькими слоями прорезиненной ткани, а внутрь их завулканизиро-ваны цилиндрические каркасы из металлической сетки. Металлические втулки 4 выступающими наружу поясками вставляют в отверстия вилок 3, 6 и крепят к ним болтами 5 с корончатыми гайками и шплинтами. Головки соединяют между собой с помощью вилок, одна из которых (3) имеет наружные, а другая (6) — внутренние шлицы. Переднюю наружную вилку соединяют с валом муфты сцепления, а заднюю наружную (6) устанавливают на шлицевой конец ведущего вала ходоуменьшителя или реверс-редуктора (в тракторах ДТ-75МБ), первичного вала коробки передач (ДТ-75МВ), вала насосного колеса гидротрансформатора (ДТ-175С).
2), в цилиндрические гнезда которых предварительно вставлены металлические втулки 4 с упругими элементами 1. Упругие элементы изготовлены из резины и для большей прочности снаружи покрыты несколькими слоями прорезиненной ткани, а внутрь их завулканизиро-ваны цилиндрические каркасы из металлической сетки. Металлические втулки 4 выступающими наружу поясками вставляют в отверстия вилок 3, 6 и крепят к ним болтами 5 с корончатыми гайками и шплинтами. Головки соединяют между собой с помощью вилок, одна из которых (3) имеет наружные, а другая (6) — внутренние шлицы. Переднюю наружную вилку соединяют с валом муфты сцепления, а заднюю наружную (6) устанавливают на шлицевой конец ведущего вала ходоуменьшителя или реверс-редуктора (в тракторах ДТ-75МБ), первичного вала коробки передач (ДТ-75МВ), вала насосного колеса гидротрансформатора (ДТ-175С).
Небольшие несоосность и перекос валов компенсируют установленные упругие резиновые элементы и крестообразно расположенные вилки.
Одинарное упругое промежуточное соединение
Рис. 1 — Одинарное упругое промежуточное соединение:
1 — Одинарное упругое промежуточное соединение:
1 — вал муфты сцепления; 2 — первичный вал коробки передач; 3 — резиновый элемент; 4 — прижим; 5 — болт.
Головка двойного упругого промежуточного соединения
Рис. 2 — Головка двойного упругого промежуточного соединения:
1 — упругий элемент; 2 – диски; 3 – внутренняя вилка; 4 – втулка; 5 – болт; 6 — наружная задняя вилка
Одинарное жесткое промежуточное соединение представляет собой соединение двух шлицевых валов с помощью втулки, имеющей внутренние шлицы, или непосредственно между собой. В последнем случае один вал имеет наружные, а другой — внутренние шлицы. Такие соединения применяют на тракторах Т-150, Т-150К, МТЗ-100, МТЗ-102.
Комбинированное промежуточное соединение двигателя с трансмиссией применено на тракторе К-701.
Карданная передача
Карданная передача служит для передачи крутящего момента от ведомого вала коробки передач или раздаточной коробки к ведущему валу главной передачи. Ее применение связано с тем, что изменяется взаимное положение осей валов трансмиссии, и они не лежат на одной прямой.
Ее применение связано с тем, что изменяется взаимное положение осей валов трансмиссии, и они не лежат на одной прямой.
Коробка передач 1 (рис. 3, а), или раздаточная коробка на автомобиле, установлена выше ведущего моста 7, в результате чего ось карданного вала 5, передающего крутящий момент, расположена под некоторым углом а к горизонтали. Коробка передач соединена с рамой неподвижно, а ведущий мост подвешен к ней при помощи рессор. Когда при прогибе рессор изменяется положение моста относительно рамы, изменяется и угол наклона карданного вала 5.
Карданная передача состоит из трех основных элементов: карданных шарниров 2, карданных валов 3 и 5 и промежуточной опоры 4. Одним из условий равномерного вращения вала 6 главной передачи ведущего моста 7 является равенство углов и ось между осью вала 5 и осями валов 3 и 6, что обеспечивается конструкцией передачи.
Схема карданной передачи (а) с шарнирами (б) неравных угловых скоростей
Рис. 3 — Схема карданной передачи (а) с шарнирами (б) неравных угловых скоростей
Карданные шарниры неравных угловых скоростей. Простейший карданный шарнир состоит из двух вилок 8 и 10 (рис. 3, б) укрепленных на валах 3 и 5, и крестовины 9 с шипами, входящими в отверстия вилок и соединяющими шарнирно валы. Вилка 10, поворачиваясь относительно оси А—А, может одновременно с крестовиной поворачиваться относительно оси Б—Б, обеспечивая передачу вращения от одного вала к другому при изменении угла между осями валов. Такой карданный шарнир называется Жестким шарниром неравных угловых скоростей. В нем при равномерном вращении ведущей вилки 8 ведомая вилка 10 вращается неравномерно: в течение одного оборота она дважды обгоняет ведущую вилку и дважды отстает от нее. В результате этого возникают дополнительные нагрузки, вызывающие изнашивание деталей шарнирного соединения и узлов трансмиссии.
Простейший карданный шарнир состоит из двух вилок 8 и 10 (рис. 3, б) укрепленных на валах 3 и 5, и крестовины 9 с шипами, входящими в отверстия вилок и соединяющими шарнирно валы. Вилка 10, поворачиваясь относительно оси А—А, может одновременно с крестовиной поворачиваться относительно оси Б—Б, обеспечивая передачу вращения от одного вала к другому при изменении угла между осями валов. Такой карданный шарнир называется Жестким шарниром неравных угловых скоростей. В нем при равномерном вращении ведущей вилки 8 ведомая вилка 10 вращается неравномерно: в течение одного оборота она дважды обгоняет ведущую вилку и дважды отстает от нее. В результате этого возникают дополнительные нагрузки, вызывающие изнашивание деталей шарнирного соединения и узлов трансмиссии.
Для устранения неравномерного вращения применяют два одинаковых карданных шарнира, причем их вилки, расположенные на противоположных концах карданного вала, должны лежать в одной плоскости. Тогда неравномерность, вызываемая одним карданным шарниром, компенсируется неравномерностью другого.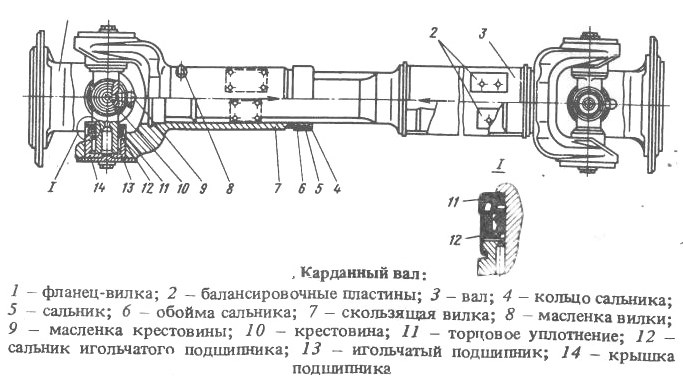 Однако и при двух карданных шарнирах угол между осями валов не должен превышать —23°.
Однако и при двух карданных шарнирах угол между осями валов не должен превышать —23°.
При движении автомобиля в результате прогиба рессор расстояние между коробкой передач и задним мостом изменяется, поэтому на валу одну из вилок карданного шарнира устанавливают на шлицах, чтобы длина карданного вала также могла изменяться.
В карданных передачах легковых автомобилей наряду с жесткими шарнирами неравных угловых скоростей применяют и Мягкие карданные шарниры, имеющие упругий элемент в виде муфты из эластичного материала, упругая деформация которого позволяет не только передавать крутящий момент между валами, пересекающимися под углом 2—5°, но и защищает трансмиссию от жестких ударов. Примером такой передачи может служить карданная передача автомобилей ВАЗ-2105, -2107 и др. Она состоит из переднего и заднего карданных валов, промежуточной опоры и трех шарниров, из которых передний представляет собой упругий элемент, соединяющий ведомый вал коробки передач с передним валом карданной передачи.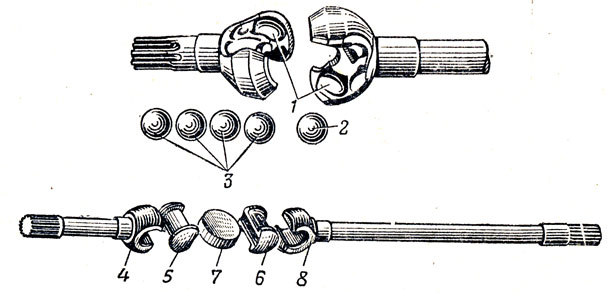
Карданные шарниры равных угловых скоростей. Условия работы карданных передач определяются в первую очередь углами наклона осей их валов (см. рис. 3, а): чем больше эти углы, тем в более тяжелых условиях работает передача. В особо тяжелых условиях работает карданная передача ведущих управляемых колес переднеприводных автомобилей, у которых угол наклона осей валов, изменяясь по величине и направлению (при повороте автомобиля), может достигать 35-40°. В таких передачах применяют
шарниры равных угловых скоростей (шариковые или кулачковые), обеспечивающие передачу крутящего момента, равномерное вращение ведомого вала и поворот управляемых колес.
Широкое распространение получили карданные шариковые шарниры (рис. 4, а) с делительными канавками. Они состоят из двух вилок 1 и 4, пяти шариков 9 и штифта 7. Вилки 1 и 4 изготовлены заодно целое со шлицевыми валами 5. При помощи торцовых сферических углублений и центрального шарика 8 вилки центрируются между собой. Положение шарика 8 фиксируется штифтом 7, удерживаемым от осевых смещений шпилькой 6.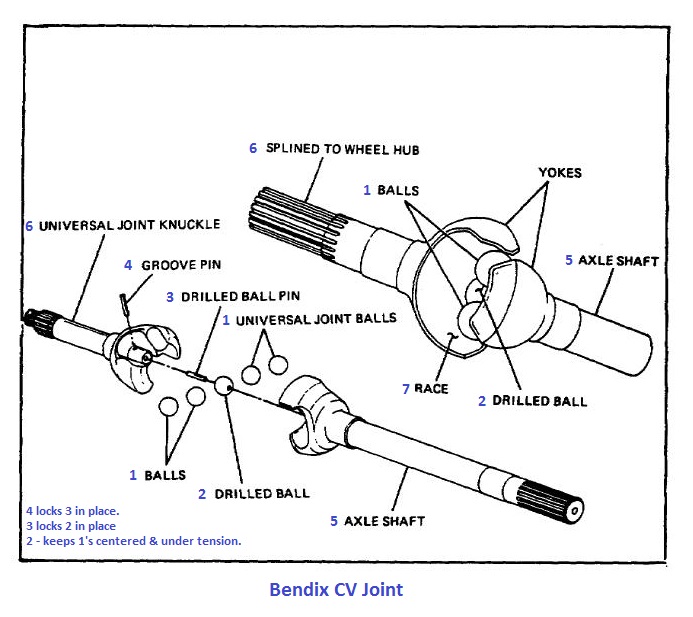 В делительные канавки 2 и 3 вилок закладываются четыре рабочих шарика 9, которые удерживаются от выкатывания из делительных канавок центральным шариком 8.
В делительные канавки 2 и 3 вилок закладываются четыре рабочих шарика 9, которые удерживаются от выкатывания из делительных канавок центральным шариком 8.
При вращении ведущего вала крутящий момент от оддой вилки к другой передается через рабочие шарики. Делительные канавки имеют такую форму, которая независимо от угловых перемещений вилок обеспечивает расположение шариков в плоскости, делящей пополам угол между осями вилок, в результате чего оба вала вращаются с равными угловыми скоростями.
Наряду с шариковыми шарнирами часто применяют и кулачковые шарниры (рис. 4, б) равных угловых скоростей. Они состоят из двух вилок 10 и 14, двух кулаков 11 и 13 и диска 12. Диск заходит в пазы кулаков и передает вращение от ведущей вилки к ведомой. В вертикальной плоскости вилки поворачиваются вокруг кулаков, а в горизонтальной — вместе с кулаками вокруг диска. Кулачковый карданный шарнир работает подобно двум сочлененным жестким карданным шарнирам, из которых первый создает неравномерность вращения, а второй устраняет эту неравномерность.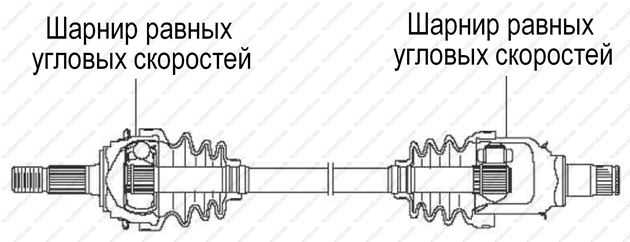 Этим и достигается вращение ведущего и ведомого валов с равными угловыми скоростями.
Этим и достигается вращение ведущего и ведомого валов с равными угловыми скоростями.
Из-за простоты конструкции и сравнительно высокой работоспособности шариковые и кулачковые карданные шарниры нашли широкое применение в приводах к ведущим управляемым колесам многих автомобилей (ЗИЛ-131, ГАЗ-66-11, КамАЗ-4310, ВАЗ-2108 «Спутник»).
Карданные шарниры равных угловых скоростей: а — шариковый; б — кулачковый
Рис. 4 — Карданные шарниры равных угловых скоростей: а — шариковый; б — кулачковый
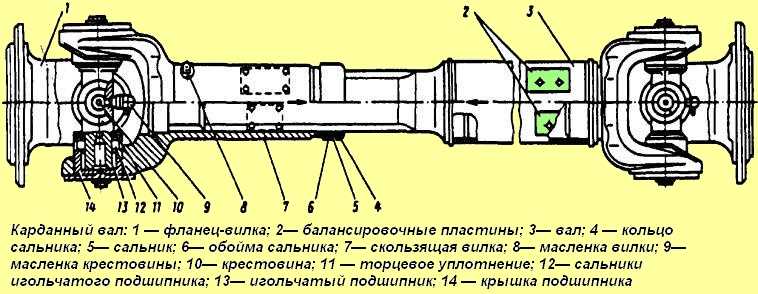
Устройство карданных передач. На современных автомобилях привод к ведущим мостам осуществляется карданными передачами с шарнирами неравных угловых скоростей. Устройство карданных передач автомобилей различных марок практически одинаково, отличие заключается главным образом в размерах и форме отдельных деталей.
Типичным примером конструкции карданной передачи является карданная передача автомобиля ЗИЛ-130 (рис. 5, а). Она состоит из промежуточного 12 и основного 21 валов, соединенных с помощью шлицев 13, промежуточной опоры 18 и трех жестких карданных шарниров /—/// неравных угловых скоростей.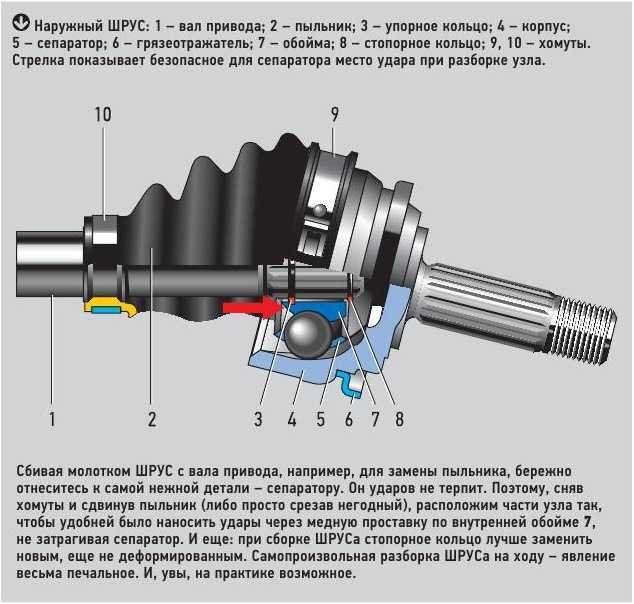
Все три карданных шарнира имеют одинаковую конструкцию, которая позволяет им работать с максимальным рабочим углом между осями валов, равным 19°. Карданный шарнир состоит из двух вилок 22 и 23, крестовины 26, четырех стаканов 34 с установленными в них подшипниками, деталей крепления и уплотнений подшипников.
Крестовина имеет четыре шипа, в центре которых просверлены несквозные смазочные каналы. На каждый шип надет игольчатый подшипник. Иглы 25 подшипника расположены в стакане 34 и внутренней обоймы не имеют. Стакан устанавливается в вилке шарнира и удерживается крышкой 27, которая крепится болтами, стопорящимися усиками пластины 24. При сборке карданных шарниров в каждое глухое отверстие шипа закладывается консистентный смазочный материал, который в процессе эксплуатации не добавляется. Для удержания смазочного материала подшипники снабжены сальниками 35: один из них (радиальный) установлен в стакане подшипника, а другой (торцовый) на шипе крестовины. В крестовинах, выпускавшихся ранее, имелись масленки для смазывания подшипников крестовин.
Промежуточный 12 и основной 21 карданные валы представляют собой тонкостенные трубы, на концах которых установлены вилки 11 карданных шарниров.
К промежуточному карданному валу 12 приварена передняя вилка 11, связанная крестовиной с фланцем-вилкой 10, при помощи которой карданный вал крепится к ведущему валу коробки передач.
Карданные передачи автомобилей
Рис. 5 – Карданные передачи автомобилей:
А – устройство карданной передачи автомобиля ЗИЛ-130; б – схема расположения валов карданной передачи полноприводного автомобиля
Задний конец промежуточного вала соединен со скользящей вилкой 28, шлицевой наконечник которой вместе со шлицевой втулкой 32 образует подвижное шлицевое соединение, компенсирующее изменение длины карданного вала в результате перемещения заднего моста. Шлицевое соединение имеет полость для смазочного материала, уплотненную сальником 19 и защищенную от попадания грязи прорезиненным кожухом 20.
К основному карданному валу 21 с обеих сторон приварены вилки, связанные через крестовины и игольчатые подшипники с промежуточным карданным валом и ведущим валом заднего моста.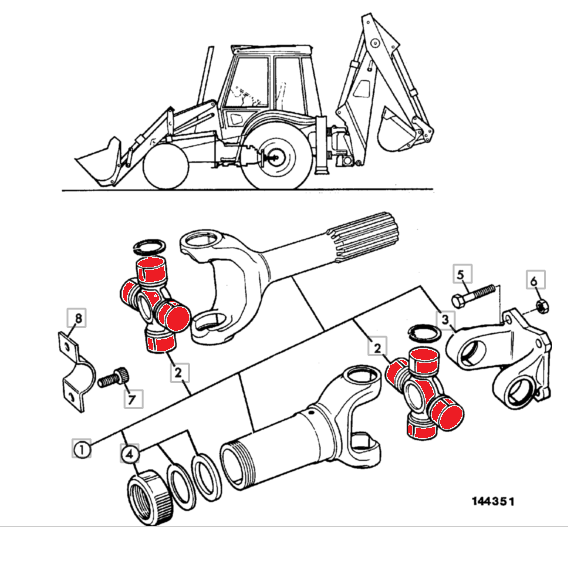 При помощи скользящей вилки 28 основной вал соединен с промежуточным карданным валом 12, а при помощи фланца вилки 23— с фланцем вала ведущей шестерни главной передачи заднего моста.
При помощи скользящей вилки 28 основной вал соединен с промежуточным карданным валом 12, а при помощи фланца вилки 23— с фланцем вала ведущей шестерни главной передачи заднего моста.
Карданные валы динамически сбалансированы, что повышает равномерность вращения (без биения) и снижает вибрацию валов. Дисбаланс промежуточного вала устраняют приваркой к его трубе пластин 33, а основного вала — привертыванием балансировочных пластин под крышки подшипников карданных шарниров.
Промежуточная опора 18 при помощи кронштейна 17 крепится болтами к поперечине рамы автомобиля.
Она расположена на заднем конце промежуточного карданного вала и является неразборной конструкцией, обеспечивающей поглощение вибрации, возникающей при
работе карданной передачи. Шарикоподшипник 16 промежуточной опоры расположен в резиновой подушке 31, закрепленной стопорными скобами и имеющей специальные прорези, повышающие ее эластичность. В крышке 15 шарикоподшипника установлены войлочные сальники 14 с отражателями 29, предохраняющими их от загрязнения, а также пресс-масленка 30 для смазывания подшипника.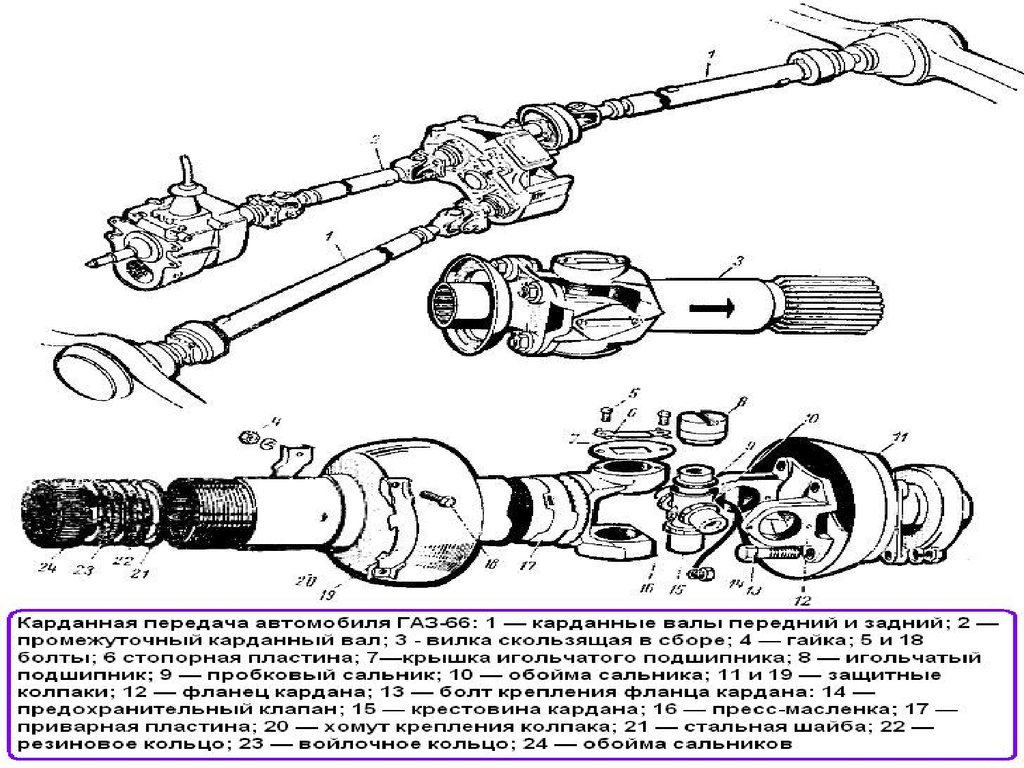 Карданные передачи полноприводных трехосных автомобилей (ЗИЛ-131, Урал-4320 и др.) состоят из четырех карданных валов (рис. 5, б): основного 4, расположенного между коробкой передач 2 и раздаточной коробкой 5, карданного вала 6 привода среднего моста 7, карданного вала 8 привода заднего моста 9 и карданного вала 3 привода переднего моста 1. Устройство всех карданных валов и шарниров этих автомобилей одинаково и аналогично описанным выше, за исключением того, что конструктивно карданный вал 6 среднего моста имеет несколько большие размеры.
Карданные передачи полноприводных трехосных автомобилей (ЗИЛ-131, Урал-4320 и др.) состоят из четырех карданных валов (рис. 5, б): основного 4, расположенного между коробкой передач 2 и раздаточной коробкой 5, карданного вала 6 привода среднего моста 7, карданного вала 8 привода заднего моста 9 и карданного вала 3 привода переднего моста 1. Устройство всех карданных валов и шарниров этих автомобилей одинаково и аналогично описанным выше, за исключением того, что конструктивно карданный вал 6 среднего моста имеет несколько большие размеры.
Контрольные вопросы.
Промежуточные соединения и их применение.
Какие могут быть промежуточные соединения по числу шарниров?
Какие могут быть промежуточные соединения по конструкции шарниров?
Устройство одинарного упругого промежуточного соединения.
Устройство двойного промежуточного соединения.
Одинарное жесткое промежуточное соединение.
Назначение и устройство карданной передачи.
Карданные шарниры неравных угловых скоростей.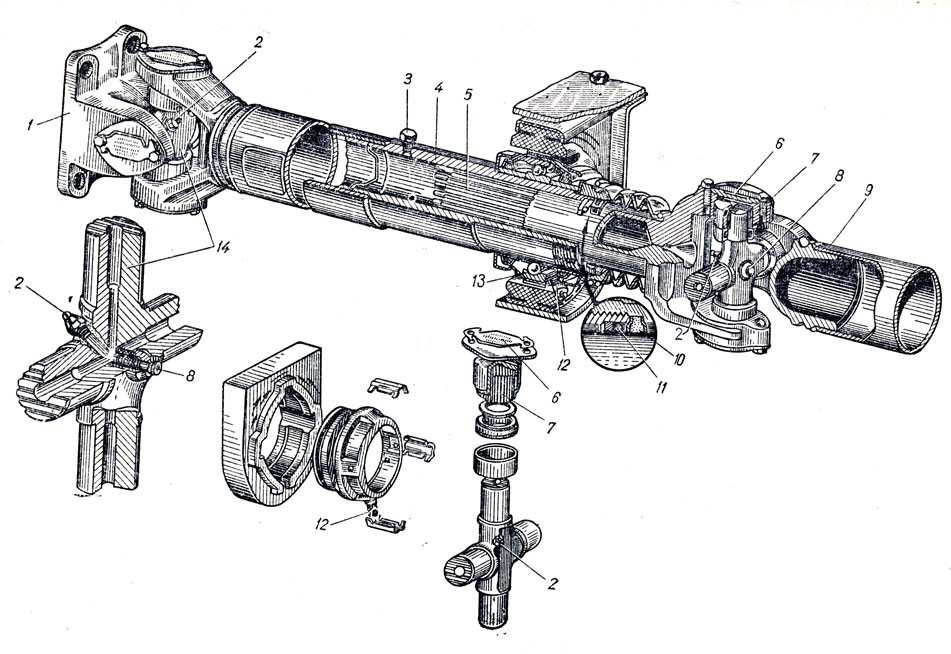
Карданные шарниры равных угловых скоростей.
Содержание отчета.
Определение промежуточного соединения.
Классификация промежуточного соединения.
Одинарное, двойное, одинарное жесткое промежуточные соединения, их устройство. Где применяются?
Определение карданной передачи.
Классификация карданных передач.
Зарисовать схему карданной передачи (рис. 3, а).
Список литературы.
1. А. М. Гуревич и др. Конструкция тракторов и автомобилей. М.: Агропромиздат, 2011г. – с. 148-151
2. В. А. Родичев. Тракторы и автомобили. М.: Колос, 1998. – с. 170-173
3. В. Л. Роговцев и др. Устройство и эксплуатация автотранспортных средств. М.: Транспорт, 1990. – с. 229-233
Несбалансированный крутящий момент: определение, примеры и уравнение
Равновесие: это то, к чему вы, вероятно, стремитесь в своей повседневной жизни, например, найти здоровый баланс между школой и жизнью в своем плотном графике. Точно так же, как ваша повседневная жизнь наполнена домашним заданием, друзьями, хобби и другими обязанностями, вокруг вас постоянно действуют всевозможные различные силы.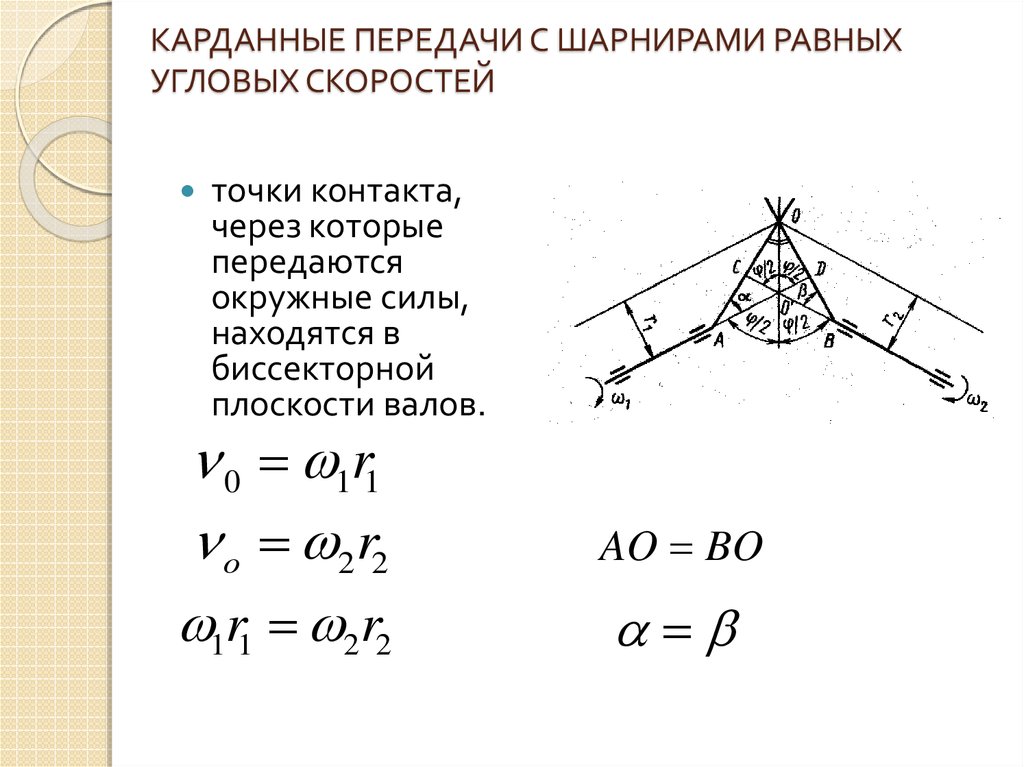 Ваш график, вероятно, кажется сбалансированным, когда у вас есть нужное количество времени для каждой задачи, а силы находятся в состоянии равновесия, когда сбалансированы до нулевой чистой силы. С другой стороны, ваше расписание, вероятно, кажется беспокойным и несбалансированным, если вам не хватает часов в сутках, чтобы все сделать, из-за чего вы отстаете от заданий, а ваше расписание выбивается из колеи. Неуравновешенный крутящий момент — то же самое — если сила не уравновешена, в результате мы станем свидетелями изменений в движении.
Ваш график, вероятно, кажется сбалансированным, когда у вас есть нужное количество времени для каждой задачи, а силы находятся в состоянии равновесия, когда сбалансированы до нулевой чистой силы. С другой стороны, ваше расписание, вероятно, кажется беспокойным и несбалансированным, если вам не хватает часов в сутках, чтобы все сделать, из-за чего вы отстаете от заданий, а ваше расписание выбивается из колеи. Неуравновешенный крутящий момент — то же самое — если сила не уравновешена, в результате мы станем свидетелями изменений в движении.
Крутящий момент — это крутящая и вращающая сила рычагов, вращающихся вентиляторов и вращающихся планет. Когда крутящий момент неуравновешен, мы наблюдаем изменения во вращательном движении. В этой статье мы рассмотрим, что такое крутящий момент, рассмотрим уравнения, которые мы используем для расчета несбалансированного крутящего момента, обсудим распространенные типы проблем и рассмотрим некоторые примеры несбалансированного крутящего момента.
Что такое крутящий момент?
Начнем обсуждение несбалансированного крутящего момента с рассмотрения определения крутящего момента. Напомним, что крутящий момент — это сила, вызывающая вращательное движение, такое как крутящее или уравновешивающее движение. 92}}\). Вы регулярно наблюдаете, испытываете и применяете крутящий момент в повседневной жизни. Каждый раз, когда вы используете ручку крана, дверную ручку или рулевое колесо, вы прикладываете силу на расстоянии, что вызывает изменение движения!
Нажатие на дверь с места расположения дверной ручки создает крутящий момент, вращая дверь вокруг ее петель, Wikimedia Commons CC BY-SA 3.0
Давайте посмотрим, как крутящий момент вызывает знакомое движение толкания двери. Дверь поворачивается вокруг своих петель, небольшой детали, которая прикрепляет дверь к раме и ограничивает диапазон ее движения. Когда вы поворачиваете дверную ручку, вы отсоединяете дверь от рамы, что затем позволяет вам приложить усилие, толкающее ее. Расстояние между петлями и точкой приложения этой силы называется плечом рычага. Результатом вашего толчка является приложенный к петлям крутящий момент, перпендикулярный силе, приложенной вашим толчком, и дверь распахивается.
Расстояние между петлями и точкой приложения этой силы называется плечом рычага. Результатом вашего толчка является приложенный к петлям крутящий момент, перпендикулярный силе, приложенной вашим толчком, и дверь распахивается.
Плечо рычага — это перпендикулярное расстояние (прямой угол) от оси вращения или точки опоры до места приложения силы.
Это расстояние обычно выражается с помощью переменных \(r\) или \(d\). Размещение дверных ручек на стороне, противоположной точкам поворота, не является ошибкой — увеличение расстояния между точкой поворота и местом, где мы прикладываем усилие, уменьшает общее количество силы, необходимой для поворота двери. Это крутящий момент в действии! Попробуйте открыть дверь на разном расстоянии от петель, чтобы убедиться в этом.
Определения сбалансированного и несбалансированного крутящего момента
Теперь, когда мы освежили наше понимание крутящего момента, давайте определим еще два связанных понятия: сбалансированный и неуравновешенный крутящий момент.
Уравновешенный крутящий момент возникает, когда крутящие моменты и силы по обе стороны от точки вращения в системе равны, что приводит к статическому равновесию системы либо в состоянии покоя, либо с нулевым ускорением вращения.
Математически мы можем записать сбалансированный крутящий момент как:
\begin{align*} \Sigma \tau=\tau_{\mathrm{net}}=0\end{align*}
где \(\tau_{\mathrm{net}}\) — чистый крутящий момент, выражается строчной греческой буквой тау .
В повседневной жизни сбалансированный крутящий момент может выглядеть как неподвижная полка, прикрепленная к стене, поддерживаемая центральным кронштейном. Размещение предметов одинакового веса по обе стороны от центральной опоры будет удерживать полку в статическом равновесии с уравновешенными крутящими моментами.
Давайте сравним это с несбалансированным крутящим моментом, который мы определяем следующим образом:
Неуравновешенный крутящий момент возникает, когда любые крутящие моменты и силы в системе не уравновешиваются, что приводит к ускорению вращения в направлении чистого крутящего момента.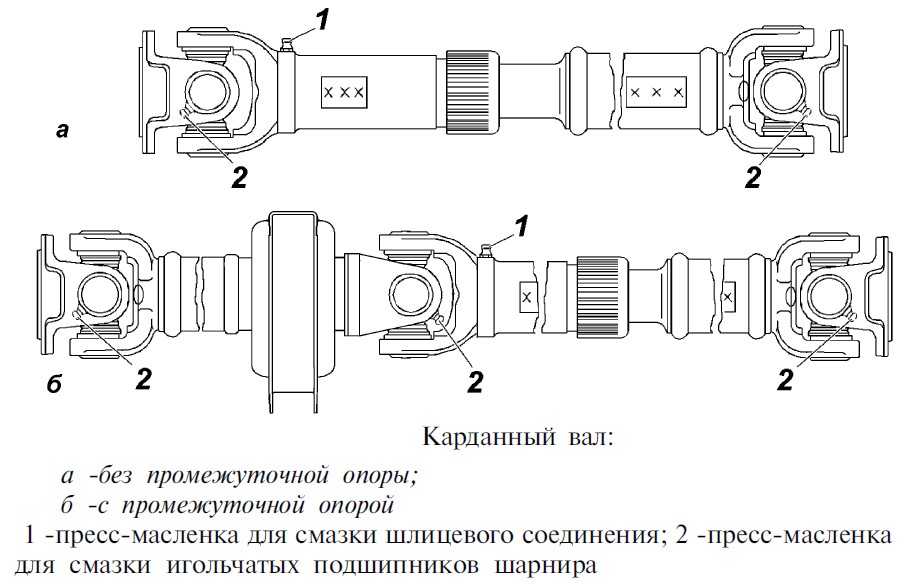
Математически мы можем записать неуравновешенный момент как:
\begin{align*} \Sigma \tau &\neq 0 \\ \tau_{\mathrm{net}}&\neq 0 \end{align*}
Опираясь на наш пример с полкой, мы можем создать несбалансированные крутящие моменты, сложив кучу объектов на левом конце полки, оставив правый конец пустым. Если длина полки равна \(L\), то вес сложенных объектов под действием силы тяжести создает чистый крутящий момент на расстоянии \(\frac{L}{2}\) от центра. Неуравновешенный крутящий момент вызывает ускорение вращения, и полка будет поворачиваться — конечно, при условии, что полка может вращаться вокруг своей опоры, а не просто отламываться от стены.
Уравнения для несбалансированного крутящего момента
Вы уже видели большинство уравнений для крутящего момента — крутящий момент является несбалансированным, когда чистый крутящий момент \(\tau_{\mathrm{net}}\) не равен нулю в расчетах. Начнем с того, что вспомним уравнение для крутящего момента, записанное как произведение приложенной силы \(F\), радиального расстояния между осью вращения и точкой приложения силы \(r\) и угла \(\theta\) между двумя:
\begin{align*} \tau=r_{\perp} F=rF\mathrm{sin\theta} \end{align*} 92}}\).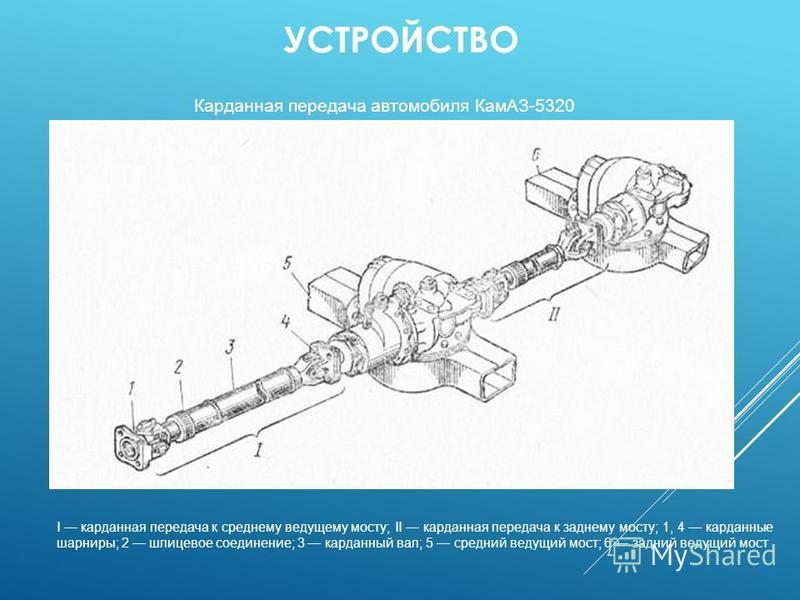 Поскольку крутящий момент зависит от момента инерции, мы не можем игнорировать форму объекта. Мы можем использовать оба этих уравнения для расчета значения приложенного крутящего момента в неуравновешенной системе. Но помните, это верно для чистого крутящего момента , поэтому обязательно обращайте внимание на то, что вы рассчитываете в задаче! У нас есть последний набор уравнений, которые мы можем использовать для расчета крутящего момента:
Поскольку крутящий момент зависит от момента инерции, мы не можем игнорировать форму объекта. Мы можем использовать оба этих уравнения для расчета значения приложенного крутящего момента в неуравновешенной системе. Но помните, это верно для чистого крутящего момента , поэтому обязательно обращайте внимание на то, что вы рассчитываете в задаче! У нас есть последний набор уравнений, которые мы можем использовать для расчета крутящего момента:
\begin{align*} \tau_1&=\tau_2 \\ F_1r_2&=F_2r_2 \end{align*}
и, если речь идет о гравитационной силе:
\begin{align*} m_1gr_1&=m_2gr_2 \\ m_1r_1&=m_2r_2 \end{align*}
Эти уравнения полезны для определения массы или радиального расстояния требуется для балансировки системы с неуравновешенными моментами.
Вращение, вызванное неуравновешенным крутящим моментом
Теперь, когда мы рассмотрели уравнения, лежащие в основе проблем неуравновешенного крутящего момента, давайте более подробно рассмотрим, как это выглядит концептуально.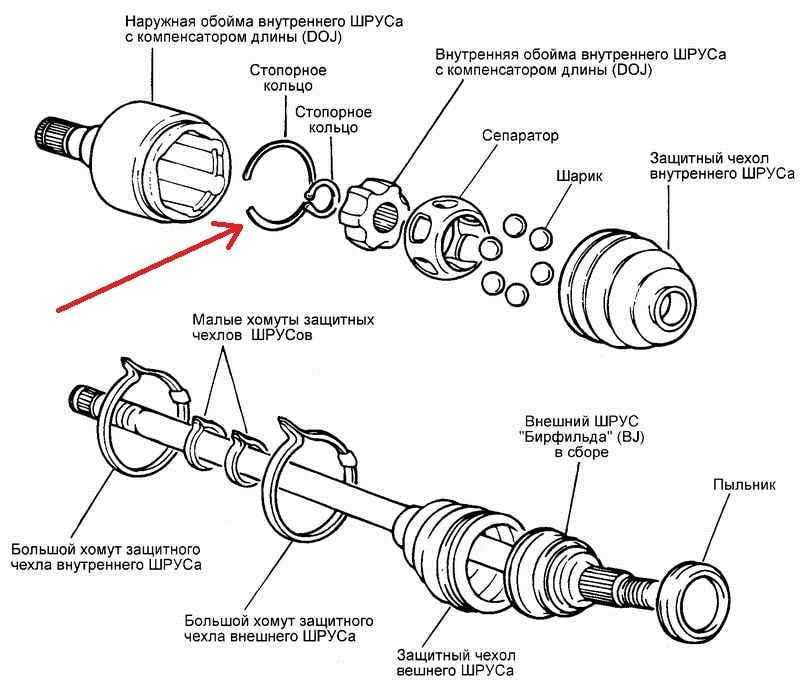 Помните уравнение, которое мы ранее ввели, \(\tau=I \alpha\)? момент инерции , \(I\), является мерой сопротивления изменению угловой скорости объекта. Это важное свойство определяется массой и распределением массы от оси вращения объекта.
Помните уравнение, которое мы ранее ввели, \(\tau=I \alpha\)? момент инерции , \(I\), является мерой сопротивления изменению угловой скорости объекта. Это важное свойство определяется массой и распределением массы от оси вращения объекта.
Если оставить момент инерции постоянным, т. е. величина останется неизменной, то получим следующую связь между крутящим моментом и угловым ускорением:
\begin{align*} \tau \propto \alpha \end{align*}
или прописью, крутящий момент пропорционален угловому ускорению. Это означает, что при увеличении крутящего момента увеличивается и угловое ускорение. Это соотношение также ясно показывает, что если чистый крутящий момент равен нулю, не может быть никакого углового ускорения!
Правило правой руки показывает направление вектора крутящего момента. Указание указательным и средним пальцами в направлении радиуса и приложенной силы при вытянутом большом пальце покажет направление крутящего момента, Wikimedia Commons CC BY-SA 3. 0
0
Итак, когда у нас есть ненулевой крутящий момент в системе, эта неуравновешенная крутящая сила приведет к изменению вращательного ускорения, заставляя систему вращаться вокруг своей оси вращения в направлении вектора чистого крутящего момента. Направление вектора крутящего момента перпендикулярно силе и радиусу \(r\) от оси . Если вы не уверены в направлении крутящего момента, используйте правило правой руки , удобный прием для проверки направления перпендикулярного вектора:
Укажите указательным пальцем в направлении радиального расстояния.
Укажите средним пальцем в направлении приложенной силы.
Держите большой палец прямо. Ваш большой палец будет указывать в направлении вектора крутящего момента.
Если приложенная сила вращается вокруг центральной оси, вместо этого согните пальцы в направлении радиального расстояния к приложенной силе. Это укажет на движение по часовой стрелке или против часовой стрелки.
 Удерживая большой палец наружу, вы укажете направление крутящего момента.
Удерживая большой палец наружу, вы укажете направление крутящего момента.
Вы будете часто сталкиваться с правилом правой руки на уроках физики, так что запишите этот трюк прямо сейчас, даже если вы еще не запомнили его! Это важный инструмент для перекрестных произведений , о котором вы узнаете больше в математических и более продвинутых курсах физики.
Расчеты несбалансированного крутящего момента и типы задач
Вы, вероятно, столкнетесь с некоторыми проблемами несбалансированного крутящего момента во время изучения физики. Давайте рассмотрим некоторые типы проблем, с которыми вы можете столкнуться, и шаги, которые вам необходимо предпринять для решения этих расчетов крутящего момента.
При решении любой проблемы всегда нужно определять, что представляет собой ваша система, и учитывать все горизонтальные и вертикальные составляющие любых задействованных сил. Крутящий момент также может быть положительным или отрицательным, так что следите за знаками!
Балансировка качелей или рычага в неравновесном состоянии
Классическая физическая задача с неуравновешенным крутящим моментом включает балансировку качелей или аналогичной установки с доской на вершине точки опоры.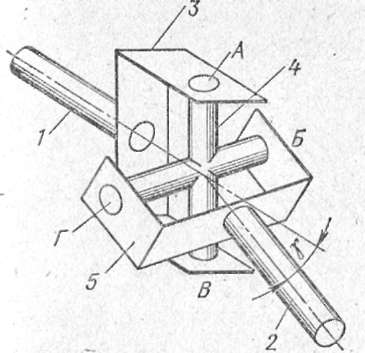 Вас могут попросить сбалансировать качели, чтобы они находились в равновесии вращения параллельно земле, основываясь на заданном наборе начальных условий.
Вас могут попросить сбалансировать качели, чтобы они находились в равновесии вращения параллельно земле, основываясь на заданном наборе начальных условий.
Давайте подумаем, какие шаги нам, возможно, придется предпринять, чтобы решить эту проблему.
Какой информацией мы располагаем? Скорее всего, вам дадут три значения, одно из которых — масса или радиальное расстояние — неизвестны.
Какое количество мы пытаемся найти? Определите недостающее количество и помните, что цель состоит в том, чтобы сбалансировать крутящий момент с обеих сторон качелей. Нарисуйте схему, если нужно.
Какое уравнение мы должны использовать? Это зависит от первоначально предоставленной информации. Во многих случаях это будет \(m_1r_1=m_2r_2\), но обратите внимание на то, с каких переменных вы начинаете!
Изолируйте неизвестную переменную и решите.
Балансировка крутящего момента в мобиле
Балансировка мобиля — это задача, похожая на балансировку качелей, но часто с несколькими ярусами подвешенных масс, где каждый ярус представляет собой отдельный рычаг. В мобильной задаче количество объектов, свисающих с каждого стержня, может быть разным. Эти типы расчета крутящего момента, по сути, являются расширением простого сценария качелей.
В мобильной задаче количество объектов, свисающих с каждого стержня, может быть разным. Эти типы расчета крутящего момента, по сути, являются расширением простого сценария качелей.
Создание мобильного телефона включает в себя уравновешивание подвешенных масс на разных рычагах, Дэниел X. О’Нил через Flickr CC BY 2.0
Как мы можем решить эту проблему? Опять же, давайте рассмотрим различные компоненты и то, что нам нужно сделать, чтобы сбалансировать крутящие моменты.
Нарисуйте или изучите схему мобильного телефона. В этих задачах вам всегда будут даны длины стержней, а также плечи рычага (расстояние от веревки до каждого висящего предмета). Плечи рычага , а не всегда будут равны половине длины стержня! Вам также будет дан вес на одной стороне самого нижнего яруса бытия.
Не обращайте внимания на вес каждого стержня и куска веревки и учитывайте только вес предметов, свисающих со стержней. Помните, что речь идет о силе гравитации, поэтому, если для начала нам дан вес , мы захотим использовать форму \(F_1r_1=F_2r_2\) уравнения крутящего момента.
Начиная с самого нижнего висящего яруса, примените уравнение балансировки крутящего момента и найдите недостающий вес.
Продвигайтесь вверх по каждому ярусу и рассчитайте следующий вес, который будет удерживать мобиль в равновесии. Когда вы продвигаетесь вверх, обязательно используйте суммируйте веса предыдущего уровня, чтобы найти значение следующего уровня.
Заполняйте диаграмму каждым значением, пока не рассчитаете все веса. Теперь вы сбалансировали подвесной мобиль!
Задачи второго закона с крутящим моментом и инерцией вращения
Последний тип задач, с которыми вы, вероятно, столкнетесь, аналогичен второму закону Ньютона. Вспомним, что второй закон движения Ньютона гласит, что сумма сил пропорциональна ускорению и обратно пропорциональна массе объекта:
\begin{align*} a=\frac{F_{\mathrm{net}}}{m} \end{align*}
где \(a\) — линейное ускорение. Второй закон Ньютона можно легко расширить, чтобы сформировать второй закон вращательного движения, зная, что сумма крутящих моментов пропорциональна угловому ускорению и обратно пропорциональна моменту инерции:
\begin{align*} a=\frac{ \tau_{\mathrm{net}}}{I} \end{align*}
В задачах такого типа вам, скорее всего, придется работать с другой информацией для начала.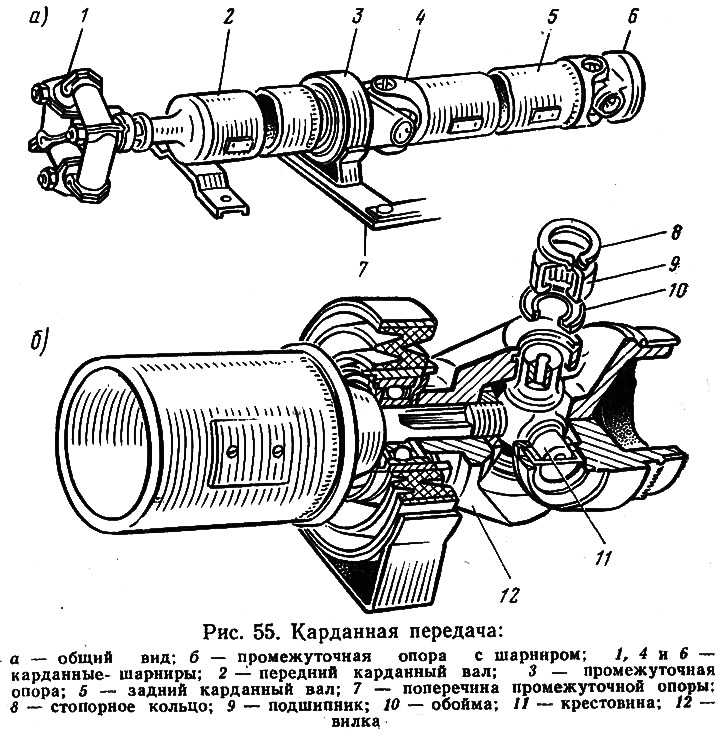 Мы все еще можем уравновешивать крутящие моменты, даже если мы не начинаем знать массы и радиальные расстояния — помните об этом, пока крутящие моменты с обеих сторон установлены равными друг другу:
Мы все еще можем уравновешивать крутящие моменты, даже если мы не начинаем знать массы и радиальные расстояния — помните об этом, пока крутящие моменты с обеих сторон установлены равными друг другу:
\begin{align*} \tau_1=\tau_2 \end{align*}
тогда мы можем найти оставшуюся неизвестную переменную.
Вы не будете балансировать систему до статического равновесия во многих задачах с крутящим моментом. Вместо этого вам будет поручено найти чистый крутящий момент, зная форму объекта и информацию об ускорении вращения или какой-либо другой вариант расчета этого крутящего момента.
Примеры неуравновешенного крутящего момента
Давайте завершим обсуждение неуравновешенного крутящего момента на примере, начиная с проблемы несбалансированных качелей.
Ребенок весом \(\mathrm{30\,кг}\) сидит на одном конце длинных \(\mathrm{2,5\,м}\) качелей. Точка опоры качелей находится точно в центре. На каком расстоянии от оси должен сесть второй ребенок весом \(\mathrm{42\,кг}\), чтобы уравновесить качели параллельно земле?
Мы хотим решить, чтобы крутящие моменты были равны по обе стороны уравнения:
\begin{align*} F_1r_1=F_2r_2 \end{align*}
и поскольку нам дан вес, мы можем подставить эти числа in для гравитационной силы, вызывающей крутящие моменты.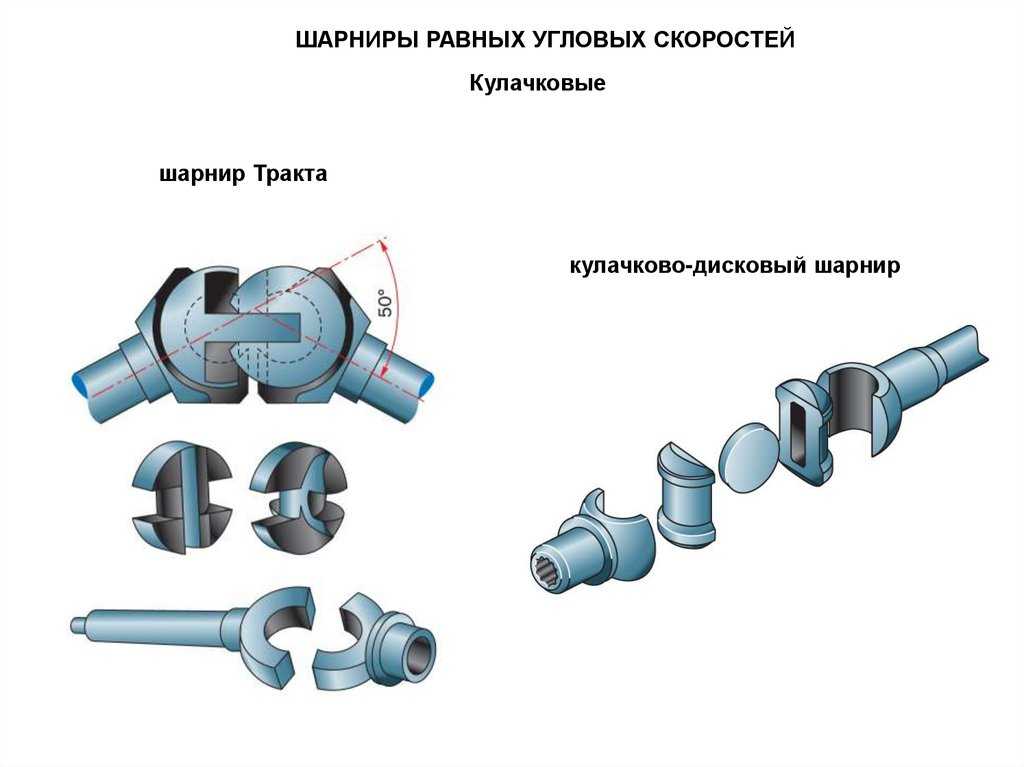 Помните, что в повседневном языке мы обычно выражаем вес в килограммах или фунтах. Однако вес из-за гравитации на самом деле равен ньютонам или фунтам силы. Еще один компонент, о котором следует подумать, — это угол; в этом сценарии угол параллели качелей с землей равен \(\theta=9\circ)=1}\), угол не влияет на наш расчет.
Помните, что в повседневном языке мы обычно выражаем вес в килограммах или фунтах. Однако вес из-за гравитации на самом деле равен ньютонам или фунтам силы. Еще один компонент, о котором следует подумать, — это угол; в этом сценарии угол параллели качелей с землей равен \(\theta=9\circ)=1}\), угол не влияет на наш расчет.
Ребенок на одном конце сидит на расстоянии \(\mathrm{\frac{2,5\,м}{2}=1,25\,м}\). Собрав все вместе, мы находим:
\[\begin{align} r_2 &= \frac{F_1r_1}{F_2} \\ \mathrm{0,89\,m} &= \mathrm{\frac{30\,N \cdot1.25\,m}{42\,N}} \end{align}\]
Таким образом, второму ребенку придется сесть гораздо ближе к центру качелей, чтобы уменьшить крутящий момент, вызванный их вес и сделать систему стабильной.
92\). Какой предмет первым достигнет дна? Какой объект будет последним?
В этой задаче мы хотим сравнить относительные моменты инерции. Запомните отношения между угловым ускорением, моментом инерции и крутящим моментом:
\begin{align*} \tau &\propto \alpha \\ \alpha &\propto \frac{1}{I} \end{align* }
Зная это, мы ожидаем, что объект с наименьшим моментом инерции быстрее достигнет подножия холма. Сопоставив это вместе, мы находим:
Сопоставив это вместе, мы находим:
\begin{align*} I _{\mathrm{solid\, cyl.}} &\geq I _{\mathrm{sph.\, shell}} \geq I _{\mathrm{cyl.\, shell}} \ \ \ alpha _ {\ mathrm {твердый \, цилиндр}} &\ geq \ alpha _ {\ mathrm {sph. \, shell}} \ geq \ alpha _ {\ mathrm {цилиндр \, shell}} \ end {align * }
Так как сплошной цилиндр имеет наибольшую массу ближе всего к своей оси вращения, сплошной цилиндр будет ускоряться быстрее всех и первым достигнет дна. Цилиндрическая оболочка имеет всю свою массу на расстоянии \(r\) от своей оси вращения и имеет наибольший момент инерции.
При расчете крутящего момента и решении задач статического равновесия помните, что крутящий момент рассчитывается в определенной точке поворота. В условиях статического равновесия чистый крутящий момент всегда будет равен нулю во всех точках разворота, а это означает, что у нас есть свобода выбора точки разворота, где расчеты самые простые, например, где некоторые крутящие моменты уже уравновешены!
Неуравновешенный крутящий момент — основные выводы
- Крутящий момент — это векторная величина, измеряющая скручивающую силу, приложенную к телу, что приводит к изменению вращательного движения.

- Сбалансированный крутящий момент возникает, когда любые действующие силы по обе стороны от точки опоры или точки вращения равны, что не приводит к изменению движения.
- Неуравновешенный крутящий момент возникает, когда любые приложенные силы не уравновешиваются и не имеют результирующей силы в одном направлении, что приводит к изменению ускорения вращения.
- Некоторые распространенные типы проблем, связанных с неуравновешенным крутящим моментом, включают балансировку качелей, балансировку многоярусного подвесного мобильного телефона и другие применения второго закона Ньютона для вращательного движения.
КРУТЯЩИЙ МОМЕНТ
Из http://www.pschweigerphysics.com/rotmot.html
— Пегги Э. Швайгер
Torque
Почему дверная ручка расположена как можно дальше от
дверная петля? Когда вы хотите толкнуть дверь, вы прикладываете силу. Где
вы прикладываете силу и в каком направлении вы нажимаете, также важны.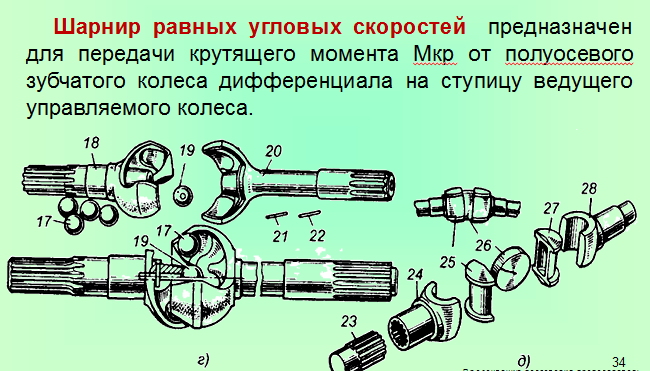
Если приложить одну и ту же силу к двум точкам, одна из которых в два раза дальше от точки
вращение, чем другое, сила, которая находится в два раза дальше, имеет вдвое больший крутящий момент
и производит вдвое большее угловое ускорение.
Крутящий момент
дюймов
круговое движение, сила, приложенная на радиальном расстоянии, которая изменяет
направление движения вращения; крутящий момент может остановить, запустить или изменить
направление кругового движения; это «неуравновешенная сила»
круговое движение
t = F d
, где t
крутящий момент в ньютонах
метров (или Н·м), F — перпендикулярная составляющая приложенной силы, а d
это радиальное расстояние (примечание: вы также можете думать о d как о r для радиуса)
Тангенциальные и радиальные
компоненты силы Сила А F действует
под углом в точке P на твердом теле, которое может свободно вращаться вокруг
ось через O расстояние r от оси вращения. Только
тангенциальная составляющая F или F T может иметь любую
воздействие на твердое тело. F R (радиальная составляющая) проходит
F R (радиальная составляющая) проходит
через ось вращения и не может заставить объект вращаться.
Угол F делает
с углом поворота называется f
Крутящий момент ( t)
вращение вокруг оси
t = r F sinf
Момент Плечо (r перпендикулярно ) Перпендикулярное расстояние линии действия силы
от оси вращения.
t = F r перпендикулярно
Или вы можете найти
составляющая силы, вызывающая крутящий момент.
Разделите силу на
его компоненты x и y. Только компонент, перпендикулярный рычагу
плечо или плечо момента вызывает крутящий момент. На изображении ниже вертикальная составляющая
F sin q перпендикулярен плечу момента и, таким образом, вызывает
крутящий момент. Горизонтальная составляющая F cos q параллельна плечу момента
и не вызывает крутящего момента.
При приложении крутящего момента
вращение происходит вокруг точки поворота , точки опоры или . Когда более
Когда более
на тело действует один крутящий момент, производимое ускорение пропорционально чистому
крутящий момент
Центр тяжести
точка
при котором кажется, что действует весь вес объекта
Крутящий момент
Движение
твердого тела относительно его центра масс
Униформа
если
объект считается однородным, его центр тяжести находится в его геометрическом центре
Вращательное равновесие
объект
называется вращательным равновесием, когда все действующие на него моменты равны
уравновешенный (или, S t = 0). Крутящий момент может вызвать движение против часовой стрелки (cc) или
вращение по часовой стрелке (cw).
St cw = St cc
где S
означает «сумма»
Центр масс (ЦМ) Точка, в которой действует вся масса объекта.
Например, если вы посмотрите на движение прыгуна в высоту, вы увидите одно особенное
пятно, которое движется по параболе. Это была бы та самая точка, где вы могли бы
уравновесить этого человека. Объект находится в равновесии, пока его ЦМ находится над его
Объект находится в равновесии, пока его ЦМ находится над его
базовый уровень. Объект считается однородным, когда ЦМ является его геометрическим
центр. Позиция СМ определяется как:
где M — полная масса, m i — масса частицы и x i
расстояние от начала координат
Статическое равновесие
Анализ статического
Равновесие очень важно в технике. Инженер-проектировщик должен определить
и изолировать все внешние силы и крутящие моменты, действующие на конструкцию. С
хороший дизайн и правильный выбор материалов, конструкции могут выдерживать нагрузки.
Шасси самолета выдерживают удары при грубых посадках, а мосты — нет.
разрушаться под транспортными нагрузками и ветром.
Поступательное равновесие Объект находится в поступательном равновесии (его импульс равен
постоянным), если сумма действующих на него сил равна нулю.
S F x = 0
S F y = 0
S F z = 0
Вращательное угловое равновесие
импульс постоянен), если сумма действующих на него моментов равна нулю.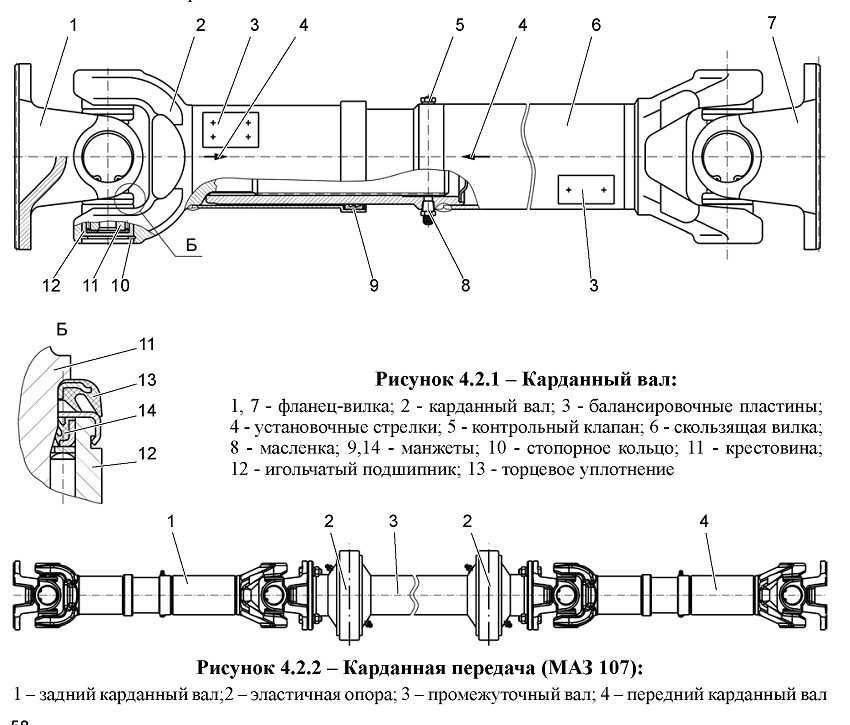
Объект будет в
равновесия, если он подвешен к своему центру тяжести или центру
сила тяжести находится ниже точки подвеса.
Эластичность Раздел физики, изучающий деформацию объектов.
при приложении к ним силы.
Предел упругости Точка, в которой деформируемый материал страдает
остаточная деформация и не вернется к своей первоначальной форме.
Есть три способа
объект может изменять свои размеры при воздействии на него сил:
1.
Объект может быть
деформируется сдвига сил. Он будет вести себя как страницы книги
когда под сдвигом. Пример: движение слоев породы при землетрясении.
2.
Объект может быть
деформируется растяжением или сжатием сил. Пример: растяжение
силы, растягивающие струну до тех пор, пока она не порвется. Пример: укладка
грузы на цилиндр, пока он не сломается.
3.
Жидкость может быть
деформируется на объемных сил. Пример: жидкость под высоким давлением может быть
сжимается со всех сторон, что приводит к изменению объема.
A стресс из-за
сил производит штамм или деформация. Напряжение пропорционально
деформации, и эта константа пропорциональности называется его модулем . стресс
является произведением модуля на деформацию. Напряжение – это отношение приложенной силы
объекта к площади поперечного сечения, на которую действует сила.
Деформация — это результирующая деформация, будь то отношение изменения
длины до исходной длины, изменение высоты до исходной высоты или изменение
объем до исходного объема.
где F — сила, A — площадь поперечного сечения в м 2 , Е есть
модуль Юнга, L — первоначальная длина, а DL — изменение
длина.
где F — сила, A — площадь поперечного сечения в м 2 , G —
модуль сдвига, h — первоначальная высота, а Dh — изменение
высота.
где F — сила, A — площадь поперечного сечения в м 2 , B — объем
модуль, V — первоначальный объем, а DV — изменение объема.
Помните, что отношение F к A — это давление (P) жидкости.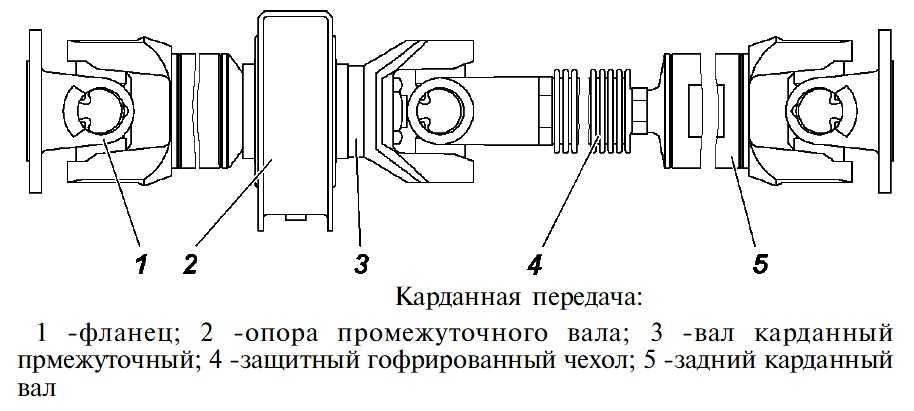
Единицей модуля является
Н/м 2 или Паскалей (Па).
Вращательное движение
Вращательное движение
движение объекта вокруг оси. До сих пор мы изучали только
прямолинейное движение (поступательное движение). Теперь будем изучать движение о
ось или вращательное движение. Объекты могут двигаться поступательно или вращательно
или оба. Они могут находиться в поступательном равновесии (сумма всех сил
действующее на объект равно нулю), но не во вращательном равновесии (сумма
все моменты, действующие на объект, равны нулю), и наоборот. Или они могут быть
как в вращательном, так и в поступательном равновесии.
Вращательное движение Поступательное движение твердого тела анализируется с помощью
описывающее движение его центра масс, а также вращательное движение вокруг
его центр масс. Каждая частица вращающегося твердого тела в любой момент имеет
линейная скорость v и линейное ускорение a . Угловой
скорость одинакова для через каждые точки вращающегося тела в любой
мгновенно, но линейная скорость больше для точек, удаленных от оси
вращение.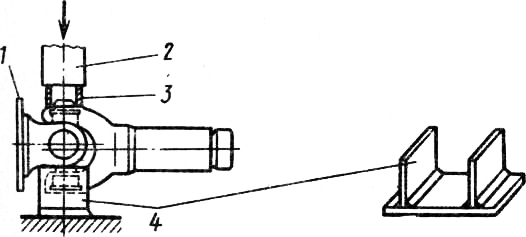
Дети на
карусели все имеют разную линейную скорость (измеряется в м/с)
в зависимости от того, насколько они удалены от оси вращения. У всех одинаковые
скорости вращения (в об/сек или рад/сек) независимо от того, где они расположены.
На изображении ниже
тело вращается вокруг неподвижной оси, проходящей через его центр. Объект, размещенный на
вращающийся объект в точке А, который вращается в точку В, вращается через то же самое
угол как объект, помещенный в точку a, который поворачивается в точку b. Оба путешествовали по
одинаковое угловое расстояние q. Они не прошли одинаковое тангенциальное расстояние. Один
прошел по дуге AB за время t, в то время как другой прошел по дуге по длине ab
вовремя т.
Угловое смещение, q
угол вокруг оси, вокруг которой вращается объект. Измеряется в градусах,
обороты или единица СИ радианы.
1
оборот = 360 = 2 p радиан
q = d/r
где d
— тангенциальное расстояние, r — радиус.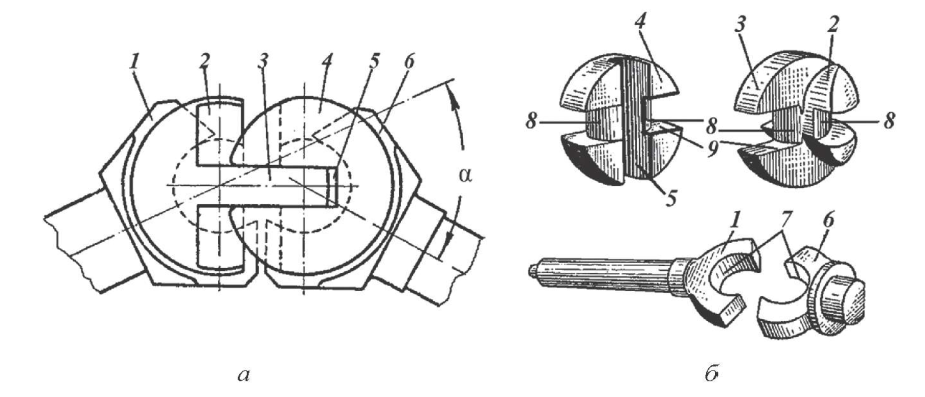
Примечание: при вращении
движения, легко использовать радиус для преобразования туда и обратно между
вращательные и поступательные величины. Также легко запомнить, что нужно
делать. Подумайте о единицах! Если бы у вас было расстояние в метрах, что бы вы сделали?
с радиусом (также в метрах), чтобы преобразовать его в радианы? ты бы разделить
расстояние в метрах на радиус в метрах. Метры отменяют оставшиеся радианы. А
радиан — это единица измерения, которая служит заполнителем.
Угловое положение Объект повернулся на некоторый угол q, когда он прошел расстояние l , измеренное вдоль
окружность его кругового пути.
Радиан Один радиан (рад) определяется как угол, образуемый
дуга, длина которой равна радиусу. Другими словами, если л = р ,
тогда q точно равно одному радиану.
Угловая скорость (или скорость), w
скорость
при котором объект вращается. Единицей СИ является рад/сек.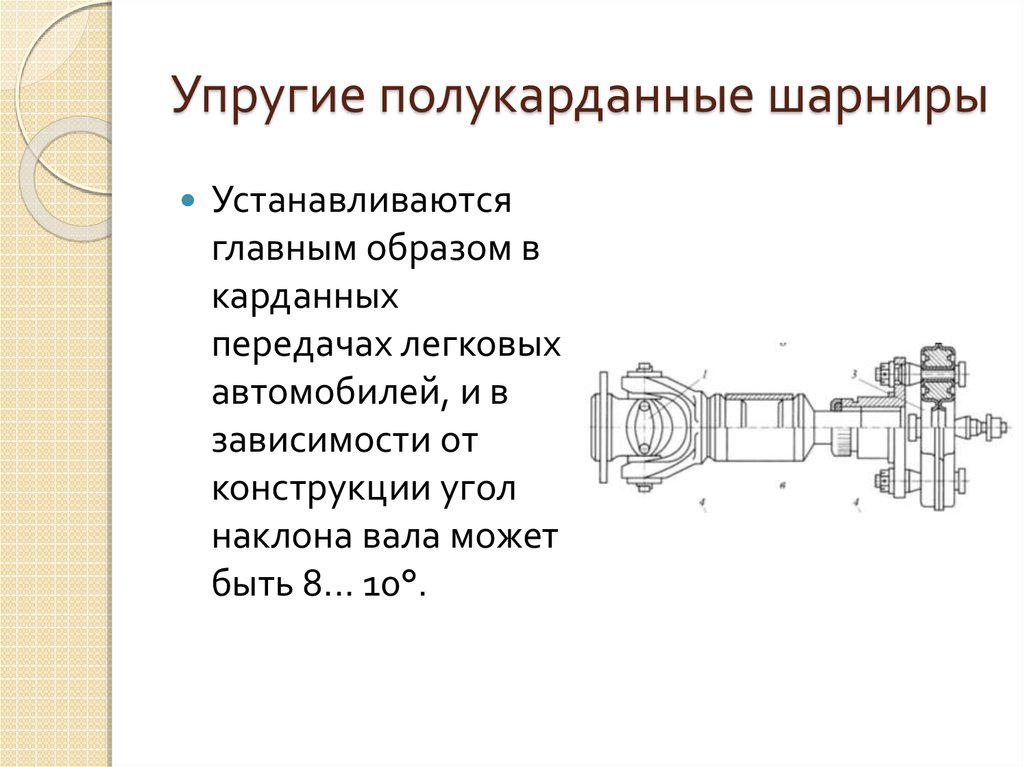 На изображении выше
На изображении выше
объект поворачивается на угол q за время t. Угловая скорость или скорость определяется выражением
(помните, при поступательном движении v = d/t)
w = q/t
Угловая скорость (скорость)
можно преобразовать в аналогичную поступательную скорость (скорость) с помощью
радиус.
w = v/r
где v
тангенциальная скорость
Угловая скорость (скорость)
и его отношение к частоте Когда
объект вращается из некоторого начального положения q i в некоторое конечное положение q f , то его угловая скорость (или скорость) w равна
равно изменению углового положения Dq = q f — q i , деленному на
изменение во времени, или w = Dq / t Угловая скорость может быть связана с частотой
вращения, f , где частота — количество полных оборотов
в секунду. Так как один оборот в секунду соответствует углу 2p
радиан в секунду, f = w / 2p
Угловое ускорение, a
скорость
при котором вращающийся объект меняет угловую скорость.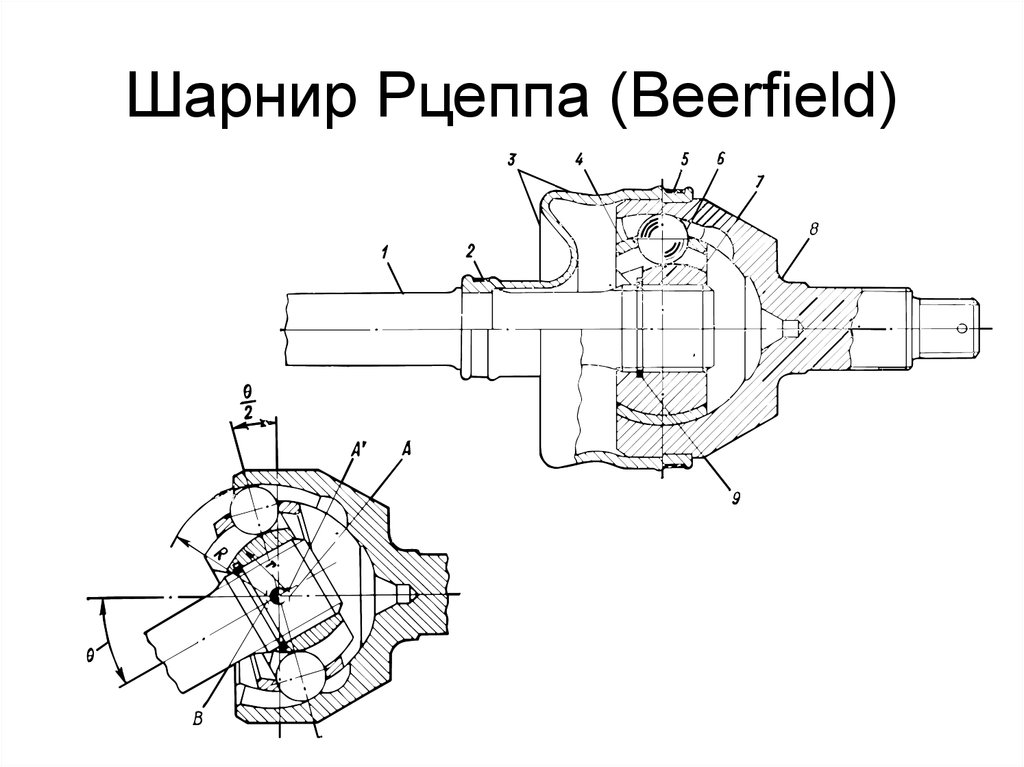 Единицей СИ является рад/с 2 .
Единицей СИ является рад/с 2 .
Угловое ускорение — это изменение угловой скорости, деленное на время
(помните, что при поступательном движении a = (v f — v i )/t)
a = (w f — w i )/t
Угловое ускорение может
преобразовать в аналогичное поступательное ускорение с помощью радиуса.
а = а/р
где а
— тангенциальное ускорение, а r — радиус
Угловое ускорение Угловое ускорение — изменение угловой скорости
разделить на время, необходимое для внесения этого изменения. Среднее угловое ускорение, а = D вт/т
Радиальная составляющая
линейное ускорение Общая линейная
ускорение a есть векторная сумма радиальной составляющей
ускорение и тангенциальная составляющая ускорения. Радиальная составляющая
линейного ускорения (или центростремительного ускорения) можно записать как a R
= w 2 r . Таким образом,
центростремительное ускорение увеличивается по мере удаления от оси
вращение. Дети, которые находятся дальше всех на карусели, испытывают самые большие
Дети, которые находятся дальше всех на карусели, испытывают самые большие
ускорение.
На изображении ниже
радиальная составляющая ускорения, a R , представляет собой центростремительную
ускорение. Тангенциальная составляющая ускорения, a tan ,
представляет собой ускорение, измеряемое по касательной к окружности. Общая
линейное ускорение вращающегося объекта есть векторная сумма двух
компоненты
Уравнения для линейных
(тангенциальное или поступательное) движение может быть преобразовано в аналогичное
ротационные формы:
д = v т | q = вес |
d = d o + v i | q = q o + w i t + a t 2 |
v f = v i + | w f = w i + a t |
v f 2 = v i 2 | w f 2 = w i 2 + 2 aq |
Так же как неуравновешенный
сила необходима для изменения движения объекта в линейном (поступательном)
движение, крутящий момент требуется, чтобы изменить движение объекта при вращении
подвижный.
t = F r
где r
радиус
ньютонов 2 9Закон 0459 и может быть преобразован в его аналог
ротационная форма:
F = мА | т = I a |
Движение качения
колесо или сфера Катящийся без
проскальзывание включает в себя как вращение, так и перемещение. Помните об отношениях
между угловой скоростью вращающегося объекта и линейной скоростью
ось, или w = v/r. В любой момент, когда вращающееся колесо находится в контакте
с землей, в этой точке контакта колесо на мгновение находится в покое.
скорость оси равна против ; скорость в верхней части колеса 2 v .
момент инерции, I
вращательная инерция вращающегося тела. Это аналог массы в поступательном
движение. Инерция вращения зависит не только от массы вращающегося тела,
но и распределение этой массы.
Расширенный взгляд на
момент инерции : Вы можете
думайте о вращающемся твердом теле, состоящем из множества частиц, расположенных в
различные радиальные расстояния от оси вращения. Момент инерции
Момент инерции
вращающееся тело — это просто сумма масс каждой частицы, умноженных на
на квадрат расстояния этой частицы от оси вращения.
Я = Смр 2
= m 1 r 2 1 + m 2 r 2 2
+ m 3 r 2 3 + m n r 2 n
До этого момента наши
изучение физики было связано с поступательным движением или движением в
xy плоскость. Стандартный английский алфавит предоставляет переменные для этого
движение. Мы используем греческий алфавит для переменных, чтобы различать вращательные
движение от поступательного движения. В следующей таблице перечислены переменные для
поступательное движение и аналогичная вращательная переменная с их СИ
переменные.
расстояние/перемещение | д в м | кв в рад |
скорость/скорость | v в м/с | Вт в рад/с |
ускорение | а в м/с 2 | а в рад/с 2 |
сила | F в ньютонах | т в Н·м |
масса | м в кг | I в кг м 2 |
Динамика вращения
Для
заставить объект начать вращаться вокруг оси. Направление силы и куда
Направление силы и куда
применяется важно. Крутящий момент создает угловое ускорение. Крутящий момент
требуется для начала вращения тела. Вращающееся твердое тело может быть
рассматривается как состоящий из множества частиц, находящихся на различных расстояниях от
ось вращения. Сумма крутящих моментов каждой из этих частиц равна
только общий крутящий момент. Момент инерции, I , говорит, как масса
тело распределено вокруг оси вращения. При вращательном движении t = I a
Некоторые вращательные моменты
инерции для твердых тел:
Тонкий обруч (велосипедное колесо или | я = мистер 2 |
Сплошной диск (сплошной цилиндр, | I = 1/2 мм 2 |
Однородная сфера (звезда) радиуса | I = 2/5 м 2 |
Длинный однородный стержень длиной L | I = 1/12 м 2 |
Длинный однородный стержень длиной L | I = 1/3 м 2 |
Кинетическая энергия вращения
Тело, вращающееся вокруг
говорят, что ось имеет вращательную кинетическую энергию. Это аналог
Это аналог
поступательная кинетическая энергия. Его единицей СИ являются джоули. Объект, который вращается
вокруг своего центра масс совершает поступательное движение, имеющее как
поступательные и вращательные КЭ, если ось закреплена. Для объекта, который катится
без скольжения по склону первоначальная потенциальная энергия равна
сумма поступательной кинетической энергии и вращательной кинетической энергии.
1/2 м v 2 | 1/2 дюйма ш 2 |
Объект, который вращается
в то время как его центр масс (ЦМ) перемещается, будет иметь как вращательное, так и
поступательные кинетические энергии. Полная кинетическая энергия такого объекта равна
дано:
KE = 1/2
mv 2 CM + 1/2 I CM w 2
Объект, скользящий по
наклон (без качения) преобразует всю свою потенциальную энергию в
поступательная кинетическая энергия. Объект, который скатывается по наклонной плоскости, трансформируется
Объект, который скатывается по наклонной плоскости, трансформируется
часть его потенциальной энергии в поступательную кинетическую энергию, а часть в
кинетическая энергия вращения. Рассмотрим несколько объектов на вершине склона:
коробка, скользящая по склону, и обруч, сплошной цилиндр и сфера
которые катятся по склону. Кто первым достигнет дна? Раздвижная коробка
который преобразует все свою потенциальную энергию в поступательную кинетическую
энергия. Обруч будет последним, потому что он преобразует наибольшее количество своего
потенциальную энергию в кинетическую энергию вращения. Более поступательная кинетика
энергия объекта, тем быстрее он достигает нижней части склона.
Угловой момент и его сохранение
У линейного импульса есть свои особенности.
аналогичная величина, угловой момент, L .
р = м v | Д = I ш |
Угловой момент
важная концепция, потому что она остается постоянной, если внешние крутящие моменты не действуют.


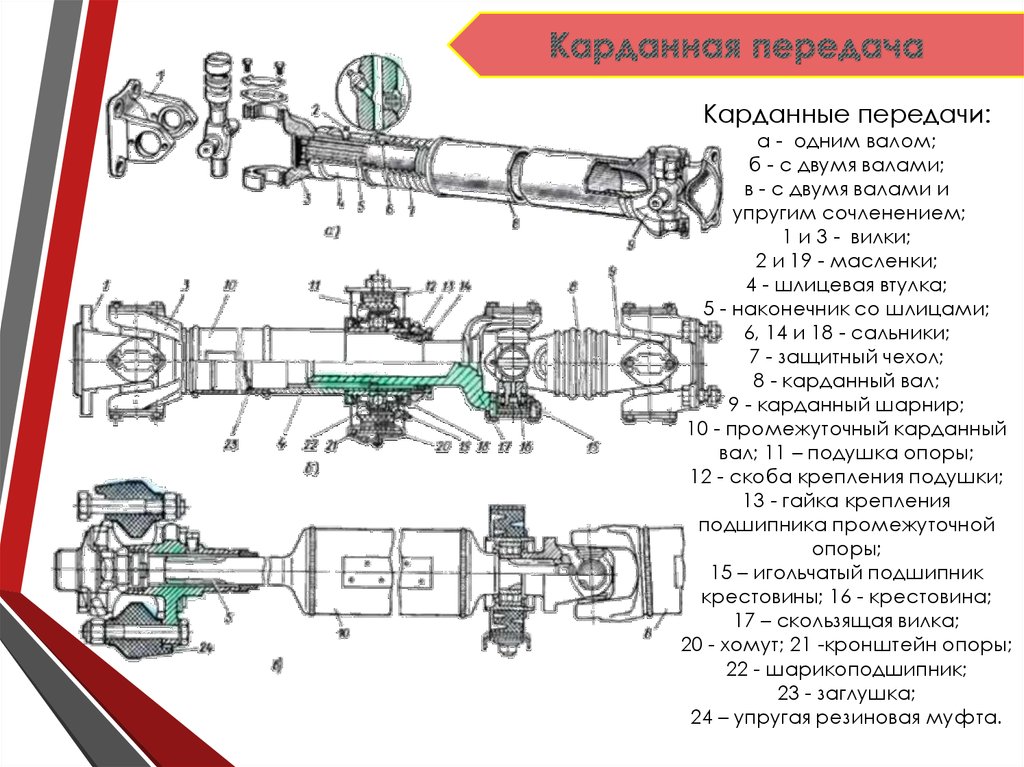 Различают карданные шарниры равных и неравных угловых скоростей.
Различают карданные шарниры равных и неравных угловых скоростей.
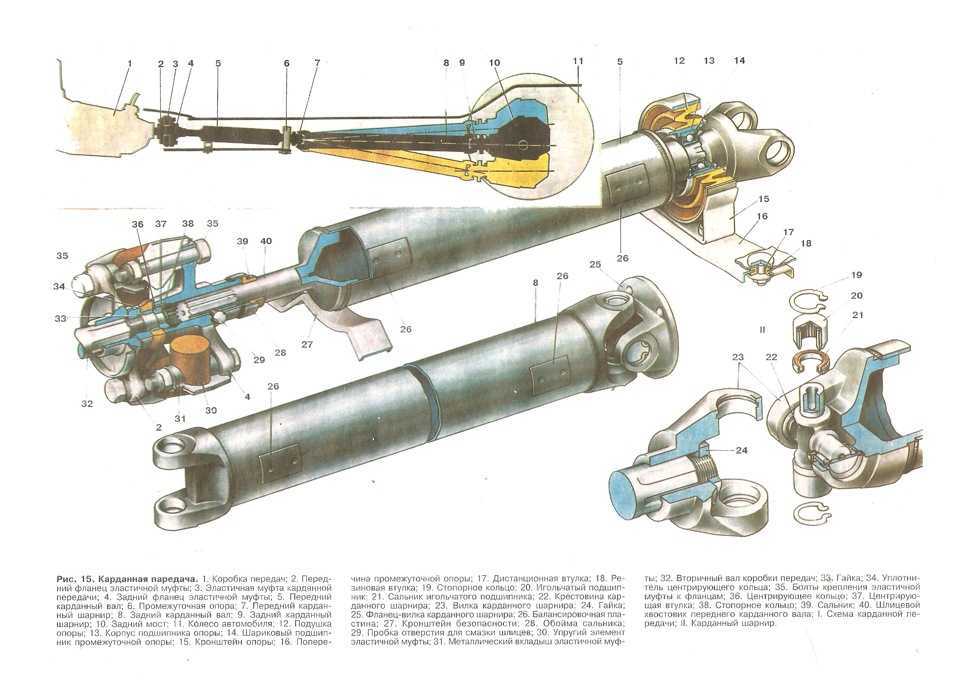 Неравномерность тем больше, чем больше угол
Неравномерность тем больше, чем больше угол
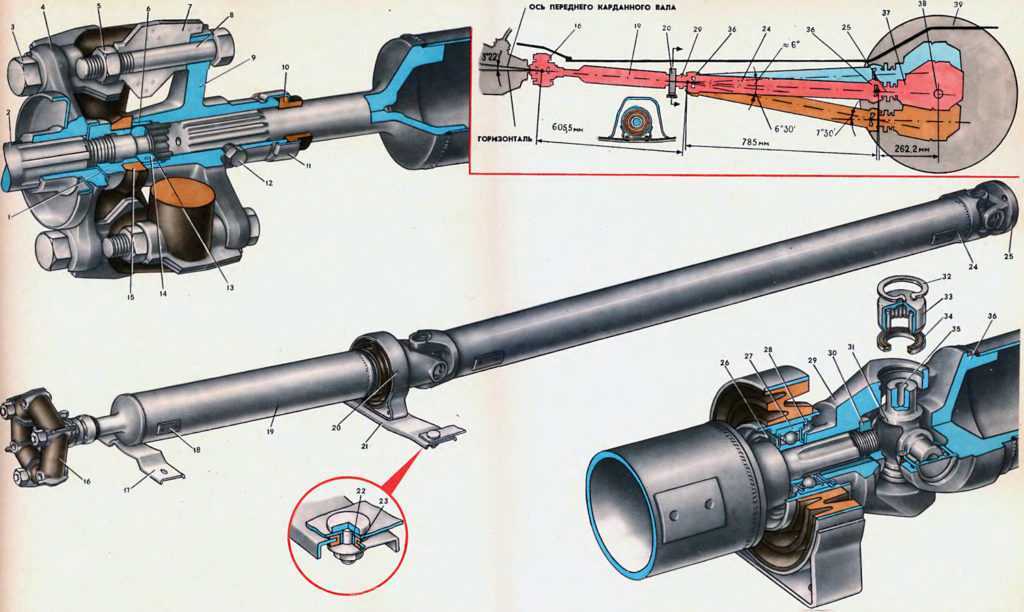 7.3.
7.3. На рис.7.5а
На рис.7.5а
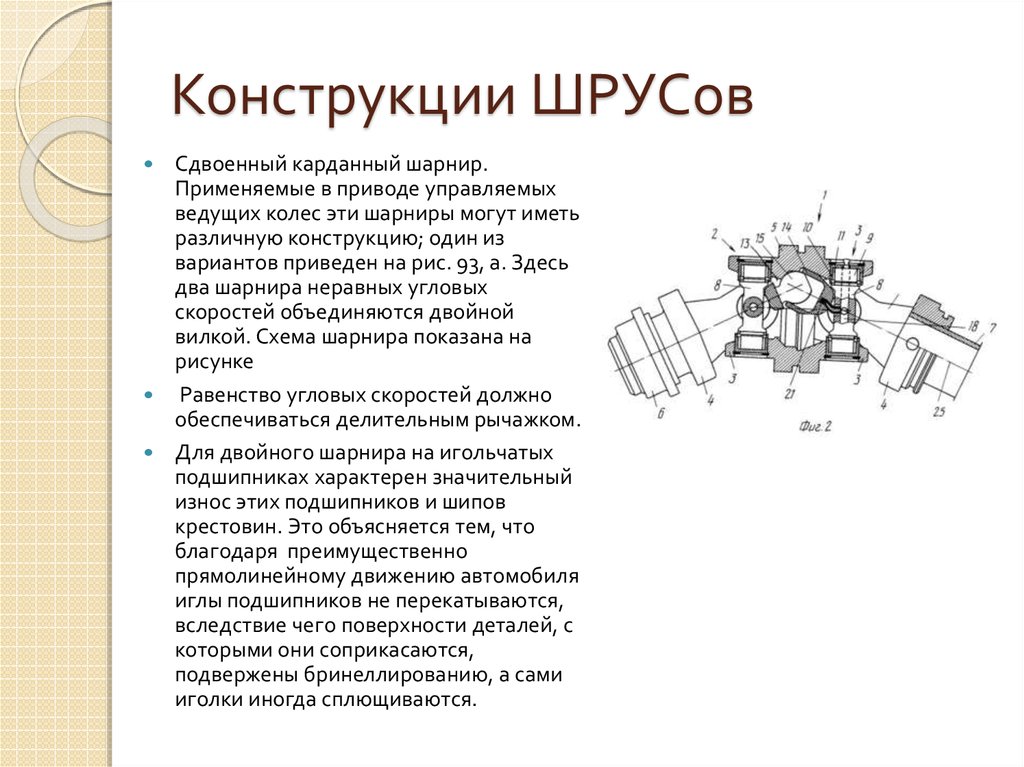 Такой шарнир работает до углов между валами до 40
Такой шарнир работает до углов между валами до 40 Пружиной 7 он прижимается к ведомому
Пружиной 7 он прижимается к ведомому
 8).
8). 7.6. Карданная передача с шарнирным карданным шарниром равных
7.6. Карданная передача с шарнирным карданным шарниром равных
