Содержание
Карданные шарниры неравных угловых скоростей (асинхронные)
Имеют
две фиксированные оси качания, используются
в карданной передаче при наклоне ведомого
вала обычно на угол не более 20′.
Универсальные шарниры отличаются от
простых тем, что в них осевая компенсация
осуществляется в самом механизме
шарнира, а не в шлицевом соединении.
Типичная конструкция карданного
шарнира
неравных угловых скоростей является
крестовина с игольчатыми подшипниками,
размещенными в колпачках. Применяемые
в современных автомобилях карданные
шарниры
неравных угловых скоростей на игольчатых
подшипниках удовлетворяют поставленным
требованиям при условии, если шарнир
имеет рациональную конструкцию,
технология производства строго
соблюдается, а игольчатые подшипники
надежно смазываются. Недостатки:
КПД
карданного
шарнира
зависит от угла g между соединяемыми
валами. С увеличением g КПД резко
снижается;Надежность
и долговечность сильно зависят от
качества смазки игольчатого подшипника;Крестовина
карданного
шарнира
должна строго центрироваться
13.
Какие основные элементы карданной
передачи Вы можете назвать?
Ответ:
Основным
элементом карданной
передачи является карданный
шарнир.
В зависимости от конструкции шарнира
различают следующие типы
карданных передач :
карданная
передача с шарниром неравных
угловых скоростей;карданная
передача с шарниром равных
угловых скоростей;карданная
передача с полукарданным упругим
шарниром;карданная
передача с полукарданным жестким
шарниром.
Карданная
передача с полукарданным жестким
шарниром на автомобилях не применяется,
т.к. не отвечает требованиям надежности
и технологичности.
14.
Под каким максимальным углом между
валами передается крутящий
момент
шарнирами неравной и равной угловой
скорости?
Ответ:
Шарнир
равных
угловых
скоростей
(сокращённо ШРУС,
в просторечии — «граната») обеспечивает
передачу крутящего
момента
при углах
поворота до 70 градусов относительно
оси.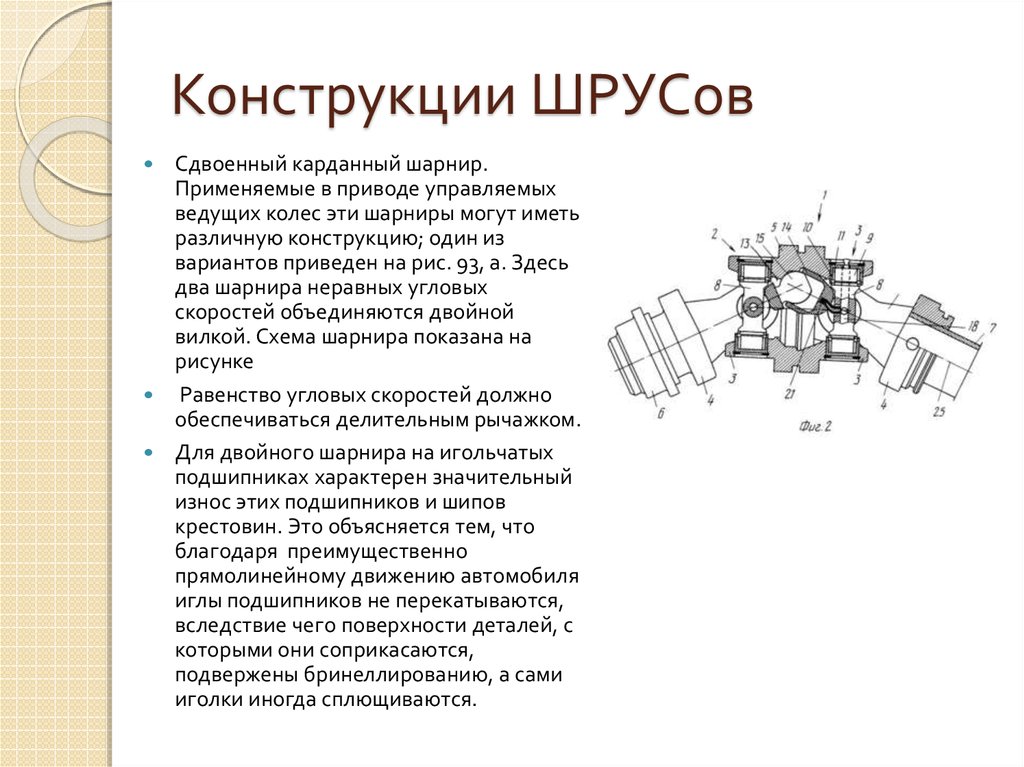 ШРУСы изредка называют «гомокинетическими
ШРУСы изредка называют «гомокинетическими
шарнирами »
(от др.-греч.
ὁμός — « равный ,
одинаковый» и
κίνησις — «движение», « скорость »).
Используется
в системах привода управляемых колёс
легковых
автомобилей
с независимой подвеской и ,
реже, задних колёс.
Первые
попытки реализовать передний
привод
осуществлялись при помощи обычных
карданных
шарниров .
Однако
если колесо перемещается в вертикальной
плоскости и
одновременно является поворотным,
наружному шарниру
полуоси приходится работать в исключительно
тяжелых условиях — с углами
30—35°. А при углах
больше 10—12° в карданной передаче резко
увеличиваются потери мощности, к тому
же вращение передаётся
неравномерно, растёт износ шарнира ,
быстро изнашиваются шины, а шестерни
и
валы
трансмиссии начинают работать с большими
перегрузками. Таким образом, требовался
особый шарнир —
шарнир
равных
угловых
скоростей —
лишенный таких недостатков, передающий
вращение равномерно вне зависимости
от угла
между
соединяемыми валами .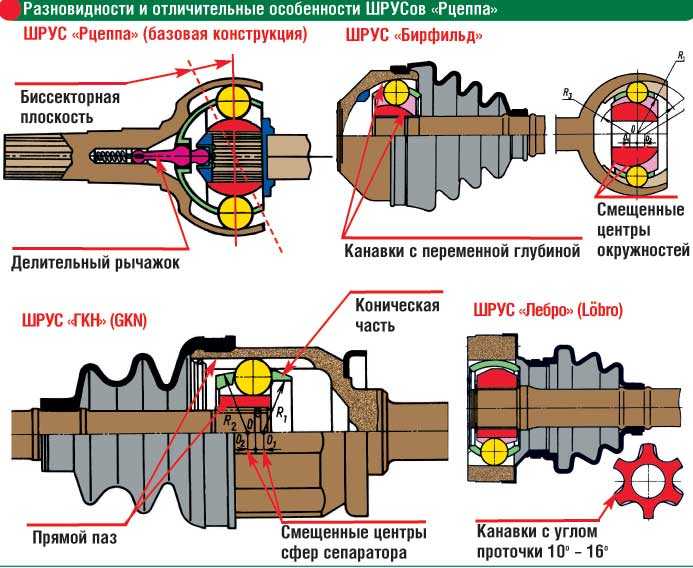
Лабораторная
работа № 4
ВЕДУЩИЙ
МОСТ
задний
мост автомобиля ВАЗ – 2107
Номер по | Название | Количество | Материал |
1 | полуось | 2 | |
2 | болт | 4х1 | |
3 | направляющий | 2х1 | |
4 | маслоотражатель | 1х1 | |
5 | тормозной | 1х1 | |
6 | подшипник | 1х1 | |
7 | запорное | 1х1 | |
8 | фланец | 1 | |
9 | сальник | 1 | |
10 | балка | 1 | |
11 | пластина | 1 | |
12 | щит | 1 | |
13 | направляющая | 1 | |
14 | регулировочная | 1 | |
15 | подшипник | 1х1 | |
16 | крышка | 1 | |
17 | сапун | 1 | |
18 | сателлит | 2х1 | |
19 | ведомая | 1 | |
20 | шестерня | 1х1 | |
21 | регулировочное | 1 | |
22 | распорная | 1 | |
23 | подшипники | 2 | |
24 | сальник | 1 | |
25 | грязеотражатель | 1 | |
26 | фланец | 1 | |
27 | маслоотражатель | 1 | |
28 | картер | 1 | |
29 | ведущая | 1 | |
30 | ось | 1 | |
31 | регулировочная | 1 | |
32 | коробка | 1 | |
33 | болт | 1 | |
34 | стопорная | 1 | |
35 | опорные | 2 | |
36 | кронштейны | 2 |
2.
Таблицу данных по форме:
Данные по | Модель | |||
ЗИЛ-4314 | КамАЗ-5320 | ВАЗ-2115 | ГАЗ-3110 | |
Тип (одинарная, центральная, | двойная | |||
Тип | межколесным | |||
Количество | ||||
Тип ные, | ||||
Тип | ||||
Передаточное главной | ||||
Наличие колесного | ||||
Устройство
и работа главных передач и межколесных
дифференциалов ведущих мостов автомобиля
КамАЗ-5320
Двойная
главная передача среднего ведущего
моста автомобиля КамАЗ-5320 (рис.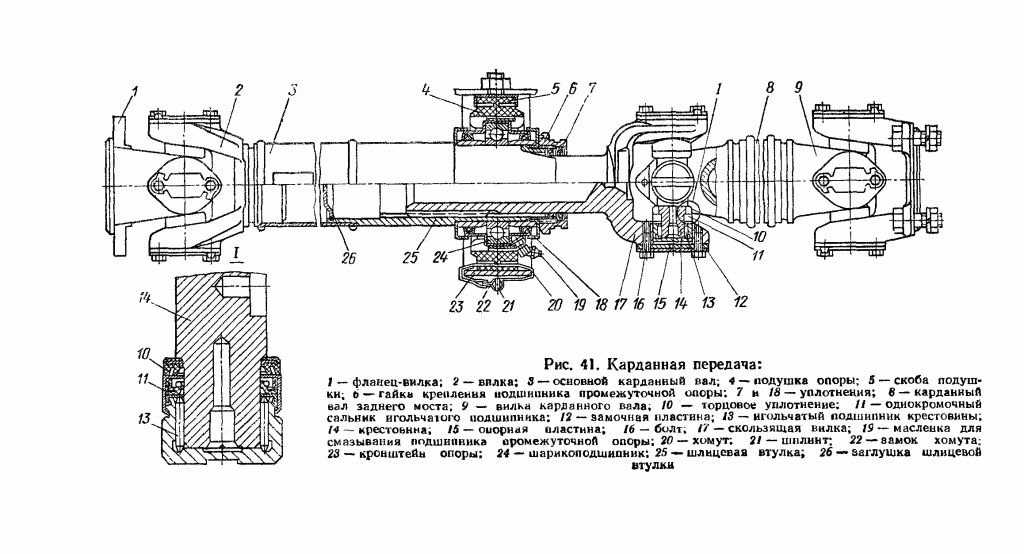 4.21)
4.21)
выполнена с проходным валом для привода
главной передачи заднего моста. Ведущая
коническая шестерня 20
установлена
в горловине картера главной передачи
на двух роликовых конических подшипниках
24,
2в, между
внутренними обоймами которых имеются
распорная втулка и регулировочные шайбы
25.
Шлифованный
конец ступицы этой шестерни соединен
с конической шестерней межосевого
дифференциала, а внутри ступицы проходит
вал 21
привода,
одним концом соединенный с кони ческой
шестерней межосевого дифференциала, а
другим при помощи карданной передачи
с ведущим валом главной передачи заднего
моста.
Промежуточный
вал опирается одним концом на два
конических роликовых подшипника 7, между
внутренними обоймами которых имеются
регулировочные шайбы 4,
а
другим на роликовый подшипник,
установленный в расточке перегородки
картера главной передачи. Конические
роликовые подшипники 7 фиксируют
промежуточный вал от смещения в осевом
направлении. Заодно с промежуточным
валом выполнена ведущая цилиндрическая
шестерня 3
с
косыми зубьями. Ведомая коническая
Ведомая коническая
шестерня / напрессована на конец
промежуточного
ведомую
цилиндрическую шестерню 16.
Крутящий
момент от корпуса межколесного
дифференциала, к которому прикреплена
ведомая цилиндрическая шестерня 16
главной
передачи, передается на крестовину
15,
а
от нее через сателлиты на шестерни
полуосей. Сателлиты, действуя с одинаковой
силой на правую и левую шестерни
полуосей, создают на них равные крутящие
моменты.
При
этом благодаря незначительному
внутреннему трению равенство моментов
практически сохраняется как при
неподвижных сателлитах, так и при их
вращении.
Поворачиваясь
на шипах крестовины, сателлиты обеспечивают
возможность вращения правой и левой
полуосей, а следовательно, и колес с
разными частотами.
Смазка
трущихся поверхностей деталей главной
передачи и дифференциала осуществляется
разбрызгиванием масла, находящегося в
картере. В дифференциал смазка поступает
через окна в его корпусе, а для подвода
масла к коническим подшипникам ведущей
конической шестерни и промежуточного
вала в стаканах, в которых установлены
подшипники, предусмотрены продольные
и радиальные каналы. Полость картера
Полость картера
главной передачи сообщается с атмосферой
через вентиляционный колпачок (сапун).
Уплотнение валов осуществляется
самоподжимными сальниками, защищенными
грязеотражательными кольцами.
Общее
устройство главной передачи и дифференциала
заднего ведущего моста (рис. 4.22) аналогично
рассмотренному выше. Отличия объясняются
главным образом тем, что задний
ведущий
мост не проходной и получает крутящий
момент от межосевого дифференциала,
установленного на среднем ведущем
мосту.
В
главной передаче заднего моста ведущая
коническая шестерня 21
отличается
от аналогичной шестерни среднего моста
тем, что ее ступица короче и имеет
внутренние шлицы для соединения с
ведущим валом 22
главной
передачи заднего моста. Опорные конические
роликовые подшипники 18
и
20
взаимозаменяемы
с соответствующими подшипниками среднего
ведущего моста. Ведущий вал лавной
передачи заднего моста задним концом
опирается на один роликовый подшипник,
установленный в расточке картера.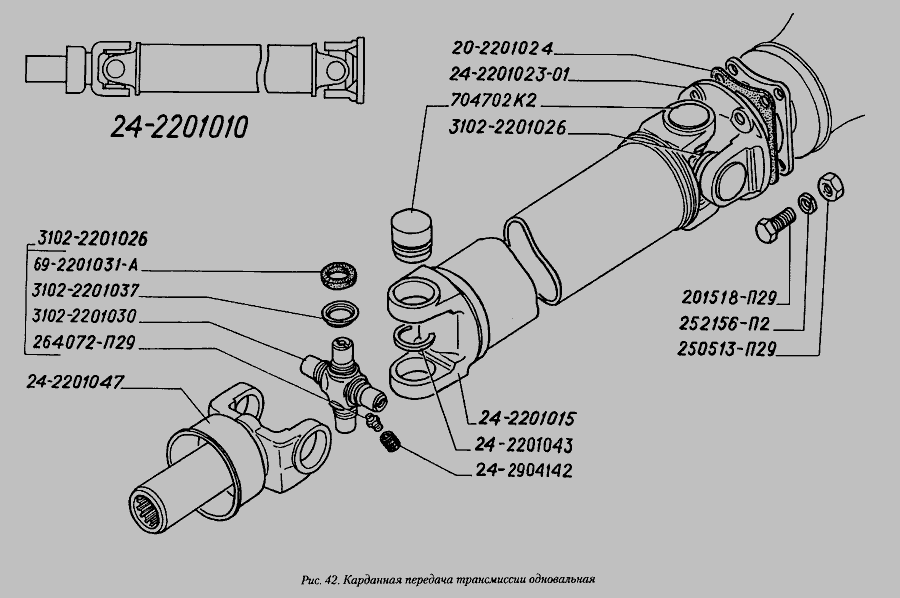 Для
Для
циркуляции смазки около подшипника в
горловине картера имеется канал. С торца
подшипник закрыт крышкой. Остальные
детали главной передачи и межколесного
дифференциала среднего и заднего ведущих
мостов аналогичны по устройству.
Устройство
и работа межосевого дифференциала
автомобиля КамАЗ-5320
Межосевой
дифференциал смонтирован в картере
(рис.4.23), который крепится к картеру
главной передачи среднего моста. Он
состоит из собственно конического
дифференциала, механизма блокировки и
привода управления блокировкой.
Корпус
5 дифференциала состоит из двух половин
(чашек), соединяемых болтами. Передняя
чашка имеет хвостовик, который опирается
на шариковый подшипник 29.
На
шлицованной части хвостовика установлен
фланец /, связывающий корпуо дифференциала
карданной передачей с коробкой передач.
Между половинами корпуса зажата
крестовина 26,
на
шипах которой установлены четыре
сателлита 6
с
опорными шайбами 7. Сателлиты находятся
в зацеплении с шестернями 24
и
27
привода
среднего и заднего мостов.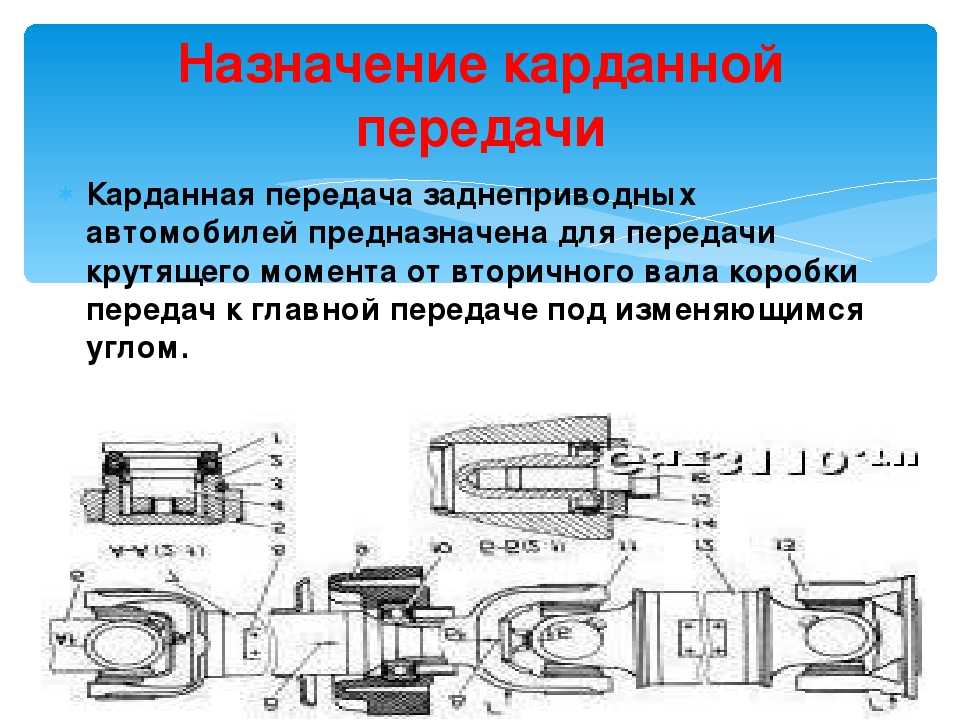 Поскольку
Поскольку
сателлиты действуют на зубья этих
шестерен с равными усилиями и размеры
их одинаковы, крутящие моменты на
шестернях привода среднего и заднего
мостов также одинаковы, т. е. дифференциал
является симметричным.
Шестерня
27 привода заднего моста установлена в
расточке корпуса дифференциала, под ее
торец поставлена опорная шайба 28,
в
корпусе имеется сверление для подвода
масла к опорной шайбе и ступице шестерни.
Шлицами, выполненными по внутренней
поверхности ступицы, шестерня 27
соединяется
со шлицованным концом проходного вала
привода заднего моста. Шестерня 24
привода
среднего моста при помощи шлицев,
выполненных на внутренней поверхности
ступицы, соединяется с удлиненной
ступицей ведущей конической шестерни
главной передачи среднего моста. На
конце ступицы шестерни 24
на
шлицах установлена зубчатая муфта 21,
по
наружной части которой может перемещаться
муфта 22
блокировки
межосевого дифференциала. Эта муфта
вилкой 20
соединяется
с ползуном 11,
связанным
с диафрагменным механизмом управления
блокировкой. Корпус 19
Корпус 19
механизма блокировки укреплен на картере
межосевого дифференциала. Между корпусом
и крышкой 18
зажата
резиновая диафрагма 15.
Полость
за диафрагмой (со стороны крышки) связана
шлангом 16
с
краном включения блокировки дифференциала.
В полости под диафрагмой размещается
ползун 11,
соединенный
со стаканом 14,
внутри
которого установлена нажимная пружина
13,
а снаружи
— возвратная пружина 12.
Рычаг
крана включения блокировки межосевого
дифференциала размещен на щитке приборов
в кабине автомобиля. На щитке приборов
имеется также контрольная лампа
блокировки межосевого дифференциала.
В
положении, показанном на рис. 4.23, межосевой
дифференциал разблокирован. Для
блокировки-дифференциала рычаг крана
включения, расположенный на щитке
приборов, водитель переводит в правое
положение. При этом сжатый воздух от
крана управления по системе трубопроводов
и шлангу 16
поступает
в полость между крышкой корпуса и
диафрагмой, которая прогибается,
перемещает стакан 14
и
ползун 11
вперед,
преодолевая сопротивление возвратной
пружины 12.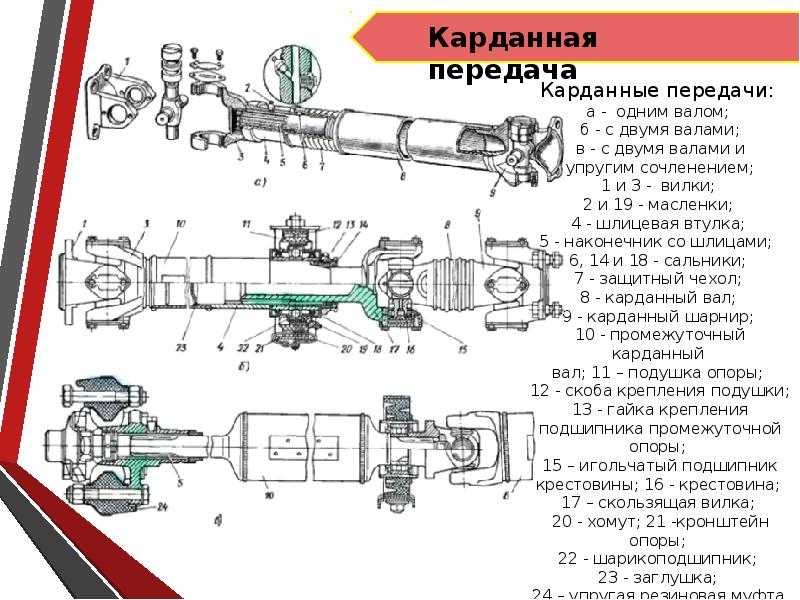
С
началом движения ползуна замыкаются
контакты включателя 8, и на щитке приборов
загорается контрольная лампа. Вместе
с ползуном перемещается и укрепленная
на нем вилка 20,
которая
вводит муфту 22
в
зацепление с зубчатым венцом на корпусе
дифференциала. При крайнем левом
положении муфты шестерня 24
привода
среднего моста и корпус 5 дифференциала
оказываются жестко соединенными, т. е.
дифференциал становится заблокированным
и шестерни 24
и
27
привода
мостов принудительно вращаются с
одинаковой частотой.
Для
разблокировки межосевого дифференциала
рычаг крана управления на щитке приборов
надо перевести влевое положение. При
этом полость за диафрагмой механизма
блокировки дифференциала через кран
управления и трубопроводы будет связана
с атмосферой. Под действием возвратной
пружины диафрагма и ползун с вилкой
перемещаются вправо (назад), смещая
одновременно муфту блокировки так, что
она разъединяется с зубчатым венцом
корпуса дифференциала.
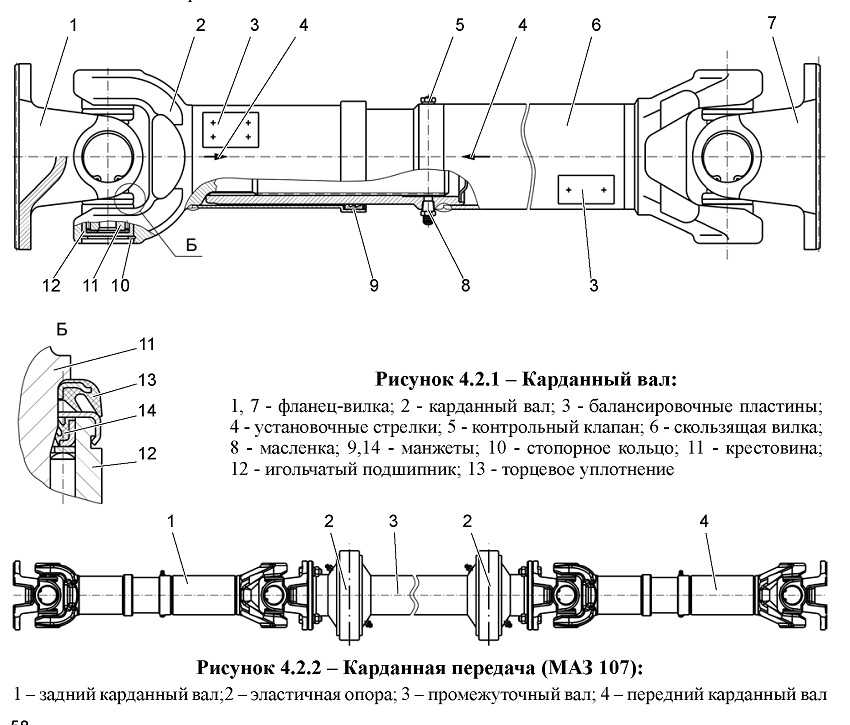
Устройство
и работа главных передач и межколесных
дифференциалов
ведущих мостов.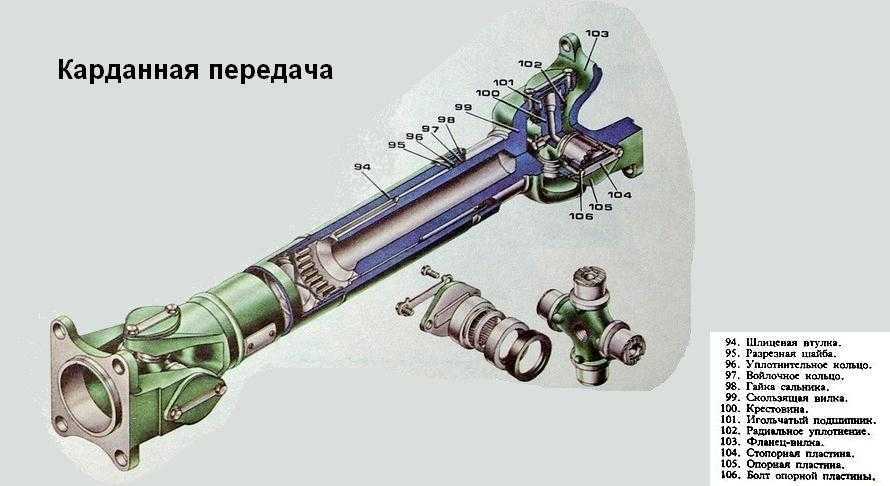
Картер
главной передачи 3
(рис.
4.24) крепится к балке моста болтами.
Плоскость разъема уплотняется паронитовой
прокладкой толщиной 0,8 мм. В полости
картера устанавливаются пара цилиндрических
с косыми зубьями шестерен. Ведущая
коническая шестерня 13
установлена
на шлицах ведущего проходного вала 15
(для
среднего моста). Этот вал опирается на
два конических роликовых подшипника
12
и
18,
которые
закрыты крышками, имеющими регулировочные
прокладки // и 16.
Выходные
концы вала уплотняются самоподжимными
сальниками, защищенными грязеотражательными
кольцами. На концах проходного вала
(для среднего моста) устанавливаются
фланцы карданных шарниров 10,
17. Фланец
17
привода
к заднему мосту меньше по размерам, чем
фланец 10,
на
который подводится крутящий момент от
межосевого дифференциала раздаточной
коробки.
Промежуточный
вал 9 главной передачи установлен на
цилиндрическом роликовом 2
и
двух конических роликовых подшипниках
6,
смонтированных
в стакане 5. Под фланец стакана и крышку
подшипников поставлены регулировочные
прокладки 7 и 8. Ведущая цилиндрическая
Ведущая цилиндрическая
шестерня 4
выполнена
заодно с промежуточным валом, а
ведомая
коническая шестерня / напрессована на
конец этого вала и дополнительно
закреплена на нем шпонкой. Ведомая
цилиндрическая шестерня 22
соединена
с половинами (чашками) корпуса
дифференциала, каждая из которых
опирается на конический подшипник.
В
корпусе дифференциала размещены
крестовина 21,
четыре
сателлита 20
на
втулках 25,
две
полуосевые шестерни 19,
под
которыми установлены опорные шайбы 23.
Полуосевые
шестерни соединяются шлицами с полуосями
привода колес. Дифференциал симметричный
и распределяет крутящий момент практически
поровну ежду правым и левым колесами.
Главные
передача и дифференциал переднего и
заднего мостов имеют аналогичное
устройство. На ведущем валу каждого из
этих мостов имеется по одному фланцу
карданного шарнира со стороны карданной
передачи, а с внешней стороны концы
валов закрыты крышками.
Ошибка
- Автомобиль — модели, марки
- Устройство автомобиля
- Ремонт и обслуживание
- Тюнинг
- Аксессуары и оборудование
- Компоненты
- Безопасность
- Физика процесса
- Новичкам в помощь
- Приглашение
- Официоз (компании)
- Пригородные маршруты
- Персоны
- Наши люди
- ТЮВ
- Эмблемы
- А
- Б
- В
- Г
- Д
- Е
- Ё
- Ж
- З
- И
- Й
- К
- Л
- М
- Н
- О
- П
- Р
- С
- Т
- У
- Ф
- Х
- Ц
- Ч
- Ш
- Щ
- Ъ
- Ы
- Ь
- Э
- Ю
- Я
Навигация
- Заглавная страница
- Сообщество
- Текущие события
- Свежие правки
- Случайная статья
- Справка
Личные инструменты
- Представиться системе
Инструменты
- Спецстраницы
Пространства имён
- Служебная страница
Просмотры
Перейти к: навигация,
поиск
Запрашиваемое название страницы неправильно, пусто, либо неправильно указано межъязыковое или интервики название. Возможно, в названии используются недопустимые символы.
Возможно, в названии используются недопустимые символы.
Возврат к странице Заглавная страница.
Если Вы обнаружили ошибку или хотите дополнить статью, выделите ту часть текста статьи, которая нуждается в редакции, и нажмите Ctrl+Enter. Далее следуйте простой инструкции.
Веб-сайт кабинета физики
Задание 2D4: Анализ статического равновесия
Цели:
- Учащийся должен уметь физически анализировать ситуации, в которых груз удерживается двумя или более тросами, расположенными под углом к горизонтали.
- Учащийся должен уметь выполнять расчеты, чтобы математически связать натяжение троса, поддерживающего знак, с углом к горизонтали и массой знака.
Чтение:
Учебный класс физики, Векторы и движение в двух измерениях Модуль, Урок 3, Часть b
Класс физики, раздел «Векторы и движение в двух измерениях», урок 3, часть c
Знак массой m симметрично подвешен на двух тросах, образующих угол тета с горизонтом (см. | |
Определение Равновесие :
| |
Если объект находится в равновесии, то отдельные силы, действующие на объект, уравновешены. Неуравновешенной силы нет — результирующая сила равна 0 ньютонов. Все вертикальные силы уравновешиваются, и все горизонтальные силы уравновешиваются. В этой ситуации действуют две силы, расположенные под углами к вертикали и горизонтали (силы растяжения). Обычная стратегия состоит в том, чтобы сначала разложить любую силу, направленную под углом к оси, на компоненты или части, направленные вдоль оси. | |
Сила натяжения имеет горизонтальную и направленную вверх составляющую или влияние на знак. Горизонтальная составляющая (F x ) можно вычислить как F десятков • косинус() где угол, который сила образует с горизонтом. Восходящая составляющая (F y ) может быть рассчитана как F десятков • синус(), где — угол, который сила образует с горизонтом. F x = F десятки • косинус() F y = F десятки • синус() | |
Сила тяжести ( F grav ), действующая на объект, может быть определена по массе объекта с помощью уравнения: F грав = масса • г где g — ускорение, вызванное только силой тяжести. | |
Что понимается под равновесием? Что верно в отношении сил, если объект находится в равновесии? Как можно применить концепции равновесия для анализа ситуации, в которой знак поддерживается тросами? |
Знак подвешивается симметрично на двух тросах, образующих угол с горизонтом (см. схему). Знак находится в состоянии статического равновесия. Какие из следующих утверждений верны? Перечислите все применимые… | |
Определение Равновесие :
| |
Если объект находится в равновесии, то отдельные силы, действующие на объект, уравновешены. Неуравновешенной силы нет — результирующая сила равна 0 ньютонов. Все вертикальные силы уравновешиваются, и все горизонтальные силы уравновешиваются. При добавлении в виде векторов их сумма должна составлять 0 Н. Имеются два троса, направленные под углами к горизонтальной и вертикальной осям. Эти тросы воздействуют на знак силами натяжения и имеют горизонтальную и вертикальную составляющие. Единственной другой силой, действующей на знак, является сила тяжести. Две вертикальные составляющие напряжения должны действовать вместе, чтобы уравновесить силу тяжести. Горизонтальные составляющие силы натяжения являются единственными горизонтальными силами и должны уравновешивать друг друга. | |
Некоторые студенты имеют неправильную привычку думать, что объект, находящийся в равновесии, — это объект, на который все силы равны. | |
Что понимается под равновесием? Что верно в отношении сил, если объект находится в равновесии? Когда знак поддерживается тросами, что можно сказать о вертикальной и горизонтальной составляющих натяжения? |
Знак массой 100 Н симметрично поддерживается двумя тросами, образующими с горизонтом угол 20,0 градусов. | |
Определение Равновесие :
| |
Если знак находится в равновесии, то отдельные силы, действующие на знак, уравновешены. Таким образом, неуравновешенной силы нет — результирующая сила равна 0 ньютонов. Чтобы результирующая сила была равна 0 Н, должен быть баланс как горизонтальных, так и вертикальных сил. Если знак поддерживается двумя тросами, каждый трос должен тянуться с достаточной восходящей силой, чтобы уравновесить вес знака (нисходящая сила тяжести). Таким образом, если знак весит 100 Н, восходящие компоненты натяжения в каждом тросе должны вместе создавать восходящую силу 100 Н. | |
Что верно в отношении сил, если объект находится в равновесии? Когда знак поддерживается двумя тросами, как соотносится вес знака с вертикальными составляющими натяжения? |
Цветочный горшок массой 20,0 Н симметрично поддерживается тремя тросами, образующими с горизонтом угол 60,0 градусов. Одиночный трос будет тянуть вверх цветочный горшок с силой ____ ньютонов. (Примечание: числа рандомизированы и, вероятно, отличаются от приведенных здесь чисел.) | |
Определение Равновесие :
| |
Если цветочный горшок находится в равновесии, то отдельные силы, действующие на горшок, уравновешены. Чистая сила равна 0 ньютонов. Чтобы результирующая сила была равна 0 Н, должен быть баланс как горизонтальных, так и вертикальных сил. Если цветочный горшок поддерживается тросами, все тросы вместе должны тянуться с достаточной восходящей силой, чтобы уравновесить вес (нисходящую силу тяжести) цветочного горшка. Таким образом, если котел весит 100 Н и имеется четыре троса, направленные вверх компоненты натяжения в каждом тросе должны вместе создавать восходящую силу 100 Н. Если тросы расположены симметрично, то вес горшка распределяется поровну между четырьмя тросами. Каждый из четырех тросов будет иметь вертикальную составляющую 25 Н, чтобы обеспечить восходящую силу в 100 Н, необходимую для балансировки веса горшка. | |
В вопросе предлагается определить величину тяги вверх , действующей на трос. | |
Что верно в отношении сил, если объект находится в равновесии? Когда знак поддерживается двумя тросами, как соотносится вес знака с вертикальными составляющими натяжения? |
Знак висит на двух тросах, каждый из которых составляет угол тета с горизонтом. Поскольку угол тета УВЕЛИЧИВАЕТСЯ (или УМЕНЬШАЕТСЯ), вес знака ____; усилие натяжения троса ____; а вертикальная составляющая силы натяжения ____. | |
Определение Равновесие :
| |
Если знак остается в равновесии, то все три отдельные силы, действующие на него, должны оставаться уравновешенными при изменении угла. Изменение угла повлияет на величину горизонтального натяжения троса, что, в свою очередь, повлияет на величину натяжения троса. Чем более горизонтально выровнен кабель, тем больше он будет тянуть по горизонтали. Таким образом, уменьшение угла увеличивает горизонтальную составляющую напряжения, а увеличение угла уменьшает горизонтальную составляющую напряжения. Эти изменения горизонтальных составляющих приведут к такому же изменению общего натяжения троса. | |
Некоторым учащимся, у которых есть трудности с понятием веса, будет трудно ответить на этот вопрос. Вес знака зависит от его массы. Не дайте себя обмануть! Изменения в кабелях, поддерживающих знак, не повлияют на вес знака. Другие трудности в этом вопросе связаны с вертикальной составляющей силы натяжения. Для знака, подвешенного симметрично на двух тросах, вес знака распределяется поровну на два троса. Таким образом, тяга тросов вверх (только по вертикали) составляет половину веса знака. Изменения угла повлияют на горизонтальную составляющую натяжения; но вертикальная составляющая напряжения должна быть достаточной, чтобы уравновесить половину веса знака. | |
Когда знак поддерживается двумя тросами, как соотносится вес знака с вертикальными составляющими натяжения? Что верно в отношении сил, если объект находится в равновесии? |
Предположим, вы повесили картину на двух тросах в своей гостиной. | |
Определение Равновесие :
| |
Если картина находится в равновесии, то все три отдельные силы, действующие на нее, должны быть уравновешены независимо от угла. Изменение угла повлияет на величину горизонтального натяжения троса, что, в свою очередь, повлияет на величину натяжения троса. Чем более горизонтально выровнен кабель, тем больше он будет тянуть по горизонтали. Это увеличенное горизонтальное натяжение увеличит натяжение троса. | |
Когда знак поддерживается двумя тросами, как соотносится вес знака с вертикальными составляющими натяжения? Что верно в отношении сил, если объект находится в равновесии? |
Знак массой 3,66 кг подвешен симметрично на двух тросах, образующих с горизонтом угол 37,2°. (Примечание: ваши номера выбраны случайным образом и, вероятно, отличаются от номеров, перечисленных здесь.) | |
Успех решения проблемы в физике зависит от тщательно продуманной стратегии. Приведенная ниже стратегия окажется полезной в этом вопросе:
| |
Все отдельные силы, действующие на знак, должны уравновешиваться. Тросы расположены под углом, поэтому каждый трос имеет вертикальную и горизонтальную составляющие натяжения. Так как знак подвешен симметрично, вес знака распределяется поровну на каждый трос. Таким образом, вертикальная составляющая натяжения в каждом тросе одинакова и равна половине веса знака. | |
Натяжение троса представляет собой вектор силы. Векторы представлены векторными стрелками. Такие векторы, как этот, имеют горизонтальную и вертикальную составляющие. Компоненты часто представляются путем построения прямоугольного треугольника вокруг вектора, так что вектор является гипотенузой прямоугольного треугольника. Тригонометрические функции можно использовать для связи значений компонентов со значением вектора. Легендарный SOH CAH TOA применяется к силовому треугольнику в этом вопросе, чтобы получить следующие результаты. F x = F десятки • косинус F y = F десятки • синус где = угол между кабелем и горизонталью | |
Сила тяжести ( F grav ), действующая на объект, может быть определена по массе объекта с помощью уравнения: F грав = масса • г где g — ускорение, вызванное только силой тяжести. Значение г на Земле составляет 9,8 м/с/с. | |
Как можно применить концепции равновесия для анализа ситуации, в которой знак поддерживается тросами? |
Знак массой 42,6 Н подвешен симметрично на двух тросах, образующих с горизонтом угол 17,5°. (Примечание: ваши номера выбраны случайным образом и, вероятно, отличаются от номеров, перечисленных здесь.) | |
Успех решения проблемы в физике зависит от тщательно продуманной стратегии. Приведенная ниже стратегия окажется полезной в этом вопросе:
| |
Все отдельные силы, действующие на знак, должны уравновешиваться. Тросы расположены под углом, поэтому каждый трос имеет вертикальную и горизонтальную составляющие натяжения. Так как знак подвешен симметрично, вес знака распределяется поровну на каждый трос. Таким образом, вертикальная составляющая натяжения в каждом тросе одинакова и равна половине веса знака. | |
Натяжение троса представляет собой вектор силы. Векторы представлены векторными стрелками. Такие векторы, как этот, имеют горизонтальную и вертикальную составляющие. Компоненты часто представляются путем построения прямоугольного треугольника вокруг вектора, так что вектор является гипотенузой прямоугольного треугольника. Тригонометрические функции можно использовать для связи значений компонентов со значением вектора. Легендарный SOH CAH TOA применяется к силовому треугольнику в этом вопросе, чтобы получить следующие результаты. F x = F десятки • косинус F y = F десятки • синус где = угол между кабелем и горизонталью. | |
Как можно применить концепции равновесия для анализа ситуации, в которой знак поддерживается тросами? |
Светильник массой 82,2 Н подвешен симметрично на трех тросах (или четырех тросах), образующих с горизонтом угол 67,1 градуса. (Примечание: ваши номера выбраны случайным образом и, вероятно, отличаются от номеров, перечисленных здесь.) | |
Успех решения проблемы в физике зависит от тщательно продуманной стратегии. Приведенная ниже стратегия окажется полезной в этом вопросе:
| |
Все отдельные силы, действующие на знак, должны уравновешиваться. Тросы расположены под углом, поэтому каждый трос имеет вертикальную и горизонтальную составляющие натяжения. Так как знак подвешен симметрично, вес знака распределяется поровну на каждый трос. Таким образом, вертикальная составляющая натяжения в каждом тросе одинакова. При наличии трех тросов вертикальная составляющая в каждом из них равна одной трети веса знака. Если тросов четыре, то вертикальная составляющая в каждом из них равна одной четвертой веса знака. | |
Натяжение троса представляет собой вектор силы. Векторы представлены векторными стрелками. Такие векторы, как этот, имеют горизонтальную и вертикальную составляющие. Тригонометрические функции можно использовать для связи значений компонентов со значением вектора. Легендарный SOH CAH TOA применяется к силовому треугольнику в этом вопросе, чтобы получить следующие результаты. F x = F десятки • косинус F y = F десятки • синус где = угол между кабелем и горизонталью. | |
Как можно применить концепции равновесия для анализа ситуации, в которой знак поддерживается тросами? |
Подписывайтесь на нас
Несбалансированный крутящий момент: определение, примеры и уравнение
Баланс: это то, к чему вы, вероятно, стремитесь в своей повседневной жизни, например, к поиску здорового баланса между школой и жизнью при напряженном графике. Точно так же, как ваша повседневная жизнь наполнена домашним заданием, друзьями, хобби и другими обязанностями, вокруг вас постоянно действуют всевозможные различные силы. Ваш график, вероятно, кажется сбалансированным, когда у вас есть нужное количество времени для каждой задачи, а силы находятся в состоянии равновесия, когда сбалансированы до нулевой чистой силы. С другой стороны, ваше расписание, вероятно, кажется беспокойным и несбалансированным, если вам не хватает часов в сутках, чтобы все сделать, из-за чего вы отстаете от заданий, а ваше расписание выбивается из колеи. Неуравновешенный крутящий момент — то же самое — если сила не уравновешена, в результате мы станем свидетелями изменений в движении.
Точно так же, как ваша повседневная жизнь наполнена домашним заданием, друзьями, хобби и другими обязанностями, вокруг вас постоянно действуют всевозможные различные силы. Ваш график, вероятно, кажется сбалансированным, когда у вас есть нужное количество времени для каждой задачи, а силы находятся в состоянии равновесия, когда сбалансированы до нулевой чистой силы. С другой стороны, ваше расписание, вероятно, кажется беспокойным и несбалансированным, если вам не хватает часов в сутках, чтобы все сделать, из-за чего вы отстаете от заданий, а ваше расписание выбивается из колеи. Неуравновешенный крутящий момент — то же самое — если сила не уравновешена, в результате мы станем свидетелями изменений в движении.
Крутящий момент — это крутящая и вращающая сила рычагов, вращающихся вентиляторов и вращающихся планет. Когда крутящий момент неуравновешен, мы наблюдаем изменения во вращательном движении. В этой статье мы рассмотрим, что такое крутящий момент, рассмотрим уравнения, которые мы используем для расчета несбалансированного крутящего момента, обсудим распространенные типы проблем и рассмотрим некоторые примеры несбалансированного крутящего момента.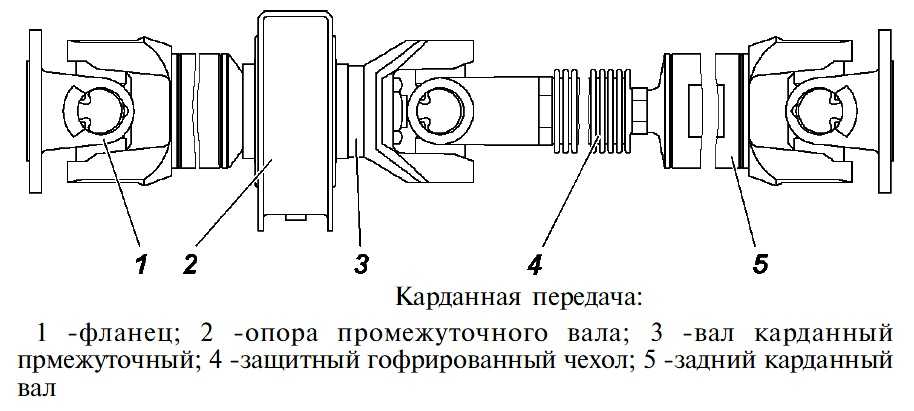
Что такое крутящий момент?
Начнем обсуждение несбалансированного крутящего момента с рассмотрения определения крутящего момента. Напомним, что крутящий момент — это сила, вызывающая вращательное движение, такое как крутящее или уравновешивающее движение. 92}}\). Вы регулярно наблюдаете, испытываете и применяете крутящий момент в повседневной жизни. Каждый раз, когда вы используете ручку крана, дверную ручку или рулевое колесо, вы прикладываете силу на расстоянии, что вызывает изменение движения!
Нажатие на дверь с места расположения дверной ручки создает крутящий момент, вращая дверь вокруг ее петель, Wikimedia Commons CC BY-SA 3.0
Давайте посмотрим, как крутящий момент вызывает знакомое движение толкания двери. Дверь поворачивается вокруг своих петель, небольшой детали, которая прикрепляет дверь к раме и ограничивает диапазон ее движения. Когда вы поворачиваете дверную ручку, вы отсоединяете дверь от рамы, что затем позволяет вам приложить усилие, толкающее ее. Расстояние между петлями и точкой приложения этой силы называется плечом рычага. Результатом вашего толчка является приложенный к петлям крутящий момент, перпендикулярный силе, приложенной вашим толчком, и дверь распахивается.
Расстояние между петлями и точкой приложения этой силы называется плечом рычага. Результатом вашего толчка является приложенный к петлям крутящий момент, перпендикулярный силе, приложенной вашим толчком, и дверь распахивается.
Плечо рычага — это перпендикулярное расстояние (прямой угол) от оси вращения или точки опоры до места приложения силы.
Это расстояние обычно выражается с помощью переменных \(r\) или \(d\). Размещение дверных ручек на стороне, противоположной точкам поворота, не является ошибкой — увеличение расстояния между точкой поворота и местом, где мы прикладываем усилие, уменьшает общее количество силы, необходимой для поворота двери. Это крутящий момент в действии! Попробуйте открыть дверь на разном расстоянии от петель, чтобы убедиться в этом.
Определения сбалансированного и несбалансированного крутящего момента
Теперь, когда мы освежили наше понимание крутящего момента, давайте определим еще два связанных понятия: сбалансированный и неуравновешенный крутящий момент.
Сбалансированный крутящий момент возникает, когда крутящие моменты и силы по обе стороны от точки вращения в системе равны, что приводит к статическому равновесию системы либо в состоянии покоя, либо с нулевым ускорением вращения.
Математически мы можем записать сбалансированный крутящий момент как:
\begin{align*} \Sigma \tau=\tau_{\mathrm{net}}=0\end{align*}
где \(\tau_{\mathrm{net}}\) — чистый крутящий момент, выражается строчной греческой буквой тау .
В повседневной жизни уравновешенный крутящий момент может выглядеть как неподвижная полка, прикрепленная к стене, поддерживаемая центральным кронштейном. Размещение предметов одинакового веса по обе стороны от центральной опоры будет удерживать полку в статическом равновесии с уравновешенными крутящими моментами.
Давайте сравним это с несбалансированным крутящим моментом, который мы определяем следующим образом:
Неуравновешенный крутящий момент возникает, когда любые крутящие моменты и силы в системе не уравновешиваются, что приводит к ускорению вращения в направлении чистого крутящего момента.
Математически мы можем записать неуравновешенный момент как:
\begin{align*} \Sigma \tau &\neq 0 \\ \tau_{\mathrm{net}}&\neq 0 \end{align*}
Опираясь на наш пример с полкой, мы можем создать несбалансированные крутящие моменты, сложив кучу объектов на левом конце полки, оставив правый конец пустым. Если длина полки равна \(L\), то вес сложенных объектов под действием силы тяжести создает чистый крутящий момент на расстоянии \(\frac{L}{2}\) от центра. Неуравновешенный крутящий момент вызывает ускорение вращения, и полка будет поворачиваться — конечно, при условии, что полка может вращаться вокруг своей опоры, а не просто отламываться от стены.
Уравнения для несбалансированного крутящего момента
Вы уже видели большинство уравнений для крутящего момента — крутящий момент является несбалансированным, когда чистый крутящий момент \(\tau_{\mathrm{net}}\) не равен нулю в расчетах. Начнем с того, что вспомним уравнение для крутящего момента, записанное как произведение приложенной силы \(F\), радиального расстояния между осью вращения и точкой приложения силы \(r\) и угла \(\theta\) между двумя:
\begin{align*} \tau=r_{\perp} F=rF\mathrm{sin\theta} \end{align*} 92}}\).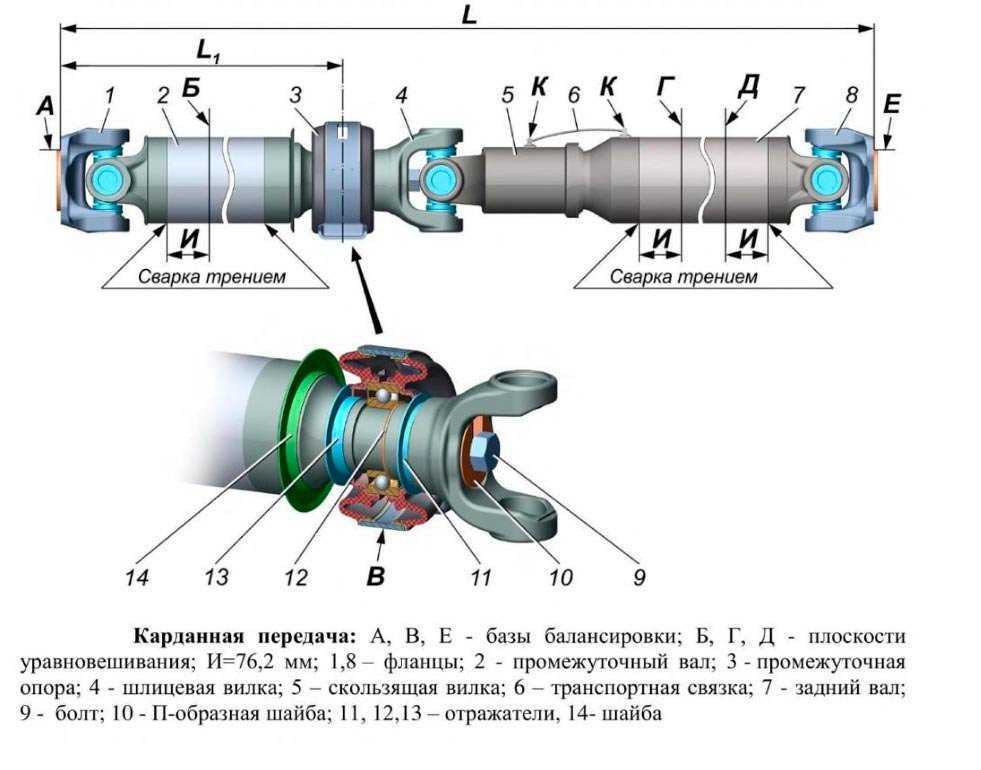 Поскольку крутящий момент зависит от момента инерции, мы не можем игнорировать форму объекта. Мы можем использовать оба этих уравнения для расчета значения приложенного крутящего момента в неуравновешенной системе. Но помните, это верно для чистого крутящего момента , поэтому обязательно обращайте внимание на то, что вы рассчитываете в задаче! У нас есть последний набор уравнений, которые мы можем использовать для расчета крутящего момента:
Поскольку крутящий момент зависит от момента инерции, мы не можем игнорировать форму объекта. Мы можем использовать оба этих уравнения для расчета значения приложенного крутящего момента в неуравновешенной системе. Но помните, это верно для чистого крутящего момента , поэтому обязательно обращайте внимание на то, что вы рассчитываете в задаче! У нас есть последний набор уравнений, которые мы можем использовать для расчета крутящего момента:
\begin{align*} \tau_1&=\tau_2 \\ F_1r_2&=F_2r_2 \end{align*}
и, если речь идет о гравитационной силе:
\begin{align*} m_1gr_1&=m_2gr_2 \\ m_1r_1&=m_2r_2 \end{align*}
Эти уравнения полезны для определения массы или радиального расстояния требуется для балансировки системы с неуравновешенными моментами.
Вращение, вызванное неуравновешенным крутящим моментом
Теперь, когда мы рассмотрели уравнения, лежащие в основе проблем неуравновешенного крутящего момента, давайте более подробно рассмотрим, как это выглядит концептуально. Помните уравнение, которое мы ранее ввели, \(\tau=I \alpha\)? момент инерции , \(I\), является мерой сопротивления изменению угловой скорости объекта. Это важное свойство определяется массой и распределением массы от оси вращения объекта.
Помните уравнение, которое мы ранее ввели, \(\tau=I \alpha\)? момент инерции , \(I\), является мерой сопротивления изменению угловой скорости объекта. Это важное свойство определяется массой и распределением массы от оси вращения объекта.
Если оставить момент инерции постоянным, т. е. величина останется неизменной, то получим следующую связь между крутящим моментом и угловым ускорением:
\begin{align*} \tau \propto \alpha \end{align*}
или прописью, крутящий момент пропорционален угловому ускорению. Это означает, что при увеличении крутящего момента увеличивается и угловое ускорение. Это соотношение также ясно показывает, что если чистый крутящий момент равен нулю, не может быть никакого углового ускорения!
Правило правой руки показывает направление вектора крутящего момента. Указание указательным и средним пальцами в направлении радиуса и приложенной силы при вытянутом большом пальце покажет направление крутящего момента, Wikimedia Commons CC BY-SA 3. 0
0
Итак, когда у нас есть ненулевой крутящий момент в системе, эта неуравновешенная крутящая сила приведет к изменению вращательного ускорения, заставляя систему вращаться вокруг своей оси вращения в направлении вектора чистого крутящего момента. Направление вектора крутящего момента перпендикулярно силе и радиусу \(r\) от оси . Если вы не уверены в направлении крутящего момента, используйте правило правой руки , удобный прием для проверки направления перпендикулярного вектора:
Укажите указательным пальцем в направлении радиального расстояния.
Укажите средним пальцем в направлении приложенной силы.
Держите большой палец прямо. Ваш большой палец будет указывать в направлении вектора крутящего момента.
Если приложенная сила вращается вокруг центральной оси, вместо этого согните пальцы в направлении радиального расстояния к приложенной силе. Это укажет на движение по часовой стрелке или против часовой стрелки.
 Удерживая большой палец наружу, вы укажете направление крутящего момента.
Удерживая большой палец наружу, вы укажете направление крутящего момента.
Вы будете часто сталкиваться с правилом правой руки во время изучения физики, так что запишите этот трюк прямо сейчас, даже если вы еще не запомнили его! Это важный инструмент для перекрестных произведений , о котором вы узнаете больше в математических и более продвинутых курсах физики.
Расчеты несбалансированного крутящего момента и типы задач
Вы, вероятно, столкнетесь с некоторыми проблемами несбалансированного крутящего момента во время изучения физики. Давайте рассмотрим некоторые типы проблем, с которыми вы можете столкнуться, и шаги, которые вам необходимо предпринять для решения этих расчетов крутящего момента.
При возникновении любой проблемы вы всегда должны определять, что представляет собой ваша система, и учитывать все горизонтальные и вертикальные компоненты любых задействованных сил. Крутящий момент также может быть положительным или отрицательным, так что следите за знаками!
Балансировка качелей или рычага в неравновесном состоянии
Классическая физическая задача с неуравновешенным крутящим моментом включает балансировку качелей или аналогичной установки с доской на вершине точки опоры. Вас могут попросить сбалансировать качели, чтобы они находились в равновесии вращения параллельно земле, основываясь на заданном наборе начальных условий.
Вас могут попросить сбалансировать качели, чтобы они находились в равновесии вращения параллельно земле, основываясь на заданном наборе начальных условий.
Давайте подумаем, какие шаги нам, возможно, придется предпринять, чтобы решить эту проблему.
Какой информацией мы располагаем? Скорее всего, вам дадут три значения, одно из которых — масса или радиальное расстояние — неизвестны.
Какое количество мы пытаемся найти? Определите недостающее количество и помните, что цель состоит в том, чтобы сбалансировать крутящий момент с обеих сторон качелей. Нарисуйте схему, если нужно.
Какое уравнение мы должны использовать? Это зависит от первоначально предоставленной информации. Во многих случаях это будет \(m_1r_1=m_2r_2\), но обратите внимание на то, с каких переменных вы начинаете!
Изолируйте неизвестную переменную и решите.
Балансировка крутящего момента в мобиле
Балансировка мобиля — это задача, похожая на балансировку качелей, но часто с несколькими ярусами подвешенных масс, каждый из которых представляет собой отдельный рычаг.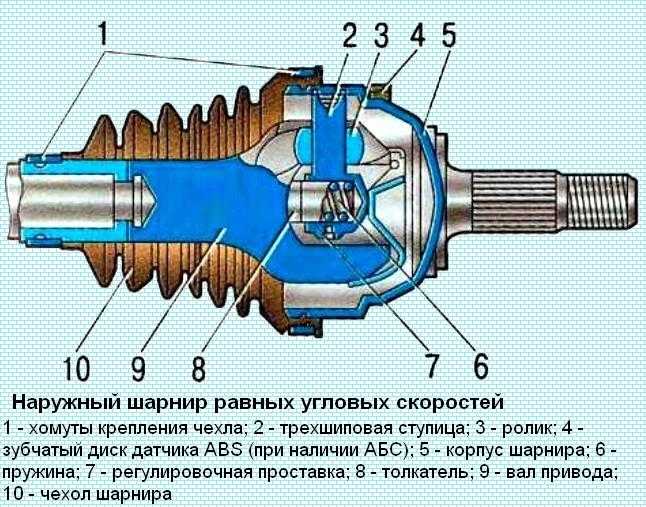 В мобильной задаче количество объектов, свисающих с каждого стержня, может быть разным. Эти типы расчета крутящего момента, по сути, являются расширением простого сценария качелей.
В мобильной задаче количество объектов, свисающих с каждого стержня, может быть разным. Эти типы расчета крутящего момента, по сути, являются расширением простого сценария качелей.
Создание мобильного телефона включает в себя балансировку подвесных масс на разных рычагах, Дэниел X. О’Нил через Flickr CC BY 2.0
Как мы можем решить эту проблему? Опять же, давайте рассмотрим различные компоненты и то, что нам нужно сделать, чтобы сбалансировать крутящие моменты.
Нарисуйте или изучите схему мобильного телефона. В этих задачах вам всегда будут даны длины стержней, а также плечи рычага (расстояние от веревки до каждого висящего предмета). Плечи рычага , а не , всегда будут равны половине длины стержня! Вам также будет дан вес на одной стороне самого нижнего яруса бытия.
Не обращайте внимания на вес каждого стержня и куска веревки и учитывайте только вес объектов, висящих на стержнях. Помните, что речь идет о силе гравитации, поэтому, если для начала нам дан вес , мы захотим использовать форму \(F_1r_1=F_2r_2\) уравнения крутящего момента.

Начиная с самого нижнего висящего яруса, примените уравнение балансировки крутящего момента и найдите недостающий вес.
Поднимитесь на каждый уровень и рассчитайте следующий вес, который будет удерживать мобиль в равновесии. Когда вы продвигаетесь вверх, обязательно используйте всего веса предыдущего уровня, чтобы найти значение следующего уровня.
Заполняйте диаграмму каждым значением, пока не рассчитаете все веса. Теперь вы сбалансировали подвесной мобиль!
Задачи второго закона с крутящим моментом и инерцией вращения
Последний тип задач, с которыми вы, вероятно, столкнетесь, аналогичен второму закону Ньютона. Вспомним, что второй закон движения Ньютона гласит, что сумма сил пропорциональна ускорению и обратно пропорциональна массе объекта:
\begin{align*} a=\frac{F_{\mathrm{net}}}{m} \end{align*}
где \(a\) — линейное ускорение. Второй закон Ньютона можно легко расширить, чтобы сформировать второй закон вращательного движения, зная, что сумма крутящих моментов пропорциональна угловому ускорению и обратно пропорциональна моменту инерции:
\begin{align*} a=\frac{ \tau_{\mathrm{net}}}{I} \end{align*}
В задачах такого типа вы, вероятно, для начала будете работать с другой информацией.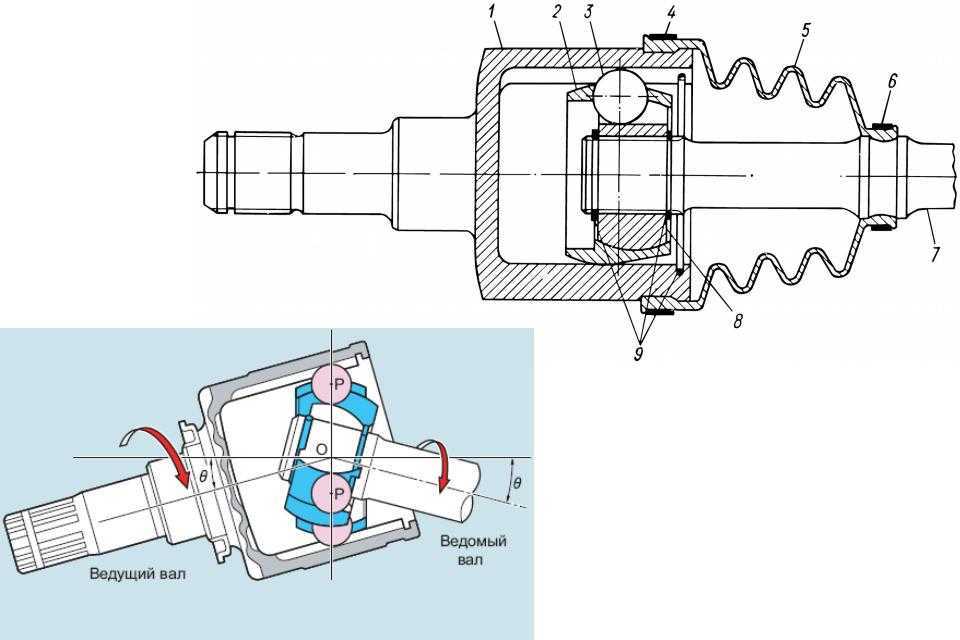 Мы все еще можем сбалансировать крутящие моменты, даже если мы не начинаем знать массы и радиальные расстояния — помните, что до тех пор, пока крутящие моменты с обеих сторон установлены равными друг другу:
Мы все еще можем сбалансировать крутящие моменты, даже если мы не начинаем знать массы и радиальные расстояния — помните, что до тех пор, пока крутящие моменты с обеих сторон установлены равными друг другу:
\begin{align*} \tau_1=\tau_2 \end{align*}
, тогда мы можем найти оставшуюся неизвестную переменную.
Вы не будете балансировать систему до статического равновесия во многих задачах с крутящим моментом. Вместо этого вам будет поручено найти чистый крутящий момент, зная форму объекта и информацию об ускорении вращения или какой-либо другой вариант расчета этого крутящего момента.
Примеры неуравновешенного крутящего момента
Давайте завершим обсуждение неуравновешенного крутящего момента на примере, начиная с проблемы несбалансированных качелей.
Ребенок весом \(\mathrm{30\,кг}\) сидит на одном конце длинных \(\mathrm{2,5\,м}\) качелей. Точка опоры качелей находится точно в центре. На каком расстоянии от оси должен сесть второй ребенок весом \(\mathrm{42\,кг}\), чтобы уравновесить качели параллельно земле?
Мы хотим сделать крутящие моменты равными по обе стороны уравнения:
\begin{align*} F_1r_1=F_2r_2 \end{align*}
и, поскольку нам дан вес, мы можем подставить эти числа in для гравитационной силы, вызывающей крутящие моменты. Помните, что в повседневном языке мы обычно выражаем вес в килограммах или фунтах. Однако вес из-за гравитации на самом деле равен ньютонам или фунтам силы. Еще один компонент, о котором следует подумать, — это угол; в этом сценарии угол параллели качелей с землей равен \(\theta=9\circ)=1}\), угол не влияет на наш расчет.
Помните, что в повседневном языке мы обычно выражаем вес в килограммах или фунтах. Однако вес из-за гравитации на самом деле равен ньютонам или фунтам силы. Еще один компонент, о котором следует подумать, — это угол; в этом сценарии угол параллели качелей с землей равен \(\theta=9\circ)=1}\), угол не влияет на наш расчет.
Ребенок на одном конце сидит на расстоянии \(\mathrm{\frac{2,5\,м}{2}=1,25\,м}\). Собрав все это вместе, мы находим:
\[\begin{align} r_2 &= \frac{F_1r_1}{F_2} \\ \mathrm{0,89\,m} &= \mathrm{\frac{30\,N \cdot1.25\,m}{42\,N}} \end{align}\]
Таким образом, второму ребенку придется сесть намного ближе к центру качелей, чтобы уменьшить крутящий момент, вызванный их вес и сделать систему стабильной.
92\). Какой предмет первым достигнет дна? Какой объект будет последним?
В этой задаче мы хотим сравнить относительные моменты инерции. Запомните отношения между угловым ускорением, моментом инерции и крутящим моментом:
\begin{align*} \tau &\propto \alpha \\ \alpha &\propto \frac{1}{I} \end{align* }
Зная это, мы ожидаем, что объект с наименьшим моментом инерции быстрее достигнет подножия холма.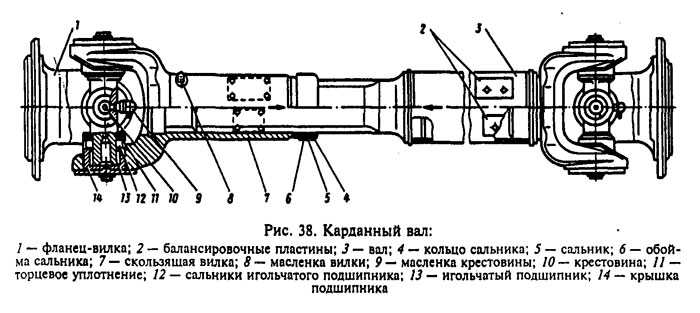 Сопоставив это вместе, мы находим:
Сопоставив это вместе, мы находим:
\begin{align*} I _{\mathrm{solid\, cyl.}} &\geq I _{\mathrm{sph.\, shell}} \geq I _{\mathrm{cyl.\, shell}} \ \ \ alpha _ {\ mathrm {твердый \, цилиндр}} &\ geq \ alpha _ {\ mathrm {sph. \, shell}} \ geq \ alpha _ {\ mathrm {цилиндр \, shell}} \ end {align * }
Поскольку сплошной цилиндр имеет наибольшую массу ближе всего к своей оси вращения, сплошной цилиндр будет ускоряться быстрее всех и первым достигнет дна. Цилиндрическая оболочка имеет всю свою массу на расстоянии \(r\) от своей оси вращения и имеет наибольший момент инерции.
При расчете крутящего момента и решении задач статического равновесия помните, что крутящий момент рассчитывается в определенной точке поворота. В условиях статического равновесия чистый крутящий момент всегда будет равен нулю во всех точках разворота, а это означает, что у нас есть свобода выбора точки разворота, где расчеты самые простые, например, где некоторые крутящие моменты уже уравновешены!
Неуравновешенный крутящий момент — основные выводы
- Крутящий момент — это векторная величина, измеряющая скручивающую силу, приложенную к телу, что приводит к изменению вращательного движения.



 схему). Натяжение каждого троса F десятки . Вертикальная составляющая силы натяжения равна F y ; горизонтальная составляющая F x . Какие из следующих математических утверждений верны?
схему). Натяжение каждого троса F десятки . Вертикальная составляющая силы натяжения равна F y ; горизонтальная составляющая F x . Какие из следующих математических утверждений верны? Таким образом, каждая сила натяжения имеет горизонтальную составляющую (F x ) и вертикальный компонент (F y ). Две вертикальные составляющие направлены вверх и вместе должны уравновешивать направленную вниз силу тяжести. Две горизонтальные составляющие направлены влево и вправо и должны уравновешивать друг друга.
Таким образом, каждая сила натяжения имеет горизонтальную составляющую (F x ) и вертикальный компонент (F y ). Две вертикальные составляющие направлены вверх и вместе должны уравновешивать направленную вниз силу тяжести. Две горизонтальные составляющие направлены влево и вправо и должны уравновешивать друг друга. Значение г на Земле составляет 9,8 м/с/с.
Значение г на Земле составляет 9,8 м/с/с.
 Ведь слово равновесие звучит так же, как слово равно . Но не дайте себя обмануть! Равновесие связано с балансом сил. Хотя возможно, что все силы могут быть равными, они не обязательно должны быть равными, чтобы быть уравновешенными. Например, объект с силой вверх 20 Н и силой вниз 20 Н, силой справа 8 Н и силой слева 8 Н находится в равновесии. Все ли силы уравновешены? Да! Все ли силы равны? Нет! 20 Н не равны 8 Н.
Ведь слово равновесие звучит так же, как слово равно . Но не дайте себя обмануть! Равновесие связано с балансом сил. Хотя возможно, что все силы могут быть равными, они не обязательно должны быть равными, чтобы быть уравновешенными. Например, объект с силой вверх 20 Н и силой вниз 20 Н, силой справа 8 Н и силой слева 8 Н находится в равновесии. Все ли силы уравновешены? Да! Все ли силы равны? Нет! 20 Н не равны 8 Н. Одиночный трос будет тянуть вверх знак с силой ____ ньютонов. (Примечание: числа рандомизированы и, вероятно, отличаются от приведенных здесь чисел.)
Одиночный трос будет тянуть вверх знак с силой ____ ньютонов. (Примечание: числа рандомизированы и, вероятно, отличаются от приведенных здесь чисел.)

 Слово вверх по имеет решающее значение для вопроса. Вопрос сосредоточен на вертикальной составляющей напряжения в знаке, а не просто на общей величине напряжения в знаке.
Слово вверх по имеет решающее значение для вопроса. Вопрос сосредоточен на вертикальной составляющей напряжения в знаке, а не просто на общей величине напряжения в знаке.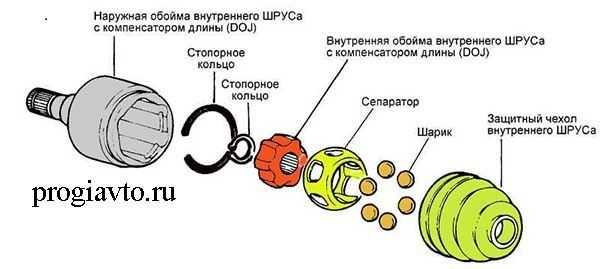

 Вы рассматриваете три различные угловые ориентации, как показано на рисунке. Какая ориентация — А, В или С — приведет к наименьшему натяжению (или наибольшему натяжению) тросов?
Вы рассматриваете три различные угловые ориентации, как показано на рисунке. Какая ориентация — А, В или С — приведет к наименьшему натяжению (или наибольшему натяжению) тросов?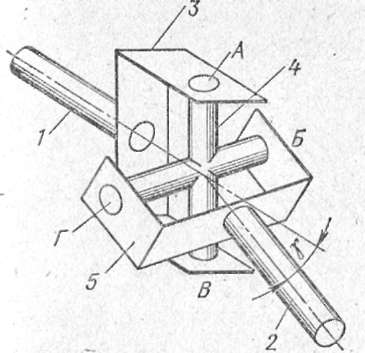 Нарисуйте диаграмму свободного тела и выполните тригонометрический анализ, чтобы определить натяжение одного из тросов.
Нарисуйте диаграмму свободного тела и выполните тригонометрический анализ, чтобы определить натяжение одного из тросов. Обозначьте угол. См. раздел Math Magic ниже.
Обозначьте угол. См. раздел Math Magic ниже. Компоненты являются катетами прямоугольного треугольника.
Компоненты являются катетами прямоугольного треугольника. Нарисуйте диаграмму свободного тела и выполните тригонометрический анализ, чтобы определить натяжение одного из тросов.
Нарисуйте диаграмму свободного тела и выполните тригонометрический анализ, чтобы определить натяжение одного из тросов.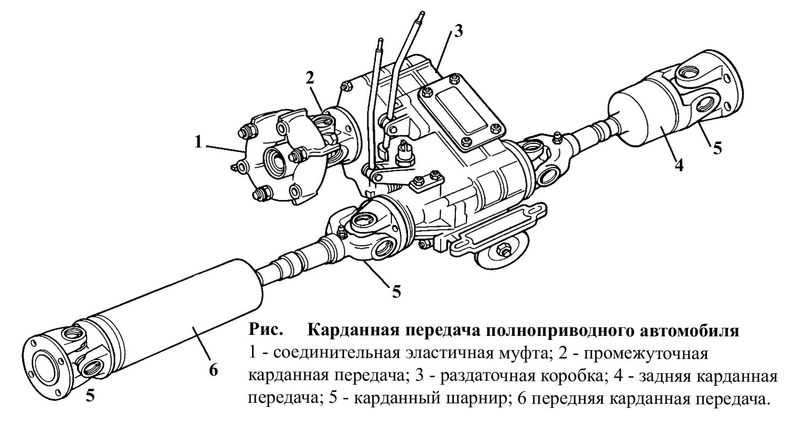
 Компоненты являются катетами прямоугольного треугольника.
Компоненты являются катетами прямоугольного треугольника. Нарисуйте диаграмму свободного тела и выполните тригонометрический анализ, чтобы определить натяжение одного из тросов.
Нарисуйте диаграмму свободного тела и выполните тригонометрический анализ, чтобы определить натяжение одного из тросов.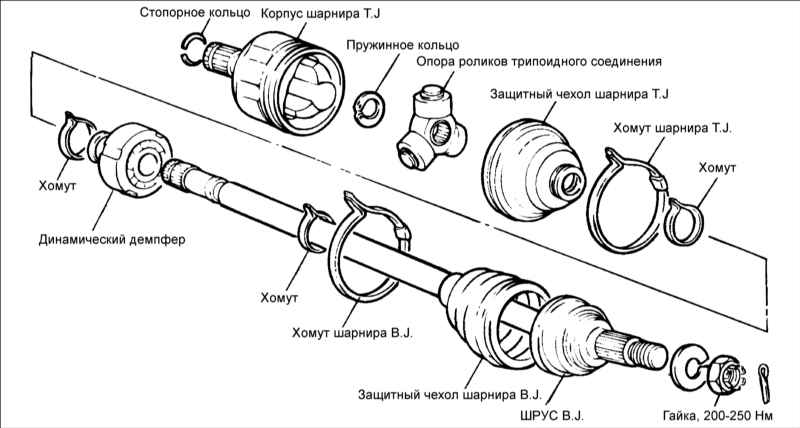
 Компоненты часто представляются путем построения прямоугольного треугольника вокруг вектора, так что вектор является гипотенузой прямоугольного треугольника. Компоненты являются катетами прямоугольного треугольника.
Компоненты часто представляются путем построения прямоугольного треугольника вокруг вектора, так что вектор является гипотенузой прямоугольного треугольника. Компоненты являются катетами прямоугольного треугольника. Удерживая большой палец наружу, вы укажете направление крутящего момента.
Удерживая большой палец наружу, вы укажете направление крутящего момента.

