Содержание
Доклад на тему «Обучение учащихся решению текстовых задач на сплавы и смеси»
Доклад
на тему «Обучение учащихся решению текстовых задач на сплавы и смеси»
Клокова
Г.А.
1.
Теоретические основы решения задач на сплавы и смеси
Задачи
на смеси, сплавы и проценты всегда вызывали сложности у учащихся.
Статистические данные по анализу результатов ЕГЭ по математике показывают, что
решаемость задания, содержащего текстовую задачу, приблизительно равна 30%.
Данные задачи
имеют практическое значение, являются хорошим средством развития мышления
учащихся. Они расширяют базовый курс математики и позволяют учащимся осознать
практическую ценность математики. Задачи на растворы, смеси и сплавы обладают
диагностической и прогностической ценностью, то есть с их помощью можно
проверить знания основных разделов школьной математики, уровень математического
и логического мышления, первоначальные навыки исследовательской деятельности,
то есть лишний раз проверить и оценить свои способности к математике. При
При
решении задач на растворы, смеси и сплавы очевидны межпредметные связи с
химией, физикой и экономикой, знание этого повышает учебную мотивацию учащихся
по всем предметам.
Трудности
при решении этих задач могут возникнуть на различных этапах:
- составления
математической модели ( уравнения, системы уравнений, неравенства) - решения
полученной модели; - анализа
математической модели ( по причине кажущейся ее неполноты: не хватает
уравнений в системе или слишком много неизвестных и пр.)
Решение задач на смеси, сплавы, растворы требует
определенной теоретической базы.
Это различные определения, такие как концентрация,
процентное содержание и др., а также и всевозможные допущения, например:
1)
всё, что мы рассматриваем, считается однородным;
2)
все процессы происходят мгновенно;
3)
полученное вещество состоит из смешиваемых веществ и равно сумме их объемов;
4)
величины, получаемые в результате вычислений, не могут быть со знаком минус.
Существует несколько способов решения задач на слияние
растворов. Например, можно воспользоваться расчетной формулой, как это делают
на уроках химии. Из области математики можно пользоваться графическим или же
алгебраическим методами. Более простым в применении является метод, в котором
указанные задачи решают по «правилу креста».
Задачи на
смеси и сплавы бывают двух видов:
1.
Две
смеси определенной массы с некоторой концентрацией вещества сливают вместе.
Нужно определить массу и концентрацию этого вещества в новой смеси.
2.
В
некоторый раствор, с некоторой концентрацией вещества, добавляют, например,
чистую воду (с нулевой концентрацией этого вещества). Нужно определить, какой
стала концентрация вещества.
В задачах
на смеси и сплавы важно уметь определять концентрацию и массу вещества.
Концентрация
вещества
— это отношение массы или объема вещества к массе или объему всего
раствора. Как правило, концентрация выражается в процентах.
Масса
раствора равна
сумме масс всех составляющих.
Алгоритм
решения задач на смеси и сплавы:
1.
Определить,
какое вещество влияет на концентрацию раствора (главное вещество).
2.
Следить
за весом главного вещества при добавлении других веществ в раствор.
3.
Исходя
из данных об изменениях состояния главного вещества — сделать выводы.
Как правило,
концентрация выражается в процентах.
Процент – это
сотая доля числа.
Она может выражаться либо в виде десятичной дроби (0,11), либо в
виде процента (11%).
Мысль 1
Масса |
Если мы смешаем 3 литра
апельсинового сока и 77 литров воды, то получим 10
10 литров
апельсинового нектара (сделаем предположение, что смешивание происходит в
автоматическом режиме, а не вручную).
Мысль 2
При |
Если мы смешаем 6 литров
яблочного сока и 66 литров
персикового сока – то получится 12 литров яблочно-персикового сока.
И еще одна
очевидность (последняя).
Мысль 3
Масса |
Если мы смешаем 3 литра
яблочного сока с 10% мякоти (0,3 л), и 55 литров
яблочного сока с 5% мякоти (0,25 л), то получим 88 литров
сока с 0,55 л мякоти
(0,3+0,25).
Перейдем к
задачам.
2.
Простейшие задачи на смеси и сплавы
Задачи на смеси и
сплавы бывают двух основных видов:
1.
Две
смеси определенной массы с некоторой концентрацией вещества сливают вместе.
Нужно определить массу и концентрацию этого вещества в новой смеси.
2.
В
некоторый раствор, с некоторой концентрацией вещества, добавляют, например,
чистую воду (с нулевой концентрацией этого вещества). Нужно определить, какой
Нужно определить, какой
стала концентрация вещества.
Строго говоря,
подход к решению от этого не меняется. Во втором случае мы тоже смешиваем две смеси,
просто в одной концентрация вещества больше 0, а в
другой равна 0.
Пример 1.
В 5% раствор
кислоты массой 3,8 кг добавили 1,2 кг чистой воды. Чему стала
равна концентрация раствора (в процентах)?
Решение:
1.
Для
начала вычислим, сколько кислоты содержится в 5% растворе.
Из 3,8 кг 5% —
это кислота, а значит в растворе 0,05 * 3,8=0,19 кг кислоты
2. Далее
определим массу нового раствора. Как мы уже знаем – масса раствора равна массе
его составляющих, т.е. 3,8 кг + 1,2 кг = 5 кг.
3. Поскольку
в чистой воде кислоты нет, то в новом растворе количество кислоты не изменилось
– 0,19 кг. Таким образом, концентрация кислоты стала равна 0,19:5=0,038
4. Теперь
выразим концентрацию в процентах — 0,038⋅100%=3,8%
Ответ: 3,8
Теперь давай
попробуем решить задачу посложнее.
Пример 2.
Смешали 3 кг 5%-го
водного раствора щелочи и 7 кг 15%-го. Какова концентрация вновь
полученного раствора? Ответ дайте в процентах.
Решение:
Давай попробуем
визуализировать ситуацию. 3 кг 5% водного раствора. Значит
воды в этом растворе 95%.
Нарисуем:
А теперь второй
раствор:
После смешивания,
вновь получившийся раствор будет весить 3кг + 7 кг = 10
кг. Обозначим количество щелочи в новом растворе за x, а
количество воды – (10−x):
Теперь выразим
количество щелочи в этих двух растворах в килограммах. В первом растворе –0,05⋅3=0,15 кг
щелочи
и 3−0,15=2,85 кг
воды,
во втором — 0,15⋅7=1,05 кг
щелочи
и 7−1,05=5,95 кг
воды:
Из картинки видно,
что количество щелочи в новом растворе равно сумме весов кислоты в старых
растворах: x=0,15+1,05=1,2 кг кислоты.
Теперь, зная
количество щелочи в новом растворе и зная его массу, мы можем легко определить
концентрацию:
1,2:10=0,12
Поскольку ответ
просят дать в процентах – умножим на 100%
0,12⋅100%=12%.
Ответ: 12.
Эту визуализацию
удобно использовать в любых задачах на растворы, смеси и сплавы.
3. Старинный метод
решения задач или «метод креста»
Впервые о нем было упомянуто в первом печатном
учебнике математики Леонтия Магницкого. Ввиду большой простоты предложенный
способ применялся купцами и ремесленниками при решении различных практических
задач. Но в задачниках и различных руководствах для мастеров и торговцев
никаких обоснований и разъяснений не приводилось. Просто давался рецепт
решения: либо, как в предыдущей задаче, рисовалась схема, либо словесно
описывалась последовательность действий — поступай так и получишь ответ.
«Правилом креста»
называют диагональную схему правила смешения для случаев с двумя растворами. Слева на
концах отрезков записывают исходные массовые доли растворов (обычно слева
вверху – большая), на пересечении отрезков – заданная, а справа на их концах
записываются разности между исходными и заданной массовыми долями. Получаемые
Получаемые
массовые части показывают, в каком отношении надо слить исходные растворы.
Пример 3.
(смешивание двух веществ, предлагалась на экзамене в 2006 году). Имеется два
сплава с разным содержанием золота. В первом сплаве содержится 35%, а во втором
60% золота. В каком отношении надо взять первый и второй сплавы, чтобы получить
из них новый сплав, содержащий 40% золота?
4. Алгебраический
метод
Под
алгебраическим методом решения задач понимается такой метод решения, когда
неизвестные величины находятся в результате решения уравнения или системы
уравнений, решения неравенства или систем неравенств, составленных по условию
задачи. Иногда алгебраическое решение задачи бывает очень сложным.
Задачи на
смешивание растворов решают с помощью составления уравнения или системы
уравнений.
Главное внимание при обучении учащихся способу решения текстовых задач методом
составления уравнений должно быть обращено на сознательную отработку этапности
решения.
В процессе
решения каждой такой задачи целесообразно действовать по следующей схеме.
1. Изучение
условия задачи. Выбор неизвестных величин (их обозначаем буквами х, у и т.д.),
относительно которых составляем пропорции. Выбирая неизвестные параметры, мы
создаем математическую модель ситуации, описанной в условии задачи.
2. Поиск плана
решения. Используя условия задачи, определяем все взаимосвязи между данными
величинами.
3. Осуществление
плана, т.е. оформление найденного решения – переход от словесной формулировки к
составлению математической модели.
4. Изучение
полученного решения, критический анализ результата.
Обратим
внимание на семь критериев полноценности решения задачи,
сформулированных
В. М. Брадисом: безошибочность, обоснованность, исчерпывающий характер,
простота, ясность пути, приведшего к решению задачи, рациональность записи, завершающее
обобщение решения.
При
решении задач удобно составлять следующую таблицу, которая помогает зрительно
воспринимать задачу.
| 1 – й р-р | 2 – й Р-р | Смесь 2 |
Масса растворов |
|
|
|
Массовая доля |
|
|
|
Масса вещества в |
|
|
|
Пример 4. В
500 кг руды содержится некоторое количество железа. После удаления из руды 200
кг примесей, содержащих в среднем 12,5 % железа, содержание железа в
оставшейся руде повысилось на 20 %. Определите, какое количество железа
Определите, какое количество железа
осталось ещё в руде?
Решение.
Сначала составим
таблицу, в которой напишем массу руды, массу железа, концентрацию (долю железа
в рудеапишем массу руды, массу железа, концентрацию
() руде?
нем
12,5 % железа, содержание железа в оставшейся руде повысилось на 20) до и
после удаления примесей.
| Масса руды, кг | Масса железа, кг | Концентрация |
Руда | 500 | х | |
Руда после | 500-200=300 | х-0,125×200= x-25 |
Пусть х кг – масса
железа в руде. Так как масса всей руды равна 500
кг, то концентрация железа в ней равна .
Так как масса
железа в 200 кг примесей равна 0,125×200=25 (кг), то его масса в руде после удаления
примесей равна (х-25) кг. Из того, что масса оставшейся руды равна 500-200=300
Из того, что масса оставшейся руды равна 500-200=300
кг следует, что концентрация железа в ней равна .
По условию,
содержание железа в оставшейся руде повысилось на 20%=1/5. Составим уравнение:
Найдём, что 212,5
кг – масса железа в руде. Найдём остаток железа в руде после удаления примесей:
212,5-25=187,5 (кг).
Ответ: 187,5
кг.
Пример 5. Имеются
два сплава меди со свинцом. Один сплав содержит 15% меди, а другой 65%. Сколько
нужно взять каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди?
Наим-е веществ, | % содержание | Масса раствора | Масса вещества |
Первый сплав | 15%=0,15 | хг | 0,15х |
Второй раствор | 65%=0,65 | (200 – х)г | 0,65(200–х)=130–0,65х |
Получившийся р-р | 30%=0,3 | 200 г | 2000,3=60 |
1 способ решения
Сумма масс меди в
двух первых сплавах (то есть в первых двух строчках) равна массе меди в полученном
сплаве (третья строка таблицы):
Решив это
уравнение, получаем х=140. При этом значении х выражение
При этом значении х выражение
200 – х=60. Это означает, что первого сплава надо взять140г, а
второго 60г.
Ответ:140г. 60г.
2 способ решения
Рассмотрим
решение этой же задачи с помощью следующей модели. Изобразим каждый из
растворов в виде прямоугольника, разбитого на два фрагмента (по числу
составляющих элементов). Для того, чтобы показать, что происходит смешивание
веществ поставим знак «+» между первым и вторым прямоугольниками, а знак «=»
между вторым и третьим прямоугольниками показывает, что третий раствор получен
в результате смешивания первых двух. Полученная схема имеет следующий вид:
Решение.
Пусть хг –
масса первого сплава. Тогда, (200-х)г – масса второго сплава.
Дополним последнюю схему этими выражениями. Получим следующую схему:
Получим следующую схему:
Сумма масс меди в
двух первых сплавах (то есть слева от знака равенства) равна массе меди в
полученном третьем сплаве (справа от знака равенства):
Решив это
уравнение, получаем х=140. При этом значении х выражение 200-х=60.
Это означает, что первого сплава надо взять140г, а второго-60г.
Ответ: 140 г
меди и 60 г свинца.
Пример 6. (Типовые
тестовые задания ЕГЭ 2012 п/р А.Л.Семенова, И.В.Ященко). Смешав 70%-й и
60%-й растворы кислоты и добавив 2 кг чистой воды, получили 50%-й раствор
кислоты. Если бы вместо 2 кг воды добавили 2 кг 90%го раствора той же кислоты,
то получили бы 70%-й раствор кислоты. Сколько килограммов 70%-го раствора
использовали для получения смеси?
Решение.
Задача содержит
два неизвестных, поэтому необходимо решить систему двух уравнений с двумя
неизвестными. Составим эти уравнения. Обозначим через х кг – массу первого
раствора, через у кг- массу второго раствора. Рассмотрим первую ситуацию:
Рассмотрим первую ситуацию:
Составим первое
уравнение: + + = . После упрощения уравнение примет вид: 2х
+у = 10.
Рассмотрим вторую
ситуацию:
Составим второе
уравнение: + + = . После упрощения уравнение примет вид: у
= 4. Тогда х = 3
Ответ: 3 кг
использовали 70%-й кислоты
Пример 7.
Первый раствор содержит 40% кислоты, а второй — 60% кислоты. Смешав эти
растворы и добавив 5 л воды, получили 20 процентный раствор. Если бы вместо
воды добавили 5 л 80 % раствора, то получился бы 70 % раствор. Сколько литров
60 % раствора кислоты было первоначально?
Пусть
х л было 40 %,
а
у л – 60 %. Тогда нового, 20 % раствора – (х + у + 5) л.
0,4х (л) –
кислоты в первом растворе;
0,6у (л) –
кислоты во втором растворе;
0,2·(х + у + 5)
(л) – кислоты в новом растворе.
Получим уравнение
кислоты в 80 процентном растворе;
кислоты в новом, 70 процентном растворе.
Получим второе
уравнение
Получим систему уравнений:
2 л 60
процентного раствора было первоначально.
Ответ: 2
л.
Подведем
итоги
Если ты заметил,
во всех задачах мы сначала определяли, какое вещество влияет на концентрацию,
назовем его «главным». А дальше следили за абсолютной величиной этого главного
вещества (в килограммах, литрах). Если в раствор (сплав) что-то доливали,
добавляли, то, в зависимости от состава «добавки», вес «главного» вещества либо
изменялся, либо нет. Важно определить, что произошло с «главным» веществом, а
дальше решение становится совсем простым.
Список
использованной литературы.
1. Кузнецова Л.В.
Сборник заданий для подготовки к государственной итоговой аттестации в 9
классе. — М.: Просвещение, 2010.
2. Прокопенко
Н.И. Задачи на смеси и сплавы.- М. :Чистые пруды, 2010 (Библиотечка «Первого
сентября». Выпуск 31 )
3. Лурье
Лурье
М.В., Александров
Б.И. Задачи на составление уравнений. Учебное руководство. – М.: Наука.
Главная редакция физико-математической литературы, 1990г.
4. Малахова
Н. А., Орлов В. В. и др. Методика работы с сюжетными задачами:
Учебно-методич. пособие. СПб.: Изд-во РГПУ, 1992. 46 с.
5. Фридман
Л.М., Турецкий Е.Н. Как научиться решать задачи: Кн. для учащихся ст. классов
сред.школы. – 3-е изд., доработанное. М.: Просвещение, 1989
6. www.mathege.ru
7. www.fipi.ru
8. www. festival.1september.ru
9. http://www.shevkin.ru/
10. http://mat-ege.ru
Реактор идеального смешения
Для
модели идеального смешения принимается
ряд допущений. Допускается, что в
результате интенсивного перемешивания
устанавливаются абсолютно одинаковые
условия в любой точке реактора:
концентрации реагентов и продуктов,
степени превращения реагентов,
температура, скорость химической реакции
и т. д. Например, в некоторый момент
времени τ, во всех точках ректора
выполняются
следующие условия:
;
;
,
где x,
y,
z
– пространственные координаты.
В
проточном реакторе идеального смешения
концентрации участников реакции в
выходном потоке в рассматриваемый
момент времени т, строго равны концентрациям
тех же веществ в реакторе.
Чтобы
перечисленные допущения могли быть
выполнены, необходимо принять еще
одно допущение: переход от одной
концентрации к другой в реакторе
идеального смешения не должен иметь
протяженности во времени. Изменение
концентрации исходного реагента от
начальной СJ,0
во
входном потоке в данный момент времени
х, до концентрации в реакторе СJ,
в
этот же момент времени должно происходить
мгновенно (скачкообразно).
Схемы реакторов идеального
смешения с механическим перемешивающим
устройством (а)
и циркуляционным контуром (б)
Приблизиться
к режиму идеального смешения можно,
обеспечив интенсивное перемешивание
реакционной смеси механическими
мешалками разного типа или циркуляционными
насосами, создающими высокую кратность
циркуляции. Смешение, близкое к идеальному,
Смешение, близкое к идеальному,
легче выполнить в емкостных аппаратах
с приблизительно равными диаметром
и высотой.
Рассмотрим
два частных случая: периодический
реактор идеального смешения и
проточный реактор идеального смешения,
работающий в стационарном режиме.
Периодический
реактор идеального смешения. В
периодический реактор все реагенты
вводят до начала реакции, а все продукты
выводят из него только по окончании
процесса. В ходе реакционного цикла
никаких веществ в реактор не вводят и
из него не выводят, так что общая масса
реакционной смеси в реакторе остается
постоянной, изменяется лишь ее состав.
Время
пребывания реагентов в реакторе
(продолжительность реакционного
цикла) определяется промежутком от
начала загрузки исходной реакционной
смеси до выгрузки конечной смеси из
реактора. В разные моменты времени
условия в периодическом реакторе
различные (концентрация реагентов,
продуктов, скорость реакции и т. д.),
д.),
однако в каждый данный момент времени
из-за допущения об идеальности эти
параметры строго одинаковы в объеме
реактора.
Для
осуществления процесса в периодическом
реакторе кроме «реакционного» времени
нужно затратить вспомогательное
время на загрузку реагентов, выведение
реактора на нужный технологический
режим, разгрузку и очистку. Полное время
одного цикла работы периодического
реактора суммируется, таким образом,
из основного τхр
и вспомогательного τвсп:
τ
= τхр
+ τвсп.
Наличие
τвсп
как составной части времени цикла
приводит к снижению производительности
химического реактора (количество
продукта, получаемого в единицу времени)
и является одним из существенных
недостатков периодических процессов
вообще. Другие их недостатки — большие
затраты ручного труда, сложность решения
задач автоматизации (так как условия в
реакторе во времени постоянно
меняются).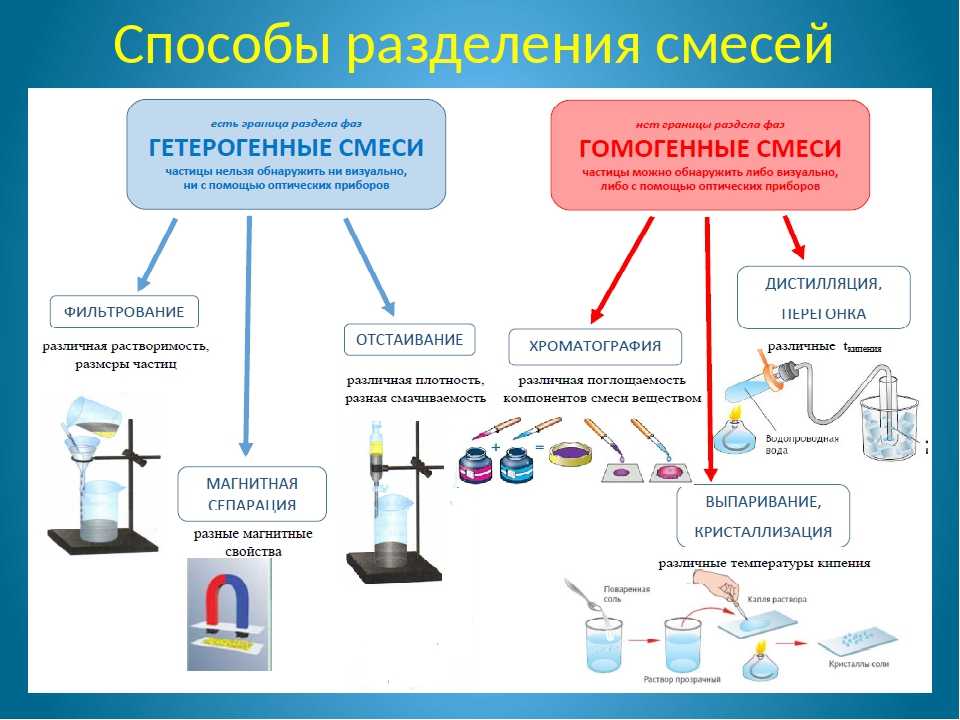
Однако
периодические реакторы обычно можно
приспособить к широкому диапазону
условий реакций, что удобно при
необходимости производить на одной
установке различные химические
продукты, например, в промышленности
химических реактивов. Периодические
реакторы с интенсивным перемешиванием,
приближающимся к идеальному смешению,
применяют в производствах реактивов,
органических красителей, лекарственных
препаратов — там, где для достижения
достаточной глубины превращения
требуется сравнительно длительное
время, а объемы производства невелики.
Периодические
реакторы смешения часто применяют в
микробиологической промышленности
для культивирования аэробных
микроорганизмов. Процесс культивирования
для большинства микроорганизмов
длится 48—72 ч, т. е. достаточно длителен.
Интенсивное перемешивание в ферментаторе
позволяет обеспечить равномерное
распределение температуры, что особенно
важно в таких процессах, так как даже
небольшие локальные разогревы могут
привести к гибели микроорганизмов.
Изолированность реакционной системы
в периодическом реакторе позволяет
устранить опасность отравления
микроорганизмов случайными примесями,
которые могут попасть в аппарат при
непрерывной подаче реагентов.
Окончательное
решение о целесообразности применения
периодического или непрерывного
процесса можно вынести лишь на основании
экономической оценки (сравнения расходов
на эксплуатацию, амортизацию,
электроэнергию, пар, сырье и т. д.). Как
правило, при проведении такого сравнения
оказывается, что периодические
процессы выгодны при относительно
невысокой производственной мощности
в тех случаях, когда получают дорогостоящие
продукты.
Проточный
реактор идеального смешения в стационарном
режиме. Если
необходимо обеспечить получение большого
количества продукта одинакового
качества, химический процесс предпочитают
проводить в непрерывнодействующих
реакторах с установившимся режимом.
Распространенным видом таких проточных
аппаратов являются реакторы смешения.
Проточный реактор смешения может
работать как в нестационарном режиме
(пуск, выход на режим, остановка), так
и в стационарном, установившемся режиме.
В
качестве элементарного объема для
реактора идеального смешения можно
принять полный объем реактора V.
При
стационарном режиме работы реактора
не происходит изменения постоянных по
объему концентраций участников реакции
и во времени, следовательно, в качестве
элементарного промежутка времени
можно принять любой конечный временной
интервал, например единицу времени (1
с,
1
мин
или 1
ч).
Стационарность
процесса в проточном реакторе можно
обеспечить, если объемные расходы на
входе v0
и
выходе vf
равны
между собой (v0
= vf
= v).
Величина
измеряется
в единицах времени и характеризует
среднее время, в течение которого
обновляется содержимое проточного
реактора. Эту величину называют средним
Эту величину называют средним
временем пребывания реагентов в проточном
реакторе.
Действительное
время пребывания частиц в проточном
реакторе смешения является случайной
величиной в отличие от времени
пребывания реагентов в периодическом
реакторе. Пусть, например, в реактор
введено N
одинаковых
частиц. В периодическом реакторе все
они будут находиться равное время от
загрузки до выгрузки. В проточном
реакторе идеального смешения эти
частицы мгновенно и равномерно
распределяются по всему объему аппарата,
и так как из аппарата непрерывно выходит
поток продуктов, то в момент ввода
частиц в реактор какое-то их количество
может сразу же оказаться в выходном
потоке. Некоторые частицы, равномерно
распределяясь в новых порциях реакционной
смеси, вошедшей в аппарат, могут находиться
в нем бесконечно долго. Отсюда можно
сделать вывод, что действительное время
пребывания частиц в проточном реакторе
— это случайная величина, которая
может изменяться от 0
до
∞. Непрерывную случайную величину
Непрерывную случайную величину
можно задать с помощью вероятностных
характеристик, в частности функций
распределения случайной величины.
Использование в качестве характеристики
времени пребывания частиц в проточном
реакторе величины
является удобным способом усреднения
действительного времени пребывания,
так как эта величина связана с
конструктивными характеристиками
реактора: его объемом и объемным расходом
реакционной смеси.
1.4 Лабораторные методы разделения смесей – CHEM 1114 – Введение в химию
Глава 1. Химия: экспериментальная наука
Цели обучения
К концу этого раздела вы сможете:
- Описывать различные методы разделения.
- Определите, какой метод разделения наиболее подходит для данной смеси.
- Определите, какие физические изменения происходят в процессе разделения.
Смесь состоит из двух или более типов вещества, которые могут присутствовать в различных количествах и могут быть физически разделены с помощью методов, использующих физические свойства для разделения компонентов смеси, таких как выпаривание, дистилляция, фильтрация и хроматография.
Испарение может использоваться в качестве метода разделения для разделения компонентов смеси с растворенным в жидкости твердым веществом. Жидкость испаряется, то есть переходит из жидкого состояния в газообразное. Для этого часто требуется тепло. Когда жидкость полностью испарится, останется только твердое вещество.
Рисунок 1. В качестве метода разделения можно использовать выпаривание.
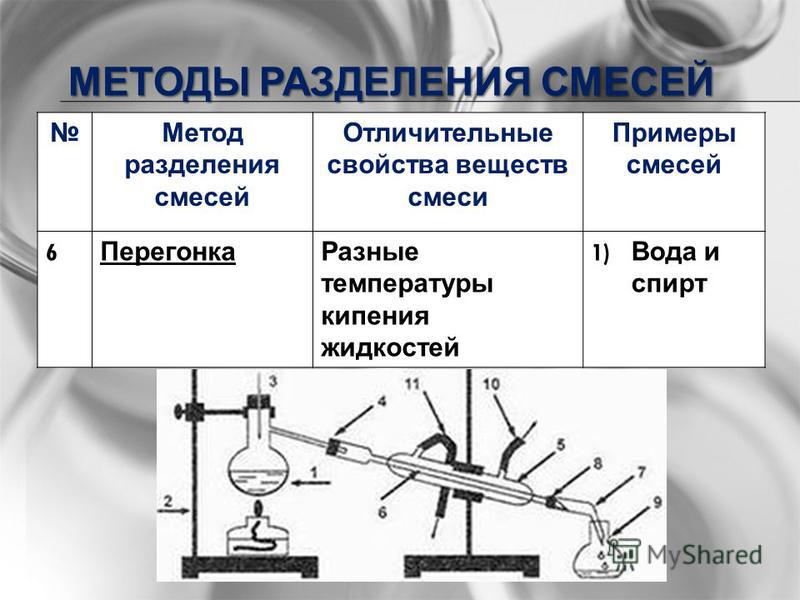
Дистилляция — это метод разделения, используемый для разделения компонентов жидкой смеси путем нагревания и охлаждения, в котором используются различия в летучести каждого из компонентов.
Рисунок 2. Перегонный аппарат.
Процедура перегонки: 1) круглодонная колба содержит жидкую смесь, которую необходимо нагреть до бурного кипения, 2) компонент с более низкой температурой кипения перейдет в газообразное состояние, 3) при контакте с водоохлаждаемым холодильником, газ будет конденсироваться, 4) просачиваться в градуированный цилиндр, где химик может восстановить конечную дистиллированную жидкость, и 5) другой жидкий компонент остается в круглодонной колбе.
Фильтрация – это метод разделения, используемый для разделения компонентов смеси, содержащей нерастворенное твердое вещество в жидкости. Фильтрацию можно проводить холодной или горячей, используя силу тяжести или вакуум, используя воронку Бюхнера или Хирша или простую стеклянную воронку. Точный используемый метод зависит от цели фильтрации, будь то выделение твердого вещества из смеси или удаление примесей из смеси.
Рисунок 3. Фильтровальный аппарат.
Процедура фильтрации: 1) смесь процеживают через воронку, выложенную фильтровальной бумагой, 2) фильтрат (жидкость) капает в колбу с фильтром, 3) твердое вещество остается в воронке.
Хотя хроматография в принципе является простой методикой, она остается наиболее важным методом разделения смесей на компоненты. Он достаточно универсален, поскольку его можно использовать для разделения смесей твердых веществ или жидкостей, или смесей твердых веществ и жидкостей вместе, или, в случае газовой хроматографии, для разделения смесей газов. Двумя элементами хроматографии являются неподвижная фаза и подвижная фаза. Существует множество вариантов неподвижных фаз, некоторые из которых представляют собой оксид алюминия, кремнезем и даже бумагу. Подвижная фаза в жидкостной хроматографии также может варьироваться. Часто это либо растворитель, либо смесь растворителей, и его часто называют элюентом. Тщательный выбор элюирующего растворителя помогает сделать разделение более успешным. Смесь помещают на неподвижную фазу. Элюант проходит над смесью и продолжает проходить через неподвижную фазу, увлекая за собой компоненты смеси. Если компонент в смеси имеет большее сродство к подвижной фазе (элюанту), чем к стационарной фазе, он будет иметь тенденцию легко уноситься вместе с элюентом. Если другой компонент смеси имеет большее сродство к неподвижной фазе, чем к подвижной, то он не будет так легко уноситься. Таким образом, разделение достигается, когда разные компоненты смеси имеют разное сродство к неподвижной и подвижной фазам. Три важных типа хроматографии, основанные на рассмотренных выше принципах, это: 1) тонкослойная хроматография (ТСХ), 2) колоночная хроматография и 3) газовая хроматография.
Двумя элементами хроматографии являются неподвижная фаза и подвижная фаза. Существует множество вариантов неподвижных фаз, некоторые из которых представляют собой оксид алюминия, кремнезем и даже бумагу. Подвижная фаза в жидкостной хроматографии также может варьироваться. Часто это либо растворитель, либо смесь растворителей, и его часто называют элюентом. Тщательный выбор элюирующего растворителя помогает сделать разделение более успешным. Смесь помещают на неподвижную фазу. Элюант проходит над смесью и продолжает проходить через неподвижную фазу, увлекая за собой компоненты смеси. Если компонент в смеси имеет большее сродство к подвижной фазе (элюанту), чем к стационарной фазе, он будет иметь тенденцию легко уноситься вместе с элюентом. Если другой компонент смеси имеет большее сродство к неподвижной фазе, чем к подвижной, то он не будет так легко уноситься. Таким образом, разделение достигается, когда разные компоненты смеси имеют разное сродство к неподвижной и подвижной фазам. Три важных типа хроматографии, основанные на рассмотренных выше принципах, это: 1) тонкослойная хроматография (ТСХ), 2) колоночная хроматография и 3) газовая хроматография.
Рисунок 4. Тонкослойная хроматография — это один из видов хроматографии. а) Неподвижная фаза может представлять собой тонкую пленку оксида алюминия или кремнезема на стекле или даже на бумаге. Планшет помещают в проявочную емкость, содержащую подвижную фазу (элюант), которая перемещается вверх по планшету за счет капиллярного действия. б) Разделение достигается за счет того, что компонент смеси, обладающий более сильным сродством к канне (соединение 2), движется вверх по пластине быстрее, чем компонент, обладающий сильным сродством к неподвижной фазе (соединение 1).
Пример 1
Определите, какой метод разделения наиболее подходит для следующих смесей:
| Методы разделения: | Смесь твердых веществ | Смесь жидкостей | Смесь твердого вещества, растворенного в жидкости | Смесь твердого вещества и жидкости |
| Испарение | ||||
| Перегонка | ||||
| Фильтрация | ||||
| Хроматография |
Раствор
| Методы разделения: | Смесь твердых веществ | Смесь жидкостей | Смесь твердого вещества, растворенного в жидкости | Смесь твердого вещества и жидкости |
| Испарение | НЕТ | НЕТ | ДА* | ДА** |
| Перегонка | НЕТ | ДА* | ДА* | НЕТ |
| Фильтрация | НЕТ | НЕТ | НЕТ | ДА |
| Хроматография | ДА* | ДА* | ДА* | ДА* |
* Успех зависит от физических свойств компонентов смеси.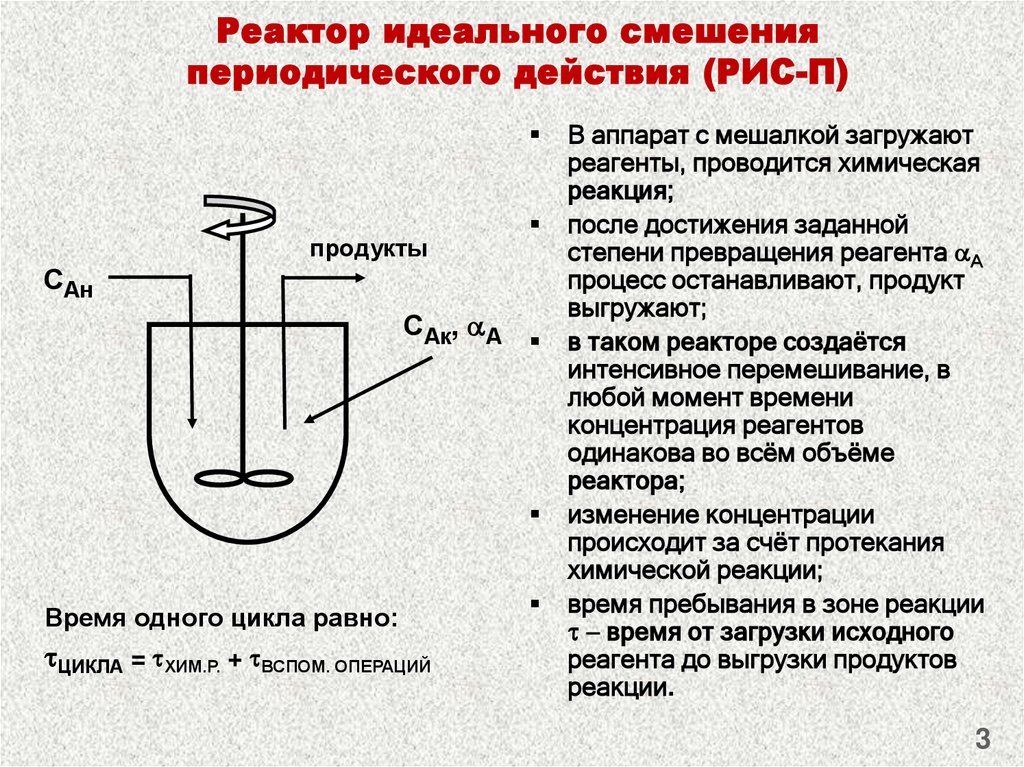
** Будет работать, но фильтрация намного быстрее.
Проверьте себя
Какой метод разделения будет наиболее эффективным для следующих смесей:
а) Морская вода
б) Золотые самородки в воде.
c) Раствор спирта (жидкости) и воды.
Ответы
а) выпаривание или перегонка (хроматография здесь неэффективна)
б) фильтрация
в) перегонка
Смеси можно физически разделить с помощью методов, использующих различия в физических свойствах для разделения компонентов смеси, таких как выпаривание, дистилляция, фильтрация и хроматография. Какой метод разделения использовать при попытке разделить смесь, зависит от того, что это за смесь (какие состояния вещества присутствуют) и от физических свойств компонентов.
Глоссарий
хроматография: – метод разделения, основанный на том, что различные компоненты смеси имеют разное сродство к неподвижной и подвижной фазам
дистилляция: – метод разделения, используемый для разделения компонентов жидкой смеси путем нагревания и охлаждения
выпаривание: – метод разделения, используемый для разделения смеси жидкости с растворенным твердым веществом, включающий удаление жидкости путем ее выпаривания и оставление твердого вещества
фильтрация: – это метод разделения, используемый для разделения компонентов смеси, содержащей нерастворенное твердое вещество в жидкости, с помощью воронки, выстланной фильтровальной бумагой, для удержания твердых частиц при пропускании жидкости.
страница не найдена — Williams College
| ’62 Центр театра и танца, ’62 Center | ||
| Касса | 597-2425 | |
| Магазин костюмов | 597-3373 | |
| Менеджер мероприятий/помощник менеджера | 597-4808 | 597-4815 факс |
| Производство | 597-4474 факс | |
| Магазин сцен | 597-2439 | |
| ’68 Центр изучения карьеры, Мирс | 597-2311 | 597-4078 факс |
| Академические ресурсы, Парески | 597-4672 | 597-4959 факс |
| Служба поддержки инвалидов, Парески | 597-4672 | |
| Приемная, Weston Hall | 597-2211 | 597-4052 факс |
| Позитивные действия, Хопкинс-холл | 597-4376 | |
| Африканские исследования, Голландия | 597-2242 | 597-4222 факс |
| Американские исследования, Шапиро | 597-2074 | 597-4620 факс |
| Антропология и социология, Холландер | 597-2076 | 597-4305 факс |
| Архивы и специальные коллекции, Sawyer | 597-4200 | 597-2929 факс |
| Читальный зал | 597-4200 | |
| Искусство (История, Студия), Spencer Studio Art/Lawrence | 597-3578 | 597-3693 факс |
| Архитектурная студия, Spencer Studio Art | 597-3134 | |
| Студия фотографии, Spencer Studio Art | 597-2030 | |
| Студия печати, Spencer Studio Art | 597-2496 | |
| Скульптурная студия, Spencer Studio Art | 597-3101 | |
| Senior Studio, Spencer Studio Art | 597-3224 | |
| Видео/фотостудия, Spencer Studio Art | 597-3193 | |
| Азиатские исследования, Голландия | 597-2391 | 597-3028 факс |
| Астрономия/астрофизика, Физика Томпсона | 597-2482 | 597-3200 факс |
| Отделение легкой атлетики, физического воспитания, отдыха, Ласелл | 597-2366 | 597-4272 факс |
| Спортивный директор | 597-3511 | |
| Лодочная пристань, озеро Онота | 443-9851 | |
| Вагоны | 597-2366 | |
| Фитнес-центр | 597-3182 | |
| Хоккейный каток Ice Line, Lansing Chapman | 597-2433 | |
| Очные занятия, Спортивный центр Чендлера | 597-3321 | |
| Физкультура | 597-2141 | |
| Влажная линия бассейна, Спортивный центр Чендлера | 597-2419 | |
| Информация о спорте, Хопкинс-холл | 597-4982 | 597-4158 факс |
| Спортивная медицина | 597-2493 | 597-3052 факс |
| Сквош-корты | 597-2485 | |
| Поле для гольфа Taconic | 458-3997 | |
| Биохимия и молекулярная биология, Биология Томпсона | 597-2126 | |
| Биоинформатика, геномика и протеомика, Бронфман | 597-2124 | |
| Биология, Биология Томпсона | 597-2126 | 597-3495 факс |
| Безопасность и безопасность кампуса, Хопкинс-холл | 597-4444 | 597-3512 факс |
| Карты доступа/Системы сигнализации | 597-4970/4033 | |
| Служба сопровождения, Хопкинс-холл | 597-4400 | |
| Офицеры и диспетчеры | 597-4444 | |
| Секретарь, удостоверения личности | 597-4343 | |
| Распределительный щит | 597-3131 | |
| Центр развития творческого сообщества, 66 Stetson Court | 884-0093 | |
| Центр экономики развития, 1065 Main St | 597-2148 | 597-4076 факс |
| Компьютерный зал | 597-2522 | |
| Вестибюль | 597-4383 | |
Центр экологических исследований, выпуск 1966 г.  |


