Архив Приложение к журналу Ключевые слова Логин Пароль ВХОД регистрация Другие журналы
| 77-30569/245694 Математическая модель гусеничного обвода # 10, октябрь 2011 Файл статьи: авторы: Сарач E. Б., Стадухин А. А. УДК 629.11.012.8 МГТУ им. Н.Э. Баумана kjlactep@ya. Введение Транспортная гусеничная машина (ГМ) является сложной механической системой. Для выяснения динамики взаимодействия ГМ и местности на этапе проектирования требуется сложная математическая модель системы машина-местность. В настоящее время существует ряд математических моделей, с большой степенью достоверностью описывающее прямолинейное движение ГМ по грунтам различного профиля [1, 2]. Увеличение быстродействия ЭВМ позволило усложнить математические модели движения ГМ: более достоверно учесть влияние гусеничного обвода; перейти, в отличие от ранних моделей, к рассмотрению большего количества конструкционных особенностей элементов системы подрессоривания. Считается, что с достаточной для практики точностью гусеницу следует считать растяжимой лентой с “нелинейной зависимостью между растягивающим усилием и удлинением”[3]. Однако часто для исследования движения ГМ необходима более подробная модель гусеничного обвода, которая не только учитывает воздействие усилий гусеницы на ходовую часть, но и реализацию этих усилий на грунт. Поэтому, важной задачей является снижение сложности такой ресурсоёмкой части математической модели ГМ как гусеничный обвод. 1. Обзор существующих моделей гусеничного обвода В [4] предложена двухшаговая схема реализации модели гусеничного обвода. В этой модели гусеницы рассматриваются как последовательно связанные между собой невесомые, растяжимые ленты. Каждая гусеница состоит из последовательно связанных между собой участков, в пределах которых растягивающее усилие неизменно. На соседних участках усилия могут быть различными. Границы участков – это места, где возможно возникновение продольных реакций связей, наложенных на обвод. А именно, места зацепления ведущих колёс и площадки контакта опорных катков с опорным основанием, которые предполагают точечными. Основной смысл реализации модели состоит в разделении перемещения гусеницы на два этапа. На первом этапе считается, что поворот ведущего колеса деформирует ленты гусеницы. На втором этапе рассчитывается перемещение системы. Ведущие колёса при этом считаются неподвижными. Построение такой модели, например, средствами Matlab/Simulink будет достаточно трудоёмким из-за того, что модель гусеницы потребует два шага расчёта, приходящихся на один шаг расчёта остальной модели. В [5] предлагается рассматривать гусеничный обвод как набор отдельных масс – траков, соединённых одномерными упруго-демпфирующими силами. В упомянутом труде подвеска и моторно-трансмиссионная установка ГМ не моделируется. Вместо этого задаются перемещения соответствующих траков по гармоническому закону. Учитывая большое количество траков в гусенице современной ГМ (97 траков в каждой гусенице танка Т-90), расчёт уравнений динамики такого же количества масс может быть неоправданно. Для работ, в которых моделирование гусеничного обвода является неосновной, сопутствующей задачей, полезна модель гусеничного обвода, имеющую более простое математическое описание и меньшие требование к вычислительным ресурсам. 2. Новая модель гусеничного обвода. Идеи описанных выше математических моделей были взяты за основу для создания новой модели гусеничного обвода. А именно, гусеничная лента представляется в виде нескольких сосредоточенных в материальных точках масс mi с одной степенью свободы, соединённых упруго-демпфирующими связями, как это сделано в работе [5]. Однако предлагается заменять массой не каждый трак, а только те точки гусеницы, в которых возможно возникновение продольных сил (рис. 1), то есть, уже упомянутые места зацепления ведущих колёс и точки контакта опорных катков с опорным основанием. При этом следует помнить, что такое разделение на массы достаточно условно и результаты расчётов сильно не изменятся, если считать все Nm масс равными друг другу, а их сумму равной общей массе гусеницы Mгус: Рис. Для определённости предлагается ввести следующую нумерацию. Опорные катки по борту, числом NOK, считать слева (от ведущего колеса) направо. Массы номеровать, начиная с той, к которой приложена сила тяги, против часовой стрелки. Положительным направлением движения масс считать движение по часовой стрелке, т.к. это совпадает с передних ходом машины при выбранной схеме (рис. 1). На каждую массу mi действуют упругие и демпфирующие силы соседних участков гусеницы: На массу на ведущем колесе кроме того действует сила тяги двигателя Pтяги. Массы под опорными катками так же испытывают дополнительные воздействия от горизонтальной реакции грунта Pгрунт(n). По большому счёту, для масс под ведущим и направляющим колёсами эта реакция тоже возможна в случае их касания грунта, однако в данной работе этот случай не рассматривается. С учётом всего вышесказанного, уравнения динамики гусеничного обвода примут вид Здесь и далее xi – перемещение соответствующей массы mi. Первая и вторая производная по времени – скорость и ускорение. Сила тяги Pтяги зависит от характеристик силовой установки и для предлагаемой модели является, по сути, задаваемым параметром. Однако для полноценной реализации системы двигатель-машина необходимо иметь обратную связь с функцией силы тяги по скорости первой массы. В большинстве случаев сила тяги будет зависеть ещё и от текущего положения гусеницы Упругие и демпфирующие силы в гусенице могут быть вычислены по удлинениям и разницам скоростей соответствующих ветвей гусеницы или . Здесь Δli– удлинение i-го участка гусеницы, ΔVi– скорость удлинения i-го участка гусеницы, с – коэффициент жёсткости гусеницы, k – коэффициент демпфирования гусеницы, aгус – удлинение каждой ветви гусеницы от сил предварительного натяжения. Удлинение гусеницы aгус предлагается задавать таким образом, чтобы статическое натяжение гусеницы составляло 0,1 веса ГМ. Это примерно соответствует предварительному натяжению гусеницы современных ГМ с резинометаллическими шарнирами [1]. При составлении модели следует учесть, что гусеница не должна работать на сжатие, а только на растяжение, т.е Упругодемпфирующие силы в гусенице будут воздействовать на подвеску, пытаясь поджать катки. Очевидно, что тут не обойтись без моделирования системы подрессоривания. Можно воспользоваться готовой моделью подвески, описанной в [1]. Эта модель, по сути, является одномерной, то есть элемент подвески воспринимает только вертикальные усилия. Подвеска представляется в виде свечной (ход опорных катков считается вертикальным), однако упругие и демпфирующие характеристики могут быть рассчитаны через передаточную функцию балансира (приведены к катку), что имитирует балансирную подвеску [1]. Из модели подвески можно выяснить взаимное положение опорных катков, а также направляющего и ведущего колеса. Для вычисления вертикальных составляющих Pгус.z достаточно знать углы направлений на следующий элемент ходовой части αi (рис. 2). Рис. 2. Влияние гусеничного обвода на подвеску Для каждого опорного катка массой mOK можно записать следующие уравнения динамики где Pп(i) – сила воздействующая на опорный каток со стороны подвески. Понятно, что это уравнение не учитывает все случаи поведения гусеничного обвода. Например, если горизонтальные составляющие сил натяжения гусеницы Pгус.z будут отрицательны, то они «потянут» опорный каток вниз. Это соответствует случаю, когда гусеница не охватывает каток и сила со стороны гусеницы на него действовать не должна. В рамках предложенной модели принято воздействие сил Pгус. Для упрощения модели воздействие сил Pгус.z на корпус через подвеску можно компенсировать, приложив к корпусу противоположные по направлению, но равные по модулю силы (-Pгус.z). В действительности эти силы компенсируются действием гусеничного обвода на ведущее и направляющее колесо. Очевидно, что именно горизонтальные реакции грунта Pгрунт(i) являются движущей силой, толкающей корпус ГМ в направлении движения. Их необходимо приложить в координатах касания опорным катком грунта (рис. 3). Можно видеть, что они будут вызывать отклонение корпуса машины φ на корму, что соответствует поведению реальной машины. Рис.3. К определению реакций грунта, движущих корпус Максимально возможные реакции грунта Pгрунт(i) можно определить, зная коэффициент сцепления φгр, зависящий от типа грунта, и нормальную реакцию грунта под катками [3]. В предлагаемой модели сила реакции грунта Pгрунт(i) является силой трения и участки, где максимальная сила реакций не реализуется, её следует считать линейно зависящей от скорости движения каждой массы гусеницы mi относительно грунта Vгус(i) (скорости буксования). Качественный вид характеристики сцепления изображён на рис. 4. Рис. 4. Простейшая характеристика сцепления гусеницы с грунтом Геометрия грунта под опорным катком задаётся вертикальной координатой грунта zгрунт. Очевидно, что если профиль грунта представляет собой кривую, то площадка под опорным катком может иметь некоторый наклон. Вычислив угол этого наклона (например, с помощью значения zгрунт на предыдущем шаге расчёта), можно разложить силу в шине на горизонтальную и вертикальную составляющую. 3. Вычислительный эксперимент Результаты работы предлагаемой модели гусеничного обвода, выполненного в программном пакете Matlab/Simulink, показан на рис.5. Рис. 5. Скорости буксования и силы в модели гусеницы Верхний график показывает зависимость скорости буксования каждой массы гусеницы от времени. Нижний график – изменение упругодемпфирующих сил, связывающих массы гусеницы, во времени. Можно видеть, что в момент нахождения системы в покое (время симуляции до 1 секунды) на массы действует только сила предварительного натяжения, одинаковая во всех ветвях гусеницы (нижний график). В момент трогания машины с места (1-я секунда симуляции) силы тяги начнут перемещать первую массу гусеницы (график жёлтого цвета), связанную с ведущим колесом. Для этой же модели на рис.6 показаны горизонтальное перемещение центра тяжести машины x (сиреневый график) и продольный наклон корпуса φ (жёлтый график). Положительное направление наклона корпуса в модели – на корму. Рис. 6. Горизонтальное перемещение центра тяжести и наклон корпуса ГМ. Расчёт четырёх секунд моделирования гусеничного обвода (в составе модели ГМ) занял около трёх секунд даже на устаревшем персональном компьютере. Заключение. Разработанная модель гусеничного обвода имеет скорость расчёта, сопоставимую с реальным временем. Взаимодействие моделируемого гусеничного обвода машины с простейшей моделью грунта качественно соответствует их поведению в реальных условиях. Модель позволяет проводить расчёт ГМ с любым количеством опорных катков на борт. Предложенная модель гусеничного обвода может быть приспособлена для трёхмерной модели ГМ, что позволит исследовать не только прямолинейное движение ГМ, но и её поворот.
Библиографический список 1. Дядченко М.Г., Котиев Г.О., Наумов В.Н. Конструкция и расчёт подвесок быстроходных гусеничных машин: учеб.пособие. – М.: Изд-во МГТУ им. Н.Э.Баумана, 2007. – 40 с. 2. Котиев Г.О., Сарач Е.Б. Комплексное подрессоривание высокоподвижных двухзвенных гусеничных машин. – М.: Изд-во МГТУ им.Н.Э.Баумана, 2010. – 184с. 3. Аврамов В.П., Калейчев Н.Б. Динамика гусеничной машины при установившемся движении по неровностям. – Харьков: Вища школа, 1989. – 112 с. 4. Котиев Г.О. Прогнозирование эксплутационных свойств систем подрессоривания военных гусеничных машин: Диссертация на соискание ученой степени доктора технических наук. 5. Платонов В.Ф. Динамика и надёжность гусеничного движителя, М., «Машиностроения», 1973. — 293 с. Поделиться: |
| ||||||||
| ||||||||||
Оптимизация параметров узлов ходовой части гусеничных машин с целью снижения их динамической нагруженности
Список источников диссертации и автореферата по механике, кандидата технических наук, Вербилов, Алексей Фёдорович, Барнаул
1. Аврамов В.П., Панкратов В.П. Математическое моделирование процесса перекатывания опорного катка гусеничной машины по звенчатой гусеничной ленте. // Теория механизмов и машин: Сб. статей / Харьков, 1983. Вып. 35.-95 с.
Аврамов В.П., Панкратов В.П. Математическое моделирование процесса перекатывания опорного катка гусеничной машины по звенчатой гусеничной ленте. // Теория механизмов и машин: Сб. статей / Харьков, 1983. Вып. 35.-95 с.
2. Андреев В.Е. Исследование нагруженности элементов ходовой части гусеничной машины. // Исследование силовых установок и шасси транспортных и тяговых машин: Темат. сб. научн. тр. / ЧПИ. -Челябинск, 1986.- С. 94 98.
3. Андреев В.Е., Харин С.Ф. Расчетно-экспериментальное исследование нагруженности элементов ходовой части гусеничной машины. // Исследование силовых установок и шасси транспортных и тяговых машин: Темат. сб. науч. тр. /ЧПИ. Челябинск, 1987. — С. 91 — 95.
4. Антонов A.C. Теория гусеничного движителя. М.: Машгиз, 1949. — С. 253.
5. Банда Б. Методы оптимизации. М.: Радио и связь, 1988. — 128 с.
6. Барсуков Ю.Н. К вопросу о приведении гусеничных цепей с резинометашшческими шарнирами при расчете крутильно-колеблющихся систем тракторов: Сб. науч. тр. / АПИ. Барнаул, 1973. -Вып. 35.-С. 47-52.
науч. тр. / АПИ. Барнаул, 1973. -Вып. 35.-С. 47-52.
7. Барсуков Ю.Н., Беседин Л.Н., Болтов А.Т., Толчинский Н.А. Влияние резинометаллической гусеницы на динамические нагрузки в силовой передаче и гусеничном обводе трактора класса Зт : Сб. науч. тр. /АПИ. -Барнаул, 1973. Вып. 23. — С. 56 — 65.
8. Безикович Я.С. Приближенные вычисления. Л.: Государственное издательство технико-теоретической литературы, 1949. — С. 421 — 456.
9. Ю.Безручко Н.П., Кутин Л.Н. Колебания остова трактора с крупнозвенчатым обводом при движении по ровному грунту. // Тракторы и сельскохозяйственные машины. М.Машиностроение, 1981. — № 6. -С. 7 — 10.
10. П.Белов В.К. Динамические нагрузки, действующие на траки гусеничной цепи быстроходной транспортной машины. // Конструирование и исследования тракторов: Вестник /ХПИ. Харьков, 1988. — Вып. 7. — С. 45-49.
11. Бердов Е.И., Гинзбург Ю.В., Егоров Ю.Д., Кормунов Г.А. Влияние подрессоривания опорных катков на тягово-сцепные показатели тракторов. // Тракторы и сельскохозяйственные машины. -М.Машиностроение, 1988. — № 8. — С. 15 — 17.
// Тракторы и сельскохозяйственные машины. -М.Машиностроение, 1988. — № 8. — С. 15 — 17.
12. Березин И.Я., Платов А.И., Рихтер Е.Е. Динамика системы «Грунт -гусеница опорный каток».// Прочность машин и аппаратов при переменных нагружениях: Темат. сб. науч. тр.-Челябинск: ЧГТУ, 1991. -156 с.
13. Болгов А.Т., Барсуков Ю.Н., Беседин Л.Н. Теоретическое исследование свободных крутильных колебаний в трансмиссии трактора класса 3 с серийной и резинометаллической гусеницами: Сб. науч. тр. / АПИ. -Барнаул, 1975. Вып. 54. — С. 79 — 54.
14. Бородкин В.А. Работоспособность асимметричных гусениц трактора Т -130Б. // Тракторы и сельхозмашины. 1985. — № 9. — С. 16 — 19.
15. Водченко О.П. К вопросу о трении в кривошипном механизме натяжения гусениц транспортной машины. // Конструирование и исследование тракторов : Вестник / ХПИ. Харьков, 1988. — Вып. 7.- С. 42 — 46.
16. Вольмир A.C., Куранов Б.А., Турбаивский А.Т. Статика и динамика сложных структур. М: Машиностроение, 1989. — 248 с.
— 248 с.
17. Вульфсон И.И., Козловский М.Э. Нелинейные задачи динамики машин. Л.: Машиностроение, 1968. С. 5 — 17.
18. Добронравов В.В. Основы аналитической механики. М.: Высшая школа, 1976,264с.
19. Докучаева E.H. Динамика задней ветви и ведущей звездочки гусеничного движителя: Сб. науч. тр. / ОНТИ НАТИ. — М., 1957. — С. 42 — 47.
20. Дружинин В.А. Моделирование динамического поведения гусеничного движителя трактора // Повышение технического уровня тракторного и сельскохозяйственного машиностроения: Межвуз. сб. Алтайского политехнического ин-та, 1989, с. 36-40.
21. Дымников С.И., Сиротин М.И., Расчет резиновых элементов резинометаллических шарниров сборного типа // Каучук и резина. -1970. -№11.- С. 36-39.
22. Емельянов А.М. и др. Аппроксимация эпюры нормального давления под гусеничным движителем // Тракторы и сельскохозяйственные машины. -1998.-№7.-С. 16-17.
23. Забавников H.A. Основы теории транспортных гусеничных машин. М.: Машиностроение, 1968. С. 396.26.3енкевич О. Метод конечных элементов в технике. М.: Мир, 1975.
С. 396.26.3енкевич О. Метод конечных элементов в технике. М.: Мир, 1975.
24. Исследование динамики гусеничного движителя сельскохозяйственного трактора: Отчет о НИР / Читинский политехнический институт; Руководитель Ю.Н. Прилуцкий. № ГР 76061202; Инв. № 02850064311. -Чита, 1989.-С. 152.
25. Каплинский Е.М., Целищев В.А. О некоторых особенностях работы упругого цепного обвода сельскохозяйственного трактора: Сб. науч. тр. / АЛИ. Барнаул, 1972. — Вып. 4. — С. 177 — 181.
26. Куликов Б.М. Исследование динамики элементов гусеничного движителя с/х трактора с полужесткой подвеской: Сб. науч. тр. / ЧИМЭСХ. -Челябинск, 1967. Вып. 28. — С. 18 — 22.
27. Куликов Б.М. О работе ведущего участка ходовой системы гусеничного трактора: Сб. науч. тр. / ЧИМЭСХ. Челябинск, 1967. — Вып. 28. — С. 23 -30.
28. Кутин JI.H., Безручко Н.П. Исследование и оценка плавности хода гусеничного трактора с крупнозвенчатым обводом. // Повышение функциональных качеств системы подрессоривания гусеничных тракторов: Тр. / НПО «НАТИ». М., 1985. — С. 37 — 40.
/ НПО «НАТИ». М., 1985. — С. 37 — 40.
29. Львов Е.Д. Теория трактора. М.: Машгиз, 1960. С. 252.
30. Ляшенко М.В., Победин A.B. Моделирование свойств грунта применительно к плавности хода МТА // Тракторы и сельскохозяйственные машины. -1999. № 9. — С. 16-17.
31. Михлин С.Г., Смолицкий X.JI. Приближенные методы решения дифференциальных и интегральных уравнений. М.: Наука, 1965, — 352с.
32. Нагибин Ю.А. К вопросу о влиянии провисания ветвей гусеничного обвода на характер свободных крутильных колебаний ведущего колеса: Сб. науч. тр. / УПИ. Свердловск, 1959. — Вып. 18. — С. 219 — 232.
33. Нагибин Ю.А. Некоторые особенности крутильно-колебательного движения совокупной системы «ведущее колесо гусеница» : Сб. науч. тр. / УПИ. — Свердловск, 1959. — Вып. 18. — С. 198 — 218.
34. Нашив А., Джоунс Д., Хендерсон Дж. Демпфирование колебаний: Пер. с англ. М.: Мир, 1988. — 448 с.40.0льхофф Н. Оптимальное проектирование конструкций: Сб. статей. М.: Мир, 1981.
35. Панин Б.Н., Сударчиков В.А., Чернин Д.Е. Влияние процесса укладки звена в грунт на колебания остова промышленного трактора. // Исследование силовых установок и шасси транспортных и тяговых машин: Сб. науч. тр. /ЧПИ. Челябинск, 1986. — С. 72 — 76.
Панин Б.Н., Сударчиков В.А., Чернин Д.Е. Влияние процесса укладки звена в грунт на колебания остова промышленного трактора. // Исследование силовых установок и шасси транспортных и тяговых машин: Сб. науч. тр. /ЧПИ. Челябинск, 1986. — С. 72 — 76.
36. Платонов В.Ф. Динамика и надежность гусеничного движителя. М.: Машиностроение, 1973. — С. 232.
37. Платонов В.Ф. Динамическая нагруженность гусеничного обвода трактора. // Тракторы и сельхозмашины. 1970. — № 10. — С. 19-21.
38. Платонов В.Ф., Герасимов B.C. Ударная нагруженность гусеничного зацепления. // Тракторы и сельхозмашины. 1973. — № 4. — С. 9 — 11.
39. Платонов В.Ф., Корвин П.И. Взаимодействие цевки гусеницы с ведущим колесом трактора. // Изв. вузов. Машиностроение. 1987. — № 11. — С. 74 -77.
40. Победил A.B., Кондаков В.Д., Расулумуна Х.М. Исследование динамики ведущего участка гусеницы. // Совершенствование рабочих органов сельхозмашин и агрегатов: Материалы международной науч.-тех. конф. — Барнаул: Изд. -во АлтГТУ, 1994. С. 81.
-во АлтГТУ, 1994. С. 81.
41. Потураев В.H. Резиновые и резинометаллические детали машин. М.: Машиностроение, 1966.- С. 299.
42. Реклейтис Г., Рейвиндран А., Регсдел К. Оптимизация в технике: В 2 х кн. : Пер. с англ.-М.: Мир, 1986. — Кн. 1 — 2.
43. Сабоннадьер Ж.-К., Кулон Ж.-Л. Метод конечных элементов и САПР. М.: Мир, 1989.- 190 с.
44. Сегерлинд JI. Применение метода конечных элементов : Пер. с англ. -М.: Мир, 1979.-392 с.
45. Спирин А.П. Потери на трение в шарнирах резинометаллической гусеницы. // Тракторы и сельхозмашины.- 1968. № 4. — С. 21 — 23.
46. Стародубцев В.Ф. Исследование влияния гусениц с резинометаллическими шарнирами на динамическую нагруженность гусеничного обвода трактора с полужесткой подвеской : Дисс. канд. техн. наук Барнаул, 1978. — 273 с.
47. Тескер Е.И., Шеховцов В.В., Зленко C.B., Кумсков Д.И. Анализ динамических воздействий на ведущие колеса гусеничного трактора // MOTOAUTO 97: Материалы международ, науч.-практ. конф. г. Русе, Болгария, 1997 г. — с.324-329.
Русе, Болгария, 1997 г. — с.324-329.
48. Тимошенко С.П., Янг Д.Х., Уивер У. Колебания в инженерном деле. -М.: Машиностроение, 1985. 472 с.
49. Толчинский Н.А., Болтов А.Т, Барсуков Ю.Н., Беседин Л.Н. Определение радиальной податливости гусеничных цепей//Исследование ходовых систем. Барнаул:АлтПИ, 1973 Вып.35, с. 35-39.
50. Толчинский В.А., Целищев В.А. К вопросу о типе гусеничного движителя для энергонасыщенных тракторов: Сб. науч. тр. / МАМИ. -М., 1976. Вып. 1. — С. 32-37.
51. Трепененков ИМ. Исследование резинометаллических шарниров: Сб. науч. тр. / НАШ. М., 1948. — Вып. 1. — С. 13 — 17.
52. Турчак Л.И. Основы численных методов. М.: Наука, 1987. — С. 213 -225.
53. Химмельблау Д. Прикладное нелинейное программирование : Пер. с англ. М.: Мир, 1975 — 534 с.
54. Хог Э., Арора Я. Прикладное оптимальное проектирование. М.: Мир, 1983.-478с.
55. Хог Э., Чой К., Комков В. Анализ чувствительности при проектировании конструкций : Пер. с англ. М.: Мир, 1988 — 428 с.
56. Ходес И.В., Победин А.В., Ляшенко М.В. Виброактивность ведущего участка гусеничного движителя // Тракторы и сельскохозяйственные машины. 1998. — № 10. — С. 38-40.
57. Akin J.E. Application and Implementation of Finite Element Methods // N. -Y.: Academic Press, 1982, — 373p.
58. Argyris J.H., Scharpf D.W. Finite Elements in Time and Space. // Nuclear Ingeneering and Design. Amsterdam: North-Holland Puplishing Company, 1969.-№10, p. 456-464.
59. Beck R.R., Wehage R.A., The Modeling and Simulation of Two Coupled M-113 Armored Personnel Carriers, Proceedings of the Tenth Annual Pittsburgh Conference on Modeling and Simulation, Vol. 10, Part 2, 1979, pp. 353-3.157
60. Box M.J. A New Method of Constrained Optimisation and A Comparison With Other Methods // The Comp. Journal, 8,42-52,1965.
61. Wehage R.A., Haug E.J. Generalized Coordinate Partitioning for Dimension Reduction in Analysis of Constrained Dynamic System // Journal of Mechanical Design, 1982, vol. 104, — PP. 247 — 255
104, — PP. 247 — 255
Определение динамических свойств гусеничного хода гидромелиоративных машин и способ шарнирного крепления рабочего органа бестраншейного трубоукладчика
Определение динамических свойств гусеничного хода гидромелиоративных машин и способ шарнирного крепления рабочего органа бестраншейного трубоукладчика
- Гасанов Т.Г.
- Батманов Е.З.
- Гусейнов М.Р.
- Нажмудинова М.Н.
;
;
;
Аннотация
Цель. Задачей исследования является определение требований к различным устройствам гидромелиоративных машин, широко применяемых при строительстве каналов и дрен, для поддержания заданного уклона, а также расчет исполнительного механизма, служащего для устранения колебательного движения рабочего органа относительно линии заданного уклона. Методика. Дано математическое описание колебаний рабочего органа гусеничных гидравлических мелиоративных машин с навесными рабочими органами.Результаты. В статье представлены результаты исследований по выявлению основных факторов, влияющих на колебания рабочего органа гусеничных мелиоративных машин. В результате теоретических и экспериментальных исследований установлено, что при пересечении гусеничной машиной с жесткой ходовой частью одиночных и множественных неровностей движение режущей кромки жестко закрепленного рабочего органа графически изображается синусоидальными кривыми. Полученные зависимости позволяют провести расчеты автоматической системы поддержания заданного уклона и установить области устойчивых режимов работы системы. Представлен геометрический метод оптимизации шарнирного соединения рабочего органа бестраншейного трубоукладчика. Заключение. Предложенные методы повышения производительности гусеничных гидравлических мелиоративных машин с навесными рабочими органами при движении по неровным грунтовым поверхностям могут быть использованы для создания широкого класса навесных землеройных машин как с пассивными, так и с активными рабочими органами.
Методика. Дано математическое описание колебаний рабочего органа гусеничных гидравлических мелиоративных машин с навесными рабочими органами.Результаты. В статье представлены результаты исследований по выявлению основных факторов, влияющих на колебания рабочего органа гусеничных мелиоративных машин. В результате теоретических и экспериментальных исследований установлено, что при пересечении гусеничной машиной с жесткой ходовой частью одиночных и множественных неровностей движение режущей кромки жестко закрепленного рабочего органа графически изображается синусоидальными кривыми. Полученные зависимости позволяют провести расчеты автоматической системы поддержания заданного уклона и установить области устойчивых режимов работы системы. Представлен геометрический метод оптимизации шарнирного соединения рабочего органа бестраншейного трубоукладчика. Заключение. Предложенные методы повышения производительности гусеничных гидравлических мелиоративных машин с навесными рабочими органами при движении по неровным грунтовым поверхностям могут быть использованы для создания широкого класса навесных землеройных машин как с пассивными, так и с активными рабочими органами.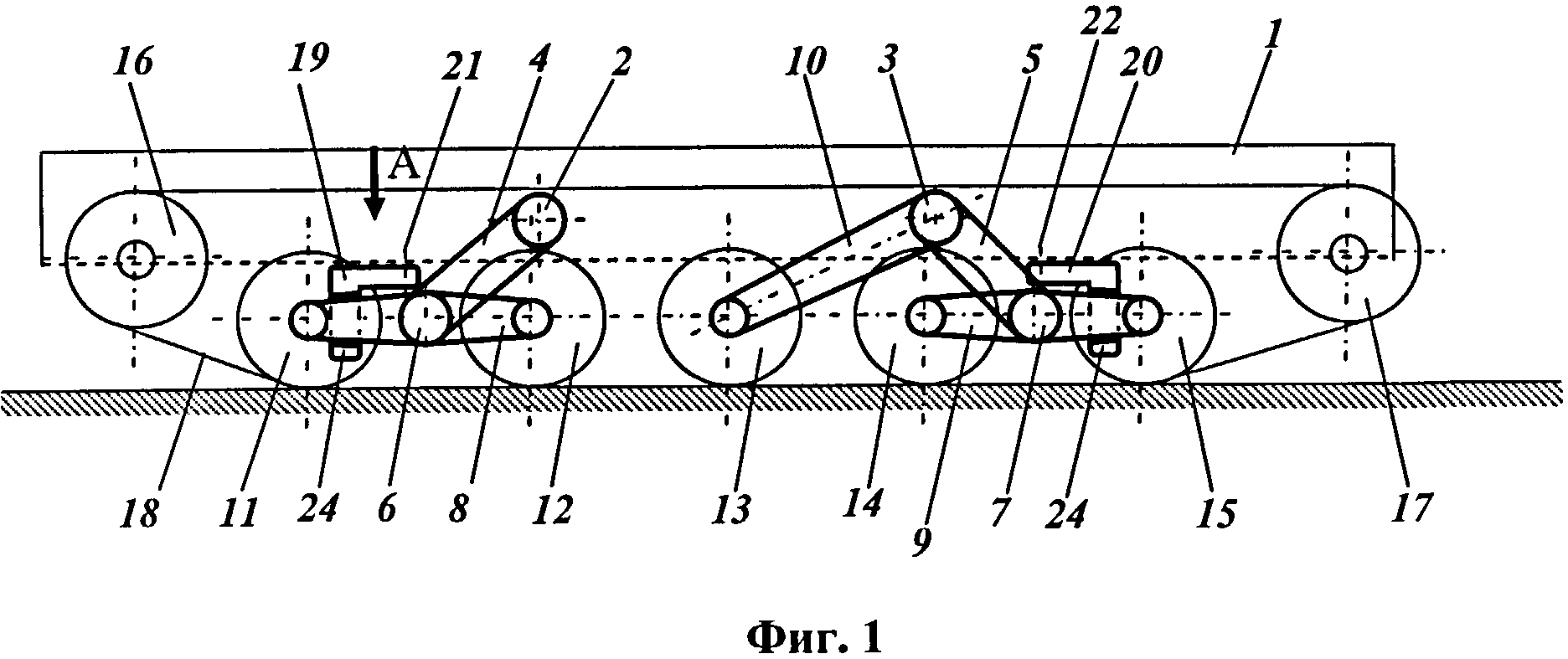
- Публикация:
Вестник Дагестанского государственного технического университета технических наук
- Дата публикации:
- Январь 2021
- DOI:
10.21822/2073-6185-2020-47-4-122-131
- Биб-код:
2021ХДСЦ..47..122Г
109 Caterpillar Dr Unit 3C, Joliet, IL 60436
Об этом доме
Факты о доме
Тип недвижимости
Кондоминиум/кооператив
Год постройки
1988
Информация о ценах
Redfin Estimate
154 868 $
Электричество и солнечная энергия
Посмотреть примерную стоимость энергии и экономию солнечной энергии для этого дома
Интернет
Посмотреть интернет-планы и провайдеров, доступных для этого дома
Просмотр улиц
Маршруты
1356 долл. США в месяц
США в месяц
Интерьер
- Тип кондиционера: Центральный
- Тип отопления: Принудительный воздух Газ
Отопление и охлаждение
- Количество комнат: 4
Информация о помещении
Внешний вид
- Количество зданий: 1
- Земельный пл. Футов: 37 798
- Название муниципалитета: TROY TWP
- Акров: 0,8677
- Описание использования округа: ЖИЛОЙ
Информация о лоте
- Тип канализации: Общественная 90 006
- Тип службы водоснабжения: Частная
Информация о коммунальных услугах
Финансовая
- История продаж
- Налоговая история
| Год | Налог на имущество | Дополнения = 900 17 | Оценочная стоимость | |||||
|---|---|---|---|---|---|---|---|---|
| 2021 | 361 долл. США (−0,1%) | 1 089 долл. США | 2 792 долл. 881 881 | |||||
| 2020 | 361 долл. (+2,7%) | 1089 долл. США | 2792 долл. 0124 | 2019 | 351 долл. США (+28,0%) | 1,045 | 2,678 | 3,723 |
| 2018 | 275 долларов (−1,9%) | 1,04 доллара 5 | 1778 долларов | 2823 долларов | ||||
| 2017 | 280 долларов (+23,9%) | 1045 долларов | 1 доллар, 778 | 2823 долл. США | ||||
| 2015 | 226 долл. США (+5,6%) | 1045 долл. США | 1114 долл. США | 2 долл. США ,159 | ||||
| 2013 | 214 долларов (−5,7%) | 1 045 долларов США | 2,127 | |||||
| 2012 | 227 долларов (+6,3%) | 1,239 долларов | 1,139 | 2,37 долларов 8 | ||||
| 2011 | 213 долларов (−7,3%) | 1 318 долларов | 1 212 долларов | 2 530 долларов США | 2010 | 230 долл. США (+1,7%) США (+1,7%) | 1 531 долл. США | 1 310 долл. США | 2 841 долл. США |
| 2008 901 41 | 226 долларов (+2,8%) | 1566 долларов США | 1 340 долларов США | 2 906 долларов США | ||||
| 2007 | 220 долларов | 1566 долларов | 1340 долларов | 2906 долларов |
Зонирование
900 16 Б-3 | Разрешено: Коммерческий
Цена продажи дома
Непогашенная ипотека
Продажа с традиционным агентомПродажа с агентом Redfin
Общая сумма выручки от продажи 145 392 долл. США 144 764 долл. США
Комиссия агента продавца 2,5% (3 872 долл. США) 4 долл. США, 500
Сравнение услуг агента
Агент с полным спектром услуг
Премиальное размещение на Redfin
Бесплатные профессиональные фотографии
Бесплатное пошаговое руководство в 3D
Показать налоги и сборы
Комиссия агента покупателя 3 872 долл. США 3 872 долл. США
США
Акцизный налог 232 долл. США 232 долл. США
Разное. сборы$1,500$1,500
Получите на 0 долларов больше, продав свой дом с агентом Redfin
Запланируйте консультацию по продаже
Сводный рейтинг GreatSchools
6/10
Troy Heritage Trail School
Public, Pre K-4 • Обслуживает этот дом • 2,1 км
6/10
Orenic Intermediate School
Public, 5-6 • Обслуживает этот дом • 4.5mi
6/10
Troy Middle School
Public, 7-8 • Обслуживает этот дом • 4.5mi
4/10 9 0017
Средняя школа Джолиет Вест
Общедоступная, 9-12 • Обслуживает этот дом • 2,1 км
Данные школы предоставлены GreatSchools, некоммерческой организацией. Redfin рекомендует покупателям и арендаторам использовать информацию и рейтинги GreatSchools в качестве первого шага, а также провести собственное расследование, чтобы определить желаемые школы или школьные округа, в том числе связавшись с самими школами и посетив их. Redfin не подтверждает и не гарантирует эту информацию. Границы школьных услуг предназначены только для справки; они могут измениться, и их точность не гарантируется. Чтобы проверить право на зачисление в школу, свяжитесь напрямую со школьным округом.
Redfin не подтверждает и не гарантирует эту информацию. Границы школьных услуг предназначены только для справки; они могут измениться, и их точность не гарантируется. Чтобы проверить право на зачисление в школу, свяжитесь напрямую со школьным округом.
Транспорт рядом с 109 Caterpillar Dr Unit 3C
61/100
В некоторой степени можно ходить пешком
Walk Score®
29/100
Некоторый общественный транспорт
9001 4 Transit Score®
55/100
Bikeable
Bike Score®
Климатические риски
Коэффициент наводнения
Мы работаем над получением актуальной и точной информации о риске наводнения для этого дома.
Fire Factor
Мы работаем над получением актуальной и точной информации о риске возгорания для этого дома.
Тепловой фактор
Мы работаем над получением актуальной и точной информации о тепловых рисках для этого дома.
Данные о климатических рисках предоставляются только в информационных целях. Если у вас есть вопросы или отзывы об этих данных, обратитесь за помощью на сайтах Riskfactor.com и Climatecheck.com.
Если у вас есть вопросы или отзывы об этих данных, обратитесь за помощью на сайтах Riskfactor.com и Climatecheck.com.
Redfin не подтверждает и не гарантирует эту информацию. Предоставляя эту информацию, Redfin и ее агенты не дают советов или рекомендаций по рискам наводнений, страхованию от наводнений или другим климатическим рискам. Redfin настоятельно рекомендует потребителям самостоятельно исследовать климатические риски недвижимости для собственного удовлетворения.
Продажи квартир (последние 30 дней)
Тенденции кондоминиумов/кооперативов в 60436
- Средняя цена продажи
- Количество проданных домов
- Среднее количество дней на рынке
90 016 Средняя цена продажи
(квартиры/кооперативы)
$186 500
+28,6% г/г | Июнь 2023
- 1 год
- 3 года
- 5 лет
На основе расчетов Redfin данных о домах из MLS и/или общедоступных записей.
$186 500
+28,6%
Подробнее о рыночных тенденциях в 60436
Рыночная конкуренция в 60436
Рассчитано за последние 3 месяца
62
Довольно конкурентоспособный
Redfin Compete Score
™
- Некоторые дома получают несколько предложений.
- В среднем дома продаются примерно на 2 % выше прейскурантной цены, а их рассмотрение занимает около 52 дней.
- Горячие дома могут быть проданы примерно на 5% выше прейскурантной цены и будут рассмотрены примерно через 35 дней.
Сравнить с ближайшими почтовыми индексами
- Некоторые дома получают несколько предложений.
- В среднем дома продаются по цене примерно на 1% выше прейскурантной цены и ожидают рассмотрения примерно через 54 дня.
- Горячие дома могут быть проданы примерно на 4% выше прейскурантной цены и будут рассмотрены примерно через 36 дней.
- Некоторые дома получают несколько предложений.

- В среднем дома продаются по цене примерно на 1% выше прейскурантной цены и ожидают рассмотрения примерно через 47 дней.
- Горячие дома могут быть проданы примерно на 4% выше прейскурантной цены и будут рассмотрены примерно через 35 дней.
Ближайшие похожие дома
Ближайшие недавно проданные дома
Данные из государственных архивов.
101 Caterpillar Drive #2C, JOLIET, IL 2 кровати | 2 ванны | — кв. футов | 155 720 $ |
109 Caterpillar Drive #1A, Джолиет, Иллинойс 2 кровати | 2 ванны | 960 кв.м. футов | 157 754 $ |
103 Caterpillar Drive #1D, Джолиет, Иллинойс 2 кровати | 2 ванны | 960 кв.м. футов | 162 610 $ |
103 Caterpillar Drive, Джолиет, Иллинойс — Кровати | 2 ванны | 960 кв.м. футов | 155 626 $ |
109 Caterpillar Drive, Джолиет, Иллинойс — Кровати | 2 ванны | 960 кв. | 136 173 $ |
103 Caterpillar Drive #3B, Джолиет, Иллинойс 2 кровати | 2 ванны | 960 кв.м. футов | 153 723 $ |
103 Caterpillar Drive #1B, Joliet, IL 2 кровати | 2 ванны | 960 кв.м. футов | 166 658 $ |
103 Caterpillar Drive #2D, Джолиет, Иллинойс 2 кровати | 2 ванны | 960 кв.м. футов | 154 710 $ |
101 Caterpillar Drive #2B, JOLIET, IL 2 кровати | 2 ванны | 960 кв.м. футов | 166 196 $ |
109 Caterpillar Drive #2C, Джолиет, Иллинойс — Кровати | 2 ванны | 960 кв.м. футов | 148 205 $ |
109 Caterpillar Drive #2D, Джолиет, Иллинойс — Кровати | 2 ванны | 960 кв.м. футов | 154 852 $ |
103 Caterpillar Drive #1A, Джолиет, Иллинойс 2 кровати | 2 ванны | 1000 кв. | 157 974 $ |
103 Caterpillar Drive, Джолиет, Иллинойс — Кровати | 2 ванны | 960 кв.м. футов | 151 824 $ |
101 Caterpillar Drive #3D, Joliet, IL 2 кровати | 2 ванны | 960 кв.м. футов | 152 233 $ |
103 Caterpillar Drive #2C, JOLIET, IL 2 кровати | 2 ванны | 960 кв.м. футов | 156 944 $ |
103 Caterpillar Drive #3D, JOLIET, IL 2 кровати | 2 ванны | 960 кв.м. футов | 158 172 $ |
109 Caterpillar Drive #1C, Джолиет, Иллинойс 2 кровати | 2 ванны | 960 кв.м. футов | 155 615 $ |
103 Caterpillar Drive #2A, Джолиет, Иллинойс — Кровати | 2 ванны | 960 кв.м. футов | 150 038 $ |
103 Caterpillar Drive #2B, Джолиет, Иллинойс 2 кровати | 2 ванны | 960 кв. | 163 493 $ |
103 Caterpillar Drive, Джолиет, Иллинойс — Кровати | 2 ванны | 960 кв.м. футов | 148 872 $ |
109 Caterpillar Drive #1D, Joliet, IL — Кровати | 2 ванны | 960 кв.м. футов | 151 190 $ |
Часто задаваемые вопросы о блоке 109 Caterpillar Dr Unit 3C
Что такое блок 109 Caterpillar Dr Unit 3C?
109 Caterpillar Dr Unit 3C — это квартира с 2 спальнями и 2 ванными комнатами. Этот дом в настоящее время не продается.
Сколько стоит этот дом?
Основываясь на данных Redfin’s Joliet, мы оцениваем стоимость дома в $154 868
Когда этот дом был построен и продан в последний раз?
109 Caterpillar Dr Unit 3C был построен в 1988 году.
Какова примерная стоимость аренды этого дома?
По нашим оценкам, стоимость аренды 109 машин Caterpillar Dr Unit 3C составит от 1338 до 1703 долларов.
Насколько конкурентоспособен рынок этого дома?
Основываясь на рыночных данных Redfin за последние 3 месяца, мы подсчитали, что рыночная конкуренция в районе 60436, где расположен этот дом, довольно высока. Дома продаются примерно на 2% выше прейскурантной цены и ожидают рассмотрения примерно через 52 дня. Горячие дома могут быть проданы примерно на 5% выше прейскурантной цены и ожидают рассмотрения примерно через 35 дней. По сравнению с соседними рынками 60436 более конкурентоспособен, чем 60585, и менее конкурентоспособен, чем 60586.
Какие похожие дома находятся рядом с этим домом?
Сопоставимые соседние дома включают 103 Caterpillar Dr Unit 1B, 2636 Crescenzo Dr Unit C и 103 Caterpillar Dr Unit 2B.
Какой полный адрес этого дома?
Полный адрес этого дома: 109 Caterpillar Drive Apartment 3C, Joliet, Illinois 60436.
Каков рынок жилья в 60436?
Рынок жилья 60436 отличается некоторой конкуренцией. Средняя цена продажи дома в 60436 в прошлом месяце составила 187 тысяч долларов, что на 28,6% больше, чем в прошлом году.


 ru
ru Такая модель должна в той или иной степени имитировать все основные системы ГМ (силовую установку, трансмиссию, подвеску, движитель), что увеличит требования математической модели к вычислительным ресурсам.
Такая модель должна в той или иной степени имитировать все основные системы ГМ (силовую установку, трансмиссию, подвеску, движитель), что увеличит требования математической модели к вычислительным ресурсам.

 1. Модель гусеничного обвода
1. Модель гусеничного обвода


 z на опорный каток нулевым при их отрицательном значении.
z на опорный каток нулевым при их отрицательном значении. Она равна силе в шине опорного катка Pш, известной из модели подвески. Тогда
Она равна силе в шине опорного катка Pш, известной из модели подвески. Тогда Вертикальные составляющие используются для расчёта сил в подвеске. Силы сцепления с грунтом Pгрунт(i) и горизонтальные составляющие определяют динамику прямолинейного движения ГМ.
Вертикальные составляющие используются для расчёта сил в подвеске. Силы сцепления с грунтом Pгрунт(i) и горизонтальные составляющие определяют динамику прямолинейного движения ГМ. На верхнем графике видно, что за этой массой с некоторым отставанием следуют остальные.
На верхнем графике видно, что за этой массой с некоторым отставанием следуют остальные.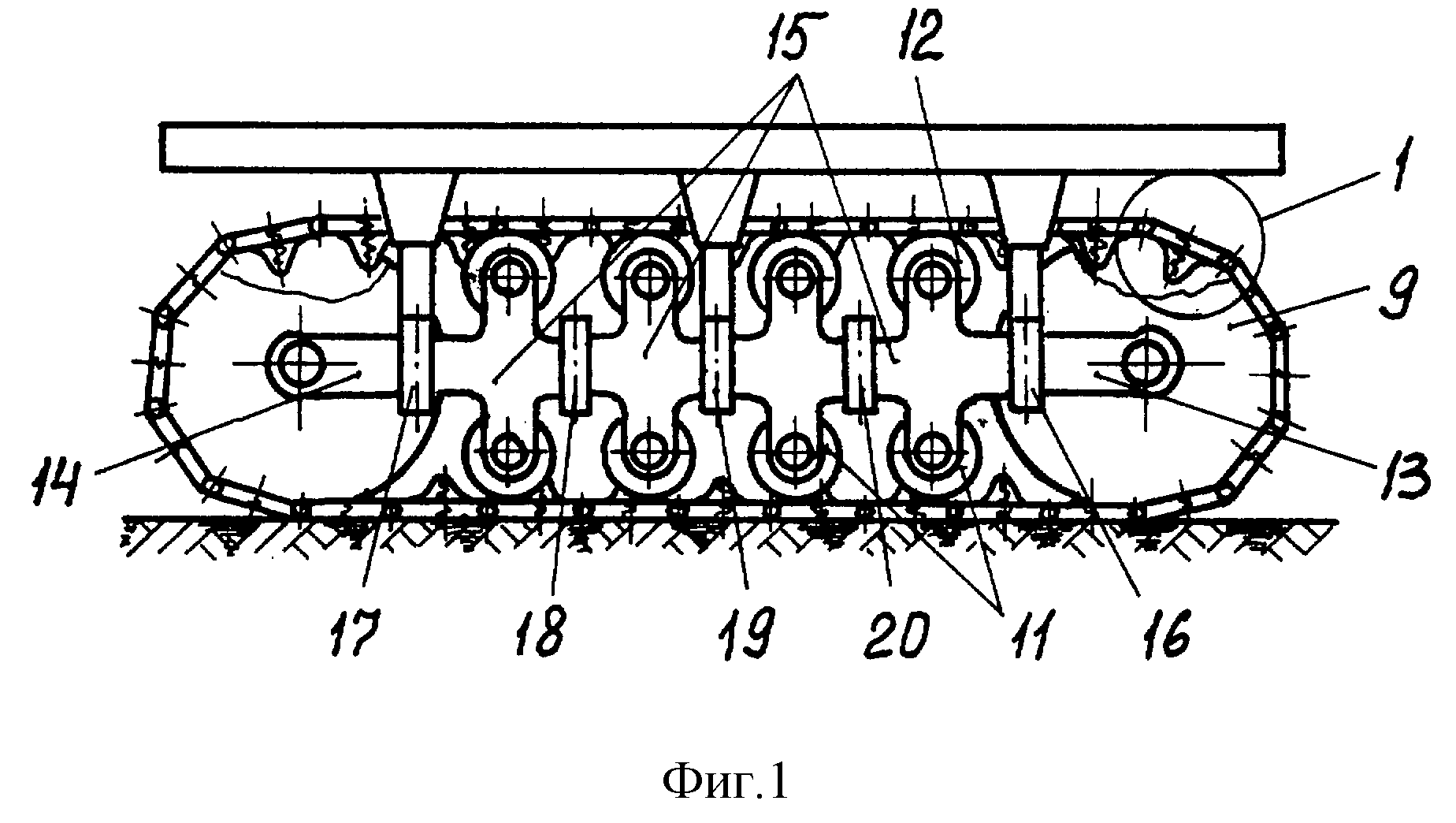 Практическая значимость модели может быть повышена, если усложнить расчёт взаимодействия гусеницы и грунта — учесть влияние большего количества характеристик грунта и грунтозацепов гусеницы. С помощью введения дополнительных масс гусеницы можно рассмотреть поведение участков гусеничного обвода между опорными катками в интересах задачи профильной проходимости.
Практическая значимость модели может быть повышена, если усложнить расчёт взаимодействия гусеницы и грунта — учесть влияние большего количества характеристик грунта и грунтозацепов гусеницы. С помощью введения дополнительных масс гусеницы можно рассмотреть поведение участков гусеничного обвода между опорными катками в интересах задачи профильной проходимости.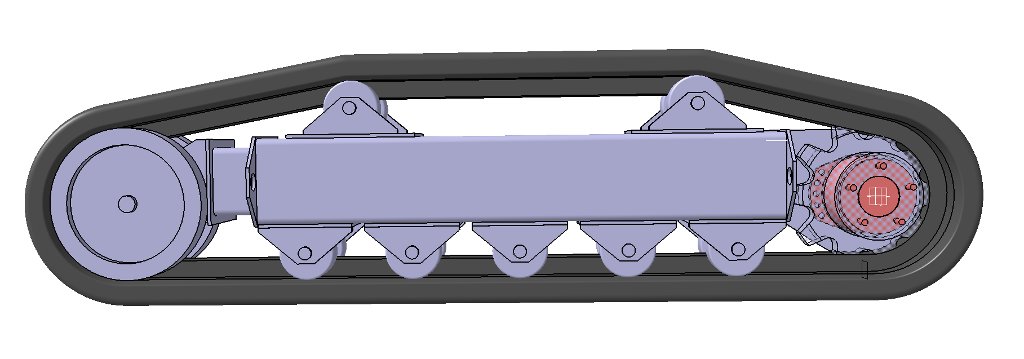 – М.: МВТУ, 2000. – 265 с.
– М.: МВТУ, 2000. – 265 с.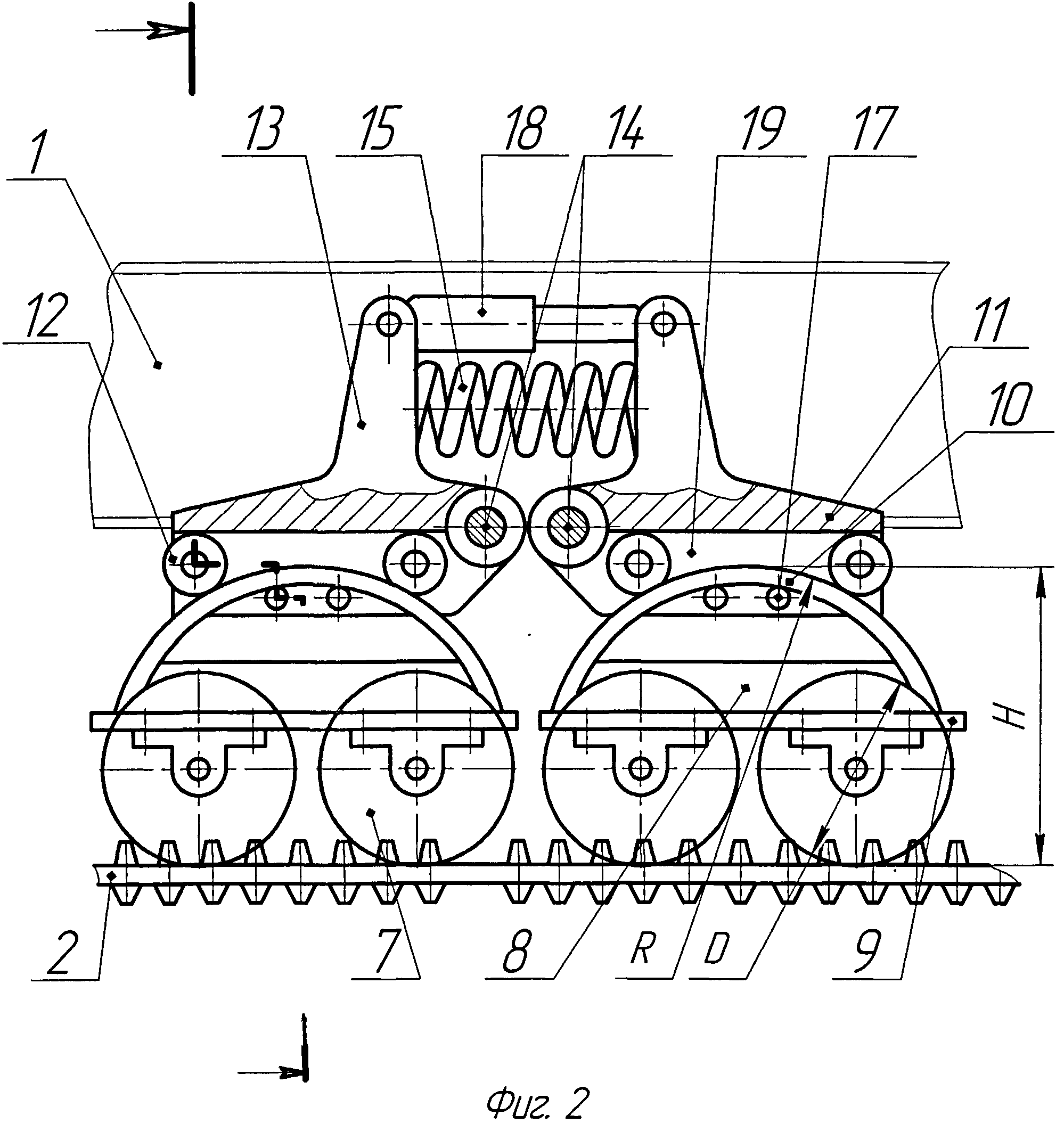 06.2018
06.2018
 м. футов
м. футов м. футов
м. футов м. футов
м. футов