Гидравлические машины. Основные определения и классификация.



Классификация гидравлических машин

Гидравлические машины — устройства для преобразования механической энергии в энергию потока и наоборот — для преобразования энергии движущейся жидкости в механическую энергию.

По функциональному назначению гидравлические машины подразделяют на две основные группы:

• насосы;
• гидравлические двигатели.

***

Насосы

Насосы являются одной из самых распространенных разновидностей машин, применяемых практически во всех отраслях машиностроения, строительства, промышленности и сельского хозяйства.

Их применяют в гидромеханических конструкциях многих механизмов и агрегатов, в трубопроводах разного назначения (нефтепроводы, газопроводы, транспортные трубопроводы и т. п.), в системах водоснабжения, отопления, охлаждения, вентиляции, в котельных установках, бытовой технике и т. д.

Насосы (как и гидродвигатели) применяют в гидропередачах, где основным элементом является гидравлический привод, назначение которого состоит в передаче энергии жидкости от насоса к исполнительному рабочему органу (гидромотору, гидроцилиндру и т. п.). Несколько иное назначение у насосов, применяемых для транспортировки жидкостей и газов (иногда — помещенных в жидкую или газообразную среду твердых объектов) по трубопроводам — здесь насосы служат для сообщения энергии движения транспортируемому веществу.

Насос преобразует механическую энергию приводного двигателя (электрического, теплового двигателя, ручного привода и т. п.) в энергию потока рабочей жидкости, т. е. насос является источником питания гидравлического привода или гидросистемы.

Согласно ГОСТ 17398-72 «Насосы. Термины и определения» по принципу действия и по виду сообщаемой жидкости энергии насосы подразделяют на две основные группы:

• насосы динамические;
• насосы объемные.

Динамические насосы преобразуют механическую энергию приводного электродвигателя преимущественно в кинетическую энергию потока рабочей жидкости за счет увеличения ее скорости.

К динамическим относят насосы, перемещающие жидкость посредством увеличивающего ее кинетическую энергию силового воздействия (лопатки и лопасти рабочего колеса, внешнее силовое поле, внешний поток, обладающий большей кинетической энергией и т. п.).

Характерная особенность динамических насосов — перемещающаяся в них жидкость имеет постоянное сообщение с входным и выходным патрубками, что конструктивно отличает их от насосов второй группы — объемных.

К динамическим относятся лопастные насосы, электромагнитные (использующие магнитное поле для ускорения потока жидкости), а также насосы, использующие силы трения и инерции (струйные, вихревые, лабиринтные, шнековые, червячные и т. п.).

Особую группу широко распространенных динамических насосов составляют насосы лопастные, передающие энергию жидкости посредством вращающегося рабочего органа — лопастного колеса.

Передача энергии в таких насосах осуществляется при динамическом взаимодействии лопастей колеса с обтекающей их жидкостью.

К лопастным относятся насосы центробежные, осевые и диагональные.

Центробежными называют лопастные насосы с движением жидкости через рабочее колесо от центра к периферии, осевыми — лопастные насосы с движением жидкости через рабочее колесо вдоль его оси.

Примером осевого лопастного насоса может послужить водометный движитель судна, винт которого является рабочим колесом.

***



Объемные насосы предназначены для преобразования механической энергии приводного электродвигателя преимущественно в потенциальную энергию потока рабочей жидкости за счет увеличения ее давления.

К объемным относят насосы, принцип работы которых основан на увеличении внешнего давления на замкнутый объем жидкости со стороны ограничивающих замкнутый объем поверхностей, и периодическим вытеснением жидкости из замкнутого объема в выходной патрубок (напорную магистраль).

Увеличение давления осуществляется за счет уменьшения замкнутого объема по пути переноса жидкости от входной (питающей) магистрали к напорной магистрали. При этом замкнутый объем попеременно сообщается то с входом (питающей магистралью), то с выходом (напорной магистралью) насоса.

Примеры наиболее распространенных конструкций объемных насосов: поршневые, плунжерные, диафрагменные, роторные и шестеренные.

К объемным насосам также относятся некоторые специальные устройства, служащие для подъема и перемещения жидкостей:

• гидравлические тараны, работа которых основана на принципе использования давления, получающегося при гидравлическом ударе;
• эрлифты — устройства для подъема жидкостей в скважинах посредством нагнетания воздуха в скважины и создания разности объемных масс в столбе воздухонасыщенной поднимаемой жидкости и жидкости, окружающей этот воздухонасыщенный столб.

Применение насосов для хозяйственных нужд человека известно с древних времен. Первые конструкции этих машин использовали мускульный (ручной или с использованием животных) привод и предназначались для водозабора из скважин, водоемов и т.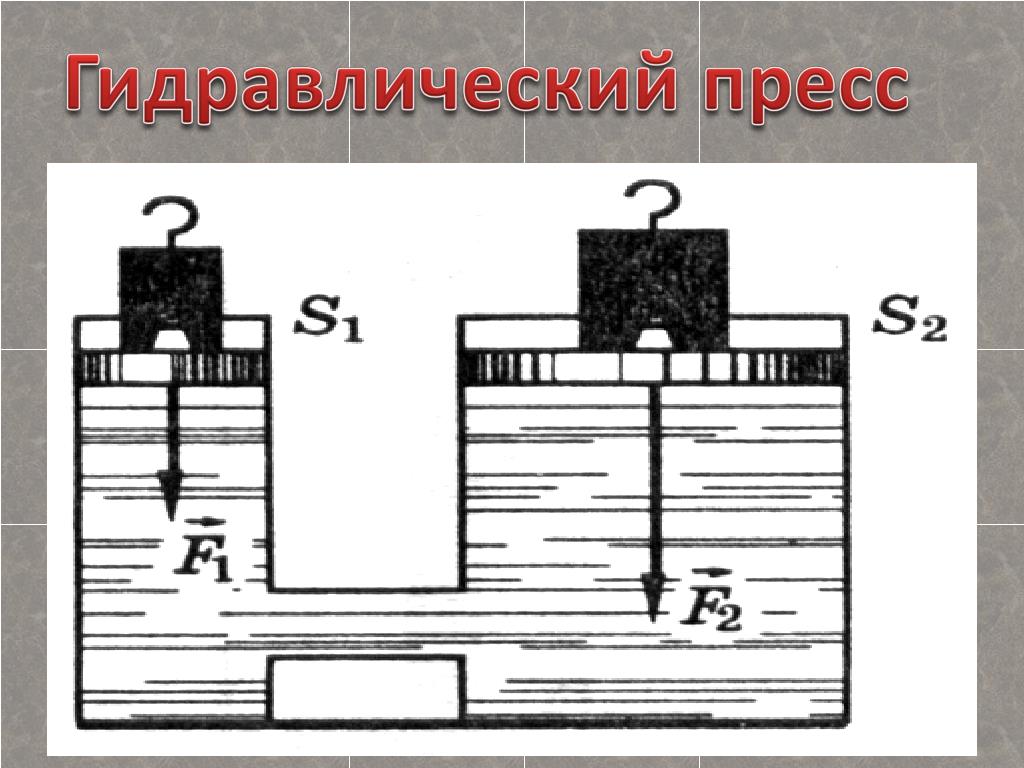 п. В настоящее время разработаны сотни разнообразных конструкций насосов, способных удовлетворить самые разнообразные потребности в машиностроении, медицине, технике, строительстве и других областях человеческой деятельности.

По создаваемому напору различают низконапорные (до 20 м), средненапорные (20..60 м) и высоконапорные (свыше 60 м) насосы.

Кроме того, насосы классифицируют по мощности и подаче (микронасосы, мелкие, малые, средние, крупные), по быстроходности (тихоходные, нормальные, быстроходные), по конструктивным и некоторым другим параметрам.

***

Гидравлические двигатели

Гидравлический двигатель преобразует энергию потока рабочей жидкости, получаемой от насоса, в механическую энергию выходного звена (например, штока цилиндра или вала гидравлического мотора), которые непосредственно или через механическую передачу приводят в действие рабочий орган машины.

Таким образом, двигатель является потребителем энергии жидкости в гидравлическом приводе.

Гидравлические двигатели, как правило, имеют «конструктивных близнецов» среди насосов, т. е. большая часть известных конструкций гидравлических насосов может быть использована в качестве гидродвигателя. Это означает, что практически любой насос может выполнять две функции — передавать энергию жидкости от механических устройств, или отбирать ее у движущейся жидкости, передавая механическим устройствам.

По этой причине гидродвигатели, как и гидронасосы, можно классифицировать на две основные группы — динамические (крыльчатки, турбины и т. п.) и объемные (по аналогу с объемными насосами).

Несколько особняком стоят объемные гидравлические двигатели — гидроцилиндры, которые, впрочем, тоже можно использовать и в качестве насосов.

***

Основными рабочими параметрами, характеризующими гидравлические машины и режимы их работы, являются напор (или давление), подача (для насоса) или расход (для гидродвигателя), мощность (потребная и полезная), а также коэффициент полезного действия.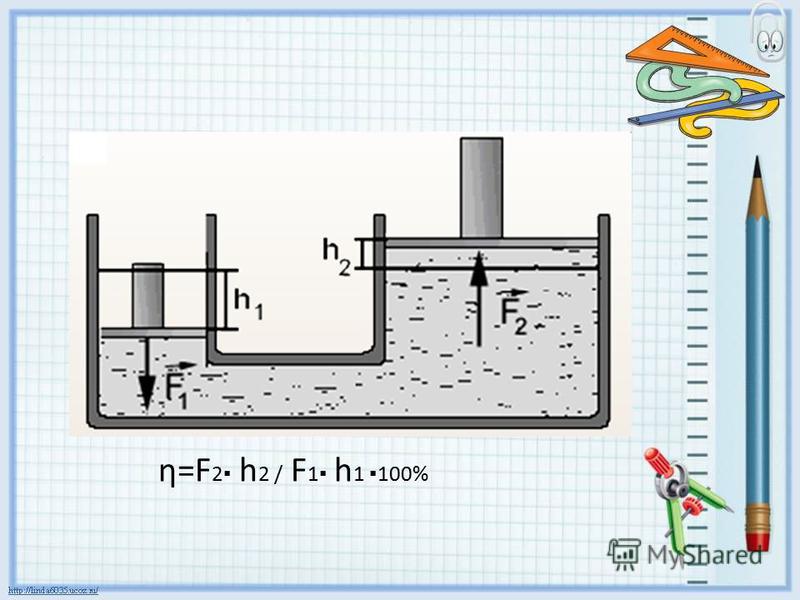

***

Объемные насосы



Главная страница

• Страничка абитуриента

Дистанционное образование

• Группа ТО-81
• Группа М-81
• Группа ТО-71

Специальности

• Ветеринария
• Механизация сельского хозяйства
• Коммерция
• Техническое обслуживание и ремонт автотранспорта

Учебные дисциплины

• Инженерная графика
• МДК.01.01. «Устройство автомобилей»
•    Карта раздела
•       Общее устройство автомобиля
•       Автомобильный двигатель
•       Трансмиссия автомобиля
•       Рулевое управление
•       Тормозная система
•       Подвеска
•       Колеса
•       Кузов
•       Электрооборудование автомобиля
•       Основы теории автомобиля
•       Основы технической диагностики




• Основы гидравлики и теплотехники
• Метрология и стандартизация
• Сельскохозяйственные машины
• Основы агрономии
• Перевозка опасных грузов
• Материаловедение
• Менеджмент
• Техническая механика
• Советы дипломнику

Олимпиады и тесты

• «Инженерная графика»
• «Техническая механика»
• «Двигатель и его системы»
• «Шасси автомобиля»
• «Электрооборудование автомобиля»

Гидравлический пресс в физике, теория и онлайн калькуляторы

Гидравлический пресс в физике, теория и онлайн калькуляторы

Определение и принцип гидравлического пресса

Определение

Гидравлический пресс — это машина, которая действует на основе законов движения и равновесия жидкостей.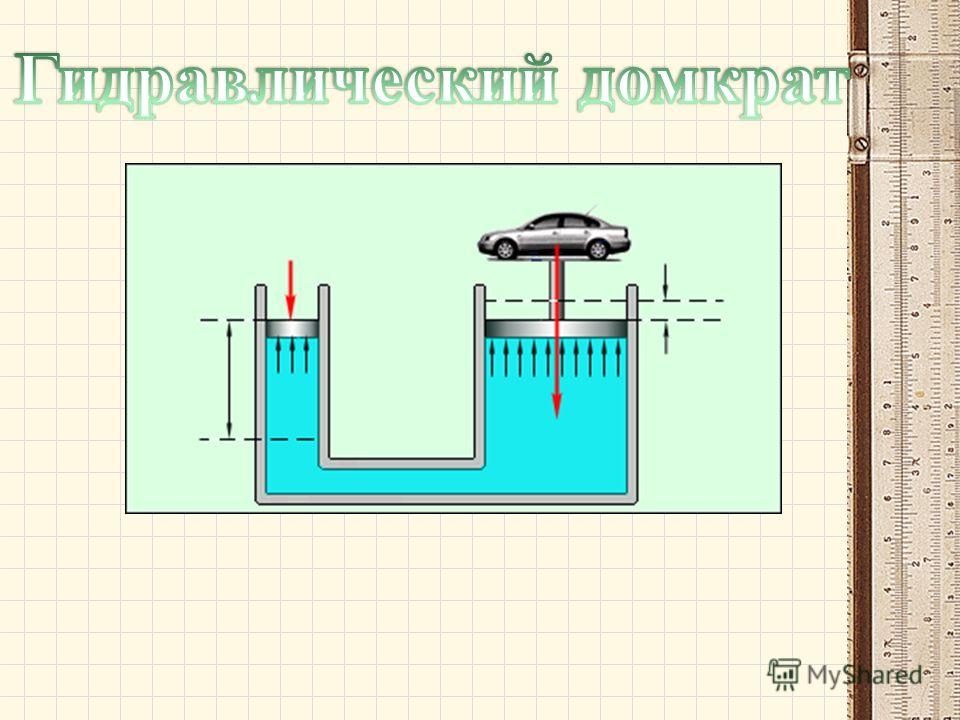 8$ньютонов.

Основу гидравлической машины составляют два цилиндра разного радиуса с поршнями (рис.1), которые соединены трубой. Пространство в цилиндрах под поршнями обычно заполняют минеральным маслом.

Для того чтобы понять принцип действия гидравлической машины следует вспомнить, что такое сообщающиеся сосуды и в чем смысл закона Паскаля.

Сообщающиеся сосуды

Сообщающимися называют сосуды, соединенные между собой и в которых жидкость может свободно перетекать из одного сосуда в другой. Форма сообщающихся сосудов может быть разной. В сообщающихся сосудах жидкость одной плотности устанавливается на одном уровне, если давления над свободными поверхностями жидкости одинаковы.

Из рис.1 мы видим, что конструктивно гидравлическая машина — это два сообщающихся сосуда разного радиуса. Высоты столбов жидкости в цилиндрах будут одинаковыми, если на поршни не действуют силы.

Закон Паскаля

Закон Паскаля говорит нам о том, что давление, которое оказывают внешние силы на жидкость, передаются ей без изменения во все ее точки. На законе Паскаля основано действие многих гидравлических устройств: прессов, тормозных систем, гидроприводов, гидроусилителей и т.д.

Принцип действия гидравлического пресса

Одним из самых простых и старых устройств основанных на законе Паскаля является гидравлический пресс, в котором небольшая сила $F_1$, прикладываемая к поршню небольшой площади $S_1$, преобразуется в большую силу $F_2$, которая воздействует на площадь большой площади $S_2$.

Давление, которое создает поршень номер один, равно:

\[p_1=\frac{F_1}{S_1}\left(1\right).\]

Давление второго поршня на жидкость составляет:

\[p_2=\frac{F_2}{S_2}\left(2\right).\]

Если поршни находятся в равновесии то давления $p_1$ и $p_2$ равны, следовательно, мы можем приравнять правые части выражений (1) и (2):

\[\frac{F_1}{S_1}=\frac{F_2}{S_2}\left(3\right).\]

Определим, каким будет модуль силы, прикладываемой к первому поршню:

\[F_1=F_2\frac{S_1}{S_2}(4)\]

Из формулы (4), видим, что величина $F_1$ больше модуля силы $F_2$ в $\frac{S_1}{S_2}$ раз.

И так, применяя гидравлический пресс можно небольшой силой уравновесить гораздо большую силу. Отношение $\frac{F_1}{F_2}$ показывает выигрыш в силе.

Пресс работает так. Тело, которое необходимо спрессовать, укладывают на платформу, которая лежит на большом поршне. С помощью малого поршня создают высокое давление на жидкость. Большой поршень вместе со сжимаемым телом поднимается, упирается в неподвижную платформу, находящуюся над ними, тело сжимается.

Из малого цилиндра в большой жидкость перекачивают повторным движением поршня малой площади. Делают это следующим образом. Малый поршень поднимается, открывается клапан, при этом в пространство под малым поршнем засасывается жидкость. Когда малый поршень опускается жидкость, оказывая на клапан давление, его закрывает, при этом открывается клапан, который пропускает жидкость в большой сосуд.

Примеры задач с решением

Пример 1

Задание. Каким будет выигрыш в силе у гидравлического пресса, если при действии на малый поршень (площадью $S_1=10\ {см}^2$) с силой $F_1=800$ Н, получают силу, воздействия на большой поршень ($S_2=1000\ {см}^2$) равной $F_2=72000\ $ Н?

Какой выигрыш в силе получался бы у этого пресса, если бы отсутствовали силы трения?

Решение. Выигрышем в силе называют отношение модулей полученной силы к приложенной:

\[\frac{F_2}{F_1}=\frac{72000}{800}=90.\]

Используя формулу, полученную для гидравлического пресса:

\[\frac{F_1}{S_1}=\frac{F_2}{S_2}\left(1.1\right),\]

найдем выигрыш в силе при отсутствии сил трения:

\[\frac{F_2}{F_1}=\frac{S_2}{S_1}=\frac{1000}{10}=100.\]

Ответ. Выигрыш в силе в прессе при наличии сил трения равен $\frac{F_2}{F_1}=90.$ Без трения он
был бы равен $\frac{F_2}{F_1}=100.$

Пример 2

Задание. Используя гидравлический подъемный механизм, следует поднять груз имеющий массу $m$. Какое число раз ($k$) нужно опустить малый поршень за время $t$, если за один раз он опускается на расстояние $l$? Отношение площадей поршней подъемника равно: $\frac{S_1}{S_2}=\frac{1}{n}$ ($n>1$). Коэффициент полезного действия машины составляет $\eta $ при мощности его двигателя $N$.

Решение. Принципиальная схема работы гидравлического подъемника изображена на рис.2., она аналогична работе гидравлического пресса.

В качестве основы для решения задачи используем выражение, связывающее мощность и работу, но при этом учтем, КПД подъемника, тогда мощность равна:

\[N=\frac{\eta A}{t}\to A=\eta Nt\left(2.1\right).\]

Работу производят с целью груз поднять, значит, ее найдем как изменение потенциальной энергии груза, за ноль потенциальной энергии будем считать энергию груза в месте начала его подъема ($E_{p1}$=0), имеем:

\[A=E_{p2}-E_{p1}=E_{p2}=mgh\ \left(2.2\right),\]

где $h$ — высота, на которую подняли груз. Приравняв правые части формул (2.1) и (2.2), найдем высоту, на которую подняли груз:

\[\eta Nt=mgh\to h=\frac{\eta Nt}{mg}\left(2. 3\right).\]

Работу, выполняемую силой $F_0$, при перемещении малого поршня найдем как:

\[А_1=F_0l\ \left(2.4\right),\]

Работа силы, которая двигает большой поршень вверх (сжимает гипотетическое тело), равна:

\[А_2=FL\ .\]
\[А_1=А_2\to F_0l=FL\]
\[\frac{F_0}{F}=\frac{L}{l}=\frac{S_1}{S_2}\left(2.5\right),\]

где $L$ — расстояние, на которое сдвигается большой поршень за один ход. Из (2.5) имеем:

\[\frac{S_1}{S_2}=\frac{L}{l}\to L=\frac{S_1}{S_2}l\ \left(2.6\right).\]

Для того чтобы найти количество ходов поршней (число раз которое опустится малый поршень или поднимется большой) следует высоту поднятия груза разделить на расстояние на которое сдвигается большой поршень за один ход:

\[k=\frac{h}{L}=\frac{\eta NtS_2}{mgS_1l}=\frac{\eta Ntn}{mgl}.\]

Ответ. $k=\frac{\eta Ntn}{mgl}$

Читать дальше: закон Архимеда.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Объясните принцип работы гидравлической машины Назовите два устройства, работающих по этому принципу…

Перейти к

• Упражнение 4А
• Упражнение 4Б

• Глава 1 – Измерения и эксперименты
• Глава 2. Движение в одном измерении
• Глава 3 Законы движения
• Глава 4 Давление в жидкостях и атмосферное давление
• Глава 5. Аптраст в жидкости. Принцип Архимеда и плавучесть.
• Глава 6 Тепло и энергия
• Глава 7 Отражение света
• Глава 8 Распространение звуковых волн
• Глава 9 Текущее электричество
• Глава 10 Магнетизм

Главная >

Селина Солюшнс
Класс 9Физика
>

Глава 4 — Глава 4 Давление в жидкостях и атмосферное давление
>

Упражнение 4А
>
Вопрос 28

Вопрос 28 Упражнение 4A

Объясните принцип работы гидравлической машины. Назовите два устройства, работающих по этому принципу.

Ответ:

Принцип действия гидравлической машины заключается в том, что небольшое усилие
приложенный к маленькому поршню передается для создания большой силы на большем
поршень.

Два устройства, работающих по этому принципу:

· Гидравлические тормоза

· Гидравлический пресс

·

Похожие вопросы

Дайте определение термину тяга. Укажите его единицу СИ.

Что понимается под давлением? Укажите его единицу СИ.

а) Какая физическая величина измеряется в бруске? (b) Как единица бар связана с единицей СИ p…

Определить один паскаль (Па) как единицу давления в системе СИ.

Укажите, является ли тяга скаляром или вектором?

Укажите, является ли давление скаляром или вектором?

Фейсбук

WhatsApp

Копировать ссылку

Было ли это полезно?

Упражнения

Упражнение 4A

Упражнение 4B

Главы

Глава 1 — Измерения и эксперименты

Глава 2 Движение в одном измерении

Глава 3 Законы движения

Глава 4 В жидкостях и атмосферном давлении

Глава.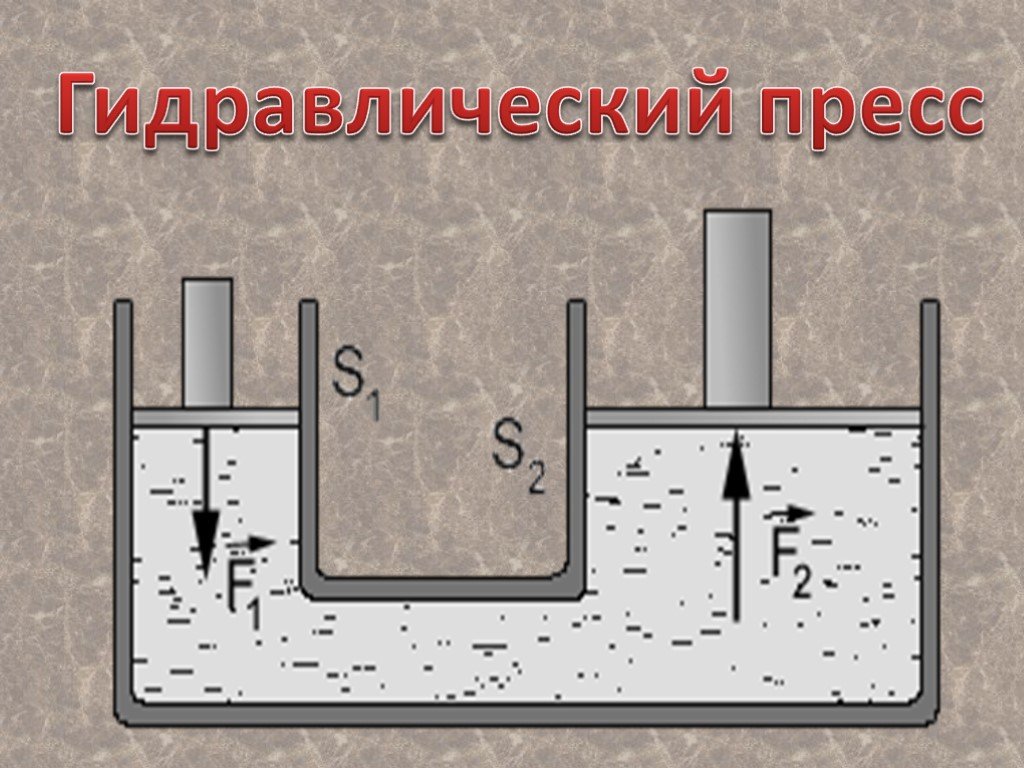 Глава. 5 Аптраст в жидкости Принцип Архимеда и плавучесть

Глава 6 Теплота и энергия

Глава 7 Отражение света

Глава 8 Распространение звуковых волн

Глава 9 Электричество

Глава 10 Магнетизм

Курсы

Быстрые ссылки

Условия и политика

Условия и политика

2022 © Quality Tutorials Pvt Ltd Все права защищены

Как работает гидравлика? — Информация о гидролинии —

Как работает гидравлика? На протяжении веков люди использовали гидроэнергию для повседневного использования. Это один из наиболее широко используемых и старейших способов использования энергии. Его области применения варьируются от полива до строительного оборудования и тяжелой техники. Это настолько распространено, что многие домашние хозяйства и офисы могут ежедневно использовать гидравлическое оборудование. Инженеры прошлого создали основу для современных гидравлических систем, отвечающих потребностям современного мира.

Кто тогда изобрел гидравлику? Трудно определить, кто именно изобрел гидравлические системы. Гидравлические системы были созданы благодаря работе таких великих умов, как Леонардо да Винчи, Галилео Галилей, Блез Паскаль и Джозеф Брама, и это лишь некоторые из них. Гидравлика нашла свое место в современном мире во время промышленной революции, предложив широкое и эффективное применение.

С началом 20-го века появились новые и разнообразные области применения гидравлики. Гидравлические системы широко используются, потому что они легко адаптируются, просты и гибки для использования с различными типами приводов. Высокая плотность мощности является одним из преимуществ системы. Помимо использования в транспортных средствах и промышленности, вы можете найти гидравлические системы повсюду. Самая сложная техника включает в себя самолеты, космические челноки, строительную технику и лифты.

Что такое гидравлическая система?

Гидравлические системы сегодня можно найти в широком диапазоне применений, от небольших сборочных процессов до комплексных сталеплавильных установок и тяжелого машиностроения. Гидравлика позволяет оператору выполнять значительную работу, поднимая тяжелые грузы, поворачивая вал, сверля прецизионные отверстия и т. д. с минимальными затратами на механическую связь благодаря применению закона Паскаля.

Гидравлический пресс обычно состоит из пары цилиндров, которые соединены между собой и заполнены гидравлической жидкостью, такой как масло. По бокам этих цилиндров установлены два поршня, которые остаются в контакте с жидкостью. Когда определенная сила приложена к меньшей части поршня, давление передается по всей жидкости. Согласно упомянутому закону Паскаля, давление будет идентично давлению жидкости в другом поршне. Для получения дополнительной информации о том, как работает гидравлический цилиндр, прочитайте этот пост в блоге.

Гидравлическая жидкость создает мощность жидкости, прокачивая жидкость через гидравлическую систему. Жидкость поступает в цилиндр через клапан, и гидравлическая энергия преобразует ее обратно в механическую энергию. Клапаны помогают направить поток жидкости, и при необходимости можно сбросить давление.

Принцип закона Паскаля реализуется в гидравлической системе с помощью гидравлической жидкости, передающей энергию от одной точки к другой. Поскольку гидравлическая жидкость практически несжимаема, она может мгновенно передавать мощность.

Британский механик по имени Джозеф Брама применил принцип закона Паскаля и разработал первый гидравлический пресс в начале промышленной революции. Его гидравлический пресс был запатентован в 1795 году, широко известный как пресс Брама. Он полагал, что давление, приложенное к небольшой площади, преобразуется в большую силу в той области, которая больше на другой стороне цилиндра.

Как работает гидравлическая система?

Гидравлическая система состоит из пяти элементов: привода, насоса, регулирующих клапанов, двигателя и нагрузки. Двигатель может быть электродвигателем или двигателем любого типа. Насос действует в основном на повышение давления.

Гидравлические системы состоят из множества частей:

• Электродвигатель приводит в действие гидравлический насос.
• Резервуар содержит гидравлическую жидкость.
• Гидравлический насос проталкивает жидкость через систему и преобразует механическую энергию в мощность гидравлической жидкости.
• Клапаны регулируют поток жидкости и при необходимости сбрасывают избыточное давление в системе.
• Гидравлический цилиндр преобразует энергию обратно в механическую энергию.

Существует много типов гидравлических систем, но каждая из них содержит одни и те же основные компоненты, перечисленные ниже. Все они предназначены для работы одинаково.

Гидравлика – принцип Паскаля

Гидравлика называется Принцип Паскаля . Закон Паскаля или принцип Паскаля, основа гидромеханики, был открыт в 1653 году и опубликован в 1663 году Блезом Паскалем. Согласно ему, если в какой-либо точке гидравлической жидкости изменится давление, энергия будет передаваться одинаково во все стороны. Когда вы оказываете давление на жидкость, она будет распределяться одинаково без уменьшения. Давление жидкости будет одинаковым во всех частях сосуда.

Согласно принципу Паскаля, давление равно силе, деленной на площадь, на которую она действует. Давление на поршень вызывает такое же увеличение давления на второй поршень в системе. Если площадь в 10 раз больше площади первой, то сила, действующая на второй поршень, в 10 раз больше, даже если давление во всем цилиндре одинаково. Гидравлический пресс создает этот эффект, основанный на принципе Паскаля. Паскаль также обнаружил, что давление в точке покоящейся жидкости одинаково во всех направлениях; давление будет одинаковым во всех плоскостях, проходящих через данную точку.

Формула закона Паскаля

Паскаль обнаружил, что изменение давления, приложенного к замкнутой жидкости, без уменьшения передается каждой точке жидкости и стенкам содержащего ее сосуда. Это происходит потому, что жидкости практически несжимаемы, поэтому при приложении давления жидкость передает его во всех направлениях по вертикали на стенки сосуда, в котором они находятся.

В этом примере небольшая сила F1, приложенная к маленькому поршню площадью A1, вызывает увеличение давления в жидкости. Согласно принципу Паскаля, это увеличение передается на больший поршень площадью А2 путем приложения к этому поршню силы F2.

Давление – это сила, приложенная к поверхности как;

P=F/A >> F — используемая сила, а A — площадь поверхности.

По обеим сторонам контейнера расположены два поршня, и контейнер заполнен несжимаемой жидкостью, например маслом. Приложенное давление будет передаваться одинаково и без уменьшения на все части системы.

Для первого поршня сила F1 приложена к площади поверхности A1. Тогда давление P1 равно;

P1=F1/A1

Давление P2 во втором цилиндре с силой F2 и площадью поверхности A2 будет равно;

P2=F2/A2

Когда вы прикладываете давление (P1) к первому поршню, оно будет в равной степени передаваться через замкнутую несжимаемую жидкость.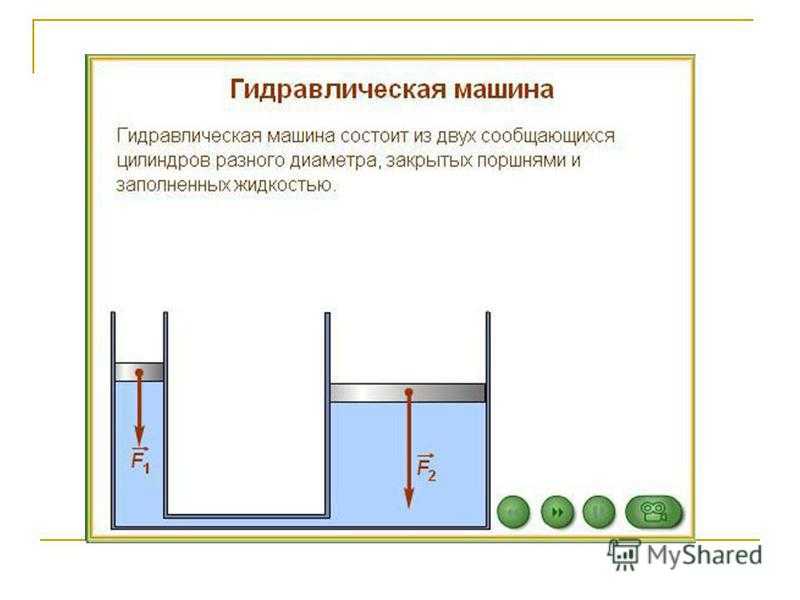

P1=P2

Гидравлическая система позволяет поднимать тяжелые грузы с небольшим усилием. Это уравнение показывает, что сила F2 больше силы F1 на коэффициент, равный отношению площадей двух поршней. Обратите внимание, что давления в обоих поршнях по существу одинаковы, и поскольку их площади различны, то и силы различны, в результате чего отношение между их величинами равно отношению между их площадями.

Блез Паскаль — отец гидравлики

Блез Паскаль (1623–1662) — французский математик, физик, изобретатель, философ и писатель. Он внес значительный вклад в науку на протяжении всей своей жизни. Паскаль внес свой вклад в несколько областей физики, в первую очередь в области гидромеханики и давления. В честь его научного вклада в его честь были названы единица давления (СИ) и закон Паскаля. Паскаль разработал теорию вероятностей, которая стала его самым влиятельным вкладом в математику.

Одно из его самых известных утверждений известно как принцип Паскаля, в котором говорится, что – 

«Давление, оказываемое на несжимаемую жидкость, находящуюся в равновесии в сосуде с недеформируемыми стенками, передается с одинаковой интенсивностью во все направлениях и во всех точках жидкости».

Его работа в области гидродинамики и гидростатики была сосредоточена на принципах гидравлических жидкостей. Он изобрел гидравлический пресс, гидравлическое давление с многократной силой и шприц, используемый в медицине. Он доказал, что гидростатическое давление зависит не от веса жидкости, а от перепада высот.

Плюсы и минусы гидравлических систем

Гидравлические системы представляют собой цепи передачи энергии, которые преобразуют механическую энергию в давление и возвращают обратно в механическое движение. Как правило, начальная механическая энергия представляет собой вращательное движение, создаваемое двигателем внутреннего сгорания или электродвигателем. Передача давления и потока создается с помощью гидравлического масла, а конечное движение может быть как вращательным, так и линейным.

Преимущества гидравлической системы: 

• Гидравлические системы самосмазывающиеся
• Хорошее соотношение мощности и веса
• Относительно небольшие компоненты
• Простая и гибкая передача энергии с помощью гидравлических трубок
• Возможность отключения привода от выработки гидравлической энергии благодаря простой передаче гидравлической энергии
• Гидравлическими системами можно управлять как вручную, так и с помощью современной электроники.

Недостатки гидравлической системы:

• Чистота трансмиссионных жидкостей
• Характеристики жидкостей, зависящие от температуры
• Передача электроэнергии на большие расстояния вызывает потери мощности в системе
• Компоненты и гидравлические жидкости требуют регулярного технического обслуживания

Каково будущее гидравлики?

Мы можем быть уверены, что гидравлика будет значительной частью машин в следующем столетии или даже дольше, потому что трудно предсказать технологии, которые появятся по мере нашего экспоненциального продвижения вперед. Например, абсолютно никто не предсказывал Интернет в 1950 лет, и теперь нас все еще ждут летающие автомобили и колонизация Марса, которые могут быть ближе, чем мы думаем, если мы попросим Илона Маска предсказать эти факты.

Наткнулись на термин « электрогидравлика »? Что, если объединить компьютеры с гидравликой? В будущем компьютеры будут часто устанавливаться на гидравлическом оборудовании. Это обеспечит точно распределенный контроль. Подумайте, что это будет означать для двигателей, цилиндров, клапанов и насосов. Электрогидравлика пробивается к современной гидравлике.

Гидравлика обладает огромной концентрацией мощности. Мы называем это плотностью мощности. Сочетание гидравлики для мускулов и компьютеров для мозга делает гидравлику умнее и эффективнее. Электроника не может сравниться с этим, по крайней мере, пока. Электроника может обеспечить гораздо лучшую координацию и контроль.

В ближайшее время подготовьтесь к гидравлическому оборудованию с еще более высоким IQ, работающему на базе ИИ. Учитывая постоянно развивающееся и быстрое развитие технологий, гидравлическое оборудование становится все более мощным. К сожалению, навыки операторов развиваются не такими темпами, поэтому срочно требуется более удобное оборудование. Для безопасности оператора и долгосрочной жизнеспособности оборудования конструкция гидравлического оборудования должна быть более удобной для пользователя. Задача будет состоять в том, чтобы сделать само гидравлическое оборудование более совершенным. Гидравлика с искусственным интеллектом справится с этой задачей.

Лидирующие на рынке инновации в области гидравлики

Развитие гидравлических технологий с 19 века было феноменальным. Основными преимуществами гидравлических систем являются простая и мощная передача энергии, гибкие и индивидуальные свойства, а также возможность многократного увеличения передачи усилия в различных промышленных целях. Гидравлические системы успешно применяются при эксплуатации и управлении станкостроительной, сельскохозяйственной, строительной и горнодобывающей техникой, а также в автомобильной и авиационной промышленности. Без сомнения, мы можем сказать, что гидравлическая энергия может успешно конкурировать с механическими и электрическими системами. Гидравлические силовые установки могут обеспечивать усилия от нескольких килограммов до тысяч тонн.

Поскольку развитие технологий в современном мире быстро развивается, а разнообразие гидравлических силовых систем становится все более конкретным и приспособленным для многих отраслей, остается еще много возможностей для дальнейшего развития использования гидравлики.