Определение центра масс, теория и онлайн калькуляторы

Определение центра масс, теория и онлайн калькуляторы

При исследовании поведения систем частиц, часто удобно использовать для описания движения такую точку, которая характеризует положение и движение рассматриваемой системы как единого целого. Такой точкой служит центр масс.

Для однородных тел обладающих симметрией центр масс часто совпадает с геометрическим центром тела. В однородном изотропном теле одной выделенной точке найдется симметричная ей точка.

Радиус-вектор и координаты центра масс

Предположим, что у нас имеются две частицы с равными массами, им соответствуют радиус-векторы: ${\overline{r}}_1\ и\ {\overline{r}}_2$ . В этом случае центр масс расположен посередине между частицами. Центр масс (точка C) определён радиус-вектором ${\overline{r}}_C$ (рис.1).

Из рис.1 видно, что:

\[{\overline{r}}_C=\frac{{\overline{r}}_1+\ {\overline{r}}_2}{2}\left(1\right).\]

Можно ожидать, что вместе с геометрическим центром системы радиус-вектор, которого равен ${\overline{r}}_C,$ играет роль точка, положение которой определяет распределение массы. N_{i=1}{m_i}}\left(7\right).\]

Формулы (4-7) совпадают с формулами, которые используют для определения тяжести тела. В том случае, если размеры тела малы в сравнении с расстоянием до центра Земли, центр тяжести считают совпадающим с центром масс тела. В большинстве задач центр тяжести совпадает с центром масс тела.

Скорость центра масс

Выражение для скорости центра масс (${\overline{v}}_c=\frac{d{\overline{r}}_c}{dt}$) запишем как:

\[{\overline{v}}_c=\frac{m_1{\overline{v}}_1+m_2{\overline{v}}_2+\dots +m_n{\overline{v}}_n}{m_1+m_2+\dots +m_n}=\frac{\overline{P}}{M}\left(8\right),\]

где $\overline{P}$ — суммарный импульс системы частиц; $M$ масса системы. Выражение (8) справедливо при движениях со скоростями которые существенно меньше скорости света.

Если система частиц является замкнутой, то сумма импульсов ее частей не изменяется. Следовательно, скорость центра масс при этом величина постоянная. Говорят, что центр масс замкнутой системы перемещается по инерции, то есть прямолинейно и равномерно, и это движение не зависимо от движения составных частей системы. В замкнутой системе могут действовать внутренние силы, в результате их действия части системы могут иметь ускорения. Но это не оказывает влияния на движение центра масс. Под действием внутренних сил скорость центра масс не изменяется.

Примеры задач на определение центра масс

Пример 2

Задание. Система составлена из материальных точек (рис.2), запишите координаты ее центра масс?

Решение. Рассмотрим рис.2. Центр масс системы лежит на плоскости, значит, у него две координаты ($x_c,y_c$). Найдем их используя формулы:

\[\left\{ \begin{array}{c}
x_c=\frac{\sum\limits_i{\Delta m_ix_i}}{m};; \\
y_с=\frac{\sum\limits_i{\Delta m_iy_i}}{m}. \end{array}
\right.\]

Вычислим массу рассматриваемой системы точек:

\[m=m+2m+3m+4m=10\ m.\]

Тогда абсцисса центра масс $x_{c\ }\ $равна:

\[x_c=\frac{0\cdot 4m+3m\cdot b+2m\cdot b}{10m}=0,5\ b.\]

Ордината $y_с$:

\[y_с=\frac{0\cdot m+m\cdot b+2m\cdot b}{10m}=0,3\ b. \]

Ответ. $x_c=0,5\ b$; $y_с=0,3\ b$

Пример 2

Задание. Космонавт, имеющий массу $m$, неподвижен относительно корабля массы $M$. Двигатель космического аппарата выключен. Человек начинает подтягиваться к кораблю при помощи легкого троса. Какое расстояние пройдет космонавт ($s_1$), какое корабль ($s_2$) до точки встречи? В начальный момент расстояние между ними равно $s$.

Решение. Центр масс корабля и космонавта лежит на прямой, соединяющей эти объекты.

В космосе, где внешние силы отсутствуют, центр масс замкнутой системы (корабль-космонавт) либо покоится, либо движется с постоянной скоростью. В избранной нами (инерциальной) системе отсчета он покоится. При этом:

\[\frac{s_1}{s_2}=\frac{m_2}{m_1}\left(2.1\right).\]

По условию:

\[s=s_1+s_2\left(2.2\right).\]

Из уравнений (2.1) и (2.2) получаем:

\[s_1=s\frac{m_2}{m_1+m_2};;\ s_2=s\frac{m_1}{m_1+m_2}.\]

Ответ. $s_1=s\frac{m_2}{m_1+m_2};;\ s_2=s\frac{m_1}{m_1+m_2}$

Читать дальше: период и частота колебаний.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Урок «Центр масс»

Урок «Центр масс»

10 класс

Регламент: 2 урока

Цель: Познакомить учащихся с понятием «центр масс» и его свойствами.

Оборудование: фигуры из картона или фанеры, «неваляшка», перочинный нож, карандаши.

План урока

Этапы урока время методы и приемы

Урок 1

I Введение учащихся 10 фронтальный опрос, работа учащихся у доски.

в проблему урока

II. Изучение нового 15-20 Рассказ учителя, решение задачи,

материала: 10 экспериментальное задание

Урок 2

III Отработка нового 10 сообщения учащихся

материала: 10-15 решение задач,

15 фронтальный опрос

IV. Выводы. Домашнее 5-10 Устное обобщение материала учителем.

задание Запись на доске

Ход урока.

I Повторение 1. Фронтальный опрос: плечо силы, момент силы, условие равновесия, виды равновесия

Эпиграф:   Центром тяжести каждого тела является некоторая располо­женная внутри его точка — такая, что если за нее мысленно подвесить тело, то оно остается в покое и сохраняет первона­чальное положение.            

Архимед

II. Объяснение нового материала

Пусть дано тело или система тел. Мысленно разобьем тело на сколь угодно малые части с массами m1, m2, m3… Каждую из этих частей можно рассматривать как материальную точку. Положение в пространстве i-ой материальной точки с массой mi определяется радиус-вектором ri (рис. 1.1). Масса тела есть сумма масс отдельных его частей: т = ∑ mi.

Центром масс тела (системы тел) называет­ся такая точка С, радиус-вектор которой определяется по формуле

r = 1/m∙∑ mi ri

Можно показать, что положение центра масс относительно тела не за­висит от выбора начала координат О, т. е. данное выше определение центра масс однозначно и корректно.

Центр масс однородных симметричных тел рас­положен в их геометрическом центре или на оси симметрии, центр масс у плоского тела в виде произвольного треугольника находится на пересече­нии его медиан.

Решение задачи

ЗАДАЧА 1. На легком стержне (рис. 1.2) закреплены однородные ша­ры массами m1 = 3 кг , m2 = 2 кг, m3 = 6 кг, и m4 = 3 кг. Расстояние между центрами любых ближайших шаров

а = 10 см . Найти положе­ние центра тяжести и центра масс конструкции.

РЕШЕНИЕ. Положение относительно шаров центра тяжести конструкции не зависит от ориентации стержня в пространстве. Для ре­шения задачи удобно располо­жить стержень горизонтально, как показано на рисунке 2. Пусть центр тяжести находится на стержне на расстоянии L от центра левого шара, т.е. от т. А . В центре тяжести приложена равнодействующая всех сил тяжести и ее момент относительно оси А равен сумме моментов сил тяжести шаров. Имеем r = (m1 + m2 + m3 + m4) g ,

R L = m2gα + m 3 g 2 а + m 4 g 3 а .

Отсюда L=α ( m1 +2m3 + 3m4)/ (m1 + m2 + m3 + m4) ≈ 16,4 см

ОТВЕТ. Центр тяжести совпадает с центром масс и находится, в точке С на расстоянии L=16,4см от центра левого шара.

Оказывается, что у центра масс тела (или системы тел) есть ряд за­мечательных свойств. В динамике показывается, что импульс произвольно движущегося тела равен произведению массы тела на скорость его центра масс и что центр масс движется так, как если бы все внешние силы, действующие на тело, были приложены в центре масс, а масса все­го тела была сосредоточена в нем.

Центром тяжести тела, находящегося в поле тяготения Земли, на­зывают точку приложения равнодействующей всех сил тяжести, дейст­вующих на все части тела. Эта равнодействующая называется силой тя­жести, действующей на тело. Сила тяжести, приложенная в центре тя­жести тела, оказывает на тело такое же воздействие, как и нее силы тя­жести, действующие на отдельные части тела.

Интересен случай, когда размеры тела намного меньше размеров Зем­ли. Тогда можно считать, что на все части тела действуют параллельные силы тяжести, т.е. тело находится в однородном поле тяжести. У парал­лельных и одинаково направленных сил всегда есть равнодействующая, что можно доказать. Но при определенном положении тела в простран­стве можно указать только линию действия равнодействующей всех параллельных сил тяжести, точка ее приложения останется пока неопреде­ленной, т.к. для твердого тела любую силу можно переносить вдоль ли­нии ее действия. Как же быть с точкой приложения?

Можно показать, что при любом положении тела в однородном поле тяжести, линия действия равнодействующей всех сил тяжести, действу­ющих на отдельные части тела, проходят через одну и ту же точку, не­подвижную относительно тела. В этой точке и прикладывается равно­действующая, а сама точка будет центром тяжести тела.

Положение центра тяжести относительно тела зависит только от фор­мы тела и распределения массы в теле и не зависит от положения тела в однородном поле тяжести. Центр тяжести не обязательно находится в са­мом теле. Например, у обруча в однородном поле тяжести центр тяжести лежит в его геометрическом центре.

В однородном поле тяжести центр тяжести те­ла совпадает с его центром масс.

В подавляющем боль­шинстве случаев один термин безбо­лезненно можно заменять другим.

Но: центр масс тела су­ществует независимо от наличия поля тяжести, а о центре тяжести мож­но говорить только при наличии силы тяжести.

Местоположение центра тяжести тела, а значит и центра масс, удобно находить, учитывая симметричность тела и используя понятие момента силы.

Вспоминая условия равновесия, мы выяснили, что

Если плечо силы равно нулю, то момент силы равен нулю и такая сила не вызывает вращательного движения тела.

Следовательно, если линия действия силы проходит через центр масс, то оно движется поступательно.

Таким образом, можно определить центр масс любой плоской фигуры. Для этого надо закрепить ее в одной точке, дав ей возможность свободно поворачиваться. Она установится так, чтобы сила тяжести, поворачивающая ее, проходила через центр масс. В точке закрепления фигуры подвесим нить с грузом (гайкой), проведем линию вдоль подвеса (т.е. линию действия силы тяжести). Повторим действия, закрепив фигуру в другой точке. Пересечение линий действия сил тяжести – центр масс тела

Экспериментальное задание: определить центр тяжести плоской фигуры (по приготовленным ранее учащимися фигурам из картона или фанеры).

Инструкция: закрепляем фигурку на штативе. Подвешиваем за один из углов фигуры отвес. Проводим линию действия силы тяжести. Поворачиваем фигуру, повторяем действие. Центр масс лежит в точке пересечения линий действия силы тяжести.

Быстро справившимся с заданием учащимся можно дать дополнительное задание: прикрепить к фигуре груз (металлический болт) и определить новое положение центра масс. Сделать вывод.

Изучение замечательных свойств «центров», которому более двух тыся­челетий, оказалось полезным не толь­ко для механики — например, при конструировании транспортных средств и военной техники, расчете устойчивости сооружений или для вывода уравнений движения реактив­ных аппаратов. Вряд ли Архимед мог даже помыслить о том, что поня­тие центра масс окажется весьма удоб­ным для исследований в ядерной фи­зике или в физике элементарных час­тиц.

Сообщения учащихся:

В своем труде «О равновесии плос­ких тел» Архимед употреблял понятие центра тяжести, фактически не опре­деляя его. Видимо, оно впервые было введено неизвестным предшественни­ком Архимеда или же им самим, но в более ранней, не дошедшей до нас работе.

Должно было пройти долгих сем­надцать столетий, прежде чем наука прибавила к исследованиям Архимеда о центрах тяжести новые результаты. Это произошло, когда Леонардо да Винчи сумел найти центр тяжести тет­раэдра . Он же, размышляя об устойчи­вости итальянских наклонных башен, в том числе — Пизанской, пришел к «теореме об опорном многоугольни­ке».

Выясненные еще Архимедом усло­вия равновесия плавающих тел впос­ледствии пришлось переоткрывать. Занимался этим в конце XVI века : голландский ученый Симон Стевин, применявший, наряду с понятием цен­тра тяжести, и понятие «центр давле­ния» — точку приложения силы давле­ния окружающей тело воды.

Прин­цип Торричелли (а его имя носят и формулы для расчета центра масс), оказывается, был предвосхищен его учителем Галилеем. В свою очередь, этот принцип лег в основу классичес­кого труда Гюйгенса о маятниковых часах, а также был использован в знаменитых гидростатических иссле­дованиях Паскаля.

Метод, позволивший Эйлеру изу­чать движение твердого тела под дей­ствием любых сил, состоял в разложе­нии этого движения на перемещение центра масс тела и вращение вокруг проходящих через него осей.

Для сохранения в неизменном по­ложении предметов при движении их опоры уже несколько столетий приме­няется так называемый карданов под­вес — устройство, в котором центр тяжести тела располагают ниже осей, вокруг которых оно может вращаться. Примером может служить корабельная керосиновая лампа.

Хотя на Луне сила тяжести в шесть раз меньше, чем на Земле, увеличить там рекорд по прыжкам в высоту уда­лось бы «всего» лишь в четыре раза. К такому выводу приводят расчеты по изменению высоты центра тяжести тела спортсмена.

Помимо суточного вращения вок­руг своей оси и годового обращения вокруг Солнца, Земля принимает уча­стие еще в одном круговом движении. Вместе с Луной она «крутится» вокруг общего центра масс, расположенного примерно в 4700 километрах от центра Земли.

Некоторые искусственные спутни­ки Земли снабжены складной штангой в несколько или даже в десятки мет­ров, утяжеленной на конце (так назы­ваемый гравитационный стабилиза­тор). Дело в том, что спутник вытяну­той формы стремится при движении по орбите повернуться вокруг своего центра масс так, чтобы его продольная ось расположилась вертикально. Тог­да он, подобно Луне, будет все время обращен к Земле одной стороной.

Наблюдения за движением неко­торых видимых звезд свидетельству­ют о том, что они входят в двойные системы, в которых происходит вра­щение «небесных партнеров» вокруг общего центра масс. Одним из невиди­мых компаньонов в такой системе мо­жет быть нейтронная звезда или, воз­можно, черная дыра.

Объяснение учителя

Теорема о центре масс: центр масс те­ла может изменить свое положение только под действием внешних сил.

Следствие теоремы о центре масс: центр масс замкнутой системы тел остается неподвижным при любых взаимодействиях тел системы.

Решение задачи (у доски)

ЗАДАЧА 2. Лодка стоит неподвижно в стоячей воде. Человек, находящийся в лодке, переходит с носа на корму. На какое расстояние h сдви­нется лодка, если масса человека m= 60кг, масса лодки М = 120кг, длина лодки L=3м? Сопротивлением воды пренебречь.

РЕШЕНИЕ. Воспользуемся условием задачи, что начальная скорость центра масс равна нулю (лодка и человек вначале покоились) и сопротивление воды отсутствует (никакие внешние силы в горизонтальном направлении на систему «человек-лодка» не действуют). Следователь­но, координата центра масс системы в горизонтальном направлении не изменилась. На рис.3 изображено начальное и конечное положение лодки и человека. Начальная координата х0 центра масс х0 = (mL+ML/2)/(m+M)

Конечная координата х центра масс х = (mh+M(h+L/2))/(m+M)

Приравнивая х0 = х, находим h= mL/(m+M) =1м

Дополнительно: сборник задач Степановой Г. Н. №393

Объяснение учителя

Вспоминая условия равновесия, мы выяснили, что

Для тел, имеющих площадь опоры, устойчивое равновесие наблюдается в том случае, когда линия действия силы тяжести проходит через основание.

Следствие: чем больше площадь опоры и ниже центр тяжести, тем устойчивее положение равновесия.

Демонстрация

Поставьте детскую игрушку неваляш­ку (Ваньку — Встаньку) на шерохова­тую доску и приподнимите правый край доски. В какую сторону откло­нится «голова» игрушки при сохране­нии ее равновесия?

Объяснение: Центр тяжести С неваляшки находится ниже геометрического центра О шарообразной поверхности «туловища». В положе­нии равновесия точка С и точка касания А игрушки с на­клонной плоскостью должны находиться на одной вертикали; следовательно «голова» неваляшки отклонится влево

Как объяснить сохранение рав­новесия в случае, показанном на ри­сунке?

Объяснение: Центр тяжести системы карандаш — нож лежит ниже точ­ки опоры

III Закрепление. Фронтальный опрос

Вопросы и задачи

1. При перемещении тела с экватора на полюс действующая на него сила тяжести меняется. Отражается ли это на положении центра тяжести тела?

Ответ: нет, т.к. относительные изменения силы тяжести всех элементов тела одинаковы.

2. Можно ли найти центр тяжести «гантели», состоящей из двух массив­ных шариков, соединенных невесо­мым стержнем, при условии, что дли­на «гантели» сравнима с диаметром Земли?

Ответ: нет. Условие существования центра тяжести — однород­ность поля тяготения. В неоднородном гравитационном поле повороты «гантели» вокруг ее центра масс приводят к тому, что линии действия L1 и L2, равнодействующих сил тяжести, приложенных к шарикам, не имеют общей точки

3. Почему при резком торможении автомобиля его передняя часть опус­кается?

Ответ: при торможении на колеса со стороны дороги действует сила трения, создающая вращающий момент вокруг центра масс автомобиля.

4. Где находится центр тяжести буб­лика?

Ответ: в дырке!

5. В цилиндрический стакан понем­ногу наливают воду. Как будет изме­няться положение центра тяжести си­стемы стакан — вода?

Ответ: Центр тяжести системы сначала будет понижаться, а потом — повышаться.

6. Какой длины конец надо отрезать от однородного стержня, чтобы его центр тяжести сместился на ∆ℓ?

Ответ: длиной 2∆ℓ.

7. Однородный стержень согну­ли посередине под прямым углом. Где оказался теперь его центр тяжес­ти?

Ответ: в точке О — середине отрезка О1О2, соединяющего сере­дины участков АВ и ВС стержня

9. Неподвижная космическая ста­ция представляет собой цилиндр. Космонавт начинает круговой обход ста­ции по ее поверхности. Что произойдет со станцией?

Ответ: станция придет во вращение в противоположную сторо­ну, причем ее центр будет описывать окружность вокруг об­щего с космонавтом центра масс.

11. Почему трудно передвигаться на ходулях?

Ответ: центр тяжести человека на ходулях значительно повыша­ется, а площадь его опоры на землю уменьшается.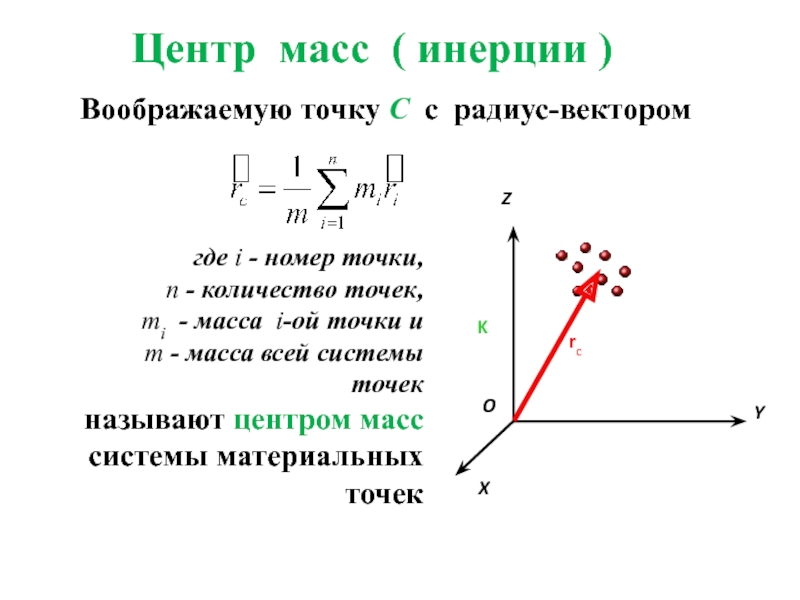

12. Когда канатоходцу легче удер­жать равновесие — при обычном пере­движении по канату или при переносе сильно изогнутого коромысла, нагру­женного ведрами с водой?

Ответ: Во втором случае, так как центр масс канатоходца с вед­рами лежит ниже, т.е. ближе к опоре — канату.

IV Домашнее задание: (выполняется желающими — задачи трудные, решившие их получают «5»). 

*1. Найдите центр тяжести системы шаров, находящихся в вершинах равностороннего невесомого треугольника, изображенного на рисунке

Ответ: центр тяжести лежит на середине биссектрисы угла, в вершине которого находится шар массой 2m

*2. Глубина лунки в доске, в кото­рую вставлен шар, в два раза меньше радиуса шара. При каком угле накло­на доски к горизонту шар выскочит из лунки?

Ответ: при α = π /3

Центр масс

Центр масс