Содержание
Как найти время, скорость и расстояние
Поможем понять и полюбить математику
Начать учиться
400.7K
Каждый день мы смотрим на часы, спидометр, фитнес-браслет и анализируем расстояние, скорость и время. Рассмотрим математические формулы, чтобы решать задачи на поиск времени, скорости и расстояния из учебников и реальной жизни.
Расстояние
Мы постоянно ходим пешком и ездим на транспорте из одной точки в другую. Давайте узнаем, как можно посчитать это пройденное расстояние.
Расстояние — это длина от одного пункта до другого.
- Например: расстояние от дома до школы 3 км, от Москвы до Петербурга 705 км.
Расстояние обозначается латинской буквой s.
Единицы расстояния чаще всего выражаются в метрах (м), километрах (км).
Формула пути Чтобы найти расстояние, нужно умножить скорость на время движения: s = v × t |
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Скорость
Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.
Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.
Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.
Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.
Сейчас мы ее сформулируем и покажем, как ее использовать.
Формула скорости Чтобы найти скорость, нужно разделить путь на время: v = s : t |
Показатели скорости чаще всего выражаются в м/сек или км/час.
Скорость сближения — это расстояние, на которое сблизились два объекта за единицу времени. Чтобы найти скорость сближения двух объектов, которые движутся навстречу друг другу, надо сложить скорости этих объектов.
Скорость удаления — расстояние, на которое отдалились друг от друга два объекта за единицу времени.
Чтобы найти скорость удаления объектов, которые движутся в противоположных направлениях, нужно сложить скорости этих объектов.
Чтобы найти скорость удаления при движении с отставанием или скорость сближения при движении вдогонку, нужно из большей скорости вычесть меньшую.
Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.
Время
Время — самое дорогое, что у нас есть. Но кроме философии, у времени есть важная роль и в математике.
Время — это продолжительность каких-то действий, событий.
- Например: от метро до дома — 10 минут, от дома до дачи — 2 часа.
Время движения обозначается латинской буквой t.
Чаще всего вам будут встречаться такие единицы времени, как секунды, минуты и часы.
Формула времени Чтобы найти время, нужно разделить расстояние на скорость: t = s : v |
Эта формула пригодится, если нужно узнать, за какое время тело преодолеет то или иное расстояние.
Взаимосвязь скорости, времени, расстояния
Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.
Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес-браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?
Как рассуждаем:
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров в минуту на 15 минут, мы определим расстояние от дома до магазина:
v = 50 м/мин
t = 15 мин
s = v × t = 50 × 15 = 750 (м)
Ответ: мы прошли 750 метров.
Если известно время и расстояние, то можно найти скорость: v = s : t.
Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние между двором и площадкой — 100 метров. Первый школьник добежал за 25 секунд, второй за 50 секунд. Кто добежал быстрее?
Как рассуждаем:
Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников — это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
100 : 25 = 4
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
В нашей задаче расстояние дано в метрах, а время в секундах. Значит, будем измерять скорость в метрах в секунду (м/с).
100 м : 25 с = 4 м/с
Так мы узнали, что скорость движения первого школьника 4 метра в секунду.
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
100 : 50 = 2
Значит, скорость движения второго школьника составляет 2 метра в секунду.
Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит, он добежал до спортивной площадки быстрее.
Ответ: первый школьник добежал быстрее.
Если известны скорость и расстояние, то можно найти время: t = s : v.
Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?
От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?
Как рассуждаем:
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос, нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое дойдем до стадиона:
s = 500 м
v = 100 м/мин
t = s : v = 500 : 100 = 5 (мин)
Ответ: от школы до стадиона мы дойдем за 5 минут.
Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
Сложение чисел с разными знаками
К следующей статье
301. 6K
6K
Объем параллелепипеда
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Расстояние, скорость, время
В этом уроке мы рассмотрим три физические величины, а именно расстояние, скорость и время.
Расстояние
Расстояние мы уже изучали в уроке единицы измерения. Говоря простым языком, расстояние это длина от одного пункта до другого. (Пример: расстояние от дома до школы 2 километра).
Имея дело с большими расстояниями, в основном они будут измеряться в метрах и километрах. Расстояние обозначается латинской буквой S. Можно обозначить и другой буквой, но буква S общепринята.
Скорость
Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Предположим, что двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 100 метров. Первый школьник добежал за 25 секунд. Второй за 50 секунд. Кто добежал быстрее?
Быстрее добежал тот, кто за 1 секунду пробежал бóльшее расстояние. Говорят, что у него скорость движения больше. В данном случае скорость школьников это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Давайте найдём скорость первого школьника. Для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
100 м : 25 с = 4
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
У нас расстояние дано в метрах, а время в секундах. Значит скорость измеряется в метрах в секунду (м/с)
Значит скорость измеряется в метрах в секунду (м/с)
100м : 25с = 4 (м/с)
Итак, скорость движения первого школьника составляет 4 метра в секунду (м/с).
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
100 м : 50 c = 2 (м/с)
Значит скорость движения второго школьника составляет 2 метра в секунду (м/с).
Скорость движения первого школьника — 4 (м/с)
Скорость движения второго школьника — 2 (м/с)
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит он добежал до спортплощадки быстрее. Скорость обозначается латинской буквой v.
Время
Иногда возникает ситуация, когда требуется узнать за какое время тело преодолеет то или иное расстояние.
Например, от дома до спортивной секции 1000 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 500 метров в минуту (500м/мин). За какое время мы доедем до спортивной секции?
Если за одну минуту мы будем проезжать 500 метров, то сколько таких минут с пятью ста метрами будет в 1000 метрах?
Очевидно, что надо разделить 1000 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 500 метров.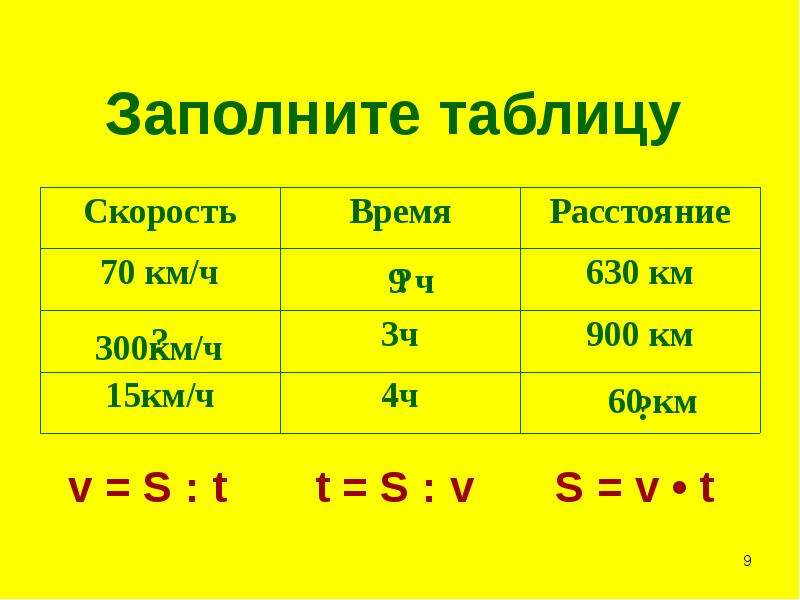 Тогда мы получим время, за которое доедем до спортивной секции:
Тогда мы получим время, за которое доедем до спортивной секции:
1000 : 500 = 2 (мин)
Время движения обозначается маленькой латинской буквой t.
Взаимосвязь скорости, времени, расстояния
Скорость принято обозначать маленькой латинской буквой v, время движения – маленькой буквой t, пройденное расстояние – маленькой буквой s. Скорость, время и расстояние связаны между собой.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:
s = v × t
Например, мы вышли из дома и направились в магазин. Мы дошли до магазина за 10 минут. Наша скорость была 50 метров в минуту. Зная свою скорость и время, мы можем найти расстояние.
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Очевидно, что умножив 50 метров на 10, мы определим расстояние от дома до магазина:
v = 50 (м/мин)
t = 10 минут
s = v × t = 50 × 10 = 500 (метров до магазина)
Если известно время и расстояние, то можно найти скорость:
v = s : t
Например, расстояние от дома до школы 900 метров.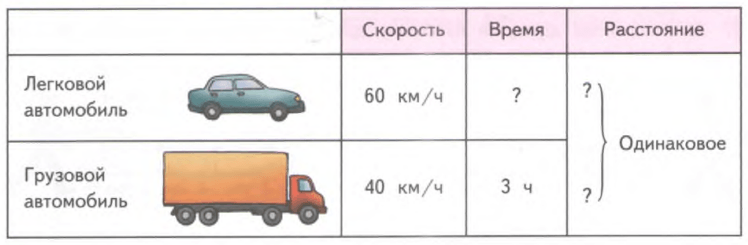 Школьник дошел до этой школы за 10 минут. Какова была его скорость?
Школьник дошел до этой школы за 10 минут. Какова была его скорость?
Скорость движения школьника это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 900 метров, то какое расстояние он преодолевал за одну минуту?
Чтобы ответить на этот, нужно разделить расстояние на время движения школьника:
s = 900 метров
t = 10 минут
v = s : t = 900 : 10 = 90 (м/мин)
Если известна скорость и расстояние, то можно найти время:
t = s : v
Например, от дома до спортивной секции 500 метров. Мы должны дойти до неё пешком. Наша скорость будет 100 метров в минуту (100 м/мин). За какое время мы дойдем до спортивной секции?
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое мы дойдем до спортивной секции:
s = 500 метров
v = 100 (м/мин)
t = s : v = 500 : 100 = 5 (минут до спортивной секции)
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Опубликовано Автор
Скорость, время и расстояние: формулы, взаимосвязь и примеры
Основная концепция скорости, времени и расстояния – это отношение между тремя переменными. Предлагаются задачи из одного-двух слов на основе скорости, времени и расстояния с вариациями, но учащиеся также должны оставаться готовыми к рассмотрению вопросов о достаточности данных и интерпретации данных, основанных на теме TDS (т. е. время, расстояние и скорость). Вопросы, связанные со скоростью, расстоянием и временем, включают в себя различные категории, такие как прямая линия, относительное движение, круговое движение, поезда, лодки, часы, гонки и т. д.
Предлагаются задачи из одного-двух слов на основе скорости, времени и расстояния с вариациями, но учащиеся также должны оставаться готовыми к рассмотрению вопросов о достаточности данных и интерпретации данных, основанных на теме TDS (т. е. время, расстояние и скорость). Вопросы, связанные со скоростью, расстоянием и временем, включают в себя различные категории, такие как прямая линия, относительное движение, круговое движение, поезда, лодки, часы, гонки и т. д.
Что такое скорость, время и расстояние?
Скорость тела – это расстояние, пройденное телом в единицу времени, т. е. скорость = расстояние/время.
Скорость: Скорость – это скорость, с которой движущийся объект преодолевает определенное расстояние.
Время: Время – это интервал, разделяющий два события.
Расстояние: Расстояние – это расстояние между двумя точками.
Единицы измерения скорости, времени и расстояния
Скорость, расстояние и время могут быть представлены в разных единицах:
- Время обычно выражается в секундах, минутах (мин) и часах (ч).
- Принимая во внимание, что расстояние обычно выражается в метрах (м), километрах (км), сантиметрах, милях, футах и т. д.
- Скорость обычно выражается в м/с, км/ч.
Пример: Если расстояние указано в км, а время в часах, то по формуле:
Скорость = Расстояние/Время; единицей скорости станет км/ч.
Связь между скоростью, временем и расстоянием
Теперь, когда мы хорошо знакомы с определением скорости, расстояния и времени, давайте поймем связь между ними. Говорят, что объект достигает движения или движения, когда он меняет свое положение по отношению к какой-либо внешней неподвижной точке. Скорость, время и расстояние — это три переменные, которые представляют математическую модель движения как s x t = d.
- Время прямо пропорционально расстоянию. Это означает, что скорость остается постоянной, если у нас есть два транспортных средства, перемещающиеся на два расстояния в течение двух разных промежутков времени, тогда время прямо пропорционально расстоянию.

- Скорость прямо пропорциональна расстоянию. Это означает, что время остается постоянным, если у нас есть два транспортных средства, перемещающиеся на два расстояния с двумя разными скоростями соответственно.
- Скорость обратно пропорциональна времени. Это означает, что расстояние остается постоянным, если у нас есть два транспортных средства, движущихся с двумя разными скоростями и затрачивающих время соответственно.
Формула для расчета скорости: Скорость = Расстояние/Время
Это показывает, насколько медленно или быстро движется цель. Он представляет собой пройденное расстояние, деленное на время, необходимое для преодоления этого расстояния.
Скорость прямо пропорциональна заданному расстоянию и обратно пропорциональна предлагаемому времени. Следовательно,
Расстояние = Скорость x Время и
Время = Расстояние / Скорость поскольку с ростом скорости необходимое время будет уменьшаться, и наоборот.
Преобразование скорости, времени и расстояния
Ниже приведено преобразование скорости, времени и расстояния в различные единицы измерения:
- Чтобы преобразовать заданные данные из км/час в м/сек, мы умножаем на 5/ 18. Поскольку 1 км/час = 5/18 м/сек.
- Чтобы преобразовать заданные данные м/сек в км/час, мы умножаем на 18/5. Так как 1 м/сек = 18/5 км/час = 3,6 км/час.
С точки зрения формулы, мы можем записать это как:
\(x\text{ км/ч}=x\times\frac{5}{18}\text{м/сек}\)
\ (x\text{ м/сек }=x\times\frac{18}{5}\text{ км/ч}\)
Аналогично, некоторые другие преобразования приведены ниже:
- 1 км/ч = 5 /8 миль/час
- 1 ярд = 3 фута
- 1 километр = 1000 метров
- 1 миля = 1,609километр
- 1 час = 60 минут = 3600 секунд
- 1 миля = 1760 ярдов
- 1 Ярд = 3 фута
- 1 миля = 5280 футов
Применение скорости, времени и расстояния
приложения скорости, времени и расстояния приведены ниже:
Средняя скорость: Средняя скорость определяется по формуле = (Общее пройденное расстояние)/(Общее затраченное время)
\(\text{Средняя скорость}=\ frac{d_1+d_2+d_3\cdots d_n}{t_1+t_2+t_3\cdots t_n}\)
Образец 1 – Когда пройденное расстояние является постоянным и задана скорость, равная двум, тогда:
Средняя скорость = \(\frac{2xy}{x+y}\)
где x и y — две скорости, с которой было пройдено соответствующее расстояние.
Образец 2 – При постоянном времени средняя скорость рассчитывается по формуле:
Средняя скорость = \(\frac{\left(x+y\right)}{2}\)
где x и y — две скорости, с которыми мы преодолели расстояние за одинаковое время.
Пример: Человек едет из одного места в другое со скоростью 40 км/ч и возвращается со скоростью 160 км/ч. Если полное необходимое время составляет 5 часов, то получите расстояние.
Решения: Здесь расстояние фиксировано, поэтому затраченное время будет обратно пропорционально скорости. Соотношение скоростей указано как 40:160, т.е. 1:4.
Следовательно, соотношение затрачиваемого времени будет 4:1.
Общее время практики = 5 часов; Таким образом, время в пути составляет 4 часа, а на обратном пути — 1 час.
Следовательно, расстояние = 40×4 = 160 км.
Если первая часть любого заданного расстояния преодолевается со скоростью v1 за время t1, а вторая часть расстояния преодолевается со скоростью v2 за время t2, то средняя скорость определяется по формуле:
Средняя скорость = \(\ frac{\left(v_{1}t_{1}+v_{2}t_{2}\right)}{t_{1}+t_{2}}\)
Относительная скорость : Как следует из названия, речь идет об относительной скорости между двумя или более вещами. Основная концепция относительной скорости состоит в том, что скорость суммируется в случае, когда объекты движутся в противоположном друг другу направлении, и скорость вычитается в случае, когда объекты движутся в одинаковом направлении.
Основная концепция относительной скорости состоит в том, что скорость суммируется в случае, когда объекты движутся в противоположном друг другу направлении, и скорость вычитается в случае, когда объекты движутся в одинаковом направлении.
Например, если два пассажирских поезда движутся в противоположном направлении со скоростью X км в час и Y километров в час соответственно. Тогда их относительная скорость определяется по формуле:
Относительная скорость = X + Y
С другой стороны, если два поезда движутся в одном направлении со скоростью X км в час и Y километров в час соответственно. Тогда их относительная скорость определяется по формуле:
Относительная скорость = X -Y
Для первого случая время, затрачиваемое поездом на прохождение друг друга, определяется по формуле:
Относительная скорость = X + Y
Время = \(\frac{L_{1}+ L_{2}}{X+Y}\)
Во втором случае время пересечения поездов определяется по формуле:
Относительная скорость = X -Y
Время = \(\frac{L_1+L_2}{X-Y}\)
Здесь \(L_{1},\ L_{2}\) — длины поездов соответственно.
Обратная пропорциональность скорости и времени: Говорят, что скорость обратно пропорциональна времени, когда расстояние фиксировано. В математическом формате S обратно пропорционально 1/T, когда D является постоянным. Для такого случая, если скорости находятся в отношении m:n, то время, затраченное на это, будет в отношении n:m.
Существует два подхода к решению вопросов:
- Применение обратной пропорциональности
- Применение правила постоянного произведения
9{th}\) нормальной скорости и достигает 55-минутного опоздания. Если бы авария произошла на 20 км дальше, она прибыла бы с опозданием на 45 минут. Получить обычную Скорость?
Решения: Применение метода обратной пропорциональности
Здесь 2 случая
Случай 1: авария на 100 км
Случай 2: авария на 120 км
Разница между двумя инцидентами только для 20 км от 100 км до 120 км. Разница во времени в 10 минут как раз из-за этих 20 км. 9{th}\) скорость.
9{th}\) скорость.
В случае 2 20 км между 100 и 120 км пройдены на обычной скорости.
Итак, обычное время «t», необходимое для прохождения 20 км, можно найти следующим образом. 4/3 t – t = 10 минут = > t = 30 минут, d = 20 км
, поэтому обычная скорость = 20/30мин = 20/0,5 = 40 км/ч
Используя метод правила постоянного произведения: Пусть фактическое затраченное время равно T.
Существует (1/4)-е уменьшение скорости, это приведет к (1/3)-му увеличению затрачиваемого времени, поскольку скорость и время обратно пропорциональны друг другу.
Увеличение одного из параметров на 1/x приведет к уменьшению другого параметра на 1/(x+1), если параметры обратно пропорциональны.
Задержка из-за этого сокращения составляет 10 минут
Таким образом, 1/3 T = 10 и T = 30 минут или 0,5 часа
Кроме того, расстояние = 20 км
Таким образом, скорость = 40 км/ч
Если два человека едут из двух точек P и Q навстречу друг другу и встречаются в точке X. Тогда общее расстояние, пройденное ими при встрече, равно PQ. Время, необходимое им обоим для встречи, будет одинаковым.
Тогда общее расстояние, пройденное ими при встрече, равно PQ. Время, необходимое им обоим для встречи, будет одинаковым.
Поскольку время постоянно, расстояния PX и QX будут пропорциональны их скорости. Предположим, что расстояние между P и Q равно d.
Если два человека делают шаг навстречу друг другу из точек P и Q соответственно, когда они встречаются в первый раз, они вместе проходят расстояние «d». Когда они встречаются во второй раз, они взаимно преодолевают расстояние «3d». Точно так же, когда они встречаются в третий раз, они дружно преодолевают расстояние «5d», и процесс продолжается.
Возьмем пример, чтобы понять концепцию:
Пример: Анкит и Арнав должны ехать из Дели в Хайдарабад на своих транспортных средствах. Анкит едет со скоростью 80 км/ч, а Арнав едет со скоростью 120 км/ч. Получите время, затраченное Арнавом на то, чтобы добраться до Хайдарабада, если Анкиту потребуется 9 часов.
Решения: Поскольку мы можем признать, что пройденное расстояние фиксировано в обоих случаях, затраченное время будет обратно пропорционально скорости. В заданном вопросе скорость Анкита и Арнава находится в соотношении 80:120 или 2:3.
В заданном вопросе скорость Анкита и Арнава находится в соотношении 80:120 или 2:3.
Таким образом, соотношение времени, потраченного Анкитом и Арнавом, будет как 3:2. Следовательно, если Анкиту потребуется 9 часов, Арнаву потребуется 6 часов.
Learn about Time and Work
Speed, Time and Distance Formulas
Some important speed, distance and time formulas are given below:
Terms | Formula |
| Скорость | \(\text{Скорость}=\frac{\text{Расстояние}}{\text{Время}}\) |
| Время | \(\text{Время}=\frac{\text{Расстояние}}{\text{Скорость}}\) |
| Расстояние | D = (Скорость x Время) |
| Средняя скорость | \(\text{Средняя скорость}=\frac{\text{Общее пройденное расстояние}}{\text{Общее затраченное время}}\) |
| Средняя скорость (когда пройденное расстояние постоянно ) | \(\frac{2xy}{x+y}\) |
| Относительная скорость (Если два поезда движутся в противоположном направлении) | Относительная скорость = X + Y Затраченное время = \(\frac{L_{1}+L_{2}}{X+Y}\) Здесь \(L_{1},\ L_{2} \) — длины поездов. |
| Относительная скорость (Если два поезда движутся в одном направлении) | Относительная скорость=X -Y Затраченное время= \(\frac{L_1+L_2}{X-Y}\) Здесь \ (L_{1},\ L_{2}\) — длины поездов. |
Некоторые дополнительные формулы скорости, расстояния и времени:
- Если отношение скоростей P и Q равно p:q, то отношение времени, затраченного ими на преодоление одного и того же расстояния, равно 1/p:1/q или q:p.
- Если два человека, автомобили или поезда отправляются в точное время в противоположном направлении из двух точек, скажем, А и В, и после пересечения друг друга им требуется время а и b соответственно, чтобы закончить путешествие, то соотношение скоростей определяется формулой :
- \(\frac{\text{Скорость первого}}{\text{Скорость второго}}=\sqrt{\frac{b}{a}}\)
- Если два человека с двумя разными скоростями x и y преодолевают одинаковое расстояние и движутся в противоположных направлениях.
 Если указано общее время и задано расстояние, то формула будет следующей:
Если указано общее время и задано расстояние, то формула будет следующей: - \(\text{Расстояние}=\frac{xy}{x+y}\times\text{Общее время}\)
Типы вопросов о скорости, времени и расстоянии
Существуют определенные типы вопросов о скорости, времени и расстоянии, которые обычно встречаются на экзаменах. Вот некоторые из важных типов вопросов о скорости, расстоянии и времени.
(a) Проблемы, связанные с поездами
Обратите внимание, что в случае проблем с поездом расстояние, которое необходимо преодолеть при пересечении объекта, равно, Расстояние, которое необходимо преодолеть = длина поезда + длина объекта .
Помните, что если рассматриваемый объект является столбом, человеком или точкой, мы можем считать их точечными объектами с нулевой длиной. Это означает, что мы не будем рассматривать длины этих объектов. Однако, если рассматриваемый объект является платформой (неточечным объектом), то его длина будет добавлена к формуле пройденного расстояния.
(b) Лодки и ручьи
В таких задачах лодки плывут либо по течению, либо против течения. Направление лодки по течению называется вниз по течению, а направление лодки против течения – вверх по течению.
Если скорость лодки в стоячей воде u км/ч, а скорость течения v км/ч, то:
1) Скорость по течению = (u + v) км/ч
2) Скорость вверх по течению = (u – v) км/ч
Узнайте о соотношении, пропорции, смешении и объединении
Советы и рекомендации по решению вопросов на основе скорости, времени и расстояния
Учащиеся могут найти ниже различные советы и рекомендации по решению вопросов на основе скорости, времени и расстояния.
Совет 1: Относительная скорость определяется как скорость движущегося тела относительно другого тела. Возможные случаи относительного движения: однонаправленные, когда два тела движутся в одном и том же направлении, относительная скорость есть разность их скоростей и всегда выражается положительной величиной. С другой стороны, противоположное направление — это когда два тела движутся в противоположном направлении, относительная скорость равна сумме их скоростей.
С другой стороны, противоположное направление — это когда два тела движутся в противоположном направлении, относительная скорость равна сумме их скоростей.
Совет 2: Средняя скорость = общее расстояние / общее время
Совет 3: Когда поезд пересекает движущееся тело,
Когда поезд проходит мимо движущегося человека/точечного объекта, расстояние, пройденное поездом во время его прохождения будет равна длине поезда, а относительная скорость будет принята как
1) Если оба движутся в одном направлении, то относительная скорость = разность обеих скоростей
2) Если оба движутся в противоположном направлении, тогда относительная скорость = Добавление обеих скоростей
Совет № 4: Поезд Проходя длинный объект или платформу, когда поезд проходит платформу или длинный объект, расстояние, пройденное поездом при пересечении этого объекта, будет равно сумме длин поезда и длина этого объекта.
Совет № 5: Поезд проезжает человека или точечный объект, когда поезд проезжает человека/объект, расстояние, пройденное поездом при прохождении этого объекта, будет равно длине поезда.
Решенные примеры скорости, времени и расстояния
Вот некоторые из решенных вопросов по теме для большей практики:
Пример 1: Скорость трех автомобилей находится в соотношении 5 : 4 : 6. Соотношение между временем, затрачиваемым ими на поездку то же расстояние равно
Решение : Отношение затраченного времени = ⅕ : ¼ : ⅙ = 12 : 15 : 10
Пример 2: Грузовик преодолевает расстояние 1200 км за 40 часов. Какова средняя скорость грузовика?
Решение : Средняя скорость = Общее пройденное расстояние/Общее затраченное время
⇒ Средняя скорость = 1200/40
∴ Средняя скорость = 30 км/ч
Пример 3: Человек проехал 12 км со скоростью 4 км/ч. ч и далее 10 км со скоростью 5 км/ч. Какова была его средняя скорость?
Решение : Общее затраченное время = Время, затраченное на скорости 4 км/ч + Время, затраченное на скорость 5 км/ч
⇒ 12/4 + 10/5 = 5 часов [∵ Время = Расстояние/ Скорость] Средняя скорость = общее расстояние/общее время
⇒ (12 + 10)/5 = 22/5 = 4,4 км/ч
Пример 4: Рахул едет из Дели в Пуну со скоростью 50 км/ч и возвращается со скоростью 75 км/ч. . Найдите его среднюю скорость пути.
. Найдите его среднюю скорость пути.
Решение : Расстояние одинаковое в обоих случаях
⇒ Требуемая средняя скорость = (2 × 50 × 75)/(50 + 75) = 7500/125 = 60 км/ч
Пример 5: Определить длину поезда А, если он пересекает столб со скоростью 60 км/ч за 30 с.
Решение : Дано, скорость поезда = 60 км/ч
⇒ Скорость = 60 × 5/18 м/с = 50/3 м/с
Дано, время пересечения полюса поездом А = 30 с
Расстояние, пройденное при пересечении полюса, будет равно длина поезда.
⇒ Расстояние = Скорость × Время
⇒ Расстояние = 50/3 × 30 = 500 м
Пример 6: Поезд длиной 150 м пересекает платформу длиной 270 м за 15 сек. За сколько времени он преодолеет платформу высотой 186 м?
Решение : При пересечении платформы длиной 270 м,
Общее расстояние, пройденное поездом = 150 + 270 = 420 м
Скорость поезда = общее пройденное расстояние/затраченное время = 420/15 = 28 м/с При пересечении платформы длиной 186 м,
Общее расстояние, пройденное поездом = 150 + 186 = 336 м
∴ Время, затраченное поездом = пройденное расстояние/скорость поезда = 336/28 = 12 сек.
Пример 7: Два поезда движутся в одном направлении со скоростями 43 км/ч и 51 км/ч соответственно. Время, за которое более быстрый поезд пересекает человека, сидящего в более медленном поезде, составляет 72 секунды. Какова длина (в метрах) более быстрого поезда?
Решение : Дано: Скорость двух поездов = 43 км/ч и 51 км/ч Относительная скорость обоих поездов = (51 – 43) км/ч = 8 км/ч Относительная скорость в м/с = 8 × (5/18) м/с
⇒ Расстояние, пройденное поездом за 72 с = 8 × (5/18) × 72 = 160 Следовательно, длина более быстрого поезда = 160 м
Пример 8: Как Сколько времени потребуется поезду длиной 100 м, движущемуся со скоростью 72 км/ч, чтобы обогнать поезд длиной 200 м, движущийся в том же направлении со скоростью 54 км/ч?
Решение : Относительная скорость = 72 – 54 км/ч (так как оба движутся в одном направлении)
= 18 км/ч = 18 × 10/36 м/с = 5 м/с
Кроме того, пройденное расстояние поездом, чтобы обогнать поезд = 100 м + 200 м = 300 м Следовательно,
Затраченное время = расстояние/скорость = 300/5 = 60 с
Пример 9: Лодке требуется 40 минут, чтобы пройти 20 км вниз по течению . Если скорость течения 2,5 км/ч, сколько времени потребуется, чтобы вернуться обратно?
Если скорость течения 2,5 км/ч, сколько времени потребуется, чтобы вернуться обратно?
Решение : Время прохождения вниз по течению = 40 мин = 40/60 = 2/3 часа. Скорость вниз по течению = 20/(2/3) = 30 км/ч.
Как мы знаем, скорость течения = 1/2 × (скорость вниз по течению – скорость вверх по течению)
⇒ скорость против течения = 30 – 2 × 2,5 = 30 – 5 = 25 км/ч.
Время, необходимое для возврата назад = 20/25 = 0,8 часа. = 0,8 × 60 = 48 мин.
∴ Лодка займет = 48 – 40 = 8 мин. больше вернуться назад.
Мы надеемся, что эта статья о скорости, времени и расстоянии была информативной и полезной, и, пожалуйста, не стесняйтесь обращаться к нам, если у вас возникнут сомнения или вопросы по этому поводу. Вы также можете скачать абсолютно бесплатное приложение Testbook и начать подготовку к любому государственному конкурсному экзамену, пройдя пробные тесты перед экзаменом, чтобы улучшить свою подготовку.
Часто задаваемые вопросы о скорости, времени и расстоянии
В. 1 Что такое скорость, время и расстояние?
1 Что такое скорость, время и расстояние?
Ответ 1 Скорость указывает нам на то, насколько медленно или быстро движется объект, а время относится к интервалу, разделяющему два события, тогда как расстояние, как следует из названия, указывает на размер пространства между двумя точками.
Q.2 Какова формула скорости, расстояния и времени?
Ответ 2 Формула скорости, времени и расстояния выглядит следующим образом:
Скорость = расстояние/время
Расстояние = скорость × время
Время = расстояние/скорость
Q.3 Какова взаимосвязь между скоростью, расстоянием и временем?
Ответ 3 Связь между скоростью, расстоянием и временем:
Скорость и время прямо пропорциональны расстоянию. Кроме того, скорость обратно пропорциональна времени.
В.4 Скорость прямо пропорциональна расстоянию?
Ответ 4 Рассмотрим основную формулу: Скорость = расстояние/время.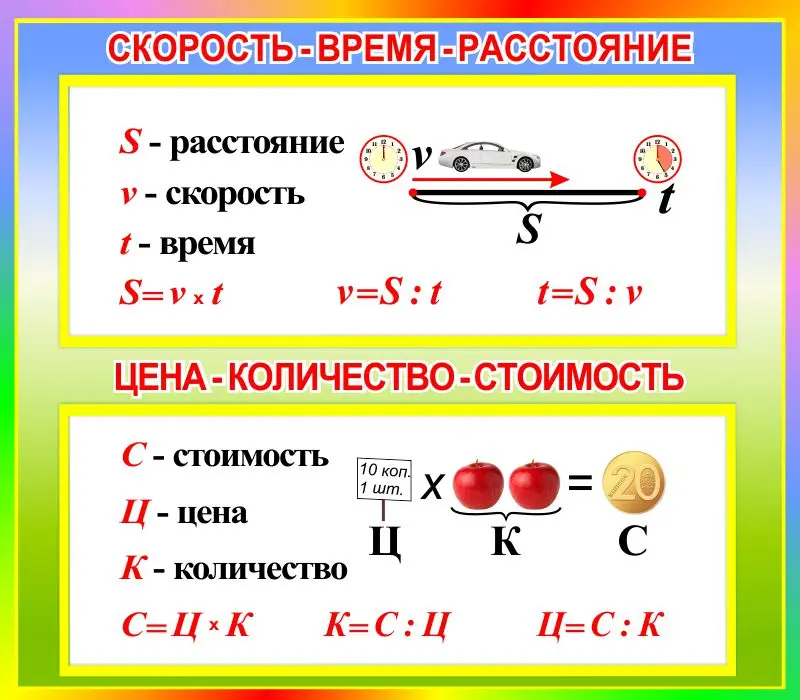
Формула утверждает, что скорость прямо пропорциональна расстоянию.
В.5 Что такое относительная скорость?
Ответ 5 Основное понятие относительной скорости состоит в том, что скорость суммируется в случае, когда объекты движутся в противоположном друг другу направлении, и скорость вычитается для случая, когда объекты движутся в одинаковом направлении. направление.
Скачать публикацию в формате PDF
| Упрощение и приближение: термины, правила, советы с примерами Примеры с советами и рекомендациями |
| Задачи на века: типы задач, приемы, вопросы с решениями |
| Труба и цистерна: концепции, примеры решений и стратегии подготовки |
Основные понятия о времени, скорости и расстоянии – Hitbullseye
В этой статье мы обсудим формулы скорости и вопросы о времени и расстоянии. Поскольку эта тема является неотъемлемой частью каждого конкурсного экзамена, вы не можете позволить себе пропустить эту тему. Эта статья поможет вам решить все задачи на время, скорость и расстояние.
Эта статья поможет вам решить все задачи на время, скорость и расстояние.
Формула средней скорости
Формула времени и расстояния
- Расстояние = скорость × время. С помощью этой формулы можно решить все основные проблемы. Однако вам необходимо убедиться в правильности использования единиц при использовании приведенных выше формул.
- Скорость обратно пропорциональна времени, затраченному на пройденное расстояние. Таким образом, при увеличении скорости время уменьшается и наоборот.
Относительная скорость:
- Относительная скорость определяется как скорость движущегося объекта относительно другого. Когда два объекта движутся в одном направлении, относительная скорость рассчитывается как их разность. Когда два объекта движутся в противоположных направлениях, относительная скорость вычисляется путем сложения двух скоростей.
Решенные проблемы средней скорости
Давайте рассмотрим несколько решенных примеров, чтобы понять применение понятий и формул для средней скорости, описанных выше: скорость 60 км/ч. Какова его средняя скорость на всем пути?
Какова его средняя скорость на всем пути?
Решение: Поскольку расстояние, пройденное с обеих сторон, одинаково, мы можем использовать формулу гармонического среднего скоростей.
Средняя скорость: 2xy/(x+y), где x — скорость при движении из A в B, а y — скорость на обратном пути.
Итак, используя эту формулу, мы получаем ответ как 48 км/ч.
Пример 2: Двигаясь со скоростью 50 км/ч, человек приходит в офис с опозданием на 10 минут. На следующий день он увеличивает скорость и движется со скоростью 60 км/ч и прибывает в свой офис на 5 минут раньше. Какое расстояние от его дома до офиса?
Решение: Мы видим, что разница во времени в оба дня составляет 15 минут (а не 5 минут, так как в один день он опаздывает, а в другой день рано)
Пусть искомое расстояние = D км. Поскольку время, затраченное на скорость 50 км/ч, больше, чем время, затраченное на скорость 60 км/ч, уравнение можно составить как D/50-D/60=15/60. Решив это уравнение, получим ответ 75 км.
Решив это уравнение, получим ответ 75 км.
Практический вопрос:
Теперь попробуйте решить следующий вопрос, используя изученную выше концепцию:
Вопрос: Два поезда NaMo Express и RaGa Express отправляются навстречу друг другу из двух городов на расстоянии 1800 м друг от друга при скорости 50 км/ч и 58. км/ч соответственно. Когда они начинают, птица по имени Демократия, сидящая в передней части RaGa, начинает лететь к NaMo, касается NaMo, а затем возвращается к RaGa и так далее, пока поезда не встретятся. Какое расстояние в общей сложности преодолела птица, если летел со скоростью 324 км/ч?
Ответ: 5400 m
Рекомендуемое действие:
Начните подготовку с БЕСПЛАТНОГО доступа к 25+ макетам, 75+ видео и 100+ тестам по главам. Зарегистрируйтесь сейчас
Время, скорость и расстояние: ключевые знания
- Хотя постановка вопроса может варьироваться, основная формула для TSD (время, скорость и расстояние) остается неизменной, и она формирует основу для ответа на любой вопрос из этой важной темы.




