В Помощь Молодому Офицеру — Проведение технического обслуживания ТО-1 и ТО-2

> Реклама на сайте Место для рекламы Вид техники Образцы выпуска до 1985 г Образцы  выпуска после 1985 г ТО-1 ТО-2 ТО-1 ТО-2 ТО-3 Автомобили, км 1200-1600 6000-8000 4000 16 000 — Колесные шасси (кроме ЗИЛ-135, БАЗ-5921), км 1200-1600 6000-8000 2500 10000 — Колесные шасси ЗИЛ-135, БАЗ-5921, км 1200-1600 6000-8000 2000 6000 — Гусеничные машины, км 800-1000 2400-3000 1000 3000 — Тракторы, км 50-60 200-240 60 240 960 Примечания: 1. ТО № 1 и № 2 машин боевой и строевой групп эксплуатации, как правило, совмещаются: первое – с очередным сезонным, второе – с сезонным обслуживанием, проводимым при подготовке машин к эксплуатации в зимний период (как правило, один раз в два года). 2. Если инструкция по эксплуатации машины рекомендует пробеги между техническими обслуживаниями меньше указанных в таблице, следует руководствоваться инструкцией. 3. При использовании машин в тяжелых дорожных условиях, а также с прицепами пробеги между техническими обслуживаниями уменьшаются. 4. Техническое обслуживание прицепов и полуприцепов проводится одновременно с обслуживанием тягачей. Наработка до ремонта или списания машин, специальное оборудование которых приводится в действие от их двигателей, рассчитывается с учетом работы этих двигателей. При этом один час работы двигателя берется: для автомобилей — до 25 км пробега; для автомобилей учебной группы — 20 км пробега; для пожарных автомобилей — 50 км пробега; для гусеничных машин, специальных колесных шасси и тягачей, — 15 км пробега; для тракторов гусеничных — 5 км пробега; для тракторов колесных — 10 км пробега.   Форма входа Блок рекламы верхний правый Календарь «  Ноябрь 2022  » Пн Вт Ср Чт Пт Сб Вс   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 Архив записей Друзья сайта
			Онлайн всего: 1 Гостей: 1 Пользователей: 0					Сайт создан О.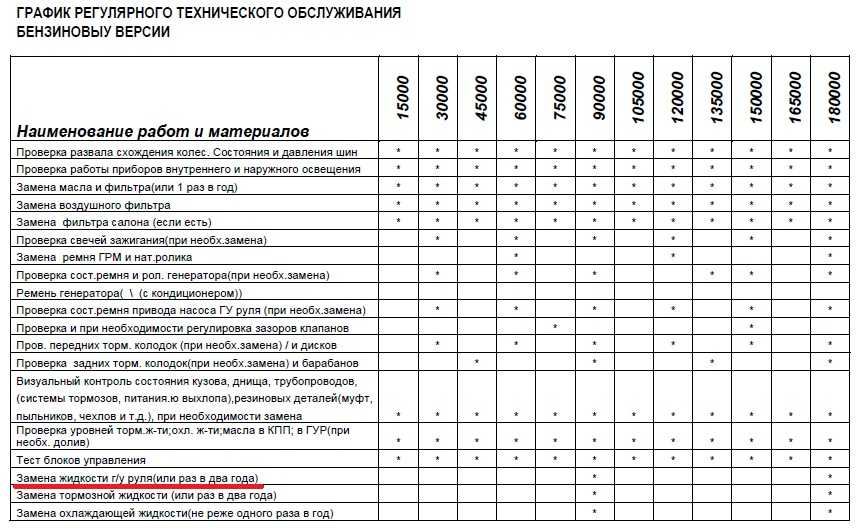 АУЛОВЫМ Copyright MyCorp © декабрь 2010 года

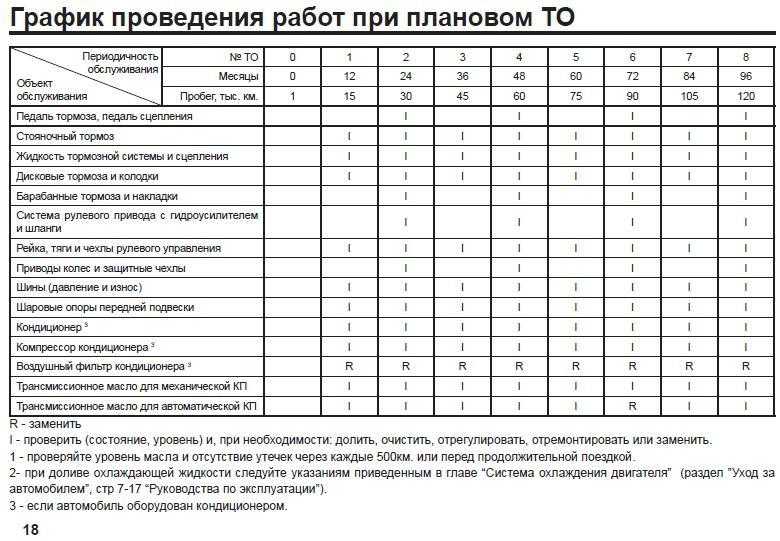
Периодичность выполнения ТО машины и требования к ней после обслуживания

ГлавнаяСтатьиПериодичность выполнения ТО машины и требования к ней после обслуживания

Цель технического обслуживания машин

• поддержать и обеспечить стабильную техническую исправность узлов, агрегатов и машины в целом;
• увеличить до максимума пробеги межремонтные;
• гарантировать безопасность перемещения;
• минимизировать затраты эксплуатационных материалов.

Чтобы поставленные цели были достижимы, есть планово-предупредительное техническое обслуживание, подразумевающее обязательное выполнение с определенной периодичностью комплекса работ при хранении, эксплуатации и транспортировке машин. Процесс обслуживания машины во время планово-предупредительных работ включает в себя и обязательные работы, и работы по необходимости, нужность которых выясняется при проверке состояния авто. Техобслуживание спецоборудования, смонтированного на автомобиле, желательно проводить вместе с обслуживанием шасси.

От периодичности выполнения работ и их объема техобслуживание бывает следующих видов: осмотр контрольный, обслуживание техническое ежедневное, обслуживание техническое № 1 (ТО-1), обслуживание техническое № 2 (ТО-2), обслуживание сезонное (СО). В случае с новыми машинами техническое обслуживание предусмотрено после первых тысячи и четырех тысяч километров. Существующее сейчас построение последовательности техобслуживания транспортных средств в Вооруженных Силах иллюстрируется диаграммой на рисунке.

Рис. Последовательность техобслуживания машин: а – виды обслуживания; б – последовательность проведения первого и второго обслуживания.

Осмотр контрольный (КО) выполняется перед каждым выходом автомобиля из парка, а также при прохождении марша на привалах для выяснения готовности автомобиля выполнять поставленные задачи.

Техобслуживание ежедневное (ЕТО) выполняется каждый день после каждого использования машины независимо от величины пробега.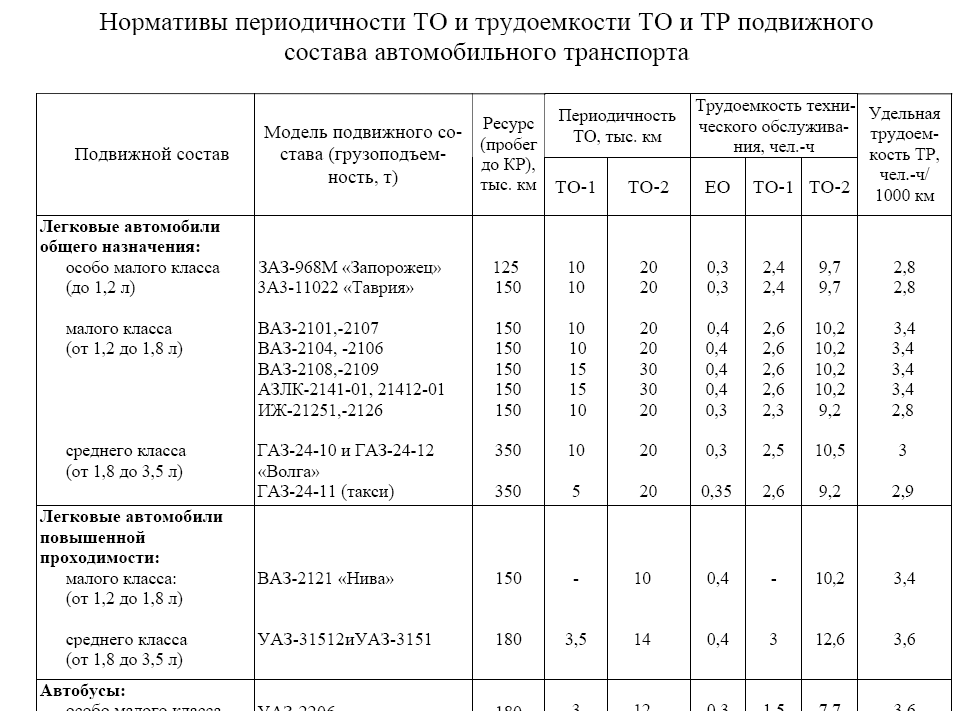 Цель такого обслуживания – подготовка автомобиля к очередному этапу его эксплуатации. Работы проводит водитель с участием автомеханика.

Первое и второе техобслуживания выполняются через каждые 1200-1600 и 7200-12000 километров пробега. Это делается для поддержки машины в постоянной эксплуатационной готовности, уменьшения интенсивности истирания деталей, предупреждения поломок путем вовремя выполняемых крепежных, контрольных, смазочных и регулировочных действий. Последовательность смен первого и второго ТО содержится в диаграмме. Видно из диаграммы, что в каждый этап обслуживания включено пять первых ТО и два вторых.

В год два раза выполняется сезонное обслуживание при подготовке автомобиля к зимнему или летнему периоду использования. Во время проведения обслуживания сезонного вместе с очередным номерным ТО проводятся и дополнительные работы, которые необходимы для подготовки автомобиля к тому или иному сезону. Сезонное и номерное обслуживание проводится водителем и мастерами по обслуживанию и ремонту машин.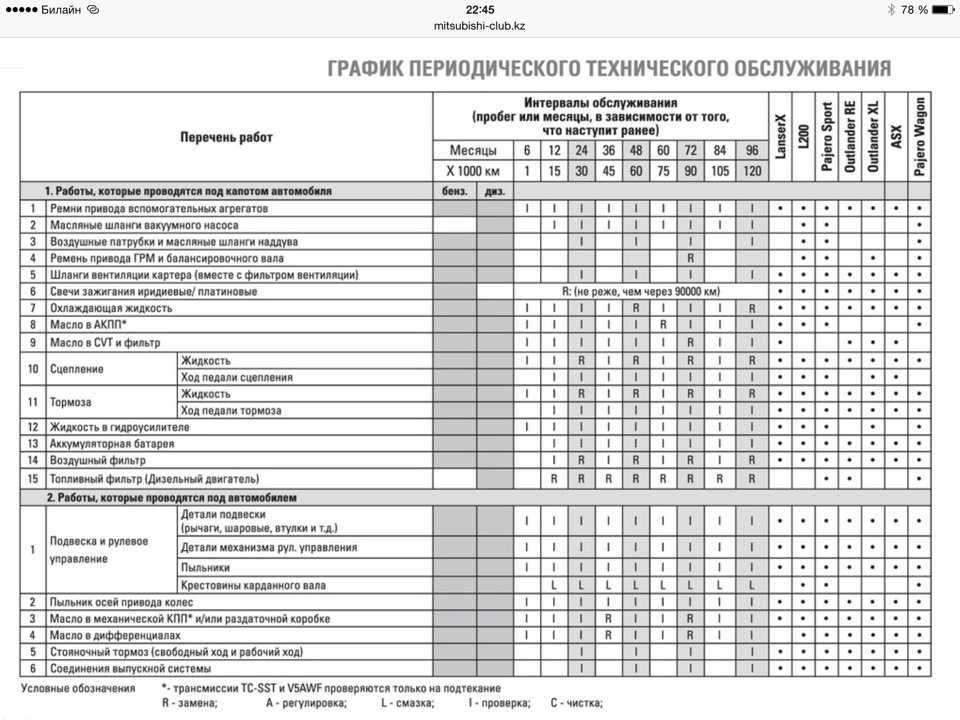

Требования к автомобилю, прошедшему ТО

• транспортное средства должно быть чистым, без поломок, заправленным необходимыми веществами, смазанным; мотор должен запускаться легко, работать устойчиво на разных оборотах коленвала;
• педали и рычаги должны ходить свободно, люфт рулевого колеса не должен превышать норму;
• тормоза должны одновременно и плавно обеспечивать остановку автомобиля на положенном по ТУ для данной модели тормозном пути;
• полностью выключаться должно сцепление, передачи при этом должны легко и бесшумно переключаться, не должно быть пробуксовки при отпущенной педали;
• в КПП, делителе коробки передач, раздаточной коробке, ведущих мостах не должно быть посторонних шумов при движении;
• в коробках раздаточной и передач не должно быть самостоятельного выключения передач;
• схождение и развал управляемых колес должны быть в норме;
• шины и давление в них должны быть в норме;
• приборы освещения, стеклоочистители, контрольные приборы, приборы сигнализации должны находиться в исправном состоянии;
• состояние аккумуляторов должно быть заряженным и уровень электролита в норме;
• подтекания топлива быть не должно, так же как и масла, тормозной и охлаждающей жидкостей;
• в исправности и пригодности к эксплуатации должны быть средства светотехнические для ночной езды и средства, повышающие проходимость, инструмент заправлен;
• абсолютно все крепления автомобиля должны быть надежными и исправными;
• сцепной прибор, лебедка автомобиля должны быть в исправном состоянии.

Начальник пункта ремонта и технического обслуживания должен при помощи измерительного инструмента и средств диагностики проверить качество проведения технического обслуживания автомобилей.

Категории статей

4.3 Распределение частот

Содержание

Текст начинается

Навигация по теме

• 4 Исследование данных
  • 4.1 Инструменты исследования данных
  • 4.2 Типы переменных
  • 4.3 Распределение частот
  • 4.4 Меры центральной тенденции
  • 4.5 Меры рассеивания
  • 4.6 Упражнения
  • 4.7 Ответы

Частота  ( f ) определенного значения – это количество раз, когда это значение встречается в данных. Распределение переменной представляет собой шаблон частот, означающий набор всех возможных значений и частот, связанных с этими значениями. Распределения частот изображаются в виде частотных таблиц или диаграмм.

Частотные распределения  могут отображать либо фактическое количество наблюдений, попадающих в каждый диапазон, либо процент наблюдений. В последнем случае распределение называется распределением относительной частоты .

Таблицы частотного распределения можно использовать как для категориальных, так и для числовых переменных. Непрерывные переменные следует использовать только с интервалами классов, что будет объяснено в ближайшее время.

Давайте рассмотрим несколько примеров частотного распределения и относительного частотного распределения для дискретных переменных.

Пример 1. Составление таблицы частотного распределения

На Мейпл-авеню было проведено обследование. В каждом из 20 домов людей спрашивали, сколько автомобилей зарегистрировано на их домохозяйства. Результаты записывались следующим образом:

1, 2, 1, 0, 3, 4, 0, 1, 1, 1, 2, 2, 3, 2, 3, 2, 1, 4, 0, 0

Используйте следующие шаги, чтобы представить эти данные в таблице частотного распределения.

1. Разделите результаты ( x ) на интервалы, а затем подсчитайте количество результатов в каждом интервале. В этом случае интервалами будут количество домохозяйств без машины (0), одна машина (1), две машины (2) и так далее.
2. Составьте таблицу с отдельными столбцами для номеров интервалов (количество автомобилей на домохозяйство), подсчитанных результатов и частоты результатов в каждом интервале. Пометьте эти столбцы Количество автомобилей , Подсчет и Частота .
3. Прочитайте список данных слева направо и поставьте отметку в соответствующей строке. Например, первый результат равен 1, поэтому поставьте отметку в строке рядом с тем местом, где в столбце интервалов стоит 1 ( Количество автомобилей ). Следующим результатом будет 2, поэтому поставьте отметку в ряду рядом с 2 и так далее. Когда вы достигнете пятой контрольной отметки, проведите контрольную линию через предыдущие четыре отметки, чтобы облегчить чтение окончательных расчетов частоты.
4. Сложите количество контрольных точек в каждой строке и запишите их в последний столбец, озаглавленный Частота .

Ваша таблица частотного распределения для этого упражнения должна выглядеть следующим образом:



Таблица 4.3.1
Таблица частоты количества автомобилей, зарегистрированных в каждом домохозяйстве
Сводка таблицы
В этой таблице отображаются результаты таблицы частоты для количества автомобилей, зарегистрированных в каждом домохозяйстве. Информация сгруппирована по количеству автомобилей (x) (отображается в виде заголовков строк), частоте (f) (отображается в виде заголовков столбцов).

Количество вагонов (х)	Частота (f)
0	4
1	6
2	5
3	3
4	2

Быстро взглянув на эту таблицу частотного распределения, мы увидим, что из 20 обследованных домохозяйств в 4 домохозяйствах не было автомобилей, в 6 домохозяйствах была 1 машина и т. д.

Пример 2. Построение таблицы

кумулятивного распределения частот Таблица кумулятивного распределения частот является более подробной таблицей. Она выглядит почти так же, как таблица распределения частот, но в нее добавлены столбцы, которые также показывают совокупную частоту и совокупный процент результатов.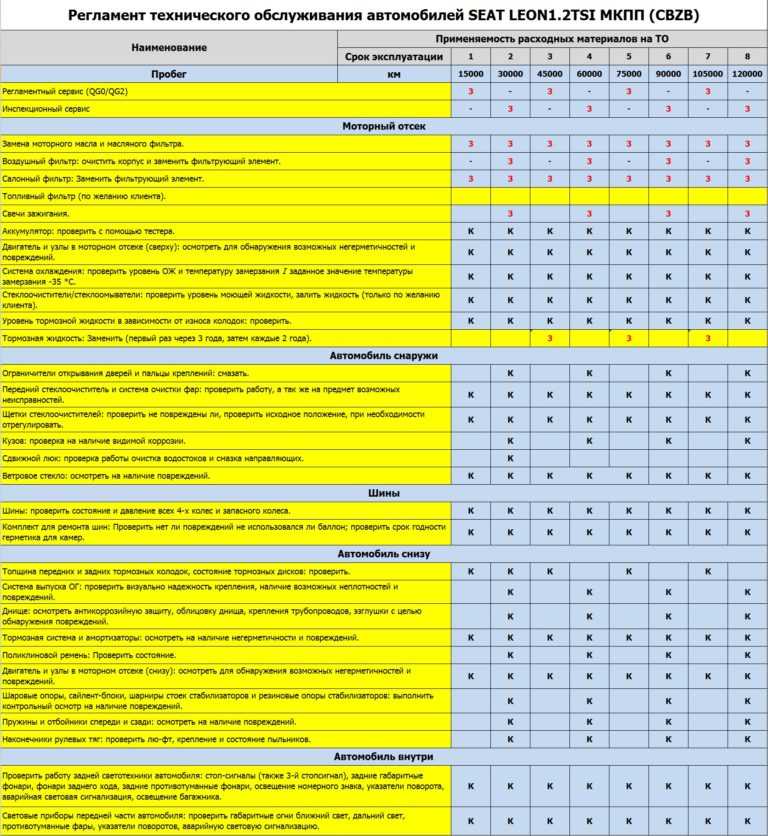

На недавнем шахматном турнире все 10 участников должны были заполнить форму, в которой были указаны их имена, адреса и возраст. Возраст участников был записан следующим образом:

36, 48, 54, 92, 57, 63, 66, 76, 66, 80

Используйте следующие шаги, чтобы представить эти данные в таблице распределения совокупной частоты.

1. Разделите результаты на интервалы, а затем подсчитайте количество результатов в каждом интервале. В этом случае подходят интервалы 10. Поскольку 36 лет — самый низкий возраст, а 92 — самый высокий, начните интервалы с 35 до 44 и закончите интервалы с 85 до 94.
2. Создайте таблицу, аналогичную таблице частотного распределения, но с тремя дополнительными столбцами.

   Совокупная таблица распределения частот должна выглядеть так:

   

   Таблица 4.3.2
   Возраст участников шахматного турнира
   Сводка таблицы
   В этой таблице отображаются результаты Возрастов участников шахматного турнира. Информация сгруппирована по нижнему значению (отображается в виде заголовков строк), верхнему значению, частоте (f), совокупной частоте, проценту и совокупному проценту (отображается в виде заголовков столбцов).

   Нижнее значение	Верхнее значение	Частота (f)	Суммарная частота	Процент	Суммарный процент
   35	44	1	1	10,0	10,0
   45	54	2	3	20,0	30,0
   55	64	2	5	20,0	50,0
   65	74	2	7	20,0	70,0
   75	84	2	9	20,0	90,0
   85	94	1	10	10,0	100,0

Интервалы классов

Если переменная принимает большое количество значений, то данные проще представлять и обрабатывать, группируя значения в интервалы классов. Непрерывные переменные с большей вероятностью будут представлены в интервалах классов, в то время как дискретные переменные могут быть сгруппированы в интервалы классов или нет.

Для иллюстрации предположим, что мы установили возрастные диапазоны для исследования молодых людей, допуская при этом возможность того, что некоторые пожилые люди также могут попасть в сферу нашего исследования.

Частота интервала класса — это количество наблюдений, происходящих в конкретном предопределенном интервале. Так, например, если в данных нашего исследования фигурируют 20 человек в возрасте от 5 до 9 лет, частота интервала 5–9 будет равна 20.

. Итак, интервалы в нашем исследовании составляют от 0 до 4 лет, от 5 до 9 лет.лет, от 10 до 14 лет, от 15 до 19 лет, от 20 до 24 лет и от 25 лет и старше. Конечные точки первого интервала равны 0 и 4, если переменная дискретна, и 0 и 4,999, если переменная непрерывна. Таким же образом будут определены конечные точки других интервалов класса.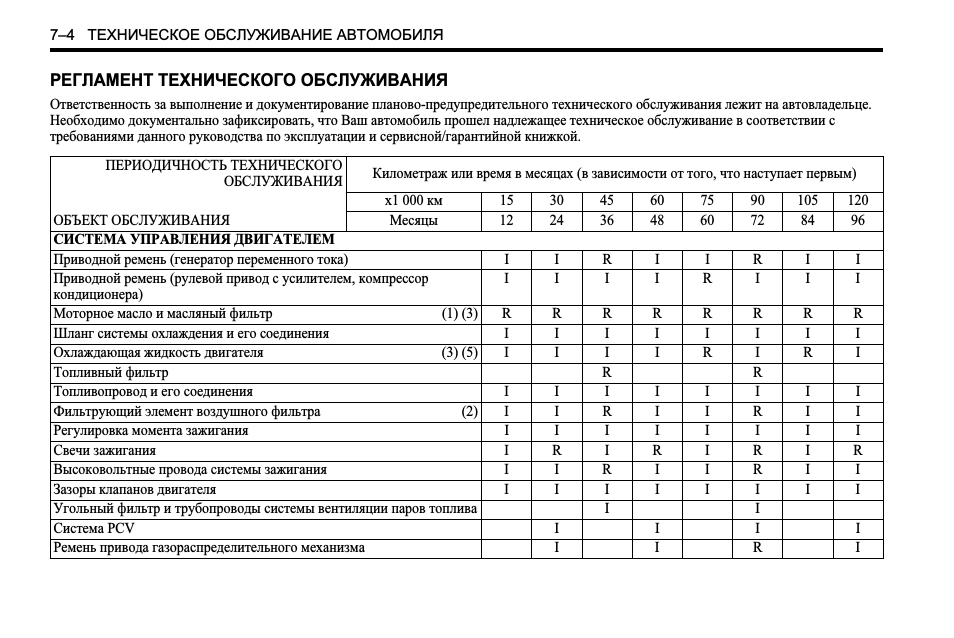

Ширина интервала класса — это разница между нижней конечной точкой интервала и нижней конечной точкой следующего интервала. Таким образом, если непрерывные интервалы нашего исследования равны от 0 до 4, от 5 до 9 и т. д., ширина первых пяти интервалов равна 5, а последний интервал открыт, поскольку ему не назначена более высокая конечная точка. Интервалы также могут быть записаны как от 0 до менее 5, от 5 до менее 10, от 10 до менее 15, от 15 до менее 20, от 20 до менее 25, от 25 и более.

Правила для наборов данных, содержащих большое количество наблюдений

Таким образом, следуйте этим основным правилам при построении таблицы распределения частот для набора данных, содержащего большое количество наблюдений:

• найдите наименьшее и наибольшее значения переменные
• принять решение о ширине интервалов классов
• включают все возможные значения переменной.

При выборе ширины интервалов классов вам придется найти компромисс между достаточно короткими интервалами, чтобы не все наблюдения попадали в один и тот же интервал, и достаточно длинными, чтобы вы не остались только с одним наблюдения за интервал.

Также важно убедиться, что интервалы классов являются взаимоисключающими и в совокупности исчерпывающими.

Пример 3. Составление таблицы частотного распределения для большого количества наблюдений

Тридцать батареек типа АА были протестированы, чтобы определить, как долго они будут работать. Результаты с точностью до минуты были записаны следующим образом:

423, 369, 387, 411, 393, 394, 371, 377, 389, 409, 392, 408, 431, 401, 363, 391, 405, 382 , 400, 381, 399, 415, 428, 422, 396, 372, 410, 419, 386, 390

Используйте шаги из примера 1 и приведенные выше правила, чтобы составить таблицу частотного распределения.

Ответ

Наименьшее значение – 363, а наибольшее – 431.

Используя данные и интервал классов, равный 10, интервал для первого класса составляет от 360 до 369 и включает 363 (наименьшее значение). Помните, всегда должно быть достаточно интервалов занятий, чтобы было включено самое высокое значение.

Заполненная таблица частотного распределения должна выглядеть следующим образом:



Таблица 4. 3.3
Ресурс батареек АА, в минутах
Сводка таблицы
В этой таблице показаны результаты срока службы батарей типа АА. Информация сгруппирована по сроку службы батареи, минутам (x) (отображается в виде заголовков строк), частоте (f) (отображается в виде заголовков столбцов).

Срок службы батареи, мин ( x )	Частота (f)
360–369	2
370–379	3
380–389	5
390–399	7
400–409	5
410–419	4
420–429	3
430–439	1
Итого	30

Пример 4. Составление таблиц относительной частоты и частоты в процентах

Аналитик, изучающий данные из примера 3, может захотеть узнать не только о том, как долго работают батареи, но и о том, какая доля батарей попадает в каждый класс интервалов срока службы батарей.

Эта относительная частота конкретного наблюдения или интервала класса находится путем деления частоты ( f ) по количеству наблюдений ( n ): то есть ( f ÷ n ). Таким образом:

Относительная частота = частота ÷ количество наблюдений

Частота в процентах находится путем умножения каждого значения относительной частоты на 100. Таким образом:

Частота в процентах = относительная частота X 100 = f ÷ n X 100

Используйте данные из Примера 3, чтобы составить таблицу, содержащую относительную частоту и процентную частоту каждого интервала срока службы батареи.

Вот как выглядит эта таблица:



Таблица 4. 3.4
Ресурс батареек АА, в минутах
Сводка таблицы
В этой таблице показаны результаты срока службы батарей типа АА. Информация сгруппирована по сроку службы батареи, минутам (x) (отображается в заголовках строк), частоте (f), относительной частоте и частоте в процентах (отображается в заголовках столбцов).

Срок службы батареи, мин ( х )	Частота (f)	Относительная частота	Процентная частота
360–369	2	0,07	7
370–379	3	0,1	10
380–389	5	0,17	17
390–399	7	0,23	23
400–409	5	0,17	17
410–419	4	0,13	13
420–429	3	0,1	10
430–439	1	0,03	3
Итого	30	1	100

Аналитик этих данных теперь может сказать, что:

• 7% батарей типа АА имеют срок службы от 360 минут до 370 минут, но менее, и что
• вероятность того, что любая случайно выбранная батарея типа АА будет иметь срок службы в этом диапазоне, составляет приблизительно 0,07.

Пример 5 – Визуализация кумулятивного распределения относительной частоты

Как показано ранее в примере 2, кумулятивная частота используется для определения количества наблюдений, которые лежат ниже определенного значения в наборе данных. Совокупная частота рассчитывается путем добавления каждой частоты из таблицы распределения частот к сумме ее предшественников. Последнее значение всегда будет равно сумме по всем наблюдениям, так как все частоты уже будут добавлены к предыдущей сумме. Давайте рассмотрим еще один пример расчета кумулятивной частоты.

Ежедневное количество скалолазов в Лейк-Луизе, Альберта, регистрировалось в течение 30-дневного периода. Результаты следующие:

31, 49, 19, 62, 24, 45, 23, 51, 55, 60, 40, 35 54, 26, 57, 37, 43, 65, 18, 41, 50, 56 , 4, 54, 39, 52, 35, 51, 63, 42.

Количество скалолазов колеблется от 4 до 65. Для составления таблицы частот данные лучше сгруппировать по классам с интервалом 10. Каждый интервал может быть одной строкой в ​​таблице частот. В столбце Частота указано количество наблюдений, найденных в пределах интервала класса. Например, в интервале от 10 до 20 всего два значения, тогда его частота равна 2 в таблице соответственно.

Используйте столбец Частота для расчета совокупной частоты.

1. Сначала добавьте число из столбца Частота к его предшественнику. Например, в первой строке у нас есть только одно наблюдение и нет предшественников. Суммарная частота равна единице.
   1 + 0 = 1
2. Однако во второй строке есть два наблюдения. Добавьте эти два к предыдущей кумулятивной частоте (один), и в результате получится три.
   1 + 2 = 3
3. Запишите результаты в столбце Суммарная частота .

Другие записи в таблице можно рассчитать аналогичным образом. Результаты представлены в таблице 4. 3.5.



Суммарная относительная частота — это еще один способ выражения частотного распределения. Он получается путем вычисления процента кумулятивной частоты в пределах каждого интервала.

Совокупный процент рассчитывается путем деления кумулятивной частоты на общее количество наблюдений ( n ), затем умножаем на 100 (последнее значение всегда будет равно 100%). Таким образом,

кумулятивная относительная частота = (кумулятивная частота ÷ n) x 100

В четвертом столбце таблицы 4.3.6 показан расчет кумулятивной относительной частоты ежедневного числа скалолазов, зарегистрированных в Лейк-Луизе.



Таблица 4.3.6
Совокупная относительная частота ежедневного количества скалолазов, зарегистрированных в Лейк-Луизе, Альберта, 30-дневный период
Сводка таблицы
В этой таблице показаны результаты кумулятивной относительной частоты ежедневного количества скалолазов, зарегистрированных в Лейк-Луизе. Информация сгруппирована по количеству скалолазов (отображается в заголовках строк), частоте (f), совокупной частоте и совокупной относительной частоте (%) (отображается в заголовках столбцов).

Количество скалолазов	Частота (f)	Суммарная частота	Кумулятивная относительная частота (%)
<10	1	1	1 ÷ 30 х 100 = 3
от 10 до <20	2	1 + 2 = 3	3 ÷ 30 х 100 = 10
от 20 до <30	3	3 + 3 = 6	6 ÷ 30 х 100 = 20
от 30 до <40	5	6 + 5 = 11	11 ÷ 30 х 100 = 37
от 40 до <50	6	11 + 6 = 17	17 ÷ 30 х 100 = 57
от 50 до <60	9	17 + 9 = 26	26 ÷ 30 х 100 = 87
>= 60	4	26 + 4 = 30	30 ÷ 30 х 100 = 100

Кумулятивное распределение относительной частоты можно визуализировать с помощью гистограммы или линейной диаграммы, как на диаграмме 4. 3.1 ниже. Значение на горизонтальной оси является верхней границей интервала класса.

Таблица данных для диаграммы 4.3.1


Из диаграммы 4. 3.1 видно, что в течение большей части дней (57%) в период количество скалолазов было меньше или равно 49.

Распределение частот можно визуализировать с помощью:

• круговой диаграммы (номинальная переменная),
• гистограмма (номинальная или порядковая переменная),
• линейная диаграмма (порядковая или дискретная переменная),
• или гистограмма (непрерывная переменная).

Эти типы диаграмм будут представлены в разделе 5 по визуализации данных. Но сначала мы рассмотрим другие методы обобщения данных с использованием показателей центральной тенденции и дисперсии.



• Статистика: сила данных! — Главная страница
• 1 Данные, статистическая информация и статистика
• 2 Источники данных
• 3 Сбор и обработка данных
• 4 Исследование данных
• 5 Визуализация данных
• Библиография
• Глоссарий

Сообщить о проблеме на этой странице

Что-то не работает? Есть ли устаревшая информация? Не можете найти то, что ищете?

Пожалуйста, свяжитесь с нами и дайте нам знать, как мы можем вам помочь.

Уведомление о конфиденциальности

Дата изменения:

2021-09-02

Частота, таблицы частот и уровни измерения

РЕЗУЛЬТАТЫ обучения

• Создание и интерпретация таблиц частот.

Когда у вас есть набор данных, вам нужно организовать его, чтобы вы могли анализировать, как часто каждый элемент данных встречается в наборе. Однако при расчете частоты вам может понадобиться округлить ответы, чтобы они были максимально точными.

Ответы и округление

Простой способ округлить ответы — добавить в окончательный ответ еще один десятичный знак по сравнению с исходными данными. Округлите только окончательный ответ. По возможности не округляйте промежуточные результаты. Если возникнет необходимость округлить промежуточные результаты, доведите их как минимум до удвоенного количества знаков после запятой, чем окончательный ответ. Например, среднее из трех оценок викторины — четыре, шесть и девять — [latex]6,3[/latex], округленное до десятых, поскольку данные представляют собой целые числа. Большинство ответов будут округлены таким образом.

Уровни измерения

Способ измерения набора данных называется его уровнем измерения . Правильные статистические процедуры зависят от того, знаком ли исследователь с уровнями измерения. Не каждую статистическую операцию можно использовать с каждым набором данных. Данные можно разделить на четыре уровня измерения. Это (от низшего к высшему уровню):

• Номинальный уровень шкалы
• Уровень порядковой шкалы
• Уровень шкалы интервалов
• Уровень шкалы отношений

Данные, измеренные с использованием номинальной шкалы , являются качественными . Категории, цвета, названия, этикетки и любимые продукты, а также ответы «да» или «нет» являются примерами данных номинального уровня. Данные номинального масштаба не упорядочены. Например, пытаться классифицировать людей по их любимой еде бессмысленно. Ставить пиццу на первое место, а суши — на второе, не имеет смысла.

Смартфоны — еще один пример данных номинальной шкалы. Некоторыми примерами являются Sony, Motorola, Nokia, Samsung и Apple. Это всего лишь список, и нет согласованного порядка. Некоторые люди могут отдать предпочтение Apple, но это вопрос мнения. Данные номинального масштаба нельзя использовать в расчетах.

Данные, измеренные с использованием порядковой шкалы , аналогичны данным номинальной шкалы, но есть большая разница. Данные порядковой шкалы можно заказать. Примером данных в порядковой шкале является список пяти лучших национальных парков США. Пять лучших национальных парков США можно ранжировать от одного до пяти, но мы не можем измерить разницу между данными.

Другим примером использования порядковой шкалы является опрос о круизах, где ответы на вопросы о круизе: «отлично», «хорошо», «удовлетворительно» и «неудовлетворительно». Эти ответы упорядочены от наиболее желаемого ответа к наименее желательному. Но различия между двумя фрагментами данных не могут быть измерены. Как и данные номинальной шкалы, данные порядковой шкалы нельзя использовать в расчетах.

Данные, измеренные с использованием интервальной шкалы , аналогичны данным порядкового уровня, поскольку они имеют определенный порядок, но между данными есть разница. Различия между данными шкалы интервалов могут быть измерены, хотя данные не имеют отправной точки.

Температурные шкалы, такие как Цельсий (C) и Фаренгейт (F), измеряются с помощью шкалы интервалов. В обоих измерениях температуры [латекс]40°[/латекс] равно [латекс]100°[/латекс] минус [латекс]60°[/латекс]. Различия имеют смысл. Но [латекс]0[/латекс] градусов не соответствует, потому что в обеих шкалах [латекс]0[/латекс] не является самой низкой температурой. Существуют такие температуры, как [латекс]-10°[/латекс] F и [латекс]-15°[/латекс] С, и они ниже, чем [латекс]0[/латекс].

Данные интервального уровня можно использовать в расчетах, но нельзя проводить один тип сравнения. [латекс]80°[/латекс] C не в четыре раза горячее, чем [латекс]20°[/латекс] C (и [латекс]80°[/латекс] F в четыре раза горячее, чем [латекс]20° [/латекс] F). Нет смысла в соотношении [латекс]80[/латекс] к [латексу]20[/латекс] (или четыре к одному).

Данные, измеренные с использованием шкалы соотношений , решают проблему соотношений и дают вам больше информации. Данные шкалы отношений аналогичны данным шкалы интервалов, но имеют точку [latex]0[/latex], и отношения можно рассчитать. Например, четыре финальных экзамена по статистике с несколькими вариантами ответов: [латекс]80[/латекс], [латекс]68[/латекс], [латекс]20[/латекс] и [латекс]92[/латекс] (из возможных [латексных]100[/латексных] баллов). Экзамены проходят машинную оценку.

Данные можно расположить в порядке от низшего к высшему: [латекс]20[/латекс], [латекс]68[/латекс], [латекс]80[/латекс], [латекс]92[/латекс].

Различия между данными имеют значение. Оценка [latex]92[/latex] больше, чем оценка [latex]68[/latex] на [latex]24[/latex] балла. Коэффициенты можно рассчитать. Наименьшая оценка — [латекс]0[/латекс]. Итак, [латекс]80[/латекс] в четыре раза больше [латекс]20[/латекс]. Оценка [latex]80[/latex] в четыре раза лучше, чем оценка [latex]20[/latex].