Содержание
Основы термодинамики. Базовый уровень 10 класс онлайн-подготовка на Ростелеком Лицей
Внутренняя энергия
Когда закипает закрытая кастрюля с водой, то можно увидеть, как приподнимается крышка – с увеличением температуры возрастает давление водяного пара внутри кастрюли. Воздушный шар поднимается вверх, когда горелка нагревает воздух внутри купола и давление внутри становится выше, чем снаружи. Сдавливая надутый воздушный шарик, мы увеличиваем давление воздуха внутри него, уменьшая при этом объем, который он занимает. Это общие наблюдения, которые позволяют сделать выводы: как связаны три основные характеристики газа – давление, температура и объем.
Но чтобы сконструировать механизм или решить прикладную задачу, нужно уметь точно рассчитать характеристики газа при заданных условиях. Для этого мы предположили (а затем подтвердили экспериментально), что вещество состоит из атомов и молекул, которые хаотично движутся. Движение мы умеем описывать с помощью инструментов механики – массы, скорости, импульса, энергии.
Когда летит рой пчел, то движение каждой пчелы по отдельности может быть разным, но все вместе они движутся как единый объект, для которого можно ввести обобщенные характеристики – скорость роя, среднюю температуру и т. д.Молекул много, описывать движение каждой, а потом суммировать полученные результаты не получится. Поэтому мы ввели усредненные характеристики газа: среднюю энергию, среднее количество ударов молекул о стенки сосуда и т. д.
Температуру газа (характеристику, которую мы можем непосредственно измерить) мы определили через среднюю кинетическую энергию движения молекул:
Энергия – это наш инструмент для описания превращений: нечто, что сохраняется и переходит из одного вида в другой.Сначала мы рассматривали закон сохранения механической энергии – то есть сохранения и превращения энергии в системе, в которой действуют только консервативные силы (силы, работа которых не зависит от вида траектории; работа таких сил определяется только начальным и конечным положением тела). Затем обобщили его: если в замкнутой системе действуют неконсервативные силы, то общая энергия системы все равно будет сохраняться, но механическая энергия может превращаться в другие виды энергии.
Затем обобщили его: если в замкнутой системе действуют неконсервативные силы, то общая энергия системы все равно будет сохраняться, но механическая энергия может превращаться в другие виды энергии.
При ударе молота о наковальню оба они в месте контакта нагреваются. Нагревание мы описываем увеличением температуры, то есть меры внутренней энергии тела. Внутренняя энергия тела – это суммарная кинетическая энергия движения его частиц. То есть кинетическая энергия движения молота как единого целого (механическая энергия молота) переходит в его внутреннюю энергию – или, как мы говорил раньше, в тепло.
Почему модель механической энергии молота – как единого объекта – нам для описания удара по наковальне не подходит? Если рассматривать только силы, работа которых определяется исключительно начальным и конечным положением тела, то наличие или отсутствие наковальни на пути молота не повлияет на механическую энергию системы (см. рис. 1).
Рис. 1. Работа силы тяжести определяется только начальным и конечным положением тела
Также во время удара произойдет неупругая деформация молота, а это смещение его частей друг относительно друга. Такое смещение в данной модели не учитывается, так как рассматривается положение всего тела как целого. Значит, чтобы описать процессы, которые происходят при ударе, нам нужна другая модель (см. рис. 2).
Такое смещение в данной модели не учитывается, так как рассматривается положение всего тела как целого. Значит, чтобы описать процессы, которые происходят при ударе, нам нужна другая модель (см. рис. 2).
Рис. 2. Энергия взаимодействия молекул
Наша задача – научиться описывать процессы, которые происходят с молекулами вещества количественно.Достаточно ли нам для этого знать температуру вещества (или, что то же самое, среднюю кинетическую энергию молекул)? Внутренняя энергия вещества – это суммарная кинетическая энергия всех молекул. Понятно, что чем больше молекул (с данной средней кинетической энергией), тем больше будет внутренняя энергия.
Вы наверняка замечали, что при повышенной влажности мороз и жара переносятся хуже. Значит, для расчета характеристик газа будет важна не только температура, но и количество вещества (или масса, их можно выразить одно через другое).Исходя из проведенного анализа, выполним расчеты для простейшей модели, с которой мы работали до этого – модели идеального газа. Она удобна тем, что с хорошей точностью описывает реальные процессы и ее несложно описать.
Она удобна тем, что с хорошей точностью описывает реальные процессы и ее несложно описать.
В модели идеального газа мы сделали такое приближение: молекулы не взаимодействуют друг с другом, то есть не обладают потенциальной энергией, а только кинетической. Поэтому внутренняя энергия идеального газа – это суммарная кинетическая энергия всех его молекул.
Если мы взяли некоторое количество газа, которое содержит атомов, то его внутренняя энергия (обозначим ее ) равна кинетической энергии одного атома (в среднем), умноженной на количество этих атомов:
Где , по определению температуры.
Зная, что в одном моле вещества молекул, выразим количество молекул:
Количество вещества можно для удобства выразить через массу, а произведение двух констант и – это газовая постоянная :
Как видим, внутренняя энергия данной массы идеального газа определяется его температурой. Выражение встречается в уравнении Менделеева – Клапейрона, оно равно , так что внутреннюю энергию можно выразить через давление и объем газа:
Эти выражения справедливы только для одноатомного идеального газа.
Следующее ответвление, в котором мы рассмотрим внутреннюю энергию двухатомного газа, обязательно к ознакомлению для учеников профильного уровня, для всех остальных – по желанию.
Внутренняя энергия двухатомного газа
Обратите внимание, что мы рассматривали именно идеальный одноатомный газ (моделирующий разреженные реальные газы гелия, аргона, неона и пр.). Для идеального газа из молекул (с двумя, тремя или большим числом атомов) нужно учесть кинетическую энергию вращения молекул (их уже нельзя считать точками или шариками). Внутренняя энергия, приходящаяся на одну степень свободы движения молекулы, равна:
А чтобы получить общую внутреннюю энергию, нужно умножить на количество степеней свободы :
Что такое степени свободы? Количество степеней свободы – это количество координат, которые полностью определяют положение частицы в пространстве. Или другими словами, количество направлений, в которых может двигаться частица. Если у нас одноатомный газ, то есть его молекула состоит из одного атома, то положение частицы в пространстве можно задать тремя координатами, она может двигаться в трех направлениях, . И внутренняя энергия такого газа равна:
И внутренняя энергия такого газа равна:
Для двухатомного газа (H2, O2, CO и пр.) количество степеней свободы больше:
каждый атом может двигаться в трех направлениях, но есть еще одна связь между атомами. В направлении этой связи молекула может двигаться только как одно целое. Поэтому для двухатомного газа :
Для газов с тремя и более атомами в молекуле (CO2, CH4 и пр.) количество степеней свободы увеличивается. Но тогда каждый добавленный атом не добавляет степеней свободы: он может двигаться в трех направлениях, но в то же время он связан как минимум с тремя другими атомами в молекуле. Поэтому внутренняя энергия всех таких газов равна:
Работа газа при изопроцессах. Первый закон термодинамики
Простота модели идеального газа позволила рассчитать его внутреннюю энергию. Кроме самой величины внутренней энергии, нас интересует ее изменение. Изменить внутреннюю энергию тела можно, передав ему теплоту или совершив им механическую работу.
Первый способ – передать теплоту. Мы выделили несколько способов теплопередачи, когда внутренняя энергия одного тела переходит во внутреннюю энергию другого тела – излучение, теплопроводность, конвекция. Результат теплопередачи, независимо от способа, состоит в том, что внутренняя энергия одного тела может перейти во внутреннюю энергию другого тела. Этот процесс мы описали с помощью величины теплоты или количество теплоты . считаем положительным, когда рассматриваемое тело получает теплоту, и отрицательным, когда теряет (см. рис. 3).
Рис. 3. Теплопередача
Второй способ – выполнение механической работы. Если газ поместить под поршень и, например, нагреть, то газ расширится и поршень переместится – будет совершена механическая работа (см. рис. 4).
Рис. 4. Работа по перемещению поршня
Мы выделили модели изопроцессов и подробно рассмотрели, как в них изменяются температура, давление и объем. Вычислим работу, которую при этом выполняет газ.
О формулировках
В физике используют формулировки «газ выполнил работу» или «над газом выполнили работу». Это сокращение, которое не нужно понимать буквально. Работу выполняет сила, по определению: . Какая сила выполняет работу при перемещении поршня?
На поршень действует сила давления . По третьему закону Ньютона, можно выделить такую же по модулю и противоположную по направлению силу, которая действует условно на газ, . Почему условно? Потому что если газ считать совокупностью атомов, то нет точки приложения для этой силы, есть много единичных столкновений с атомами. Но так можно сказать о любом теле, состоящем из атомов, а силы мы все же в разных моделях выделяем. Эта сила равна сумме внешних сил, действующих на поршень: силы тяжести, силы, создаваемой атмосферным давлением.
Так вот, пусть газ расширяется. Работа силы равна , она положительна. Эту работу мы и называем работой, которую совершает газ, чтобы не называть ее «работа силы действия на поршень, создаваемой давлением газа». А работа внешних сил равна . Эту работу мы называем работой, которая совершается над газом. Они равны по модулю и противоположны по знаку, .
А работа внешних сил равна . Эту работу мы называем работой, которая совершается над газом. Они равны по модулю и противоположны по знаку, .
Проще всего с изохорным процессом. Объем газа не изменяется, перемещения нет, значит, работа равна нулю, .
Вычислим работу газа при изобарном процессе. Пусть газ находится в цилиндре под поршнем. Давление на поршень, по определению, равно силе, деленной на площадь. Распишем силу через давление:
Перемещение поршня обозначим , чтобы не путать с площадью . Положительным считаем , когда газ расширяется, тогда сила и перемещение сонаправлены. Запишем работу:
А изменение высоты умноженное на площадь – это изменение объема газа, тогда:
Соответственно, если газ будет изобарно сжиматься, то (а это ) будет отрицательным, или если мы записываем модуль , то поставим знак минус. В любом случае получим отрицательную работу (см. рис. 5).
Рис. 5. График зависимости при изобарном процессе
Значение давления постоянно. Видно, что – это площадь прямоугольника. Это удобно: мы можем оценить работу, совершаемую газом, по площади фигуры под графиком процесса в координатах . А знак этой работы определяется направлением процесса: увеличивается объем (тогда точка движется по графику вправо) или уменьшается (тогда влево).
Видно, что – это площадь прямоугольника. Это удобно: мы можем оценить работу, совершаемую газом, по площади фигуры под графиком процесса в координатах . А знак этой работы определяется направлением процесса: увеличивается объем (тогда точка движется по графику вправо) или уменьшается (тогда влево).
Рассмотрим работу газа при изотермическом процессе. Здесь изменяется и давление, и объем, такая задача решается немного сложнее. Оценим работу газа по графику. График изотермы – это гипербола , и работа газа равна площади фигуры под графиком (см. рис. 6).
Рис. 6. График зависимости при изотермическом процессе
Следующее ответвление, в котором мы получим уравнение для работы газа при изотермическом процессе, обязательно к ознакомлению для учеников профильного уровня, для всех остальных – по желанию.
Работа газа при изотермическом процессе
Вычислить работу газа можно по площади фигуры под графиком процесса в координатах . Даже если график не прямой, как в случае с изотермой, его можно разбить на небольшие промежутки, на каждом из которых давление можно считать постоянным. Тогда можно вычислить работу на каждом участке как площадь прямоугольника и сложить.
Тогда можно вычислить работу на каждом участке как площадь прямоугольника и сложить.
Мы так уже делали неоднократно: скорость при равноускоренном движении, работа изменяющейся силы упругости. Только график у нас обычно был прямой и сложных вычислений не было. Чтобы можно было работать с графиками любой формы, придумали математический инструмент – интегрирование (см. рис. 7). Он основан на том же процессе, который мы только что описали: разбиение на малые участки и сложение площадей, только специальные формулы позволяют делать это быстрее и точнее.
Рис. 7. Интегрирование на графике
Вы научитесь это делать позже на уроках математики в разделе «Интегралы», а сейчас для графика изотермы запишем готовый результат:
Первый закон термодинамики
Итак, мы научились вычислять внутреннюю энергию , рассчитали работу газа при разных процессах. А может еще передаваться теплота Q. Чтобы разобраться в этих переходах, осталось эти величины связать: как одно превращается в другое.
Как изменяются и превращаются друг в друга разные виды энергии, описывает закон сохранения энергии, это для нас не новость. Мы формулировали его для механических процессов как закон сохранения полной механической энергии. В ядерной физике мы рассматривали переход массы в энергию. Это все разные формы общего принципа, который можно упрощенно сформулировать так: энергия не возникает из ниоткуда и не исчезает бесследно. Запишем закон сохранения энергии для тепловых процессов.
Изменение внутренней энергии системы при ее переходе из одного состояния в другое равно количеству теплоты, подведенному к системе извне, плюс работе внешних сил, действующих на нее:
Другими словами, внутренняя энергия газа изменяется на количество теплоты, переданное газу, и на величину работы, совершенной над газом. В таком виде закон сохранения энергии назвали первым законом термодинамики (их мы рассмотрим два) – уравнение простое, но оно позволяет описать множество процессов, связанных с тепловыми явлениями.
Перепишем уравнение в другом виде. Мы чуть раньше в ответвлении разобрались с тем, что работа внешних сил над газом равна работе, совершенной над газом, которая взята со знаком минус:
Тогда:
Читаем уравнение: количество теплоты, переданное системе, идет на изменение ее внутренней энергии и на совершение ею работы. В ответвлении применим нашу модель для решения задачи.
Задача 1
Задача 1. Определите количество теплоты, полученное одноатомным газом в ходе процесса, график которого изображен на рисунке 8.
Рис. 8. Условие задачи
Анализ условия. В задаче описан процесс, в ходе которого газ получает теплоту, выполняет работу (так как на графике видно, что объем изменяется). И наверняка изменяется внутренняя энергия: на графике температура не видна, но процесс явно не изотермический. Такие превращения энергии мы описываем с помощью первого закона термодинамики. Работу газа мы умеем вычислять как площадь фигуры под графиком (см. рис. 9).
рис. 9).
Рис. 9. Работа газа на графике
Уравнение для внутренней энергии одноатомного газа мы тоже знаем. Перейдем к физической части решения, запишем в виде уравнений то, что обсудили.
По первому закону термодинамики, количество теплоты, переданное газу, идет на изменение его внутренней энергии и совершение им работы:
Вычислим работу газа как площадь фигуры под графиком. Можем выделить прямоугольник и треугольник, можем рассматривать полностью трапецию – как удобно. Рассмотрим трапецию: ее основания равны и , а высота равна . Из уроков геометрии помним, что площадь трапеции равна (см. рис. 10):
Рис. 10. Площадь трапеции
Внутренняя энергия одноатомного идеального газа определяется температурой:
У нас нет температуры, можем переписать, применим уравнение Менделеева – Клапейрона:
Тогда при переходе из состояния 1 в состояние 2 изменение внутренней энергии равно:
Математическая часть решения задачи осталась простая: подставляем и в первое уравнение и находим количество теплоты. Значения давлений и объемов находим на графике и переводим в СИ: , , , .
Значения давлений и объемов находим на графике и переводим в СИ: , , , .
Вычислим:
Получили ответ 775 кДж, задача решена.
Применим первый закон термодинамики к изопроцессам. При изобарном процессе давление постоянно, а температура и объем изменяются. Пусть газ нагревается и расширяется. Нагревается – значит, увеличивается внутренняя энергия. Расширяется – значит, выполняет работу. И , и работу при изобарном процессе мы вычислять умеем, поэтому по формуле: сможем рассчитать количество теплоты.
При изохорном процессе не выполняется работа, , потому что объем не меняется. Поэтому первый закон термодинамики примет вид: , то есть вся переданная газу теплота идет на изменение внутренней энергии.
При изотермическом процессе не изменяется температура, а значит, не изменяется внутренняя энергия, . Тогда уравнение примет вид: . Вся переданная газу теплота идет на выполнение газом работы.
В следующем ответвлении мы рассмотрим еще один процесс, адиабатный, оно обязательно к ознакомлению для учеников профильного уровня, для всех остальных – по желанию.
Адиабатный процесс
Выделим еще одну модель, с помощью которой можно описать реальные процессы. Представим себе процесс, при котором газ не обменивается теплотой с окружающими телами, . Может такое быть? Например, когда процесс происходит быстро и вкладом теплообмена можно пренебречь, считаем почти равным нулю. Такой процесс назвали адиабатным. Тогда:
Это значит, что уменьшение внутренней энергии тела равно работе, выполненной этим телом. При этом изменяются все три макропараметра газа: уменьшается температура, увеличивается объем и уменьшается давление. В координатах график адиабаты идет круче, чем график изотермы: так как тепло извне не подводится и не отводится, температура падает и, соответственно, растет быстрее (см. рис. 11).
Рис. 11. График зависимости при адиабатном процессе
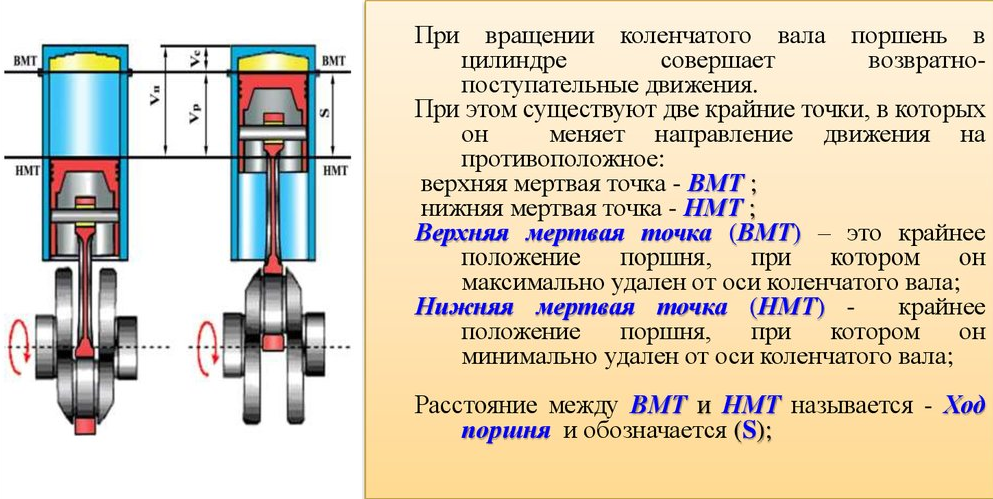
Когда мы открываем бутылку с газированным напитком, в которой воздух был под давлением, воздух быстро расширяется, выполняется работа (может даже отскочить крышка), за счет того что уменьшается внутренняя энергия газа – закон сохранения энергии выполняется.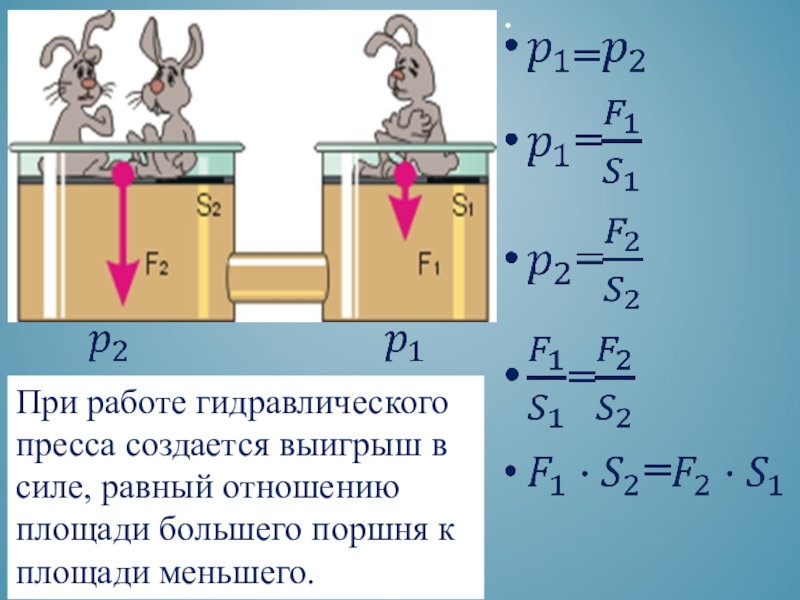 И газ охлаждается: мы видим даже конденсацию пара из-за этого охлаждения. И наоборот, если быстро сжать газ, то есть выполнить над ним работу, его внутренняя энергия (а значит, и температура) увеличится. Так при резком сжатии под поршнем воспламеняется топливо в дизельных двигателях (а не от искры, как в бензиновых).
И газ охлаждается: мы видим даже конденсацию пара из-за этого охлаждения. И наоборот, если быстро сжать газ, то есть выполнить над ним работу, его внутренняя энергия (а значит, и температура) увеличится. Так при резком сжатии под поршнем воспламеняется топливо в дизельных двигателях (а не от искры, как в бензиновых).
Второй закон термодинамики
С количественными характеристиками тепловых процессов разобрались, ответили на вопрос «сколько?». Конечно, эта модель, как и любая другая, имеет ограничения, идеализация не совпадает с реальностью.
Обратим внимание вот на что. Под поршнем есть некоторое количество газа комнатной температуры. Представим, что он расширился, то есть выполнил работу , и нагрел окружающий воздух в комнате (то есть полученное им количество теплоты отрицательно, ). При этом он должен охладиться. Из уравнения изменение внутренней энергии равно . отрицательное, еще и минус , получается отрицательным. В уравнении все сходится, внутренняя энергия уменьшилась, а разность выделилась в виде теплоты и пошла на выполнение газом работы. Но опыт нам подсказывает, что такой процесс самопроизвольно не протекает. Да, вещества обладают внутренней энергией, но не всегда мы ею можем управлять. Мы не можем забрать часть энергии у холодной батареи, чтобы она стала еще холоднее, а руки нагрелись. Воздух, который вырвался из воздушного шарика, самопроизвольно в нем не соберется. Так что помимо количественных характеристик тепловых процессов важно еще направление этих процессов.
Но опыт нам подсказывает, что такой процесс самопроизвольно не протекает. Да, вещества обладают внутренней энергией, но не всегда мы ею можем управлять. Мы не можем забрать часть энергии у холодной батареи, чтобы она стала еще холоднее, а руки нагрелись. Воздух, который вырвался из воздушного шарика, самопроизвольно в нем не соберется. Так что помимо количественных характеристик тепловых процессов важно еще направление этих процессов.
Опыт подсказывает нам, что теплота самопроизвольно не передается от холодных тел к теплым, но это можно сделать с помощью холодильника. Строго это утверждение сформулировано в виде второго закона термодинамики, он отображает необратимость процессов в природе – они самопроизвольно протекают только в одном направлении. Этот закон имеет множество формулировок, приведем несколько.
Невозможен процесс перехода теплоты от тела с более низкой температурой к телу с более высокой.
Невозможен процесс, результатом которого было бы совершение работы за счет теплоты, взятой от одного какого-то тела. Еще другими словами – невозможно существование вечного двигателя второго рода (вечный двигатель первого рода предполагает создание энергии из ничего, а второго рода – полное превращение тепловой энергии в механическую).
Еще другими словами – невозможно существование вечного двигателя второго рода (вечный двигатель первого рода предполагает создание энергии из ничего, а второго рода – полное превращение тепловой энергии в механическую).
Эти и другие формулировки следуют одни из другой и описывают одно и то же с разных сторон. Еще несколько формулировок второго закона термодинамики мы приведем в следующем ответвлении, которое обязательно к ознакомлению для учеников профильного уровня, для всех остальных – по желанию.
Второй закон термодинамики
Мы применили второй закон термодинамики к тепловым процессам. Но мы же знаем, что для описания тепловых явлений можно использовать модель механики для большого количества частиц. Поэтому можно распространить второй закон термодинамики и на механические явления.
Для систем с большим количеством элементов, к которым можно применить инструменты статистики, ввели понятие энтропии. Если упрощенно, то это величина, характеризующая неупорядоченность, хаотичность. Например, если весь воздух из комнаты был бы сосредоточен в одном открытом сосуде, энтропия такой системы была бы низкой. Если в одной части комнаты собран весь азот, в другой кислород, а внутри флакона молекулы духОв – энтропия тоже низкая. Но если воздух распределен равномерно и смешан, энтропия такой системы выше.
Например, если весь воздух из комнаты был бы сосредоточен в одном открытом сосуде, энтропия такой системы была бы низкой. Если в одной части комнаты собран весь азот, в другой кислород, а внутри флакона молекулы духОв – энтропия тоже низкая. Но если воздух распределен равномерно и смешан, энтропия такой системы выше.
Так вот, есть такая формулировка второго закона термодинамики: в замкнутых системах (без поступления энергии извне) энтропия не может уменьшаться. То есть неупорядоченность только увеличивается: хаотично движущиеся молекулы не могут сами прийти в порядок, распределившаяся теплота не может передаться назад к источнику, разбитая ваза не может собраться из осколков, разбежавшееся стадо без команды или дрессировки не соберется в стойле и так далее.
Тепловой двигатель
Второй закон термодинамики ограничивает нас в использовании энергии, и возникает задача. Есть энергия, которая содержится в любом веществе – внутренняя энергия. И было бы замечательно научиться как-то ее использовать, превращать в механическую, электрическую и т.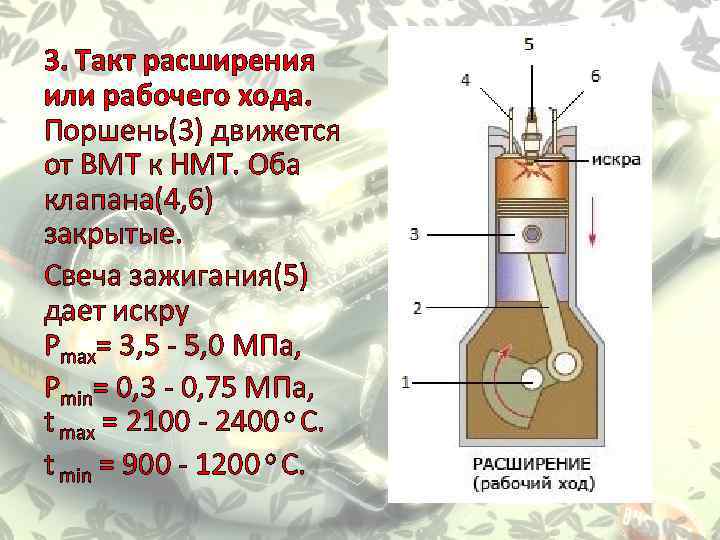 д. – в какую нужно. Но как это сделать, если самопроизвольное превращение внутренней энергии в работу невозможно?
д. – в какую нужно. Но как это сделать, если самопроизвольное превращение внутренней энергии в работу невозможно?
Мы эту задачу уже решили и придумали, на каком принципе должен работать тепловой двигатель (см. рис. 12). Вкратце напомним, о чем мы договорились. Чтобы газ выполнял работу, его нужно нагревать, а затем охлаждать, чтобы привести в исходное состояние.
Рис. 12. Принцип работы теплового двигателя за цикл
В итоге тепловой двигатель работает в замкнутом цикле, и он, помимо рабочего тела, должен содержать нагреватель и холодильник. Тогда на разных этапах работы двигателя второй закон термодинамики выполняется: теплота переходит от нагревателя к рабочему телу и от рабочего тела к холодильнику. Превращения энергии мы описывали уравнением:
Часть теплоты , полученной от нагревателя, идет на выполнение работы , а остальная () передается холодильнику. КПД теплового двигателя мы вычисляем по стандартной формуле: полезная работа, деленная на затраченную энергию, и для теплового двигателя эта формула принимает вид:
Работу выразим из предыдущего уравнения:
Можем сформулировать второй закон термодинамики еще одним способом. КПД теплового двигателя не может быть равен 100 %. Конечно, у любого механизма есть потери. Но здесь речь о том, что даже идеальный тепловой двигатель должен отдавать теплоту холодильнику, чтобы тот охлаждал рабочее тело, а значит, числитель всегда будет меньше знаменателя и КПД будет меньше 1. Так мы пришли к предыдущим формулировкам второго закона термодинамики.
КПД теплового двигателя не может быть равен 100 %. Конечно, у любого механизма есть потери. Но здесь речь о том, что даже идеальный тепловой двигатель должен отдавать теплоту холодильнику, чтобы тот охлаждал рабочее тело, а значит, числитель всегда будет меньше знаменателя и КПД будет меньше 1. Так мы пришли к предыдущим формулировкам второго закона термодинамики.
Следующее ответвление, в котором мы рассмотрим модель теплового двигателя с максимально возможным КПД, обязательно к ознакомлению для учеников профильного уровня, для всех остальных – по желанию.
Цикл Карно
Попробуем построить по возможности наиболее эффективную тепловую машину. Что для этого нужно? Тепловая энергия должна максимально полно превращаться в механическую, без лишних потерь.
Теплота, подводимая к рабочему телу нагревателем, должна полностью идти на выполнение им работы, , . Такое условие выполняется при изотермическом расширении, это будет первый этап, отметим его на графике (см. рис. 13). , .
рис. 13). , .
Сделаем вторым этапом адиабатическое расширение: прекратим подвод теплоты , и уже работа будет совершаться за счет охлаждения газа, . Здесь , .
Теперь начнем возвращать машину в исходное состояние. На этапе 3 сожмем газ, совершив над ним работу, одновременно отводя тепло при помощи холодильника. Отводим все тепло, которое возникает из-за сжатия – так, чтобы внутренняя энергия газа не менялась. То есть процесс идет при постоянной температуре, по изотерме. , , .
И наконец, на этапе 4 сожмем газ, совершив над ним работу, не отводя и не подводя тепло, то есть процесс адиабатический. , , . Таким образом, получили цикл из двух изотерм и двух адиабат.
Рис. 13. Цикл Карно
Построенная тепловая машина была предложена французским инженером Сади Карно, и описанный цикл носит его имя. КПД этой машины максимально возможный для тепловой машины, работающей при данных температурах нагревателя и холодильника и . Ее КПД равен:
Реализовать такую машину в точности нельзя.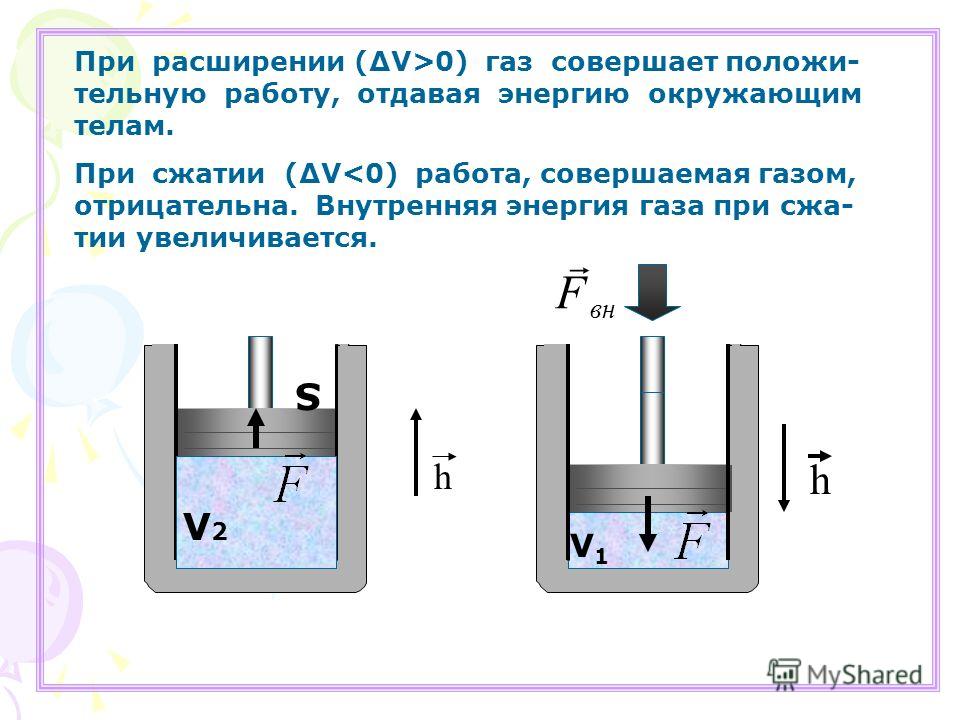 Например, в реальности нельзя сжимать газ и отводить тепло так, чтобы газ все время оставался при одной температуре. Теоретически, если тепло передается между телами при равных температурах, оно может передаваться в обоих направлениях (нет более теплого и более холодного). Для такой модели придумали название квазиобратимый процесс: его не существует, но если бы он существовал, то мог бы быть обратимым. А в реальности могут протекать процессы, только с некоторой степенью точности похожие на описанные идеальные: температура почти не меняется или меняется очень медленно, теплообмен почти не происходит, почти все тепло переходит в работу.
Например, в реальности нельзя сжимать газ и отводить тепло так, чтобы газ все время оставался при одной температуре. Теоретически, если тепло передается между телами при равных температурах, оно может передаваться в обоих направлениях (нет более теплого и более холодного). Для такой модели придумали название квазиобратимый процесс: его не существует, но если бы он существовал, то мог бы быть обратимым. А в реальности могут протекать процессы, только с некоторой степенью точности похожие на описанные идеальные: температура почти не меняется или меняется очень медленно, теплообмен почти не происходит, почти все тепло переходит в работу.
Зачем нам эта модель? Чтобы оценить максимальный КПД, который теоретически возможен при данных температурах. Например, мы получили для двигателя на цикле Карно значение КПД 30 %. Это значит, что какой бы мы ни сделали двигатель с данными рабочими температурами, его КПД даже теоретически не может достичь и тем более превысить 30 %. На практике он будет меньше.
Список литературы
- Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. Физика 10. – М.: Просвещение, 2008.
- Касьянов В.А. Физика 10. – М.: Дрофа, 2000.
- М.М. Балашов, А.И. Гомонова, А.Б. Долицкий и др. Физика: Механика 10. – М.: Дрофа, 2004.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «class-fizika.ru» (Источник)
- Интернет-портал «class-fizika.ru» (Источник)
- Интернет-портал «class-fizika.ru» (Источник)
Домашнее задание
- Определите температуру кислорода массой 64 г, находящегося в сосуде объемом 1 л при давлении Па. Молярная масса кислорода М = 0,032 кг/моль.
- Опишите способы изменения внутренней энергии газа и приведите к каждому практический пример.
Тепловые явления — Физика — Презентации
Беспорядочное перемещение частиц тела, не
прекращающееся при любой температуре выше
Абсолютного нуля (- 273 о С). V частиц Т тела
V частиц Т тела
Отличие от механического движения:
очень м н о г о частиц, каждая движется б е с п о р я д о ч н о.
Жидкость
Газ
Твёрдое тело
Сохраняет форму и объём,
сжимаемо.
Сохраняет объём, течёт, несжимаема.
1 см 3 воды содержит 3*10 28 молекул.
Не сохраняет объёма, формы,
течёт, легко сжимается.
Молекулы беспорядочно перемещаются, почти не
взаимодействуют.
Молекулы совершают
только колебания.
Перескоки молекул из одного слоя в другой.
«бродяги»
« кочевники»
«оседлые»
А г р е г а т н ы е с о с т о я н и я в е щ е с т в а
Опишите превращения энергии в данных примерах
Составьте текст из фрагментов А, Б, В, Г, Д:
А. Средняя кинетическая энергия молекул…
1. в твёрдых телах…
2. в жидкостях…
3. газах…
Б. 1. при постоянной температуре…
2. с увеличением температуры…
с увеличением температуры…
3. с понижением температуры…
В. 1. уменьшается.
2. увеличивается.
3. не изменяется.
Г. Поэтому внутренняя энергия этих тел…
1. с понижением температуры…
2. при постоянной температуре…
3. с ростом температуры…
Д. 1. увеличивается.
2. уменьшается.
3. не изменяется.
Ответы: А1Б1В3Г2Д3; А2Б2В2Г3Д1 А3Б3В1Г1Д2
Спички
Одинаково ли для брусков изменение внутренней энергии при погружении их в горячую воду?
В каком сосуде температура выше?
В каком манометре
мех. работа по подъёму
жидкости выше?
Если быстро
скользить по
канату, то можно
обжечь руки.
Почему?
В чём сходство и различие причин
загорания спичек?
Что является причиной сгорания искусственных спутников Земли
при их вхождении в плотные слои а т м о с ф е р ы ?
Процесс изменения внутренней энергии без совершения работы
над телом или самим телом
- Чем отличаются приведённые
примеры в передаче теплоты?
- Что общего?
3. Происходит ли теплопередача,
Происходит ли теплопередача,
если температура тел одинакова?
Внутренняя энергия
Вам известны следующие теоретические положения:
- Как внутренняя энергия тела зависит от его кинетической и
потенциальной энергии.
II . Может ли тело совершать работу за счёт своей внутренней
энергии.
- Как изменяется внутренняя энергия при совершении
механической работы над телом или самим телом.
- Изменяется ли внутренняя энергия тела при теплопередаче.
- Какая физическая величина служит мерой внутренней энергии.
Какими из приведённых ниже примеров их можно подтвердить?
1. При сверлении на токарном станке сверло и заготовку
надо охлаждать.
2. Нагретый воздух выталкивает пробку из сосуда независимо
от того, на каком этаже он находится.
3. У кипящего на плите чайника крышка подскакивает.
4. Воздух комнаты нагревается за счёт горячей воды, проте-
кающей через батареи.
5. При соприкосновении двух тел их температура выравнивается.
Ответы: I — 2 ; II — 3; III — 1; IV — 4; V — 5.
Перенос энергии от более нагретых участков тела
к более холодным за счёт теплового движения
и взаимодействия ч а с т и ц т е л а
- При теплопроводности само вещество не перемещается от
нагретого конца тела к холодному. Как же передаётся тепло?
- Будет ли происходить перенос тепла в условиях невесомости?
- Разные вещества проводят тепло по-разному. Почему?
Проводники тепла:
х о р о ш и е
металлы, их расплавы,
твёрдые тела и др.
п л о х и е
Жидкости, газы, пористые
тела, земля…
В какой обуви
больше мёрзнут ноги зимой:
в просторной или тесной?
Объясните.
В каком чай-
нике скорее
нагреется вода:
в новом или
старом, на
стенках которого
имеется накипь?
(Чайники
одинаковые)
Почему
в одинаковых
условиях металл
на морозе кажется
холоднее дерева и
горячее – при нагреве?
Деревянная
ложка в стакане с
горячей водой
нагревается меньше, чем
металлическая.
ρ в
Почему водоёмы зимой не
промерзают до дна?
Попробуйте ответить, используя
график изменения плотности воды
с температурой.
4 0 С
t 0 C
Зачем
жители Средней
Азии в жару
носят ватные
халаты и
папахи?
Какое из указанных ниже веществ является…
А. лучшим проводником теплоты?
Б.самым плохим проводником теплоты?
В каком состоянии вода обладает…
В. наименьшей теплопроводностью?
Г. наибольшей теплопроводностью?
1. В твёрдом состоянии. 2. В жидком состоянии.
3. В газообразном состоянии.
Д. Каков механизм передачи теплоты при контакте по-разному
нагретых твёрдых тел?
1.Быстрые частицы перемещаются из нагретых частей
тела в более холодные.
2.Быстрые частицы отдают часть своей энергии менее
подвижным из слоя в слой последовательно.
1. Пенопласт 2. Железо
3. Стекло 4. Серебро
Стекло 4. Серебро
ОТВЕТЫ : А4; Б1; В3; Г1; Д2
Перенос тепла от нагретых тел к более
холодным струями жидкости или газа.
- У горячих слоёв жидкости (газа) плотность
уменьшается, и они поднимаются вверх, уступая место более холодным. Возникает
циркуляция («движение по кругу») слоёв.
- Будет ли происходить конвекция между телами с одинаковой температурой?
- Возможна ли конвекция в вакууме?
- От чего зависит быстрота теплообмена?
В каком состоянии вещества теплота передаётся преимуще-
Составьте тексты из фрагментов А, Б, В, Г, Д, Е, Ж:
ственно… А. конвекцией? Б. теплопроводностью?
1. Твёрдом состоянии. 2. Жидком и газообразном.
3. Независимо от состояния вещества.
В чём состоит явление…
В. конвекции? Г. теплопроводности?
1. В том, что молекулы с большей энергией движения пере-
дают её менее энергичным молекулам во взаимодействии.
2. Теплота переносится струями жидкости или газа.
В состоянии невесомости…
Д . не происходит… Е. осуществляется…
1. теплопроводность. 2. конвекция.
Ж. Объясняется это тем, что причиной…
1. является архимедова сила.
2. тепловое хаотическое движение молекул.
ОТВЕТЫ: А2; Б1; В2; Г1; Д2;Ж1; Е1;Ж2.
Наблюдаются ли
конвективные потоки у
поверхности Луны?
Марса?
Что теплее: земля или
воды океана? Днем?
Ночью?
Играет ли конвекция важную р о л ь
1) в образовании облаков?
2) в нагревании поверхностных
вод океана?
Как образуются бризы?
День
Ночь
Составьте текст из фрагментов А, Б, В, Г:
А .1. При нагревании воздуха снизу…
2. В случае нагревания одного конца металлического
стержня… 3. При охлаждении жидкости снизу…
Б . 1. в данной части вещества увеличиваются колебания
частиц и их средняя кинетическая энергия растёт.
2. циркуляции вещества практически не идёт.
3. в данной части вещества растёт средняя скорость
поступательного движения молекул и их средняя
кинетическая энергия.
В . 1. Процесс выравнивания температуры идёт очень
медленно, т.к. не происходит перемешивания слоёв.
2. вещество в этом слое расширяется, его плотность
уменьшается и оно поднимается вверх в виде струй,
уступая место внизу более холодным слоям.
3. Быстро колеблющиеся частицы одного слоя переда-
ют энергию соседним частицам, и так от слоя к слою.
Г . 1. Такой способ теплопередачи называют конвекцией.
2. Это явление называется теплопроводностью.
ОТВЕТЫ: 1) А1;Б3;В2;Г1. 2) А2;Б1;В3;Г2. 3) А3;Б2;В1;Г2.
Это особое инфракрасное
( тепловое ) излучение , подобное
свету, но невидимое глазу
- Передаётся через вакуум на большие расстояния.

- Любое тело «светится», излучая тепловые лучи.
- Чем больше температура тела, тем сильнее оно излучает.
4. Поглощают тепло разные тела неодинаково.
П о г л о щ е н и е т е л а м и:
х о р о ш е е
п л о х о е (лучше отражают)
Белые тела, блестящие,
зеркальные поверхности
Чёрные тела, шероховатые
поверхности, сажа и др.
Каким способом нагревается вода
в ведре?
Как змея обнаруживает свою добычу?
1
Специальный орган, улавливающий
тепло животных
А сами туристы?
В какой
одежде менее
жарко летом: в белой или
тёмной?
Зачем крылья самолётов и воздушные
шары красят серебряной краской?
Вам известно, как происходит передача теплоты…
А. в вакууме. Б. в случае конвекции.
В. при разной теплопроводности веществ.
Различают…
Г. хорошие проводники теплоты.
Д. плохие проводники теплоты.
Какие из этих положений Вы используете для объ-
яснения приведённых ниже конкретных фактов?
- Жидкости и газы всегда нагревают снизу.
2. Главным источником энергии для Земли служит Солнце.
3. В доме зимой лучше сберегают тепло двойные рамы, чем
одинарные рамы с толстым стеклом.
4. Батареи отопления изготавливают из металла (чугуна и др.)
5. Железный гвоздь невозможно сильно нагреть, держа в
руке, а спичку можно держать почти до полного сгорания.
Ответы: А2; Б1; В5;Г4; Д3
Энергия, которую получает или теряет тело при теплопередаче
называют к о л и ч е с т в о м т е п л о т ы
Тело
получило
(отдало)
количество
теплоты
20 кДж
Произошёл процесс ,
в результате которого
внутренняя энергия
тела увеличилась
(или уменьшилась) на
20 000 Дж без соверше-
ния работы.
t 2 0 С Q 1 Q 1 Q 2 Q 1 Q 2 Разное время нагревания Разная температура Разные вещества Q ~ т Q ~ t 0 C Q ~ роду вещества количество теплоты, которое получает (или отдаёт) тело, зависит от его массы , рода вещества , и изме — нения температуры . показывает, какое количество теплоты требуется для изменения температуры вещества массой 1 кг на 1 0 С. Обозначается: С . Единица измерения: 1 Дж / кг 0 С Q = cm(t 2 0 – t 1 0 ) «
t 1
m 1 = m 2
t 1 0 С t 2 0 С
Q 1
Q 1 Q 2
Q 1 Q 2
Разное время нагревания
Разная температура
Разные вещества
Q ~ т
Q ~ t 0 C
Q ~ роду вещества
количество теплоты, которое получает (или отдаёт)
тело, зависит от его массы , рода вещества , и изме —
нения температуры .
показывает, какое количество теплоты требуется для изменения
температуры вещества массой 1 кг на 1 0 С.
Обозначается: С . Единица измерения: 1 Дж / кг 0 С
Единица измерения: 1 Дж / кг 0 С
Q = cm(t 2 0 – t 1 0 )
А. Какая из указанных величин не используется при вычислении
количества теплоты:
1. разность начальной и конечной температур.
2. объём тела. 3. масса тела. 4. удельная теплоёмкость тела.
Б. Можно ли от куска льда отнять некоторое количество теплоты?
1. Нет, т. к. он и так холодный.
2. Да, но только когда окружающие тела имеют ещё более
низкую температуру.
В. Может ли бочка с водой служить регулятором постоянной
температуры в погребе?
1. Нет, погреб недостаточно утеплён для зимних температур.
2. Да. Благодаря высокой теплоёмкости массы воды в бочке
выделяемое (поглощаемое) тепло сглаживает колебания тем-
пературы в погребе в сравнении с наружной.
Укажите единицы измерения…
Г. удельной теплоёмкости. Д. количества теплоты.
1. Градус ( 0 С). 2. Дж. 3. Дж / (кг 0 С). 4. кг.
Ответы: А2; Б2; В2;Г3; Д2.
В
А
Керосин из мензурок А и В перелили в стакан. Определите
температуру керосина в стакане. Нагреванием стакана и
объёмом термометра пренебречь.
Задача . Латунное тело М опустили в мензурку с водой так, как пока-
зано на рисунке. Определить, на сколько градусов повысилась тем-
пература тела М, считая неизменной температуру мензурки.
Объёмом термометра пренебречь. ОТВЕТ: ~ 1,1 0 С
Какой из воробьёв
Пробка
Какие виды
теплопередачи
устраняет
пробка?
Вакуум?
Зеркало?
Вакуум
изображён летом, а какой- зимой?
Зеркало
З е мляне
В каком направлении движется
вода (вверх или вниз) при работе двигателя автомобиля?
Объясните,
что такое «парниковый эффект»?
Вреден или полезен для планеты?
Примерная схема поглощения и излучения (в %) энергии у
поверхности Земли.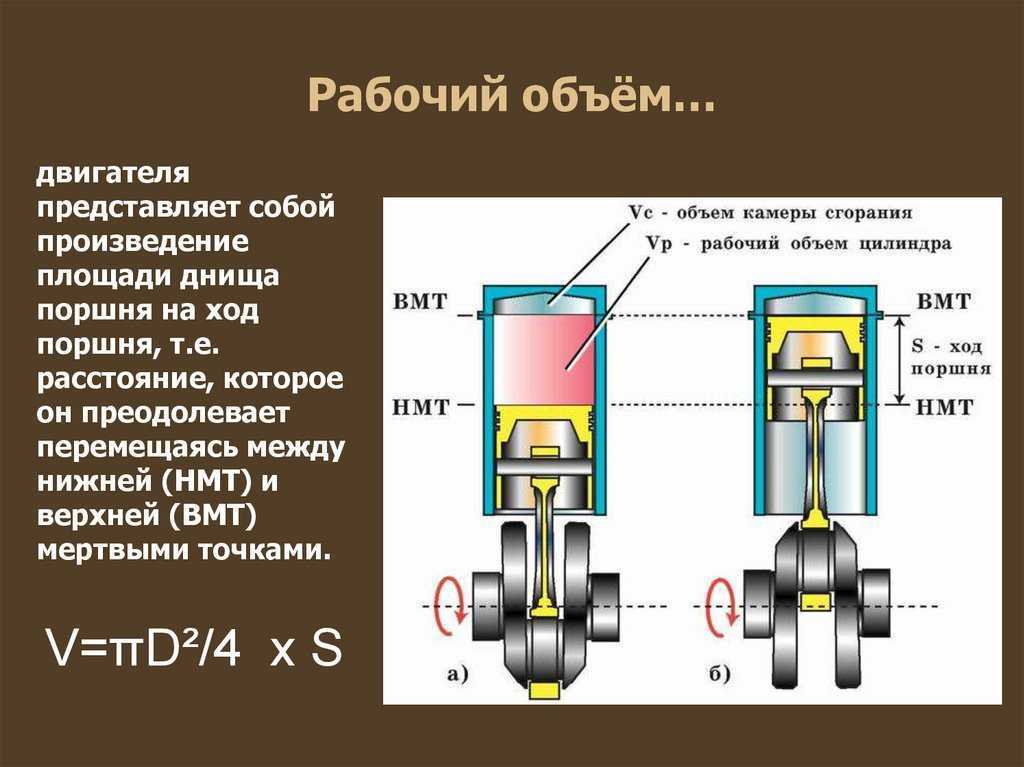 Благодаря атмосфере, средняя темпе-ратура планеты + 1 4,5 0 C ( без атмосферы – 18,7 0 С ).
Благодаря атмосфере, средняя темпе-ратура планеты + 1 4,5 0 C ( без атмосферы – 18,7 0 С ).
2
В железный душевой бак,
масса которого70 кг, налили
холодной воды объёмом 200 л.
В результате нагревания солнечным излучением темпе-
ратура воды повысилась с 4 до
30 0 С. Какое количество тепло-ты получили бак и вода?
t, 0 C
1
2
3
3
t, мин.
Какое количество теплоты
передаст окружающим телам
кирпичная печь массой 1,5 Т
при охлаждении от 30 0 С до 20 0 С?
На одинаковых горелках нагревались вода, медь, железо равной массы.
Какой график соответствует
каждому веществу?
t, 0 C
t, 0 C
Г
1200
В
Б
600
Б
В
Г
300
А
0
t, мин.
А
2 4 6 8 10 14 16
Вопросы:
Д
0
t , мин.
- Какую t 0 имело тело в т. А,В,Г?
- Какой процесс описывают участки АБ? БВ? ВГ?
- При какой t 0 начался процесс? Закончился?
- Какую t 0 имело тело на 4 мин.?
- Сколько времени длился процесс охлаждения тела?
- Что происходило с телом на
отрезке БВ графика?
7. Что происходило быстрее: нагревание или охлаждение?
- На каком участке телу сообщается
некоторое количество теплоты Q ?
- Когда тело отдаёт Q ?
- Какую t 0 имеет тело к концу процесса?
- Сравните количество теплоты, приобретённое телом в ходе процесса и отданное.
- Сообщалось ли телу некоторое Q
на участке БВ? Зачем?
О
О
С
Q
При горении топлива (угля, нефти, газа, сланцев) один
атом углерода соединяется
с двумя атомами кислорода.
При образовании этой
молекулы выделяется
э н е р г и я.
С
m
q
СО 2
показывает, какое количество теплоты выделяется при
полном сгорании 1 кг топлива. О б о з н а ч а е т с я : q
О б о з н а ч а е т с я : q
Е д и н и ц а и з м е р е н и я : 1 Дж / кг.
Воду из мензурки
перелили в сосуд и
довели до кипения.
Определить массу
сгоревшего спирта.
П о м о щ ь:
- Определите массу
воды.
2. Рассчитайте количе-
ство теплоты, необхо-
димое для её нагрева-
ния до 100 0 С.
3. Найдите, какое коли-
чество спирта выделя-
ет столько же энергии
при своём сгорании.
Холодильник
Паровая машина
1 – испаритель
2 – морозильная
камера
3 – регулирующий клапан испарителя
4 – змеевик
5 – мотор
6 – компрессор
1
3
2
4
5
6
Турбореактивный двигатель
Турбина
3
3
1 – вал турбины
2 – турбокомпрессор
3 – форсунки для
подачи топлива
4 – камеры сгорания
5 – воздушный поток
6 – турбина
7 — сопло
5
1
2
1 – вал
2 – ротор
3 – лопатка
4 — сопло
1
1
2
2
4
4
3
4
6
7
Первый паровоз был сконструирован в
1803 г. английским изобретателем
английским изобретателем
Ричардом Т р е в и т и к о м.
Масса паровоза составляла 5 т. Когда его стали использовать на конной чугунной
дороге, он начал ломать рельсы. Второй
паровоз Тревитика развивал скорость 30
км/ч, но нашёл место только в качестве аттракциона на небольшой кольцевой дороге.
Первоначальное название парохода – пироскаф . Он имел ещё паруса.
Первый пароход «Клермонт» построен в Сев. Америке (1807 г.).
В России впервые пароход «Елиза- вета» курсировал между Санкт – Петербургом и Кронштадтом (1815 г.)
Решающая роль в развитии парового
железнодорожного транспорта принад-
лежит английскому конструктору и изо-
бретателю Д. Стефенсону (1781 – 1848).
Строить паровозы он начал с 1814 г.
Уже в 1823 г. им был основан первый в мире паровозостроительный завод. Под руководством Стефенсона были построены железные дороги.
В 1829 г. состоялись соревнования
лучших локомотивов. Первое место
Первое место
среди них занял паровоз Стефенсона
«Ракета». Его мощность составляла 3 л.с., а наибольшая скорость – 47 км/ч.
В России первый паровоз был создан крепостными мастерами-самоучками от-
цом и сыном Е.А. и М.Е. Черепановыми
в 1834 г.
Первым паровым автомобилем была
самодвижущаяся тележка французского инженера Ж. Кюньо (1770 г.).
Она предназначалась для перевозки артиллерийских орудий. Устройство бы- ло громоздким, трудноуправляемым и при первом испытании тележка налетела
на стену. Несмотря на это, все были в восторге от нового вида транспорта.
Первый автомобиль с бензиновым
двигателем внутреннего сгорания
был создан в 1886 г. Г. Даймлером .
В том же году появился трёхколёсный
автомобиль К. Бенца .
В 1892 г. свой первый автомобиль
построил Г. Форд (США). Через 11 лет
его автомобили были запущены в се-
рийное производство и распространи-
нились по всему миру.
В 1908 г. автомобили начали произ-
водить в России («Руссо-Балт», Рига).
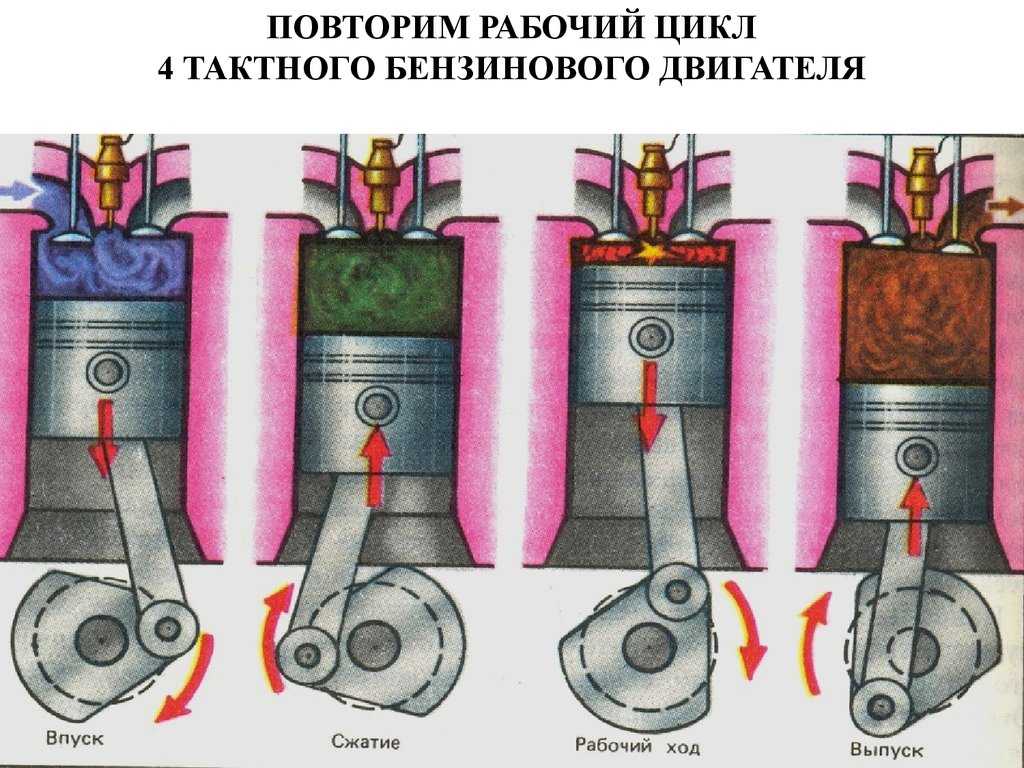
4
I такт
III такт
Впуск
Рабочий
ход
1 – впускной
клапан
2 — поршень
4 – свеча
зажигания
2
IV такт
II такт
Выпуск
Сжатие
5
3 — шатун
5 – выпускной
клапан
6 – коленчатый
вал
3
6
Вы знаете устройство…
А. паровой машины. Б. двигателя внутреннего сгорания.
В. паровой и газовой турбины. Г. реактивного двигателя.
Д. дизеля.
Укажите приведённые ниже особенности работы каждого из них.
- Истечение продуктов сгорания приводит в движение машину в сто-
рону, противоположную направлению вылетающих продуктов сго-
рания.
- В цилиндре периодически происходит воспламенение от искры
смеси бензина с воздухом.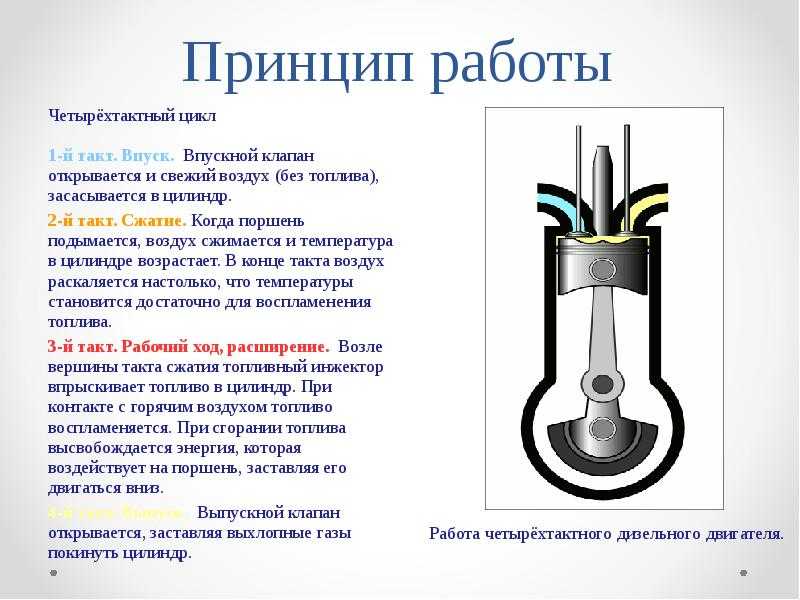 Расширяющиеся газы толкают поршень,
Расширяющиеся газы толкают поршень,
приводящий в движение коленчатый вал.
3. В котле подогревают воду. Сжатый пар давит на поршень, его дви-
жение приводит через шатун во вращение маховик.
- Нагретый пар (или газ) вращает устройство со специальными лопат-
ками без помощи поршня и шатуна.
- В цилиндр впрыскивается топливо, происходит самовоспламенение
смеси при сжатии. Расширяющиеся газы толкают поршень, приводя-
щий в движение коленчатый вал.
Ответы: А3; Б2; В4; Г1; Д5.
В природе нет процессов создания и уничтожения энергии
Энергия превращается из одного вида в другой, при этом её
количество с о х р а н я е т с я
Как сохраняется и преобразуется энергия
в приведённых ниже примерах?
- При забивании гвоздя молотком гвоздь нагревается.
- Падение воды с плотины электростанции на турбину.
- Закручивание пружины механических часов.

- Вылет пробки из пробирки при закипании в ней воды.
- Нагревание ладоней при интенсивном натирании.
- При быстром расширении жидкая углекислота становится
«сухим льдом».
Вам известно :
- Внутренняя энергия тела может превращаться в механическую.
- Механическая энергия может превращаться во внутреннюю.
- Потенциальная энергия может превращаться в кинетическую
и наоборот.
- Часть внутренней энергии одного тела может передаваться
другим телам разными способами.
- Механическая энергия одного тела может передаваться другим
телам.
Какими из приведённых ниже примеров это можно подтвердить:
А. Автомобиль приводится в движение энергией горящей смеси.
Б. Падающая вода вращает турбины электростанции.
В. При резком торможении шины автомобиля сильно нагреваются.
Г. Для закалки свёрла сначала нагревают в печи, а потом резко
охлаждают в специальном растворе.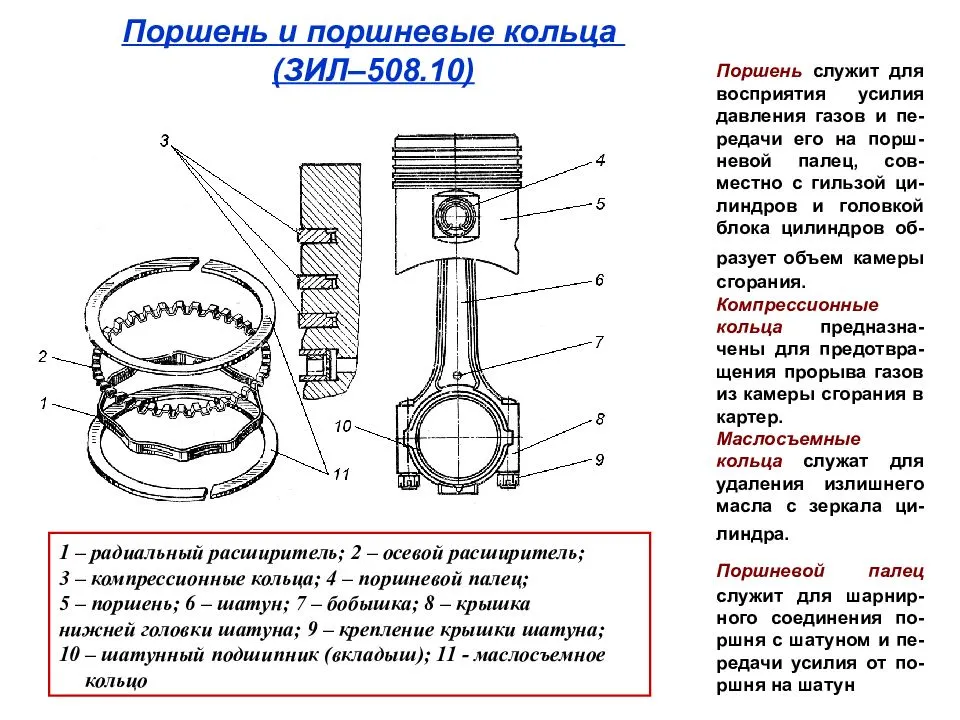
Д. Костёр для туриста – главное средство обогревания и приготов-
ления пищи.
Ответы: 1А; 2В; 3Б; 4Г, 4Д; 5Б.
Задача 1. Какое количество теплоты получит турист, выпив чашку чая массой
200 г, нагретого до t = 46 ,5 0 С? ( t тела человека = 36,5 0 С).
- Можно ли быстро согреться таким чаем, если замёрзнешь?
- Что может случиться в бане, если выпьешь очень холодной воды?
Задача 2. Какое количество энергии приобретёт турист, если к чаю съест
ещё бутерброд с маслом? (масса хлеба 100 г, масла – 20 г.; удельная
теплота сгорания хлеба — 9 260 000 Дж/кг, а масла – 32 690 000 Дж/кг).
Задача 3. На какую высоту в гору может подняться школьник
массой 40 кг за счёт энергии бутерброда, если его организм
всю эту энергию превратит в мышечную?
Дополнительно рассчитать ,
если за плечами рюкзак
массой 5 кг; 10 кг.
Ответы:
1. 8,4 кДж
2. ~ 1,6 МДж
3. h = Q/mg,
4000 м;
3556 м;
3200 м.
Куда потратится
дополнительная
энергия, если в
гору не идти, а
лечь под кустом
отдыхать?
Сухой лёд
При сгорании угля можно полу-
чить не жар, а наоборот, холод. Для этого уголь сжигают в котлах, образующийся дым очищают и улавливают в нём углекислый газ. Его охлаждают и сжимают до давления 7*10 6 Па. Получается жидкая углекислота. Её хранят в толстостенных баллонах.
При открывании крана жидкая углекислота резко расширяется и охдаждается, превращаясь в твёр-
дую углекислоту – «сухой лёд».
Под влиянием теплоты хлопья сухого льда сразу переходят в газ, минуя жидкое состояние.
Горячий лёд
Мы привыкли считать, что вода
не может быть в твёрдом состоянии
при t выше 0 0 С.
Английский физик Бриджмен по-
казал, что вода под давлением р ~
2*10 9 Па остаётся твёрдой даже при
t = 76 0 С.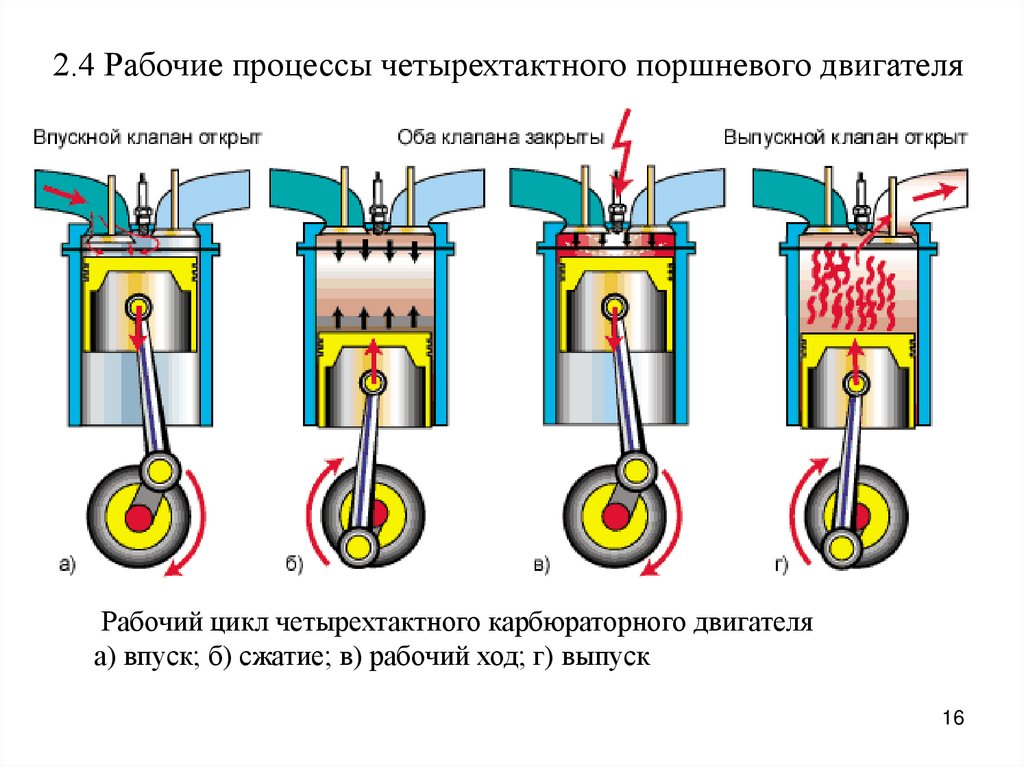 Это так называемый « го-
Это так называемый « го-
рячий лёд — 5». Взять его в руки не-
льзя, о свойствах этой разновидно-
сти льда узнали косвенным образом.
«Горячий лёд» плотнее воды (1050
кг/м 3 ), он тонет в воде.
Сегодня известно более 10 разно-
видностей льда с удивительными
качествами.
термодинамика — Почему газ нагревается при внезапном сжатии? Что происходит на молекулярном уровне?
Потому что вы выполняете работу по сжатию газа, а энергия должна куда-то деваться. Молекулы ускоряются, потому что они сталкиваются со стеной, движущейся вперед — если вы двигаете стену вперед, мяч, который отскакивает от стены, движется быстрее на удвоенную скорость стены, потому что, если вы двигаетесь вместе со стеной, он отражается с той же скоростью.
Ответы на вопросы в комментариях
- После охлаждения молекулы газа движутся с той же скоростью, что и раньше.
- Второй вопрос — это форма демона Максвелла.
 Если вы знаете, когда молекулярные столкновения происходят с такой точностью, что можете сдвинуть стену, когда молекулы не будут отскакивать, вы сможете сжать газ, не совершая никакой работы. Но чтобы сделать это, вы должны получить и сохранить информацию о том, где находятся все молекулы, а это процесс, который требует производства огромного количества энтропии. Информация о молекулах позволяет уменьшить их объем без увеличения их энергии.
Если вы знаете, когда молекулярные столкновения происходят с такой точностью, что можете сдвинуть стену, когда молекулы не будут отскакивать, вы сможете сжать газ, не совершая никакой работы. Но чтобы сделать это, вы должны получить и сохранить информацию о том, где находятся все молекулы, а это процесс, который требует производства огромного количества энтропии. Информация о молекулах позволяет уменьшить их объем без увеличения их энергии. - В любой ситуации, когда работает классическая механика, в частности, для кинетической энергии газов температура равна средней молекулярной кинетической энергии. Для всех нерелятивистских систем средняя кинетическая энергия каждого атома составляет $3T\over 2$ в больцмановских единицах (k=1). Это частный случай закона равнораспределения — каждая квадратичная степень свободы получает ${kT\over 2}$ энергии в равновесии. Из-за связи между температурой и кинетической энергией скорости молекул в двух газах при одной и той же температуре одинаковы.
 Таким образом, после того, как газ приходит в равновесие с окружающей средой, он имеет одинаковую среднюю скорость для молекул, не зависящую от его объема (это теорема разделения потенциальной энергии молекулярной кинетической энергии, которая верна даже тогда, когда материал сжижается или затвердевает, при по крайней мере при комнатной температуре, когда нормальные твердые тела подчиняются закону Дюлонга-Пти).
Таким образом, после того, как газ приходит в равновесие с окружающей средой, он имеет одинаковую среднюю скорость для молекул, не зависящую от его объема (это теорема разделения потенциальной энергии молекулярной кинетической энергии, которая верна даже тогда, когда материал сжижается или затвердевает, при по крайней мере при комнатной температуре, когда нормальные твердые тела подчиняются закону Дюлонга-Пти).
Увеличение энтропии
Есть второй способ понять увеличение температуры. Когда вы сжимаете газ, вы увеличиваете свои знания о том, где находятся молекулы, вы уменьшаете их блуждающий объем. Это означает, что если ничего не произойдет, вы уменьшите их энтропию. Значит, должно было произойти что-то, из-за чего вы меньше знаете о состоянии Вселенной. Если им не позволять сбрасывать тепло и энтропию во внешнюю вселенную, единственное, что может случиться, это то, что они будут двигаться быстрее, увеличивая вашу неуверенность в том, насколько быстро они движутся. 9{C_v}$ постоянна, то есть отношение абсолютных температур до и после есть некоторая степень отношения объемов после и до.
9{C_v}$ постоянна, то есть отношение абсолютных температур до и после есть некоторая степень отношения объемов после и до.
Должен отметить, что если вы двигаете поршень чрезвычайно быстро, со скоростью, сравнимой со скоростью звука газа, вы будете производить дополнительных тепла в дополнение к минимуму, необходимому для того, чтобы энтропия не падала. Дополнительное тепло можно понимать двумя эквивалентными способами:
- вы чрезмерно сжимаете тонкую оболочку газа возле поршня, которая на мгновение оказывает большее противодавление на поршень, чем обычно, если бы вы действовали медленно. Таким образом, вы делаете больше работы, чтобы быстро сжать газ.
- Вы узнаете больше о положении молекул по медленной релаксации давления — вы знаете, что большая часть объема газа сжимается около поршня.
Это классическое утверждение, что чем точнее вы знаете, где находятся молекулы газа, тем менее точно вы знаете, с какой скоростью они движутся (тем горячее становится газ), при постоянной информации (энтропии). Это не , а не принцип неопределенности Гейзенберга, это просто классическая термодинамика, и здесь интерпретация знаний точна, потому что энтропия — это мера классического знания, которое у вас есть о микросостоянии. Квантово-механический принцип неопределенности не является заявлением о незнании скрытых переменных, по крайней мере, не очевидным образом, поэтому он не имеет точной информационной интерпретации, как это имеет место.
Это не , а не принцип неопределенности Гейзенберга, это просто классическая термодинамика, и здесь интерпретация знаний точна, потому что энтропия — это мера классического знания, которое у вас есть о микросостоянии. Квантово-механический принцип неопределенности не является заявлением о незнании скрытых переменных, по крайней мере, не очевидным образом, поэтому он не имеет точной информационной интерпретации, как это имеет место.
термодинамика — Что происходит с температурой при сжатии идеального газа?
Задавать вопрос
спросил
Изменено
4 года назад
Просмотрено
109 тысяч раз
$\begingroup$
Меня это немного смущает. Из закона Шарля я знаю, что при постоянном давлении объем газа прямо пропорционален его абсолютной температуре, то есть
Из закона Шарля я знаю, что при постоянном давлении объем газа прямо пропорционален его абсолютной температуре, то есть
$$\frac{V_1}{T_1} = \frac{V_2}{T_2}$$
Таким образом соответственно, при сжатии температура газа будет снижаться. Но в Лекциях по физике, том 1 Фейнмана написано:
Предположим, что поршень движется внутрь, так что атомы медленно сжимаются в меньшее пространство. Что происходит, когда атом попадает в движущийся поршень? Очевидно, он набирает скорость от столкновения. […] Таким образом, атомы «горячее», когда они отрываются от поршня, чем они были до удара по нему. Следовательно, все атомы, находящиеся в сосуде, наберут скорость. Это означает, что когда мы медленно сжимаем газ, температура газа увеличивается .
(Постоянное давление?) Итак, это противоречит закону Чарльза. Почему это происходит? Кто прав? Или они оба правильные? Я смущен. Помощь.
- термодинамика
- давление
- температура
- идеальный газ
- объем
$\endgroup$
3
$\begingroup$
На ваш вопрос нет однозначного ответа, поэтому вы немного запутались. Чтобы полностью определить вашу проблему, вы должны точно указать, как и обменивается ли газ теплом с окружающей средой и как и даже сжимается ли он. При рассуждениях всегда следует ссылаться на полный газовый закон $P\,V=n\,R\,T$. Обычно рассматриваются следующие ситуации:
Чтобы полностью определить вашу проблему, вы должны точно указать, как и обменивается ли газ теплом с окружающей средой и как и даже сжимается ли он. При рассуждениях всегда следует ссылаться на полный газовый закон $P\,V=n\,R\,T$. Обычно рассматриваются следующие ситуации:
Закон Шарля: Давление на объемный газ постоянно . Никакой работы газ не совершает над своим окружением, и при этом газ не совершает никакой работы над своим окружением, поршнем или чем-то еще во время любого изменения. Температура газа равна температуре окружающей среды. При повышении/понижении температуры окружающей среды тепло передается газу/отводу и соответственно увеличивается/уменьшается его объем, так что давление газа может оставаться постоянным: $V = n\,R\,T/P$; с константой $P$ вы можете получить закон Чарльза; 9{-1}$;
Адиабатический: Теплота не передается между газом и окружающей средой, когда он сжимается / совершает работу. Опять же, вы думаете о газе в цилиндре с поршнем.
 Это прототипическая ситуация, о которой говорит Фейнман. Нажимая на поршень и изменяя объем $V\maps на V-{\rm d}V$, вы выполняете работу $-P\,{\rm d}V$. Эта энергия остается с газом, поэтому она должна проявляться как увеличение внутренней энергии, поэтому температура должна повышаться. Возьмите насос для велосипедных шин, держите палец над выпускным отверстием и сильно и быстро сожмите его другой рукой: вы обнаружите, что можете значительно нагреть воздух внутри него (осторожно прикоснитесь губами к стенке цилиндра, чтобы почувствовать поднимающийся воздух). температура). Эта ситуация описывается $P\,{\rm d}V = -n\,\tilde{R}\,{\rm d} T$. Внутренняя энергия пропорциональна температуре и количеству молекул газа и отрицательна, если объем увеличивается (в этом случае газ действует на окружающую среду). Но константа $\tilde{R}$ не совпадает с $R$: она зависит от внутренних степеней свободы. Например, двухатомные молекулы могут накапливать колебательную, а также кинетическую энергию, поскольку длина их связи колеблется (вы можете думать о них как о удерживаемых вместе упругими пружинами, накапливающими энергию).
Это прототипическая ситуация, о которой говорит Фейнман. Нажимая на поршень и изменяя объем $V\maps на V-{\rm d}V$, вы выполняете работу $-P\,{\rm d}V$. Эта энергия остается с газом, поэтому она должна проявляться как увеличение внутренней энергии, поэтому температура должна повышаться. Возьмите насос для велосипедных шин, держите палец над выпускным отверстием и сильно и быстро сожмите его другой рукой: вы обнаружите, что можете значительно нагреть воздух внутри него (осторожно прикоснитесь губами к стенке цилиндра, чтобы почувствовать поднимающийся воздух). температура). Эта ситуация описывается $P\,{\rm d}V = -n\,\tilde{R}\,{\rm d} T$. Внутренняя энергия пропорциональна температуре и количеству молекул газа и отрицательна, если объем увеличивается (в этом случае газ действует на окружающую среду). Но константа $\tilde{R}$ не совпадает с $R$: она зависит от внутренних степеней свободы. Например, двухатомные молекулы могут накапливать колебательную, а также кинетическую энергию, поскольку длина их связи колеблется (вы можете думать о них как о удерживаемых вместе упругими пружинами, накапливающими энергию). Итак, когда мы используем газовый закон для исключения $P = n\,R\,T/V$ из уравнения $P\,{\rm d}V = -n\,\tilde{R}\,{\ rm d} T$ получаем дифференциальное уравнение: 9{\gamma-1} = \text{const}$, где $\gamma=\frac{R}{\tilde{R}}+1$ называется показателем адиабаты и представляет собой отношение удельной теплоемкости газа при постоянном давлении к удельной теплоемкости при постоянном объеме.
Итак, когда мы используем газовый закон для исключения $P = n\,R\,T/V$ из уравнения $P\,{\rm d}V = -n\,\tilde{R}\,{\ rm d} T$ получаем дифференциальное уравнение: 9{\gamma-1} = \text{const}$, где $\gamma=\frac{R}{\tilde{R}}+1$ называется показателем адиабаты и представляет собой отношение удельной теплоемкости газа при постоянном давлении к удельной теплоемкости при постоянном объеме.$\endgroup$
1
$\begingroup$
Рассмотрим два устройства:
Демонстрационный прибор газового закона измеряет температуру и давление во время сжатия. Это устройство медленно опускает поршень в тонкостенном контейнере, что в основном приводит к увеличению давления при повышении температуры менее чем на один градус.
Сравните это с пожарным шприцем, в котором поршень в хорошо изолированном контейнере забивается молотком, вызывая достаточно сильное изменение температуры, чтобы зажечь хлопок.
Объяснение: Демонстрационный прибор газового закона в первую очередь представляет собой устройство изотермического сжатия (медленное и плохо изолированное), а пожарный шприц представляет собой устройство адиабатического сжатия (быстрое и хорошо изолированное).
Процесс является адиабатическим, когда система не обменивается теплом. Это может происходить двумя путями: либо вы можете изолировать систему настолько хорошо, что теплопередача будет незначительной, либо вы можете сделать процесс настолько быстрым, что не будет хватать времени для теплообмена (все механизмы теплопередачи — теплопроводность). , конвекция, диффузия и излучение — требуют много времени).
Насколько быстрым должен быть процесс, чтобы он был адиабатическим, зависит от того, насколько хорошо изолирована система. Если система очень хорошо изолирована, адиабатические процессы могут быть намного медленнее, чем при плохой изоляции системы. Даже если система вообще не изолирована, существует некоторая временная шкала, ниже которой любой процесс становится адиабатическим.
 Например, расширение взлетающего в атмосферу воздушного посылки примерно адиабатическое.
Например, расширение взлетающего в атмосферу воздушного посылки примерно адиабатическое.Напротив, изотермические процессы обязательно протекают медленно, поскольку они требуют теплопередачи для поддержания одной и той же температуры, что достигается при нахождении в тепловом равновесии с некоторым резервуаром. Процесс будет изотермическим только в том случае, если он происходит в масштабах времени, превышающих масштаб времени, необходимый для эффективной теплопередачи.
$\endgroup$
$\begingroup$
Вам нужно прочитать об эффекте Джоуля-Томпсона в Википедии. В идеальном газе не происходит изменения температуры ни при сжатии, ни при расширении. Единственными газами, которые приближаются к идеальным при комнатной температуре, являются гелий, водород и неон. На самом деле они слегка охлаждаются при сжатии и нагреваются при расширении при комнатной температуре. Это можно изменить при очень низких температурах.





 Если вы знаете, когда молекулярные столкновения происходят с такой точностью, что можете сдвинуть стену, когда молекулы не будут отскакивать, вы сможете сжать газ, не совершая никакой работы. Но чтобы сделать это, вы должны получить и сохранить информацию о том, где находятся все молекулы, а это процесс, который требует производства огромного количества энтропии. Информация о молекулах позволяет уменьшить их объем без увеличения их энергии.
Если вы знаете, когда молекулярные столкновения происходят с такой точностью, что можете сдвинуть стену, когда молекулы не будут отскакивать, вы сможете сжать газ, не совершая никакой работы. Но чтобы сделать это, вы должны получить и сохранить информацию о том, где находятся все молекулы, а это процесс, который требует производства огромного количества энтропии. Информация о молекулах позволяет уменьшить их объем без увеличения их энергии. Таким образом, после того, как газ приходит в равновесие с окружающей средой, он имеет одинаковую среднюю скорость для молекул, не зависящую от его объема (это теорема разделения потенциальной энергии молекулярной кинетической энергии, которая верна даже тогда, когда материал сжижается или затвердевает, при по крайней мере при комнатной температуре, когда нормальные твердые тела подчиняются закону Дюлонга-Пти).
Таким образом, после того, как газ приходит в равновесие с окружающей средой, он имеет одинаковую среднюю скорость для молекул, не зависящую от его объема (это теорема разделения потенциальной энергии молекулярной кинетической энергии, которая верна даже тогда, когда материал сжижается или затвердевает, при по крайней мере при комнатной температуре, когда нормальные твердые тела подчиняются закону Дюлонга-Пти).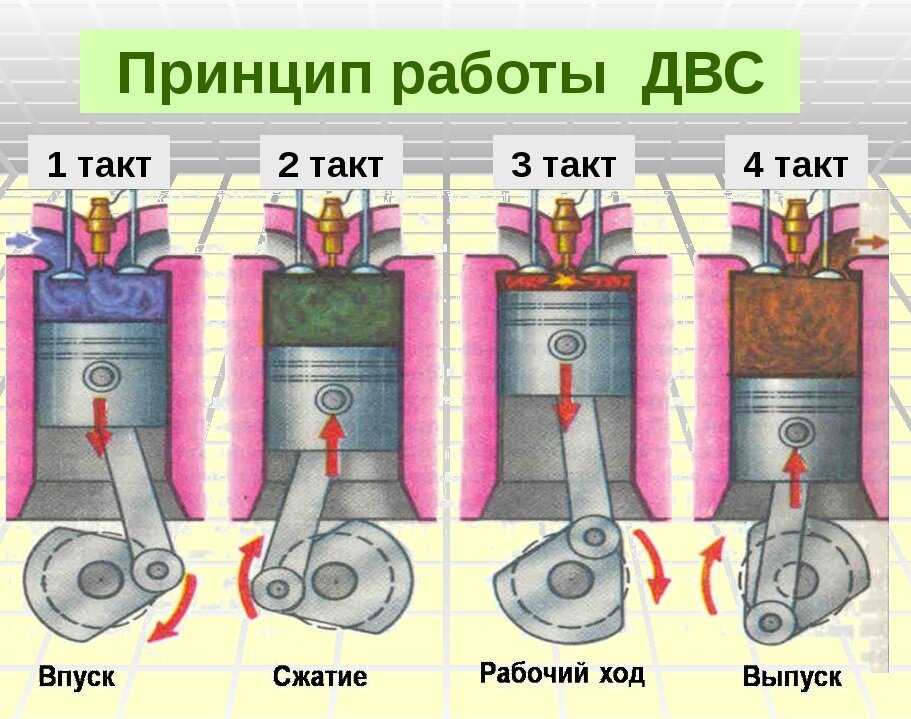 Это прототипическая ситуация, о которой говорит Фейнман. Нажимая на поршень и изменяя объем $V\maps на V-{\rm d}V$, вы выполняете работу $-P\,{\rm d}V$. Эта энергия остается с газом, поэтому она должна проявляться как увеличение внутренней энергии, поэтому температура должна повышаться. Возьмите насос для велосипедных шин, держите палец над выпускным отверстием и сильно и быстро сожмите его другой рукой: вы обнаружите, что можете значительно нагреть воздух внутри него (осторожно прикоснитесь губами к стенке цилиндра, чтобы почувствовать поднимающийся воздух). температура). Эта ситуация описывается $P\,{\rm d}V = -n\,\tilde{R}\,{\rm d} T$. Внутренняя энергия пропорциональна температуре и количеству молекул газа и отрицательна, если объем увеличивается (в этом случае газ действует на окружающую среду). Но константа $\tilde{R}$ не совпадает с $R$: она зависит от внутренних степеней свободы. Например, двухатомные молекулы могут накапливать колебательную, а также кинетическую энергию, поскольку длина их связи колеблется (вы можете думать о них как о удерживаемых вместе упругими пружинами, накапливающими энергию).
Это прототипическая ситуация, о которой говорит Фейнман. Нажимая на поршень и изменяя объем $V\maps на V-{\rm d}V$, вы выполняете работу $-P\,{\rm d}V$. Эта энергия остается с газом, поэтому она должна проявляться как увеличение внутренней энергии, поэтому температура должна повышаться. Возьмите насос для велосипедных шин, держите палец над выпускным отверстием и сильно и быстро сожмите его другой рукой: вы обнаружите, что можете значительно нагреть воздух внутри него (осторожно прикоснитесь губами к стенке цилиндра, чтобы почувствовать поднимающийся воздух). температура). Эта ситуация описывается $P\,{\rm d}V = -n\,\tilde{R}\,{\rm d} T$. Внутренняя энергия пропорциональна температуре и количеству молекул газа и отрицательна, если объем увеличивается (в этом случае газ действует на окружающую среду). Но константа $\tilde{R}$ не совпадает с $R$: она зависит от внутренних степеней свободы. Например, двухатомные молекулы могут накапливать колебательную, а также кинетическую энергию, поскольку длина их связи колеблется (вы можете думать о них как о удерживаемых вместе упругими пружинами, накапливающими энергию). Итак, когда мы используем газовый закон для исключения $P = n\,R\,T/V$ из уравнения $P\,{\rm d}V = -n\,\tilde{R}\,{\ rm d} T$ получаем дифференциальное уравнение: 9{\gamma-1} = \text{const}$, где $\gamma=\frac{R}{\tilde{R}}+1$ называется показателем адиабаты и представляет собой отношение удельной теплоемкости газа при постоянном давлении к удельной теплоемкости при постоянном объеме.
Итак, когда мы используем газовый закон для исключения $P = n\,R\,T/V$ из уравнения $P\,{\rm d}V = -n\,\tilde{R}\,{\ rm d} T$ получаем дифференциальное уравнение: 9{\gamma-1} = \text{const}$, где $\gamma=\frac{R}{\tilde{R}}+1$ называется показателем адиабаты и представляет собой отношение удельной теплоемкости газа при постоянном давлении к удельной теплоемкости при постоянном объеме.
 Например, расширение взлетающего в атмосферу воздушного посылки примерно адиабатическое.
Например, расширение взлетающего в атмосферу воздушного посылки примерно адиабатическое.