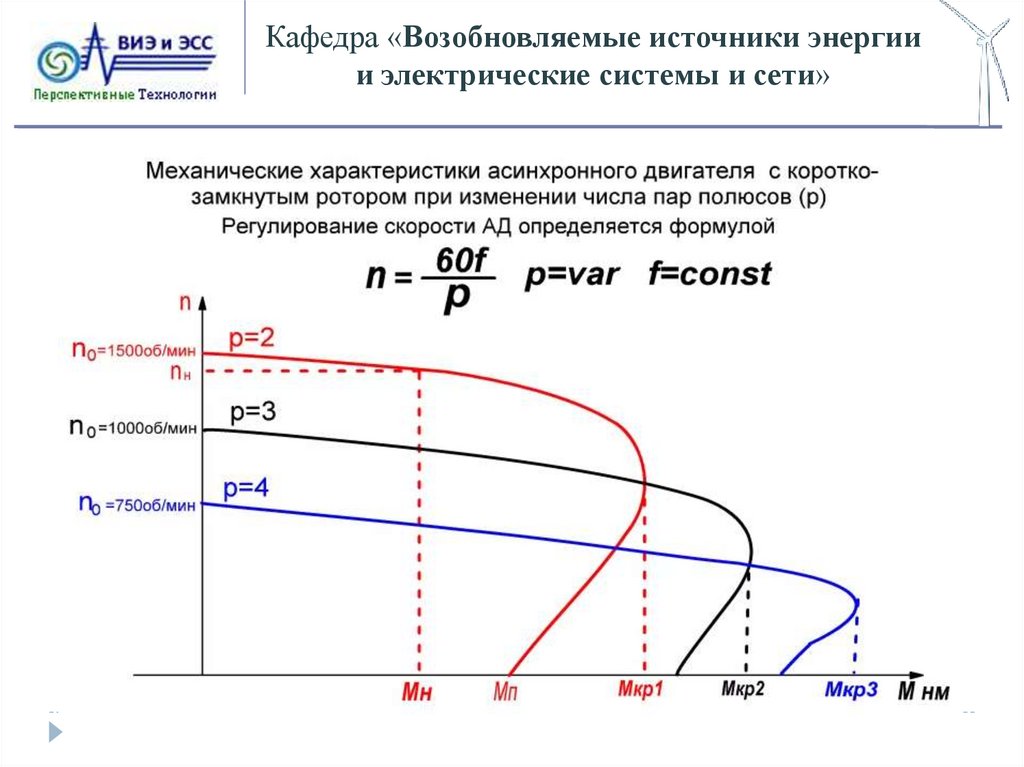
Механическая характеристика асинхронного двигателя

Механической характеристикой называется зависимость скорости асинхронного двигателя от момента на его валу.

Выражение механической характеристики можно получить из выражения потерь для асинхронного двигателя.

Δp₂ = P_эм – P₂ = M·ω₀ – M·ω = M·(ω₀ – ω) = M·ω₀·s

P_эм – электромагнитная мощность – мощность, передаваемая через воздушный зазор из статора двигателя в ротор. Она может быть электрической и механической.

P₂ – полезная мощность, может быть только механическая, и равна произведению момента на валу двигателя на его скорость.

ω₀ – ω₀·(1 – s) = ω₀ – ω₀ + ω₀·s

Δp₂ = 3·(I₂’)²·r₂’

3·(I₂’)²·r₂’ = M·ω₀·s

Упрощенная формула механической характеристики асинхронного двигателя:

M = [3·(I₂’)²·r₂’] / [ω₀·s] (1)

Подставим в формулу (1) значения тока I₂’, определенного по схеме замещения.

Выражение полной формулы механической характеристики:

M = [3·U_ф²·(r₂’/s)] / [ω₀·[(r₁ + r₂’/s)² + x_к²]] (2)

Если в формулу (2) подставить s от 0 до ±∞, то получится механическая характеристика асинхронного двигателя.

Механическая характеристика асинхронного двигателя.

Как видно из механической характеристики, она имеет два экстремума: первый в области положительных скольжений, второй в области отрицательных скольжений.

dM/ds = 0, можно определить максимальное значение момента, которое называют критическим моментом.

M_max = M_кр = [3·U_ф²] / [2·ω₀·(r₁ ± √(r₁² + x_к²))] (3)

s_кр = ±(r₂’/x_к) (4)

Как видно из формулы (3), момент критический будет иметь разные значения, в области скольжений больше нуля будет знак «+», в области скольжений меньше нуля будет знак «–».

Величина критического скольжения одинаковая и в двигательном и в генераторном режимах, только имеет разные знаки.

Если выражение (1) разделить на выражение (2), можно получить, так называемую, формулу Клосса:

M = [2·M_к·(1 + a·s_кр)] / [s/s_кр + s_кр/s + 2·a·s_кр] (5)

a – это коэффициент.

a = r₁/r₂’

Обычно у асинхронных двигателей активное сопротивление статора r₁ на порядок меньше активного сопротивления ротора r₂’, поэтому с достаточной степенью точности можно записать, что r₁=0, и тогда a=0.

M = [2·M_к] / [s/s_кр + s_кр/s] (6)

Если (5) называется полной формулой Клосса, то (6) называется упрощенной формулой Клосса.

Упрощенная формула критического момента:

M_кр = [3·U_ф²] / [2·ω₀·x_кр]

В двигательном режиме скольжение изменяется от 1 до 0.

Рассмотрим анализ формулы Клосса для двигательного режима работы. Как видно из характеристики, ее можно разбить на два участка: s > s_кр и s < s_кр.

Рассмотрим участок s > s_кр, тогда отношением s_кр/s можно пренебречь:

M = 2·M_к· s_кр / s = A/s

Как видно из получившейся формулы, связь между моментом и скольжением носит гиперболический характер. Это нелинейная не рабочая часть механической характеристики.

Рассмотрим участок s < s_кр, тогда отношением s/s_кр можно пренебречь:

M = 2·M_к·s / s_кр = B·s

На участке s < s_кр связь между моментом и скольжением линейная.

Из анализа формулы Клосса видно, что механическая характеристика имеет два участка: линейный рабочий и нелинейный нерабочий.

Для того чтобы определить характеристику двигателя в генераторном режиме, которая имеет также два участка: линейный и нелинейный, достаточно знать значение критического момента в генераторном режиме. Нелинейная область в генераторном режиме не может быть использована из-за больших значений токов и моментов.

λ = M_кр.д./M_н

Критический момент можно определить для двигательного режима по паспортным данным, в них задается отношение M_кр.д./M_н.

M_кр.г. = M_кр.д. · [r₁ + √(r₁² + x_к²)] / [r₁ – √(r₁² + x_к²)]

• Схема включения и электромеханическая характеристика асинхронного двигателя

Рабочие характеристики асинхронного двигателя.

Рабочими
характеристиками называются зависимости
эксплуатационных параметров двигателя
от полезной мощности Р₂
на его валу. К этим параметрам относятся:

— скорость вращения
или скольжение;

— вращающий момент;

— коэффициент
мощности;

— коэффициент
полезного действия;

— ток, потребляемый
двигателем из сети (ток статора).

Характерный вид
рабочих характеристик асинхронного
двигателя приведен на рис.12.

Рис.12. Рабочие
характеристики асинхронного двигателя.

Р₁
— активная мощность, потребляемая из
сети;

Q₁
– реактивная мощность, потребляемая
из сети;

Р₂
— полезная мощность на валу;

Р_2ном
— номинальная полезная мощность на
валу;

I₁
– ток статора;

I_1ном
– номинальный ток статора;

М – вращающий
момент двигателя;

М_ном
– номинальный вращающий момент двигателя;

— коэффициент
полезного действия;

– коэффициент
мощности.

— относительная
скорость вращения ротора;

— относительный
потребляемый ток;

— относительный
вращающий момент двигателя.

Скоростная
характеристика.
При идеальном холостом ходе, т.е. при
Р₂=0,
ротор вращается со скоростью магнитного
поля. По мере увеличения нагрузки
скорость вращения ротора уменьшается,
а скольжение увеличивается. Асинхронный
двигатель имеет жесткую скоростную
характеристику. Скорость двигателя
изменяется незначительно при изменении
нагрузки от холостого хода до номинального
значения.

Потребляемый
двигателем ток.
Ток холостого хода двигателя большой
и составляет 0,2-0,5 от номинального
значения. По мере увеличения нагрузки
увеличивается и ток статора.

Коэффициент
мощности.
Коэффициент мощности асинхронного
двигателя всегда меньше единицы. При
холостом ходе его значение не превышает
0,2-0,3. Из-за малого значения коэффициента
мощности нежелательна длительная работа
двигателя без нагрузки.

Коэффициент
полезного действия. При отсутствии
нагрузки коэффициент полезного действия
равен нулю. КПД повышается по мере
увеличения нагрузки и достигает максимума
при нагрузках, близких к номинальным.

Пусковые свойства
асинхронного двигателя определяются
особен­ностями его конструкции, в
частности устройством ротора.

В большинстве
случаев двигатели с короткозамкнутым
ротором пус­кают в ход прямым включением
обмоток статора к питающей сети. Этот
способ пуска прост и быстр. Для его
осуществления необходим лишь простейший
коммутирующий аппарат — выключатель.
Однако следует помнить, что при прямом
включении двигателя кратность пускового
тока составляет от 4 до 7 номинального
значения тока. Кратко­временный толчок
пускового тока безопасен для двигателя.
Однако он вызывает кратковременное
понижение напряжение в сети, что может
оказать неблагоприятное влияние на
работу других потребителей электрической
энергии. Следует иметь в виду еще один
недостаток прямого пуска асинхронного
двигателя —
это кратность пускового момента, которая
составляет 1,1…1,4.

Таким образом,
асинхронный двигатель с короткозамкнутым
ротором при пуске имеет большую силу
тока при относительно небольшом вращающем
моменте.

Для уменьшения
величины пусковых токов двигатели с
короткозамкнутым ротором пускают в ход
при пониженном напряжении пи­тающей
сети. Практическая реализация данного
способа требует не только дополнительных
элементов, например регулируемых
трехфазных трансформаторов, но и приводит
к снижению величины пускового момента.
Наибольшее распространение получил
способ, при котором двигатель, работающий
при соединении обмоток статора по схеме
треугольник, пускают в ход без нагрузки
путем переключения схемы соединения
его об­моток. При пуске обмотки статора
соединяют по схеме звезда, а при достижении
им частоты вращения, близкой к номинальной,
при помощи специального переключателя
обмотки соединяют по схеме «треугольник»
и нагружают двигатель. Пусковые свойства
двигателя с фазным ротором существенно
от­личаются от двигателя с короткозамкнутым
ротором за счет возмож­ности включения
в цепь ротора внешнего пускового
реостата.

Сопротивление
каждой фазы пускового реостата выбирается
таким, чтобы обеспечить при пуске
максимальный момент. По мере разго­на
ротора уменьшается скольжение, а вместе
с ним ЭДС и сила тока ротора, вследствие
чего падает и вращающий момент. Для
получения вращающего момента, близкого
к максимальному, сопротив­ление
пускового реостата постепенно уменьшают.
Наконец, когда ротор двигателя достигает
нормальной скорости, сопротивления
пусковых реостатов замыкаются накоротко.

ЛАБОРАТОРНАЯ
РАБОТА №1.

ИССЛЕДОВАНИЕ
АСИНХРОННОГО ЭЛЕКТРОДВИГАТЕЛЯ С
КОРОТКОЗАМКНУТЫМ РОТОРОМ.

Цель
работы:
Экспериментальное определение
механических и рабочих характеристик
асинхронного двигателя с короткозамкнутым
ротором.

Рабочие характеристики трехфазного асинхронного двигателя

1. Полная характеристика крутящий момент-скорость
3. Рабочая точка и стабильная и нестабильная область работы
2. Влияние сопротивления ротора на характеристику скорости и крутящего момента.

Рабочие характеристики трехфазного асинхронного двигателя

Эквивалентные схемы, полученные в предыдущем разделе, можно использовать для прогнозирования рабочих характеристик асинхронного двигателя. Важными рабочими характеристиками в установившемся режиме являются КПД, коэффициент мощности, ток, пусковой момент, максимальный (или пусковой) момент.

1. Полная характеристика момент-скорость

Для оценки скоростно-моментной характеристики предположим, что на машину подается синусоидальное напряжение . Учитывая, что эквивалентная схема представляет собой пофазное представление машины, ток, потребляемый схемой, определяется как

, где Vs — вектор фазного напряжения, а Isis — вектор тока. Током намагничивания пренебрегаем. Поскольку этот ток протекает через R′r/s, мощность воздушного зазора равна

Было показано, что выходная механическая мощность равна (1-s)Pg (мощность, рассеиваемая в Р’р/с). Крутящий момент получается путем деления его на скорость вала ωm. Таким образом, мы имеем

Где ωm – синхронная скорость в радианах в секунду, а s – скольжение. Кроме того, это крутящий момент, создаваемый на фазу. Следовательно, общий крутящий момент определяется как

. машина.

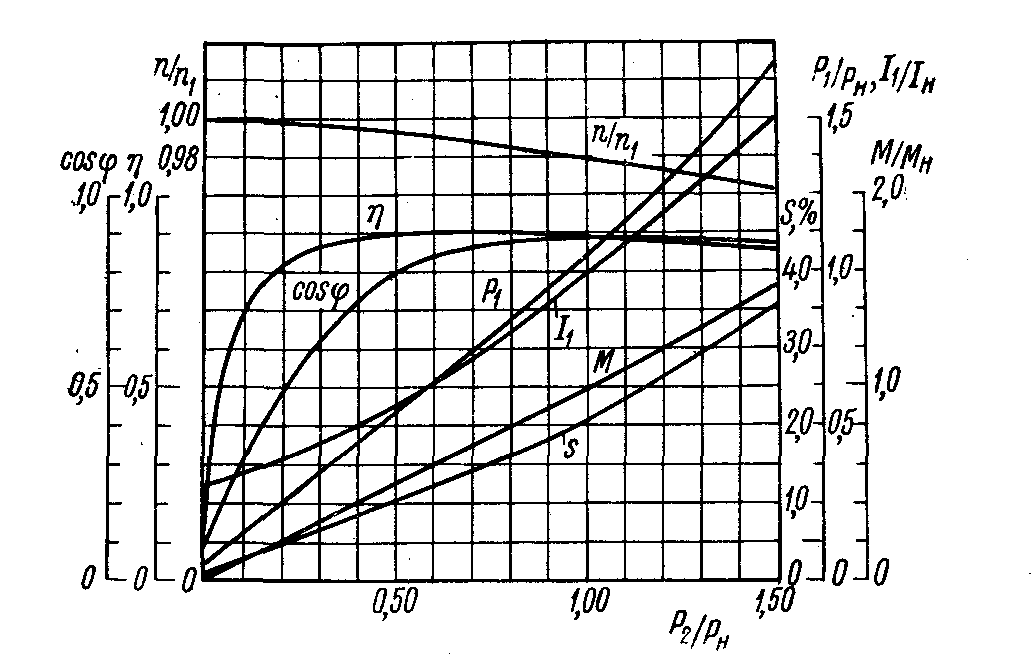
Типичная характеристика момент-скорость показана на рис. 3.18. Этот график соответствует машине мощностью 3 кВт, 4 полюса и 60 Гц. Номинальная рабочая скорость 1780 об/мин.

Кроме того, эта кривая получена путем изменения скольжения при неизменном приложенном напряжении. В сочетании с тем фактом, что это эквивалентная схема, действующая в установившемся режиме, это означает, что если эта характеристика должна быть измерена экспериментально, нам нужно посмотреть на крутящий момент для данной скорости после того, как все переходные процессы утихли. Например, нельзя попытаться получить эту кривую, запустив двигатель напрямую с полным напряжением, подаваемым на клеммы, и динамически измеряя крутящий момент и скорость по мере того, как он достигает установившейся скорости.

Что касается направления вращения потока в воздушном зазоре, ротор может приводиться в движение с более высокими скоростями с помощью первичного двигателя или также может вращаться в обратном направлении. Отношение момент-скорость для машины во всем диапазоне скоростей называется полной характеристикой скорости-момент.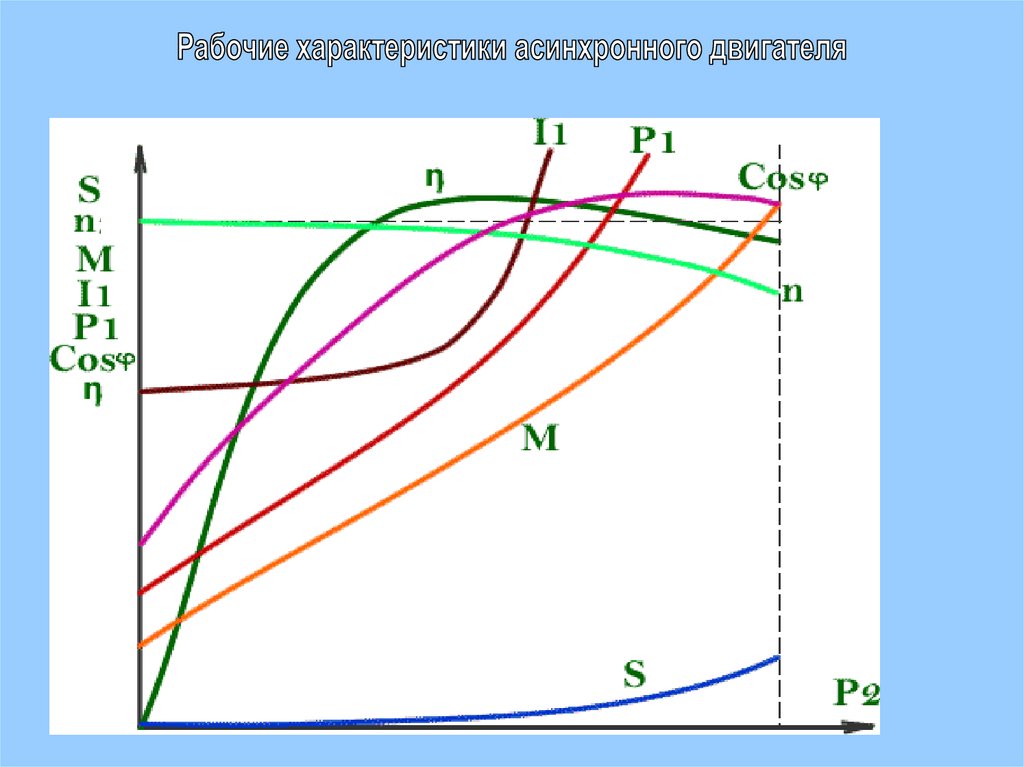 Типичная кривая показана на рис. 3.19 для четырехполюсной машины с синхронной скоростью 1500 об/мин. Обратите внимание, что отрицательные скорости соответствуют значениям скольжения больше 1, а скорости больше 1500 об/мин соответствуют отрицательному скольжению. На графике также показаны режимы работы асинхронной машины в различных регионах. Ось скольжения также показана для удобства.

2. Влияние сопротивления ротора на характеристику скорости и момента

Ограничение к положительным значениям скольжения, мы видим, что кривая имеет точку пика. Это максимальный крутящий момент, который может создать машина, и он называется крутящим моментом. Если момент нагрузки превышает это значение, машина перестает вращаться или глохнет. Это происходит при скольжении ˆs, которое для машины рис. 3.19 равно 0,38. При значениях скольжения ниже ˆs кривая круто падает до нуля при s = 0. Таким образом, крутящий момент при синхронной скорости равен нулю. При значениях скольжения выше s = ˆs кривая медленно спадает до минимального значения при s = 1. Момент при s = 1 (скорость = 0) называется пусковым моментом. Значение крутящего момента можно получить, продифференцировав выражение для крутящего момента по отношению к нулю и приравняв его к нулю, чтобы найти значение ˆs. Используя этот метод, мы можем написать

Подстановка ˆs в выражение для крутящего момента дает значение опрокидывающего момента ˆ Te,

Из выражения видно, что ˆ Te не зависит от R′r, а ˆs прямо пропорционально R′ р. Этот факт удобно использовать для изменения ˆs. Если можно изменить R′r, то можно получить целый ряд моментно-скоростных характеристик, при этом максимальный крутящий момент все время остается постоянным.

Заметим, что если R′r выбрано равным =

ˆs, становится единицей, что означает, что максимальный крутящий момент возникает при пуске. Таким образом, изменение R′r, где это возможно, может служить средством управления пусковым моментом Рис: 3. 20.

При рассмотрении области отрицательного скольжения (генераторный режим) мы отмечаем, что максимальный крутящий момент выше, чем в области положительного скольжения (двигательный режим).

3. Рабочая точка и стабильная и нестабильная область работы

Рассмотрим характеристику крутящего момента, показанную на рис. 25 для асинхронной машины, на которую также наложена нагрузочная характеристика. Нагрузка представляет собой нагрузку с постоянным крутящим моментом, т. е. крутящий момент, необходимый для работы, является фиксированным независимо от скорости.

Система, состоящая из двигателя и нагрузки, будет работать в точке, где эти две характеристики совпадают. Из приведенного выше графика мы замечаем, что таких точек две. Поэтому нам нужно выяснить, какая из них является фактической рабочей точкой. Чтобы ответить на этот вопрос, мы должны отметить, что на практике характеристики никогда не бывают фиксированными; они незначительно меняются со временем. Уместно было бы рассмотреть небольшую полосу вокруг проведенной кривой, где будут лежать фактические точки характеристики. В этом случае будем считать, что система работает в точке 1, и требуемый момент нагрузки немного увеличивается. Это показано на рис. 3.22, где изменение преувеличено для ясности. Это сместит точку срабатывания в точку 1′, в которой проскальзывание будет меньше, а развиваемый крутящий момент выше.

Разница в развиваемом крутящем моменте △Т.е. положительная величина ускорит машину. Любое превышение скорости по мере приближения к точке 1′ приведет к дальнейшему ускорению, поскольку развиваемый крутящий момент увеличивается. Аналогичные аргументы можно использовать, чтобы показать, что если по какой-то причине развиваемый крутящий момент Положительная разница в развиваемом крутящем моменте △Te ускорит машину. Любое превышение становится меньше, скорость падает, и эффект накапливается. Поэтому мы можем заключить, что 1 не является стабильной рабочей точкой.

Рассмотрим точку 2. крутящий момент ускорит машину. Такое поведение приведет к тому, что рабочая точка снова приблизится к 2. Другими словами, возмущения в точке 2 не вызовут эффекта разгона. Аналогичные аргументы могут быть приведены для случая, когда характеристика нагрузки смещается вниз. Поэтому делаем вывод, что точка 2 является стабильной рабочей точкой.

Из приведенных рассуждений можно сказать, что вся область скоростно-моментной характеристики от s = 0 до s = ˆs является неустойчивой областью, а область от s = ˆs до s = 0 является устойчивой область, край. Поэтому машина всегда будет работать между s = 0 и s = ˆs.

.

Учебный материал, Лекционные заметки, Задание, Справочник, Вики-описание, объяснение, краткая информация

Электрические машины: Трехфазный асинхронный двигатель: Рабочие характеристики трехфазного асинхронного двигателя |

Производительность трехфазного асинхронного двигателя

Хотите создать сайт? Найдите бесплатные темы и плагины WordPress.

Используя эквивалентную схему трехфазного асинхронного двигателя и некоторую дополнительную информацию о механических потерях и потерях в сердечнике, можно рассчитать производительность трехфазного асинхронного двигателя от холостого хода до полной нагрузки. На рис. 1 показан набор общих кривых эффективности, тока, коэффициента мощности и скольжения для асинхронного двигателя. Рассмотрим каждую из этих кривых.

РИСУНОК 1     Характеристики асинхронного двигателя.

Эффективность

Эффективность равна выходной мощности, деленной на входную мощность. Очевидно, что если двигатель не загружен, выходная мощность и эффективность равны нулю.

На холостом ходу машина потребляет энергию из системы, потому что в машине все еще есть потери (вращательные, сердечник и немного меди). Когда на вал двигателя возлагается нагрузка, из системы потребляется больше энергии, и эффективность должна повышаться, потому что выходная мощность теперь больше нуля. Эффективность будет продолжать расти до тех пор, пока выходная мощность будет увеличиваться быстрее, чем входная мощность.

В конце концов, однако, достигается точка, в которой потери начинают расти быстрее, а эффективность падает. Важно отметить, что КПД довольно ровный от 50% до 100% номинальной нагрузки и достигает максимума где-то от 70% до 80%, поэтому указание немного увеличенного двигателя не приводит к слишком большому снижению эффективности.

Коэффициент мощности

Коэффициент мощности – это фактическая мощность машины, деленная на полную мощность. Рассматривая эквивалентную схему, представленную на рис. 2, отметим, что для малых нагрузок член R _r /с становится очень большим из-за малого значения скольжения. В частности, цепь ротора фактически представляет собой разомкнутую цепь на холостом ходу, а эквивалентная цепь сводится к сопротивлению статора последовательно с реактивным сопротивлением рассеяния статора и реактивным сопротивлением намагничивания.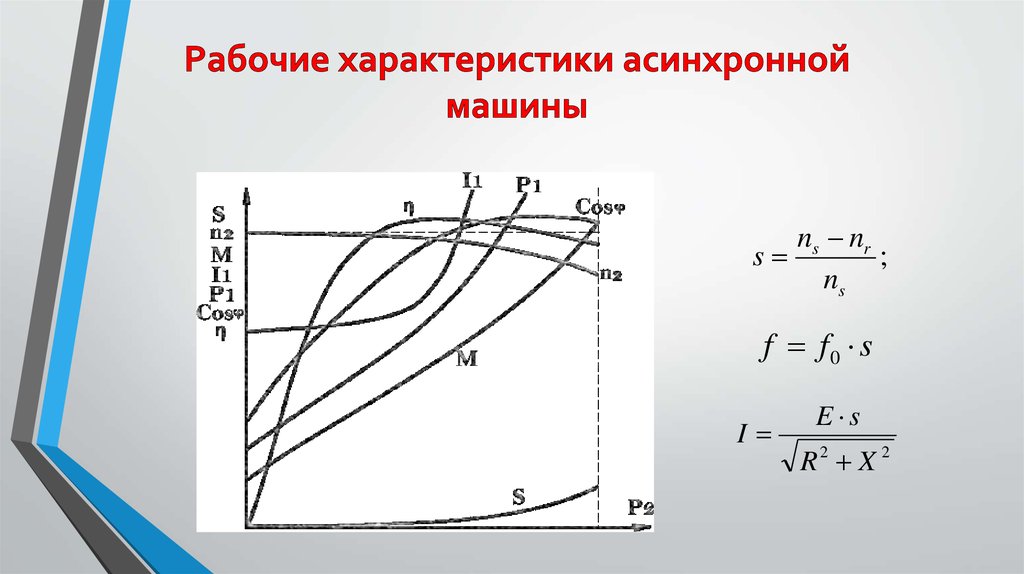 Реактивное сопротивление намагничивания намного больше, чем сопротивление статора, поэтому коэффициент мощности очень низкий. Однако оно не равно нулю, потому что мощность поступает в двигатель, чтобы компенсировать потери холостого хода.

По мере увеличения нагрузки активная мощность в машине должна увеличиваться, в то время как реактивная мощность не изменяется слишком сильно. Реактивная мощность поддерживает магнитное поле и практически не зависит от нагрузки. Следовательно, мы ожидаем, что коэффициент мощности будет увеличиваться по мере увеличения нагрузки на двигатель. Работа двигателя при нагрузке ниже номинальной приводит к более низкому коэффициенту мощности, что может усугубить проблемы с коэффициентом мощности на предприятии.

РИСУНОК 2     Эквивалентная схема пофазного асинхронного двигателя.

Ток

Ток необходим для обеспечения реактивной мощности магнитного поля, а также активной мощности для работы нагрузки. Ток холостого хода может составлять значительную часть тока полной нагрузки, поскольку воздушный зазор двигателя относительно велик. По мере увеличения нагрузки составляющая тока, совпадающая по фазе с напряжением, увеличивается, в результате чего величина тока увеличивается, а угол коэффициента мощности уменьшается.

На рис. 3 показана векторная диаграмма с фазным напряжением в качестве опорного вектора. Ток I _nl представляет линейный ток без нагрузки. Поскольку реальная мощность не передается, коэффициент мощности очень низкий. Ток можно разделить на две составляющие: одну совпадающую по фазе с напряжением, а другую отстающую от напряжения на 90 ^o .

РИСУНОК 3     Векторы тока и напряжения для асинхронного двигателя.

Составляющая, совпадающая по фазе с напряжением, производит активную мощность, которая в данном случае представляет собой просто потери двигателя. Компонент, который отстает на 90° — это ток намагничивания, который создает магнитное поле и, таким образом, связан с реактивной мощностью.

Когда двигатель работает с полной нагрузкой, ток намагничивания остается примерно одинаковым, поскольку для создания вращающегося магнитного поля требуется только определенный ток.

Составляющая тока, совпадающая по фазе с напряжением, значительно увеличивается, однако для обеспечения фактической мощности, необходимой нагрузке. Результирующий линейный ток при полной нагрузке показан как I _fl .

Обратите внимание, что активная мощность изменяется пропорционально компоненту тока, совпадающему по фазе с напряжением, а полная мощность изменяется пропорционально линейному току. Поскольку коэффициент мощности увеличивается с нагрузкой, величина линейного тока не увеличивается так быстро, как реальная мощность в машине.

Скольжение

Скольжение — это процентная разница между синхронной скоростью двигателя и скоростью ротора. Когда к двигателю добавляется нагрузка, вал немного замедляется, а скольжение увеличивается. 9{2}}} & {} & \left( a \right)  \\\end{matrix}\]

Это выражение несколько громоздко, и с ним трудно работать.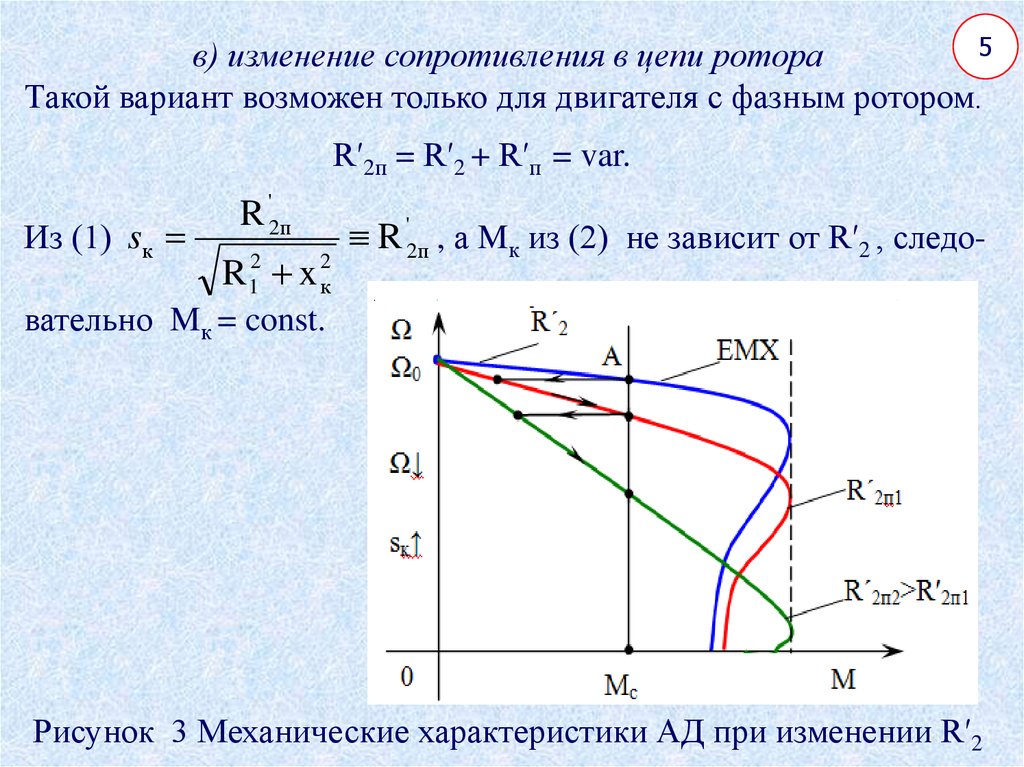 {2}}s}{f} & {} & \left( 4 \right)  \\\end{matrix}\]

Уравнение 4 говорит нам, что развиваемый крутящий момент пропорционален скольжению и квадрату напряжения и обратно пропорционален частоте. Это уравнение справедливо только для малых значений проскальзывания, менее 3 % или около того.

Мы можем использовать уравнение 4, чтобы посмотреть на характеристики двигателя, когда он подвергается отклонениям от своих нормальных условий, как показано в следующем примере.

Пример характеристик асинхронного двигателя

Двигатель мощностью 50 л.с., 60 Гц, 460 В, четыре полюса. При работе в номинальных условиях:

$\begin{array}{l}\eta  = 89,6\% \\{F_p} = 79,5\% \\s = 3\%\end{array}$

Если двигатель работает на частоте 55 Гц, 430 В, а n _r =1605 RMP, какая примерно развиваемая л.с.?

Решение

Мы знаем, что это четырехполюсная машина, поэтому

\[4\text{ }pole\text{ }at\text{ }60\text{ }Hz\to {{n}_{ s}}=\frac{120\times f}{P}=1800\text{ }RPM\]

Решение для скорости ротора,

\[{{n}_{r}}={{n} _{с}}(1-с)=1800(1-0,03)=1746 об/мин\]

При номинальной нагрузке и скорости номинальный крутящий момент определяется как

\[{{T}_{rated}}=\frac{HP\times 5252}{{{n}_{r}}}=150,4\ text{ }lb.