Маз схождение: Передняя ось и рулевые тяги МАЗ — обслуживание и ремонт

Передняя ось и рулевые тяги МАЗ — обслуживание и ремонт

Содержание

Техническое обслуживание передней оси и рулевых тяг МАЗ

При осмотрах передней оси обращать внимание на степень затяжки конусного соединения шкворня и на состояние упорного подшипника. При износе упорного подшипника увеличивается зазор между верхним ушком поворотной цапфы и балкой, который не должен превышать 0,4 мм. При необходимости следует ставить металлические прокладки.

Особое внимание обращать на величину износа шкворня и втулок поворотной цапфы. Изношенные бронзовые втулки цапфы заменять новыми.

Регулярно проверять крепление пальцев шаровых сочленений продольной и поперечной тяг, крепление рычагов рулевой трапеции к поворотным цапфам. При осмотре деталей шаровых сочленений проверить, нет ли трещин на пружинах и сухарях. Пальцы с вмятинами, сухари и пружины с трещинами обязательно заменять новыми.

Регулярно проверять правильность углов установки передних колес, так как вследствие износа и деформации деталей углы во время эксплуатации могут изменяться.

Угол схождения колес в горизонтальной плоскости устанавливают регулировкой длины поперечной рулевой тяги, на концах которой имеется правая и левая резьба.

При установке передних колес для движения по прямой расстояние Б между торцами тормозных барабанов в горизонтальной плоскости сзади должно быть больше расстояния А спереди на 3—5 мм (см. рис. 86).

Схождение колес рекомендуется регулировать в следующем порядке:

  • установить колеса в положение, соответствующее движению по прямой;
  • ослабить затяжку болтов обоих наконечников поперечной рулевой тяги;
  • вращением тяги (ввертывая ее в наконечник при большом схождении и вывертывая при недостаточном) изменить ее длину так, чтобы величина схождения колес стала нормальной;
  • затянуть стяжные болты обоих наконечников.

После регулировки схождения колес проверить углы поворота колес и отрегулировать положение обоих болтов (упорных), ограничивающих поворот колеса. Угол поворота левого колеса при повороте влево, а правого при повороте вправо должен быть 38°.

При регулировке шарового сочленения продольной рулевой тяги пробку 6 (см. рис. 84) завернуть до отказа (до выбора зазора между сухарем 4 и ограничителем 2 пружины), после чего отвернуть на 1/8 — 1/4 оборота (до первого положения, при котором возможна шплинтовка) и зашплинтовать.

При регулировке шаровых сочленений поперечной рулевой тяги завернуть до отказа опорную пяту (см. рис. 85) до выбора зазора между сухарем 7 и опорной пятой 9, после чего отвернуть на 1/2 — 1 оборот (до первого положения, при котором возможно стопорение) и застопорить.

Проверять и регулировать углы поворота колес следует, как правило, после регулировки схождения колес. При регулировке углов поворота колес изменяют положение упорных болтов, ввернутых в выступы балки передней оси.

После регулировки углов проверить, не задевают ли шины при осадке рессор и поворотах колес в крайнее положение за детали.

Установочные параметры передних колес МАЗ

Устойчивость движения автомобиля, легкость управления им, более равномерный износ шин передних колес зависят от углов установки колес (рис. 86).

Продольный угол наклона шкворня 2°30′ обеспечивается за счет того, что нижний конец шворня вынесен вперед. Его положение определяется креплением рессоры в кронштейнах рамы.

Продольный угол наклона шкворня обеспечивает хорошую устойчивость автомобиля вследствие возникновения стабилизирующего момента, что особенно заметно при повороте, а также облегчает управление автомобилем. При изменении этого угла во время эксплуатации возможно виляние колес, ухудшение управляемости автомобиля (автомобиль «плохо держит дорогу») и затруднение выхода из поворота на прямолинейный участок. Указанные явления могут возникнуть при значительной неравномерности в осадке и прогибе передних рессор, скручивании балки передней оси или износе шкворневого соединения. В этом случае требуется восстановить продольный угол шкворня, заменив или исправив изношенные детали.

Поперечный угол наклона шкворня, равный 8°, обеспечивается наклоном оси отверстия под шкворень в балке передней оси.

Стабилизирующий эффект от поперечного угла наклона шкворня проявляется в способности колес сохранять нейтральное положение при движении автомобиля.

Поперечный угол наклона шкворня может быть нарушен при прогибе балки передней оси. В этом случае следует устранить прогиб балки.

Угол развала колеса 1° определяется заданным при обработке положением оси поворотной цапфы по отношению к отверстиям под шкворень в ушках.

При наличии угла развала колес создается горизонтальная составляющая вертикальной нагрузки, направленная к оси автомобиля. Эта сила всегда прижимает ступицу колеса к внутреннему роликовому подшипнику. В случае отсутствия угла развала колес и наличия некоторого осевого зазора в подшипниках ступиц возможно осевое перемещение ступиц на подшипниках, в результате чего ухудшается устойчивость автомобиля при движении и возрастает износ шин.

На угле развала колес отражается износ шкворневого соединения, а также чрезмерные зазоры в подшипниках колес.

Для проверки развала колес измерить расстояния В и Г соответственно верхней и нижней частей ободьев колес от какой-либо вертикальной плоскости или отвеса. Разность этих расстояний при правильном угле развала должна быть 7—11 мм.

Рис. 86. Установочные параметры колес МАЗ

Схождение колес в горизонтальной плоскости необходимо для того, чтобы передние колеса катились строго в продольной плоскости, так как при наличии угла развала колеса автомобиля стремятся катиться по расходящимся дугам в сторону от автомобиля. Схождение колес зависит от угла развала, с увеличением которого возрастает схождение. Неправильное (увеличенное) схождение колес может привести к интенсивному износу шин.

Устройство передней оси и рулевых тяг МАЗ

Передняя ось автомобиля воспринимает нагрузку вертикальную, а также силы и момент, возникающие при торможении и повороте автомобиля. Колеса передней оси являются управляемыми.

Основной несущей деталью, через которую с помощью рессор передаются указанные силы на раму автомобиля, является балка 21 (рис. 83) передней оси.

Она изготовляется методом горячей штамповки из стали 40 и имеет двутавровое сечение с площадками на верхней полке для крепления рессор.

По концам балка имеет утолщения цилиндрической формы, в которых выполнены конические отверстия с вершиной конуса, обращенной вверх. Балка передней оси соединена с поворотными цапфами 7 с помощью шкворней 27. Концы шкворня представляют собой цилиндрические шейки разных диаметров, соединенные конической частью. Верхняя шейка шкворня на конце имеет резьбу. Шейка шкворня большего диаметра соединена с нижним ушком поворотной цапфы, а меньшего диаметра — с верхним ушком. Средней конической частью шкворень входит в коническое отверстие балки передней оси, обеспечивая ее связь с поворотной цапфой.

С целью повышения износостойкости поверхность шкворня подвергается закалке т. в. ч. до твердости HRC 56—63. Нижняя цилиндрическая шейка шкворня опирается на бронзовую втулку, запрессованную в ушко поворотной цапфы. Так как ушки поворотной цапфы обработаны в линию и имеют одинаковый диаметр, а диаметр верхнего конца шкворня меньше диаметра нижнего, то сверху на шкворень устанавливается стальная втулка, которая компенсирует разность в указанных диаметрах и одновременно является распорной втулкой. Втулка вместе со шкворнем поворачивается в бронзовой втулке 26 верхнего ушка поворотной цапфы.

Торцы распорной и бронзовой втулок, помещенных в верхнем ушке поворотной цапфы, защищены уплотнительным резиновым кольцом, закрытым металлической обоймой. На резьбовой конец шкворня навернута гайка, с помощью которой устраняют зазор в коническом соединении шкворня с балкой передней оси. Гайка стопорится замковой шайбой.

Между нижним ушком поворотной цапфы и балкой расположен упорный шариковый подшипник 28. Балка опирается на этот подшипник через опорную шайбу 31, прилегающую к нему плоской стороной, а к балке — сферической поверхностью, что обеспечивает правильную самоустановку подшипника. При таком соединении балки передней оси с поворотной цапфой горизонтальные нагрузки воспринимаются бронзовыми втулками, запрессованными в ушки поворотной цапфы, а вертикальные нагрузки — упорным шариковым подшипником.

Рис. 83. Передняя ось и ступица переднего колеса МАЗ:

1 — болт крепления колеса; 2 и 12 — гайки; 3 — гайка крепления колеса; 4 — внутренний подшипник; 5 — наружный подшипник; 6 — крышка ступицы; 7 — поворотная цапфа; 5 — ступица; 9 — контргайка; 10 — замковая шайба; 11 — замковое кольцо; 13 — обод колеса; 14 — замочное кольцо; 15 — бортовое кольцо; 16 — колесо; 17 — самоподжимный сальник; 18 — продольная рулевая тяга; 19 — рычаг поперечной рулевой тяги; 20 — поперечная рулевая тяга; 21 — балка передней оси; 22 — рычаг продольной рулевой тяги; 23 — суппорт колесного тормоза; 24 — тормозная накладка; 25 — тормозной барабан; 26 — бронзовая втулка; 27 — шкворень; 28 — шариковый подшипник шкворня; 29 — распорная втулка; 30 — регулировочные шайбы; 31 — опорная шайба

Для свободного вращения при ограниченном вертикальном перемещении поворотной цапфы и связанного с ним колеса на шкворне между верхним ушком поворотной цапфы и балкой передней оси имеется зазор, который должен быть в пределах 0,1—0,4 мм. Для обеспечения заданного зазора между верхним ушком поворотной цапфы и балкой установлены металлические регулировочные шайбы 30. Поворотные цапфы соединены с рулевой трапецией.

Ушки поворотной цапфы переходят в цилиндрические утолщения, в которых сделаны конические отверстия. На левой цапфе утолщения имеются у верхнего и нижнего ушков, а на правой — только у. нижнего. В коническое отверстие верхнего ушка левой поворотной цапфы вставлен конический хвостовик поворотного рычага 22 продольной рулевой тяги, а в конические отверстия нижних ушков обеих поворотных цапф — конический хвостовик рычага 19 поперечной рулевой тяги.

Рычаги соединены с ушками поворотной цапфы на шпонках и затянуты по конусу гайками, а с тягами рулевой трапеции — с помощью шаровых сочленений. Для этого на концах рычагов имеются площадки, в которых сделаны конические отверстия под хвостовики сферических пальцев, соединяющих рычаги с тягами. Сферические пальцы коническими хвостовиками плотно входят в конические отверстия рычагов и надежно по конусу притянуты к ним корончатыми гайками, которые зашплинтованы.

Задний конец продольной рулевой тяги соединен с поворотным рычагом, а передний конец ее с помощью шарового пальца — с корпусом шарнира гидроусилителя рулевого механизма.

Продольная рулевая тяга (рис. 84) изготовлена из трубы 1, в передний торец которой вварен наконечник 10, для сферического пальца 11, соединяющего тягу с гидроусилителем рулевого механизма. С другого конца труба на небольшой длине обжимается и образует гнездо для вкладыша-заглушки. Сферическая часть пальца 8, входящего в продольную тягу, охватывается двумя сухарями 4, наружная поверхность которых несколько меньше внутренней поверхности конца трубы, а внутренние поверхности сухарей, так же как и пальца, сферические. Для повышения износостойкости соединения сферические поверхности сухаря и пальца обработаны до высокой чистоты и, кроме того, палец закален т. в. ч., а сухарь подвергнут цементации и объемной закалке.

Сферическая головка пальца поджимается к сухарям пружиной 3, натяжение которой регулируется пробкой 6, ввернутой в конец трубы. Благодаря пружине автоматически устраняется зазор, возникающий при износе деталей, а также смягчается ударная нагрузка на детали рулевого механизма.

Чтобы обеспечить качание шарового пальца, с внутренней стороны в сухарях сделаны выемки. Шаровые пальцы с сухарями смазываются через масленку и уплотняются защитным резиновым уплотнителем 7.

Поперечная рулевая тяга (рис. 85), так же как и продольная, трубчатая. В отличие от продольной тяги длину поперечной тяги можно регулировать, что необходимо для регулировки схождения колес. Поэтому на концы трубы 10 поперечной тяги навернуты стальные наконечники 1 и 13, отличающиеся между собой только направлением резьбы.

Шаровая головка пальца 3 поперечной тяги охватывается сухарями 2 и 7, поджимаемыми пружиной 8, установленной в стакане большого сухаря 7. Натяжение пружины регулируется гайкой до сборки наконечника с трубой поперечной тяги.

Рис. 84. Продольная рулевая тяга МАЗ:

1 — труба; 2 — ограничитель пружины; 3 — пружина; 4 — сухарь пальца; 5 — хомут уплотнителя; 6 — пробка; 7 — уплотнитель; 8 — шаровой палец; 9 — масленка; 10 — наконечник; 11 — палец

Рис. 85. Поперечная рулевая тяга МАЗ:

1 — левый наконечник тяги; 2 — малый сухарь пальца; 3 — шаровой палец; 4 — сальник пальца; 5 — обойма сальника; 6 — пружина сальника; 7 — большой сухарь пальца; 8 — пружина сухаря; 9 — опорная пята; 10 — труба; 11 — стопорный болт; 12 — стяжные болты; 13 — правый наконечник тяги

Самоотвертыванию гайки препятствует болт 11, который вставляется в прорезь гайки при совпадении прорези с отверстием в наконечнике. После регулировки длины поперечной тяги навернутые на трубу наконечники фиксируются в нужном положении двумя стяжными болтами 12 на каждом наконечнике. Для этого на наконечнике сделаны разрезные бобышки, стягиваемые стяжными болтами.

Шаровые пальцы смазываются через масленки, ввернутые в головки наконечников тяги.

Уплотнение шаровых сочленений обеспечивается резиновым сальником 4, поджимаемым к наконечнику конической пружиной 6.

Поворотные цапфы имеют развитые фланцы прямоугольной формы, к которым крепятся суппорты 23 (см. рис. 83) колесных тормозов, являющиеся одновременно тормозными щитами:

Поворотная цапфа 7 имеет плавный переход к фланцу, обрабатываемый до высокой чистоты и подвергаемый поверхностной закалке т. в. ч. для повышения усталостной прочности детали. На большой цилиндрической шейке цапфы установлен внутренний конический роликовый подшипник ступицы переднего колеса, на меньшую шейку — наружный роликовый подшипник. Эти подшипники воспринимают как радиальную, так и осевую нагрузку, действующую на колесо.

На конических роликовых подшипниках поворотной цапфы вращается ступица 8 переднего колеса. Подшипники закреплены на цапфе гайкой 12 с замковым кольцом 11 и контргайкой 9 с шайбой 10.

Уплотнение подшипников с внутренней стороны обеспечивается самоподжимным сальником 17, размещенным в крышке, привернутой к внутреннему торцу ступицы. Для уплотнения подшипников с наружной стороны служит крышка 6, привернутая через прокладку к внешнему торцу ступицы колеса.

Ступицы колес, отлитые из ковкого чугуна, с наружной стороны имеют шесть фигурных спиц, к которым при помощи прижимов закреплен обод 13 колеса.

К внутреннему фланцу ступицы прикреплен тормозной барабан 25.

 

Устройство передней оси и уход за ней

Устройство передней оси и ступицы переднего колеса:

Рисунок 1 — Передняя ось и ступица переднего колеса

Рисунок 2 — Продольная рулевая тяга

Уход за рулевыми тягами и передней осью

Для установки угла схождения управляемых колес, необходимо отрегулировать длину поперечной рулевой тяги (концы с резьбой). 

Если обнаружили люфт в шарнирах рулевой тяги и подшипниках, то о проверке схождения, до устранения люфтов, можете забыть.

Схождение = разность расстояний между торцами левого и правого барабана спереди и сзади при измерении на уровне геометрической оси колес.

Чтобы добраться к торцам тормозных барабанов, при замере необходимо снять резиновые заглушки на щитках тормозов.

Если Вы запланировали схождение колес, отрегулируйте в следующем порядке:

  1. положение колес должно соответствовать движению по прямой;
  2. гайку стяжных болтов обоих наконечников поперечной тяги нужно ослабить;
  3. ввертывайте или вывертывайте наконечники установите схождение в задаваемых пределах

*Важно: вывертывание наконечников на один оборот увеличивает разность расстояний ориентировочно на 5мм, а ввертывание, соответственно, уменьшает на те же 5мм. Когда отрегулируете схождение, не забудьте затянуть стяжные болты наконечников и проверить  (отрегулировать) углы поворота колес с ограничением их упорными болтами.

Чтобы определить зазор в шарнирах рулевых тяг, осмотрите соединения при проворачивании рулевого колеса право и влево. 

*У Вас продольная тяга? Делайте операцию при неработающем двигателе. С поперечной — двигатель стоит завести.

Заверните регулировочную пробку №5(рисунок №2) до упора моментом 118-157 Нм, когда регулируете шаровое соединение продольной рулевой тяги, а после отверните на 1/8 — 1/12 оборота.

Что делать после регулировки?

— Верните крышку №6  (рисунок №2) на место и поверните её на 120 градусов относительно первоначального положения.
— Обожмите край в паз наконечника №3 (рисунок №2) чтобы застопорить крышку №5 (рисунок №2).

*Каждый раз, когда регулируете шаровое соединение, проворачивайте крышку №6 (рисунок №2) на 120 градусов, выпрямив деформированный участок.

Регулировка подшипников ступиц передних колес

Рисунок 2 — Передняя ось и ступица переднего колеса 

  1. Снимите крышечку №8 (рисунок №3) и ослабьте гайку №9 (рисунок №3) подшипника
  2. Отверните болт №10 (рисунок №3)
  3. Проверьте ступицу на легкость вращения. Если ступица вращается туго — выясняйте причину, возможно Вам понадобится снимать ступицу.
  4. Установите шайбу №12 (рисунок №3). Следите чтобы лыска на шайбе совпадала с лыской на поворотном кулаке №11 (рисунок №3)
  5. Затяните гайку №9 (рисунок №3), проворачивая ступицу, до тугого вращеия моментом 240Нм. После этого отверните гайку на 90 градусов
  6. Проверьте, насколько легко вращается ступица, есть ли осевой люфт (осевой зазор в подшипниках 0,02- 0,08 мм). Если что-то не так, повторите регулировку
  7. застопорите гайку №9 (рисунок №3) болтом №10 (рисунок №3) с пружинной шайбой. Заверните его моментом 50-70 Нм
  8. Внутреннюю полость крышки №8 (рисунок №3) необходимо заполнить специальной смазкой (исключение — пространство под гайку).  
  9. Установите крышку с прокладкой на ступицу.

* (кстати, если у Вас течет ступица — рекомендую прочитать нашу статью с подробным описанием проблемы и её устранением.  Жмите вот сюда

А Если Вы ищите запчасти для передней оси по выгодным ценам, компания ООО «МАЗИК» является официальным дилером МАЗ более 10 лет и предоставляет экспертную консультацию, гарантию качества, мгновенную комплектацию и доставку запчастей + у нас есть региональные склады

« Преимущества автомобилей МАЗ

Таблица примененяемости сцеплений на автобусах отечественного производства »

Сходимость гамильтонового градиентного спуска и оптимизация на основе консенсуса

Джейкоб Абернети, Кевин А. Лай, Андре Вибисоно

Материалы 32-й Международной конференции по теории алгоритмического обучения , PMLR 132:3-47, 2021.

Аннотация

В то время как классическая работа по выпукло-вогнутой минимаксной оптимизации опирается на результаты сходимости в среднем итерации, появление невыпуклых приложений, таких как обучение генеративно-состязательных сетей, привело к возрождению интереса к гарантиям сходимости на последней итерации. Доказательство сходимости на последней итерации является сложной задачей, потому что многие естественные алгоритмы, такие как одновременный градиентный спуск/подъем, доказуемо расходятся или зацикливаются даже в простых выпукло-вогнутых минимаксных настройках, и относительно немного работ доказывают глобальные скорости сходимости на последней итерации за пределами билинейная и выпукло-сильно вогнутая установки. В этой работе мы показываем, что алгоритм гамильтонова градиентного спуска (HGD) достигает линейной сходимости в различных более общих условиях, включая выпукло-вогнутые задачи, которые удовлетворяют условию «достаточно билинейности». Мы также доказываем скорость сходимости для стохастического HGD ​​и для некоторых параметров алгоритма оптимизации консенсуса Mescheder et al. (2017).

Процитировать эту статью

БибТекс


@InProceedings{pmlr-v132-abernethy21a,
title = {Коэффициенты сходимости на последней итерации для оптимизации минимума и максимума: сходимость гамильтонового градиентного спуска и оптимизация на основе консенсуса},
автор = {Абернети, Джейкоб и Лай, Кевин А. и Вибисоно, Андре},
booktitle = {Материалы 32-й Международной конференции по теории алгоритмического обучения},
страницы = {3--47},
год = {2021},
редактор = {Фельдман, Виталий и Лигетт, Катрина и Сабато, Сиван},
объем = {132},
серия = {Материалы исследования машинного обучения},
месяц = ​​{16--19март},
издатель = {PMLR},
pdf = {http://proceedings.mlr.press/v132/abernethy21a/abernethy21a.pdf},
URL = {https://proceedings.mlr.press/v132/abernethy21a.html},
abstract = {В то время как классическая работа по выпукло-вогнутой минимаксной оптимизации опирается на результаты сходимости в среднем итерации, появление невыпуклых приложений, таких как обучение генеративно-состязательных сетей, привело к возобновлению интереса к гарантиям сходимости на последней итерации. Доказательство сходимости на последней итерации является сложной задачей, потому что многие естественные алгоритмы, такие как одновременный градиентный спуск/подъем, доказуемо расходятся или зацикливаются даже в простых выпукло-вогнутых минимаксных настройках, и относительно немного работ доказывают глобальные скорости сходимости на последней итерации за пределами билинейная и выпукло-сильно вогнутая установки. В этой работе мы показываем, что алгоритм гамильтонова градиентного спуска (HGD) достигает линейной сходимости в различных более общих условиях, включая выпукло-вогнутые задачи, которые удовлетворяют условию «достаточно билинейности». Мы также доказываем скорость сходимости для стохастического HGD ​​и для некоторых параметров алгоритма оптимизации консенсуса Mescheder et al. (2017).}
}

Сноска

%0 Документ конференции
%T Скорость сходимости последней итерации для оптимизации минимум-макс: сходимость гамильтонового градиентного спуска и оптимизация на основе консенсуса
%A Джейкоб Абернети
%A Кевин А. Лай
%A Андре Вибисоно
%B Материалы 32-й Международной конференции по теории алгоритмического обучения
%C Материалы исследования машинного обучения
%D 2021
%E Виталий Фельдман
%E Катрина Лигетт
%E Сиван Сабато
%F pmler-v132-abernethy21a
%I PMLR
%Р 3--47
%U https://proceedings.mlr.press/v132/abernethy21a.html
%V 132
%X В то время как классическая работа по выпукло-вогнутой минимаксной оптимизации опирается на результаты сходимости средних итераций, появление невыпуклых приложений, таких как обучение генеративно-состязательных сетей, привело к возрождению интереса к гарантиям сходимости последней итерации. Доказательство сходимости на последней итерации является сложной задачей, потому что многие естественные алгоритмы, такие как одновременный градиентный спуск/подъем, доказуемо расходятся или зацикливаются даже в простых выпукло-вогнутых минимаксных настройках, и относительно немного работ доказывают глобальные скорости сходимости на последней итерации за пределами билинейная и выпукло-сильно вогнутая установки. В этой работе мы показываем, что алгоритм гамильтонова градиентного спуска (HGD) достигает линейной сходимости в различных более общих условиях, включая выпукло-вогнутые задачи, которые удовлетворяют условию «достаточно билинейности». Мы также доказываем скорость сходимости для стохастического HGD ​​и для некоторых параметров алгоритма оптимизации консенсуса Mescheder et al. (2017).

АПА


Абернети, Дж., Лай, К.А. и Вибисоно, А.. (2021). Скорость сходимости на последней итерации для оптимизации минимум-макс: сходимость гамильтонового градиентного спуска и оптимизация на основе консенсуса. Proceedings of the 32nd International Conference on Algorithmic Learning Theory , in Proceedings of Machine Learning Research 132:3-47 Доступно по адресу https://proceedings.mlr.press/v132/abernethy21a.html.

Сопутствующий материал

Оптимизация геометрии

Автор кода: Роллин А. Кинг и Александр Г. Хайде

Автор раздела: Роллин А. Кинг, Александр Г. Хайде и Лори А. Бернс

Модуль: Ключевые слова, OPTKING

PSI4 выполняет молекулярную оптимизацию с использованием модуля Python под названием
выбор. Программа optking принимает в качестве входных данных ядерные градиенты и,
необязательно, ядерные вторые производные — обе в декартовых координатах.
Алгоритм минимизации по умолчанию использует эмпирическую модель Гессе,
избыточные внутренние координаты, шаг RFO с масштабированием радиуса доверия и обновление BFGS Hessian.

Основные литературные ссылки включают введение избыточных
внутренние координаты Peng et al. [Пэн: 1996: 49].
Общий подход, используемый в этом коде
аналогичен «методу модели Гессе плюс РЧ», описанному и протестированному Баккеном и
Хельгакер [Bakken:2002:9160]. Однако для разделенных
фрагментов, мы решили не использовать их «лишние» координаты.

Внутренние координаты генерируются автоматически на основе предполагаемой связи
подключение. Связность определяется путем проверки межатомных
расстояние меньше суммы атомных радиусов, умноженной на значение
COVALENT_CONNECT. Если пользователь обнаружит, что некоторые
подключение по умолчанию отсутствует, то это значение можно увеличить.

Предупреждение

Выбор входа Z-матрицы и, в частности, включение
фиктивных атомов, не влияет на поведение оптимизатора, который начинает
из декартова представления системы.

В настоящее время по умолчанию отдельные фрагменты склеиваются
ближайшие атомы, и вся система рассматривается как часть одного
молекула. Однако с параметром FRAG_MODE фрагменты
вместо этого может быть связан минимальным набором межфрагментных координат, определяемым
опорные точки внутри каждого фрагмента. Опорные точки могут быть атомарными
позиции (текущее значение по умолчанию) или линейные комбинации позиций атомов
(автоматическое использование главных осей находится в разработке).
Эти координаты димера можно указать напрямую через INTERFRAG_COORDS)
См. здесь для двух примеров их использования.

Основные ключевые слова

ОПТ_ТИП

Указывает минимальный поиск, поиск в переходном состоянии или IRC после

ШАГ_ТИП

Тип шага оптимизации геометрии, Ньютона-Рафсона или Rational Function Optimization

  • Тип : строка

  • Возможные значения : RFO, P_RFO, NR, SD, LINESEARCH

  • По умолчанию : RFO

GEOM_MAXITER

Максимальное количество шагов оптимизации геометрии

  • Тип : целое число

  • По умолчанию : 50

Г_КОНВЕРГЕНЦИЯ

Набор критериев оптимизации. Спецификация любых параметров MAX_*_G_CONVERGENCE или RMS_*_G_CONVERGENCE будет добавлена ​​для перезаписи установленных здесь критериев, если также не включен параметр FLEXIBLE_G_CONVERGENCE. Подробнее см. в разделе Конвергенция геометрии таблицы.

  • Тип : строка

  • Возможные значения : QCHEM, MOLPRO, GAU, GAU_LOOSE, GAU_TIGHT, INTERFRAG_TIGHT, GAU_VERYTIGHT, TURBOMOLE, CFOUR, NWCHEM_LOOSE

  • По умолчанию : QCHEM

ПОЛНЫЙ_HESS_КАЖДЫЙ

Частота, с которой вычисляется полный гессиан в ходе оптимизации геометрии. 0 означает вычислять только начальный гессиан, 1 означает пересчитывать каждый шаг, а N означает пересчитывать каждые N шагов. Значение по умолчанию (-1) никогда не вычисляет полный гессиан.

  • Тип : целое число

  • По умолчанию : -1

Оптимизация минимумов

Сначала определите молекулу и базис во входных данных.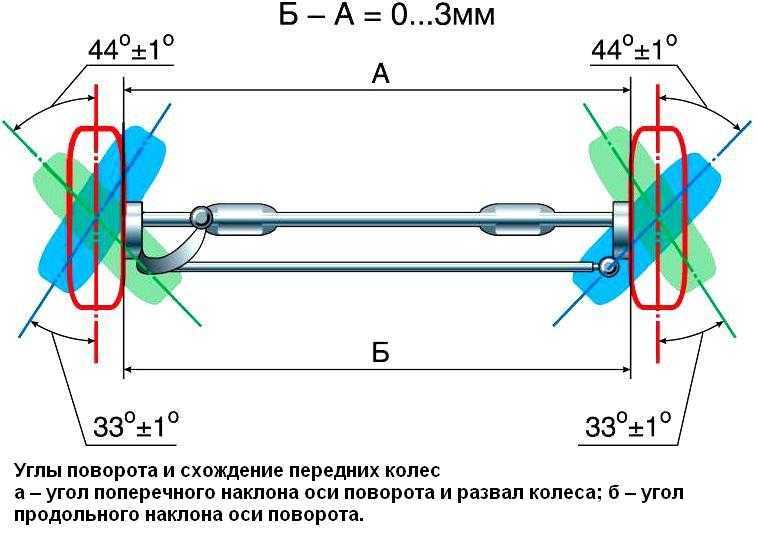

 молекула h3o {
  О
  Н 1 1,0
  Н 1 1,0 2 105,0
}
установить базис дз

Далее приведены примеры различных типов вычислений, которые можно выполнить.

  • Оптимизация геометрии с использованием методов по умолчанию (шаг RFO):

     оптимизировать('scf')

  • Оптимизация с использованием шагов Ньютона-Рафсона вместо шагов RFO:

     установить номер типа шага
оптимизировать ('scf')

  • Оптимизация с использованием конечных разностей энергий вместо градиентов:

     оптимизировать('scf', dertype='энергия')

  • Оптимизировать, ограничивая начальный размер шага до 0,1 а.е.:

     установить intrafrag_step_limit 0,1
оптимизировать ('scf')

  • Оптимизировать, всегда ограничивая размер шага до 0,1 а.е.:

 набор {
  intrafrag_step_limit 0,1
  intrafrag_step_limit_min 0,1
  intrafrag_step_limit_max 0,1
}
оптимизировать ('scf')
 
 установить full_hess_every 1
оптимизировать ('scf')
 
 выбор импорта

Гессен

Если доступны декартовы вторые производные, optking может их прочитать
и преобразовать их во внутренние координаты, чтобы сделать начальный гессиан в
внутренние координаты. В противном случае доступны несколько эмпирических гессианов,
в том числе у Шлегеля [Шлегель:1984:333] и Фишер и Альмлоф
[Фишер: 1992: 9770].
Любой из них или простой диагональный гессиан можно выбрать с помощью
Ключевое слово INTRAFRAG_HESS.

Доступны все распространенные схемы обновления Hessian. Формулы см.
Шлегеля [Schlegel:1987:AIMQC] и Бофилла [Bofill:1994:1].

Гессе можно вычислить во время оптимизации с использованием
ключевое слово FULL_HESS_EVERY.

Переходные состояния и пути реакции

  • Рассчитать начальный гессиан и оптимизировать «переходное состояние»
    линейная вода (обратите внимание, что без разумной стартовой геометрии и
    Hessian, такой прямой поиск часто не удается):

     молекула h3o {
   О
   Н 1 1,0
   Н 1 1,0 2 160,0
}
набор {
   базис дз
   full_hess_every 0
   opt_type тс
}
оптимизировать ('scf')

  • В переходном состоянии (плоский HOOH) вычислите вторую производную и
    затем следуйте внутреннему пути реакции до минимума:

     молекула хух {
   симметрия с1
   ЧАС
   О 1 0,946347
   О 2 1,397780 1 107,243777
   Н 3 0,946347 2 107,243777 1 0,0
}
набор {
   базис дзп
   opt_type irc
   geom_maxiter 50
}
частоты ('scf')
оптимизировать ('scf')

Оптимизация с ограничениями

  • Оптимизация геометрии (HOOH) при зафиксированном двугранном угле 90 градусов.

     молекула {
  ЧАС
  О 1 0,90
  О 2 1,40 1 100,0
  Н 3 0,90 2 100,0 1 90,0
}
установить выбор {
  замороженный_диэдральный = ("
    1 2 3 4
  ")
}
оптимизировать ('scf')

  • Чтобы вместо этого заморозить два расстояния связи O-H

     установить выбор {
  замороженное_расстояние = ("
    1 2
    3 4
  ")
}

Для изгибов соответствующее ключевое слово «frozen_bend».

 заморозка_списка = """
  2 xyz
"""
установить выбор замороженного_картезиана $freeze_list
 
 заморозка_списка = """
  2 года
  3 года
"""
установить выбор замороженного_картезиана $freeze_list
 
 установить выбор {
  диапазонное_расстояние = ("
    1 3 0,949 0,95
    2 4 0,949 0,95
  ")
}

Примечание

Эффект фиксированных и ранжированных ключевых слов обычно не зависит от
как была введена геометрия молекулы (будь то Z-матрица или декартова и т. д.).
В это время; однако применение декартовых ограничений при использовании zmatrix для
молекулярный ввод не поддерживается. Замораживание или ограничение декартовых координат
требует ввода декартовой молекулы. Если численные ошибки приводят к симметрии
разрыва, пока активны декартовы связи, симметризация не может произойти и
появится сообщение об ошибке, предлагающее перезапустить задание.

 молекула хух {
  0 1
  Н 0,850718 0,772960 0,563468
  О 0,120432 0,684669 -0,035503
  О -0,120432 -0,684669 -0,035503
  Н -0,850718 -0,772960 0,563468
}
набор {
  основа cc-pvdz
  intrafrag_step_limit 0,1
}
нижняя граница = [99,99, 109,99, 119,99, 129,99, 149,99]
upper_bound = [100, 110, 120, 130, 140, 150]
ПЭС = []
для нижнего, верхнего в zip(lower_bound, upper_bound):
my_string = f"1 2 3 4 {нижний} {верхний}"
установить выбор ranged_dihedral = $my_string
E = оптимизировать ('scf')
PES.append((верхний, E))
print("\n\tcc-pVDZ энергия СКФ как функция phi\n")
для точки в PES:
  print("\t%5.1f%20.10f" % (точка[0], точка[1]))

Предупреждение

Вращение двугранных граней с большими приращениями без возможности релаксации молекулы
между приращениями может привести к нефизической геометрии с перекрывающимися функциональными группами в более крупных молекулах,
что может помешать успешной оптимизации с ограничениями. Кроме того, такое расслабленное сканирование ПЭС делает
не всегда дают результат, близкий к ИРК, или даже путь реакции, по которому энергия изменяется в
непрерывный путь.

 молекула хух {
  0 1
  ЧАС
  О 1 0,95
  О 2 1,391 103
  Н 3 0,95 2 103 1 Д
  Д = 99
  единицы анг
}
набор {
  основа cc-pvdz
  intrafrag_step_limit 0,1
  Frozen_dihedral ("1 2 3 4")
}
двугранники = [100, 110, 120, 130, 140, 150]
ПЭС = []
для фи в двугранниках:
  хох.Д = фи
  E = оптимизировать ('scf')
  PES.append((фи, Е))
print("\n\tcc-pVDZ энергия СКФ как функция phi\n")
для точки в PES:
  print("\t%5.1f%20.10f" % (точка[0], точка[1]))

Многофрагментная оптимизация

В предыдущих версиях optking метрика соединения атомов была увеличена до тех пор, пока все атомы
были связаны. Это текущее поведение для FRAG_MODE 9.0063 одиночный .
Установка FRAG_MODE на multi теперь добавит специальный
набор межмолекулярных координат между фрагментами — внутри называется DimerFrag
координаты (см. здесь для краткого описания).
Для каждой пары молекулярных фрагментов набор до 3 реперных точек
выбираются на каждом фрагменте. Каждая опорная точка будет либо атомом, либо линейной комбинацией
положения атомов внутри этого фрагмента. Растяжения, изгибы и двугранные углы между двумя
фрагменты будут созданы с использованием этих опорных точек. Видеть
Таблица координат Dimer для того, как создаются контрольные точки.
Для набора из трех димеров A, B и C между каждой парой создаются наборы координат:
АВ, АС и ВС. Каждая DimerFrag может использовать разные контрольные точки.
Созданием межмолекулярных координат можно управлять через FRAG_REF_ATOMS
и INTERFRAG_COORDS. FRAG_REF_ATOMS указывает, какие атомы
(или линейная комбинация атомов) для использования в качестве опорных точек и INTERFRAG_COORDS,
который включает в себя FRAG_REF_ATOMS, позволяет добавлять ограничения и метки к
межмолекулярные координаты.

Примечание

Ручное задание межфрагментных координат поддерживается для опытных пользователей,
и обеспечивает полный контроль относительной ориентации фрагментов.
Установка INTERFRAG_MODE на multi должно хватить почти во всех случаях.
Координатная таблица димеров. предоставляет имя и порядок
соглашение о координатах.

 память 4 ГБ
молекула моль {
    0 1
    О -0,5026452583 -0,9681078610 -0,4772692868
    Н -2,32929 -1,1611084524 -0,4772692868
    Н -0,8887241813 0,8340933116 -0,4772692868
    --
    0 1
    С 0,8853463281 -5,2235996493 0,5504918473
    С 1,8139169342 -2,1992967152 3,8040686146
    С 2,8624456357 -4,1143863257 0,54010
    С -0,6240195463 -4,8153482424 2,1
2137
    С -0,1646305764 -3,3031992532 3,8141619690
    С 3,3271056135 -2,6064153737 2,1669340785
    Н 0,5244823836 -6,4459192939 -0,7478283184
    Н 4,0823309159 -4,4449979205 -0,7680411190
    Н -2,2074914566 -5,7109913627 2,2110247636
    Н -1,3768100495 -2,9846751653 5,1327625515
    Н 4,9209603634 -1,7288723155 2,1638694922
    Н 2.1923374156 -0,9964630692 5,1155773223
    ноком
    единицы а.е.
}
набор {
    основа 6-31+Г
    frag_mode МУЛЬТИ
}
оптимизировать("mp2")

Предупреждение

Ввод молекулы для psi4 не влияет на выбор, ожидается предоставление декартова
координаты. Указание независимых фрагментов с разделителем — не сработает
выбор для добавления определенных межфрагментных координат. Используйте FRAG_MODE мульти .

  • Укажите контрольные точки для использования в качестве координат через FRAG_REF_ATOMS.
    Каждый список соответствует фрагменту. Список индексов обозначает линейную комбинацию
    атомов. В этом случае первой точкой отсчета для второго фрагмента является центр
    бензольного кольца. Индексация начинается с 1, поэтому второй фрагмент в этом примере начинается с индекса 4.

 память 4 ГБ
молекула моль {
    0 1
    О -0,5026452583 -0,9681078610 -0,4772692868
    Н -2,32929 -1,1611084524 -0,4772692868
    Н -0,8887241813 0,8340933116 -0,4772692868
    --
    0 1
    С 0,8853463281 -5,2235996493 0,5504918473
    С 1,8139169342 -2,1992967152 3,8040686146
    С 2,8624456357 -4,1143863257 0,54010
    С -0,6240195463 -4,8153482424 2,1
2137
    С -0,1646305764 -3,3031992532 3,8141619690
    С 3,3271056135 -2,6064153737 2,1669340785
    Н 0,5244823836 -6,4459192939 -0,7478283184
    Н 4,0823309159 -4,4449979205 -0,7680411190
    Н -2,2074914566 -5,7109913627 2,2110247636
    Н -1,3768100495 -2,9846751653 5,1327625515
    Н 4,9209603634 -1,7288723155 2,1638694922
    Н 2,1923374156 -0,9964630692 5,1155773223
    ноком
    единицы а. е.
}
набор {
    основа 6-31+Г
    frag_mode МУЛЬТИ
    # Строка ниже указывает опорные точки, которые будут использоваться для построения
    # межфрагментные координаты между двумя фрагментами (называемые A и B).
    # Формат следующий:
    # [[А-1], [А-2], [А-3]], [[Б-1], [Б-2], [Б-3]]
    #
    # С точки зрения атомов в каждом фрагменте, строка ниже выбирает для воды:
    # h4 воды для первой контрольной точки, O1 воды для второй контрольной точки и
    # h3 воды для третьей опорной точки.
    # Для бензола: среднее значение положений всех атомов C, C2, одного из атомов углерода,
    # и C6, еще один из атомов углерода.
    фрагмент_ref_атомы [
        [[3], [1], [2]], [[4, 5, 6, 7, 8, 9], [5], [9]]
    ]
}
оптимизировать("mp2")

Для еще большего контроля можно передать словарь в INTERFRAG_COORDS

Координаты, которые создаются между двумя димерами, зависят от количества присутствующих атомов.
Фрагменты A и B содержат до 3 эталонных атомов каждый, как показано на рис.
Координатная таблица димеров.
Межфрагментные координаты именуются и могут быть зафиксированы в соответствии с их именами, как показано на рис.
пример ниже. Для указания контрольных точек используйте индексацию на основе 1.

Координаты димера

имя

тип

атомные метки

присутствует, если

РАБ

расстояние

А0-В0

всегда

тета_А

уголок

А1-А0-В0

А содержит > 1 атома

тета_B

уголок

А0-В0-В1

В содержит > 1 атома

тау

двугранный

А1-А0-В0-В1

А и В содержат > 1 атома

фи_А

двугранный

А2-А1-А0-В0

А содержит > 2 атомов. Нелинейный

фи_Б

двугранный

А0-В0-В1-В2

B имеет > 2 атомов. Нелинейный

  • Выполняется оптимизация с ограничениями, при которой ориентация двух фрагментов фиксирована, но
    расстояние между фрагментами и все внутрифрагментные координаты ослабляются. В этом
    например, центры бензольного и тиофенового колец выбраны в качестве первых реперных точек.
    Метильные группы углерода и один водород выбраны для двух других опорных точек на
    первые фрагменты. Для второго фрагмента в качестве других реперных точек выбраны два атома углерода бензольного кольца.

 память 4 ГБ
молекула моль {
  С -1,258686 0,546935 0,436840
  Н -0,683650 1,200389 1,102833
  С -0,699036 -0,349093 -0,396608
  С -2,693370 0,550414 0,355311
  Н -3,336987 1,206824 0,952052
  С -3,159324 -0,343127 -0,536418
  Н -4,199699 -0,558111 -0,805894
  S -1,883829 -1,212288 -1,301525
  С 0,786082 -0,656530 -0,606057
  Н 1,387673 -0,016033 0,048976
  Н 1,054892 -0,465272 -1,651226
  Н 0,978834 -1,708370 -0,365860
  --
  С -6,955593 -0,119764 -1,395442
  С -6,977905 -0,135060 1,376787
  С -7,111625 1,067403 -0,697024
  С -6,810717 -1,314577 -0,707746
  С -6,821873 -1,322226 0,678369
  С -7,122781 1,059754 0,689090
  Н -7,226173 2,012097 -1,240759
  Н -6,687348 -2,253224 -1,259958
  Н -6,707325 -2,266920 1. 222105
  Н -7,246150 1,998400 1,241304
  О -6,944245 -0,111984 -2,805375
  Н -7,058224 0,807436 -3,049180
  С -6,9

-0,143507 2,4
Н -8,018305 -0,274985 3,264065
Н -6,592753 0,807024 3,281508
Н -6,368443 -0,968607 3,273516
ноком
единица ангстрем
}
# Создать словарь Python и преобразовать его в строку для передачи в optking
МТдимер = «»»{
«Натомов на фраг»: [12, 16],
«Фраг»: 1,
«A Ref Atoms»: [[1, 3, 4, 6, 8], [8], [11]],
«Этикетка»: «метилтиофен»,
«Б Фраг»: 2,
«Атомы B Ref»: [[13, 14, 15, 16, 17, 18], [13], [15]],
«Этикетка B»: «тирозин»,
«Замороженный»: [«theta_A», «theta_B», «tau», «phi_A», «phi_B»],
}»»»
набор {
основа 6-31+Г
frag_mode МУЛЬТИ
interfrag_coords $MTdimer
}
оптимизировать(«mp2»)

Работа с проблемными оптимизациями

Несмотря на то, что optking постоянно совершенствуется с учетом надежности, некоторые
попытки оптимизации неизбежно не сойдутся к желаемым минимумам.
Для сложных случаев даются следующие рекомендации.

  • Как и для любого оптимизатора, вычисление гессиана и ограничение размера шага
    успешно сходятся более высокий процент случаев. Настройки по умолчанию имеют
    были выбраны потому, что они эффективно работают с общими репрезентативными наборами тестов.
    Иногда необходимы более ограничительные и осторожные шаги.

  • DYNAMIC_LEVEL позволяет изменить метод оптимизации
    к алгоритмам, которые, хотя зачастую и менее эффективны, могут помочь свести сложные
    случаи. Если изначально установлено значение 1, то при обнаружении плохих шагов
    повысит динамический уровень с помощью нескольких форм более надежных и осторожных алгоритмов.
    Изменения уменьшат радиус доверия, разрешат шаги назад (частичная строка
    поиск), добавить декартовы координаты, переключиться на декартовы координаты и взять
    ступени самого крутого спуска.

  • Разработчики обнаружили, что параметру OPT_COORDINATES присвоено значение «ОБА», что
    включает в себя как избыточный набор внутренних координат, так и декартовы координаты,
    хорошо работает для систем с длинными «плечами» или гибкими частями молекулы плохо
    описывается местными интерналами.

  • Optking поддерживает спецификацию призрачных атомов. Некоторые внутренние координаты, такие
    поскольку кручения становятся плохо определенными, когда они содержат почти линейные изгибы.
    Внутренняя ошибка AlgError 9В таких случаях может быть поднят номер 0064. Optking позволит избежать таких
    координаты при выборе исходной системы координат; однако они могут возникать в ходе
    оптимизации. В таких случаях попробуйте перезапустить с самой последней геометрии.
    В качестве альтернативы установка OPT_COORDINATES на декартову позволит избежать каких-либо внутренних
    координировать трудности в целом. Эти изменения координат могут быть автоматически
    выполняется путем установки DYNAMIC_LEVEL на 1.

Предупреждение

В некоторых случаях, например, при проблемах с координатами, описанных выше, опция optking будет сброшена для сохранения
последовательная история. Если в Psi4 возникает ошибка из-за превышения GEOM_MAXITER, но
отчет о последнем шаге показывает, что optking не предпринял шагов GEOM_MAXITER, например
произошел сброс. Проверка покажет, что счетчик шагов был сброшен на 1 где-то в
оптимизация.

Критерии сходимости

Optking отслеживает пять параметров для оценки хода геометрии
оптимизация. Это (с их ключевыми словами) изменение энергии
(MAX_ENERGY_G_CONVERGENCE), максимальный элемент
градиент (MAX_FORCE_G_CONVERGENCE), среднеквадратичное
градиента (RMS_FORCE_G_CONVERGENCE), максимальный элемент
смещения (MAX_DISP_G_CONVERGENCE) и
среднеквадратичное смещение (RMS_DISP_G_CONVERGENCE),
все во внутренних координатах и ​​атомных единицах. Обычно эти варианты не
устанавливаться напрямую. Первичный контроль сходимости геометрии лежит на ключевом слове
G_CONVERGENCE, который устанавливает вышеупомянутое в соответствии
с конвергенцией геометрии таблицы. 9{-6}\)

Сноски

[1]

По умолчанию

[2]

Критерии сходимости Бейкера одинаковы.

[3]
(1,2)

Критерии сходимости аналогов NWCHEM такие же.

[4]
(1,2,3)

Конвергенция достигается, когда выполняются все активные критерии.

[5]
(1,2,3)

Конвергенция достигается при выполнении Max Force и одного из Max Energy или Max Disp .

[6]
(1,2,3,4,5)

Нормальная сходимость достигнута, когда все четыре критерия ( Максимальное усилие , Среднеквадратичное усилие ,
Max Disp и RMS Disp ). Чтобы помочь с квартирой
потенциальные поверхности, попеременная конвергенция достигается при 100\(\кратах\) действующей силы меньше
чем критерий RMS Force .

[7]

Компенсирует трудности оптимизации сходящейся геометрии надмолекулярных комплексов
плотно, где большие среднеквадратичные значения disp и max disp могут быть результатом плоских потенциальных поверхностей, даже когда
max force и/или rms force малы.

Для полного контроля, указание значения для любой из пяти контролируемых опций активирует это
критерий и перезаписывает/добавляет его к критериям, установленным G_CONVERGENCE.
Обратите внимание, что это отменяет специальные меры сходимости, подробно описанные в примечаниях [5] и [6].
и вместо этого требует, чтобы все активные критерии были выполнены для
добиться сходимости. Чтобы избежать отзыва, включите ключевое слово FLEXIBLE_G_CONVERGENCE.

Интерфейс к GeomeTRIC

Оптимизатор GeomeTRIC, разработанный Wang and Song [Wang:2016:214108], можно использовать вместо
Собственный оптимизатор Psi4 Optking. GeomeTRIC использует внутреннюю координату перемещения-вращения (TRIC).
система, которая хорошо работает для оптимизации геометрии систем, содержащих нековалентные взаимодействия.

Использование оптимизатора GeomeTRIC указано с аргументом engine для
оптимизировать() . Оптимизация будет учитывать ключевые слова G_CONVERGENCE.
и GEOM_MAXITER. Любые другие специфичные для GeomeTRIC параметры (включая ограничения)
можно указать с помощью optimizer_keywords аргумент для optimize() .
Ограничения могут быть наложены на декартовы координаты, связи, углы и двугранники, и они могут быть
используется, чтобы заморозить координату или установить для нее определенное значение. См. GitHub GeomeTRIC
для получения дополнительной информации о ключевых словах и спецификации ограничений JSON.

  • Оптимизация молекулы воды с помощью GeomeTRIC:

     молекула h3o {
   О
   Н 1 1,0
   Н 1 1,0 2 160,0
}
набор {
   макситер 100
   g_convergence гау
}
оптимизировать('hf/cc-pvdz', engine='геометрический')

  • Оптимизация молекулы воды с помощью GeomeTRIC, с ограничением одной из двух связей ОН до 2,0 а.е.
    и угол HOH, ограниченный 104,5 градусами:

     молекула h3o {
   О
   Н 1 1,0
   Н 1 1,0 2 160,0
}
набор {
   макситер 100
   g_convergence гау
}
геометрические_ключевые слова = {
  'coordsys' : 'трик',
  «ограничения»: {
  'установить': [{'тип': 'расстояние',
            «индексы»: [0, 1],
            «значение»: 2,0},
           {'тип' : 'угол',
            «индексы»: [1, 0, 2],
            «значение»: 104,5 }]
   }
}
оптимизировать('hf/cc-pvdz', engine='geometric', optimizer_keywords=geometric_keywords)

  • Оптимизация димера бензола/воды с помощью GeomeTRIC с замороженными 6 атомами углерода бензола.
    место:

     молекула h3o {
  С 0,833 1,221 -0,504
  Н 1,482 2,086 -0,518
  С 1,379 -0,055 -0,486
  Н 2,453 -0,184 -0,483
  С 0,546 -1,167 -0,474
  Н 0,971 -2,162 -0,466
  С -0,833 -1,001 -0,475
  Н -1,482 -1,867 -0,468
  С -1,3790,275 -0,490
  Н -2,453 0,404 -0,491
  С -0,546 1,386 -0,506
  Н -0,971 2,381 -0,524
  --
  О 0,000 0,147 3,265
  Н 0,000 -0,505 2,581
  Н 0,000 0,965 2,790
  no_com
  нет_переориентировать
}
набор {
   макситер 100
   g_convergence гау
}
геометрические_ключевые слова = {
  'coordsys' : 'трик',
  «ограничения»: {
  'заморозить': [{'тип': 'xyz',
               'индексы': [0, 2, 4, 6, 8, 10]}]
   }
}
оптимизировать('hf/cc-pvdz', engine='geometric', optimizer_keywords=geometric_keywords)

Выход

Ход оптимизации геометрии можно отслеживать, выполнив поиск выходного файла для
символ тильды ( ~ ). Это создает таблицу, подобную приведенной ниже, которая показывает
для каждой итерации значение каждой из пяти величин и соответствие критерию
является активным и выполненным ( * ), активным и невыполненным ( ) или неактивным ( o ).

 -------------------------------------------------- -------------------------------------------- ~
 Шаг Суммарная энергия Delta E MAX Force RMS Force MAX Disp RMS Disp ~
-------------------------------------------------- ------------------------------------------- ~
  Критерии сходимости 1.00e-06 * 3.00e-04 * o 1.20e-03 * o ~
-------------------------------------------------- ------------------------------------------- ~
    1 -38,91591820 -3.89e+01 6.91e-02 5.72e-02 о 1.42e-01 1.19e-01 о ~
    2 -38.92529543 -9.38e-03 6.21e-03 3.91e-03 о 2.00e-02 1.18e-02 о ~
    3 -38.92540669 -1.11е-04 4.04е-03 2.46е-03 о 3.63е-02 2.12е-02 о ~
    4 -38.92548668 -8.00e-05 2.30e-04 * 1.92e-04 о 1.99e-03 1.17e-03 о ~
    5 -38.92548698 -2.98е-07*3.95е-05*3.35е-05о 1.37е-04*1.05е-04о~

Полный список ключевых слов для optking приведен в Приложении OPTKING.

Предоставляется информация о функции Psithon, которая управляет оптимизацией геометрии.
в оптимизировать() .