Технические характеристики козлового крана КК 20-25

Технические характеристики козлового крана КК 20-25

Современные грузоподъемные механизмы отличаются широким функционалом. Рабочие характеристики козлового крана КК 20-25 позволяет использовать его для широкого спектра грузоподъемных работ:

• Монтаж строительных сооружений, промышленных установок.
• Погрузка и выгрузка крупногабаритных грузов.
• Загрузка в морские суда и железнодорожные вагоны с высокими бортами.
• Штабирование леса.
• Обслуживание цехов и складов.

Общие технические характеристики козлового крана КК-20

• Максимальная грузоподъемность – 20 тонн.
• Длина несущего пролета – 32 метра.
• Предельная высота подъема груза – 8,65 метра.
• Вылет консоли – 7 метров.
• Скорость поднятия груза – 4,4 метра в минуту.
• Скорость передвижения ходовой тележки – 24 метра в минуту.
• Питание от переменного тока мощностью 380 В и частотой 50 Гц.

Рис. 1. Козловый кран КК-20-32

Управление производится из стационарной или передвижной кабины. Мобильный аппаратный пункт позволяет полностью контролировать весь процесс работы – погрузку, транспортировку и опускание груза.

Помимо технических характеристик козловой кран КК-20 оценивается по исполнению, в котором он произведен: общепромышленном или специальном. В стандартной комплектации кран оснащается противоугонным устройством, температурным реле. В нормальном режиме допустимой температурой является диапазон от -20 до +40 градусов.

При необходимости кран выпускается в пожаробезопасном, взрывобезопасном, химическом, тропическом исполнении. Сейсмическоустойчивые модели способны выдерживать колебания до 8 баллов и нормально функционировать при 6.

Рис. 2. Козловой кран

Рельсовые пути устанавливаются на бетонной или мягкой подушке.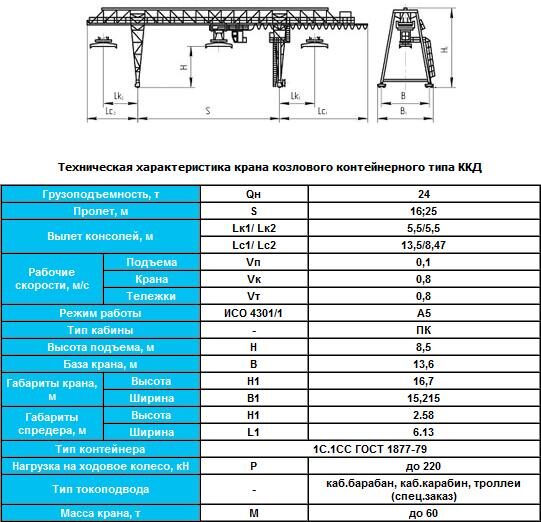 Для прокладки применяются стандартные рельсы серии Р, также возможен монтаж специальных крановых рельс КР.

Электричество подается с помощью гибкого кабеля или троллеи. Все электрические устройства управление помещены в защищенный шкаф.

При выпуске крана на производстве к нему прилагаются электрические схемы управления и подключения. Они позволяют быстро настроить подъемно-транспортный механизм.

КК-20 выпускается в климатическом исполнении У и устойчив к различным климатическим условиям. Это обеспечивает длительный период эксплуатации.

Вернуться к списку статей

Наши услуги

Подкрановые пути

Модернизация и реконструкция крана

Радиоуправление краном

Ремонт кранового оборудования

Монтаж кранового оборудования

Техническое обслуживание грузоподъемных кранов

Обследование грузоподъемных кранов

Ремонт крановых колес

Мехобработка деталей

Наши товары

Крановое оборудование

Кран мостовой

Литейные производства

Изготовление металлоконструкций

Оборудование для аэропортов

Сергеев Евгений Иванович

Коммерческий директор ООО Машиностроительно-Литейное Объединение Буревестник

О компании

Мы рады приветствовать вас на интерактивной площадке нашего завода и благодарны за внимание к нашему предприятию и его деятельности в бизнесе.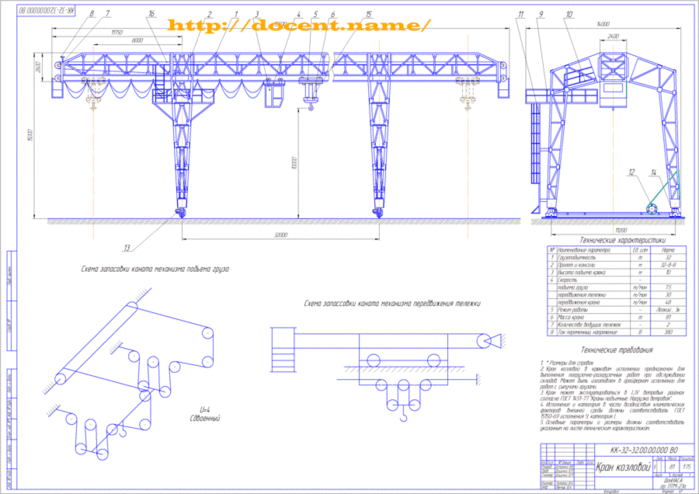

Наш завод производит широкий ассортимент машиностроительной и металлургической продукции для различных отраслей отечественной экономики и многих зарубежных стран.

Высокий технический уровень, качество и надежность изделий с маркой нашего предприятия получили широкую известность и признание, создали заводу высокий авторитет в промышленном мире.

Читать подробнее о компании

Кран козловой 20 т (тн, тонн) КК / ККС / ККТ

Производство кранов:

Кран-балка

Кран мостовой

Кран консольный

Кран козловой

Тельферы (электрические тали)

Тали

Монтаж

Ремонт

Комплектующие

• Кран-балка

• Кран мостовой

• Кран консольный

• Кран козловой

  • Кран козловой КК (ККТ, ККС)

    • Кран козловой КК (ККТ, ККС) 3. 2 т
    • Кран козловой КК (ККТ, ККС) 5 т
    • Кран козловой КК (ККТ, ККС) 6.3 т
    • Кран козловой КК (ККТ, ККС) 10 т
    • Кран козловой КК (ККТ, ККС) 12 т
    • Кран козловой КК (ККТ, ККС) 16 т
    • Кран козловой КК (ККТ, ККС) 20 т
    • Кран козловой КК (ККТ, ККС) 24 т
    • Кран козловой КК (ККТ, ККС) 25 т
    • Кран козловой КК (ККТ, ККС) 32 т
    • Кран козловой КК (ККТ, ККС) 40 т
    • Кран козловой КК (ККТ, ККС) 50 т
    • Кран козловой КК (ККТ, ККС) 80 т
    • Кран козловой КК (ККТ, ККС) 100 т

  • Легкий козловой кран ККЛ (ККМ)

• Тельферы (электрические тали)

• Тали

• Монтаж

• Ремонт

• Комплектующие

Главная

/

Кран козловой

/

Кран козловой КК (ККТ, ККС)

/
Кран козловой КК-20 — 20 тонн

( электрический козловой кран ККС-20 / ККТ-20 )

Цена по запросу
* Зависит от ваших технических требований — Уточняйте у специалиста!

  Предварительный расчет стоимости

Цена — расчет

  Заказать, или задать вопрос

Продукты и услуги — KK Steel

Продукты

ПЭБ

Мезонин

EOT

Предварительно спроектированные здания (PEB) — это здания, которые проектируются на заводе и собираются на месте. Обычно ПЭБ представляют собой стальные конструкции. Составные секции изготавливаются на заводе по точным размерам, транспортируются на место и собираются на месте с помощью болтовых соединений. Этот тип структурной концепции обычно используется для строительства промышленных зданий, станций метро, ​​складов и т. д.

Принятие PEB вместо традиционной концепции проектирования стальных зданий дало множество преимуществ, включая экономичность и простоту изготовления. Строительные конструкции такого типа могут быть отделаны внутри для выполнения любых функций, которые на самом деле помогают в проектировании малоэтажных зданий. Примерами быстровозводимых зданий являются склады, навесы, фабрики, мосты и т. д.

Наши специальности

Промышленное здание крана E O T
Склады / Годауны
Rail Yards
Логитистический двор
Cold Stores
Промышленное стальное здание
Семинары
Транспортные терминалы
Выставочные залы
Стации

Спортивные залы
Auditoriv
. Стальное здание гостиницы

Мезонин

Антресоль — это промежуточный уровень или уровни между полом и потолком любого этажа в соответствии с разделом 505 Международного строительного кодекса. Значение мезонина происходит от итальянского слова mezza, что означает «половина» или «середина».

Типы применения антресольных этажей включают складские, складские, офисные, производственные и производственные помещения. Мезонины можно использовать для увеличения полезной площади в здании без необходимости пристройки к самому зданию. Они могут быть изготовлены из стали, дерева, бетона или других материалов.

Мезонин помогает повысить эффективность использования пространства внутри здания. Антресольный этаж может представлять собой большую антресольную систему из конструкционной стали, удлиненную платформу для оборудования или рабочую платформу или небольшую платформу для хранения. Однако не следует путать антресоли с площадками для оборудования. Разница между мезонином и платформой оборудования может иметь важные последствия для строительства и требований строительных норм и правил.

Мезонины часто проектируются с использованием различных материалов, таких как сталь, дерево или бетон. Большинство промышленных антресолей изготовлены из высокопрочной стали для легкой сборки в конструкции здания.

На промышленные мезонины можно попасть по стальным мезонинным лестницам. Для небольших антресолей, расположенных в ограниченном пространстве внутри здания, лестницы с чередующимися ступенями являются безопасным и эффективным способом доступа к антресолям.

Стальные антресоли являются распространенным типом антресольных конструкций для складских помещений, площадок для оборудования и других промышленных помещений. Стальная конструкция обеспечивает высокую прочность для долговечной и безопасной конструкции.

Стальные антресоли и платформы для оборудования могут быть спроектированы как отдельно стоящие конструкции с болтовым соединением для легкой сборки внутри существующего здания. Это делает сталь лучшим выбором для добавления антресольного этажа к существующему пространству.

Кран EOT

Электрический мостовой кран или кран EOT является одним из наиболее распространенных типов мостовых кранов, также называемых мостовыми кранами, которые состоят из параллельных путей с передвижным мостом, перекрывающим зазор. Краны EOT обычно питаются от электричества.

Краны EOT широко используются на складах и в промышленности. Кран EOT может переносить тяжелые предметы в любое место на заводе, а также может использоваться для подъема. Однако его можно использовать не во всех отраслях.
Рабочая температура ограничена диапазоном от -20 C до 40 C.

Однобалочный кран EOT

Однобалочный кран EOT используется для погрузочно-разгрузочных работ легкой и средней грузоподъемности; подъем и перемещение грузов, погрузка и разгрузка транспортных средств могут быть целью установки этих кранов.

Эти краны также устанавливаются в ограниченном пространстве.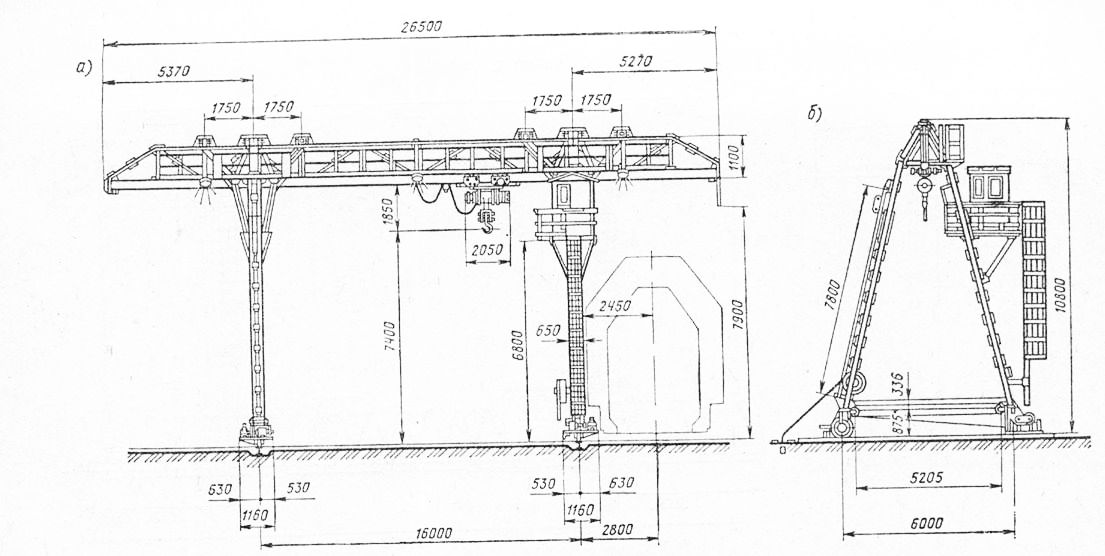 Рекомендуемые пролеты до 20м. max и высота подъема от 3м до 9м.

Производитель однобалочных кранов EOT в Гуджарате, Индия, грузоподъемностью от 1 до 20 тонн производится компанией KK Steel.

Двухбалочный кран EOT

Двухбалочный кран EOT используется для средних и тяжелых условий эксплуатации. Двухбалочные краны EOT отличаются прочной конструкцией и конструкцией, благодаря чему достигаются функции, не требующие обслуживания. Для клиентов это идеальный продукт, который можно забыть из-за его долговечности. Преимуществом является простота обслуживания каждого компонента на установленной высоте.

Стандартная грузоподъемность составляет от 3 до 200 тонн в зависимости от требований заказчика. Им отдают предпочтение практически во всех отраслях промышленности.

KK Steel – крупнейший двухбалочный кран EOT Производственная мощность до 200 тонн в Гуджарате.

Козловой кран

Козловые краны в основном используются для погрузочно-разгрузочных работ на открытом воздухе. В районах, где строительство навесов невозможно/не требуется, устанавливаются такие краны. Складские площадки, железнодорожные станции, порты, доки и строительство

промышленность. Установка этого типа крана выгодна покупателям, поскольку под рабочим пространством крана покрывается большая площадь. Краны с большими пролетами и высотой могут соответствовать требованиям.

 KK Steels — лучший производитель козловых кранов грузоподъемностью до 100 т в Гуджарате.

Услуги

Полное управление проектами

Мы предоставляем полное обслуживание проекта, начиная с планирования проекта и заканчивая полной реализацией проекта в соответствии с планом без какого-либо стресса для вас.
Просто оставьте все это на нас, и мы завершим проект в соответствии с вашей мечтой.

Получить предложение

Электроника | Бесплатный полнотекстовый | Стабильность характеристик управления трехмерными мостовыми кранами при неопределенности массы полезной нагрузки

1.

Введение

Трехмерный (3D) мостовой кран, также называемый козловым краном, все чаще играет решающую роль в подъеме и транспортировке грузов и контейнеров в морских портах или портах. мануфактуры, где его операции должны быть предельно точными и безопасными [1]. Тем не менее, мостовой кран моделируется как механическая система с недостаточным приводом, в которой количество управляющих сигналов меньше, чем количество его степеней свободы (DoF). Недостаточное срабатывание может привести к неожиданным колебаниям полезной нагрузки. Что еще более важно, учитывая неопределенность массы полезной нагрузки, неожиданные колебания могут поставить под угрозу жизнь людей и разрушить окружающие механизмы и товары [2]. Чтобы гарантировать безопасность и точность работы козлового крана, надежность и стабильность закона управления краном являются обязательными показателями при разработке контроллера.

За последние десятилетия было предложено множество стратегий управления краном. Достаточно простой регулятор может быть представлен разомкнутым законом управления, где реализовать его на кране несложно, так как датчик не требуется [3,4,5,6]. Тем не менее, мостовой кран, использующий контроллер с разомкнутым контуром, может быть весьма чувствительным к внешним воздействиям, таким как дождь и ветер, когда он работает на открытом воздухе [7]. Напротив, контроллер с обратной связью может использовать показания встроенных датчиков для регулировки приводов крана, чтобы его работа стабилизировалась даже в условиях внешних шумов или системных неопределенностей [8]. Первым примером замкнутого регулятора является пропорционально-дифференциальный закон управления, основанный на теореме Ласалля об инвариантности множества, который был предложен для крана с двумя степенями свободы [9].]. Аналогичным образом была предложена нелинейная схема управления с двумя обратными связями [10] для уменьшения углов поворота крана при перемещении объекта на новое место. Авторы работы [11] линеаризовали частичную обратную связь нелинейной динамики на 2-мерном (2D) кране, что позволило разработать контроллер для мгновенного управления как положением тележки, так и углами ее качания. Расширяя двухмерный нелинейный подход к управлению с частичной обратной связью из [11], Le et al. [12,13] разработали асимптотически стабилизированные стратегии управления трехмерным козловым краном.

На самом деле, ожидается, что краном можно будет надежно управлять из-за его нелинейности и неопределенностей, включая недостаточно активный механизм, неопределенные системные параметры и внешние помехи от рабочей среды. С этой целью в некоторых других работах было предложено использовать метод управления скользящим режимом (SMC) [14, 15, 16, 17, 18, 19, 20, 21, 22] при разработке надежного контроллера для козлового крана. Например, авторы в [17,19] предложили закон управления с поверхностью скольжения, линейно составленной из скользящей подповерхности активированного состояния и ошибок недоактивированного состояния. Точно так же Qian et al. [18,23] использовали ошибки состояния в качестве промежуточной переменной для разработки поверхности скольжения второго порядка. Однако метод иерархического SMC (HSMC) привлек больше внимания исследователей, практиков и инженеров, которые разработали надежный контроллер для системы с недостаточной активацией. По сути, метод HSMC состоит из нескольких слоев поверхностей скольжения. В [24] авторы предложили, чтобы поверхность скольжения первого уровня строилась по переменным состояния и их весам, а поверхность второго уровня просто линейно комбинировалась несколькими слоями первого порядка [24]. Некоторые другие исследователи разработали схему HSMC по-другому. Например, Ван и др. [25] использовали поверхности скольжения первой и второй подсистем для построения поверхности скольжения второго порядка; затем они использовали сформированную поверхность скольжения второго порядка и поверхность скольжения третьей подсистемы для построения поверхности скольжения третьего порядка. Построение продолжалось до последней подсистемы, где доказали устойчивость иерархических поверхностей скольжения.

Основной недостаток использования метода SMC для проектирования контроллера, особенно для мостового крана, заключается в том, что все параметры модели должны быть детерминированными. Однако очевидно, что параметры крановой системы очень неопределенны и нелинейны, особенно при внешних возмущениях. Чтобы решить эту непрактичность использования подхода управления SMC, были предложены некоторые адаптивные стратегии для оценки параметров крана в режиме онлайн. Например, авторы [26] использовали теорию Ляпунова для получения адаптивной методики оценки неизвестных параметров мостового крана. Парк и др. [27] предложил нечеткую логику на основе наблюдателя для представления неопределенностей и нелинейностей приводов крана. Кроме того, адаптивный закон SMC, основанный на нейронных сетях с нечеткими вейвлетами, был предложен для трехмерного козлового крана, как обсуждалось другими авторами [28]. В наших предыдущих работах [29,30], мы представили адаптивные схемы HSMC для 2D и 3D мостовых кранов, соответственно, где мы использовали сеть нечетких наблюдателей и радиальных базисных функций для адаптивной оценки неизвестных и неопределенных параметров крана. Тем не менее, насколько нам известно, ни одна из предыдущих схем адаптивного управления трехмерным мостовым краном не учитывала постоянство характеристик управления замкнутой системы управления при неопределенной массе полезного груза.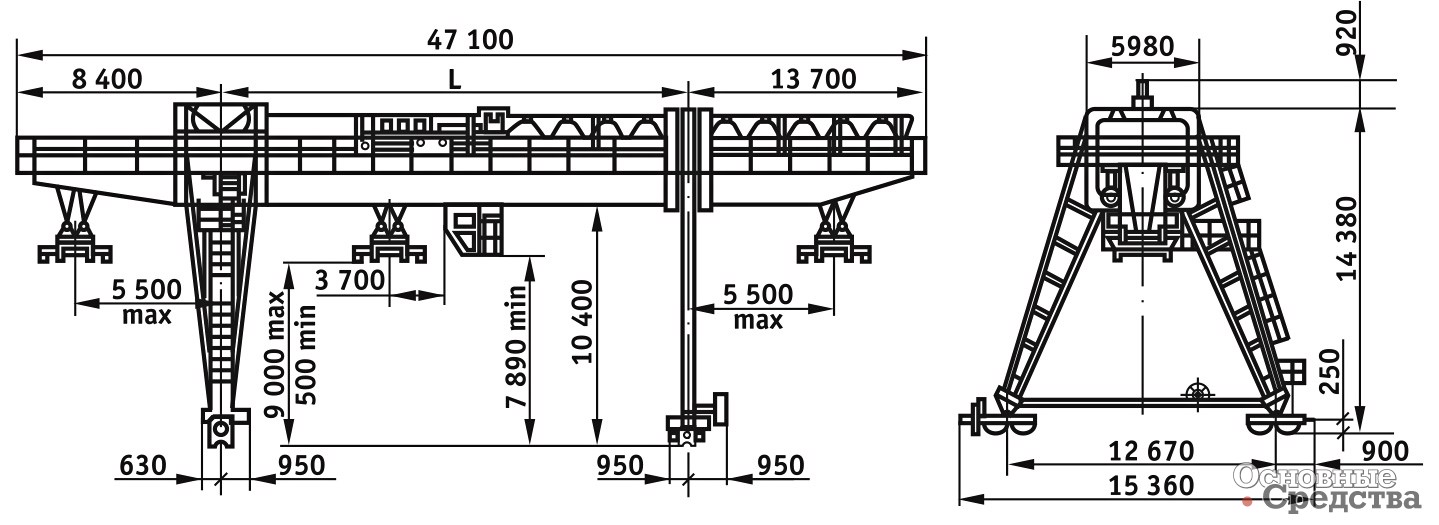

В результате в этой работе для эффективного и надежного управления трехмерным мостовым краном даже в условиях неопределенности массы полезного груза мы сначала предлагаем использовать нейронную сеть радиальной базисной функции для адаптивной оценки неизвестных и неопределенных кинетических параметров системы. контроллера, который разработан на основе технологии SMC. Что еще более важно, мы затем предлагаем включить механизмы адаптации [31] в закон управления, который позволяет контроллеру адаптивно оценивать и обновлять массу полезной нагрузки в режиме онлайн, чтобы вычислить ее другие неизвестные параметры. Затем математически доказана устойчивость предлагаемой системы управления с обратной связью с использованием теории Ляпунова, которая подтверждает, что трехмерный козловой кран может надежно работать при неопределенной массе полезной нагрузки. Предложенный алгоритм был оценен в экспериментах по синтетическому моделированию, где полученные результаты показывают, что характеристики управления были постоянными, хотя масса полезной нагрузки варьировалась.

Оставшаяся часть этого документа организована следующим образом: Раздел 2 описывает, как спроектировать контроллер SMC для трехмерного мостового крана. В разделе 3 представлены предлагаемые адаптивные методы оценки неизвестных и неопределенных параметров системы, в которых масса полезного груза обновляется в режиме онлайн, а также обсуждается устойчивость замкнутой системы управления трехмерным мостовым краном. В разделе 4 обсуждаются подтвержденные результаты, полученные с помощью предлагаемого подхода, прежде чем будут сделаны выводы в разделе 5.

2. Контроллер скользящего режима для трехмерных мостовых кранов с неопределенной грузоподъемностью

2.1. Трехмерная динамическая модель мостового крана

На практике трехмерный козловой кран состоит из трех основных компонентов, как показано на рис. 1: мост, который может перемещаться влево или вправо; тележка, скользящая вперед или назад по мосту; и подъемник для перевозки предметов или груза. Обозначим массу тележки как mc, сосредоточенную массу моста как mr, массу груза как m и длину подъемного каната как l. Для простоты предположим, что длина подъемного троса фиксирована. Силы, действующие на тележку в направлениях x и y, определяются как ux и uy соответственно. Обозначим также θx как угол качания полезной нагрузки и θy как косвенно зависимый параметр колебательной составляющей крана. Без ограничения общности предполагается, что трение покоя в козловом кране определено, а масса подъемного каната тривиальна и ею пренебрегают. И тележка, и груз рассматриваются как материальные частицы.

Если положения тележки на плоскости xy декартовой системы координат определяются x и y, то мостовой кран представляет собой систему с несколькими входами и несколькими выходами (MIMO), где входы и выходы f_1=uxuyT∈R2 и q_=xyθxθy∈R4 соответственно. Учитывая входы и выходы мостового крана, очевидно, что его механическая система недостаточно активна.

Учитывая приведенные выше определения, динамическую модель мостового крана в 3D можно представить с помощью уравнений движения Лагранжа второго рода следующим образом:

где

q_=xyθxθyT — вектор состояния системы.

Взяв производную от (1) по q_, можно получить динамическую модель трехмерной портальной системы в матричной форме, заданной выражением

где Mq_ — матрица инерции, Cq_,q_˙ — матрица Кориолиса, g_q_=00mglsinθx0T — вектор силы тяжести, u_=uxuy00T — вектор управления. Эти матрицы и векторы вычисляются

2.2. Контроллер скользящего режима для трехмерного мостового крана

Надежное управление трехмерным мостовым краном заключается в эффективном перемещении как моста, так и тележки по заданным траекториям в направлениях x и y, а также в эффективном минимизации колебаний полезной нагрузки (θx, θy) с учетом неизвестной массы груза и неопределенных матриц Mq_, Cq_,q_˙, g_q_. Чтобы иметь дело с системой с высокой неопределенностью трехмерного козлового крана, подход SMC обеспечит замечательную надежность в характеристиках управления [30]. Если мы разделим матрицы и векторы в (3) на подматрицу R2×2 и подвектор R2×1, то (3) можно представить в виде

, где M11,M12,M21,M22∈R2×2, C11,C12,C21,C22∈R2×2, D11,D12,D21,D22∈R2×2 и G1,G2∈R2×1.

Обратите внимание, что

Таким образом, теперь мы можем представить (4) в виде двух матричных уравнений следующим образом:

Поскольку M22 положительно, уравнение (6) можно переписать в виде

Из (5) и (7) получается

или же

куда

Если поверхность скольжения определяется

где q_1d — желаемое положение тележки, постоянное в рабочем цикле, тогда λ и α — положительные диагональные матрицы. Следовательно, производная поверхности скольжения равна

Если выбрать закон управления s˙=−M¯1K1sgn(s)+K2s, где K1,K2∈R2×2 — положительные диагональные матрицы, а sign() — знаковая функция, то управляющий вход, который может поддерживать устойчивость поверхности скольжения определяется выражением

На практике, чтобы уменьшить явление вибрации, функция насыщения используется вместо функции знака следующим образом:

где τs и τ — выход привода и управляющий вход соответственно.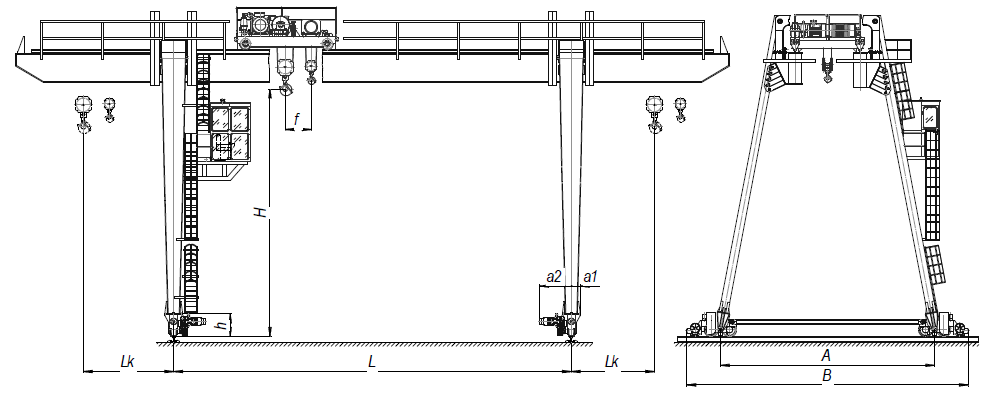 τmax и τmin — верхняя и нижняя границы τ. Для получения дополнительной информации о функции насыщения при проектировании схемы SMC заинтересованные читатели могут обратиться к нашим предыдущим работам [30].

3. Адаптивный контроллер режима скольжения для трехмерных мостовых кранов с неопределенной грузоподъемностью и массой

Хотя контроллер SMC, разработанный в предыдущем разделе, обеспечивает надежность и устойчивость крановой системы с неопределенностями и нелинейностями, он не имеет механизма для оценки неопределенные и неизвестные параметры системы, что не позволяет использовать ее в реальных приложениях управления, особенно в трехмерном мостовом кране. С этой целью мы предлагаем использовать нейронную сеть радиальной базисной функции (RBFNN) для адаптивной оценки неизвестных и неопределенных параметров для разработанного контроллера SMC. 92T∈R2 определяется как выход RBFNN. Внутри RBFNN мы обозначаем W∈Rl×2 как матрицу идеальных весов, где l — количество нейронов в скрытом слое. — ошибка весовой матрицы. 91=m˜Λ и

Следовательно,

Если механизмы адаптации для массы полезной нагрузки и весовой матрицы выбраны

тогда

где λmin — наименьшее значение матрицы M¯1K1.

3.2. Адаптивный контроллер

Эффективность предложенного адаптивного регулятора массы полезной нагрузки с неопределенностью для трехмерного мостового крана может быть математически продемонстрирована устойчивостью замкнутой системы управления в следующей теореме:

4. Моделирование и экспериментальные результаты

Чтобы продемонстрировать эффективность предложенного нами алгоритма адаптивного контроллера скользящего режима на основе нейронной сети (ANNSMC) при управлении трехмерным мостовым краном в условиях неопределенности массы полезной нагрузки, мы провели эксперименты в среде синтетического моделирования, и представлены полученные результаты. в этой секции. Отмечается, что эффективность управления измеряется тем, насколько эффективно мост, тележка и лебедка трехмерного козлового крана реагируют на управляющее воздействие и можно ли привести тележку в желаемое положение с минимальными углами качания.

В экспериментах предполагалось, что массы тележки и моста известны. Также была известна длина подъемного троса, хотя предполагалось, что он будет безмассовым. Приведены некоторые постоянные параметры предлагаемого адаптивного регулятора. Эти параметры приведены в таблице 1.

Важно отметить, что в наших экспериментах мы предполагали, что полезная нагрузка неизвестна и что контроллер должен был ее адаптивно оценивать.

Для оценки неопределенных и неизвестных параметров мы разработали двухслойную RBFNN с десятью нейронными компонентами. Все веса RBFNN были инициализированы 0,1. Блок-схема моделирования в наших экспериментах представлена ​​на рис. 3.9.0003

Чтобы проверить согласованность характеристик управления в трехмерной крановой системе с учетом неопределенности массы полезной нагрузки, мы установили два разных значения массы груза, равные 10 кг и 20 кг соответственно, в двух разных операциях транспортировки, которые были неизвестны диспетчеру. Можно видеть, что хотя масса полезной нагрузки была неизвестна, в обоих сценариях работы по транспортировке сигналы управляющей силы в каждом направлении, как показано на рисунке 4, были весьма схожими. То есть управляющий ввод в основном не зависел от массы полезной нагрузки.

Теперь давайте рассмотрим выходные данные трехмерной системы мостового крана в двух проведенных сценариях транспортировки. Эта механическая система с недостаточным приводом имеет четыре выхода, включая две координаты положения тележки, как показано на рис. 5 и рис. 6, и два угла качания в каждом эксперименте, как показано на рис. 7 и рис. 8, для моделирования полезной нагрузки. массы 10 кг и 20 кг соответственно.

Из Рис. 5 и Рис. 6 ясно видно, что примерно через 5 с в обоих сценариях тележка достигла 99% от желаемой позиции. Что еще более важно, в обоих проиллюстрированных примерах реакции тележки были очень сопоставимы, хотя кран перевозил разные массы полезной нагрузки. Сходство в реакциях тележки было результатом сходных управляющих входных данных, которые были адаптивно рассчитаны с помощью RBFNN и механизмов адаптации, как показано на рисунке 4.

В дополнение к положениям тележки, два других выхода крана учитывались углы поворота полезной нагрузки, как показано на рис. 7, и постоянство характеристик управления, как показано на рис. 8, где максимальные углы раскачивания в двух представленных направлениях в любом сценарии составляли около 8 и 4 градусов. Эти характеристики предлагаемого алгоритма управления являются практически решающими с точки зрения обеспечения надежности, устойчивости и робастности замкнутой системы управления. Другими словами, разработанный контроллер очень применим.

5. Выводы

В данной статье предложена адаптивная схема управления, основанная на структуре SMC для трехмерного мостового крана с неопределенностью в условиях неопределенности массы полезной нагрузки. Кроме того, неизвестные и неопределенные параметры динамики системы предлагается адаптивно оценивать с помощью RBFNN. Предлагая механизмы адаптации, основанные на теории Ляпунова, для аппроксимации неизвестной массы полезной нагрузки и весовой матрицы, статья математически доказывает устойчивость замкнутой системы управления.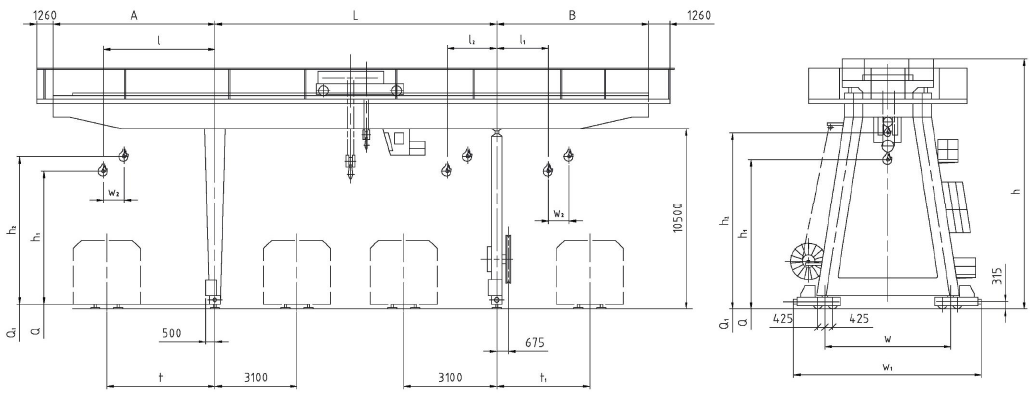 Результаты, полученные при реализации предложенного алгоритма при моделировании, показали, что тележка может достичь исходного положения за 5 с, а максимальные углы раскачивания в обе стороны составляют 8 и 4 градуса соответственно. Что еще более важно, результаты не зависели от полезной нагрузки, что продемонстрировало постоянство характеристик управления, несмотря на то, что кран перевозил полезные нагрузки с разной массой. В будущих работах мы проверим метод на реальных системах.

Вклады авторов

Все авторы проводили исследования и обсуждали решение проблемы. У.Т.Т.Х., Л.Н. и H.X.L. провел анализ и написал Раздел 2 и Раздел 3. N.H.T., H.V.P. и Л.Н. провел моделирование и написал остальную часть статьи. Все авторы прочитали и согласились с опубликованной версией рукописи.

Финансирование

Это исследование не получило внешнего финансирования.

Конфликт интересов

Авторы заявляют об отсутствии конфликта интересов.

Ссылки

1. «> Батлер, Х.; Хондэрд, Г.; Ван Амеронген, Дж. Справочная модель адаптивного управления масштабной моделью козлового крана. Система управления IEEE. Маг. 1991 , 11, 57–62. [Google Scholar] [CrossRef][Зеленая версия]
2. Юн, Дж.; Нация, С.; Синхоз, В .; Воан, Дж. Э. Контроль полезной нагрузки крана, которая подпрыгивает во время подъема. IEEE транс. Система управления Технол. 2014 , 22, 1233–1238. [Google Scholar] [CrossRef]
3. Lee, HH Планирование движения трехмерных мостовых кранов с высокоскоростным подъемом груза. Междунар. Дж. Контроль 2005 , 78, 875–886. [Google Scholar] [CrossRef]
4. Sun, N.; Ян, Т .; Чен, Х .; Фанг, Ю.К.; Цянь, Ю.З. Адаптивное управление вращением и позиционированием для поворотных кранов с четырьмя степенями свободы с учетом неопределенных/неизвестных параметров с аппаратными экспериментами. IEEE транс. Сист. Человек Киберн. Сист. 2019 , 49, 1309–1321. [Google Scholar] [CrossRef]
5. Sun, N.; Ян, Т .; Фанг, Ю.К.; Ву, Ю.М.; Чен, Х. Управление транспортировкой двухмаятниковых кранов с нелинейной квази-ПИД-схемой: проектирование и эксперименты. IEEE транс. Сист. Человек Киберн. Сист. 2019 , 49, 1408–1418. [Google Scholar] [CrossRef]
6. Саиди, Х.; Нараги, М .; Рэй, А.А. Самонастройка нейронной сети, основанная на поведении формирователей входных данных для системы предотвращения раскачивания козловых кранов. Дж. Виб. Контроль 2013 , 19, 1936–1949. [Google Scholar] [CrossRef]
7. Омар, Х.М. Управление козловыми и башенными кранами. Докторская диссертация, Политехнический институт и государственный университет Вирджинии, Блэксбург, Вирджиния, США, 2003 г. [Google Scholar]
8. Omar, H.M.; Найфех, А. Х. Противоповоротное управление козловыми и башенными кранами с использованием нечеткой обратной связи с задержкой по времени и компенсацией трения. Шок Виб. 2005 , 12, 73–89. [Google Scholar] [CrossRef][Green Version]
9. Fang, Y.; Диксон, У.Э.; Доусон, Д.М.; Зергероглу, Э. Нелинейные законы управления муфтой для системы мостового крана с недостаточным приводом. IEEE/ASME Trans. Мехатрон. 2003 , 8, 418–423. [Google Scholar] [CrossRef][Зеленая версия]
10. Ю, Дж.; Льюис, Флорида; Хуанг Т. Нелинейное управление козловым краном с обратной связью. В материалах Американской конференции по управлению IEEE, Сиэтл, Вашингтон, США, 21–23 июня 1995 г .; стр. 4310–4315. [Академия Google] [CrossRef]
11. Парк, Х.; Чва, Д.; Хонг, К.С. Управление линеаризацией контейнерных кранов с обратной связью: изменение длины каната. Междунар. J. Управление автоматом. Сист. 2007 , 5, 379–387. [Google Scholar]
12. Ле, Т.А.; Ли, С.Г.; Данг, В.Х.; Мун, С .; Ким, Б.С. Управление линеаризацией с частичной обратной связью трехмерного мостового крана. Междунар. J. Управление автоматом. Сист. 2013 , 11, 718–727. [Google Scholar] [CrossRef]
13. Ле, Т.А.; Ким, GH; Ким, М.Ю.; Ли, С.Г. Управление линеаризацией мостовых кранов с частичной обратной связью с тросами различной длины. Междунар. Дж. Точность. англ. Произв. 2012 , 13, 501–507. [Google Scholar] [CrossRef]
14. Ле, Х.; Нгуен, Л.; Тиягараджан, К.; Фам, Х. Контроллер динамической поверхности на основе адаптивной нейронной сети для роботов с двумя руками. В материалах Международной конференции IEEE по промышленной электронике и приложениям, Кристиансанд, Норвегия, 21–25 июня 2020 г. Принято. [Google Scholar]
15. Фам, Д.Т.; Нгуен, Т.В.; Ле, HX; Нгуен, Л.; Тайский, Нью-Хэмпшир; Фан, Т.А.; Фам, HT; Дуонг, А.Х.; Буй, Л.Т. Адаптивное управление динамической поверхностью на основе нейронной сети для неопределенных роботов с двумя руками. Междунар. Дж. Динам. Контроль 2019 . [Google Scholar] [CrossRef][Зеленая версия]
16. «> Ван Нгуен, Т.; Тайский, Нью-Хэмпшир; Фам, HT; Фан, Т.А.; Нгуен, Л.; Ле, HX; Нгуен, Х.Д. Адаптивный подход к управлению скользящим режимом обратного шага на основе нейронной сети для роботов с двумя руками. J. Управление автоматом. электр. Сист. 2019 , 30, 512–521. [Google Scholar] [CrossRef][Green Version]
17. Shyu, KK; Джен, CL; Шанг, Л. Дж. Проектирование скользящего регулятора для противораскачивания мостовых кранов. В материалах 31-й ежегодной конференции IEEE Industrial Electronics Society, Роли, Северная Каролина, США, 6–10 ноября 2005 г.; стр. 147–152. [Академия Google] [CrossRef]
18. Цянь, Д.В.; Йи, JQ; Чжао, Д.Б. Управление системами мостовых кранов путем комбинирования скользящего режима с нечетким регулятором. Протокол МФБ. Том. 2011 , 44, 9320–9325. [Google Scholar] [CrossRef][Зеленая версия]
19. Ле, Т.А.; Ким, Джей Джей; Ли, С.Г.; Лим, Т.Г.; Луонг, Северная Каролина. Управление скользящим режимом второго порядка трехмерного мостового крана с неопределенными параметрами системы. Междунар. Дж. Точность. англ. Произв. 2014 , 15, 811–819. [Google Scholar] [CrossRef]
20. Ngo, QH; Хонг, К.С. Плавное управление противораскачиванием морского контейнерного крана. IEEE/ASME Trans. Мехатрон. 2012 , 17, 201–209. [Google Scholar] [CrossRef]
21. Бартолини, Г.; Пизано, А .; Усаи, Э. Управление скользящим режимом контейнерных кранов второго порядка. Automatica 2002 , 38, 1783–1790. [Google Scholar] [CrossRef]
22. Махджуб, С.; Мниф, Ф .; Дербель, Н. Подходы скользящего режима второго порядка для управления классом систем с недостаточным приводом. Междунар. Дж. Автомат. вычисл. 2015 , 12, 134–141. [Google Scholar] [CrossRef]
23. Xu, WM; Чжэн, X .; Лю, YQ; Чжан, MJ; Луо, Ю.Ю. Адаптивное динамическое управление режимом скольжения для мостовых кранов. В материалах 34-й Китайской конференции по управлению IEEE, Ханчжоу, Китай, 28–30 июля 2015 г . ; стр. 3287–329.2. [Google Scholar] [CrossRef]
24. Wang, W.; Йи, Дж.; Чжао, Д .; Лю, Д. Проект стабильного регулятора скользящего режима для класса систем с недостаточным приводом второго порядка. IEEE Proc. Приложение теории управления. 2004 , 151, 630–690. [Google Scholar] [CrossRef][Зеленая версия]
25. Ван, В.; Лю, XD; Йи, Дж.К. Структурный расчет двух типов скользящих регуляторов для одного класса малоприводных механических систем. IET Control Theory Appl. 2007 , 1, 163–172. [Академия Google] [CrossRef]
26. Ян, Дж. Х.; Ян, К.С. Адаптивное управление муфтой для мостовых кранов. Мехатроника 2007 , 17, 143–152. [Google Scholar] [CrossRef]
27. Park, MS; Чва, Д.; Эом, М. Адаптивное управление противораскачиванием в скользящем режиме неопределенных мостовых кранов с высокоскоростным подъемным движением. IEEE транс. Нечеткая сист. 2014 , 22, 1262–1271. [Google Scholar] [CrossRef]
28. Tsai, C.C.; Ву, HL; Чуанг, К.Х. Интеллектуальное управление движением в скользящем режиме с использованием сетей нечетких вейвлетов для автоматических трехмерных мостовых кранов. В материалах ежегодной конференции IEEE SICE, Акита, Япония, 20–23 августа 2012 г.; стр. 1256–1261. [Академия Google]
29. Ле, Х.Х.; Ле, А.В.; Нгуен, Л. Адаптивное управление иерархическим скользящим режимом на основе нечеткого наблюдателя для неопределенных двухмерных мостовых кранов. Кибер-физ. Сист. 2019 , 5, 191–208. [Google Scholar] [CrossRef]
30. Ле, В.; Ле, Х .; Нгуен, Л.; Фан, М. Эффективная адаптивная иерархическая стратегия управления скользящим режимом с использованием нейронных сетей для трехмерных мостовых кранов. Междунар. Дж. Автомат. вычисл. 2019 , 16, 614–627. [Google Scholar] [CrossRef][Зеленая версия]
31. Туан, Лос-Анджелес; Ли, С.-Г.; Нхо, LC; Ким, Д. Х. Эталонная модель адаптивного управления режимом скольжения для трехмерных мостовых кранов. Междунар. Дж. Точность. англ. Произв. 2013 , 14, 1329–1338. [Google Scholar] [CrossRef]

Рисунок 1.
Физическая модель трехмерного мостового крана.

Рисунок 1.
Физическая модель трехмерного мостового крана.

Рисунок 2.
Нейронная сеть с радиальной базисной функцией.

Рисунок 2.
Нейронная сеть с радиальной базисной функцией.

Рисунок 3.
Блок-схема моделирования.

Рис. 3.
Блок-схема моделирования.

Рисунок 4.
Сигналы управляющей силы.

Рисунок 4.
Сигналы управляющей силы.

Рисунок 5.
Положение тележки при массе полезного груза 10 кг.

Рисунок 5.
Положение тележки при массе полезного груза 10 кг.

Рисунок 6.
Положение тележки при массе полезного груза 20 кг.

Рисунок 6.
Положение тележки при массе полезного груза 20 кг.

Рисунок 7.
Углы поворота при массе полезной нагрузки 10 кг.

Рис. 7.
Углы поворота при массе полезной нагрузки 10 кг.

Рисунок 8.
Углы поворота при массе полезной нагрузки 20 кг.

Рис. 8.
Углы поворота при массе полезной нагрузки 20 кг.

Таблица 1.
Параметры трехмерного мостового крана и характеристики его контроллера.

Таблица 1.
Параметры трехмерного мостового крана и характеристики его контроллера.

Parameters	Values ​​
Crane’s dynamic model properties
mr	50 (kg)
mc	30 (kg)
l	1 ( M)
G	9,81 (M/S2)
Характеристики адаптивного контроллера.