|
||||
|
|
звонок бесплатный
Наши сотрудники:
[email protected]
Екатерина - специалист по продаже а/м КАМАЗ
 [email protected]
[email protected]






Техника в наличии

Тягач КАМАЗ 44108-6030-24
2014г, 6х6, Евро3, дв.КАМАЗ 300 л.с., КПП ZF9, бак 210л+350л, МКБ,МОБ,рестайлинг.
цена 2 220 000 руб.,

КАМАЗ 4308-6063-28(R4)
4х2,дв. Cummins ISB6.7e4 245л.с. (Е-4),КПП ZF6S1000, V кузова=39,7куб.м., спальное место, бак 210л, шк-пет,МКБ, ТНВД BOSCH, система нейтрализ. ОГ(AdBlue), тент, каркас, рестайлинг, внутр. размеры платформы 6112х2470х730 мм
цена 1 950 000 руб.,

Самосвал КАМАЗ 6520-057
2014г, 6х4,Евро3, дв.КАМАЗ 320 л.с., КПП ZF16, ТНВД ЯЗДА, бак 350л, г/п 20 тонн, V кузова =20 куб.м.,МКБ,МОБ, со спальным местом.
цена 2 700 000 руб.,

Самосвал 6522-027
2014, 6х6, дв.КАМАЗ 740.51,320 л.с., КПП ZF16,бак 350л, г/п 19 тонн,V кузова 12куб.м.,МКБ,МОБ,задняя разгрузка,обогрев платформы.
цена 3 190 000 руб.,
СУПЕР ЦЕНА
на АВТОМОБИЛИ КАМАЗ
| 43118-010-10 (дв.740.30-260 л.с.) | 2 220 000 |
| 43118-6033-24 (дв.740.55-300 л.с.) | 2 300 000 |
| 65117-029 (дв.740.30-260 л.с.) | 2 200 000 |
| 65117-6010-62 (дв.740.62-280 л.с.) | 2 350 000 |
| 44108 (дв.740.30-260 л.с.) | 2 160 000 |
| 44108-6030-24 (дв.740.55,рест.) | 2 200 000 |
| 65116-010-62 (дв.740.62-280 л.с.) | 1 880 000 |
| 6460 (дв.740.50-360 л.с.) | 2 180 000 |
| 45143-011-15 (дв.740.13-260л.с) | 2 180 000 |
| 65115 (дв.740.62-280 л.с.,рест.) | 2 190 000 |
| 65115 (дв.740.62-280 л.с.,3-х стор) | 2 295 000 |
| 6520 (дв.740.51-320 л.с.) | 2 610 000 |
| 6520 (дв.740.51-320 л.с.,сп.место) | 2 700 000 |
| 6522-027 (дв.740.51-320 л.с.,6х6) | 3 190 000 |

подробнее про услугу перегона можно прочесть здесь.

|
Нужны самосвалы? Обратите внимание на Ford-65513-02. |
КАМАЗы в лизинг
ООО «Старт Импэкс» имеет возможность поставки грузовой автотехники КАМАЗ, а так же спецтехники на шасси КАМАЗ в лизинг. Продажа грузовой техники по лизинговым схемам имеет определенные выгоды для покупателя грузовика. Рассрочка платежа, а так же то обстоятельство, что грузовики до полной выплаты лизинговых платежей находятся на балансе лизингодателя, и соответственно покупатель автомобиля не платит налогов на имущество. Мы готовы предложить любые модели бортовых автомобилей, тягачей и самосвалов по самым выгодным лизинговым схемам.Контактная информация.
г. Набережные Челны, Промкомзона-2, Автодорога №3, база «Партнер плюс».
тел/факс (8552) 388373.
Схема проезда
fizika / Сопротивление проводников. Параллельное и последовательное соединение проводников. Какое соединение называется параллельным
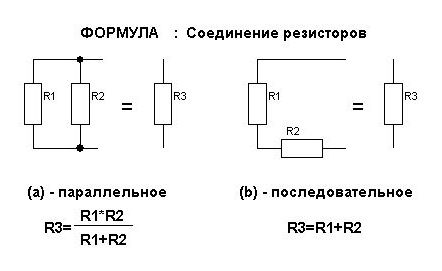
Последовательное и параллельное соединение резисторов
Последовательное соединение резисторов
Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.
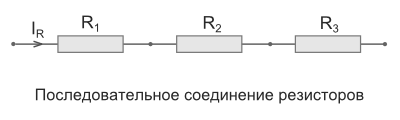
Общее сопротивление Rобщ
При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.
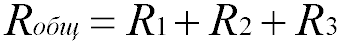
Напряжение при последовательном соединении
Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:
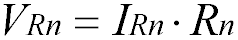
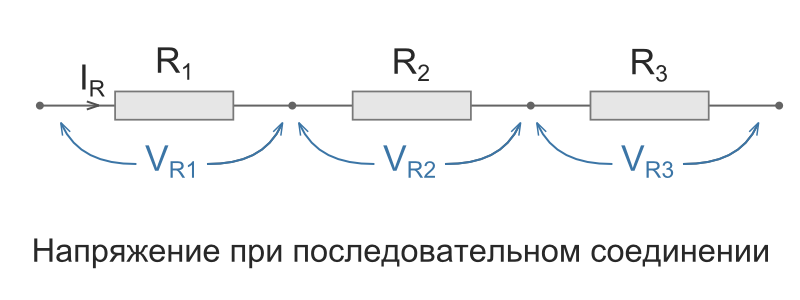
Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.
Параллельное соединение резисторов
Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.
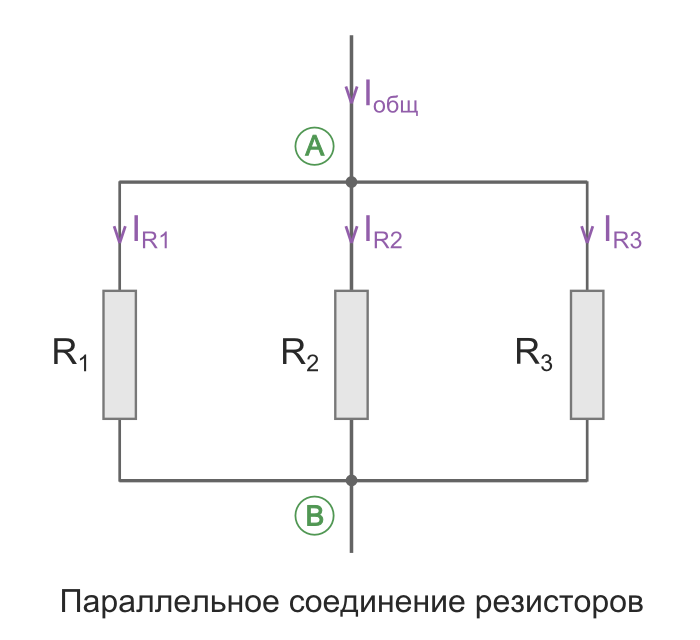
Общее сопротивление Rобщ
При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.
Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.
Формула общей проводимости при параллельном соединении резисторов:
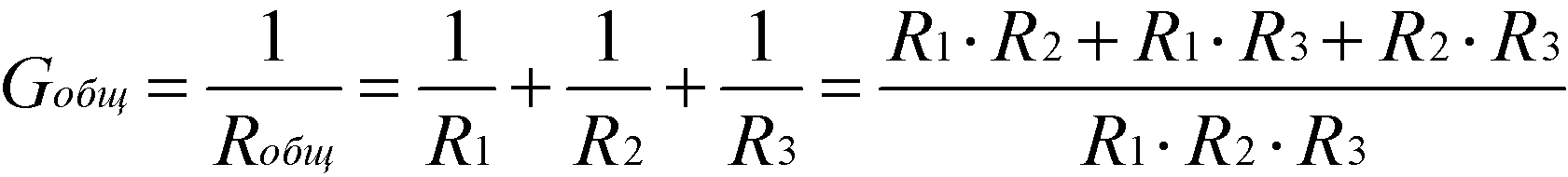
Формула эквивалентного общего сопротивления при параллельном соединении резисторов:
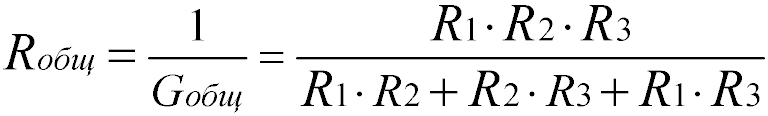
Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:
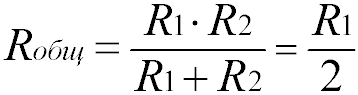
Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.
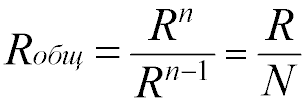
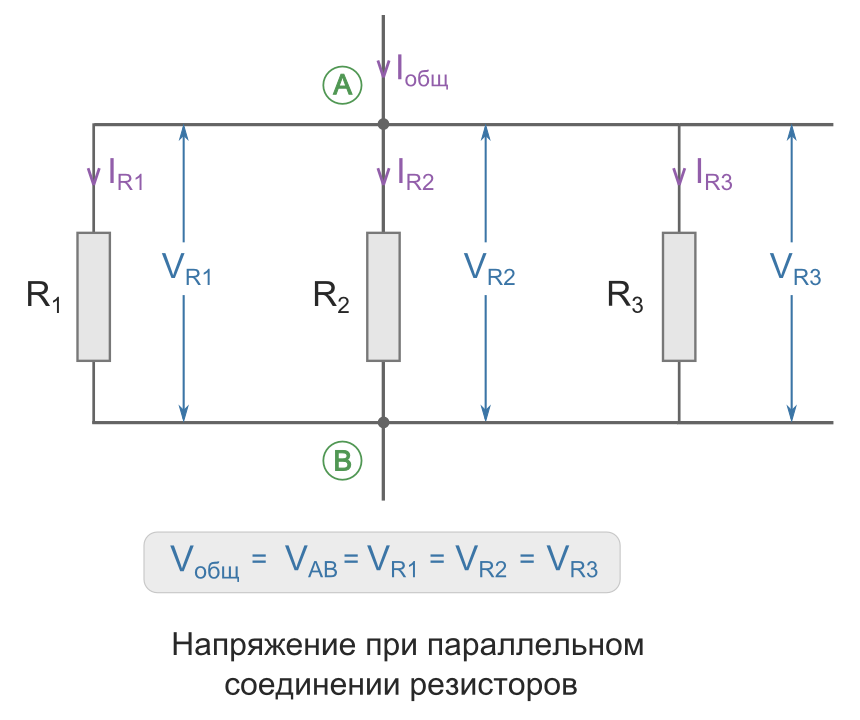
Напряжение при параллельном соединении
Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.
Электрический ток при параллельном соединении
Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора. Для того чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:
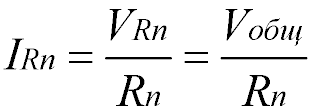
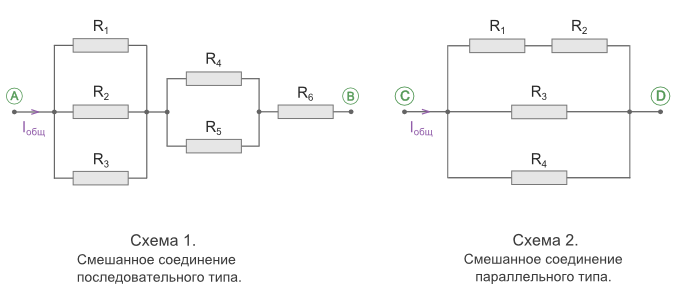
Смешанное соединение резисторов
Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно. В свою очередь, смешанное соединение бывает последовательного и параллельного типов.
Общее сопротивление Rобщ
Для того чтобы посчитать общее сопротивление смешанного соединения:
- Цепь разбивают на участки с только пареллельным или только последовательным соединением.
- Вычисляют общее сопротивление для каждого отдельного участка.
- Вычисляют общее сопротивление для всей цепи смешанного соединения.
Так это будет выглядеть для схемы 1:
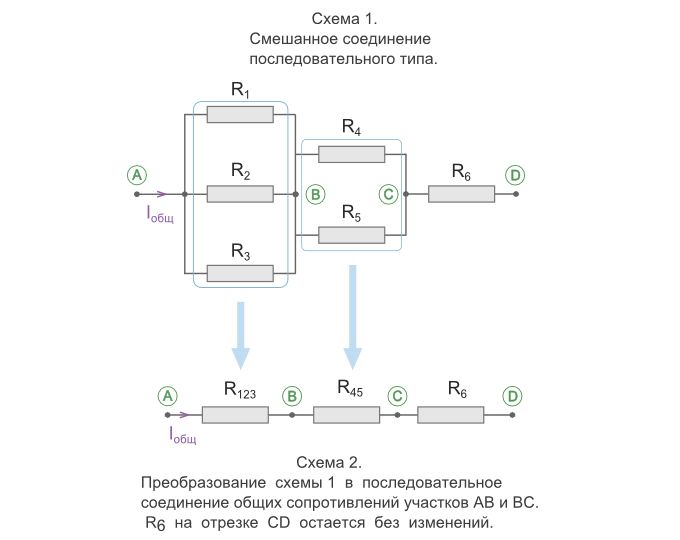
Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Можно, в соответствии схеме, сразу записывать формулу следующим образом:
- Если резисторы соединяются последоватеьно — складывать.
- Если резисторы соединяются параллельно — использовать условное обозначение «||».
- Подставлять формулу для параллельного соединения где стоит символ «||».
Так это будет выглядеть для схемы 1:
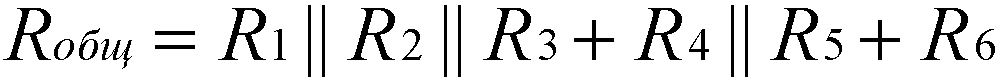
После подстановки формулы параллельного соединения вместо «||»:
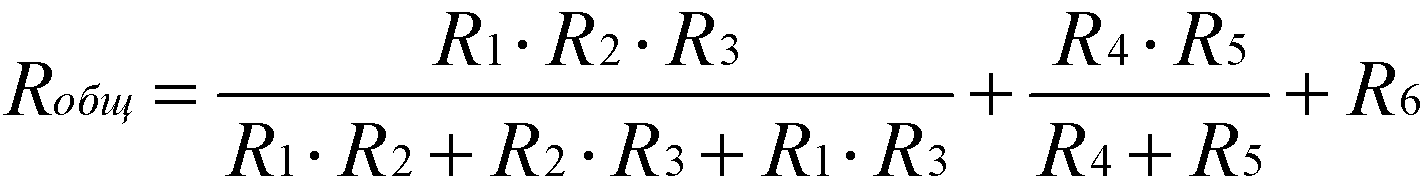
hightolow.ru
Параллельное и последовательное соединение. Последовательное и параллельное соединения проводников
В физике изучается тема про параллельное и последовательное соединение, причем это могут быть не только проводники, но и конденсаторы. Здесь важно не запутаться в том, как выглядит каждое из них на схеме. А уже потом применять конкретные формулы. Их, кстати, нужно помнить наизусть.
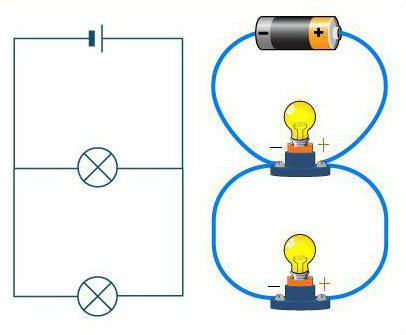
Как различить эти два соединения?
Внимательно посмотрите на схему. Если провода представить как дорогу, то машины на ней будут играть роль резисторов. На прямой дороге без каких-либо разветвлений машины едут одна за другой, в цепочку. Так же выглядит и последовательное соединение проводников. Дорога в этом случае может иметь неограниченное количество поворотов, но ни одного перекрестка. Как бы ни виляла дорога (провода), машины (резисторы) всегда будут расположены друг за другом, по одной цепочке.
Совсем другое дело, если рассматривается параллельное соединение. Тогда резисторы можно сравнить со спортсменами на старте. Они стоят каждый на своей дорожке, но направление движения у них одинаковое, и финиш в одном месте. Так же и резисторы — у каждого из них свой провод, но все они соединены в некоторой точке.
Формулы для силы тока
О ней всегда идет речь в теме «Электричество». Параллельное и последовательное соединение по-разному влияют на величину силы тока в резисторах. Для них выведены формулы, которые можно запомнить. Но достаточно просто запомнить смысл, который в них вкладывается.
Так, ток при последовательном соединении проводников всегда одинаков. То есть в каждом из них значение силы тока не отличается. Провести аналогию можно, если сравнить провод с трубой. В ней вода течет всегда одинаково. И все препятствия на ее пути будут сметаться с одной и той же силой. Так же с силой тока. Поэтому формула общей силы тока в цепи с последовательным соединением резисторов выглядит так:
I общ = I 1 = I 2
Здесь буквой I обозначена сила тока. Это общепринятое обозначение, поэтому его нужно запомнить.
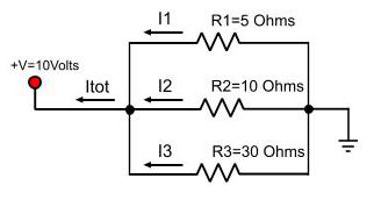
Ток при параллельном соединении уже не будет постоянной величиной. При той же аналогии с трубой получается, что вода разделится на два потока, если у основной трубы будет ответвление. То же явление наблюдается с током, когда на его пути появляется разветвление проводов. Формула общей силы тока при параллельном соединении проводников:
I общ = I 1 + I 2
Если разветвление составлено из проводов, которых больше двух, то в приведенной формуле на такое же количество станет больше слагаемых.
Формулы для напряжения
Когда рассматривается схема, в которой выполнено соединение проводников последовательно, то напряжение на всем участке определяется суммой этих величин на каждом конкретном резисторе. Сравнить эту ситуацию можно с тарелками. Удержать одну из них легко получится одному человеку, вторую рядом он тоже сможет взять, но уже с трудом. Держать в руках три тарелки рядом друг с другом одному человеку уже не удастся, потребуется помощь второго. И так далее. Усилия людей складываются.
Формула для общего напряжения участка цепи с последовательным соединением проводников выглядит так:
U общ = U 1 + U 2, где U - обозначение, принятое для электрического напряжения.
Другая ситуация складывается, если рассматривается параллельное соединение резисторов. Когда тарелки ставятся друг на друга, их по-прежнему может удержать один человек. Поэтому складывать ничего не приходится. Такая же аналогия наблюдается при параллельном соединении проводников. Напряжение на каждом из них одинаковое и равно тому, которое на всех них сразу. Формула общего напряжения такая:
U общ = U 1 = U 2
Формулы для электрического сопротивления
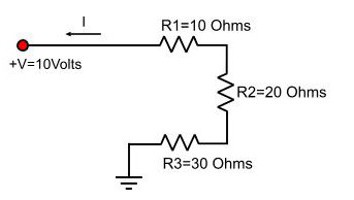
Их уже можно не запоминать, а знать формулу закона Ома и из нее выводить нужную. Из указанного закона следует, что напряжение равно произведению силы тока и сопротивления. То есть U = I * R, где R — сопротивление.
Тогда формула, с которой нужно будет работать, зависит от того, как выполнено соединение проводников:
- последовательно, значит, нужно равенство для напряжения — Iобщ * Rобщ = I1 * R1 + I2 * R2;
- параллельно необходимо пользоваться формулой для силы тока — Uобщ / Rобщ = U1 / R1 + U2 / R2 .
Далее следуют простые преобразования, которые основываются на том, что в первом равенстве все силы тока имеют одинаковое значение, а во втором — напряжения равны. Значит, их можно сократить. То есть получаются такие выражения:
- R общ = R 1 + R 2 (для последовательного соединения проводников).
- 1 / R общ = 1 / R 1 + 1 / R 2 (при параллельном соединении).
При увеличении числа резисторов, которые включены в сеть, изменяется количество слагаемых в этих выражениях.
Стоит отметить, что параллельное и последовательное соединение проводников по-разному влияют на общее сопротивление. Первое из них уменьшает сопротивление участка цепи. Причем оно оказывается меньше самого маленького из использованных резисторов. При последовательном соединении все логично: значения складываются, поэтому общее число всегда будет самым большим.
Работа тока
Предыдущие три величины составляют законы параллельного соединения и последовательного расположения проводников в цепи. Поэтому их знать нужно обязательно. Про работу и мощность необходимо просто запомнить базовую формулу. Она записывается так: А = I * U * t, где А — работа тока, t — время его прохождения по проводнику.
Для того чтобы определить общую работу при последовательном соединении нужно заменить в исходном выражении напряжение. Получится равенство: А = I * (U 1 + U 2) * t, раскрыв скобки в котором получится, что работа на всем участке равна их сумме на каждом конкретном потребителе тока.
Аналогично идет рассуждение, если рассматривается схема параллельного соединения. Только заменять полагается силу тока. Но результат будет тот же: А = А 1 + А 2.
Мощность тока
При выведении формулы для мощности (обозначение «Р») участка цепи опять нужно пользоваться одной формулой: Р = U * I. После подобных рассуждений получается, что параллельное и последовательное соединение описываются такой формулой для мощности: Р = Р 1 + Р 2.
То есть, как бы ни были составлены схемы, общая мощность будет складываться из тех, которые задействованы в работе. Именно этим объясняется тот факт, что нельзя включать в сеть квартиры одновременно много мощных приборов. Она просто не выдержит такой нагрузки.
Как влияет соединение проводников на ремонт новогодней гирлянды?
Сразу же после того, как перегорит одна из лампочек, станет ясно, как они были соединены. При последовательном соединении не будет светиться ни одна из них. Это объясняется тем, что пришедшая в негодность лампа создает разрыв в цепи. Поэтому нужно проверить все, чтобы определить, какая перегорела, заменить ее - и гирлянда станет работать.
Если в ней используется параллельное соединение, то она не перестает работать при неисправности одной из лампочек. Ведь цепь не будет полностью разорвана, а только одна параллельная часть. Чтобы отремонтировать такую гирлянду, не нужно проверять все элементы цепи, а только те, которые не светятся.
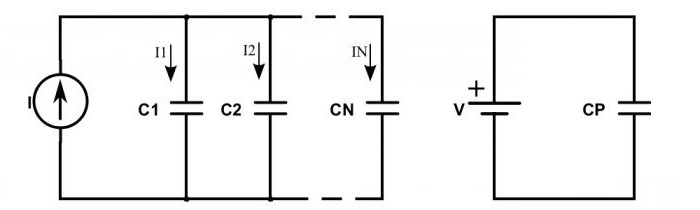
Что происходит с цепью, если в нее включены не резисторы, а конденсаторы?
При их последовательном соединении наблюдается такая ситуация: заряды от плюсов источника питания поступают только на внешние обкладки крайних конденсаторов. Те, что находятся между ними, просто передают этот заряд по цепочке. Этим объясняется то, что на всех обкладках появляются одинаковые заряды, но имеющие разные знаки. Поэтому электрический заряд каждого конденсатора, соединенного последовательно, можно записать такой формулой:
q общ = q 1 = q 2.
Для того чтобы определить напряжение на каждом конденсаторе, потребуется знание формулы: U = q / С. В ней С — емкость конденсатора.
Общее напряжение подчиняется тому же закону, который справедлив для резисторов. Поэтому, заменив в формуле емкости напряжение на сумму, мы получим, что общую емкость приборов нужно вычислять по формуле:
С = q / (U 1 + U 2).
Упростить эту формулу можно, перевернув дроби и заменив отношение напряжения к заряду емкостью. Получается такое равенство: 1 / С = 1 / С 1 + 1 / С 2.
Несколько по-другому выглядит ситуация, когда соединение конденсаторов — параллельное. Тогда общий заряд определяется суммой всех зарядов, которые накапливаются на обкладках всех приборов. А значение напряжения по-прежнему определяется по общим законам. Поэтому формула для общей емкости параллельно соединенных конденсаторов выглядит так:
С = (q 1 + q 2 ) / U.
То есть эта величина считается, как сумма каждого из использованных в соединении приборов:
С = С 1 + С 2.
Как определить общее сопротивление произвольного соединения проводников?
То есть такого, в котором последовательные участки сменяют параллельные, и наоборот. Для них по-прежнему справедливы все описанные законы. Только применять их нужно поэтапно.
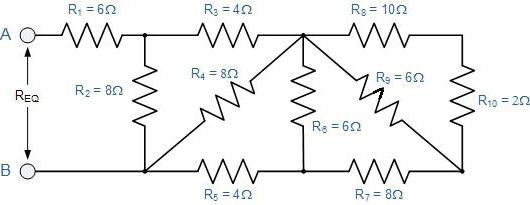
Сперва полагается мысленно развернуть схему. Если представить ее сложно, то нужно нарисовать то, что получается. Объяснение станет понятнее, если рассмотреть его на конкретном примере (см. рисунок).
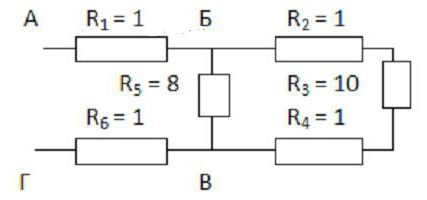
Ее удобно начать рисовать с точек Б и В. Их необходимо поставить на некотором удалении друг от друга и от краев листа. Слева к точке Б подходит один провод, а вправо направлены уже два. Точка В, напротив, слева имеет два ответвления, а после нее расположен один провод.
Теперь необходимо заполнить пространство между этими точками. По верхнему проводу нужно расположить три резистора с коэффициентами 2, 3 и 4, а снизу пойдет тот, у которого индекс равен 5. Первые три соединены последовательно. С пятым резистором они параллельны.
Оставшиеся два резистора (первый и шестой) включены последовательно с рассмотренным участком БВ. Поэтому рисунок можно просто дополнить двумя прямоугольниками по обе стороны от выбранных точек. Осталось применить формулы для расчета сопротивления:
- сначала ту, которая приведена для последовательного соединения;
- потом для параллельного;
- и снова для последовательного.
Подобным образом можно развернуть любую, даже очень сложную схему.
Задача на последовательное соединение проводников
Условие. В цепи друг за другом подсоединены две лампы и резистор. Общее напряжение равно 110 В, а сила тока 12 А. Чему равно сопротивление резистора, если каждая лампа рассчитана на напряжение в 40 В?
Решение. Поскольку рассматривается последовательное соединение, формулы его законов известны. Нужно только правильно их применить. Начать с того, чтобы выяснить значение напряжения, которое приходится на резистор. Для этого из общего нужно вычесть два раза напряжение одной лампы. Получается 30 В.
Теперь, когда известны две величины, U и I (вторая из них дана в условии, так как общий ток равен току в каждом последовательном потребителе), можно сосчитать сопротивление резистора по закону Ома. Оно оказывается равным 2,5 Ом.
Ответ. Сопротивление резистора равно 2,5 Ом.
Условие. Имеются три конденсатора с емкостями 20, 25 и 30 мкФ. Определите их общую емкость при последовательном и параллельном соединении.
Решение. Проще начать с параллельного подключения. В этой ситуации все три значения нужно просто сложить. Таким образом, общая емкость оказывается равной 75 мкФ.
Несколько сложнее расчеты будут при последовательном соединении этих конденсаторов. Ведь сначала нужно найти отношения единицы к каждой из этих емкостей, а потом сложить их друг с другом. Получается, что единица, деленная на общую емкость, равна 37/300. Тогда искомая величина получается приблизительно 8 мкФ.
Ответ. Общая емкость при последовательном соединении 8 мкФ, при параллельном — 75 мкФ.
fb.ru
Последовательное и параллельное соединение резисторов.
Как я и обещал в статье про переменные резисторы (ссылка), сегодня речь пойдет о возможных способах соединения резисторов, в частности о последовательном соединении и о параллельном.
Последовательное соединение резисторов.
Давайте начнем с рассмотрения цепей, элементы которой соединены последовательно. И хоть мы и будем рассматривать только резисторы в качестве элементов цепи в данной статье, но правила, касающиеся напряжений и токов при разных соединениях будут справедливы и для других элементов. Итак, первая цепь, которую мы будем разбирать выглядит следующим образом:
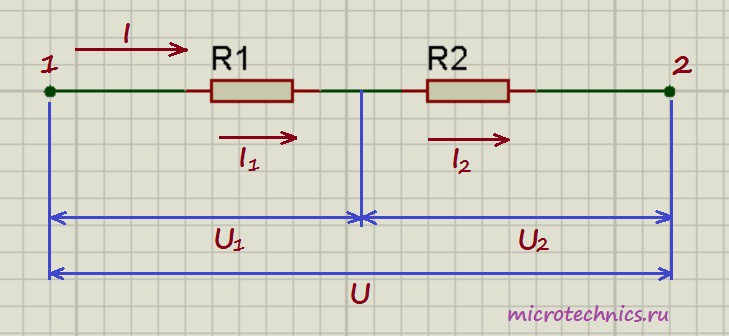
Здесь у нас классический случай последовательного соединения – два последовательно включенных резистора. Но не будем забегать вперед и рассчитывать общее сопротивление цепи, а для начала рассмотрим все напряжения и токи. Итак, первое правило заключается в том, что протекающие по всем проводникам токи при последовательном соединении равны между собой:
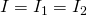
А для определения общего напряжения при последовательном соединении, напряжения на отдельных элементах необходимо просуммировать:
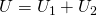
В то же время, по закону Ома для напряжений, сопротивлений и токов в данной цепи справедливы следующие соотношения:
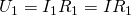
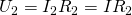
Тогда для вычисления общего напряжения можно будет использовать следующее выражение:
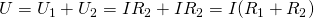
Но для общего напряжение также справедлив закон Ома:
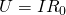
Здесь 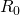 – это общее сопротивление цепи, которое исходя из двух формул для общего напряжения равно:
– это общее сопротивление цепи, которое исходя из двух формул для общего напряжения равно:
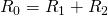
Таким образом, при последовательном соединении резисторов общее сопротивление цепи будет равно сумме сопротивлений всех проводников.
Например для следующей цепи:
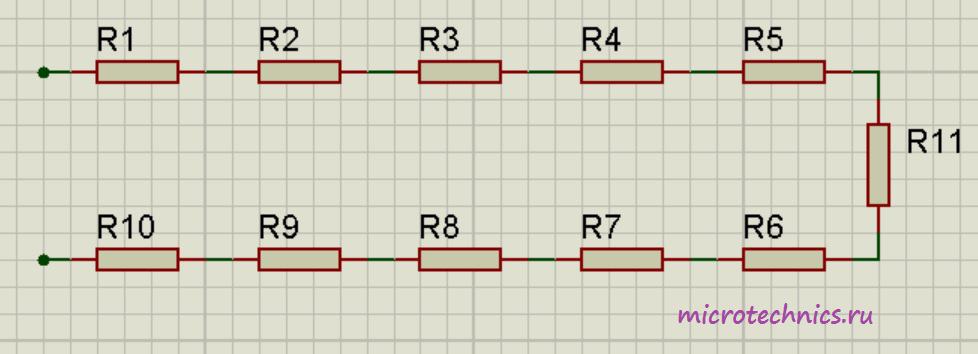
Общее сопротивление будет равно:
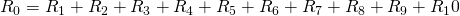
Количество элементов значения не имеет, правило, по которому мы определяем общее сопротивление будем работать в любом случае 🙂 А если при последовательном соединении все сопротивления равны (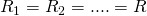 ), то общее сопротивление цепи составит:
), то общее сопротивление цепи составит:
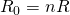
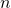 в данной формуле равно количеству элементов цепи.
в данной формуле равно количеству элементов цепи.
С последовательным соединением резисторов мы разобрались, давайте перейдем к параллельному.
Параллельное соединение резисторов.
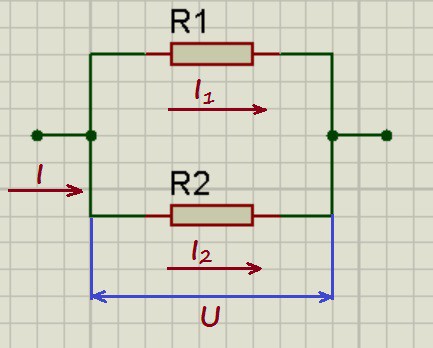
При параллельном соединении напряжения на проводниках равны:
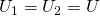
А для токов справедливо следующее выражение:
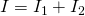
То есть общий ток разветвляется на две составляющие, а его значение равно сумме всех составляющих. По закону Ома:
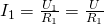
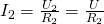
Подставим эти выражения в формулу общего тока:
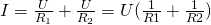
А по закону Ома ток:
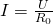
Приравниваем эти выражения и получаем формулу для общего сопротивления цепи:
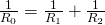
Данную формулу можно записать и несколько иначе:
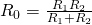
Таким образом, при параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Аналогичная ситуация будет наблюдаться и при большем количестве проводников, соединенных параллельно:
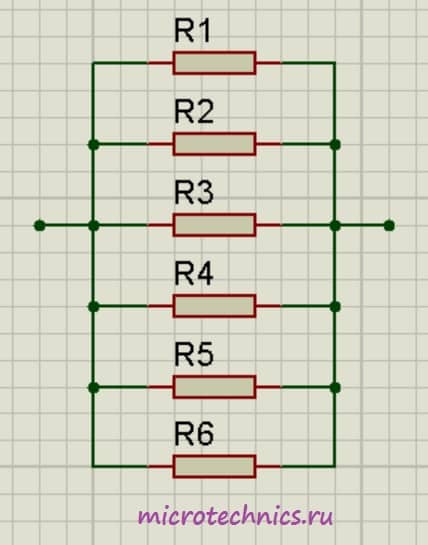
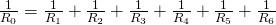
Смешанное соединение резисторов.
Помимо параллельного и последовательного соединений резисторов существует еще смешанное соединение. Из названия уже понятно, что при таком соединении в цепи присутствуют резисторы, соединенные как параллельно, так и последовательно. Вот пример такой цепи:
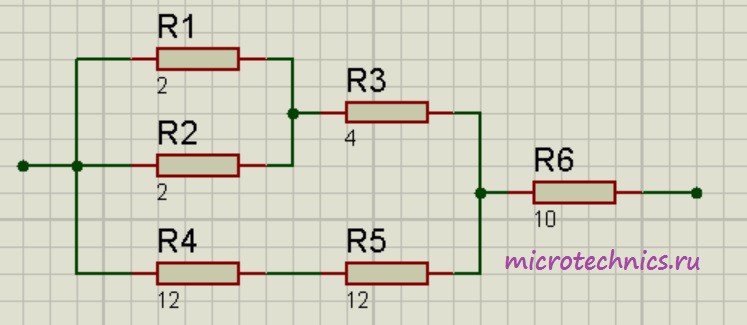
Давайте рассчитаем общее сопротивление цепи. Начнем с резисторов 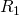 и
и 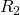 – они соединены параллельно. Мы можем рассчитать общее сопротивление для этих резисторов и заменить их в схеме одним единственным резистором
– они соединены параллельно. Мы можем рассчитать общее сопротивление для этих резисторов и заменить их в схеме одним единственным резистором 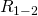 :
:
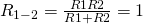
Теперь у нас образовались две группы последовательно соединенных резисторов:
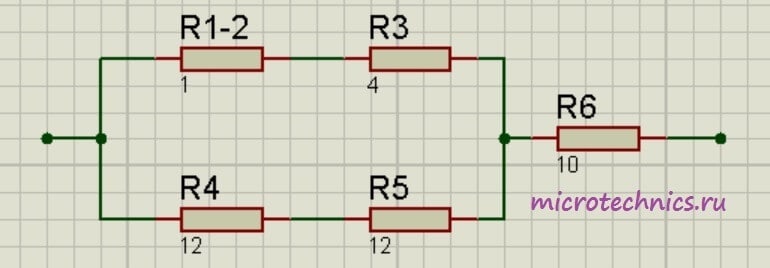
Заменим эти две группы двумя резисторами, сопротивление которых равно:
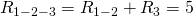
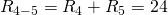
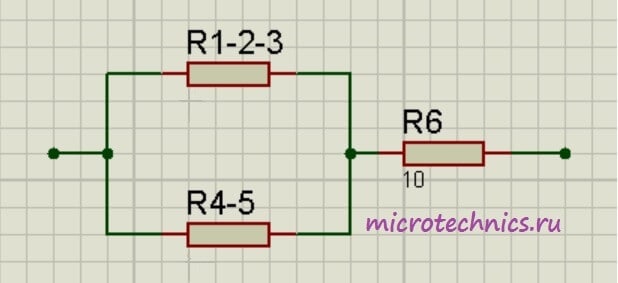
Как видите, схема стала уже совсем простой ) Заменим группу параллельно соединенных резисторов 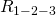 и
и 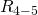 одним резистором
одним резистором 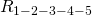 :
:
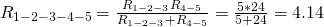
И в итоге у нас на схеме осталось только два резистора соединенных последовательно:
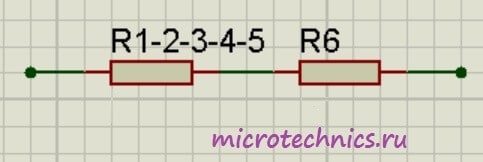
Общее сопротивление цепи получилось равным:
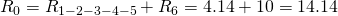
Таким вот образом достаточно большая схема свелась к простейшему последовательному соединению двух резисторов 😉
Тут стоит отметить, что некоторые схемы невозможно так просто преобразовать и определить общее сопротивление – для таких схем нужно использовать правила Кирхгофа, о которых мы обязательно поговорим в будущих статьях. А сегодняшняя статья на этом подошла к концу, до скорых встреч на нашем сайте!
microtechnics.ru
Виды соединения проводников
При решении задач принято преобразовывать схему, так, чтобы она была как можно проще. Для этого применяют эквивалентные преобразования. Эквивалентными называют такие преобразования части схемы электрической цепи, при которых токи и напряжения в не преобразованной её части остаются неизменными.
Существует четыре основных вида соединения проводников: последовательное, параллельное, смешанное и мостовое.
Последовательное соединение – это такое соединение, при котором сила тока на всем участке цепи одинакова. Ярким примером последовательного соединения является старая елочная гирлянда. Там лампочки подключены последовательно, друг за другом. Теперь представьте, одна лампочка перегорает, цепь нарушена и остальные лампочки гаснут. Выход из строя одного элемента, ведет за собой отключение всех остальных, это является существенным недостатком последовательного соединения.

При последовательном соединении сопротивления элементов суммируются.

Параллельное соединение – это соединение, при котором напряжение на концах участка цепи одинаково. Параллельное соединение наиболее распространено, в основном потому, что все элементы находятся под одним напряжением, сила тока распределена по-разному и при выходе одного из элементов все остальные продолжают свою работу.

При параллельном соединении эквивалентное сопротивление находится как:

В случае двух параллельно соединенных резисторов
В случае трех параллельно подключенных резисторов:


Смешанное соединение – соединение, которое является совокупностью последовательных и параллельных соединений. Для нахождения эквивалентного сопротивления нужно, “свернуть” схему поочередным преобразованием параллельных и последовательных участков цепи.

Сначала найдем эквивалентное сопротивление для параллельного участка цепи, а затем прибавим к нему оставшееся сопротивление R3. Следует понимать, что после преобразования эквивалентное сопротивление R1R2 и резистор R3, соединены последовательно.

Итак, остается самое интересное и самое сложное соединение проводников.
Мостовая схема соединения представлена на рисунке ниже.

Для того чтобы свернуть мостовую схему, один из треугольников моста, заменяют эквивалентной звездой.

И находят сопротивления R1, R2 и R3.

Затем находят общее эквивалентное сопротивление, учитывая, что резисторы R3,R4 и R5,R2 соединены между друг другом последовательно, а в парах параллельно.

На этом всё! Примеры расчета сопротивления цепей тут.
electroandi.ru
fizika / Сопротивление проводников. Параллельное и последовательное соединение проводников
Сопротивление проводников. Параллельное и последовательное соединение проводников.
Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношениюнапряжения на концах проводника к силе тока, протекающего по нему[1]. Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиями импеданса и волнового сопротивления. Сопротивлением (резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления.
Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как
где
R — сопротивление;
U — разность электрических потенциалов (напряжение) на концах проводника;
I — сила тока, протекающего между концами проводника под действием разности потенциалов.
При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:
| Рисунок 1.9.1. Последовательное соединение проводников |
По закону Ома, напряжения U1 и U2 на проводниках равны
| U1 = IR1, U2 = IR2. |
Общее напряжение U на обоих проводниках равно сумме напряжений U1 и U2:
| U = U1 + U2 = I(R1 + R2) = IR, |
где R – электрическое сопротивление всей цепи. Отсюда следует:
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Этот результат справедлив для любого числа последовательно соединенных проводников.
При параллельном соединении (рис. 1.9.2) напряжения U1 и U2 на обоих проводниках одинаковы:
Сумма токов I1 + I2, протекающих по обоим проводникам, равна току в неразветвленной цепи:
Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд IΔt, а утекает от узла за то же время заряд I1Δt + I2Δt. Следовательно,I = I1 + I2.
| Рисунок 1.9.2. Параллельное соединение проводников |
Записывая на основании закона Ома
где R – электрическое сопротивление всей цепи, получим
| |
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Этот результат справедлив для любого числа параллельно включенных проводников.
Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.
| Рисунок 1.9.3. Расчет сопротивления сложной цепи. Сопротивления всех проводников указаны вомах (Ом) |
Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.
| Рисунок 1.9.4. Пример электрической цепи, которая не сводится к комбинации последовательно и параллельно соединенных проводников |
studfiles.net
Соединяем проводники в электроустановках: последовательно или паралелльно
Прохождение тока в любых электрических цепочках реализуется посредством отдельных электротехнических проводников (кабелей), подключаемых по определённой схеме. В зависимости от поставленной задачи, в линейной электрической цепи применяются различные виды включения потребителей, которые могут подсоединяться как последовательно, так и параллельно.
Последовательное соединение
В отдельных случаях возможно использование обоих видов соединения проводников (так называемое «смешанное» подключение), которое, наряду с другими способами, должно учитываться при разработке и ремонте любой электроустановки.
Последовательное соединение
Широкое распространение в электротехнике получили последовательные и параллельные схемы соединения радиотехнических деталей, входящих в те или иные устройства. При рассмотрении вопроса о том, какое соединение проводников называют последовательным, следует учитывать, что в этом случае они располагаются в цепочку чередующихся один за другим компонентов. Их механическое сопряжение, или спайка, осуществляется согласно действующему в электротехнике стандарту (ПУЭ). Рассмотрим особенности такого включения на примере линии с двумя пассивными составляющими (обычными резисторами).
Для обозначения протекающего в ней тока, приложенного напряжения и сопротивления каждой из деталей используем общепринятые символы I1, U1, R1 и I2, U2, R2 соответственно.
Воспользовавшись законом Кирхгофа, получим:
I = I1 = I2, U = U1 + U2, R = R1 + R2.
К сведению. Все эти выкладки подтверждаются экспериментальной проверкой, состоящей в измерении электрических параметров посредством обычного мультиметра.
Анализ уже рассмотренных ранее формул, иллюстрирующих такое соединение проводов и нагрузок, позволяет отметить следующие особенности:
- Значение тока во всех включённых в линию элементах цепочки будет иметь одну и ту же величину;
- Разность потенциалов между входной и выходной её точками складывается из падений напряжений на каждом отдельном (дискретном) элементе;
- Общее или суммарное сопротивление всего участка находится как сумма тех же значений для каждого из проводников.
Указанные соотношения справедливы для любого числа потребителей, соединенных по простейшей линейной схеме. При этом значение суммарного сопротивления будет всегда иметь большую величину, чем тот же параметр для любого отдельного элемента.
При включении в обследуемую линию N одинаковых по номиналу пассивных элементов общее их сопротивление можно представить формулой:
R = N х R1,
где R1 – номинал отдельно взятой детали. Напряжение U здесь распределяется между резисторами равномерно, образуя падение на каждом из них, в N раз меньшее приложенного ко всему участку значения.
В качестве примера рассмотрим ситуацию, когда в бытовую сеть с действующим напряжением 220 В включены последовательно десять лампочек с одинаковой мощностью. При таком варианте подключения напряжение на каждой из них будет составлять:
U1 = U/10 = 22 В.
Обратите внимание! Особенностью соединённых в одну линию проводников или нагрузок является её аварийный обрыв при сгорании хотя бы одного из соединённых таким образом компонентов.
Следствием повреждения одного элемента линейной цепочки является пропадание тока во всей схеме.
Параллельное включение
Для того чтобы определиться с тем, какое соединение называется параллельным, следует представить себе схему, в которой все входные и выходные контакты каждого из N проводников собраны вместе (в один узел).
Параллельное включение
Такая схема может содержать любое разумное количество «ответвлений» из всевозможных потребителей. Общий ток в этом случае может быть представлен как сумма отдельных составляющих, протекающих по каждой из N цепочек. При таком подключении ток в одном потребителе определяется приложенным к нему общим напряжением и сопротивлением каждого отдельного ответвления.
Важно! Общий ток в линии распределяется между этими N проводниками-потребителями пропорционально сопротивлению каждого из них. При этом он всегда вычисляется как сумма составляющих, протекающих по любому из N ответвлений.
Известные правила подключения параллельных цепей также вытекают из закона Кирхгофа, согласно которому сумма втекающих в узел токов должна быть равна сумме вытекающих. В частном случае, когда сопротивления всех N проводников равны по величине, токи через каждый из них будут иметь одинаковые величины, равные N-ой части общего токового значения.
Суммарное сопротивление цепочки из нескольких соединённых «в параллель» проводников вычисляется по следующей формуле:
Расчёт сопротивления
Исходя из этого значения, легко рассчитать суммарный ток через всю образованную таким образом сложную цепочку, воспользовавшись уже полученными ранее данными. Он будет равен приложенному к линии напряжению, делённому на определённое согласно формуле сопротивление.
Дополнительная информация. Иногда для удобства расчётов вместо сопротивлений пассивных элементов (резисторов) используется обратная им величина, называемая проводимостью.
После введения показателя проводимости все расчётные формулы, используемые ранее, заметно упрощаются. Проводимости в этом случае просто складываются подобно тому, как ранее это делалось для резистивных номиналов деталей, включённых в последовательную цепочку.
Смешанное подключение
Схема
С примером смешанного соединения нескольких нагрузок (потребителей) можно ознакомиться на размещённой ниже картинке.
Смешанное подсоединение
Такое включение отдельных звеньев потребления наиболее часто встречается в типовых электрических схемах или на их участках. Последовательно-параллельное расположение проводников предполагает сложный расчёт величин токов и сопротивлений, включающий в себя уже рассмотренные выше варианты.
Расчёт
Методика таких вычислений построена на следующих принципах:
- Сначала электрическая схема разбивается на более простые и поддающиеся элементарному расчёту части;
- После этого каждый из таких участков, представленных простым типом включения, рассчитывается независимо от остальных частей;
Важно! В результате этой операции звенья с параллельно соединенными нагрузками приводятся к последовательному виду.
- На завершающей стадии расчёта все полученные для отдельных участков параметры суммируются по методике, описанной ранее для последовательного соединения.
В результате такого подхода расчёт сложных последовательно-параллельных цепей удаётся свести к элементарным или типовым операциям, производимым на основании законов Кирхгофа и Ома.
В заключение несколько слов о практическом применении рассмотренных видов включения. Так, самый распространённый из них (смешанный) применяется при изготовлении обмоток таких широко распространенных электротехнических изделий, как известные всем электродвигатели (смотрите ПУЭ). С его же помощью обустраиваются промышленные осветительные сети, обслуживающие значительные по площади объекты, а также типовая квартирная электропроводка.
Видео
Оцените статью:elquanta.ru
Параллельное соединение сопротивлений в электрической цепи. Параллельное соединение конденсаторов и катушек.
Определение параллельного соединения
Параллельное соединение электрических элементов (проводников, сопротивлений, емкостей, индуктивностей) - это такое соединение, при котором подключенные элементы цепи имеют два общих узла подключения.
Другое определение: сопротивления подключены параллельно, если они подключены одно и той же паре узлов.
Графическое обозначение схемы параллельного соеднинения
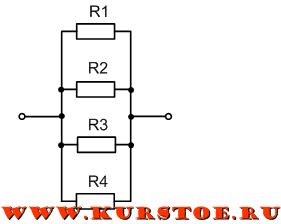
На приведенном рисунке показана схема параллельное подключения сопротивлений R1, R2, R3, R4. Из схемы видно, что все эти четыре сопротивления имеют две общие точки (узла подключения).
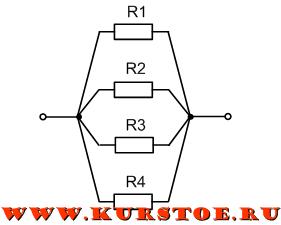
В электротехнике принято, но не строго требуется, рисовать провода горизонтально и вертикально. Поэтому эту же схему можно изобразить, как на рисунке ниже. Это тоже параллельное соединение тех же самых сопротивлений.
Формула для расчета параллельного соединения сопротивлений
При параллельном соединении обратная величина от эквивалентного сопротивления равна сумме обратных величин всех параллельно подключенных сопротивлений. Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.
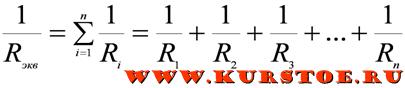
Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:
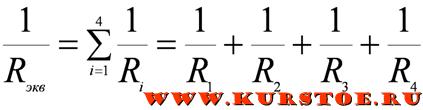
В частном случае при подключении параллельно двух сопротивлений:
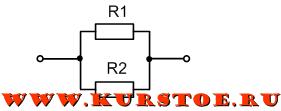
Эквивалентное сопротивление цепи определяется по формуле:
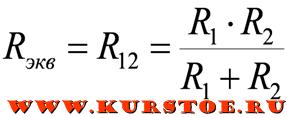
В случае подключения "n" одинаковых сопротивлений, эквивалентное сопротивление можно рассчитать по частной формуле:
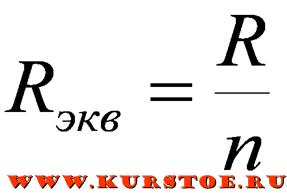
Формулы для частного рассчета вытекают из основной формулы.
Формула для расчета параллельного соединения емкостей (конденсаторов)
При параллельном подключении емкостей (конденсаторов) эквивалентная емкость равна сумме параллельно подключенных емкостей:
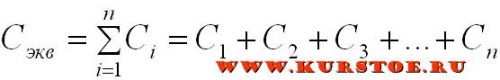
Формула для расчета параллельного соединения индуктивностей
При параллельном подключении индуктивностей, эквивалентная индуктивность рассчитывается так же, как и эквивалентное сопротивление при параллельном соединении:
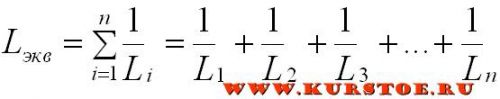
Необходимо обратить внимание, что в формуле не учтены взаимные индуктивности.
Пример свертывания параллельного сопротивления
Для участка электрической цепи необходимо найти параллельное соединение сопротивлений выполнить их преобразование до одного.
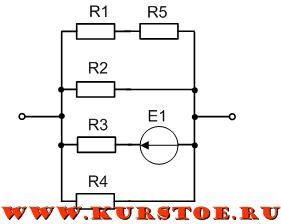
Из схемы видно, что параллельно подключены только R2 и R4. R3 не параллельно, т.к. одним концом оно подключено к источнику ЭДС E1. R1 - одним концом подключено к R5, а не к узлу. R5 - одним концом подключено к R1, а не к узлу. Можно так же говорить, что последовательное соединение сопротивлений R1 и R5 подключено параллельно с R2 и R4.
Рассчитать эквивалентное сопротивлений R14 можно по формуле для двух сопротивлений.
Ток при параллельном соединении
При параллельном соединении сопротивлений ток через каждое сопротивление в общем случае разный. Величина тока обратно пропорциональна величине сопротивления.
Напряжение при параллельном соединении
При параллельном соединении разность потенциалов между узлами, объединяющими элементы цепи, одинакова для всех элементов.
Применение параллельного соединения
1. В промышленности изготавливаются сопротивления определенных величин. Иногда необходимо получить значение сопротивления вне данных рядов. Для этого можно подключить несколько сопротивлений параллельно. Эквивалентное сопротивление всегда будет меньше самого большого номинала сопротивления.
2. Делитель токов.
www.kurstoe.ru
423800, Набережные Челны , база Партнер Плюс, тел. 8 800 100-58-94 (звонок бесплатный)






