|
Двигатель Игоря Высоцкого. Буквой F обозначена центробежная сила, ускоряющая жидкость.
Спиральный центробежный двигатель
Спиральный центробежный двигатель
Боковое сечение спирального центробежного двигателя. Rc — радиус колеса (спирали), расстояние от оси вращения до центра сопла; Rз — радиус от оси вращения до центра заборника; Sз — площадь забора жидкости на входе трубки; Sc — площадь сопла на выходе трубки.
Sз · vз · ρз = Sc · vc · ρc (1),
где S — площадь сечения трубки в выбранном месте, v — скорость потока в этом месте, а ρ — его плотность в рассматриваемом сечении.
v = f · (2 · π · r) (2),
где f — частота вращения (обороты в секунду), r — радиус вращения (здесь и далее маленькой буквой r будем обозначать текущий радиус для рассматриваемого в данный момент участка спирали).
Sз / Sc > Rc / Rз (3).
U(r) = Rr∫ aц(x) · dx = Rr∫ (f · 2 · π · x)2 / x · dx = (f · 2 · π)2 · (r – R)2 / 2 = 2 · (f · π · (r – R))2 (4),
где r — радиус вращения рассматриваемого сечения, R = Rc — радиус спирали, равный расстоянию от центра сопла до оси вращения (радиус нулевого потенциала, у оси вращения потенциал максимален), aц — центростремительное ускорение, f — частота вращения спирали вокруг оси.
ΔP = ρ · Uз = ρ · 2 · (f · π · (Rс – Rз))2 (5).
Δvc2 / 2 = (f · 2 · π)2 · (Rс – Rз)2 / 2,
откуда следует, что скорость возле сопла превышает скорость возле заборника на
Δv = f · 2 · π · (Rс – Rз) (6).
Pатм + ρ · vс2 / 2 = ρ · Uз + Pатм + ρ · vт2 / 2,
сократив подобные члены (атмосферное давление), поделив всё на плотность (которая для жидкости является величиной практически неизменной), получаем
(k · vт)2 / 2 = Uз + vт2 / 2.
Переносим скорости в одну часть уравнения и, умножая обе части на 2, получаем
(k · vт)2 – vт2 = 2 · Uз.
Теперь выносим квадрат скорости за скобки и заменяем потенциал на формулу (4):
vт2 · (k2 – 1) = (f · 2 · π · (Rт – Rс))2,
откуда вычисляем скорость потока внутри трубки
vт2 = (2 · π · f · (Rз – Rс))2 / (k2 – 1) (7).
Кстати, если давление на входе спирали будет превышать давление на выходе сопла на ΔP (жидкость подаётся в спираль под давлением), то формула примет следующий вид:
vт2 = ((2 · π · f · (Rз – Rс))2 + 2 · ΔP / ρ) / (k2 – 1) (8).
Таблица 1. Расчёт скорости потока для различных параметров вращения
Спираль или «рога»?
Вариант с твёрдыми шарами (одна ветвь, вид сверху).
Немного истории
Резюме
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
последняя правка 17.11.2009 22:22:13 |
|
Статья легализует центробежные двигатели,
|
|
|
|
Рассмотрим свободно вращающуюся массу
|
|
|
|
Таким образом произошло преобразование вращения в
|
|
|
|
Чтобы тело под действием ЦБСИ начало
|
|
|
|
(и количества движения mV) из-за
|
|
|
|
В сечениях I-I и II-II уравнение
|
|
|
|
где
|
|
|
|
и
|
|
|
|
а -
|
|
|
|
и
|
|
|
|
Если же тело движется под действием ЦБСИ от центра
1. Слепая и примитивная вера в ЗСЭ, в частности, что
Автор:
|
|
|
Центробежная сила — что это такое?
Перейти к содержимому Центробежная сила — что это такое?
Слова «центробежная сила» впервые были использованы в 1698 году, так что это далеко не новое понятие. Словарное определение — это «кажущаяся сила, которую ощущает объект, движущийся по криволинейной траектории, действующей наружу от центра вращения».
Все мы ощущали действие центробежной силы, когда вели машину или грузовик и поворачивали на высокой скорости.
Пока мы движемся по прямой линии, мы не чувствуем эту силу, но когда мы съезжаем с шоссе на высокой скорости на круговой пандус 270 градусов, мы чувствуем, как сила тянет нас в противоположном направлении, в котором мы поворачиваем. .
В промышленном мире эта сила постоянно присутствует во всем вращающемся оборудовании. Ротор каждого двигателя испытывает действие центробежной силы по мере увеличения скорости вращения. На вращающихся элементах центробежные силы возрастают с квадратом скорости. То есть сила не линейна со скоростью — она квадратична по мере увеличения скорости или оборотов в минуту. Как ремонтная компания, мы динамически балансируем все вращающиеся части двигателя – ротор, вентилятор, муфту или шкив. Путем балансировки мы уменьшаем центробежную силу тяжелого места, оказывающего чрезмерную силу на вращающуюся часть, что приводит к чрезмерной вибрации и преждевременному выходу из строя подшипников, посадки вала и т. д. Все промышленное оборудование имеет максимальные обороты в минуту (об/мин) на заводской табличке.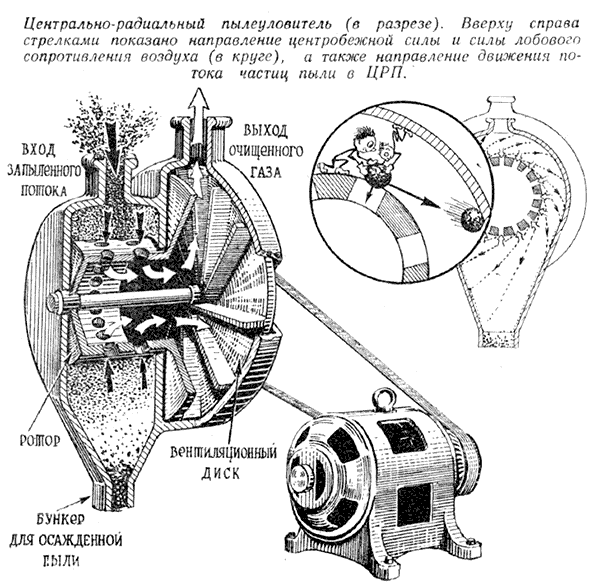 . Это определяет безопасный диапазон скоростей, в котором оборудование было разработано для работы. Когда скорость вращения превышает номинальную, центробежные силы могут привести к выходу из строя вращающихся компонентов с разрушительными последствиями. Наша компания предоставила комплексному заказчику двигатель постоянного тока мощностью 600 л.с. для выемки гравия из карьера. Двигатель приводит в действие редуктор, который приводит в движение барабан подъемного троса, который поднимает большой ковш, полный материала. Когда загруженный ковш находится в точке максимального подъема, стопорный тормоз фиксирует груз, а двигатель останавливается. Что ж, стопорный тормоз вышел из строя, и загруженный ковш упал с предельной скоростью — 120 + миль в час. Теперь, когда нагрузка приводит в движение коробку передач, она становится средством увеличения скорости, а не редуктором, в результате чего число оборотов двигателя приближается к 10 000 об/мин. Обратите внимание, что двигатель рассчитан на максимальную скорость 2700 об/мин, поэтому превышение скорости двигателя составило примерно 3-кратное номинальное число оборотов в минуту.
. Это определяет безопасный диапазон скоростей, в котором оборудование было разработано для работы. Когда скорость вращения превышает номинальную, центробежные силы могут привести к выходу из строя вращающихся компонентов с разрушительными последствиями. Наша компания предоставила комплексному заказчику двигатель постоянного тока мощностью 600 л.с. для выемки гравия из карьера. Двигатель приводит в действие редуктор, который приводит в движение барабан подъемного троса, который поднимает большой ковш, полный материала. Когда загруженный ковш находится в точке максимального подъема, стопорный тормоз фиксирует груз, а двигатель останавливается. Что ж, стопорный тормоз вышел из строя, и загруженный ковш упал с предельной скоростью — 120 + миль в час. Теперь, когда нагрузка приводит в движение коробку передач, она становится средством увеличения скорости, а не редуктором, в результате чего число оборотов двигателя приближается к 10 000 об/мин. Обратите внимание, что двигатель рассчитан на максимальную скорость 2700 об/мин, поэтому превышение скорости двигателя составило примерно 3-кратное номинальное число оборотов в минуту.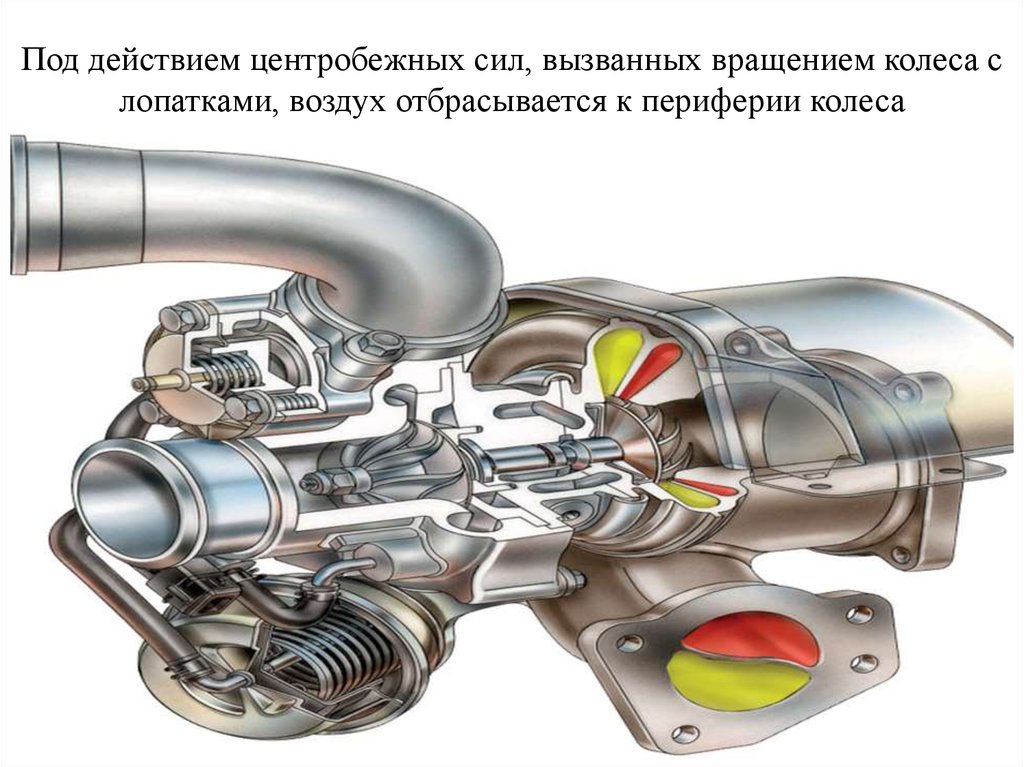 На фотографиях видно, как коллекторные стержни взорвались с такой силой, что сломали отливку толщиной ½ дюйма 9.0005 железная рама двигателя. Повреждение мотора выглядит так, будто взорвалась взрывчатка, такая как ручная граната или C-4.
На фотографиях видно, как коллекторные стержни взорвались с такой силой, что сломали отливку толщиной ½ дюйма 9.0005 железная рама двигателя. Повреждение мотора выглядит так, будто взорвалась взрывчатка, такая как ручная граната или C-4.
Другим примером превышения скорости двигателя является ситуация, когда двигатель постоянного тока теряет ток шунтирующего поля, но привод постоянного тока не отключает ток якоря. Когда возникает такая ситуация, двигатель постоянного тока становится двигателем последовательного типа, и число оборотов в минуту продолжает увеличиваться до тех пор, пока центробежная сила не остановит его, разорвав бандаж и позволив обмоткам якоря выйти из сердечника якоря. Я был свидетелем этой ситуации на объекте заказчика во время выездного обслуживания. Мотор звучал, как реактивный двигатель, разгоняющийся перед взлетом, пока не дошел до 9.0005 внезапная остановка с очень громким хлопком. Маленькая подкладка к этому темному облаку заключалась в том, что мы получили хороший мотор и отремонтировали машину из этой плохой ситуации!
Жаклин Кин2021-01-10T16:32:56-05:00 Ссылка для загрузки страницы
В начало
Что такое центробежные и центростремительные силы?
(Изображение предоставлено: Энтони Чинг/Getty Images)
Центростремительные и центробежные силы — это силы, действующие на вращающиеся объекты. Центростремительная сила заставляет объект двигаться по кругу и всегда направлена к центру этого круга. Например, гравитационная сила Солнца является центростремительной силой, удерживающей Земля вращается вокруг нее. Между тем, центробежная сила — это кажущаяся внешняя сила, действующая на объект, который движется по кругу. Примером центробежной силы может быть ощущение, возникающее при езде на карусели, которое заставляет вас лететь наружу.
Центростремительная сила заставляет объект двигаться по кругу и всегда направлена к центру этого круга. Например, гравитационная сила Солнца является центростремительной силой, удерживающей Земля вращается вокруг нее. Между тем, центробежная сила — это кажущаяся внешняя сила, действующая на объект, который движется по кругу. Примером центробежной силы может быть ощущение, возникающее при езде на карусели, которое заставляет вас лететь наружу.
Разница между центростремительной и центробежной силами
Основное различие между центростремительной и центробежной силами заключается в том, что центростремительная сила — это сила, направленная к центру окружности, которая заставляет объект двигаться по круговой траектории, а центробежная сила — это сила, направленная к центру окружности. ощущение, которое испытывает объект, когда он движется по этой круговой траектории, причем это ощущение как бы отталкивает его от центра круга.
Люди испытывают на себе действие центробежной силы, когда поворачивают за угол в автомобиле или когда самолет входит в поворот. Это происходит при отжиме стиральной машины или когда дети катаются на каруселях. Однажды она может даже обеспечить искусственную гравитацию для космических кораблей и космических станций — если мы сможем заставить космический корабль вращаться достаточно быстро, центробежная сила может обеспечить некоторое подобие нормального ощущения гравитации.
Это происходит при отжиме стиральной машины или когда дети катаются на каруселях. Однажды она может даже обеспечить искусственную гравитацию для космических кораблей и космических станций — если мы сможем заставить космический корабль вращаться достаточно быстро, центробежная сила может обеспечить некоторое подобие нормального ощущения гравитации.
Но центробежную силу часто путают с ее аналогом, центростремительной силой, потому что они очень тесно связаны — по сути, это две стороны одной медали.
Центростремительная сила — это название, данное любой силе, которая заставляет объект двигаться по кругу — подумайте о камне, привязанном к концу веревки, а другой конец — к чему-то или в вашей руке. Когда струна закручена, натяжение этой струны не дает камню улететь по прямой линии. Это напряжение направлено внутрь, к центру круга. В качестве другого примера, гравитация Солнца обеспечивает центростремительную силу, которая заставляет планеты двигаться по своим орбитам.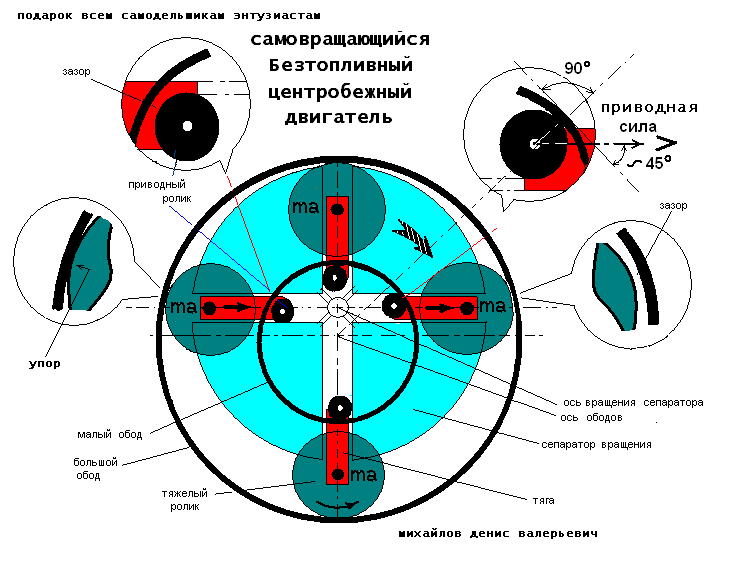
Центростремительная сила всегда направлена перпендикулярно направлению движения объекта. Если вы едете в машине, а дорога изгибается и поворачивает влево, нормальная сила от дороги с креном будет толкать машину влево. Если бы центростремительная сила внезапно исчезла, автомобиль продолжал бы двигаться прямолинейно.
С другой стороны, центробежная сила — это кажущаяся сила, которую ощущает объект, когда он движется по криволинейной траектории, и эта кажущаяся сила направлена в направлении от центра траектории вращения, согласно Кристоферу С. Бэрду. в West Texas A&M University (открывается в новой вкладке).
Центробежная сила направлена наружу, а центростремительная притягивает вращающийся объект внутрь. (Изображение предоставлено: Future)
Обратите внимание, что хотя центростремительная сила является фактической силой, центробежная сила определяется как кажущаяся сила. Другими словами, при вращении массы на струне струна воздействует на массу внутренней центростремительной силой, в то время как масса «кажется» воздействующей на струну внешней центробежной силой.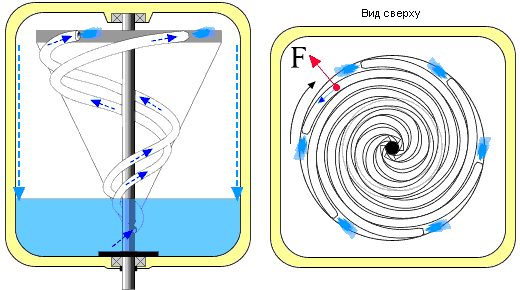
«Разница между центростремительной и центробежной силой связана с разными «системами отсчета», то есть с разными точками зрения, с которых вы что-то измеряете», — сказал Эндрю А. Ганс, физик-исследователь из Вашингтонского университета. «Центростремительная сила и центробежная сила на самом деле являются одной и той же силой, только в противоположных направлениях, потому что они воспринимаются из разных систем отсчета».
Если вы наблюдаете за вращающейся системой снаружи, вы видите внутреннюю центростремительную силу, которая заставляет вращающееся тело двигаться по круговой траектории. Однако, если вы являетесь частью вращающейся системы, вы испытываете кажущуюся центробежную силу, отталкивающую вас от центра круга, хотя на самом деле вы ощущаете внутреннюю центростремительную силу, которая не дает вам буквально уйти по касательной. .
Вернемся к примеру с автомобилем после поворота с креном. Если вы наблюдаете снаружи, вы можете наблюдать центростремительную силу, толкающую автомобиль внутрь к центру, заставляя его двигаться по кругу. 2/r.
2/r.
Третий закон Ньютона гласит, что «на каждое действие есть равное и противоположное противодействие». Точно так же, как гравитация заставляет вас воздействовать на землю, кажется, что земля оказывает равную и противоположную силу на ваши ноги. Когда вы едете в разгоняющемся автомобиле, сиденье оказывает на вас силу, направленную вперед, точно так же, как кажется, что вы оказываете на сиденье силу, направленную назад.
В случае вращающейся системы центростремительная сила притягивает массу внутрь, следуя по кривой траектории, в то время как масса, кажется, выталкивается наружу из-за своей инерции. Однако в каждом из этих случаев прилагается только одна реальная сила, а другая — только кажущаяся сила.
Примеры центростремительной силы
Центростремительная сила используется во многих приложениях. Одним из них является моделирование ускорения космического запуска для подготовки космонавтов. Когда ракета запускается впервые, она настолько загружена топливом и окислителем, что едва может двигаться.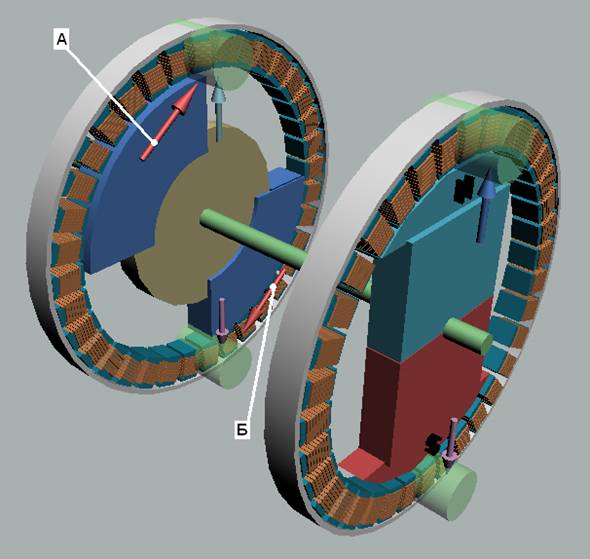 Однако по мере подъема он сжигает топливо с огромной скоростью, постоянно теряя массу. Второй закон Ньютона гласит, что сила равна массе, умноженной на ускорение, или F = ma.
Однако по мере подъема он сжигает топливо с огромной скоростью, постоянно теряя массу. Второй закон Ньютона гласит, что сила равна массе, умноженной на ускорение, или F = ma.
В большинстве случаев масса остается постоянной. Однако у ракеты ее масса резко меняется, а сила — в данном случае тяга ракетных двигателей — остается почти постоянной. Это приводит к тому, что ускорение к концу фазы разгона увеличивается в несколько раз по сравнению с нормальной гравитацией. НАСА использует большие центрифуги (открывается в новой вкладке), чтобы подготовить астронавтов к этому экстремальному ускорению. В этом случае центростремительная сила создается за счет того, что спинка сиденья давит на космонавта внутрь.
Лабораторные центрифуги быстро вращаются и воздействуют центростремительной силой на жидкости, такие как кровь, которые затем разделяются в зависимости от их плотности. (Изображение предоставлено Shutterstock)
Статьи по теме
Другой пример применения центростремительной силы — лабораторные центрифуги, которые используются для ускорения осаждения взвешенных в жидкости частиц. Одним из распространенных применений этой технологии является подготовка образцов крови для анализа. Согласно Веб-сайт Experimental Biosciences Университета Райса (открывается в новой вкладке): «Уникальная структура крови позволяет очень легко отделить эритроциты от плазмы и других форменных элементов с помощью дифференциального центрифугирования».
Одним из распространенных применений этой технологии является подготовка образцов крови для анализа. Согласно Веб-сайт Experimental Biosciences Университета Райса (открывается в новой вкладке): «Уникальная структура крови позволяет очень легко отделить эритроциты от плазмы и других форменных элементов с помощью дифференциального центрифугирования».
При нормальной силе тяжести тепловое движение вызывает непрерывное перемешивание, что предотвращает осаждение клеток крови из образца цельной крови. Однако типичная лабораторная центрифуга может развивать ускорение в 600-2000 раз больше, чем .нормальная гравитация . Это вынуждает тяжелые эритроциты оседать на дно и расслаивает различные компоненты раствора на слои в соответствии с их плотностью.
Эта статья была обновлена 11 ноября 2021 г. редактором Live Science Беном Биггсом.
Дополнительные ресурсы
Подробнее об основах центростремительной силы можно прочитать в Технологического университета Суинберна (открывается в новой вкладке).


 Это, безусловно, более удобно для расчётов, поэтому именно такой вариант и следует взять за основу. Нельзя не отметить и В.Н.Власова, проанализировавшего и оценившего некоторые параметры такого двигателя и высказавшего ряд интересных идей. Именно его анализ и подтолкнул меня серьёзно заняться центробежным двигателем Высоцкого и двигателем Клема. Сразу скажу, результат оказался весьма неожиданным: если двигатель Высоцкого является именно механическим центробежным двигателем и потому не работоспособен, как и другие чисто механические конструкции, то двигатель Клема на самом деле использует совсем другие принципы, и конус со спиралью играет там гораздо более сложную роль, чем простой центробежный нагнетатель рабочего тела (по некоторым сведениям, в двигателе Клема спиральный канал как таковой вообще не являлся одной деталью или её частью, а формировался при сопряжении поверхностей двух деталей, движущихся друг относительно друга).
Это, безусловно, более удобно для расчётов, поэтому именно такой вариант и следует взять за основу. Нельзя не отметить и В.Н.Власова, проанализировавшего и оценившего некоторые параметры такого двигателя и высказавшего ряд интересных идей. Именно его анализ и подтолкнул меня серьёзно заняться центробежным двигателем Высоцкого и двигателем Клема. Сразу скажу, результат оказался весьма неожиданным: если двигатель Высоцкого является именно механическим центробежным двигателем и потому не работоспособен, как и другие чисто механические конструкции, то двигатель Клема на самом деле использует совсем другие принципы, и конус со спиралью играет там гораздо более сложную роль, чем простой центробежный нагнетатель рабочего тела (по некоторым сведениям, в двигателе Клема спиральный канал как таковой вообще не являлся одной деталью или её частью, а формировался при сопряжении поверхностей двух деталей, движущихся друг относительно друга). Скомпонуем всю спираль (за исключением заборника жидкости) в одной плоскости чуть выше уровня этой жидкости. В результате получился вариант спирали Архимеда, т.е. такой спирали, у которой шаг между витками одинаков по всему радиальному сечению. Допустим, что вся спираль состоит из одной трубки и вращается по часовой стрелке.
Скомпонуем всю спираль (за исключением заборника жидкости) в одной плоскости чуть выше уровня этой жидкости. В результате получился вариант спирали Архимеда, т.е. такой спирали, у которой шаг между витками одинаков по всему радиальному сечению. Допустим, что вся спираль состоит из одной трубки и вращается по часовой стрелке. На внешнем конце спирали она вылетает из сопла с достаточно высокой скоростью, за счёт чего создаёт реактивную тягу, разгоняющую спираль.
На внешнем конце спирали она вылетает из сопла с достаточно высокой скоростью, за счёт чего создаёт реактивную тягу, разгоняющую спираль. Поскольку жидкости практически несжимаемы, то если рабочее тело всё время будет оставаться в жидком состоянии, ρз ~ ρс, так что плотности можно будет исключить.
Поскольку жидкости практически несжимаемы, то если рабочее тело всё время будет оставаться в жидком состоянии, ρз ~ ρс, так что плотности можно будет исключить. Отсюда для обеспечения разгона спирали при безнапорном заборе неподвижной жидкости следует соотношение размеров входного и выходного отверстий:
Отсюда для обеспечения разгона спирали при безнапорном заборе неподвижной жидкости следует соотношение размеров входного и выходного отверстий: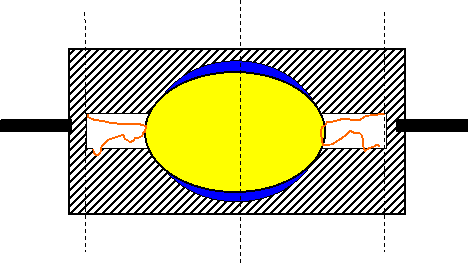



 Попробуем теперь найти «золотую середину» — чтобы сопло не перекрывало поток полностью, но создавало давление, достаточное для достижения нужной скорости истечения струи. Обозначим отношение площади заборника и внутреннего диаметра трубки спирали к площади отверстия сопла Sз / Sс = k. В соответствии с формулой (1) получаем vc = k · vз. Предполагая внутренний диаметр спирали по всей длине до самого сопла одинаковым и равным диаметру заборника, перед входом сопла мы имеем сечение S = Sз и скорость потока vт = vз (vт — это скорость потока жидкости в трубке, и не следует путать её с линейной скоростью самого заборника — это разные вещи). Давление возле сопла повышено относительно атмосферного на входе заборника, однако, если сопло ориентировать строго тангенциально, потенциалы центробежных сил с обоих сторон сопла можно считать одинаковыми и равными 0 (ведь именно сопло мы ранее выбрали в качестве точки отсчёта потенциала).
Попробуем теперь найти «золотую середину» — чтобы сопло не перекрывало поток полностью, но создавало давление, достаточное для достижения нужной скорости истечения струи. Обозначим отношение площади заборника и внутреннего диаметра трубки спирали к площади отверстия сопла Sз / Sс = k. В соответствии с формулой (1) получаем vc = k · vз. Предполагая внутренний диаметр спирали по всей длине до самого сопла одинаковым и равным диаметру заборника, перед входом сопла мы имеем сечение S = Sз и скорость потока vт = vз (vт — это скорость потока жидкости в трубке, и не следует путать её с линейной скоростью самого заборника — это разные вещи). Давление возле сопла повышено относительно атмосферного на входе заборника, однако, если сопло ориентировать строго тангенциально, потенциалы центробежных сил с обоих сторон сопла можно считать одинаковыми и равными 0 (ведь именно сопло мы ранее выбрали в качестве точки отсчёта потенциала). Кстати, такая ориентация сопла является технически оптимальной, поскольку вся реактивная тяга будет направлена именно на раскрутку спирали. С другой стороны, в заборнике давление равно атмосферному, зато имеется максимальный потенциал, рассчитываемый по формуле (4). На выходе сопла сечением Sc = Sз / k вследствие уравнения непрерывности (точнее, закона сохранения расхода) мы имеем скорость vc = vт · k при атмосферном давлении и нулевом потенциале. Наша цель — найти зависимость возможной скорости течения рабочего тела в трубке спирали от её радиуса и скорости вращения и соотношения диаметров трубки (заборника) и сопла.
Кстати, такая ориентация сопла является технически оптимальной, поскольку вся реактивная тяга будет направлена именно на раскрутку спирали. С другой стороны, в заборнике давление равно атмосферному, зато имеется максимальный потенциал, рассчитываемый по формуле (4). На выходе сопла сечением Sc = Sз / k вследствие уравнения непрерывности (точнее, закона сохранения расхода) мы имеем скорость vc = vт · k при атмосферном давлении и нулевом потенциале. Наша цель — найти зависимость возможной скорости течения рабочего тела в трубке спирали от её радиуса и скорости вращения и соотношения диаметров трубки (заборника) и сопла.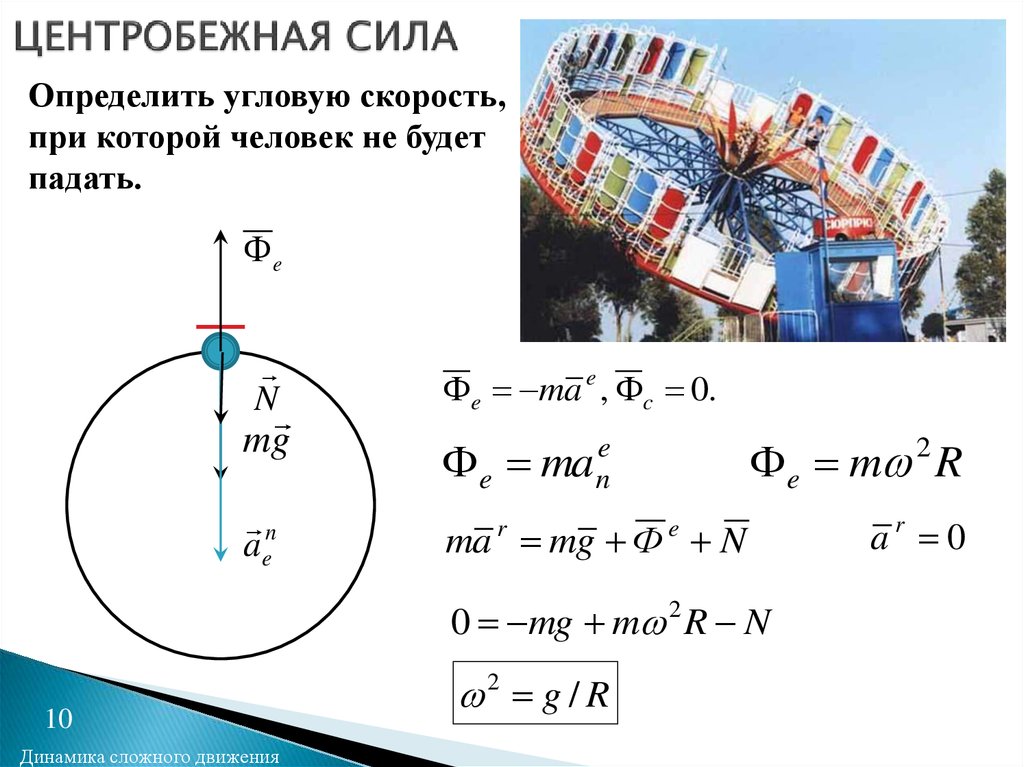
 Так что эффектный вывод В.Н.Власова о необходимости соотношения Sз < Sс представляется ошибочным!
Так что эффектный вывод В.Н.Власова о необходимости соотношения Sз < Sс представляется ошибочным!
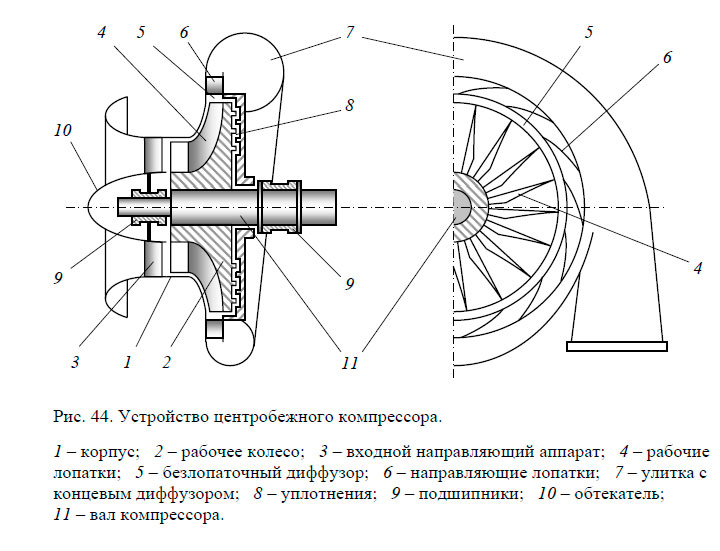
 А из этого следует, что многовитковая спираль вроде бы и не нужна — вполне работоспособной должна быть и следующая конструкция (разве что радиус изгиба трубок возле сопел можно сделать побольше для уменьшения потерь на поворот жидкости перед соплом).
А из этого следует, что многовитковая спираль вроде бы и не нужна — вполне работоспособной должна быть и следующая конструкция (разве что радиус изгиба трубок возле сопел можно сделать побольше для уменьшения потерь на поворот жидкости перед соплом).
 Расчёт специально приведён подробно и ошибок в нём я не нашёл. Это говорит о том, что слепо использовать полученную формулу нельзя, а надо понять её физический смысл и, стало быть, границы применимости. Дело в том, что vТ — это возможная максимальная скорость идеальной жидкости (без трения) относительно спирали при отсутствии дополнительного давления на входе. Кроме того, необходимо напомнить, что жидкость рассматривалась как идеальная несжимаемая, неиспаряемая и сверхтекучая — без трения и без кавитационных эффектов. Поэтому, когда диаметр сопла равен диаметру трубки, никаких препятствий сверхтекучей жидкости нет, и её скорость теоретически может быть бесконечно большой. Если же сопло начинает уменьшаться, то оно будет ограничивать максимальную скорость даже для сверхтекучей жидкости.
Расчёт специально приведён подробно и ошибок в нём я не нашёл. Это говорит о том, что слепо использовать полученную формулу нельзя, а надо понять её физический смысл и, стало быть, границы применимости. Дело в том, что vТ — это возможная максимальная скорость идеальной жидкости (без трения) относительно спирали при отсутствии дополнительного давления на входе. Кроме того, необходимо напомнить, что жидкость рассматривалась как идеальная несжимаемая, неиспаряемая и сверхтекучая — без трения и без кавитационных эффектов. Поэтому, когда диаметр сопла равен диаметру трубки, никаких препятствий сверхтекучей жидкости нет, и её скорость теоретически может быть бесконечно большой. Если же сопло начинает уменьшаться, то оно будет ограничивать максимальную скорость даже для сверхтекучей жидкости. Рассчитаем по формуле (7) значения vт для нескольких значений радиуса сопла Rс и скорости вращения f. Площадь сопла Sс при этом будем выбирать так, чтобы соотношение сечений k = Sз / Sс примерно вдвое превосходило соотношение радиусов Rс / Rз с тем, чтобы скорость струи из сопла во столько же раз превышала его линейную скорость для создания реактивной тяги.
Рассчитаем по формуле (7) значения vт для нескольких значений радиуса сопла Rс и скорости вращения f. Площадь сопла Sс при этом будем выбирать так, чтобы соотношение сечений k = Sз / Sс примерно вдвое превосходило соотношение радиусов Rс / Rз с тем, чтобы скорость струи из сопла во столько же раз превышала его линейную скорость для создания реактивной тяги. 2 см2 = 2·10–5 м2
2 см2 = 2·10–5 м2 2 см2 = 2·10–5 м2
2 см2 = 2·10–5 м2 1 см2 = 10–5 м2
1 см2 = 10–5 м2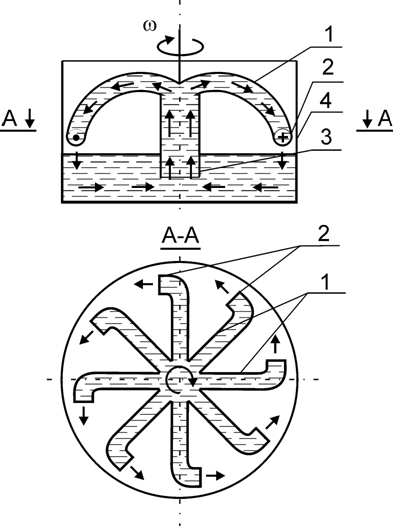 Но, прежде чем заняться изменением фазового состояния, необходимо уточнить геометрию устройства.
Но, прежде чем заняться изменением фазового состояния, необходимо уточнить геометрию устройства. е. преобразует тангенциальную скорость того участка трубки, по которому он катится, в свою нормальную скорость, отбирая на этом этапе кинетическую энергию ротора. Если посмотреть на него с точки зрения неподвижной оси вращения ротора, мы увидим, что шарик начинает двигаться не только от центра к периферии, но и вокруг оси вращения вместе с ротором, причём по мере удаления от центра вращения ротора его тангенциальная скорость нарастает, соответствуя тангенциальной скорости проходимого им участка трубки, которая прямо пропорциональна расстоянию до центра вращения. Передавая на завершающем участке траектории свою энергию стенкам трубки, а через неё — ротору, он лишь возвращает эту накопленную энергию обратно. Так что реально никакой прибавки энергии, а значит ускорения и возможности получить дополнительную работу, здесь нет.
е. преобразует тангенциальную скорость того участка трубки, по которому он катится, в свою нормальную скорость, отбирая на этом этапе кинетическую энергию ротора. Если посмотреть на него с точки зрения неподвижной оси вращения ротора, мы увидим, что шарик начинает двигаться не только от центра к периферии, но и вокруг оси вращения вместе с ротором, причём по мере удаления от центра вращения ротора его тангенциальная скорость нарастает, соответствуя тангенциальной скорости проходимого им участка трубки, которая прямо пропорциональна расстоянию до центра вращения. Передавая на завершающем участке траектории свою энергию стенкам трубки, а через неё — ротору, он лишь возвращает эту накопленную энергию обратно. Так что реально никакой прибавки энергии, а значит ускорения и возможности получить дополнительную работу, здесь нет. Поэтому он не сможет отобрать у ротора так много энергии, но и передаст спирали также немного. Так что конечный результат будет таким же, как и в первом случае: при полном отсутствии трения шарик не наберёт тангенциальной скорости и просто «выпадет» из внешнего конца спирали, но часть энергии спирали (весьма малая) будет израсходована на то, чтобы придать шарику небольшую (по сравнению со скоростью шарика относительно самой спирали) нормальную скорость, перемещая его от центра вращения к периферии. Глядя от оси вращения ротора, мы увидим, что шарик не будет вращаться вокруг этой оси, а просто начнёт смещаться к периферии, чем-то напоминая звукоснимающую головку на граммофонной пластинке.
Поэтому он не сможет отобрать у ротора так много энергии, но и передаст спирали также немного. Так что конечный результат будет таким же, как и в первом случае: при полном отсутствии трения шарик не наберёт тангенциальной скорости и просто «выпадет» из внешнего конца спирали, но часть энергии спирали (весьма малая) будет израсходована на то, чтобы придать шарику небольшую (по сравнению со скоростью шарика относительно самой спирали) нормальную скорость, перемещая его от центра вращения к периферии. Глядя от оси вращения ротора, мы увидим, что шарик не будет вращаться вокруг этой оси, а просто начнёт смещаться к периферии, чем-то напоминая звукоснимающую головку на граммофонной пластинке. до н.э.). Однако эолипил работал на пару. А в 1750 г. его гидравлический вариант изобрёл венгерский учёный Янош Сегнер, поэтому сейчас такую конструкцию называют «сегнеровым колесом».
до н.э.). Однако эолипил работал на пару. А в 1750 г. его гидравлический вариант изобрёл венгерский учёный Янош Сегнер, поэтому сейчас такую конструкцию называют «сегнеровым колесом».
 Вот эту суть совершенно не понял наш критик.
Вот эту суть совершенно не понял наш критик.
 Центробежные силы инерции (ЦБСИ) есть неизбежный спутник вращения
Центробежные силы инерции (ЦБСИ) есть неизбежный спутник вращения
 Однако, у ЦБСИ есть свой истинный антипод. это сила гравитации
Однако, у ЦБСИ есть свой истинный антипод. это сила гравитации

 е. произошла
е. произошла
 Одна из таких сил будет активной, если
Одна из таких сил будет активной, если
 Это заблуждение длится уже два века. Легко доказать, что работа
Это заблуждение длится уже два века. Легко доказать, что работа

 Наличие сил инерции говорит о том, что рассматриваемая
Наличие сил инерции говорит о том, что рассматриваемая
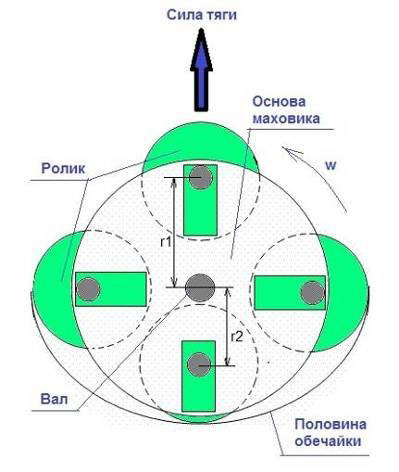
 Чтобы количество
Чтобы количество
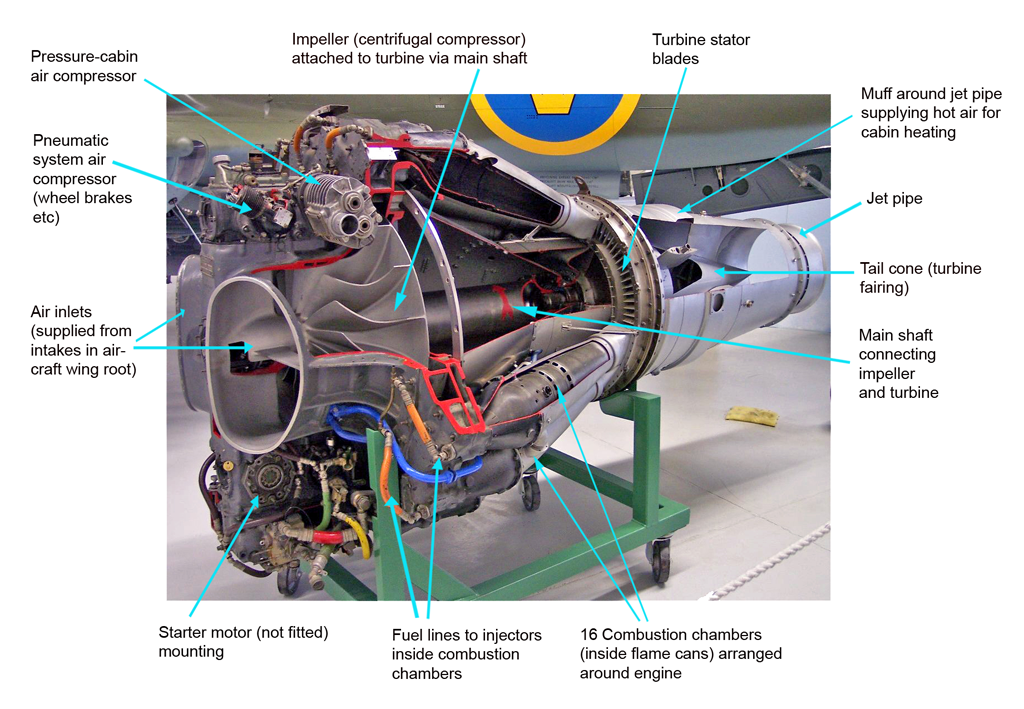 е. ЦБСИ. Эту закаченную энергию при желании можно
е. ЦБСИ. Эту закаченную энергию при желании можно
 е. окружной кинетической энергии тела. Два века это создавало
е. окружной кинетической энергии тела. Два века это создавало
 е.
е.
 к. реально радиус ЦБ-двигателя (генератора энергии) конечен, то
к. реально радиус ЦБ-двигателя (генератора энергии) конечен, то
 На раскрутку рабочего тела и возникновение ЦБСИ требуется привод
На раскрутку рабочего тела и возникновение ЦБСИ требуется привод
 ЦБ-ротор насоса засасывает, раскручивает и под действием ЦБСИ
ЦБ-ротор насоса засасывает, раскручивает и под действием ЦБСИ


 Самолеты без горючего могут крутиться
Самолеты без горючего могут крутиться
 Считалось, что ЦБСИ являются внутренними силами и система с ЦБСИ –
Считалось, что ЦБСИ являются внутренними силами и система с ЦБСИ –

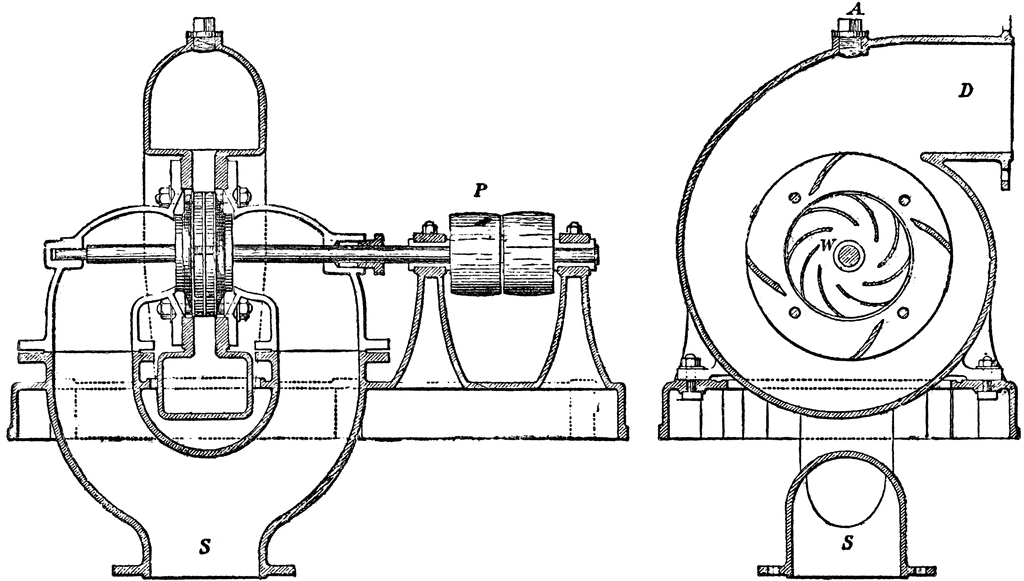 Судьями должно быть все научное
Судьями должно быть все научное
