Фрезерование Зубчатых Колес

Главная / Фрезерный станок с ЧПУ / Фрезерование Зубчатых Колес

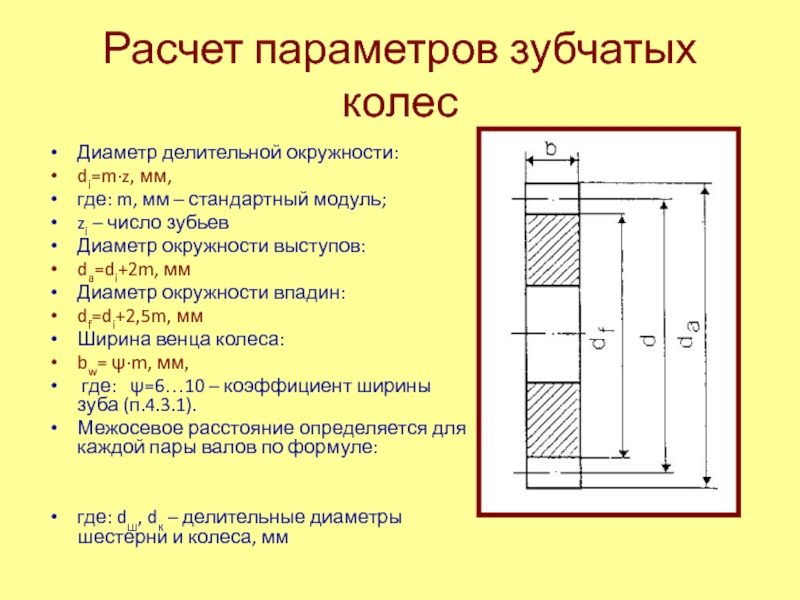
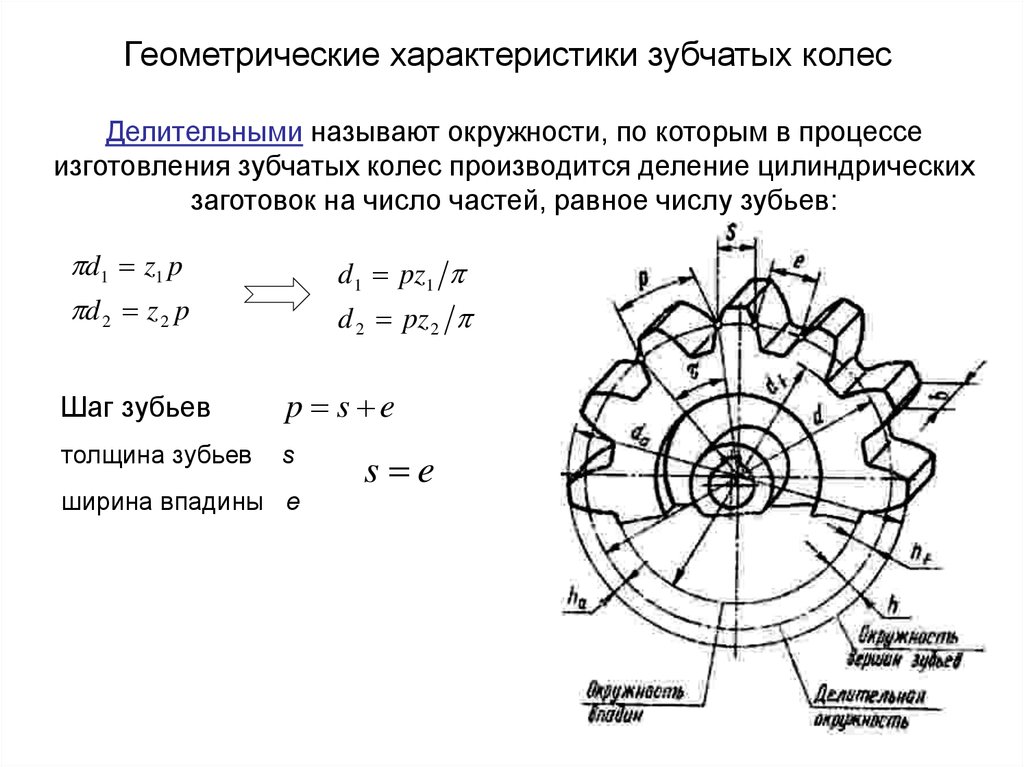
Перед изучением процесса фрезерования зубчатых колес, рассмотрим элементы зубчатого колеса. Боковые стороны профиля зубьев изготавливаются по кривой, называемой эвольвентной. В зубчатом колесе различают головку окружности выступов, впадин и делительную (рис. 1).

Окружностью выступов называется окружность, описанная из центра колеса и проходящая по выступам зубьев. Окружность впадин описывается из центра колеса и проходит по основанию впадин. В делительной окружности шаг и угол зацепления зубчатого колеса соответственно равны теоретическому шагу и углу зацепления исходной (зуборезной) рейки. Она делит высоту зуба на две неравные части (головку и ножку).

Шагом зубчатого колеса называется расстояние, измеренное между одноименными боковыми поверхностями двух смежных зубьев по дуге делительной окружности. Эта величина измеряется в мм и определяется по формуле: Pt = πd/z, где Р — шаг колеса; d — диаметр делительной окружности; z — число зубьев колеса; π — постоянное число, равное 3,14.

Основной характеристикой зубчатого колеса является модуль. Модулем называется часть диаметра делительной окружности, приходящаяся на один зуб колеса, мм.

Модуль численно равен отношению диаметра делительной окружности к числу зубьев колеса m = d/z.

Использовав формулу, можно выразить шаг через модуль: Pt = πm,  или модуль через шаг: m = Pt/π.

Таким образом, модуль можно определить, разделив шаг колеса на постоянное число π=3,14.

Зуб колеса состоит из головки и ножки. Высотой головки зуба ha называется расстояние, измеренное по радиусу между делительной окружностью и окружностью выступов. Эта величина численно равна модулю (мм) ha = m.

Рис. 1. Элементы зубчатого колеса

Высота ножки зуба һ1 — это расстояние, измеренное по радиусу между диаметром делительной окружности и окружностью впадин. Она численно равна 1,25м (мм): h = 1,25m.

Полная высота зуба 1 (мм) равна h = ha+h2 = m+1,25m = 2,25m.

Длина дуги, измеренная по делительной окружности между боковыми сторонами профиля зуба, называется толщиной зуба S (мм) и определяется по формуле S = Pt/2.

Зная число зубьев колеса и его модуль, можно определить диаметр окружности выступов da = m (z+2).

Соотношения между элементами зубчатого колеса приведены в таблице на рис. 2.

Рис. 2. Соотношение между элементами зубчатого колеса

Пример. Определить значения основных элементов зубчатого колеса с модулем m = 2 и числом зубьев z = 50.

Решение:

• Диаметр делительной окружности d = m*z = 2*50 = 100 мм.
• Диаметр окружности выступов da = m (z + 2) = 2 (50 + 2) = 104 мм.
• Высота головки зуба , hа = m = 2 мм.
• Высота ножки зуба h2 = 1,25m = 1,25 * 2 = 2,5 мм.
• Полная высота зуба h = ha + hf = m +1,25m = 2,25m = 2,25 + 2 = 4,5 мм.
• Шаг зубчатого колеса Рt = πm = 3,14 * 2 = 6,28 мм.
• Толщина зуба S = Pt/2 = 6.28/2*3,14 мм.

Обработка зубчатых колес фрезерованием

Зубчатые колеса должны работать плавно, бесшумно, равномерно вращаясь и сохраняя постоянство передаточного отношения передачи.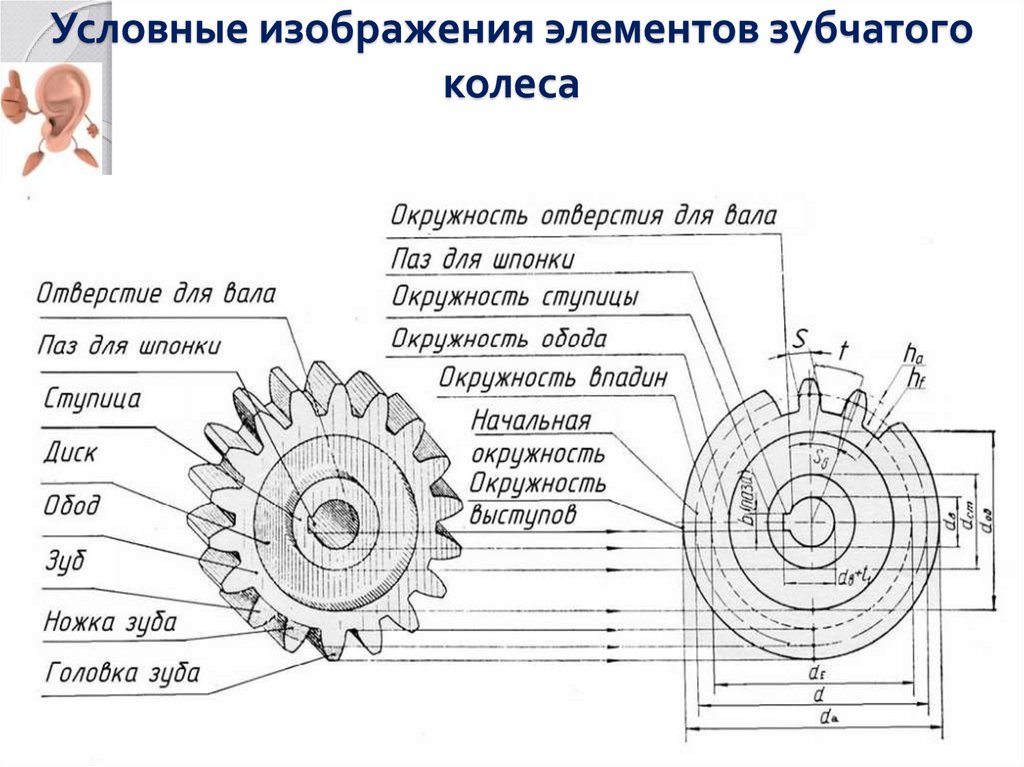 Эти требования определяются и устанавливаются в зависимости от условий эксплуатации зубчатых колес. Для обеспечения этих качеств обработка зубчатых колес фрезерованием должна быть выполнена согласно техническим условиям рабочего чертежа. Особое внимание должно быть обращено на допустимые биения диаметра делительной окружности и толщину зуба, допуск на изготовление которых, в зависимости от степени точности, указывается на чертеже.

Существуют два метода нарезания зубчатых колес: обкаткой и копированием. Методом обкатки нарезают колеса на зубофрезерных станках. Он основан на воспроизведении движений червячной передачи, у которой червяк в виде фрезы является режущим инструментом, а сопрягаемое колесо — нарезаемой заготовкой. Для нарезания зубчатых колес методом обкатки служат червячные модульные фрезы.

Сущность данного метода зубчатого фрезерования копирования состоит в том, что режущим инструментом — дисковой модульной фрезой последовательно нарезают впадины зубчатого колеса. Профиль впадин зубьев в точности соответствует профилю режущего инструмента.

Режущий инструмент для зубчатого фрезерования

Для фрезерования цилиндрических зубчатых колес методом копирования на консольно-фрезерных станках используют дисковые модульные фрезы (рис. 3), которые представляют собой фасонную фрезу с затылованными зубьями. Профиль режущих кромок таких фрез должен соответствовать профилю впадин нарезаемого колеса. Они изготавливаются из быстрорежущих сталей марок Р6М5, Р6М5К5 и подразделяются на фрезы для предварительного нарезания (черновые) и окончательного (чистовые). У черновых фрез для облегчения условий резания передний угол ү принимают равным 8-10°, у чистовых он равен нулю. Значение задних углов для всех видов фрез принимают равным 15°, что соответствует величине вспомогательных задних углов на боковых сторонах зубьев не менее 3°. По конструкции дисковые модульные фрезы бывают цельные и сборные (для модулей свыше 8). Чтобы сохранить профиль зуба, перетачивают их только по передней поверхности.

Рис. 3. Дисковая модульная фреза

Фрезы выбираются в зависимости от величины модуля и числа зубьев нарезаемого колеса. Так как у двух зубчатых колес одного и того же модуля, но с разным числом зубьев форма впадины не одинакова, то для каждого модуля нарезаемых колес требуется столько фрез, сколько различных чисел зубьев нужно нарезать.

Для сокращения номенклатуры фрез их изготавливают наборами (см. таблицу на рис. 4). Комплект из 8 фрез применяется для нарезания зубьев колес с модулем до 8 мм, из 15 — для колес с модулем 9-16 мм и из 26 — для колес с модулем свыше 16 мм.

На каждой фрезе комплекта на торцовой поверхности указано, из какого материала она сделана, нарезаемый модуль колеса, номер фрезы из комплекта и количество нарезаемых зубьев данной фрезой.

Рис. 4. Наборы дисковых модульных фрез

Установка и закрепление заготовок и фрезы при зубчатом фрезеровании

Заготовки зубчатых колес, имеющие цилиндрические отверстия, закрепляют на конических, или цилиндрических оправках, а со шлицевыми отверстиями внутри — на шлицевых оправках, в центрах делительной головки и задней бабки.

Перед установкой заготовки в центрах делительной головки необходимо проверить соосность осей центров шпинделя и задней бабки в горизонтальной плоскости и их параллельность относительно направления продольной подачи фрезерного станка. Это производится с помощью цилиндрической оправки и индикатора или штангенрейсмаса.

Дисковую модульную фрезу следует закрепить на центровой оправке по возможности ближе к шпинделю станка, ее свободный конец вставить в подшипник подвески.

Для обеспечения симметричного расположения нарезаемых зубьев к диаметральной плоскости обрабатываемого колеса ось профиля зубьев модульной фрезы также должна совместиться с осью заготовки. Предварительно это можно выполнить по вершинам центров делительной головки или задней бабки. Для окончательной выверки фрезы относительно оси заготовки можно воспользоваться следующим способом. Пробным проходом предварительно нарезают одну впадину. Затем снимают оправку с заготовкой и, повернув ее другой стороной, закрепляют в центрах, вводят зубья фрезы в обработанную впадину. При правильной установке заготовки зубья фрезы и впадины колеса должны совместиться.

Установка заготовки на конической центровой оправке в центрах делительной головки и задней бабки (рис. 5, а) производится следующим образом. На цилиндрическую часть центра 3, вставленного в шпиндель делительной головки, надевают поводковый хомутик 5, который через отогнутый хомутик 4, скрепленный с оправкой 1 и заготовкой 2, передает заготовке вращательное движение от шпинделя при повороте ее на расчетную часть окружности.

В тех случаях, когда требуется выполнить фрезерование зубчатого колеса диаметра превосходящего, чем допускает высота оси шпинделя делительной головки над столом станка, оно может быть закреплено на концевой оправке или в патроне с вертикальным положением оси шпинделя делительной головки (рис. 5, б).

Во всех случаях после закрепления заготовки следует обязательно проверить радиальное биение ее поверхности. Оно, как правило, не должно превышать 0,03 мм.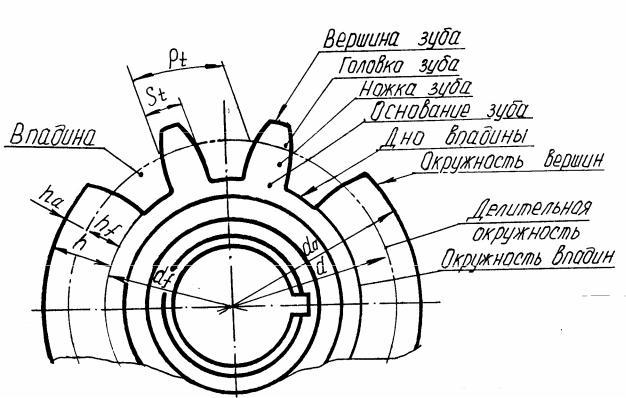

Рис. 5. Способы установки зубчатых колес

Режим фрезерования зубчатых колес

В зависимости от величины модуля нарезаемого колеса и требуемой шероховатости боковых сторон зубьев фрезеровать каждую впадину можно за один или несколько проходов. Когда модуль колеса не превышает 3 мм, глубину фрезерования устанавливают из расчета t = 2,25m. При фрезеровании каждой впадины за несколько проходов припуск на чистовой проход не должен превышать 0,2 мм на сторону.

Учитывая довольно трудные условия работы дисковых модульных фрез, их высокую стоимость, следует устанавливать подачу на зуб не более 0,05 мм/зуб, а скорость резания — 15-20 м/мин. По принятой скорости резания определяют частоту вращения фрезы в минуту и минутную подачу, на которые настраивают станок.

Приемы и способы зубчатого фрезерования

До начала зубчатого фрезерования необходимо определить число оборотов рукоятки универсальной делительной головки, выбрать требуемую окружность с отверстиями на боковом делительном диске, настроить его сектор и в отверстие выбранной окружности вставить фиксатор рукоятки. Включив вращение шпинделя, рукояткой продольной и вертикальной подач стола подводят заготовку до легкого соприкосновения ее наивысшей точки с фрезой. После этого продольной подачей отводят стол с заготовкой из-под фрезы, лимбовое кольцо вертикальной подачи устанавливают на нулевое деление и поднимают стол на глубину резания, равную 2,25т (при фрезерований за один проход). Затем стопорят консоль на станине, перемещают стол с заготовкой до фрезы, производят врезание, включают продольную механическую подачу и фрезеруют первую впадину на необходимую длину. После этого выключают вращение фрезы, возвращают стол в первоначальное положение, освобождают шпиндель делительной головки, вращением рукоятки относительно бокового делительного диска поворачивают заготовку на необходимое число оборотов (или части оборота), снова закрепляют шпиндель и обрабатывают вторую и последующие впадины колеса.

После фрезерования первых двух впадин колеса рекомендуется проверить толщину зуба и при необходимости произвести корректировку размеров.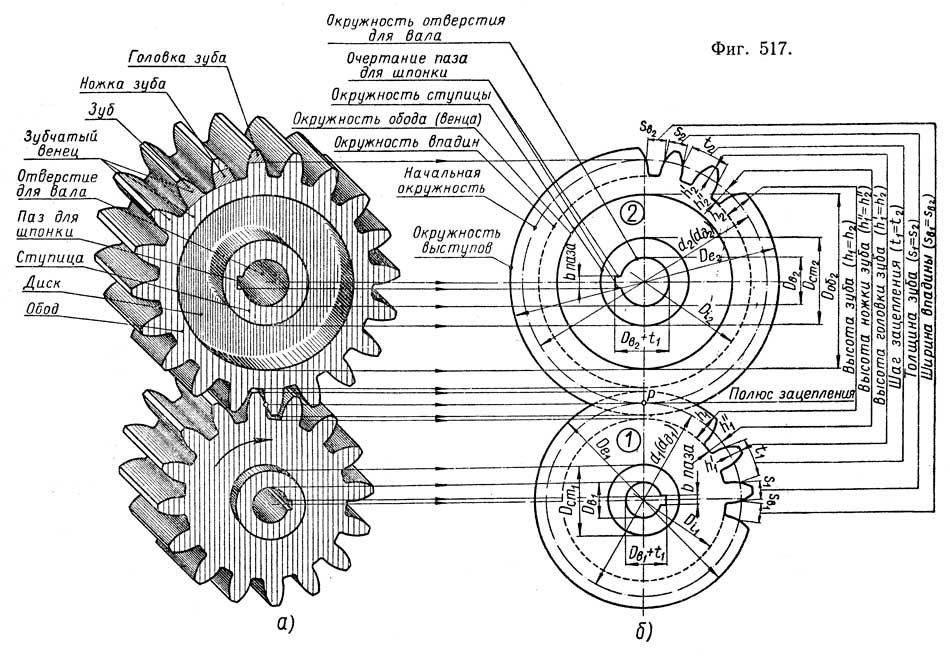

Контроль элементов зубчатых колес

Обычно у зубчатых колес, обрабатываемых на универсально-фрезерных станках дисковыми модульными фрезами (в случае, если точность их изготовления не превышает 9-11 степени точности), достаточно проверить толщину зуба по постоянной хорде и радиальное биение профиля зубьев.

Толщину зуба с точностью измерения 0,02 мм проверяют кромочным штангензубомером (рис. 6, а). Он состоит из двух взаимно перпендикулярных штанг 1 и 9, на которые нанесены деления в миллиметрах, рамок 3 и 7 с нониусами. Нониус и рамка 7 связаны с губкой 6, а нониус и рамка 3 — с высотной линейкой 5. Точную установку нониуса на размер производят с навинчиванием гаек 2 и 8 на микрометрические винты, связанные с рамками 3 и 7.

Для измерения толщины зуба штангензубомером по постоянной хорде необходимо рассчитать высоту от вершины зуба колеса до постоянной хорды по формуле hп.х = 0,747m и установить высотную линейку штангензубомера на этот размер.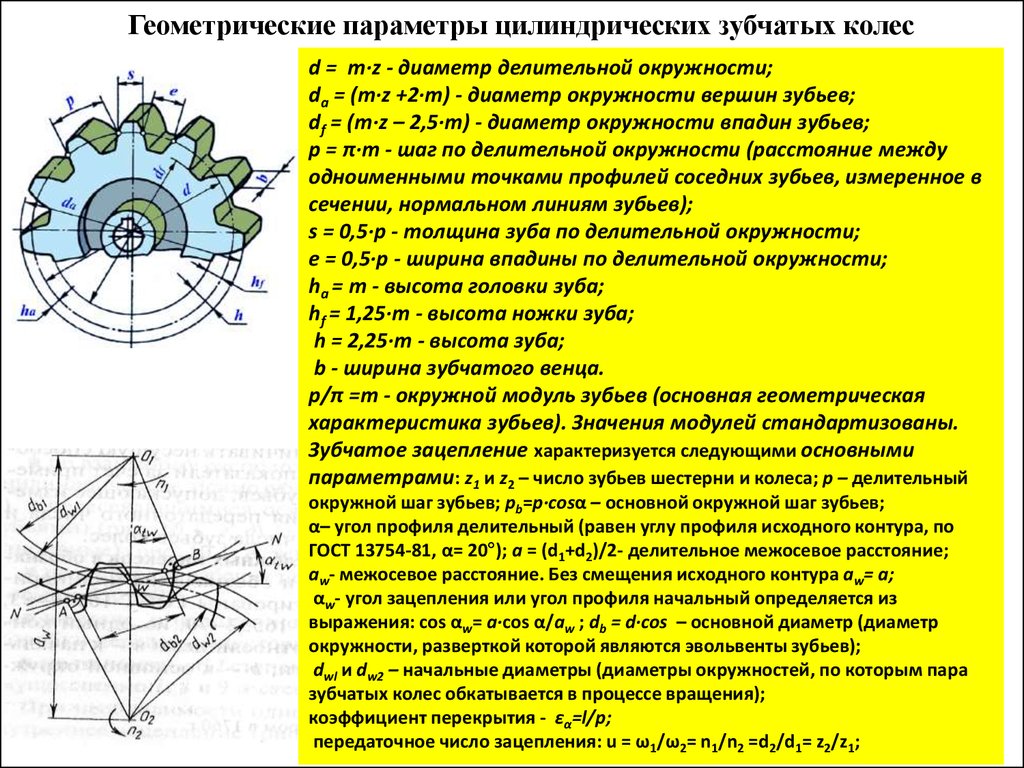

Толщина зуба по постоянной хорде определяется по формуле Sп.х = 1,387m.

Чтобы измерить толщину зуба, ребро высотной линейки устанавливают на его выступ и при помощи губок 4 и 6 измеряют его толщину. По разности между полученной величиной и расчетной или заданной чертежом (с учетом проставленных отклонений) судят о правильности размера.

Важным показателем годности зубчатого колеса является радиальное биение профиля зубьев в пределах допустимой нормы. При наличии биения нарушается нормальная работа зубчатой передачи и нередко по этой причине происходит поломка механизма. Величина радиального биения профиля зубьев обрабатываемого колеса зависит от многих причин, основными из которых являются: биение оправки, на котором закреплена заготовка, биение переднего центра шпинделя делительной головки.

В условиях единичного производства радиальное биение профиля зубьев на делительной окружности измеряется индикатором с использованием стального шлифованного цилиндрического ролика (рис.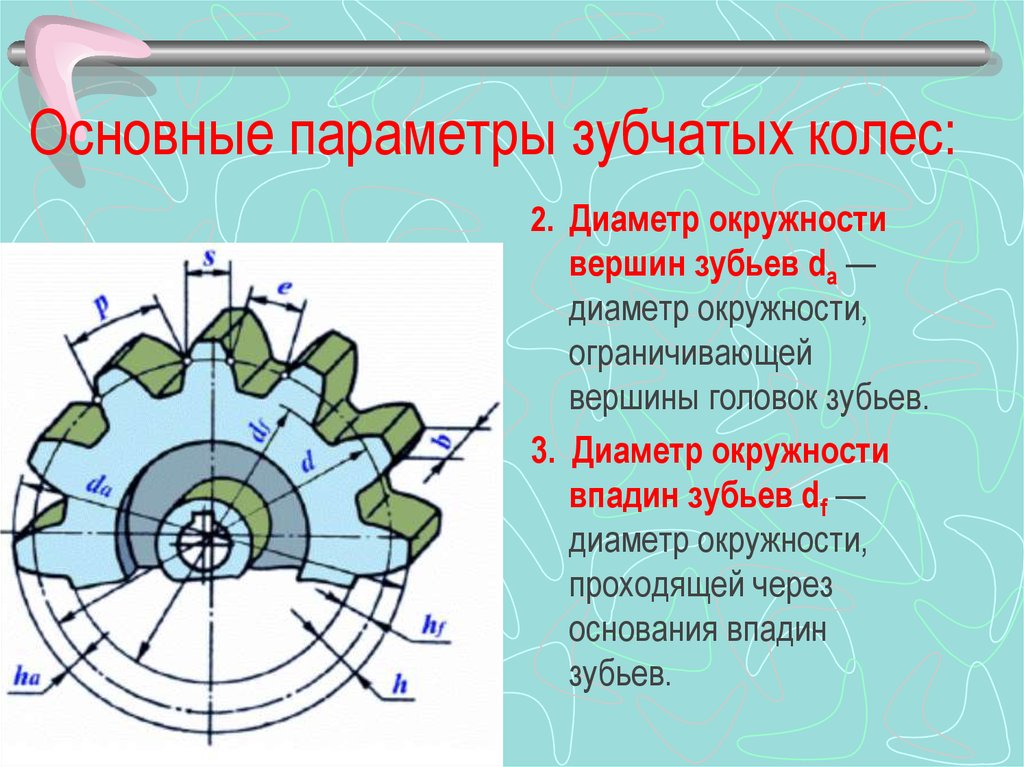 6, б). Зубчатое колесо 1 закрепляется на оправке 2, в центрах 3 и 7 приспособления или делительной головки и задней бабки.

Ролик 6, диаметр которого принимается равным 1,475m, размещают во впадине зубьев колеса. Измерительным штифтом индикатора 5, закрепленного на стойке 4 и установленного на столе контрольного приспособления или станка, касаются (с небольшим натягом) ролика. Поворачивают зубчатое колесо с оправкой в центрах и по отклонению стрелки индикатора определяют наивысшую точку ролика, который затем помещают в соседнюю впадину и поворачивают колесо до тех пор, пока стрелка индикатора не покажет его наивысшую точку во второй впадине. Обычно ролик размещают в четырех, расположенных в диаметральных плоскостях, впадинах. По разности отклонений стрелки индикатора определяют радиальное биение профиля зубьев на делительной окружности.

Рис. 6. Контроль зубчатых колес

Виды и причины брака при зубчатом фрезеровании

При фрезеровании зубчатых колес могут быть допущены следующие виды брака:

• Количество зубьев нарезанного колеса оказалось больше или меньше заданного, причиной чего является ошибка при расчете числа оборотов рукоятки или при делении.
• Неравномерный шаг зубьев с разной их толщиной, что бывает из-за небрежности фрезеровщика при отсчете числа промежутков по диску, из-за неумения пользоваться раздвижным сектором или если при делении вращение рукоятки универсальной делительной головки производилось в разных направлениях.
• Неправильная высота и толщина зуба, что происходит из-за ошибки при установке глубины фрезерования или если лимбовое кольцо не обеспечивает точность отсчета.
• Профиль зубьев несимметричен относительно диаметральной плоскости, что бывает, если не произведена установка фрезы по центру шпинделя делительной головки.
• Размеры зубьев по толщине, высоте и шагу не соответствуют требованиям чертежа вследствие неверного выбора фрезы номера из комплекта или по модулю.
• Завышенная шероховатость боковых сторон профиля, что происходит при работе затупившейся фрезой или если принята большая подача на зуб.
• Биение диаметра делительной окружности, причиной которого является биение центра делительной головки или оправки, на котором закреплена заготовка.

Следующая статья

Остались вопросы?

Заполните форму и наши менеджеры свяжутся с вами

Как к вам обращаться:

Ваш номер телефона:

Нажимая кнопку «Отправить», Вы принимаете Условия и даёте своё согласие на обработку Ваших персональных данных, в соответствии с Политикой конфиденциальности

Цилиндрические зубчатые передачи,основные термины и обозначения

Термины и обозначения приведены в табл. 1, определения терминов см. ГОСТ 16530—83 и 16531-83.

[gview file=»https://www.cb-online.ru/wp-content/uploads/2014/05/GOST-16530—83.pdf»]

[gview file=»https://www.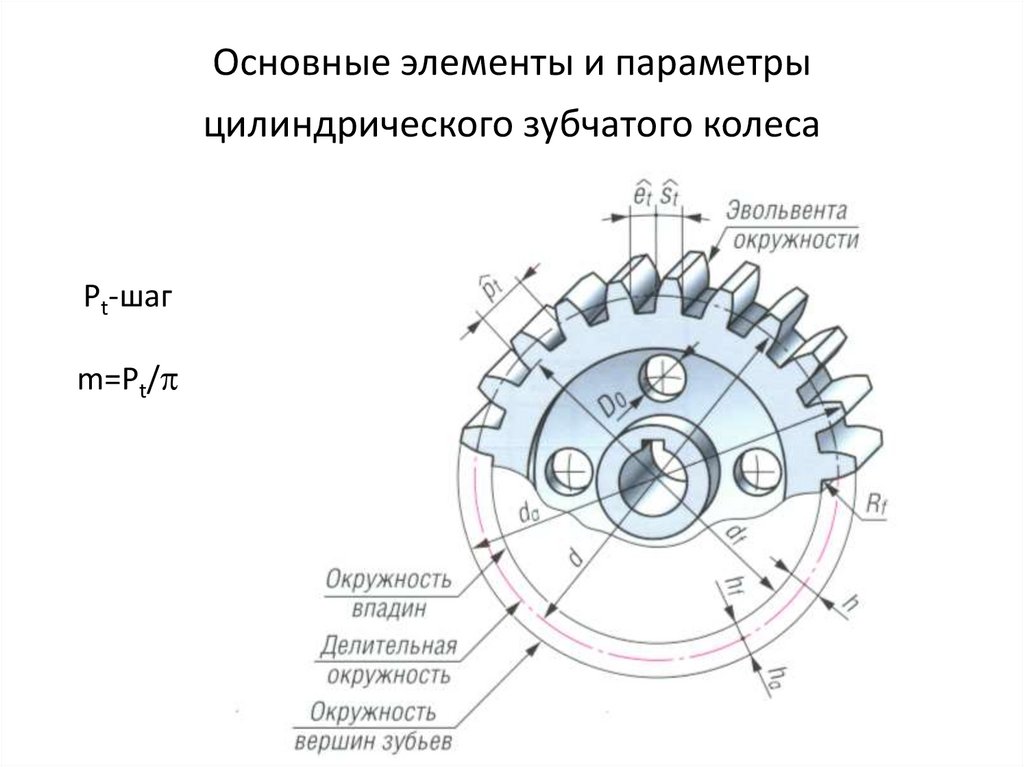 cb-online.ru/wp-content/uploads/2014/05/GOST-16531—83.pdf»]

1. Термины и обозначения цилиндрических зубчатых передач

Делительное межосевое расстоя­ние — a

Межосевое расстояние — a_w

Ширина венца цилиндрического зубчатого колеса — b

Рабочая ширина венца зубчатой передачи — b_w

Радиальный зазор пары исходных контуров — c

Коэффициент радиального зазора нормального исходного контура – c*

Высота зуба цилиндрического зубчатого колеса — h

Высота делительной головки зуба цилиндрического зубчатого колеса — h_a

Коэффициент высоты головки исходного контура – h_a*

Высота до хорды зуба колеса —

Высота до постоянной хорды зуба —

Высота до хорды дуги окруж­ности —

Глубина захода зубьев колеса, а также глубина захода зубьев ис­ходных реек —

Высота делительной ножки зуба колеса — h_f

Граничная высота зуба колеса — h_l

Делительный диаметр зубчатого колеса — d

Диаметр вершин зубьев колеса — d_a

Основной диаметр зубчатого ко­леса — d_b

Диаметр впадин зубчатого колеса — d_f

Диаметр окружности граничных точек зубчатого колеса — d_l

Начальный диаметр зубчатого ко­леса — d_w

Радиус зубчатого колеса — r

Расчетный модуль цилиндриче­ского зубчатого колеса — m

Нормальный модуль зубьев — m_n

Окружной модуль зубьев (торцо­вый) — m_t

Шаг эвольвентного зацепления — p_b

Нормальный шаг зубьев рейки — p_n

Торцовый шаг зубьев рейки — p_t

Осевой шаг зубьев рейки — p_x

Основной нормальный шаг зубьев — p_bn

Основной окружной шаг зубьев — p_bt

Основная нормальная толщина зуба — s_bn

Постоянная хорда зуба —

Нормальная толщина зуба рейки — s_n

Осевая толщина зуба рейки — s_x

Торцовая толщина зуба рейки — s_t

Толщина по хорде зуба —

Окружная толщина на заданном диаметре d_y — s_ty

Толщина по хорде —

Длина обшей нормали зубчатого колеса — W

Коэффициент смещения исход­ного контура — x

Коэффициент наименьшего сме­щения исходного контура — x_min

Коэффициент суммы смещений х_Σ

Коэффициент воспринимаемого смещения — у

Коэффициент уравнительного смещения — Δу

Число зубьев зубчатого колеса (число зубьев секторно-зубчатого колеса) — z

Наименьшее число зубьев, сво­бодное от подрезания — z_min

Число зубьев в длине обшей нор­мали — z_w

Нормальный боковой зазор эвольвентной цилиндрической зубчатой передачи — j_n

Эвольвентный угол профиля зуба – inv a

Эвольвентный угол, соответст­вующий точке профиля на окруж­ности d_y– inv a_y

Частота вращения зубчатого колеса в минуту — n

Передаточное число зубчатой передачи (z₂/z₁; d₂/d₁; n₁/n₂) — u

Угол профиля зуба исходного кон­тура в нормальном сечении — a

Угол профиля зуба в торцовом сечении — a_t

Угол зацепления — a_tw

Угол профиля в точке на концен­трической окружности заданного диаметра d_y — a_y

Угол наклона линии зуба соосной цилиндрической поверхности диа­метраd_y— β_y

Угол наклона линии зуба — β

Основной угол наклона линии зуба (косозубого колеса на его основ­ном цилиндре) — β_b

Угол развернутости эвольвенты зуба — v

Половина угловой толщины зуба — ψ

Половина угловой толщины зуба эквивалентного зубчатого колеса, соответствующая концентрической окружности диаметра d_y/cos²β_y — ψ_yv

Угловая скорость — ω

Шестерня — зубчатое колесо передачи с меньшим числом зубьев, колесо — с боль­шим числом зубьев. При одинаковом числе зубьев зубчатых колес передачи шестерней называют ведущее зубчатое колесо, а коле­сом — ведомое. Индекс 1 — для величин, относящихся к шестерне, индекс 2 — относя­щихся к колесу.

Исходный контур зубчатых цилиндрических колес эвольвентного зацепления и конических колес с прямыми зубьями

Рис. 1. Исходный контур зубчатых цилиндрических колес эвольвентного зацепления по ГОСТ 13755—81 и конических колес с прямыми зубьями по ГОСТ 13754— 81

Индекс n — для величин, относящихся к нормальному сечению, t — к окружному (торцовому) сечению. В тех случаях, когда не может быть разночтения и неясности, индексы n и t можно исключить.

Термины параметров нормального ис­ходного контура и нормального исходного производящего контура, выраженных в до­лях модуля нормального исходного контура, образуют добавлением слова «коэффициент» перед термином соответствующего парамет­ра.

Обозначения коэффициентов соответст­вуют обозначениям параметров с добавлением знака «*», например коэффициент радиального зазора пары исходных контуров с*.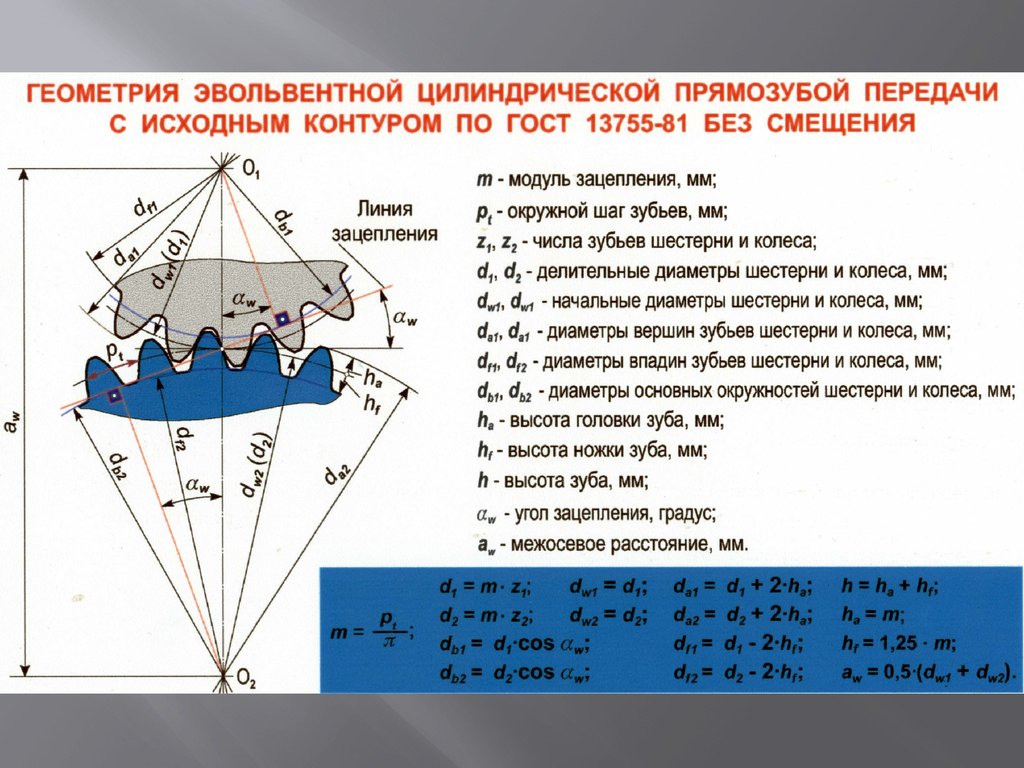

Модули (по ГОСТ9563—60). Стандарт распространяется на эвольвентные цилинд­рические зубчатые колеса и конические зубчатые колеса с прямыми зубьями и устанав­ливает:

для цилиндрических колес — значения нормальных модулей;

для конических колес — значения внеш­них окружных делительных модулей.

Числовые значения модулей:

Примечания:

1. При выборе модулей ряд 1 следует предпочитать ряду 2.

2. Для цилиндрических зубчатых колес допускается:

а) в тракторной промышленности при­менение модулей 3,75; 4,25 и 6,5мм;

б) в автомобильной промышленности применение модулей, отличающихся от ус­тановленных в настоящем стандарте;

в) в редукторостроении применение мо­дулей 1,6; 3,15; 6,3; 12,5м.

3. Для конических зубчатых колес до­пускается:

а) определять модуль на среднем конус­ном расстоянии;

б) в технически обоснованных случаях применение модулей, отличающихся от ука­занных в таблице.

4. Стандарт предусматривает применение модулей в диапазоне значений от 0,05 до 100мм.

Исходный контур цилиндрических зубча­тых колес. Под исходным контуром колес (рис. 1) подразумевают контур зубьев рейки в нормальном к направлению зубьев сечении. Радиальный зазор с = 0,25m, радиус кривизны переходной кривой зуба p_f = 0.4m. Допускается увеличение радиуса р_fесли это не нарушает правильности зацепления, и увеличение с до 0,35m при обработке колес долбяками и шеверами и до 0,4m при шлифовании зубьев.

Для цилиндрических колес внешнего зацепления при окружной скорости более указанной в табл. 2 применяют исходный контур с модификацией профиля головки зуба (рис.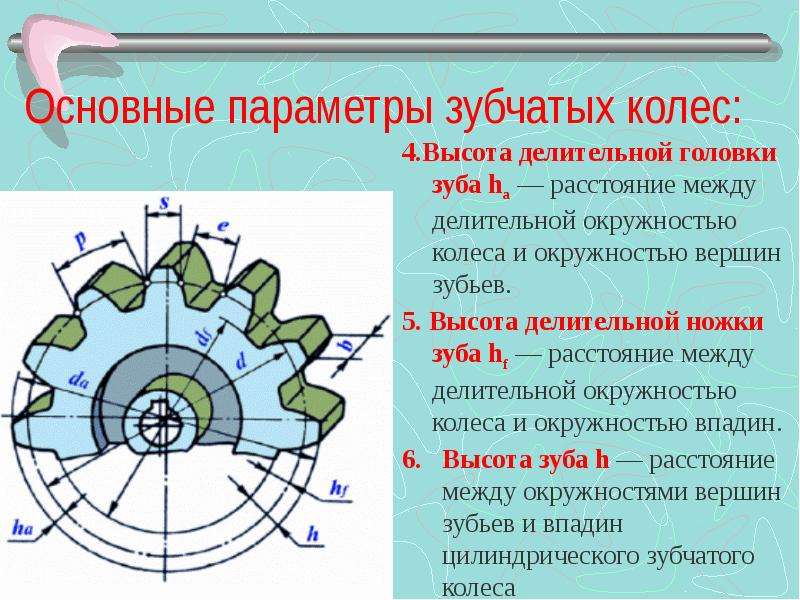 2). При этом линия модификации — прямая, коэффициент модификации h_g* должен быть не более 0,45, а коэффициент глубины модификации Δ* — не более 0,02.

Рекомендуемые значения коэффициента Δ* приведены в табл. 3.

Основные элементы зубчатого зацепле­ния указаны на рис. 3 и 4 в соответствии с обозначением по табл. 1.

Смещение колес зубчатых передач с внешним зацеплением. Чтобы повысить прочность зубьев на изгиб, снизить кон­тактные напряжения на их поверхности и уменьшить износ за счет относительного скольжения профилей, рекомендуется про­изводить смешение инструмента для цилин­дрических (и конических) зубчатых передач, у которых z₁ ≠ z₂. Наибольший результат достигается в следующих случаях:

Исходный контур с профильной модификацией

Рис. 2. Исходный контур с профильной модификацией

2. Окружная скорость колес в зависимости от их точности

3. Коэффициент глубины модификации Δ* в зависимости от модуля и степени точности

1) при смещении передач, у которых шестерня имеет малое число зубьев (z₁ < 17), так как при этом устраняется под­рез у корня зуба;

2) при больших передаточных числах, так как в этом случае значительно снижается относительное скольжение профилей.

Рис. 3

Рис. 4

Положение исходного производящего контура относительно нарезаемого колеса, при котором делительная прямая рейка ка­сается делительной окружности колеса, на­зывают номинальным положением (рис. 5, а). Колесо, зубья которого образованы при номинальном положении исходной произ­водящей рейки, называют колесом, наре­занным без смешения исходного контура (по старой терминологии — некорригированное колесо).

Положение производящего реечного контура относительно заготовки

Рис. 5. Положение производящего реечного контура относительно заготовки:

а — номинальное; б — с отрицательным смещением; в — с положительным смещением

График для определения нижнего предельного значения z1 в зависимости от z2 при которых

Рис. 6. График для определения нижнего предельного значения z₁ в зависимости от z₂ при которых

ε_а = 1,2 (x₁= х₂ = 0,5)

График для определения хmin в зависимости от z и β или zmin — х и β

Рис. 7. График для определения х_min в зависимости от z и β или z_min — х и β

(округляется до ближайшего большего целого числа)

Примеры.

1. Дано: z = 15; β = 0. По графику определяем х_min = 0,12 (см. штриховую линию).

2. Дано: х = 0; β = 30°. По графику определяем наименьшее число зубьев = 12 (cм. штриховую линию)

Влияние смещения исходного контура на геометрию зубьев

Рис. 8. Влияние смещения исходного контура на геометрию зубьев

Если исходная производящая рейка в станочном зацеплении смещена из номи­нального положения и установлена так, что ее делительная прямая не касается дели­тельной окружности нарезаемого колеса, то в результате обработки получится колесо, нарезанное со смещением исходного конту­ра (по старой терминологии — корригиро­ванное колесо).

Зацепление (в сечении, параллельном торцовому) зубчатого колеса со смещением с исходной производящей рейкой

Рис. 9. Зацепление (в сечении, параллельном торцовому) зубчатого колеса со смещением с исходной производящей рейкой

4. Коэффициенты смещения у зубчатых колес прямозубой передачи

5. Коэффициент смещения у зубчатых колес косозубой и шевронной передач

Толщина зуба по постоянной хорде и высота до постоянной хорды в нормальном сечении

Рис.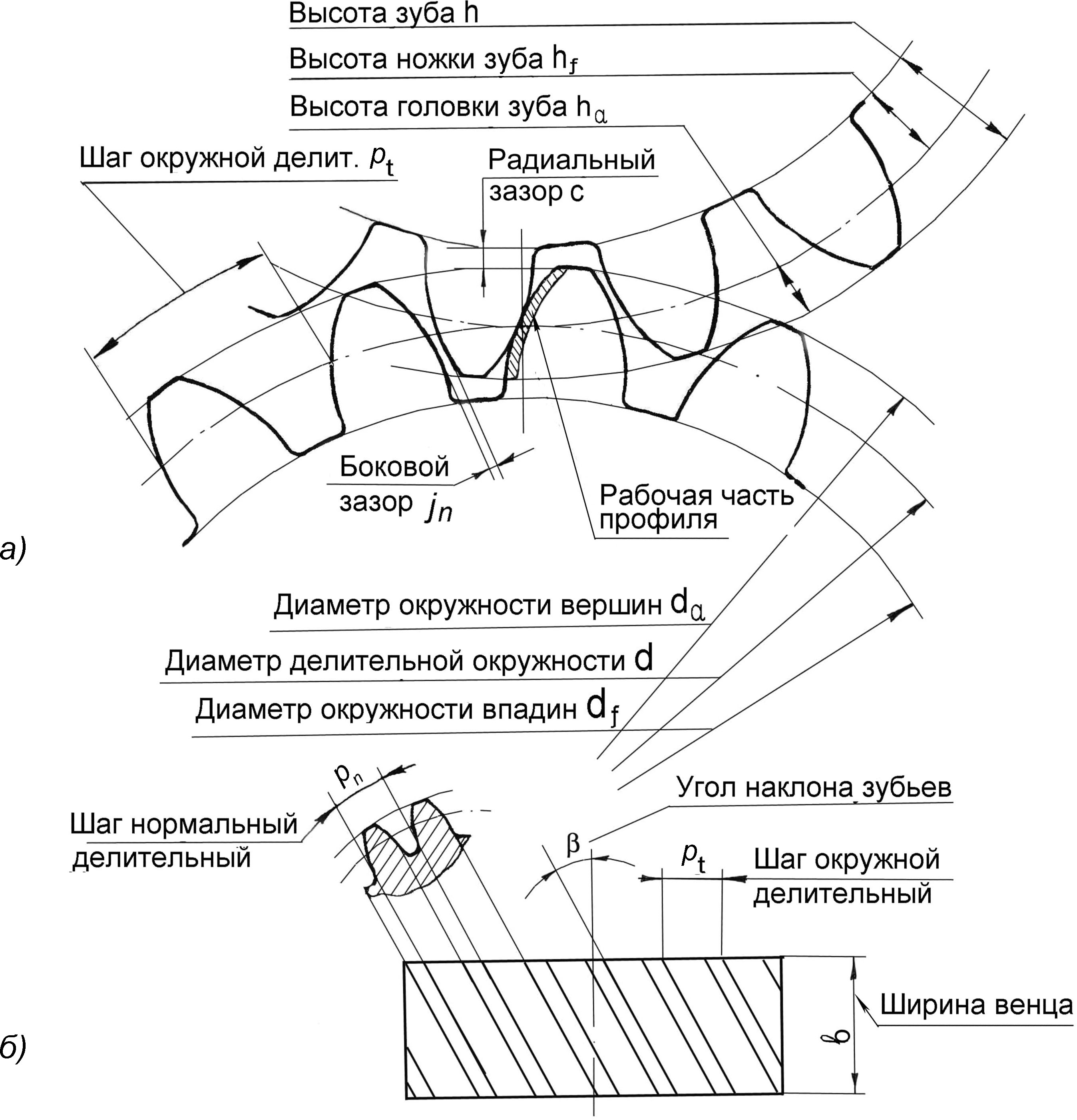 10. Толщина зуба по постоянной хорде и высота до постоянной хорды в нормальном сечении

Расстояние от делительной прямой исходной производящей рейки (или исходного контура) до делительной окружности колеса является величиной смещения.

Отношение смещения исходного контура к расчетному модулю называют коэффици­ентом смещения (х).

Если делительная прямая исходного контура пересекает делительную окружность зубчатого колеса (рис. 5, б), смещение назы­вают отрицательным (х < 0), если не пере­секает и не соприкасается (рис. 5, в) — по­ложительным (х > 0). При номинальном положении исходного контура смещение равно нулю (х = 0).

Коэффициент смещения х обеспечивает­ся установкой инструмента относительно заготовки зубчатого колеса в станочном за­цеплении.

Коэффициенты смещения у зубчатых колес рекомендуется выбирать по табл. 4 для прямозубой передачи и по табл. 5 — для косозубой и шевронной передач.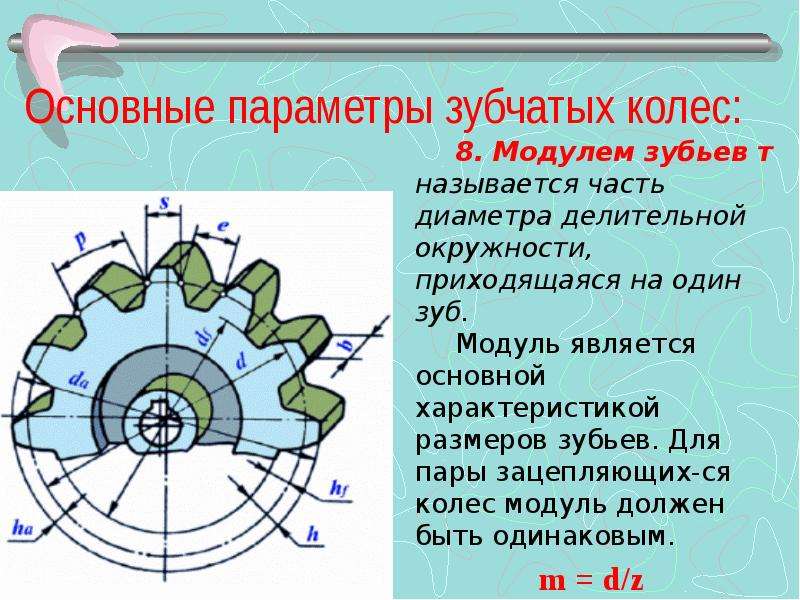

Основные элементы зубчатого зацепле­ния со смещением указаны на рис. 8, 9, 10.

6. Разбивка коэффициента суммы смещения x_Σ у прямозубой передачи на составляющие х₁ и х₂

Примечания:

1. При заданном межосевом расстоянии a_w требуемое значение коэффи­циента суммы смещений х_Σ можно получить за счет изменения числа зубьев z₁ или z₂, если это изменение допускается.

2. При 0.3 < х_Σ < 0,7 и u < 2 наибольшая скорость скольжения в зацеплении будет большей, чем в передаче без смещения.

3. При u = 1 рекомендуется x₁ = x₂ = 0,5х_Σ.

7. Разбивка коэффициента суммы смещения x_Σ у косозубой или шевронной передачи на составляющие х₁ и x₂

Примечания:

1. При заданном межосевом расстоянии a_w требуемое значение коэффи­циента суммы смещений х_Σ можно получить за счет изменения числа зубьев z₁ или z₂, угла на­клона β, если эти изменения допускаются.

2. При х_Σ > 0,3 и u < 2 наибольшая скорость скольжения в зацеплении будет большей, чем в передаче без смещения.

3. При u = 1 рекомендуется х₁ = х₂ = 0,5x_Σ.

8. Значения наименьшего числа зубьев z_min зубчатого колеса с коэффициентом смещения х = 0 при станочном зацеплении с исходной производящей рейкой

[Цилиндрические зубчатые передачи] Далее »

Терминология зубчатых колес, знание своих зубов

Вы когда-нибудь смотрели на чертеж зубчатого колеса и были поражены всеми различными спецификациями, задаваясь вопросом, что все это значит? В этом блоге будут перечислены и объяснены несколько общих терминов для передач.

Количество зубьев – количество зубьев на шестерне.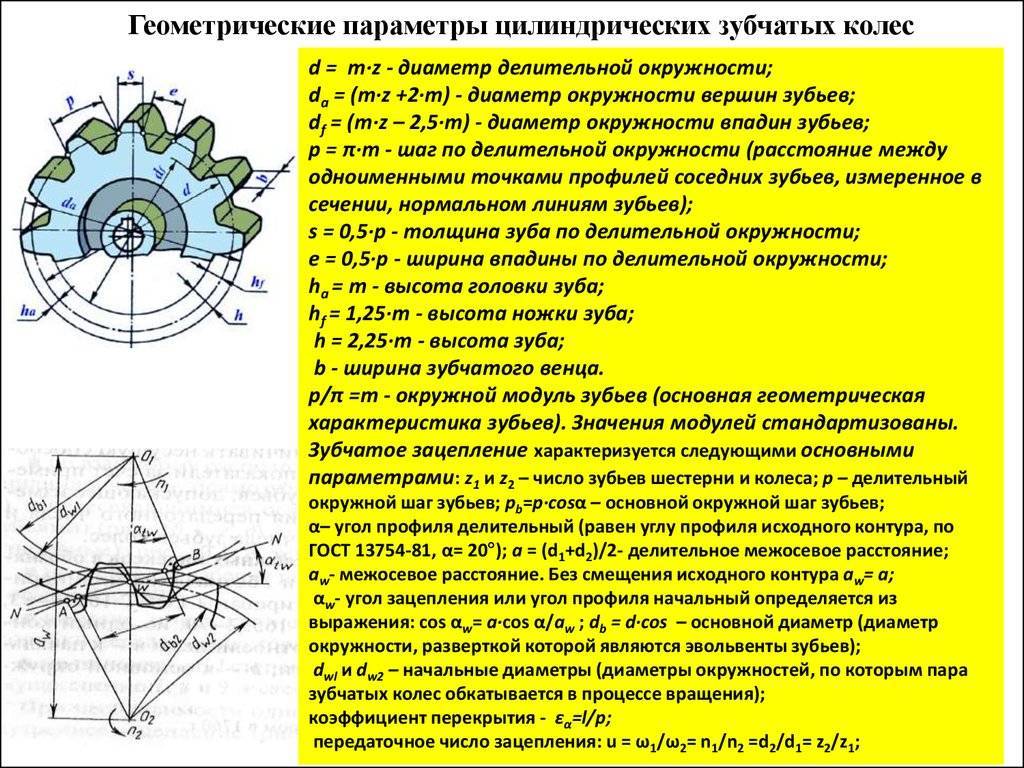 Этот термин несколько усложняется, если указываются секторные шестерни, и в этом случае вместе с общим количеством зубьев полной шестерни будет названо изготовленное количество зубьев.

Диаметральный шаг – количество зубьев на дюйм.

Модуль – метрическая версия диаметрального шага с единицами измерения в миллиметрах (мм). Вместо этого это расстояние (мм) на зуб, обратное диаметральному шагу.

Угол давления – контактный угол между линией действия зубчатой ​​пары и направлением скорости в точке тангажа.

Helix Angle – угол зуба относительно центральной оси. Углы спирали обычно составляют от 10° до 45° в зависимости от конструктивных требований. Зубчатые колеса с углом наклона спирали  0° называются прямозубыми. Косозубые шестерни (свыше 0°) увеличивают коэффициент контакта и снижают уровень шума шестерен, но также создают осевую нагрузку, которую необходимо учитывать при проектировании подшипника.

Helix Hand – направление угла спирали, выраженное как правое или левое. Глядя вниз на центральную ось шестерни, правая спираль наклоняется слева направо вниз по поверхности зуба от вас. Противоположное верно для левой спирали.

Шаг – осевое расстояние, необходимое для того, чтобы зуб винтовой шестерни совершил один полный оборот вокруг шестерни.

Диаметр шага – теоретический диаметр без допуска, определяемый делением числа зубьев зубчатого колеса на диаметральный шаг. Делительный диаметр обычно проходит через среднюю часть зуба шестерни.

Внешний диаметр – диаметр вершин зубьев шестерни.

Диаметр основания – диаметр самой нижней части или основания зубчатого колеса.

Приложение – расстояние от делительного диаметра до вершины зуба или наружного диаметра.

Дедендум – расстояние от делительного диаметра до диаметра корня зубчатого колеса.

Полная глубина – глубина зуба шестерни от вершины до основания.

Толщина зуба – толщина зуба, измеренная на делительном диаметре.

Нормальная толщина зуба s – толщина зуба, измеренная перпендикулярно или перпендикулярно центральной оси зубчатого колеса, а также на делительном диаметре.

Поперечная толщина зуба – толщина зуба, измеренная перпендикулярно или перпендикулярно углу наклона спирали, а также по делительному диаметру.

Эффективная толщина зуба – теоретическая толщина зуба, учитывающая погрешности производственного процесса.

Измеренная или фактическая толщина зуба – указанная толщина зуба, не учитывающая погрешности производственного процесса и используемая для измерения и проверки зубчатого колеса.

Измерение по штифтам – этот предварительно рассчитанный допуск используется для определения толщины зуба. Обычно два небольших цилиндрических штифта помещаются между двумя зубьями шестерни напротив друг друга. Затем измеряется расстояние между двумя штифтами и сравнивается с теоретически рассчитанным допуском.

Master Gear – шестерня очень высокого качества, которая прикатывается с плотным зацеплением к детали шестерни для проверки межцентрового расстояния, погрешности между зубьями и общей комплексной погрешности.

Межцентровое расстояние проверки — предварительно заданный допуск, основанный на межосевом расстоянии в плотном зацеплении (без люфта) между ведущей и неполной шестернями для проверки толщины зубьев неполной шестерни.

Tooth-Tooth Error – измеренная погрешность между соседними зубьями детали зубчатого колеса с помощью ведущего зубчатого колеса. Зазубрины или вмятины на зубах будут отображаться как ошибка зуба к зубу.

Total Composite Erro r – ошибка в детализированном зубчатом колесе, состоящая как из биения, так и из межзубцовой ошибки, проверяемая с помощью ведущего зубчатого колеса.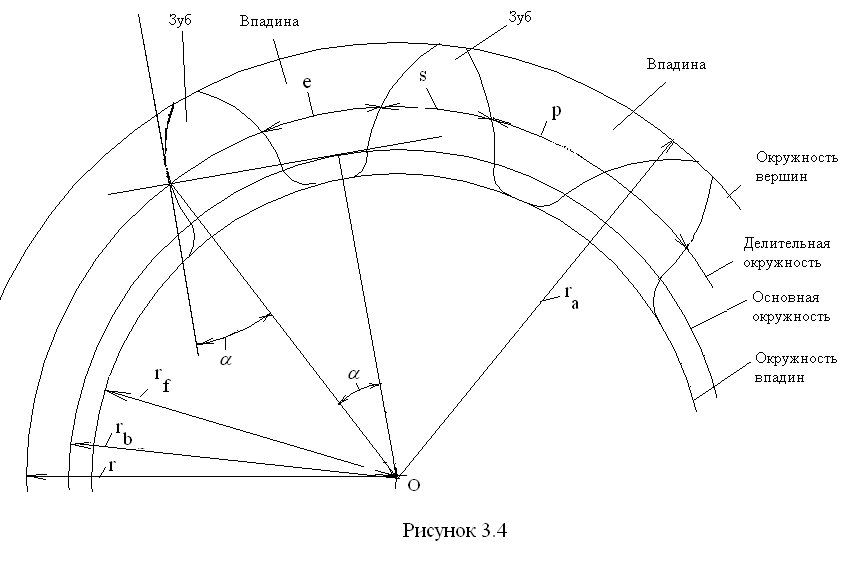

Методы определения диаметра фасонной части зубчатых наружных эвольвентных зубчатых колес

Чтобы помочь разработчикам зубчатых колес мгновенно проверить технологичность своих конструкций, представлены два метода расчета диаметра фасонного профиля с учетом конструктивных параметров шестерни и червячной втулки.

В нестандартных конструкциях прямозубых или косозубых зубчатых колес конструкторы обычно предпочитают меньший диаметр формы для большего коэффициента поперечного контакта. Больший радиус галтели корня и больший диаметр корня также предпочтительны для более высокой прочности корня на изгиб. Комбинация трех вышеуказанных требований может привести к тому, что конструкции зубчатых колес не могут быть изготовлены методом зубофрезерной обработки с последующей чистовой обработкой только боковой поверхности. Чтобы помочь разработчикам зубчатых колес мгновенно проверить технологичность своих конструкций, в этой работе представлены два метода расчета диаметра изготовленной формы с учетом конструктивных параметров зубчатого колеса и червячной втулки.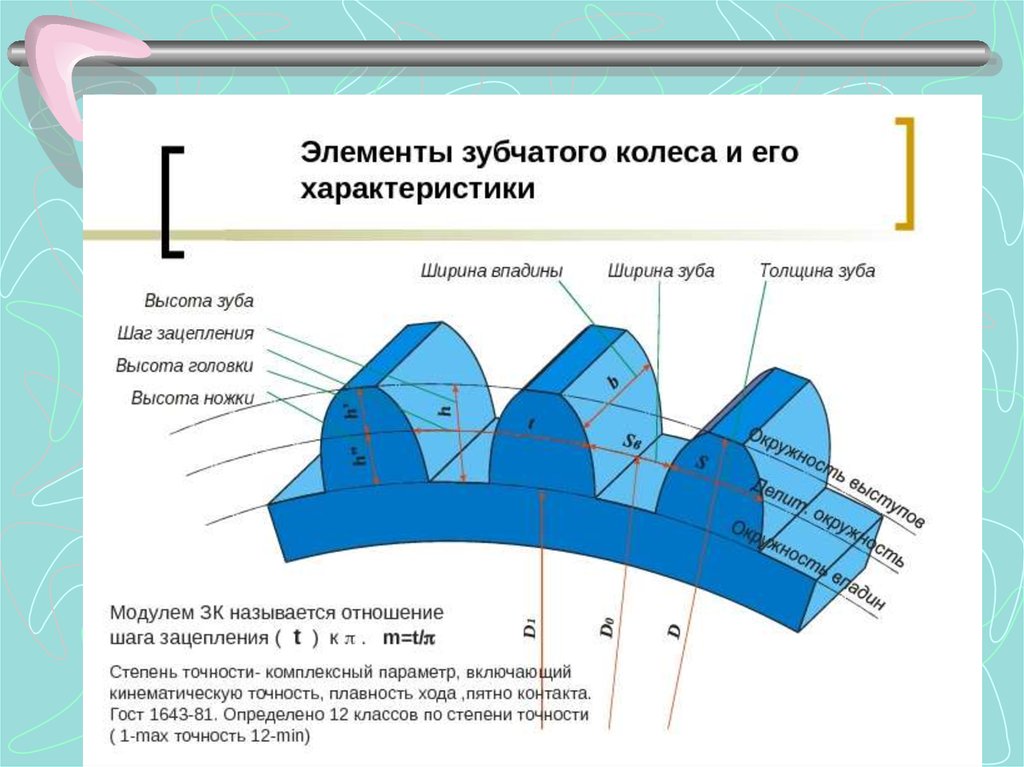 В частности, второй метод не требует итерационных вычислений или графического моделирования, принятых во многих публикациях и программах. Вместо этого пользователям предоставляется ряд эмпирических формул, позволяющих напрямую определить диаметр изготовленной формы, используя параметры конструкции зубчатого колеса и геометрию червячной втулки. В широком диапазоне конструктивных параметров зубчатых колес по формулам можно рассчитать диаметр формы с относительной погрешностью менее 0,1 %. Также представлены примеры применения формул.

1  Введение

Для эвольвентных зубчатых колес фасонный диаметр – это диаметр окружности, на которой кривая корневого скругления пересекает эвольвенту или присоединяется к ней [1]. В большинстве случаев кривая скругления корня представляет собой одну непрерывную трохоиду, образованную кончиком образующего режущего инструмента. В некоторых случаях кривая скругления корня также может состоять из трохоиды и еще одной эвольвенты с меньшим углом давления. Диаметр формы также известен как истинный диаметр формы эвольвенты (TIF) или диаметр в начале эвольвенты (SOI) [2].

Конструкторы нестандартных наружных эвольвентных зубчатых колес обычно указывают максимальный диаметр формы, который необходим для поперечного коэффициента контакта зубчатого зацепления при различных условиях. Между тем, больший диаметр корня и больший радиус галтели корня также предпочтительны для более высокой прочности корня на изгиб. Однако, когда указанные выше три требования указаны одновременно, они могут вызвать проблемы при изготовлении зубчатого колеса, особенно если надрез на галтели, вызванный чистовой операцией, не допускается. Если конструкторы зубчатых колес могут мгновенно определить, можно ли изготовить заданный диаметр формы вместе с указанным радиусом галтели и диаметром основания, можно предотвратить создание конструкций зубчатых колес, которые невозможно изготовить.

Некоторые коммерческие программы могут точно моделировать производственные процессы. Обычно они представляют собой графическое моделирование генерирующего процесса резания на основе параметров зубчатых колес и режущих инструментов. Однако, если конструкция зубчатого колеса не создается с использованием таких программ, выполнение моделирования производства с их помощью может потребовать дополнительных затрат и времени.

В предыдущих работах было представлено множество методов для определения диаметра формы. Герпен и Рис представили метод с упрощающим предположением, что диаметр формы создается конечной точкой круглого наконечника [3]. Мат и Чанд представили метод для червячных фрез, у которых есть два других прямых сегмента, соединяющих круглый наконечник и основную режущую сторону фрезы [4]. Лиан представил метод определения диаметра формы косозубых или прямозубых, внутренних и наружных зубчатых колес, нарезанных фрезами или червячными фрезами [5], если корневая галтель состоит только из трохоиды, образованной круглым наконечником фрезы, без вторичной эвольвенты, образуемой переходной прямой кромкой рядом с круглым наконечником на фрезе. Кроме того, все вышеперечисленные методы предполагают итеративное решение ряда уравнений для определения диаметра формы.

В этом документе представлены два метода, A и B, для определения диаметра изготовленной формы на наружных косозубых или цилиндрических зубчатых колесах, изготовленных методом червячной обработки, с возможным последующим процессом чистовой обработки только боковой поверхности, таким как шлифование или шлифование. В методе А используются уравнения для описания трех ключевых кривых: трохоида, образованная круглым наконечником червячной фрезы, первичная эвольвента, образованная основной режущей поверхностью фрезы, и вторичная эвольвента, образованная переходной прямой кромкой, соединяющей круглую вершину и фрезу. основная режущая кромка на плите. Затем определяется нижняя точка на первичной эвольвенте, которую может пересекать либо трохоида, либо вторичная эвольвента. Метод А включает в себя итеративное решение для поиска точки пересечения, как и в предыдущих публикациях.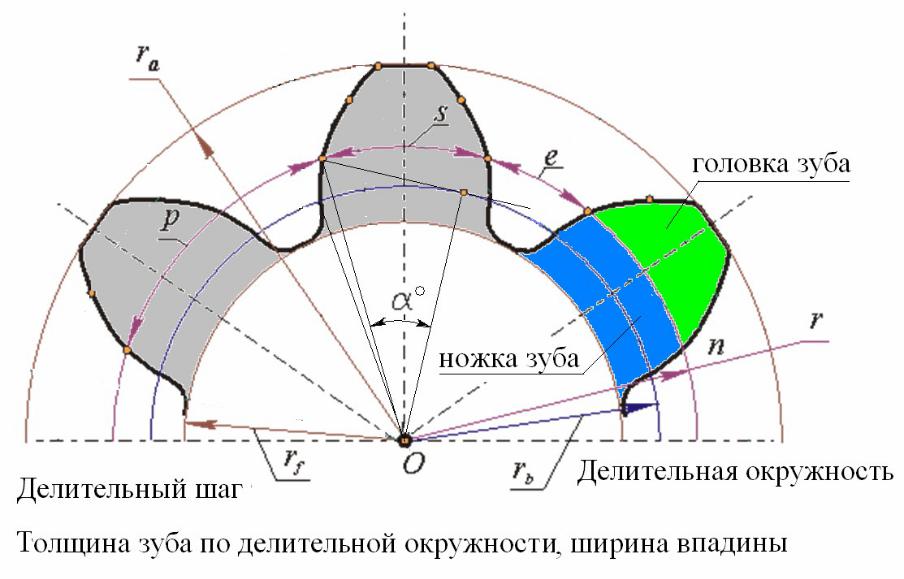

Метод B состоит из ряда эмпирических формул и блок-схемы, показывающей, как применять формулы для расчета диаметра формы без повторения. Формулы находятся путем регрессии большого количества примеров, созданных с использованием метода А, которые состоят из диаметров формы и параметров конструкции зубчатого колеса и параметров фрезы. Из-за характера эмпирической формулы диаметры формы по методу B имеют относительные ошибки, которые составляют менее 0,1% в широком диапазоне входных параметров, как указано, и менее 0,05% для обычных конструкций зубчатых колес. Толщина зуба не требуется ни для метода A, ни для метода B. Показаны примеры применения обоих методов.

2 Определения символов

Таблица 1: Символы, используемые в методе A. Таблица 2: Символы, используемые только в методе B. Таблица 3: Описание ключевых точек и кривых на рисунках.

3 Методы определения диаметра формы

Представленные методы применимы к наружным косозубым или прямозубым зубчатым колесам, изготовленным методом червячной обработки с последующей чистовой обработкой боковой поверхности.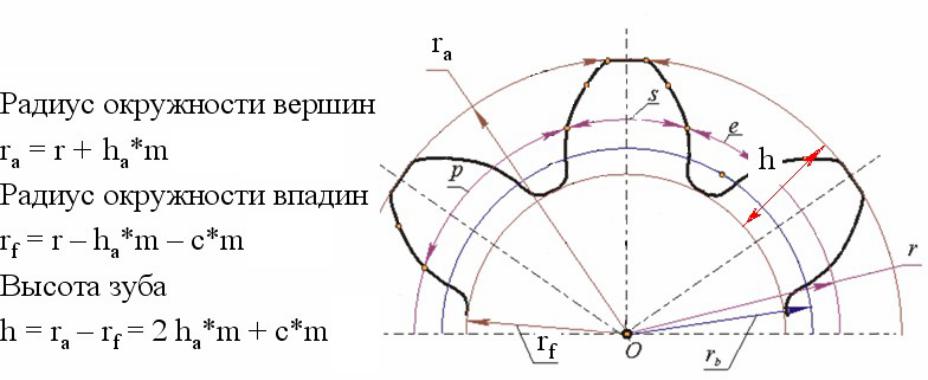 Методы представлены в разделах 3.1 и 3.2, предполагая, что зубчатое колесо прямозубое. В разделе 3.3 обсуждается, как обращаться с косозубыми зубчатыми колесами. Пример зуба шестерни показан на рисунке 1.

Рисунок 1: Пример зубчатого колеса. Рисунок 2: Геометрия фрезы.

В методах предполагается, что рассматриваемая геометрия фрезы может быть представлена ​​на рисунке 2. В нормальной плоскости фрезы круглый наконечник с радиусом ρ _a0 имеет две конечные точки M и N и центральную точку H. Переходная линейка NQ касается MN в точке N и соединяется с основной режущей кромкой PQ в точке Q.

В обоих методах используются следующие входные переменные, которые предполагаются известными проектировщикам:

• В отношении редуктора: r _f , r _b , Z , β _b

• В отношении варочной панели: φ , φ ₂ , ρ _а0 , δ ₀

В методе A угол давления NQ, φ ₂ , может варьироваться от 0° до φ . В методе B для простоты φ ₂ принимается равным 10°, поэтому не является входной переменной. Если на варочной панели нет выступа,  δ ₀ = 0, и φ ₂ = φ .

Если δ ₀ — фактический выступ на фрезе, расчетный диаметр формы соответствует состоянию зубчатого колеса после фрезы и перед чистовой обработкой. Если необходимо рассчитать фасонный диаметр зубчатого колеса после операции чистовой обработки только боковой поверхности, δ ₀ необходимо заменить на δ _или , прежде чем применять любой метод:

, где u _s — удаление припуска только для боковой поверхности чистовой обработки вдоль делительной окружности процесса зубофрезерной обработки.

В нестандартных конструкциях зубчатых колес угол давления зубчатого колеса не является существенным параметром. Одна и та же передача может быть выражена с использованием различных углов давления. Следовательно, угол давления зубчатого колеса, нормальный или поперечный, не является входной переменной ни в одном из методов. Нормальный угол давления фрезы φ важен и не должен равняться углу давления шестерни. Обратите внимание, что переменная r представляет собой радиус делительной окружности зубчатого колеса, который можно найти с помощью уравнения 2 для цилиндрического зубчатого колеса:

Для косозубого зубчатого колеса радиус делительной окружности r можно найти, решив уравнение 3:

3.1 Метод A

В методе A необходимо аналитически выразить три ключевые кривые. Трохоида MN’, образованная круглой вершиной фрезы, выражается с помощью уравнения A1-A4 [6], первичная эвольвента PQ’, генерируемая основной режущей поверхностью фрезы, и вторичная эвольвента NQ’, генерируемая переходной прямой кромкой соединение круглого наконечника и основной режущей кромки на варочной панели. Чтобы правильно расположить три кривые друг к другу, угловое расстояние от осевой линии трохоиды MN’ до обеих эвольвентных кривых указано в уравнениях A5 и A6.

Затем определяется нижняя точка X на первичной эвольвенте PQ’, которую может пересекать либо трохоида MN’, либо вторичная эвольвента NQ’. Метод А включает в себя итеративное решение для поиска точки пересечения, как и в предыдущих публикациях.

Рисунок 3: Корневая трохоида и эвольвента. Рисунок 4: Траектория H’ центра окружности наконечника фрезы и огибающая движения наконечника MN’.

В процессе зубофрезерной обработки в системе отсчета зубчатого колеса центр конца фрезы H имеет траекторию H’, которая симметрична ее центральной линии, как показано на рисунках 3 и 4. Кривая трохоиды H может быть выражена с использованием переменных θ _T и r _T :

Огибающая MN’ круглого наконечника MN представляет собой эквидистантную кривую от H’ с интервалом, равным радиусу наконечника фрезы ρ _a0 . Следовательно, MN’ можно выразить с помощью уравнения A2-A4:

. Угол между центральной линией H’ и начальной точкой эвольвенты PQ’ определяется уравнением A5:

. Аналогично, угол между центральной линией H’ и начальной точкой эвольвента NQ’ определяется уравнением A6:

Существует несколько вариантов относительного положения трех кривых. Немчек и Дейл провели их углубленный анализ [7]. На рис. 5 представлены два репрезентативных условия, а также диаметр формы в этих условиях. Чтобы найти самую низкую точку X на первичной эвольвенте, рекомендуется сначала итеративно найти точку пересечения X ₀ первичной эвольвенты PQ’ и корневой трохоиды MN’. Обязательно найдите более высокую, когда есть две точки пересечения. Затем определите, имеет ли отрезок NQ’ за пределами MN’ точку пересечения с PQ’. Если да, то новая точка пересечения будет выше, чем X ₀ и становится самой нижней точкой X на первичной эвольвенте, как показано на рисунке 5(b). В противном случае X ₀ является самой нижней точкой X на первичной эвольвенте, как показано на рисунке 5(a).

Рис. 5 (a), (b): Возможные позиционные соотношения ключевых кривых MN’, NQ’ и PQ’.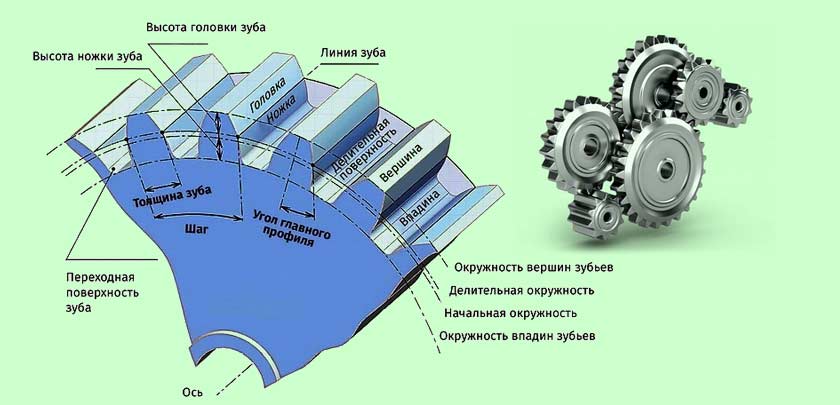

Когда итерации полностью сойдутся, диаметр формы из метода А будет очень точным. Их сравнили с результатами KISSsoft на нескольких примерах, и почти все видимые цифры совпадают. См. раздел 4 для примера деталей.

3.2 Метод B

С помощью метода A создается большое количество наборов данных, охватывающих широкий диапазон входных параметров. Каждый набор данных включает в себя входные параметры и расчетный диаметр формы. Затем эти данные используются в регрессии для создания ряда эмпирических формул для прямого расчета диаметра формы из входных параметров без необходимости аналитического построения нескольких кривых и использования математических соотношений для определения, где находится самая нижняя точка первичной эвольвенты. Считается, что метод Б намного проще в применении.

Из-за характера эмпирической формулы диаметры формы по методу B имеют относительные погрешности, которые обычно составляют менее 0,1 % в указанных диапазонах входных параметров и менее 0,05 % для обычных конструкций зубчатых колес. Точность достаточна для большинства практических применений, особенно когда конструкторам необходимо проверить возможность изготовления заданного диаметра формы, диаметра основания и радиуса вершины фрезы.

Рисунок 6: Блок-схема применения уравнений метода B.

18 уравнений следует применять в последовательности, показанной на рисунке 6. 135 коэффициентов d _ijkm приведены в таблице 4, которые используются для расчета 45 коэффициентов c _ijk , которые в дальнейшем используются для расчета 15 коэффициентов b _ij , которые впоследствии используются для расчета 5 коэффициентов a _i , которые позже используется для расчета диаметра потенциальной формы d _TIF,C . В зависимости от входных параметров и логического решения, показанного на рисунке 6, могут потребоваться аналогичные процессы для нахождения диаметра потенциальной формы, когда C=0,0005, d _TIF,C5 , и диаметр потенциальной формы, когда выпуклость равна нулю d _TIF,C0 , и диаметр потенциальной формы, если он получен как пересечение двух эвольвентных кривых, d _TIF,S . Наконец, этот метод определяет, какой диаметр потенциальной формы является фактическим диаметром формы, и сообщает об этом как d _TIF . Хотя метод B требует от 75 до 178 шагов расчета для определения диаметра формы, все шаги просты и понятны.

Иметь относительную погрешность менее 0,1%, переменные φ , A, B, C должны находиться в следующих диапазонах:

φ : [15°, 30°]

A: [0,01, 0,2]

B: [0, 0,6] 9000 5

C: [0, 0,005]

Ниже приведены уравнения для метода B:

Коэффициенты, используемые в уравнении B6, показаны в таблице 4.

Таблица 4: dijkm, используемые в уравнении B6.

Коэффициенты, использованные в уравнении B11, показаны в таблице 5.

Таблица 5: dijk’, использованный в уравнении B11.

Коэффициенты, использованные в уравнении B15, показаны в таблице 6.

Таблица 6: dijk, используемый в уравнении B15.

3.3 Применение методов A и B к косозубым зубчатым колесам

Методы A или B нельзя применять в поперечной плоскости для точного определения диаметра косозубого зубчатого колеса из-за того, что в обоих методах предполагается, что вершина червячной фрезы имеет круглую форму. Когда червячная фреза имеет круглый наконечник в своей нормальной плоскости, наконечник имеет эллиптическое поперечное сечение в поперечной плоскости при нарезке косозубого колеса.

Оба метода могут быть применены к косозубым зубчатым колесам в нормальной плоскости с использованием концепции виртуального цилиндрического зубчатого колеса. Окружности, образующие делительную окружность косозубого колеса и его виртуального прямозубого колеса, пересекаются в точке R на рисунке 3. Однако, если уравнение 4 используется для количества зубьев виртуального прямозубого колеса, результаты определения диаметра формы могут иметь относительную погрешность более 0,1. %. Несколько иной метод расчета количества зубьев в виртуальном цилиндрическом зубчатом колесе Z 9.0129 V использует уравнение 5, которое обеспечивает более высокую точность сгенерированной геометрии корня для самых разных конструкций зубчатых колес. Относительная погрешность определения диаметра косозубого зубчатого колеса с использованием уравнения 5 и метода А составляет менее 0,01%.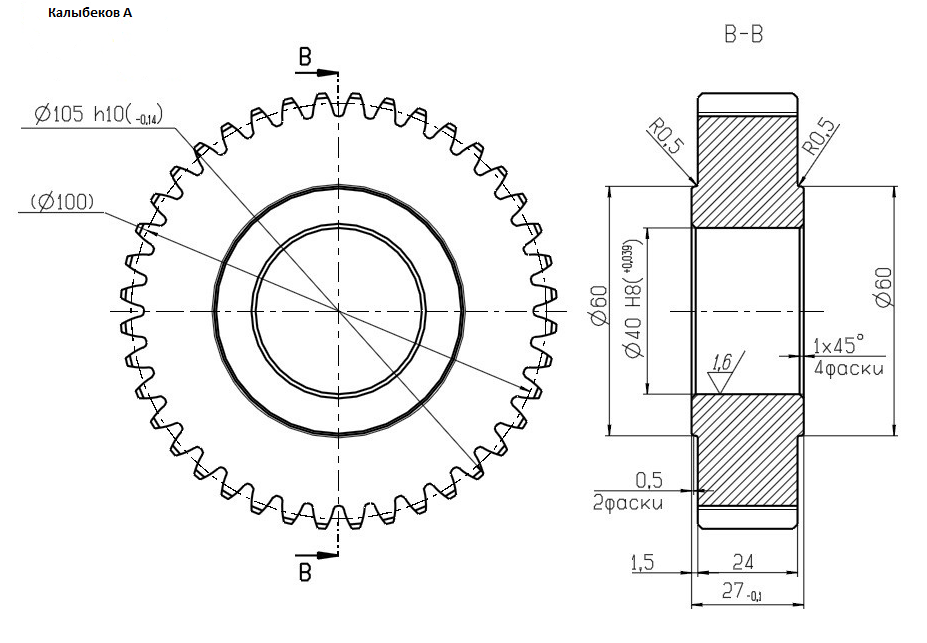 Относительная погрешность диаметра формы косозубого зубчатого колеса с использованием уравнения 5 и метода B в основном связана с самим методом и составляет менее 0,1%, если расчетные параметры находятся в указанных диапазонах.

Угол подъема спирали при различных диаметрах может быть связан с основным углом спирали с помощью уравнения 6.

Расстояние между центрами косозубого колеса и его виртуального прямозубого колеса равно разнице между образующими делительными радиусами двух колес:

В котором r и β _r можно найти с помощью уравнения 3.

После фасонный диаметр виртуального цилиндрического зубчатого колеса d _TIF,V находится с помощью метода A или B, для определения фасонного диаметра фактического косозубого колеса с помощью уравнения 8 требуется регулировка межосевого расстояния:

Рекомендуется следовать процесс, показанный на рисунке 7, для расчета диаметра формы косозубого колеса.

Рисунок 7: Процесс расчета диаметра формы косозубого зубчатого колеса.

4  Примеры с использованием методов A и B

Создано десять примеров для сравнения результатов диаметра формы, полученных методом A, методом B и KISSsoft. Каждый пример представляет собой довольно экстремальную особенность конструкции зубчатой ​​передачи, как указано в описании, с надеждой охватить широкий спектр практических конструкций зубчатой ​​передачи. дед. коэффициент равен (r – r _f ) Z cos φ ⁄ (2r _b ).

Графическое представление 10 приведенных выше примеров создано с помощью KISSsoft и представлено на рисунках 8-17. Две дуги окружности на рисунках 8-17 представляют базовую окружность (нижняя) и формируют окружность диаметра (верхняя).

Таблица 7: Примеры применения методов A и B.Рисунок 8: Пример 1, типичный ответвление.Рисунок 9: Пример 2, угол высокого давления.Рисунок 10: Пример 3, угол низкого давления.Рисунок 11: Пример 4, небольшое количество Рисунок 12: Пример 5, большое количество зубов. Рисунок 13: Пример 6, большой выступ. Рисунок 14: Пример 7, небольшой выступ. .Рисунок 17: Пример 10, косозубая шестерня.

5 Обсуждение

Некоторые общие выводы можно сделать из параметрических исследований с использованием методов. Если другие параметры остаются неизменными, больший выступ, больший радиус вершины фрезы, больший радиус корня и больший угол вторичного давления фрезы имеют тенденцию к увеличению диаметра формы. Это доказывает, что меньший диаметр формы и более высокая прочность на изгиб являются компромиссом по производственным причинам.

Для изготовления целевого зубчатого колеса нижний угол нормального давления фрезы обычно имеет тенденцию к уменьшению диаметра профиля, но только до определенного угла давления, после которого дальнейшее снижение нормального угла давления фрезы будет увеличивать диаметр профиля. Большое количество зубьев, малая дедендум, большой выступ, большой радиус вершины фрезы и большой вторичный угол давления приводят к тому, что основная эвольвента пересекается вторичной эвольвентой, а не трохоидой.

Применяя любой метод несколько раз с различными выступами в диапазоне от нуля до фактического выступа, можно построить форму верхней части кривой скругления корня, от диаметра формы до максимального диаметра выточки или диаметра базовой окружности, в зависимости от того, что больше. Форма кривой скругления может быть полезна при конструировании инструмента для чистовых операций.

6  Выводы и дальнейшая работа

Представлены два метода определения диаметра формы наружных косозубых или прямозубых шестерен по конструктивным параметрам шестерни и параметрам фрезы. Метод А может быть очень точным, но его применение сопряжено с некоторыми трудностями. С помощью метода А необходимо итеративно найти одну конкретную точку пересечения из нескольких точек пересечения среди трех кривых, которые выражены неявными функциями. Для сравнения, метод B проще в применении, так как все уравнения и шаги являются прямыми расчетами. Метод Б имеет большие относительные ошибки, приемлемые для большинства практических целей. Одно из возможных применений таких методов заключается в том, что разработчики зубчатых колес, не имеющие доступа к передовому программному обеспечению для моделирования, могут оценить технологичность предлагаемых конструкций и сопоставить достижимое отношение контакта с радиусом корня и толщиной зуба в критическом сечении на ранней стадии проектирования. Другие способы использования этих методов включают помощь в проектировании червячных дисков и выполнение параметрического исследования параметров зубчатых колес и червячных дисков, что требует много времени даже при наличии доступа к передовому программному обеспечению для моделирования.

Для будущей работы такие методы могут быть расширены для учета зубчатых колес с внутренним зацеплением и зубчатых колес с зубчатым зацеплением.

7 Благодарность

Автор благодарит Джека Ценга, основателя и владельца GearShopPro LLC за помощь от себя и своей программы. Автор благодарит ООО «Стар-СУ» за их вклад. KISSsoft используется в качестве эталона и инструмента для построения графиков.

Библиография

1. ANSI/AMGA, 2005 г., «Номенклатура передач, определение терминов с помощью символов», ANSI/AGMA 1012-G05.
2. ISO, 2006 г., «Расчет грузоподъемности прямозубых и косозубых зубчатых колес. Часть 1: Основные принципы, введение и общие факторы влияния», ISO 6336-1.
3. Герпен, Х.В. и Рис, С.К., 1989, «Диаметр формы зубчатых колес», Gear Technology, стр. 38-44.
4. Математика, В.Б. и Чанд, С., 2004 г., «Подход к определению галтели корня зуба цилиндрической шестерни», ASME. Дж. Мех. Des., 126(2), стр. 336-340.
5. Лиан Г., 2005 г., «Определение профиля скругления косозубого зубчатого колеса с формообразующей нарезкой», Осеннее техническое совещание, AGMA, 05FTM14.
6. Buckingham, E., 1988, Analytical Mechanics of Gears, Dover Publications, New York, Chap. 3
7. Немчек, М. и Дейл, З., 2011 г., «Геометрические расчеты скошенной вершины и выточки выступа профиля зуба», Международные технические конференции по проектированию и Компьютеры и информация в инженерной конференции, ASME.