Содержание
Центр тяжести — методы нахождения.
Наиболее часто для нахождения центра тяжести тела или фигуры применяют следующие методы:
- метод симметрии;
- метод разбиения;
- метод отрицательных масс.
Рассмотрим приемы, применяемые в каждом из перечисленных методов.
***
Метод симметрии
Представим себе однородное тело, которое имеет плоскость симметрии. Выберем такую систему координат, чтобы оси x и z лежали в плоскости симметрии (см. рисунок 1).
В этом случае каждой элементарной частице силой тяжести Gi с абсциссой yi = +a соответствует такая же элементарная частица с абсциссой yi = -a, тогда:
yC = Σ(Gixi)/ΣGi = 0.
Отсюда вывод: если однородное тело имеет плоскость симметрии, то центр тяжести тела лежит в этой плоскости.
Аналогично можно доказать и следующие положения:
- Если однородное тело имеет ось симметрии, то центр тяжести тела лежит на этой оси;
- Если однородное тело имеет две оси симметрии, то центр тяжести тела находится в точке их пересечения;
- Центр тяжести однородного тела вращения лежит на оси вращения.

***
Метод разбиения
Этот метод заключается в том, что тело разбивают на наименьшее число частей, силы тяжести и положение центров тяжести которых известны, после чего применяют приведенные ранее формулы для определения общего центра тяжести тела.
Допустим, что мы разбили тело силой тяжести G на три части G’, G», G»’, абсциссы центров тяжести этих частей x’C, x»C, x»’C известны.
Формула для определения абсциссы центра тяжести всего тела:
xC = Σ(Gixi)/ΣGi.
Перепишем ее в следующем виде:
xCΣGi = Σ(Gixi) или GxC = Σ(Gixi).
Последнее равенство запишем для каждой из трех частей тела отдельно:
G’x’C = Σ(G’x’i), G»x»C = Σ(G»ix»i), G»’x»’C = Σ(G»’ix»’i).
Сложив левые и правые части этих трех равенств, получим:
G’x’C + G»x»C + G»’x»’C = Σ(G’ix’i) + Σ(G»x»i) + Σ(G»’ix»’i) = Σ(Gixi).
Но правая часть последнего равенства представляет собой произведение GxC, так как
GxC = Σ(Gixi),
Следовательно, xC = (G’x’C + G»x»C + G»’x»’C)/G, что и требовалось доказать.
Аналогично определяются координаты центра тяжести на координатных осях y и z:
yC = (G’y’C + G»y»C + G»’y»’C)/G,
zC = (G’z’C + G»z»C + G»’z»’C)/G.
Полученные формулы аналогичны формулам для определения координат цента тяжести, выведенные выше. Поэтому в исходные формулы можно подставлять не силы тяжести элементарных частиц Gi, а силы тяжести конечных частей; под координатами xi, yi, zi понимают координаты центров тяжести частей, на которые разбито тело.
***
Метод отрицательных масс
Этот метод заключается в том, что тело, имеющее свободные полости, считают сплошным, а массу свободных полостей – отрицательной. Вид формул для определения координат центра тяжести тела при этом не меняется.
Таким образом, при определении центра тяжести тела, имеющего свободные полости, следует применять метод разбиения, но считать массу полостей отрицательной.
***
Практические методы определения центра тяжести тел
На практике для определения центра тяжести плоских тел сложной формы часто применяют метод подвешивания, который заключается в том, что плоское тело подвешивают на нити за какую-нибудь точку. Прочерчивают вдоль нити линию, и тело подвешивают за другую точку, не находящуюся на полученной линии.
Затем вновь проводят линию вдоль нити.
Точка пересечения двух линий и будет являться центром тяжести плоского тела.
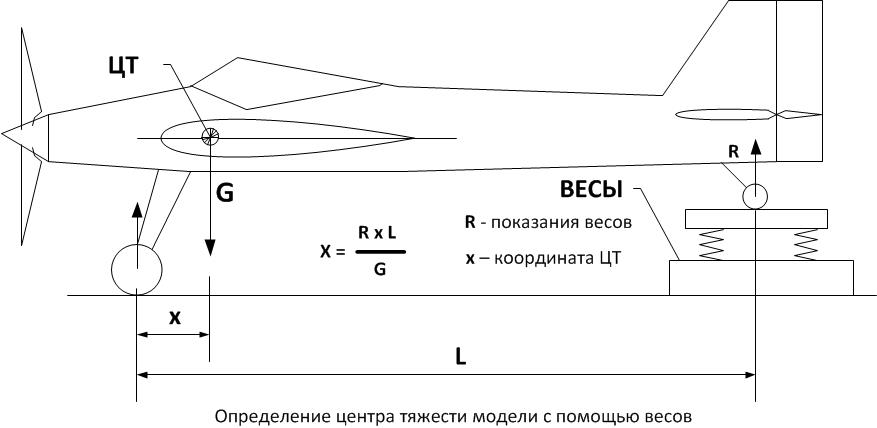
Еще один способ определения центра тяжести, применяемый на практике, называется метод взвешивания. Этот метод часто применяется для определения центра тяжести крупных машин и изделий – автомобилей, самолетов, колесных тракторов и т. п., которые имеют сложную объемную форму и точечную опору на грунт.
Этот метод часто применяется для определения центра тяжести крупных машин и изделий – автомобилей, самолетов, колесных тракторов и т. п., которые имеют сложную объемную форму и точечную опору на грунт.
Метод заключается в применении условий равновесия, исходя из того, что сумма моментов всех сил, действующих на неподвижное тело равна нулю.
Практически это осуществляется взвешиванием одной из опор машины (задние или передние колеса устанавливаются на весы), при этом показания весов, по сути, являются реакцией опоры, которая учитывается при составлении уравнения равновесия относительно второй точки опоры (находящейся вне весов).
По известной массе (соответственно – весу) тела, показанию весов в одной из точек опоры, и расстоянию между точками опоры можно определить расстояние от одной из точек опоры до плоскости, в которой расположен центр тяжести.
Чтобы найти подобным образом линию (ось), на которой расположен центр тяжести машины, необходимо произвести два взвешивания по принципу, изложенному выше для метода подвешивания (см. рис. 1а).
рис. 1а).
***
Положение центра тяжести некоторых фигур
Прямоугольник. Так как прямоугольник имеет две оси симметрии, то центр тяжести его площади находится в точке пересечения этих осей, иначе говоря, в точке пересечения диагоналей прямоугольника.
Треугольник. Пусть дан треугольник АBD (см. рисунок 2).
Разобьем его на элементарные (бесконечно узкие) полоски, параллельные стороне AD. Центр тяжести каждой полоски будет лежать на медиане Bd (т. е. в середине каждой полоски), следовательно, на этой медиане будет лежать и центр тяжести всей площади треугольника. Разбив треугольник на элементарные полоски, параллельные стороне AB, увидим, что искомый центр тяжести лежит и на медиане aD.
Проделав аналогичное действие с треугольником относительно стороны ВD, получим тот же результат – центр тяжести находится на соответствующей медиане.
Следовательно, центр тяжести всей площади треугольника лежит на точке пересечения его медиан, поскольку эта точка является единственной общей точкой для всех трех медиан данной геометрической фигуры.
Из геометрии известно, что медианы треугольника пересекаются в одной точке и делятся в соотношении 1:2 от основания. Следовательно, центр тяжести треугольника расположен на расстоянии одной трети высоты от каждого основания.
Дуга окружности. Возьмем дугу окружности АВ радиусом R с центральным углом 2α (см. рисунок 3). Систему координат выберем так, чтобы начало координат было в центре окружности, а ось x делила дугу пополам, тогда yC= 0 вследствие симметрии дуги относительно оси x. Определим координату центра тяжести xC.
Разобьем дугу АВ на элементарные части li, одна из которых изображена на рисунке. Тогда, согласно сделанным выше выводам,
xC =Σ(lixCi)/Σli.
Дугу li вследствие малости примем за отрезок прямой. Из подобия треугольника ODiCi и элементарного треугольника S (на рисунке заштрихован) получим:
Li/Δyi = R/xCi или lixi = RΔyi.
Тогда:
xC =Σ(lixCi)/Σli = Σ(RΔyi)/l = RΣΔyi/l = R×AB/l,
поскольку RΣΔyi = AB, а Σli = l – длина дуги АВ. Но АВ = 2R sinα, а l = 2Rα, следовательно,
xC = (R sinα)/α.
При α = π/2 рад (полуокружность), xC = 2R/π.
Круговой сектор. Возьмем сектор радиусом R с центральным углом 2α (см. рисунок 3а). Проведем оси координат, как показано на рисунке (ось x направлена вдоль оси симметрии сектора), тогда yC = 0.
Определим xC, для чего разобьем сектор на ряд элементарных секторов, каждый из которых из-за малости дуги li можно принять за равнобедренный треугольник с высотой R. Тогда центр тяжести каждого элементарного сектора будет находиться на дуге радиуса 2R/3 и задача определения центра тяжести сектора сводится к определению центра тяжести этой дуги.
Очевидно, что
xC = 2 R sinα/(3α).
При α = π/2 рад (полукруг): xC = 4R/(3π).
***
Пример решения задачи на определение центра тяжести
Задача:
Определить положение центра тяжести сечения, составленного из двутавра № 22 и швеллера № 20, как показано на рисунке 4.
Решение.
Из курса инженерной графики известно, что номер проката соответствует наибольшему габаритному размеру его сечения, выраженного в сантиметрах.
Так как сечение, составленное из двутавра и швеллера, представляет собой фигуру, симметричную относительно оси y, то центр тяжести такого сечения лежит на этой оси, т. е. xC = 0.
По справочнику определим площади и координаты центров тяжести двутавра 1 и швеллера 2.
Для двутаврового сечения: А1 = 15,2 см2; y1 = 22/2 = 11 см.
Для швеллерного сечения: А2 = 12 см2; y2 = 22 + d – z0 = 22 + 0,32 – 1,25 = 21,07 см,
где d – толщина стенки швеллера; z0 – размер, определяющий положение центра тяжести швеллера.
Применим формулу для определения координаты центра тяжести всего сечения:
yC = Σ(Aiyi)/ΣAi,
тогда:
yC = (A1y1 +A2y2)/(A1 +A2) = (15,2×11 + 12×21,07)/(15,2 + 12) = 15,4 см.
Задача решена.
***
Кинематика точки
Главная страница
- Страничка абитуриента
Дистанционное образование
- Группа ТО-81
- Группа М-81
- Группа ТО-71
Специальности
- Ветеринария
- Механизация сельского хозяйства
- Коммерция
- Техническое обслуживание и ремонт автотранспорта
Учебные дисциплины
- Инженерная графика
- МДК.
 01.01. «Устройство автомобилей»
01.01. «Устройство автомобилей» - Карта раздела
- Общее устройство автомобиля
- Автомобильный двигатель
- Трансмиссия автомобиля
- Рулевое управление
- Тормозная система
- Подвеска
- Колеса
- Кузов
- Электрооборудование автомобиля
- Основы теории автомобиля
- Основы технической диагностики
- Основы гидравлики и теплотехники
- Метрология и стандартизация
- Сельскохозяйственные машины
- Основы агрономии
- Перевозка опасных грузов
- Материаловедение
- Менеджмент
- Техническая механика
- Советы дипломнику
Олимпиады и тесты
- «Инженерная графика»
- «Техническая механика»
- «Двигатель и его системы»
- «Шасси автомобиля»
- «Электрооборудование автомобиля»
|
КАТЕГОРИИ: Археология
ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы.
|
⇐ ПредыдущаяСтр 4 из 30Следующая ⇒ Наиболее часто для нахождения центра тяжести тела или фигуры применяют следующие методы: · метод симметрии; · метод разбиения; · метод отрицательных масс. Рассмотрим приемы, применяемые в каждом из перечисленных методов. *** Метод симметрии Представим себе однородное тело, которое имеет плоскость симметрии. Выберем такую систему координат, чтобы оси x и z лежали в плоскости симметрии (см. рисунок 1). В этом случае каждой элементарной частице силой тяжести Giс абсциссой yi = +a соответствует такая же элементарная частица с абсциссой yi = -a, тогда: yC = Σ(Gixi)/ΣGi = 0. Отсюда вывод: если однородное тело имеет плоскость симметрии, то центр тяжести тела лежит в этой плоскости. Аналогично можно доказать и следующие положения: · Если однородное тело имеет ось симметрии, то центр тяжести тела лежит на этой оси; · Если однородное тело имеет две оси симметрии, то центр тяжести тела находится в точке их пересечения; · Центр тяжести однородного тела вращения лежит на оси вращения. *** Метод разбиения Этот метод заключается в том, что тело разбивают на наименьшее число частей, силы тяжести и положение центров тяжести которых известны, после чего применяют приведенные ранее формулы для определения общего центра тяжести тела. Допустим, что мы разбили тело силой тяжести G на три части G’, G», G»’, абсциссы центров тяжести этих частейx’C, x»C, x»’C известны. xC = Σ(Gixi)/ΣGi. Перепишем ее в следующем виде: xCΣGi = Σ(Gixi) или GxC = Σ(Gixi). Последнее равенство запишем для каждой из трех частей тела отдельно: G’x’C = Σ(G’x’i), G»x»C = Σ(G»ix»i), G»’x»’C = Σ(G»’ix»’i). Сложив левые и правые части этих трех равенств, получим: G’x’C + G»x»C + G»’x»’C = Σ(G’ix’i) + Σ(G»x»i) + Σ(G»’ix»’i) = Σ(Gixi). Но правая часть последнего равенства представляет собой произведение GxC, так как GxC = Σ(Gixi), Следовательно, xC = (G’x’C + G»x»C + G»’x»’C)/G, что и требовалось доказать. yC = (G’y’C + G»y»C + G»’y»’C)/G, Полученные формулы аналогичны формулам для определения координат цента тяжести, выведенные выше. Поэтому в исходные формулы можно подставлять не силы тяжести элементарных частиц Gi, а силы тяжести конечных частей; под координатами xi, yi, zi понимают координаты центров тяжести частей, на которые разбито тело. *** Метод отрицательных масс Этот метод заключается в том, что тело, имеющее свободные полости, считают сплошным, а массу свободных полостей – отрицательной. Таким образом, при определении центра тяжести тела, имеющего свободные полости, следует применять метод разбиения, но считать массу полостей отрицательной. *** Практические методы определения центра тяжести тел На практике для определения центра тяжести плоских тел сложной формы часто применяют метод подвешивания, который заключается в том, что плоское тело подвешивают на нити за какую-нибудь точку. Прочерчивают вдоль нити линию, и тело подвешивают за другую точку, не находящуюся на полученной линии. Еще один способ определения центра тяжести, применяемый на практике, называется метод взвешивания. Этот метод часто применяется для определения центра тяжести крупных машин и изделий – автомобилей, самолетов, колесных тракторов и т.
Вопрос 12 Момент инерции тела. МОМЕНТ ИНЕРЦИИ — величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. В механике различают M. и. осевые и центробежные. Осевым M. и. тела относительно оси z наз. величина, определяемая равенством где mi — массы точек тела, hi — их расстояния от оси z, r — массовая плотность, V — объём тела. Величина Iz является мерой инертности тела при его вращении вокруг оси (см. Вращательное движение). Осевой M. и. можно также выразить через линейную величину rz, наз. радиусом инерции относительно оси z, по ф-ле Iz = Mr2z, где M — масса тела. Размерность M. и.- L2M;единицы измерения -кг.м2. Центробежными M. и. относительно системы прямоуг. осей х, у, z, проведённых в точке О, наз. или соответствующими объёмными интегралами. Эти величины являются характеристиками динамич. неуравновешенности тела. Напр., при вращении тела вокруг оси z от значений Ixz и Iyz зависят силы давления на подшипники, в к-рых закреплена ось. M. и. относительно параллельных осей z и z’ связаны соотношением (теорема Гюйгенса) где z’ — ось, проходящая через центр массы тела, d — расстояние между осями. M. и. относительно любой проходящей через начало координат О оси Ol с направляющими косинусами a, b, g находится по ф-ле Зная шесть величин Ix, Iy, Iz, Ixy, Iyz, Izx, можно последовательно, используя ф-лы (4) и (3), вычислить всю совокупность M. и. тела относительно любых осей. Эти шесть величин определяют т. н. тензор инерции тела. Через каждую точку тела можно провести 3 такие взаимно перпендикулярные оси, наз. Вопрос 12.1 ⇐ Предыдущая12345678910Следующая ⇒ Читайте также: Организация работы процедурного кабинета Статус республик в составе РФ Понятие финансов, их функции и особенности Сущность демографической политии |
|
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 3260; Нарушение авторского права страницы; Мы поможем в написании вашей работы!
infopedia.
|
Определение положения центра тяжести фигур и тел сложной формы
Оглавление:
Определение положения центра тяжести фигур и тел сложной формы
Аналитический способ
Для определения положения центра тяжести фигур и тел сложной геометрической формы их мысленно разбивают на такие части простейшей формы (если, конечно, это возможно), для которых положения центров тяжести известны. Затем определяют положение центра тяжести всей фигуры или тела по формулам § 39, понимая в этих формулах под и объемы, площади и длины частей, на которые разбито данное тело, фигура или линия, а под и — координаты центров тяжести этих частей.
Если рассматриваемые фигуры или тела неоднородны, то, разделив их па однородные части, умножают входящие в формулы (43), (44) и (47) объемы, площади и длины этих частей на соответствующий каждой части удельный вес. Если в данном теле или фигуре имеются полости или отверстия, то для определения центра тяжести такого тела или фигуры пользуются теми же приемами и формулами, считая при этом объемы и площади вырезанных частей отрицательными.
Если в данном теле или фигуре имеются полости или отверстия, то для определения центра тяжести такого тела или фигуры пользуются теми же приемами и формулами, считая при этом объемы и площади вырезанных частей отрицательными.
В тех случаях, когда данное тело нельзя разбить на такие части, для которых было бы известно положение их центров тяжести, для вычисления координат центра тяжести тела приходится пользоваться методами интегрального исчисления.
Экспериментальный способ
Для определения центра тяжести неоднородных тел сложной формы существуют различные экспериментальные методы. Рассмотрим на примерах два из них.
I. Метод взвешивания. Для определения положения центра тяжести шатун (рис. 93) подвешиваем в точке и опираем точкой на платформу десятичных весов, так чтобы он занял горизонтальное положение. Сила давления шатуна на платформу, найденная путем взвешивания, оказалась равной по модулю . К находящемуся в равновесии шатуну приложены силы: сила тяжести шатуна, проходящая через его центр тяжести, вертикальная реакция платформы, проходящая через точку и равная по модулю силе давления шатуна на платформу, и сила натяжения нити .
Зная вес шатуна и расстояние между его точками и , теперь нетрудно найти и расстояние от точки до центра тяжести шатуна. Одним из уравнений равновесия шатуна будет:
- Метод подвешивания. Тело подвешивают на нити за какую-либо его точку (рис. 94, а) к неподвижной точке . После того как тело придет в равновесие, проводят вертикальную линию , составляющую продолжение направления нити . При равновесии центр тяжести тела должен находиться на одной
вертикали с неподвижной точкой и, следовательно, будет лежать на линии . Вновь подвесив тело к другой его точке (рис. 94,6), мы точно так же найдем, что его центр тяжести лежит на линии , являющейся продолжением направления нити . Точка пересечения линий и и будет являться центром тяжести тела. Способ подвешивания удобен для определения положения центра тяжести тонких пластинок.
Пример задачи:
Найти статические моменты относительно координатных осей площади листа и координаты его центра тяжести.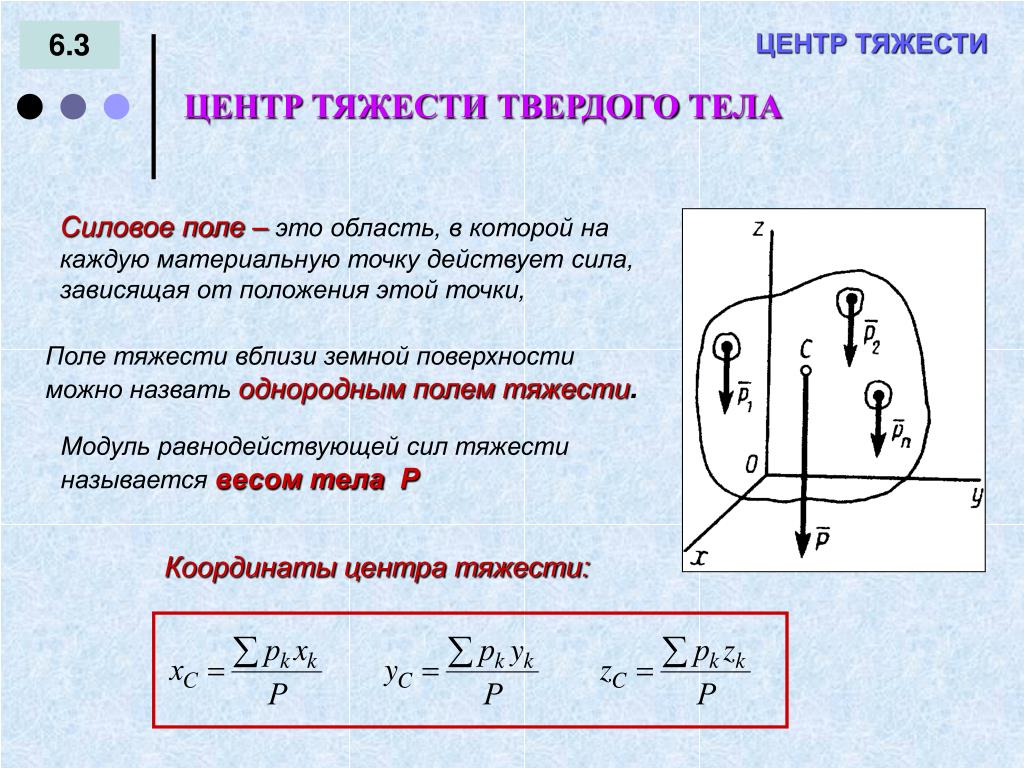 Размеры листа (в сантиметрах) указаны на рис. 95.
Размеры листа (в сантиметрах) указаны на рис. 95.
Решение:
Разобьем данную площадь на три прямоугольника. Центр тяжести каждого из прямоугольников лежит на пересечении его диагоналей. Координаты этих центров, так же как и площади прямоугольников, легко определяются из чертежа.
По формулам (45) находим статические моменты площади данной фигуры
Определяем теперь по формулам (46) координаты центра тяжести площади фигуры:
Пример задачи:
Найти центр тяжести площади кругового сегмента радиуса , если (рис. 96).
Решение:
Искомый центр тяжести лежит на оси симметрии, проходящей через центр круга и середину дуги . Направим вдоль прямой ось . Начало координат возьмем в точке Будем рассматривать круговой сегмент как состоящий из двух фигуp: кругового сектора и треугольника , причем вторую площадь надо считать отрицательной.
Площадь кругового сектора
Абсцисса его центра тяжести
Площадь треугольника
Абсцисса его центра тяжести
По формуле (44) определяем абсциссу центра тяжести данного кругового сегмента:
Пример задачи:
Тело состоит из деревянного цилиндра II, радиус которого высота и двух скрепленных с ним стальных шаров I и III с радиусами и (рис. 97). Определить положение центра тяжести этого тела, если удельный вес дерева и удельный вес стали .
97). Определить положение центра тяжести этого тела, если удельный вес дерева и удельный вес стали .
Решение:
Искомый центр тяжести лежит на оси симметрии, проходящей через центры шаров и . Начало координат возьмем в центре большого шара и ось симметрии примем за ось . Разобьем тело на три части и составим для них таблицу объемов и координат (абсцисс) центров тяжести.
Для определения абсциссы центра тяжести всего неоднородного тела воспользуемся формулой (42):
Пример задачи:
Определить статические моменты относительно координатных осей и положение центра тяжести сечения (рис. 98, я), составленного из равнобокого уголка 100 X 100 X 10, швеллера №24 и полосы 190 X 10.
Решение:
Из таблиц нормального сортамента для прокатной стали ‘) выпишем следующие данные:
I. Равнобокий уголок (рис. 98,6), ГОСТ 8509-57. Профиль № 10. Ширина полки Толщина полки . Площадь поперечного сечения Расстояние центра тяжести от оснований полки .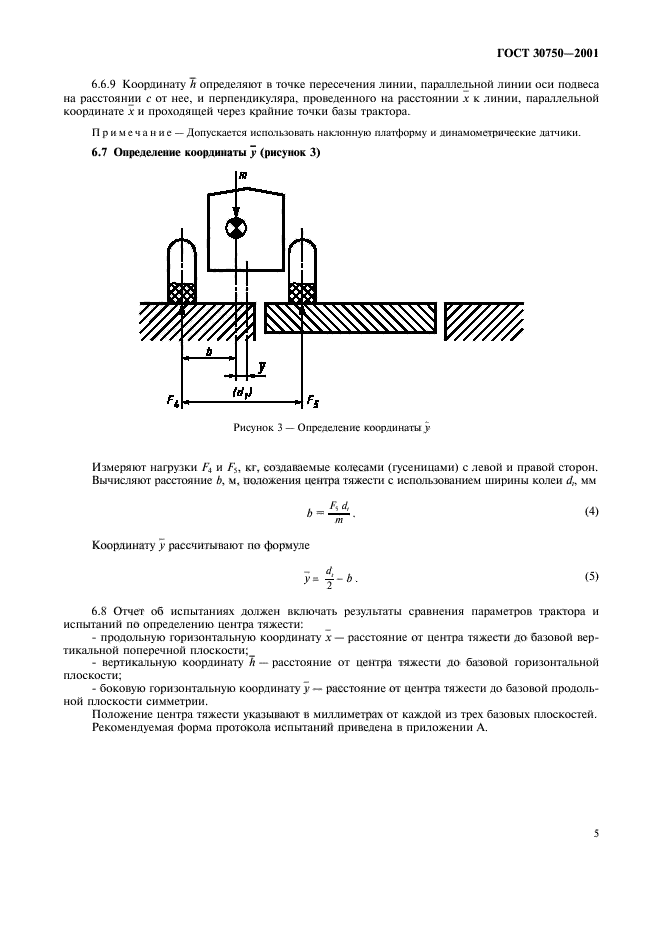
II. Швеллер (рис. 98, в), ГОСТ 8509-57. Профиль № 24. Высота стенки Ширина полки Толщина стенки Площадь поперечного сечения . Расстояние центра тяжести от наружного края вертикальной стенки . (Швеллер имеет горизонтальную ось симметрии и, следовательно, его центр тяжести лежит на этой оси.)
III. Полосовая сталь, ГОСТ 103-57. Сечение — прямоугольник. Ширина полосы 190 мм. Толщина 10 мм. Площадь поперечного сечения
Нумеруем отдельные части сечения и на основании записанных выше данных проставляем соответствующие размеры (в см) на рис. 98, а. Оси координат выбираем так, как указано на этом рисунке.
Статический момент сечения относительно оси :
Статический момент сечения относительно оси :
Координаты центра тяжести сечения:
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
|
222 ВЗВЕШИВАНИЕ САМОЛЕТА
2221 Взвешивание и определение центра тяжести производится в двух вариантах: I. Пустой самолет с несъемным оборудованием, но с водой в системе и маслом в картере мотора. II. Самолет имеет нормальную полетную нагрузку. 2222 Взвешивание для определения центра тяжести производится в трех положениях самолета: 1. При угле, близком к стояночному. 2. В линии полета или близкой к ней. 3. В положении самолета, когда нагрузка на костыль небольшая. ПРИМЕЧАНИЕ. Для самолетов с весом до 2,5 т поднятие хвоста производится до тех пор, пока на костыле не будет достигнута нулевая нагрузка. 2223 Самолет устанавливается на двух весах (весы под шасси и весы под костыль), а если платформа весов не позволяет установить на нее оба колеса шасси, то на трех (весы в трех точках). 2224 Измерения производятся с помощью нивелира. Нивелир устанавливается таким образом, чтобы линия горизонта проходила несколько выше оси колес и ниже задней кромки крыла в месте хорды обмера при стоянке самолета на трех точках. 2225 За хорду обмера обычно выбирается хорда разъема или хорда любого сечения крыла, где нет зализов. 2226 При каждом положении самолета производятся измерения, приведенные на схеме фиг. 2226. Измерения производятся в следующем порядке: Между колесами вдоль их оси натягивается тонкая проволока, которая должна быть горизонтальна. В случае, если колеса имеют развалку, проволока должна находиться на линии. Проходящей через точки пересечения плоскости симметрии колес с их осями вращения.
Проверяется вертикальность плоскости симметрии самолета и обязательно заклиниваются амортизаторы шасси. В носовой части крыла отмечается (на-глаз) передняя точка выбранной хорды обмера (как наиболее удаленная точка от задней кромки крыла). При помощи примитивного штангенциркуля или ровно выстроганной планки и двух столярных угольников измеряется длина хорды обмера. ПРИМЕЧАНИЕ. Штангенциркуль или планку следует прикладывать параллельно (на — глаз) хорде обмера. При помощи натянутой ленты рулетки измеряются расстояния n и m (фиг. 2226) от проволоки, соединяющей оси колес, до передней и задней точек хорды обмера.
При помощи нивелира, отвесов и измерительной линейки определяются при каждом положении взвешивания величины h1 и h2(фиг. 2226) — расстояния от линии горизонта до передней и задней точек хорды обмера. При помощи отвесов и рулетки измеряется расстояние L между проволокой, натянутой между колесами, и перпендикуляром, опущенным на линию горизонта из точки касания костылем платформы весов или подставки. Результаты обмеров заносят в протокол (табл. 2226).
В протоколе, помимо записей измерений, производятся подсчеты значений х:
где Рхв — чистый вес хвостовой части при данном положении самолета. При взвешивании самолета с трехколесным шасси операции производятся в том же порядке, как для самолета с двухколесным шасси, причем роль хвостового колеса играет переднее колесо. При взвешивании самолета на лыжах необходимо освобождать их амортизаторы.
ОПРЕДЕЛЕНИЕ ЦЕНТРА ТЯЖЕСТИ САМОЛЕТА
Определение положения центра тяжести относительно хорды обмера производится по схеме, представленной на фиг. 2231. Чертеж делается для больших самолетов в 1/10 и для небольших самолетов в 1/5 натуральной величины. Порядок построения указан в подписи к фиг. 2231. Если центр тяжести самолета ранее определен относительно хорды разъема (как часто бывает в заводской практике), то хорду разъема нужно наложить на чертеж в соответствии с чертежом крыла самолета. Можно сделать такое же наложение и средней аэродинамической хорды. Опустив перпендикуляр па хорду разъема или САХ из центра тяжести самолета, можно определить координаты центра тяжести относительно носка той или другой хорды и положение центра тяжести но оси x и по оси у в процентах хорды по формулам:
Для определения угла капотажа проводится касательная к окружности колеса так, чтобы она проходила под углом αст к хорде крыла, и опускается из точки O перпендикуляр OD на эту касательную.
На чертеже откладывается длина b хорды обмера. Из точек А и В (носик и хвостик профиля) радиусами n и m делаются засечки, пересечение которых дает точку О — центр оси колес. Из тех же точек А и В проводятся дуги окружностей радиусами h1, и h2, для каждого взвешивания (на чертеже это произведено только для одного взвешивания). К этим окружностям проводится общая касательная, которая отмечается I’- I’ (или II’— II’ и III’ — III’). Параллельно линиям I’- I’, I’— II’ и III’ — III’ проводятся линии I—I, II—II и III — III через точку О. Линии I—I, II -II и III — III являются линиями горизонта, проходящего через ось колес для каждого взвешивания. 224 ЗАМЕЧАНИЯ ОБ ОПРЕДЕЛЕНИИ ЦЕНТРА ТЯЖЕСТИ САМОЛЕТА ДЛЯ КАЖДОГО ПОЛЕТА
2241 Положение центра тяжести должно быть известно для каждого полета. Для этого ведущий инженер обязан вести в своем дневнике или особом журнале учет всего оборудования, находящегося на самолете, а борттехник обязан знать точно вес горючего в баках дэ и после каждого полета, для чего лучше всего протарнровать баки и иметь специальные мерные линейки. 2242 Определение центра тяжести для каждого полета производится расчетным путем. Для этого необходимо подсчитывать величины статических моментов от веса пустого самолета и всех грузов относительно осей координат с началом в какой-либо жестко фиксированной точке на самолете.
По балансировочному чертежу самолета и таблицам весов и размещений грузов, полученных летной станцией от копструкторского бюро, можно составить заранее таблицу статических моментов съемных грузов относительно указанной точки. Алгебраическая сумма всех моментов относительно этой точки, включая момент от веса пустого самолета, будет равна моменту относительно той же точки для нагруженного самолета. Отсюда легко найти координаты центра тяжести самолета относительно осей, имеющих начало координат в выбранной точке. Они определяются по формулам (фиг. 2242):
Взвешивание самолета производится обычно на колесах, поэтому при убирании шасси или при замене колес на лыжи центр тяжести самолета изменяется, что необходимо учитывать при определении центра тяжести в таких случаях. Для этого из чертежей самолета берутся соответствующие изменения весов и центров тяжести шасси и лыж, подечнтываются статические моменты и определяются положения центра тяжести по вышеуказанным формулам.
Дата публикации на сайте: 08.09.2012
|
Методы нахождения центров тяжести тел — КиберПедия
Из соображений симметрии.
Если тело имеет центр материальной симметрии, то его центр тяжести совпадает с этим центром симметрии. Отсюда, например, следует, что центр тяжести однородного шара совпадает с центром шара (см. рис. 116).
Рис. 116
Если тело имеет ось материальной симметрии, то его центр тяжести лежит на оси симметрии. Исходя из этого, легко найти центр тяжести однородной прямоугольной пластинки (см. рис. 117).
Рис. 117
Если тело имеет плоскость материальной симметрии, то его центр тяжести лежит в плоскости симметрии. Пользуясь этим, легко найти центр тяжести однородного кругового цилиндра (см. рис. 118).
рис. 118).
Рис. 118
Метод разбиения тела на части.
Пусть тело можно разбить на несколько частей, для каждой из которых положение центра тяжести известно (см. рис. 119). Тогда общий центр тяжести тела может быть найден по формуле
(86)
Рис. 119
Метод отрицательных масс.
Этот метод является обобщением метода разбиения тела на части на случай, когда тело имеет пустые полости с известным положением их центров тяжести, если эти полости заполнить веществом. В этом случае можно считать тело с пустыми полостями состоящим из воображаемого тела с заполненными полостями и телами в виде полостей, которым следует приписать отрицательную массу. После этого центр тяжести исходного тела можно найти по формуле (86). Поясним этот метод на примере.
Пример 10
Определим положение центра тяжести однородной прямоугольной пластинки с вырезанным полукругом ( см. рис. 120 ). Пусть задан радиус
120 ). Пусть задан радиус
Рис. 120
вырезанного полукруга R=1 м. Выберем оси координат, как показано на рисунке. Эту пластинку можно рассматривать как фигуру, составленную из прямоугольной пластинки и полукруга с отрицательной массой. Площади таких фигур и координаты их центров тяжести равны:
Далее в соответствии с формулой (86) найдем координаты центра тяжести пластинки:
Метод подвешивания.
Это экспериментальный метод, с помощью которого удобно находить положение центров тяжести плоских, в том числе и неоднородных, тел. Тело, подвешенное на нити, находится в равновесии под действием двух сил: силы тяжести, приложенной в центре тяжести, и силы натяжения, направленной вдоль нити. Эти две силы равны по величине и направлены вдоль одной прямой, являющейся продолжением нити. Поэтому для нахождения центра тяжести достаточно два раза подвесить тело за две различные точки и в условиях равновесия отметить на теле продолжение нити (см. рис. 121).
рис. 121).
Рис. 121
В результате центр тяжести найдем как точку пересечения двух полученных прямых.
Метод взвешивания.
Этот экспериментальный метод используют для нахождения центров тяжести транспортных средств. Для его реализации используются весы, приспособленные для взвешивания транспортных средств. Для нахождения центра тяжести снимают два показания весов: Р – для случая, когда транспортное средство опирается на платформу весов четырьмя колесами, и — для случая, когда транспортное средство опирается на платформу весов двумя колесами (см. рис. 122).
Рис. 122
В результате первого взвешивания определяется вес транспортного средства Р. Результат второго взвешивания дает силу давления передних колес на платформу весов при втором взвешивании.
Рассмотрим теперь в качестве объекта равновесия транспортное средство при втором взвешивании. Оно находится в равновесии под действием трех сил Обозначим — колесную базу транспортного средства и — расстояние по горизонтали от центра тяжести до оси задних колес (см. рис. 122). Для такой системы сил сумма алгебраических моментов относительно точки касания задними колесами опорной поверхности равна нулю:
рис. 122). Для такой системы сил сумма алгебраических моментов относительно точки касания задними колесами опорной поверхности равна нулю:
Отсюда, учитывая, что , найдем
Библиографический список
1. Тарг, С.М. Краткий курс теоретической механики/ С.М. Тарг. М.: Высшая школа, 2007. 416с.
2. Яблонский, А.А. Курс теоретической механики/ Яблонский, А.А., Никифорова, В.М. СПб.: Лань, 2001. 764 с.
3. Мещерский, И.В. Сборник задач по теоретической механике/ И.В. Мещерский.: Лань, 2001. 448с.
4. Сборник заданий для курсовых работ по теоретической механике/ Под ред. А.А. Яблонского. М.: Интеграл-Пресс, 2001. 382с.
5. Сборник коротких задач по теоретической механике/ Под ред. О.Э. Кепе. СПб.: Лань, 2008. 368с.
О Г Л А В Л Е Н И Е
Введение 3
Раздел 1. КИНЕМАТИКА 4
Глава 1. КИНЕМАТИКА ТОЧКИ 4
1.1. Векторный способ задания движения точки 4
Векторный способ задания движения точки 4
1.2. Задание движения точки в декартовых координатах 6
1.3.Задание движения точки естественным способом 8
Глава 2. ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА 14
2.1. Поступательное движение твердого тела 14
2.2. Вращательное движение твердого тела 16
2.2.1. Основные понятия 16
2.2.2. Угловая скорость и угловое ускорение тела 17
2.2.3. Простейшие случаи вращательного движения твердого тела 18
2.2.4. Определение скоростей и ускорений точек тела 19
2.2.5. Векторные формулы для скоростей и ускорений точек тела 20
Глава 3. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ 23
3.1. Основные понятия 23
3.2. Связь между полной и локальной производными от вектора 25
3.3. Теорема сложения скоростей при сложном движении точки 27
3.4. Теорема сложения ускорений при сложном движении точки 30
Глава 4. ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА 37 4.1. Основные понятия 37
4. 2. Скорости точек тела при плоском движении 40
2. Скорости точек тела при плоском движении 40
4.3. Мгновенный центр скоростей 42
4.4. Ускорения точек тела при плоском движении 47
4.5. Мгновенный центр ускорений 48
4.6. Вычисление угловой скорости и углового ускорения тела при
плоском движении 52
Раздел 2. СТАТИКА 54
Глава 1. ВВЕДЕНИЕ В СТАТИКУ 54
1.1.Основные понятия 54
1.2. Аксиомы статики 56
1.3. Основные виды связей и их реакции 58
Глава 2. СИСТЕМА СХОДЯЩИХСЯ СИЛ 62
2.1. Классификация систем сил 62
2.2. Приведение сходящейся системы сил к равнодействующей 62
2.3. Уравнения равновесия 63
Глава 3. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ И ОСИ 66
3.1. Векторный момент силы относительно точки 66
3.2. Момент силы относительно оси 67
3.3. Алгебраический момент силы относительно точки 70
Глава 4. ПАРА СИЛ И ЕЕ СВОЙСТВА 71
4.1. Понятие о паре сил 71
4. 2. Основные свойства пар сил 72
2. Основные свойства пар сил 72
Глава 5. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ЦЕНТРУ 74
5.1. Приведение произвольной пространственной системы сил к центру 74
5.2. Частные случаи приведения системы сил к центру 76
Глава 6. УРАВНЕНИЯ РАВНОВЕСИЯ 79
6.1. Независимые уравнения равновесия для различных систем сил 79
6.2. Различные формы независимых уравнений равновесия для плоской произвольной системы сил 81
6.3. Непрерывно распределенная нагрузка 85
6.4. Равновесие системы тел 88
Глава 7. ТРЕНИЕ И ФЕРМЫ 93
7.1. Трение скольжения 93 7.2. Трение качения 95 7.3. Расчет ферм 97
Глава 8. ЦЕНТР ТЯЖЕСТИ 103
8.1. Основные понятия 103 8.2. Центры тяжести простейших однородных тел 106 8.3. Методы нахождения центров тяжести тел 108
Библиографический список 112
Центр тяжести твердого тела и способы нахождения его положения. Центр тяжести твердого тела
Если твердое тело находится вблизи поверхности Земли, то к каждой материальной точке этого тела приложена сила тяжести. При этом размеры тела по сравнению с размером Земли настолько малы, что силы земного притяжения, действующие на все частицы тела, можно считать параллельными между собой
При этом размеры тела по сравнению с размером Земли настолько малы, что силы земного притяжения, действующие на все частицы тела, можно считать параллельными между собой
Центр (точка С
) системы параллельных сил тяжести всех точек тела называется центром тяжести твердого тела
, а сумма сил тяжести всех его материальных точек называется силой тяжести
, действующей на него
Координаты центра тяжести твердого тела определяются по формулам:
где — координаты точек приложения сил тяжести , действующих на k
-ю материальную точку.
Для однородного тела:
где V — объем всего тела;
V k
— объем k
-й частицы.
Для однородной тонкой пластины:
где S – площадь пластины;
S k –
площадь k-
ой части пластины.
Для линии:
где L
— длина всей линии;
L k
— длина k
-ой части линии.
Способы определения координат центров тяжести тел:
Теоретические
Симметрия.
Если однородное тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно или в плоскости симметрии, или на оси, или в центре симметрии.
Разбиение.
Если тело можно разбить на конечное число таких частей, для каждой из которых положение центра тяжести известно, то координаты центра тяжести всего тела можно непосредственно вычислить по выше приведенным формулам.
Дополнение.
Этот способ является частным случаем способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. В расчеты их включают со знаком «-».
Интегрирование
.
Когда тело нельзя разбить на составные части, центры тяжести которых известны, используют метод интегрирования, являющийся универсальным.
Экспериментальные
Метод подвешивания.
Тело подвешивают за две-три точки, проводя из них вертикали. Точка их пересечении – центр масс.
Метод взвешивания
. Тело разными частями помещают на весы, определяя тем самым опорные реакции. Составляют уравнения равновесия, из которых определяют координаты центра тяжести.
С помощью теоретических методов выведены формулы для определения координат центра тяжести
наиболее распространенных однородных тел:
Дуга окружности
Просмотр:
эта статья прочитана 11269 раз
Pdf
Выберите язык…
Русский
Украинский
Английский
Краткий обзор
Полностью материал скачивается выше, предварительно выбрав язык
Обзор
Рычаг
— это твердое тело, имеющее недвижимую ось вращения и находящееся под действием сил, лежащих в плоскости, перпендикулярной этой оси.
Если рычаг находится в состоянии покоя, то алгебраическая сумма моментов всех сил, приложенных к рычагу относительно опорной точки, равняется нулю
Произвольная плоская система сил
— это система сил, линии действия которых расположены в плоскости независимо.
Методом Пуансо в центре приведения О будет получена система сил и система пар, моменты каждой из которых равняют моментам соответствующей силы относительно центра приведения.
Главным вектором системы
называется вектор, который равняется геометрической сумме всех сил системы.
Главным моментом системы
относительно центра О в плоскости называется алгебраическая сумма моментов сил системы относительно центра приведения О.
Главный вектор не зависит от выбора центра приведения О. Главный момент сил зависит от центра приведения.
Основная теорема статики о приведении системы сил к данному центру
: Какая-либо плоская произвольная система сил, действующих на абсолютно твердое тело, при приведении к произвольно избранному центру О, может быть заменена одной силой, равняющейся главному вектору системы и приложенной в центре приведения О, и одной парой с моментом, равняющемуся главному моменту системы относительно центра О.
Рассмотрены случаи приведения плоской системы сил к более простому виду
Условия равновесия произвольной плоской системы сил.
1. Геометрические условия равновесия
: для равновесия плоской произвольной системы сил необходимо и достаточно, чтобы главный вектор и главный момент системы равнялись нулю
2. Аналитические условия равновесия
.
Основная форма условий равновесия
: Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на координатные оси и сумма их моментов относительно любого центра, который лежит в плоскости действия сил, равнялись нулю.
Вторая форма условий равновесия
: Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех сил относительно любых двух центров А и В и сумма их проекций на ось, не перпендикулярную прямой АВ, равнялись нулю.
Третья форма условий равновесия (уравнение трех моментов)
: Для равновесия плоской произвольной системы сил необходимо и достаточно, чтобы суммы моментов всех сил относительно любых трех центров А, В и С, не лежащих на одной прямой, равнялись нулю.
Центр параллельных сил
Система параллельных сил, направленных в одну сторону, не может быть уравновешена или приводиться к паре сил, она всегда имеет равнодействующую.
Линия действия равнодействующей параллельна силам. Положение точки ее приложение зависит от величин и положения точек приложения сил системы.
Центр параллельных сил
— точка С точка приложения равнодействующей системы параллельных сил.
Положение центра параллельных сил — точки С, определяется координатами этой точки
Центр тяжести твердого тела и его координаты
Центр тяжести тела
— неизменно связанная с этим телом геометрическая точка, в которой приложена равнодействующая сил тяжести отдельных частиц тела, т.е. вес тела в пространстве.
Координаты центра тяжести определяются аналогично координатам центра параллельных сил С (), составленных силами тяжести частиц тела.
Положение центра тяжести однородного тела зависит только от его геометрической формы и размеров, и не зависит от свойств материала, из которого тело выполнено.
Сумма произведений элементарных площадей, входящих в состав плоской фигуры, на алгебраические значения их расстояний до некоторой оси, называется статическим моментом площади плоской фигуры.
Статический момент
площади плоской фигуры равняется произведению площади фигуры на алгебраическое расстояние от центра тяжести до этой оси. Единица измерения статического момента [см3].
статический момент площади плоской фигуры относительно оси, которая проходит через центр тяжести фигуры, равняется нулю.
Вес тела это равнодействующая сил тяжести отдельных частиц тела.
Способы определения положения центра тяжести
.
- Метод симметрии
: Если однородное тело имеет плоскость, ось или центр симметрии, то центр тяжести лежит соответственно или в плоскости симметрии, или на оси симметрии, или в центре симметрии.Центр тяжести линии длиной — по середине. Центр тяжести окружности (или круга) радиуса — в его центре, т.е. в точке пересечения диаметров. Центр тяжести параллелограмма, ромба или параллелепипеда — в точке пересечения диагоналей. Центр тяжести правильного многоугольника — в центре вписанного или описанный круга.
Центр тяжести параллелограмма, ромба или параллелепипеда — в точке пересечения диагоналей. Центр тяжести правильного многоугольника — в центре вписанного или описанный круга. - Метод разбивки
:
Если тело можно разбить на конечное количество элементов (объемов, плоскостей, линий), для каждой из которых положение центра тяжести известно, то координаты центра тяжести всего тела можно определить зная значения для элементов непосредственно по формулам - Метод дополнения
(отрицательных плоскостей): Если тело имеет вырезанные элементы, то при разбивке на элементы, вырезанная часть (площадь, объем) отнимаются из общей, т.е. вырезанным элементам даются отрицательные значения площади или объема
Формат: pdf
Размер: 700 КВ
Язык: русский, украинский
Пример расчета прямозубой цилиндрической передачи
Пример расчета прямозубой цилиндрической передачи. Выполнен выбор материала, расчет допускаемых напряжений, расчет на контактную и изгибную прочность.
Пример решения задачи на изгиб балки
В примере построены эпюры поперечных сил и изгибающих моментов, найдено опасное сечение и подобран двутавр. В задаче проанализировано построение эпюр с помощью дифференциальных зависимостей, провелен сравнительный анализ различных поперечных сечений балки.
Пример решения задачи на кручение вала
Задача состоит в проверке прочности стального вала при заданном диаметре, материале и допускаемых напряжениях. В ходе решения строятся эпюры крутящих моментов, касательных напряжений и углов закручивания. Собственный вес вала не учитывается
Пример решения задачи на растяжение-сжатие стержня
Задача состоит в проверке прочности стального стержня при заданных допускаемых напряжениях. В ходе решения строятся эпюры продольных сил, нормальных напряжений и перемещений. Собственный вес стержня не учитывается
Применение теоремы о сохранении кинетической энергии
Пример решения задачи на применение теоремы о сохранение кинетической энергии механической системы
Определение скорости и ускорения точки по заданным уравнениям движения
Пример решение задачи на определение скорости и ускорения точки по заданным уравнениям движения
Определение скоростей и ускорений точек твердого тела при плоскопараллельном движении
Пример решения задачи на определение скоростей и ускорений точек твердого тела при плоскопараллельном движении
Тема относительно проста для усвоения, однако крайне важна при изучении курса сопротивления материалов. Главное внимание здесь необходимо обратить на решение задач как с плоскими и геометрическими фигурами, так и со стандартными прокатными профилями.
Главное внимание здесь необходимо обратить на решение задач как с плоскими и геометрическими фигурами, так и со стандартными прокатными профилями.
Вопросы для самоконтроля
1. Что такое центр параллельных сил?
Центр параллельных сил есть точка, через которую проходит линия равнодействующей системы параллельных сил, приложенных в заданных точках, при любом изменении направления этих сил в пространстве.
2. Как найти координаты центра параллельных сил?
Для определения координат центра параллельных сил воспользуемся теоремой Вариньона.
Относительно оси x
M x (R) = ΣM x (F k)
, — y C R = Σy kFk
и y C = Σy kFk /Σ Fk
.
Относительно оси y
M y (R) = ΣM y (F k)
, — x C R = Σx kFk
и x C = Σx kFk /Σ Fk
.
Чтобы определить координату z C
, повернем все силы на 90° так, чтобы они стали параллельны оси y
(рисунок 1. 5, б). Тогда
5, б). Тогда
M z (R) = ΣM z (F k)
, — z C R = Σz kFk
и z C = Σz kFk /Σ Fk
.
Следовательно, формула для определения радиус-вектора центра параллельных сил принимает вид
r C = Σr kFk /Σ Fk
.
3. Что такое центр тяжести тела?
Центр Тяжести—
неизменно связанная с твердым телом точка, через которую проходит равнодействующая сил тяжести, действующих на частицы этого тела при любом положении тела в пространстве. У однородного тела, имеющего центр симметрии (круг, шар, куб и т. д.), центр тяжести находится в центре симметрии тела. Положение центра тяжести твердого тела совпадает с положением его центра масс.
4. Как найти центр тяжести прямоугольника, треугольника, круга?
Для нахождения центра тяжести треугольника, необходимо нарисовать треугольник – фигуру, состоящую из трех отрезков, соединенных между собой в трех точках. Перед тем, как найти центр тяжести фигуры, необходимо, используя линейку, измерить длину одной стороны треугольника. В середине стороны поставьте отметку, после чего противоположную вершину и середину отрезка соедините линией, которая называется медианой. Тот же самый алгоритм повторите со второй стороной треугольника, а затем и с третьей. Результатом вашей работы станут три медианы, которые пересекаются в одной точке, которая будет являться центром тяжести треугольника. Если необходимо определить центр тяжести круглого диска однородной структуры, то для начала найдите точку пересечения диаметров круга. Она и будет центром тяжести данного тела. Рассматривая такие фигуры, как шар, обруч и однородный прямоугольный параллелепипед, можно с уверенностью сказать, что центр тяжести обруча будет находиться в центре фигуры, но вне ее точек, центр тяжести шара — геометрический центр сферы, и в последнем случае, центром тяжестью считается пересечение диагоналей прямоугольногопараллелепипеда.
В середине стороны поставьте отметку, после чего противоположную вершину и середину отрезка соедините линией, которая называется медианой. Тот же самый алгоритм повторите со второй стороной треугольника, а затем и с третьей. Результатом вашей работы станут три медианы, которые пересекаются в одной точке, которая будет являться центром тяжести треугольника. Если необходимо определить центр тяжести круглого диска однородной структуры, то для начала найдите точку пересечения диаметров круга. Она и будет центром тяжести данного тела. Рассматривая такие фигуры, как шар, обруч и однородный прямоугольный параллелепипед, можно с уверенностью сказать, что центр тяжести обруча будет находиться в центре фигуры, но вне ее точек, центр тяжести шара — геометрический центр сферы, и в последнем случае, центром тяжестью считается пересечение диагоналей прямоугольногопараллелепипеда.
5. Как найти координаты центра тяжести плоского составного сечения?
Метод разбиения:
если плоскую фигуру можно разбить на конечное число таких частей, для каждой из которых положение центра тяжести известно, то координаты центра тяжести всей фигуры опредляются по формулам:
Х C = ( s k x k) / S; Y C = ( s k y k) / S,
где x k , y k — координаты центров тяжести частей фигуры;
s k — их площади;
S = s k — площадь всей фигуры.
6. Центр тяжести
1. В каком случае для определения центра тяжести достаточно определить одну координату расчетным путем?
В первом случае для определения центра тяжести достаточно определить одну координату Тело разбивается на конечное число частей, для каждой из которых положение центра тяжести C
и площадь S
известны. Например, проекцию тела на плоскость xOy
(рисунок 1.) можно представить в виде двух плоских фигур с площадями S 1
и S 2
(S = S 1 + S 2
). Центры тяжести этих фигур находятся в точках C 1 (x 1 , y 1)
и C 2 (x 2 , y 2)
. Тогда координаты центра тяжести тела равны
Так как центры фигур лежат на оси ординат (х = 0), то находим только координату Ус
.
2 Как учитывается площадь отверстия в фигуре 4 в формуле для определения центра тяжести фигуры?
Метод отрицательных масс
Этот метод заключается в том, что тело, имеющее свободные полости, считают сплошным, а массу свободных полостей – отрицательной. Вид формул для определения координат центра тяжести тела при этом не меняется.
Вид формул для определения координат центра тяжести тела при этом не меняется.
Таким образом, при определении центра тяжести тела, имеющего свободные полости, следует применять метод разбиения, но считать массу полостей отрицательной.
иметь представление
о центре параллельных сил и его свойствах;
знать
формулы для определения координат центра тяжести плоских фигур;
уметь
определять координаты центра тяжести плоских фигур простых геометрических фигур и стандартных прокатных профилей.
ЭЛЕМЕНТЫ КИНЕМАТИКИ И ДИНАМИКИ
Изучив кинематику точки, обратите внимание на то, что прямолинейное движение точки как неравномерное, так и равномерное всегда характеризуется наличием нормального (центростремительного) ускорения. При поступательном движении тела (характеризуемом движением любой его точки) применимы все формулы кинематики точки. Формулы для определения угловых величин тела, вращающегося вокруг неподвижной оси, имеют полную смысловую аналогию с формулами для определения соответствующих линейных величин поступательно движущегося тела.
Тема 1.7. Кинематика точки
При изучении темы обратите внимание на основные понятия кинематики: ускорение, скорость, путь, расстояние.
Вопросы для самоконтроля
1. В чем заключается относительность понятий покоя и движения?
Механическое движение -это изменение движения тела, или (его частей) в пространстве относительно др. тел с течением времени. Полет брошенного камня, вращение колеса- примеры механического движения.
2. Дайте определение основных понятий кинематики: траектории, расстоянию, пути, скорости, ускорению, времени.
Скорость – это кинематическая мера движения точки, характеризующая быстроту изменения ее положения в пространстве. Скорость является векторной величиной, т. е. она характеризуется не только модулем (скалярной составляющей), но и направлением в пространстве.
Как известно из физики, при равномерном движении скорость может быть определена длиной пути, пройденного за единицу времени: v = s/t = const (предполагается, что начало отсчета пути и времени совпадают).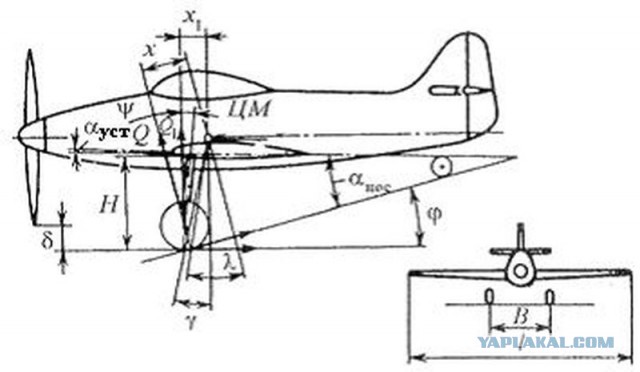 При прямолинейном движении скорость постоянна и по модулю, и по направлению, а ее вектор совпадает с траекторией.
При прямолинейном движении скорость постоянна и по модулю, и по направлению, а ее вектор совпадает с траекторией.
Единица скорости в системе СИ
определяется соотношением длина/время, т. е. м/с.
Ускорение есть кинематическая мера изменения скорости точки во времени. Другими словами — ускорение — это скорость изменения скорости.
Как и скорость, ускорение является величиной векторной, т. е. характеризуется не только модулем, но и направлением в пространстве.
При прямолинейном движении вектор скорости всегда совпадает с траекторией и поэтому вектор изменения скорости тоже совпадает с траекторией.
Из курса физики известно, что ускорение представляет собой изменение скорости в единицу времени. Если за небольшой промежуток времени Δt скорость точки изменилась на Δv, то среднее ускорение за данный промежуток времени составило: а ср = Δv/Δt.
Среднее ускорение не дает представление об истинной величине изменения скорости в каждый момент времени. При этом очевидно, что чем меньше рассматриваемый промежуток времени, во время которого произошло изменение скорости, тем ближе значение ускорения будет к истинному (мгновенному).
Отсюда определение: истинное (мгновенное) ускорение есть предел, к которому стремится среднее ускорение при Δt, стремящемся к нулю:
а = lim а ср при t→0 или lim Δv/Δt = dv/dt.
Учитывая, что v = ds/dt, получим: а = dv/dt = d 2 s/dt 2 .
Истинное ускорение в прямолинейном движении равно первой производной скорости или второй производной координаты (расстояния от начала отсчета перемещения) по времени. Единица ускорения — метр, деленный на секунду в квадрате (м/с 2).
Траектория
— линия в пространстве, вдоль которой движется материальная точка.
Путь
— это длина траектории. Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t. Путь – скалярная величина.
Расстояние
определяет положение точки на ее траектории и отсчитывается от некоторого начала отсчета. Расстояние является алгебраической величиной, так как в зависимости от положения точки относительно начала отсчета и от принятого направления оси расстояний оно может быть и положительным, и отрицательным. В отличие от расстояния путь, пройденный точкой, всегда определяется положительным числом. Путь совпадает с абсолютным значением расстояния только в том случае, когда движение точки начинается от начала отсчета и совершается по траектории в одном направлении.
В отличие от расстояния путь, пройденный точкой, всегда определяется положительным числом. Путь совпадает с абсолютным значением расстояния только в том случае, когда движение точки начинается от начала отсчета и совершается по траектории в одном направлении.
В общем случае движения точки путь равен сумме абсолютных значений пройденных точкой расстояний за данный промежуток времени:
3. Какими способами может быть задан закон движения точки?
1.Естественный способ задания движения точки.
При естественном способе задания движения предполагается определение параметров движения точки в подвижной системе отсчета, начало которой совпадает с движущейся точкой, а осями служат касательная, нормаль и бинормаль к траектории движения точки в каждом ее положении. Чтобы задать закон движения точки естественным способом необходимо:
1) знать траекторию движения;
2) установить начало отсчета на этой кривой;
3) установить положительное направление движения;
4) дать закон движения точки по этой кривой, т. е. выразить расстояние от начала отсчета до положения точки на кривой в данный момент времени ∪OM=S(t)
е. выразить расстояние от начала отсчета до положения точки на кривой в данный момент времени ∪OM=S(t)
.
2.Векторный способ задания движения точки
В этом случае положение точки на плоскости или в пространстве определяется вектором-функцией. Этот вектор откладывается от неподвижной точки, выбранной за начало отсчета, его конец определяет положение движущейся точки.
3.Координатный способ задания движения точки
В выбранной системе координат задаются координаты движущейся точки как функции от времени. В прямоугольной декартовой системе координат это будут уравнения:
4. Как направлен вектор истинной скорости точки при криволинейном движении?
При неравномерном движении точки модуль ее скорости с течением времени меняется.
Представим себе точку, движение которой задано естественным способом уравнением s = f(t).
Если за небольшой промежуток времени Δt точка прошла путь Δs, то ее средняя скорость равна:
vср = Δs/Δt.
Средняя скорость не дает представления об истинной скорости в каждый данный момент времени (истинную скорость иначе называют мгновенной). Очевидно, что чем меньше промежуток времени, за который определяется средняя скорость, тем ближе ее значение будет к мгновенной скорости.
Очевидно, что чем меньше промежуток времени, за который определяется средняя скорость, тем ближе ее значение будет к мгновенной скорости.
Истинная (мгновенная) скорость есть предел, к которому стремится средняя скорость при Δt, стремящемся к нулю:
v = lim v ср при t→0 или v = lim (Δs/Δt) = ds/dt.
Таким образом, числовое значение истинной скорости равно v = ds/dt.
Истинная (мгновенная) скорость при любом движении точки равна первой производной координаты (т. е. расстояния от начала отсчета перемещения) по времени.
При Δt стремящемся к нулю, Δs тоже стремится к нулю, и, как мы уже выяснили, вектор скорости будет направлен по касательной (т. е. совпадает с вектором истинной скорости v). Из этого следует, что предел вектора условной скорости v п, равный пределу отношения вектора перемещения точки к бесконечно малому промежутку времени, равен вектору истинной скорости точки.
5. Как направлены касательное и нормальное ускорения точки?
Направление вектора ускорения совпадает с направлением изменения скорости Δ = — 0
Касательное ускорение в данной точке направлено по касательной к траектории движения точки; если движение ускоренное, то направление вектора касательного ускорения совпадает с направлением вектора скорости; если движение замедленное – то направление вектора касательного ускорения противоположно направлению вектора скорости.
6. Какое движение совершает точка, если касательное ускорение равно нулю, а нормальное не изменяется с течением времени?
Равномерное криволинейное движение
характеризуется тем, что численное значение скорости постоянно (v
= const
), скорость меняется лишь по направлению. В этом случае касательное ускорение равно нулю, так как v
= const
(рис.б),
а нормальное ускорение не равно нулю, так как r
— конечная величина.
7. Как выглядят кинематические графики при равномерном и равнопеременном движении?
При равномерном движении тело за любые равные промежутки времени проходит равные пути. Для кинематического описания равномерного прямолинейного движения координатную ось OX
удобно расположить по линии движения. Положение тела при равномерном движении определяется заданием одной координаты x
. Вектор перемещения и вектор скорости всегда направлены параллельно координатной оси OX
. Поэтому перемещение и скорость при прямолинейном движении можно спроецировать на ось OX
и рассматривать их проекции как алгебраические величины.
При равномерном движении путь изменяется, согласно линейной зависимости . В координатах . Графиком является наклонная линия.
В результате изучения темы студент должен:
иметь представление
о пространстве, времени, траектории; средней и истиной скорости;
знать
способы задания движения точки; параметры движения точки по заданной траектории.
Центр тяжести твердого тела
Центром тяжести
твердого тела называется геометрическая точка, жестко связанная с этим телом, и являющаяся центром параллельных сил тяжести, приложенных к отдельным элементарным частицам тела (рисунок 1.6).
Радиус-вектор этой точки
Рисунок 1.6
Для однородного тела положение центра тяжести тела не зависит от материала, а определяется геометрической формой тела.
Если удельный вес однородного тела γ
, вес элементарной частицы тела
P k = γΔV k (P = γV)
подставить в формулу для определения r C
, имеем
Откуда, проецируя на оси и переходя к пределу, получаем координаты центра тяжести однородного объема
Аналогично для координат центра тяжести однородной поверхности площадью S
(рисунок 1. 7, а)
7, а)
Рисунок 1.7
Для координат центра тяжести однородной линии длиной L
(рисунок 1.7, б)
Способы определения координат центра тяжести
Исходя из полученных ранее общих формул, можно указать способы определения координат центров тяжести твердых тел:
Рисунок 1.8
Рисунок 1.9
11. Основные понятия кинематики. Кинематика точки. Способы задания движения точки. Скорость и ускорение точки.
Основные понятия кинематики
Кинематика
— раздел механики, изучающий движение тел без учета причин, вызвавших это движение.
Основной задачей кинематики является нахождение положения тела в любой момент времени, если известны его положение, скорость и ускорение в начальный момент времени.
Механическое движение
— это изменение положения тел (или частей тела) относительно друг друга в пространстве с течением времени.
Для описания механического движения надо выбрать систему отсчета.
Тело отсчета
— тело (или группа тел), принимаемое в данном случае за неподвижное, относительно которого рассматривается движение других тел.
Система отсчета
— это система координат, связанная с телом отсчета, и выбранный способ измерения времени (рис. 1).
Положение тела можно определить с помощью радиуса-вектора r⃗ r→ или с помощью координат.
Радиус-вектор
r⃗ r→ точки Μ
— направленный отрезок прямой, соединяющий начало отсчета О
с точкой Μ
(рис. 2).
Координата
x точки Μ
— это проекция конца радиуса-вектора точки Μ
на ось Ох
. Обычно пользуются прямоугольной системой ко ординат. В этом случае положение точки Μ
на линии, плоскости и в пространстве определяют соответственно одним (x
), двумя (х
, у
) и тремя (х
, у
, z
) числами — координатами (рис. 3).
В элементарном курсе физики изучают кинематику движения материальной точки.
Материальная точка
— тело, размерами которого в данных условиях можно пренебречь.
Этой моделью пользуются в тех случаях, когда линейные размеры рассматриваемых тел много меньше всех прочих расстояний в данной задаче или когда тело движется поступательно.
Поступательным
называется движение тела, при котором прямая, проходящая через любые две точки тела, перемещается, оставаясь параллельной самой себе. При поступательном движении все точки тела описывают одинаковые траектории и в любой момент времени имеют одинаковые скорости и ускорения. Поэтому для описания такого движения тела достаточно описать движение его одной произвольной точки.
В дальнейшем под словом «тело» будем понимать «материальная точка».
Линия, которую описывает движущееся тело в определенной системе отсчета, называется траекторией
. На практике форму траектории задают с помощью математических формул (y
= f
(x
) — уравнение траектории) или изображают на рисунке. Вид траектории зависит от выбора системы отсчета. Например, траекторией тела, свободно падающего в вагоне, который движется равномерно и прямолинейно, является прямая вертикальная линия в системе отсчета, связанной с вагоном, и парабола в системе отсчета, связанной с Землей.
Вид траектории зависит от выбора системы отсчета. Например, траекторией тела, свободно падающего в вагоне, который движется равномерно и прямолинейно, является прямая вертикальная линия в системе отсчета, связанной с вагоном, и парабола в системе отсчета, связанной с Землей.
В зависимости от вида траектории различают прямолинейное и криволинейное движение.
Путь
s
— скалярная физическая величина, определяемая длиной траектории, описанной телом за некоторый промежуток времени. Путь всегда положителен: s
> 0.
Перемещение
Δr⃗ Δr→ тела за определенный промежуток времени — направленный отрезок прямой, соединяющий начальное (точка M
0) и конечное (точка М
) положение тела (см. рис. 2):
Δr⃗ =r⃗ −r⃗ 0, Δr→=r→−r→0,
где r⃗ r→ и r⃗ 0 r→0 — радиусы-векторы тела в эти моменты времени.
Проекция перемещения на ось Ox
Δrx=Δx=x−x0 Δrx=Δx=x−x0
Где x
0 и x
— координаты тела в начальный и конечный моменты времени.
Модуль перемещения не может быть больше пути
|Δr⃗ |≤s |Δr→|≤s
Знак равенства относится к случаю прямолинейного движения, если направление движения не изменяется.
Зная перемещение и начальное положение тела, можно найти его положение в момент времени t:
r⃗ =r⃗ 0+Δr⃗ ; r→=r→0+Δr→;
{x=x0+Δrx;y=y0+Δry. {x=x0+Δrx;y=y0+Δry.
Скорость
Средняя скорость hυ⃗ i hυ→i — векторная физическая величина, численно равная отношению перемещения к промежутку времени, за который оно произошло, и направленная вдоль перемещения (рис. 4):
hυ⃗ i=Δr⃗ Δt;hυ⃗ i⇈Δr⃗ . hυ→i=Δr→Δt;hυ→i⇈Δr→.
В СИ единицей скорости является метр в секунду (м/с).
Средняя скорость, найденная по этой формуле, характеризует движение только на том участке траектории, для которого она определена. На другом участке траектории она может быть другой.
Иногда пользуются средней скоростью пути
hυi=sΔt hυi=sΔt
Где s — путь, пройденный за промежуток времени Δt
. Средняя скорость пути — это скалярная величина.
Средняя скорость пути — это скалярная величина.
Мгновенная скорость
υ⃗ υ→ тела — скорость тела в данный момент времени (или в данной точке траектории). Она равна пределу, к которому стремится средняя скорость за бесконечно малый промежуток времени υ⃗ =limΔt→0Δr⃗ Δt=r⃗ ′ υ→=limΔt→0Δr→Δt=r→ ′. Здесь r⃗ ′ r→ ′ — производная от радиуса-вектора по времени.
В проекции на ось Ох
:
υx=limΔt→0ΔxΔt=x′. υx=limΔt→0ΔxΔt=x′.
Мгновенная скорость тела направлена по касательной к траектории в каждой ее точке в сторону движения (см. рис. 4).
Ускорение
Среднее ускорение
— физическая величина, численно равная отношению изменения скорости ко времени, за которое оно произошло:
ha⃗ i=Δυ⃗ Δt=υ⃗ −υ⃗ 0Δt. ha→i=Δυ→Δt=υ→−υ→0Δt.
Вектор ha⃗ i ha→i направлен параллельно вектору изменения скорости Δυ⃗ Δυ→ (ha⃗ i⇈Δυ⃗ ha→i⇈Δυ→) в сторону вогнутости траектории (рис. 5).
Мгновенное ускорение
:
a⃗ =limΔt→0Δυ⃗ Δt=υ⃗ ′. a→=limΔt→0Δυ→Δt=υ→ ′.
a→=limΔt→0Δυ→Δt=υ→ ′.
В СИ единицей ускорения является метр на секунду в квадрате (м/с 2).
В общем случае мгновенное ускорение направлено под углом к скорости. Зная траекторию, можно определить направление скорости, но не ускорения. Направление ускорения определяется направлением равнодействующей сил, действующих на тело.
При прямолинейном движении с возрастающей по модулю скоростью (рис. 6, а) векторы a⃗ a→ и υ⃗ 0 υ→0 сонаправлены (a⃗ ⇈υ⃗ 0 a→⇈υ→0) и проекция ускорения на направление движения положительна.
При прямолинейном движении с убывающей по модулю скоростью (рис. 6, б) направления векторов a⃗ a→ и υ⃗ 0 υ→0 противоположны (a⃗ ↓υ⃗ 0 a→↓υ→0) и проекция ускорения на направление движения отрицательна.
Вектор a⃗ a→ при криволинейном движении можно разложить на две составляющие, направленные вдоль скорости a⃗ τ a→τ и перпендикулярно скорости a⃗ n a→n (рис. 1.7), a⃗ τ a→τ — тангенциальное ускорение, характеризующее быстроту изменения модуля скорости при криволинейном движении, a⃗ n a→n — нормальное ускорение, характеризующее быстроту изменения направления вектора скорости при криволинейном движении Модуль ускорения a=a2τ+a2n−−−−−−√ a=aτ2+an2.
Способы задания движения точки
Для задания движения точки можно применять один из следующих трех способов:
1) векторный, 2) координатный, 3) естественный.
1. Векторный способ задания движения точки.
Пусть точка М
движется по отношению к некоторой системе отсчета Oxyz
. Положение этой точки в любой момент времени можно определить, задав ее радиус-вектор , проведенный из начала координат О
в точку М
(рис. 3).
Рис.3
При движении точки М
вектор будет с течением времени изменяться и по модулю, и по направлению. Следовательно, является переменным вектором (вектором-функцией), зависящим от аргумента t:
Равенство определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий вектор и найти положение движущейся точки.
Геометрическое место концов вектора , т.е. годограф
этого вектора, определяет траекторию движущейся точки.
2. Координатный способ задания движения точки.
Положение точки можно непосредственно определять ее декартовыми координатами х, у, z
(рис.3), которые при движении точки будут с течением времени изменяться. Чтобы знать закон движения точки, т.е. ее положение в пространстве в любой момент времени, надо знать значения координат точки для каждого момента времени, т.е. знать зависимости
x=f 1 (t), y=f 2 (t), z=f 3 (t).
Уравнения представляют собой уравнения движения точки в прямоугольных декартовых координатах. Они определяют закон движения точки при координатном способе задания движения.
Чтобы получить уравнение траектории надо из уравнений движения исключить параметр t.
Нетрудно установить зависимость между векторным и координатным способами задания движения.
Разложим вектор на составляющие по осям координат:
где r x , r y , r z — проекции вектора на оси; – единичные векторы направленные по осям, орты осей.
Так как начало вектора находится в начале координат, то проекции вектора будут равны координатам точки M
. Поэтому
Поэтому
Если движение точки задано в полярных координатах
r=r(t), φ = φ(t),
где r — полярный радиус, φ — угол между полярной осью и полярным радиусом, то данные уравнения выражают уравнение траектории точки. Исключив параметр t, получим
r = r(φ).
Пример 1.
Движение точки задано уравнениями
Рис.4
Чтобы исключить время, параметр t
, найдём из первого уравнения sin2t=x/2, из второго cos2t=y/3. Затем возведём в квадрат и сложим. Так как sin 2 2t+cos 2 2t=1, получим . Это уравнение эллипса с полуосями 2 см и 3 см (рис.4).
Начальное положение точки M
0 (при t
=0) определяется координатами x 0 =0, y 0 =3 см.
Через 1 сек. точка будет в положении M
1 с координатами
x 1 =2sin2=2∙0,91=1,82 см, y 1 =2cos2=3∙(-0,42)= -1,25 см.
Примечание.
Движение точки может быть задано с помощью и других координат. Например, цилиндрических или сферических. Среди них будут не только линейные размеры, но и углы. При необходимости, с заданием движения цилиндрическими и сферическими координатами можно познакомиться по учебникам.
Среди них будут не только линейные размеры, но и углы. При необходимости, с заданием движения цилиндрическими и сферическими координатами можно познакомиться по учебникам.
3. Естественный способ задания движения точки.
Рис.5
Естественным способом задания движения удобно пользоваться в тех случаях, когда траектория движущейся точки известна заранее. Пусть кривая АВ
является траекторией точки М
при ее движении относительно системы отсчета Oxyz
(рис.5) Выберем на этой траектории какую-нибудь неподвижную точку О»
, которую примем за начало отсчета, и установим на траектории положительное и отрицательное направления отсчета (как на координатной оси).
Тогда положение точки М
на траектории будет однозначно определяться криволинейной координатой s
, которая равна расстоянию от точки О’
до точки М
, измеренному вдоль дуги траектории и взятому с соответствующим знаком. При движении точка М
перемещается в положения M
1 , М
2 ,.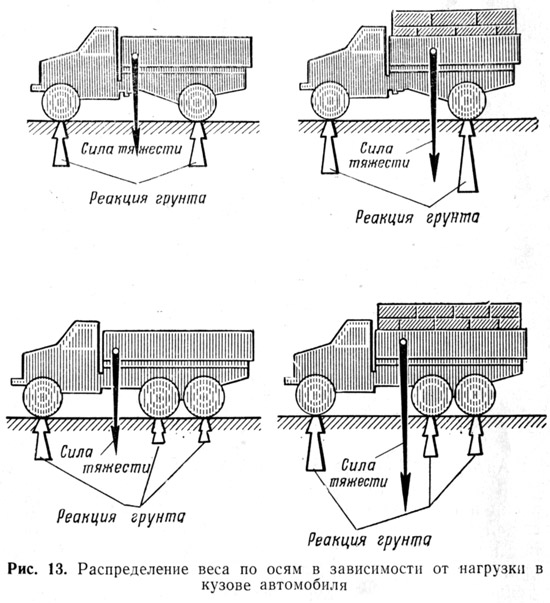 .. . следовательно, расстояние s
.. . следовательно, расстояние s
будет с течением времени изменяться.
Чтобы знать положение точки М
на траектории в любой момент времени, надо знать зависимость
Уравнение выражает закон движения точки М
вдоль траектории. Функция s= f(t) должна быть однозначной, непрерывной и дифференцируемой.
За положительное направление отсчета дуговой координаты s принимают направление движения точки в момент, когда она занимает положение О. Cледует помнить, что уравнение s=f(t) не определяет закон движения точки в пространстве, так как для определения положения точки в пространстве нужно знать еще траекторию точки с начальным положением точки на ней и фиксированное положительное направление. Таким образом, движение точки считается заданным естественным способом, если известна траектория и уравнение (или закон) движения точки по траектории.
Важно заметить, что дуговая координата точки s отлична от пройденного точкой по траектории пути σ. При своем движении точка проходит некоторый путь σ, которой является функцией времени t. Однако пройденный путь σ совпадает с расстоянием s лишь тогда, когда функция s = f(t) монотонно изменяется со временем, т.е. при движении точки в одном направлении. Допустим, что точка М переходит из М 1 в М 2 . Положению точки в М 1 соответствует время t 1 , а положению точки в М 2 — время t 2 . Разложим промежуток времени t 2 — t 1 на весьма малые промежутки времени ∆t 1 (i = 1,2, …n) так, чтобы в каждый из них точка совершала движение в одном направлении. Соответствующее приращение дуговой координаты обозначим ∆s i . Пройденной точкой путь σ будет положительной величиной:
Однако пройденный путь σ совпадает с расстоянием s лишь тогда, когда функция s = f(t) монотонно изменяется со временем, т.е. при движении точки в одном направлении. Допустим, что точка М переходит из М 1 в М 2 . Положению точки в М 1 соответствует время t 1 , а положению точки в М 2 — время t 2 . Разложим промежуток времени t 2 — t 1 на весьма малые промежутки времени ∆t 1 (i = 1,2, …n) так, чтобы в каждый из них точка совершала движение в одном направлении. Соответствующее приращение дуговой координаты обозначим ∆s i . Пройденной точкой путь σ будет положительной величиной:
Если движение точки задано координатным способом, то пройденный путь определяется по формуле
где dx=xdt, dy= ydt, dz=zdt.
Следовательно,
Пример 2.
Точка движется по прямой линии, по закону s=2t+3 (см) (рис. 6).
Рис.6
В начале движения, при t=0 s=OM 0 =s 0 =3 см. Положение точки M
0 называется начальным положением
.
При t=1 с, s=OM 1 =5 см.
Конечно, за 1 сек. точка прошла расстояние M
0 M
1 =
2см.Так что s
– это не путь пройденный точкой, а расстояние от начала отсчёта до точки.
Вектор скорости точки
Одной из основных кинематических характеристик движения точки является векторная величина, называемая скоростью точки. Понятие скорости точки в равномерном прямолинейном движении относится к числу элементарных понятий.
Скорость
— мера механического состояния тела. Она характеризует быстроту изменения положения тела относительно данной системы отсчета и является векторной физической величиной.
Единица измерения скорости – м/с. Часто используют и другие единицы, например, км/ч: 1 км/час=1/3,6 м/с.
Движение точки называется равномерным, если приращения радиуса-вектора точки за одинаковые промежутки времени равны между собой. Если при этом траекторией точки является прямая, то движение точки называется прямолинейным.
Для равномерно-прямолинейного движения
∆r=v
∆t, (1)
где v
– постоянный вектор.
Вектор v
называется скоростью прямолинейного и равномерного движения полностью его определяет.
Из соотношения (1) видно, что скорость прямолинейного и равномерного движения является физической величиной, определяющей перемещение точки за единицу времени. Из (1) имеем
Направление вектора v
указано на рис. 6.1.
Рис.6.1
При неравномерном движении эта формула не годится. Введем сначала понятие о средней скорости точки за какой-нибудь промежуток времени.
Пусть движущаяся точка находится в момент времени t
в положении М
, определяемом радиусом-вектором , а в момент t 1 приходит в положение M
1 определяемое вектором (рис.7). Тогда перемещение точки за промежуток времени ∆t=t 1 -t определяется вектором который будем называть вектором перемещения точки. Из треугольника ОММ
1 видно, что ; следовательно,
Рис. 7
7
Отношение вектора перемещения точки к соответствующему промежутку времени дает векторную величину, называемую средней по модулю и направлению скоростью точки за промежуток времени ∆t:
Скоростью точки в данный момент времени t называется векторная величина v, к которой стремится средняя скорость v ср при стремлении промежутка времени ∆t к нулю:
Итак, вектор скорости точки в данный момент времени равен первой производной от радиуса-вектора точки по времени.
Так как предельным направлением секущей ММ
1 является касательная, то вектор скорости точки в данный момент времени направлен по касательной к траектории точки в сторону движения.
Определение скорости точки при координатном способе задания движения
Вектор скорости точки , учитывая, что r x =x, r y =y, r z =z, найдем:
Таким образом, проекции скорости точки на координатные оси равны первым производным от соответствующих координат точки по времени.
Зная проекции скорости, найдем ее модуль и направление (т. е. углы α, β, γ, которые вектор v образует с координатными осями) по формулам
е. углы α, β, γ, которые вектор v образует с координатными осями) по формулам
Итак, численная величина скорости точки в данный момент времени равна первой производной от расстояния (криволинейной координаты) s
точки по времени.
Направлен вектор скорости по касательной к траектории, которая нам наперед известна.
Определение скорости точки при естественном способе задания движения
Величину скорости можно определить как предел (∆r – длина хорды ММ
1):
где ∆s – длина дуги ММ
1 . Первый предел равен единице, второй предел – производная ds/dt.
Следовательно, скорость точки есть первая производная по времени от закона движения:
Направлен вектор скорости, как было установлено ранее, по касательной к траектории. Если величина скорости в данный момент будет больше нуля, то вектор скорости направляется в положительном направлении
Вектор ускорения точки
Ускорение
— векторная физическая величина, характеризующая быстроту изменения скорости. Оно показывает, на какую величину изменяется скорость тела за единицу времени.
Оно показывает, на какую величину изменяется скорость тела за единицу времени.
В СИ единицей ускорения является метр на секунду в квадрате . к соответствующему промежутку времени ∆t определяет вектор среднего ускорения точки за этот промежуток времени:
Вектор среднего ускорения имеет то же направление, что и вектор , т.е. направлен в сторону вогнутости траектории.
Ускорением точки в данный момент времени t
называется векторная величина , к которой стремится среднее ускорение при стремлении промежутка времени ∆t к нулю: Вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиуса-вектора точки по времени.
Ускорение точки равно нулю лишь тогда, когда скорость точки v
постоянна как по величине, так и по направлению: это соответствует только прямолинейному и равномерному движению.
Найдем, как располагается вектор по отношению к траектории точки. При прямолинейном движении вектор направлен вдоль прямой, по которой движется точка. направлен в сторону вогнутости траектории и лежит в плоскости, проходящей через касательную к траектории в точке М
направлен в сторону вогнутости траектории и лежит в плоскости, проходящей через касательную к траектории в точке М
и прямую, параллельную касательной в соседней точке M
1 (рис. 8). В пределе, когда точка М
стремится к М
, эта плоскость занимает положение так называемой соприкасающейся плоскости, т.е. плоскости, в которой происходит бесконечно малый поворот касательной к траектории при элементарном перемещении движущейся точки. Следовательно, в общем случае вектор ускорения лежит в соприкасающейся плоскости и направлен в сторону вогнутости кривой.
Определение ускорения при координатном способе задания движения
Вектор ускорения точки в проекции на оси получаем:
т.е. проекция ускорения точки на координатные оси равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени. Модуль и направление ускорения найдутся из формул
Рис.10
Проекции ускорения a x = =0, a y = =-8 см∙с -2 . Так как проекция вектора ускорения на ось x
Так как проекция вектора ускорения на ось x
равна нулю, а на ось y
– отрицательна, то вектор ускорения направлен вертикально вниз, и величина его постоянна, не зависит от времени.
Первым открытием Архимеда в механике было введение понятия центра тяжести, т.е. доказательство того, что в любом теле есть единственная точка, в которой можно сосредоточить его вес, не нарушив равновесного состояния.
Центр тяжести тела – точка твердого тела, через которую проходит равнодействующая всех сил тяжести, действующих на элементарные массы этого тела при любом его положении в пространстве.
Центром тяжестимеханической системы
называется точка, относительно которой суммарный момент сил тяжести, действующих на все тела системы, равен нулю.
Проще говоря, центр тяжести
– это точка, к которой приложена сила тяжести независимо от положения самого тела. Если тело однородное, центр тяжести
обычно расположен в геометрическом центре тела. Таким образом, центр тяжести в однородном кубе или однородном шаре совпадает с геометрическим центром этих тел.
Если размеры тела малы по сравнению с радиусом Земли, то можно считать, что силы тяжести всех частиц тела образуют систему параллельных сил. Их равнодействующая называется силой тяжести
, а центр этих параллельных сил – центром тяжести тела
.
Координаты центра тяжести тела могут быть определены по формулам (рис. 7.1):
, , ,
где – вес телаx i
, y i
, z i
– координаты элементарной частицы, весом Р i
;.
Формулы для определения координат центра тяжести тела являются точными, строго говоря, лишь при разбиении тело на бесконечное число бесконечно малых элементарных частиц весом Р i
. Если же число частиц, на которые мысленно разбито тело, конечное, то в общем случае эти формулы будут приближенными, так как координаты x i , y i , z i
при этом могут быть определены лишь с точностью до размеров частиц. Чем меньше эти частицы, тем меньше будет ошибка, которую мы сделаем при вычислении координат центра тяжести. К точным выражениям можно прийти лишь в результате предельного перехода, когда размер каждой частицы стремится к нулю, а число их неограниченно возрастает. Как известно, такой предел называется определенным интегралом. Поэтому фактическое определение координат центров тяжести тел в общем случае требует замены сумм соответствующими им интегралами и применения методов интегрального исчисления.
К точным выражениям можно прийти лишь в результате предельного перехода, когда размер каждой частицы стремится к нулю, а число их неограниченно возрастает. Как известно, такой предел называется определенным интегралом. Поэтому фактическое определение координат центров тяжести тел в общем случае требует замены сумм соответствующими им интегралами и применения методов интегрального исчисления.
Если масса внутри твердого тела или механической системы распределяется неоднородно, то центр тяжести смещается в ту часть, где оно тяжелее.
Центр тяжести тела не всегда даже может находиться внутри самого тела. Так, например, центр тяжести бумеранга находится где-то посередине между оконечностей бумеранга, но вне самого тела бумеранга.
Для крепления грузов положение центра тяжести очень важно. Именно в эту точку приложены силы тяжести и инерционные силы, действующие на груз в процессе движения. Чем выше находится центр тяжести тела или механической системы, тем более оно склонно к опрокидыванию.
Центр тяжести тела совпадает с центром масс.
Шкала центра тяжести
Что такое центр тяжести
Центр тяжести (или центр масс) объекта — это среднее положение веса (или массы) объекта в пространстве. Объект, подвешенный в пространстве над центром тяжести, будет идеально сбалансирован. Сила, приложенная к центру тяжести, вызывает чистое смещение. Сила, приложенная не через центр тяжести, заставляет объект вращаться вокруг своего центра тяжести. Когда дело доходит до проектирования самолетов, космических кораблей и даже автомобилей, расчет центра тяжести является важной частью процесса.
Зачем нужно находить Центр тяжести?
Управление полетом объекта требует хорошего знания положения его центра тяжести. Например, выравнивание направления тяги ракетного двигателя таким образом, чтобы он проходил точно через центр тяжести ракеты, необходимо для достижения прямого полета. Это может иметь огромное значение для устойчивости самолета, а также для его топливной эффективности при перемещении из одной точки в другую.
В автомобильной конструкции чем ниже центр тяжести, тем выше устойчивость автомобиля или грузовика. Это объясняет, почему у грузовиков и внедорожников больше проблем с опрокидыванием, чем у автомобилей, потому что они находятся выше над дорогой, поэтому их центр тяжести выше. Гоночные автомобили всегда имеют очень низкий центр тяжести, чтобы избежать опрокидывания на поворотах на высокой скорости.
Совершенно очевидно, что расчет центра тяжести является важной частью процесса проектирования. Тогда вопрос, как лучше это сделать?
Как рассчитать центр тяжести объекта?
Центр тяжести объекта можно рассчитать, поместив объект на весы с несколькими датчиками — обычно это делается с помощью весов с четырьмя или тремя датчиками веса. Объект помещается в центр платформы весов. Вес объекта измеряется в четырех углах по отдельности, и расположение четырех тензодатчиков по отношению к началу координат используется для вычисления суммы моментов, и эта сумма делится на общий вес для вычисления местоположения его x и положение Y.
X = (W1*X1 + W2*X2 + W3*X3 + W4*X4)/(W1+W2+W3+W4)
И
Y = (W1*Y1 + W2*Y2 + W3*Y3 + W4 *Y4)/(W1+W2+W3+W4)
Объект можно повернуть на 90 градусов, и тот же процесс повторить для вычисления центра тяжести в другой плоскости.
- Платформенные весы с четырьмя весоизмерительными ячейками USB
- Питание и данные через порт USB
- Простое в использовании программное обеспечение LV-4000CG
- Калибровка по стандартам NIST с сертификатом
- Калибровка сохранена в датчике
- Программное обеспечение, совместимое с Win 8/10
- Данные обновляются с частотой до 150 Гц
- Отображение, регистрация и построение данных в удобном графическом интерфейсе пользователя
- Точность каждого тензодатчика порядка +/- 0,25% от полной шкалы
- Общая точность весов составляет около +/- 1% от емкости
- Просмотр центра тяжести в режиме реального времени с отслеживанием в реальном времени
- Сохранить данные в файле CSV и открыть в Excel, Matlab и т.
 д.
д. - Просто поставьте весы на стол или пол и выровняйте перед использованием
- Изготовлен из легкого алюминиевого материала с протравленной сеткой
Весы центра тяжести
Весы CG 2 фута x 2 фута включают в себя платформу с квадратной сеткой 1 дюйм, четыре тензодатчика, адаптеры, выравнивающие ножки, четырехканальный интерфейс USB для тензодатчиков и программное обеспечение LV-4000CG, поставляемое на USB-накопителе. Диск или как ссылка для скачивания. Прилагаются калибровочные сертификаты для каждого тензодатчика, демонстрирующие соответствие стандартам NIST. Используйте с ПК или планшетом с операционной системой Win 8/10, 8 ГБ ОЗУ и достаточным местом на диске для записи данных (500 ГБ должно быть более чем достаточно).
Если вы хотите создать собственную компьютерную шкалу нестандартного размера, взгляните на комплект компьютерной графики.
Купить
- Весы состоят из четырех тензодатчиков, установленных в четырех углах платформы, построенной из жесткого алюминиевого каркаса.
 Платформа имеет вытравленную сетку на поверхности для определения CG.
Платформа имеет вытравленную сетку на поверхности для определения CG.
Верхняя часть весов CG с метками сетки
Нижняя часть весов CG с датчиками
Весы построены с использованием четырех тензодатчиков iLoad Pro, установленных в четырех углах платформы, построенной с использованием алюминиевого каркаса, и одного четырехпортового USB-концентратора.
Максимальная частота обновления с датчика – 150 Гц. Но при необходимости мы можем предоставить максимальное обновление данных до 500 Гц.
Расположение центра тяжести рассчитывается по простой формуле:
X = (W1*X1 + W2*X2 + W3*X3 + W4*X4)/(W1+W2+W3+W4)
А
Y = (W1*Y1 + W2*Y2 + W3*Y3 + W4*Y4)/(W1+W2+W3+W4)
Вы можете вычислить ЦТ объекта в 3D, вычислив сначала ЦТ в двух измерениях, а затем затем наклон платформы на известный угол, а затем снова измерение новой ЦТ и определение ЦТ в 3D с использованием преобразований. Мы пока не предлагаем 3D-решение в качестве стандартного продукта, но можем предложить решение заинтересованным клиентам в будущем. Пожалуйста, свяжитесь с нами для получения информации о ваших пользовательских масштабах CG.
Пожалуйста, свяжитесь с нами для получения информации о ваших пользовательских масштабах CG.
Весы CG показаны с гирями
Программное обеспечение для весов CG
Программное обеспечение LoadVUE Pro Center of Gravity должно использоваться с весами CG для расчета и отображения центра тяжести объектов в двух измерениях. Отображается индивидуальный вес или сила на каждом тензодатчике, а центр тяжести объекта в 2D-пространстве отображается в виде точки, диаметр которой зависит от общего веса силы объекта.
Может использоваться для отслеживания статических и динамических изменений ЦТ в режиме реального времени с целью изучения распределения веса и баланса людей или животных. Размер весов, а также мощность весов могут быть изменены в соответствии с вашими потребностями. Для покупки доступны несколько стандартных конфигураций. Пожалуйста, свяжитесь с нами для получения информации о ваших пользовательских масштабах CG.
Создайте свои собственные весы центра тяжести
Если стандартные варианты, которые мы предлагаем в качестве весов центра тяжести, не соответствуют вашим потребностям, вы можете создать свои собственные, используя наш набор цифровых USB-тензодатчиков! Вам просто нужно сначала построить жесткую раму и установить четыре тензодатчика по четырем углам рамы. Затем вы можете создать платформу (добавить сетку для удобного определения местоположения и определить систему координат), где вы можете разместить объекты, которые хотите измерить. Используйте прилагаемые кнопки загрузки (выравнивающие ножки), чтобы выровнять весы, прежде чем обнулить их и использовать.
Затем вы можете создать платформу (добавить сетку для удобного определения местоположения и определить систему координат), где вы можете разместить объекты, которые хотите измерить. Используйте прилагаемые кнопки загрузки (выравнивающие ножки), чтобы выровнять весы, прежде чем обнулить их и использовать.
Комплект CG средней точности
В этот комплект входят четыре тензодатчика iLoad Pro, концентратор USB с четырьмя портами и программное обеспечение LV-4000-CG. Комплект поставляется предварительно откалиброванным в режиме сжатия с отслеживаемыми сертификатами калибровки NIST. Вам просто нужно построить крепкую, жесткую раму, разместить на ней платформу и разместить на ней объект, который вам нужно измерить CG. Вам понадобится ПК или планшет WIn 8/10 с 8 ГБ оперативной памяти и не менее 500 ГБ дискового пространства. Мы включили четыре кнопки загрузки, чтобы помочь вам выровнять весы после их установки на поверхность, на которую вы будете их устанавливать.
Купить сейчас
Высокоточный комплект компьютерной графики с 16-битным цифровым интерфейсом
В этот комплект входят четыре тензодатчика RSB6, концентратор USB с четырьмя портами и программное обеспечение LV-4000-CG. Комплект поставляется предварительно откалиброванным в режиме сжатия с отслеживаемыми сертификатами калибровки NIST. Вам просто нужно построить крепкую, жесткую раму, разместить на ней платформу и разместить на ней объект, который вам нужно измерить CG. Вам понадобится ПК или планшет WIn 8/10 с 8 ГБ оперативной памяти и не менее 500 ГБ дискового пространства. Мы включили четыре кнопки загрузки, чтобы помочь вам выровнять весы после их установки на поверхность, на которую вы будете их устанавливать.
Комплект поставляется предварительно откалиброванным в режиме сжатия с отслеживаемыми сертификатами калибровки NIST. Вам просто нужно построить крепкую, жесткую раму, разместить на ней платформу и разместить на ней объект, который вам нужно измерить CG. Вам понадобится ПК или планшет WIn 8/10 с 8 ГБ оперативной памяти и не менее 500 ГБ дискового пространства. Мы включили четыре кнопки загрузки, чтобы помочь вам выровнять весы после их установки на поверхность, на которую вы будете их устанавливать.
Высокоточный комплект компьютерной графики с 24-битным цифровым интерфейсом
В этот комплект входят четыре тензодатчика RSB6, четыре 24-битных цифровых интерфейса DI-1000U, 1 USB-концентратор HX-400 и программное обеспечение LV-4000-CG. Комплект поставляется предварительно откалиброванным в режиме сжатия с отслеживаемыми сертификатами калибровки NIST. Вам просто нужно построить крепкую, жесткую раму, разместить на ней платформу и разместить на ней объект, который вам нужно измерить CG. Вам понадобится ПК или планшет WIn 8/10 с 8 ГБ оперативной памяти и не менее 500 ГБ дискового пространства. Мы включили четыре кнопки загрузки, чтобы помочь вам выровнять весы после их установки на поверхность, на которую вы будете их устанавливать.
Вам понадобится ПК или планшет WIn 8/10 с 8 ГБ оперативной памяти и не менее 500 ГБ дискового пространства. Мы включили четыре кнопки загрузки, чтобы помочь вам выровнять весы после их установки на поверхность, на которую вы будете их устанавливать.
Что входит в комплект компьютерной шкалы?
В комплект весов CG входят четыре тензодатчика iLoad Pro, регулируемые ножки (кнопки нагрузки) для выравнивания платформы, один 4-портовый USB-концентратор и программное обеспечение LV-4000CG, поставляемое на USB-накопителе или загружаемое по ссылке. Прилагаются калибровочные сертификаты для каждого тензодатчика, демонстрирующие соответствие стандартам NIST. Вам просто нужно создать свою платформу и раму и получить ПК с операционной системой Win 8/10, 8 ГБ ОЗУ и достаточным местом на диске для сбора данных (500 ГБ должно быть более чем достаточно).
Купить
Свяжитесь с нами
Центр тяжести является геометрическим свойством любого объекта. Определение центра тяжести очень важно В общем, определение центра тяжести (cg) является сложной задачей. Для объекта общей формы существует простой механический способ
Если масса объекта распределена неравномерно, мы должны использовать исчисление cg * W = S x dw где x — расстояние от опорной линии, dw это ш = м * г где м — масса объекта, а г — гравитационная м = ро * V Мы можем объединить последние два уравнения: ш = г * ро * V тогда dw = g * ро * dV dw = g * rho(x, y, z) * dx dy dz Если у нас есть функциональная форма для распределения массы, мы можем решить cg * W = g * SSS x * rho(x,y,z) dx dy dz где SSS указывает тройной интеграл по dx . dy . и дз . Экскурсии с гидом
Деятельность: Связанные сайты: |
Как легко найти центр тяжести груза
Центр тяжести по определению — это точка, из которой можно считать, что вес тела или системы действует.
В такелаже центр тяжести — это точка внутри груза, в которой объект равномерно уравновешивается во всех направлениях. Вы также можете услышать, что центр тяжести — это точка, в которой сосредоточен весь вес груза. Знание местоположения центра тяжести груза является важной частью безопасной такелажа, поскольку груз наиболее стабилен, когда он поднимается непосредственно над точкой центра тяжести.
Иногда найти центр тяжести груза довольно просто. Для объектов одинаковой формы и состава, таких как цельный кусок трубы, центр тяжести обычно находится в середине объекта. Конечно, даже если вы уверены, что установили точку захвата выше центра тяжести, все же рекомендуется провести быструю проверку перед выполнением подъема. Это включает подъем груза на несколько дюймов за раз, чтобы обеспечить его устойчивость. Если груз начинает свободно раскачиваться, вам, возможно, придется снова опустить его и переустановить перед повторным тестированием. Подробнее о тестировании нагрузки можно прочитать здесь .
Определение центра тяжести груза для объектов необычной конфигурации потребует немного больше работы. Вы можете выбрать метод проб и ошибок, при котором вы устанавливаете груз в точке, в которой, по вашим оценкам, находится центр тяжести, а затем выполняете вышеупомянутый пробный запуск, пока не сможете надежно поднять груз, но это может занять значительное время. времени.
времени.
Более эффективным способом может быть расчет центра тяжести груза с помощью простой математической формулы. Хотя из-за длинных объяснений это может звучать как ракетостроение, на самом деле все довольно просто. Ниже мы собираемся разбить его шаг за шагом. Зная шаги, вы можете легко определить центр тяжести груза за считанные минуты, используя пару загрузите ссылки , рулетку и калькулятор вашего телефона. Обратите внимание, что в этом примере мы находим ЦТ восток/запад. Эти шаги можно повторить, чтобы найти север/юг CG.
Для определения центра тяжести сложных или нетвердых объектов необходимо сначала прикрепить звено нагрузки к каждому концу груза. Измерьте нагрузку с левой и с правой стороны (WL и WR в нашем примере). Затем объедините оба, чтобы рассчитать общий вес (TW).
Вот как должна выглядеть формула на данный момент, используя случайно сгенерированные числа из нашего примера.
WL (вес левого конца) = 3500 фунтов
WR (вес правого конца) = 8 650 фунтов
TW (общий вес) = 12150 фунтов
. ближе к самому тяжелому концу груза. Это правильный конец в нашем примере. Следующий шаг в определении центра тяжести — взять более тяжелый конечный вес и разделить его на общий вес.
ближе к самому тяжелому концу груза. Это правильный конец в нашем примере. Следующий шаг в определении центра тяжести — взять более тяжелый конечный вес и разделить его на общий вес.
(WR / TW) = X
8 650 / 12 150 = 0,71
Это говорит нам о том, что центр тяжести в 0,71 раза больше расстояния между двумя точками захвата, в сторону более тяжелого конца или вправо в этот пример. * Если ваша нагрузка тяжелее на левом конце, просто замените WR на WL в каждом месте, где мы написали эту формулу. Вам нужно только рассчитать одну сторону, чтобы найти CG. *
На последнем этапе измерьте расстояние между двумя точками выбора. Это называется SPAN, и в нашем примере он рассчитан на 126 дюймов. Теперь вы возьмете наш предыдущий расчет и умножите его на SPAN, как показано ниже шаг за шагом.
(WR / TW) x Span
(8 650 /12150) x 126 ”
(0,71) x 126” = 89 ”
Вы уже обнаружили, что центр гравитации 89 дюймов
40004. слева в нашем примере, так как правый конец был более тяжелым. Теперь вы можете установить груз вокруг центра тяжести и, как обычно, выполнить быструю пробную нагрузку, чтобы убедиться, что груз сбалансирован.
слева в нашем примере, так как правый конец был более тяжелым. Теперь вы можете установить груз вокруг центра тяжести и, как обычно, выполнить быструю пробную нагрузку, чтобы убедиться, что груз сбалансирован.
Обратите внимание, что вы также можете использовать десятые доли фута или любую другую метрическую единицу вместо дюймов. Формула будет работать одинаково со всеми этими единицами измерения при условии, что все используемые единицы измерения одинаковы. Полная формула выглядит следующим образом. Какой из них вы используете, будет зависеть от того, тяжелее ли ваш груз с левой или правой стороны.
(WL / TW) x SPAN = CG
(WR / TW) x SPAN = CG
Дополнительные советы по такелажированию см. в нашей публикации 5 правил безопасности при такелаже 9.
Если у вас остались вопросы о том, как рассчитать центр тяжести груза, обратитесь к местному представителю LGH по телефону или позвоните нам по телефону 800-878-7305 , чтобы поговорить с одним из наших специалистов по аренде. Мы можем помочь вам найти центр тяжести для сложных нагрузок, центр тяжести которых должен располагаться горизонтально, как показано здесь, а также вдоль осей y и z для трехмерных/коробчатых нагрузок.
Мы можем помочь вам найти центр тяжести для сложных нагрузок, центр тяжести которых должен располагаться горизонтально, как показано здесь, а также вдоль осей y и z для трехмерных/коробчатых нагрузок.
Информация и иллюстрации, авторские права принадлежат Джерри Клинке, все права защищены.
Как рассчитать положение центра тяжести – Как отрегулировать и настроить – Секреты подвески ручки автомобиля и почему он так себя ведет. Определение положения центра тяжести — это первый шаг в определении того, почему ваш автомобиль так сильно кренится, а также помогает рассчитать момент крена. Это также один из этапов, необходимых, если вы хотите рассчитать оптимальную жесткость пружины для своего гоночного автомобиля. Ниже приведен метод, используемый для расчета статического положения центра тяжести вашего автомобиля.
Необходимое оборудование
Для точного определения положения центра тяжести вам потребуется следующее оборудование:
- Набор угловых грузов
- Рулетка
- Гидравлический домкрат или подъемное оборудование
Прежде чем приступить к работе
Чтобы получить точный результат, перед началом работы необходимо выполнить следующие шаги:
- Подготовьте жесткие металлические блокировочные стержни, которые эффективно заблокируют передние амортизаторы.
 Они потребуются позже.
Они потребуются позже. - Убедитесь, что все жидкости заполнены
- Масса места водителя, эквивалентная массе водителя
- Отсоедините стабилизатор поперечной устойчивости
Элементы для измерения
Есть несколько параметров, которые необходимо измерить либо с помощью рулетки, либо с помощью угловых грузов, чтобы рассчитать положение центра тяжести.
В приведенной ниже таблице показаны все элементы, которые необходимо измерить, и ее можно использовать для отслеживания измерений, которые будут использоваться в уравнениях, приведенных ниже.
| Измеренный параметр | Вес (кг) | Длина (м) | Угол (градусы) | Процент (%) |
| Передний левый угол | ————– | ——————- | ——————- | |
| Передний правый угол | ————– | ——————- | ——————- | |
| Задний левый угол | ————– | ——————- | ——————- | |
| Задний правый угол | ————– | ——————- | ——————- | |
| Процент переднего веса | —————- | ————– | ——————- | |
| Левый процент веса | —————- | ————– | ——————- | |
| Колесная база | —————- | ——————- | ——————- | |
| Ширина передней гусеницы | —————- | ——————- | ——————- | |
| Ширина задней колеи | —————- | ——————- | ——————- | |
| Общий вес | ————– | ——————- | ——————- | |
| Передний груз поднят | ————– | ——————- | ——————- | |
| Высота поднята по вертикали | —————- | ——————- | ——————- | |
| Длина смежного этажа | —————- | ——————- | ——————- | |
| Угол подъема | —————- | ————– | ——————- | |
| Передняя массовая замена | ————– | ——————- | ——————- | |
| Высота оси | —————- | ——————- | ——————- |
Прежде чем продолжить, вы должны убедиться, что все ваши высоты дорожного просвета установлены на желаемые значения и не будут изменены после этого расчета. Кроме того, аналогично тому, как вы утяжеляете свой автомобиль в повороте, стабилизаторы поперечной устойчивости должны быть отсоединены из стороны в сторону, чтобы устранить любое статическое кручение из системы подвески.
Кроме того, аналогично тому, как вы утяжеляете свой автомобиль в повороте, стабилизаторы поперечной устойчивости должны быть отсоединены из стороны в сторону, чтобы устранить любое статическое кручение из системы подвески.
Этап измерения
Первые измерения, которые необходимо снять с автомобиля, — это ширина колеи и колесная база. Самый простой способ измерить это — провести рулеткой от центра переднего колеса вниз по боку автомобиля к центру заднего колеса. Это даст вам колесную базу. Запишите это в таблице выше в метрах. Далее измерьте ширину дорожки. Для этого проведите рулетку от центра шины спереди по ширине автомобиля к центру шины с другой стороны автомобиля. Если ваши передние колеса расставлены шире, чем задние, или наоборот, запишите ширину передней и задней колеи в приведенную выше таблицу.
Когда эти измерения завершены и записаны в таблицу, пришло время измерить некоторые веса.
Поставьте автомобиль на угловые весы, убедившись, что давление во всех шинах установлено на то, которое вы будете использовать на треке. Кроме того, убедитесь, что все остальные проверки настройки выполнены, как указано в статье «Как утяжелить автомобиль на поворотах». Это обеспечит точное измерение.
Кроме того, убедитесь, что все остальные проверки настройки выполнены, как указано в статье «Как утяжелить автомобиль на поворотах». Это обеспечит точное измерение.
Угловые грузики точно покажут 5 вещей:
- Масса переднего правого колеса
- Передняя левая масса
- Масса задняя правая
- Масса задняя левая
- Общая масса
Снимите эти показания с весов и поместите их в приведенную выше таблицу, убедившись, что масса измеряется в кг. Если нет, то перед вводом данных в таблицу переведите свои показания в кг.
Некоторые весы также рассчитывают процентное соотношение массы спереди и сзади и процентное соотношение массы слева направо. Если это так, то поместите переднюю процентную массу в приведенную выше таблицу в процентах и поместите левую процентную массу в приведенную выше таблицу в процентах.
Если ваши весы не имеют возможности расчета процентного деления и показывают только массу на каждом углу, то можно предпринять следующие шаги, чтобы получить требуемые процентные значения.
Чтобы было проще, ниже приведены некоторые примеры цифр для одноместного гоночного автомобиля:
- Передняя правая масса = 92 кг
- Передняя левая масса = 88 кг
- Масса заднего левого колеса = 123 кг
- Задний правый Масса = 122 кг
- Общая масса автомобиля = 425 кг
Используя эти цифры, мы можем определить, что:
- Общая передняя масса = 180 кг
- Общая масса задней части = 245 кг
- Общая левая масса = 211 кг
- Общая правая масса = 214 кг
Расчет положения центра тяжести спереди назад и сбоку
Теперь нам нужно рассчитать процент веса передней и левой части. Поэтому нам нужно выбрать нашу общую переднюю массу и нашу общую массу и подставить числа в следующее уравнение:
Следовательно:
Теперь для левого процентного разделения нам потребуется общая масса слева и общая масса транспортного средства, которые будут использоваться аналогичным образом в следующем уравнении:
Следовательно:
4
4 Эти цифры теперь можно поместить в приведенную выше таблицу.
Следующим этапом определения положения центра тяжести спереди назад и слева направо является использование ранее записанных измерений ширины колеи и колесной базы. Неважно, какое значение ширины колеи используется для этого, поэтому мы будем использовать измерение ширины передней колеи.
Для целей будущих расчетов в приведенной ниже таблице будут использованы примерные цифры, взятые из одноместного гоночного автомобиля, чтобы сделать рабочие примеры, чтобы показать, как использовать уравнения и суммы.
| Измеряемый параметр | Вес (кг) | Длина (м) | Угол (градусы) | Процент (%) |
| Передний левый угол | 88 | ————– | ——————- | ——————- |
| Передний правый угол | 92 | ————– | ——————- | ——————- |
| Задний левый угол | 123 | ————– | ——————- | ——————- |
| Задний правый угол | 122 | ————– | ——————- | ——————- |
| Передний вес, процент | —————- | ————– | ——————- | 42,35 |
| Левый процент веса | —————- | ————— | ——————- | 49,64 |
| Колесная база | —————- | 2,65 | ——————- | ——————- |
| Ширина передней гусеницы | —————- | 1,45 | ——————- | ——————- |
| Ширина задней колеи | 1,45 | ——————- | ——————- | |
| Общий вес | 425 | ————– | ——————- | ——————- |
| Передний груз поднят | ————– | ——————- | ——————- | |
| Высота поднята по вертикали | —————- | ——————- | ——————- | |
| Длина смежного этажа | —————- | ——————- | ——————- | |
| Угол подъема | —————- | ————— | ——————- | |
| Передняя массовая замена | ————– | ——————- | ——————- | |
| Высота оси | —————- | 0,24 | ——————- | ——————- |
Чтобы рассчитать положение центра тяжести слева направо, мы можем использовать следующее уравнение, используя измерение ширины дорожки и процент массы слева:
Следовательно:
Теперь нам нужно найти центральную линию оси, разделив ширину колеи на 2: ЦТ от центральной линии:
Следовательно:
Если ответ положительный, это означает, что ЦТ смещен от центра на указанную величину в сторону правого колеса. Если значение отрицательное, это говорит вам, что COG смещен от центра на эту величину в сторону левого колеса. Следовательно, в этом примере ЦТ смещен от центра на 5,2 мм в сторону правого колеса.
Если значение отрицательное, это говорит вам, что COG смещен от центра на эту величину в сторону левого колеса. Следовательно, в этом примере ЦТ смещен от центра на 5,2 мм в сторону правого колеса.
Далее нам нужно определить положение центра тяжести спереди назад. Это делается аналогично предыдущему, но вместо этого используется колесная база и процент передней массы.
Таким образом:
Теперь нам нужно найти центральную линию автомобиля, разделив колесную базу на 2.
центральная линия автомобиля COG сидит спереди назад:
Следовательно:
Если ответ положительный, это означает, что центр тяжести смещен на указанную величину в сторону задних колес. Если ответ отрицательный, это означает, что положение ЦТ смещено от центра на указанную величину по направлению к передним колесам. В этом случае положение центра тяжести смещено от центра на 203 мм по направлению к задним колесам.
На приведенной ниже диаграмме вида сверху показано текущее положение центра тяжести автомобиля.
Расчет высоты положения центра тяжести
Расчет высоты положения центра тяжести очень важен, если вы хотите понять характеристики крена вашего автомобиля и если вы хотите рассчитать идеальные жесткости пружин.
Когда автомобиль все еще находится на угловых весах, заднюю часть автомобиля необходимо приподнять на определенную величину, чтобы в идеале автомобиль находился под углом от 15 до 20 градусов от горизонтали, а передние колеса все еще находились на весах. .
Чтобы поднять заднюю часть автомобиля на правильную величину, нам нужно использовать математический принцип под названием СОХКАТОА. Мы будем использовать часть SOH, которая означает Sin (угол), противоположную длину и длину гипотенузы. Длина гипотенузы равна длине колесной базы. Для этого примера мы будем использовать угловую фигуру 18 градусов, так как она находится в середине нашего идеального диапазона. Угол, используемый для функции Sin, равен 18 градусам.
Чтобы рассчитать, насколько высоко вам нужно поднять заднюю часть автомобиля, можно использовать следующее уравнение:
Следовательно, в нашем примере:
Это показывает, что нам нужно поднять заднюю часть автомобиля на 81,9. см по вертикали, чтобы добиться правильного угла. Эта цифра будет меняться в зависимости от величины колесной базы, которую вы измерили для своего конкретного автомобиля.
см по вертикали, чтобы добиться правильного угла. Эта цифра будет меняться в зависимости от величины колесной базы, которую вы измерили для своего конкретного автомобиля.
Самый простой способ сделать это точно — вставить блокировочные стержни в передние амортизаторы, чтобы предотвратить их сжатие при поднятии задних. Также увеличьте давление в передней шине, чтобы исключить из измерений изгиб боковины. Затем установите домкрат между обоими задними колесами на подрамник или дифференциал в центре автомобиля. Поднимите гидравлический домкрат до тех пор, пока он не коснется подрамника, но до того, как он начнет поднимать автомобиль. Измерьте высоту головки домкрата от пола. Теперь поддомкратьте автомобиль вверх, пока головка домкрата не станет на 81,9.см выше, чем когда он просто соприкасался с подрамником. Для достижения такого высокого уровня подъема требуется домкрат с большой высотой подъема. Если у вас есть обычный домкрат, вам, возможно, придется поднимать автомобиль поэтапно, чтобы достичь этой высоты, поднимая его до максимального хода, устанавливая автомобиль на осевые опоры, затем подкладывая дерево между домкратом и автомобилем и снова поднимая его до тех пор, пока высота достигнута. На изображении выше используется пандус для достижения подъема, необходимого для точного измерения. Если вы выберете аналогичный метод, позаботьтесь о том, чтобы задняя ось была надежно закреплена на рампе. Если вам трудно достичь высоты, используйте 15 градусов в нижней части диапазона, что потребует меньшей подъемной силы.
На изображении выше используется пандус для достижения подъема, необходимого для точного измерения. Если вы выберете аналогичный метод, позаботьтесь о том, чтобы задняя ось была надежно закреплена на рампе. Если вам трудно достичь высоты, используйте 15 градусов в нижней части диапазона, что потребует меньшей подъемной силы.
Что делать, если я не могу поднять свой автомобиль на такую высоту
Если вы не можете поднять свой автомобиль достаточно высоко, чтобы поднять его под углом 15 градусов, тогда можно использовать меньшие высоту и угол, но это будет меньше точнее, чем если бы вы находились в диапазоне от 15 до 20 градусов. Однако, если вы не можете подняться на такую высоту, это все равно даст вам близкое приближение к высоте вашего центра тяжести.
Абсолютный минимум, на который вы должны поднять свой автомобиль, составляет 26 см. Все, что меньше этого, приведет к неточному результату. Поэтому лучше всего поднять автомобиль как можно выше и принять во внимание поднятую вертикальную высоту. Теперь можно использовать следующие уравнения для получения значения «Tan θ», которое нам понадобится для расчета высоты центра тяжести позже.
Теперь можно использовать следующие уравнения для получения значения «Tan θ», которое нам понадобится для расчета высоты центра тяжести позже.
Сначала нам нужно вычислить прилегающую длину под автомобилем для поднятой высоты по теореме Пифагора.
Где:
- WB = Колесная база (м)
- Z = Вертикальная высота с поднятой задней частью (м)
Теперь с этим значением мы можем использовать его, чтобы получить значение «Tan θ» для нашего основного уравнения ниже. Используя SOHCATOA, мы можем определить, что:
Где:
- Z = вертикальная высота в поднятом положении сзади (м)
- Adj = Прилегающая длина, рассчитанная по приведенному выше уравнению (м)
Число для «Tan θ» будет десятичным числом. Это можно сохранить и полностью вставить в основное уравнение ниже вместо «Tan θ». После завершения этого раздела мы можем снова присоединиться к исходной процедуре.
Уравнение
Когда автомобиль находится в этом положении, обратите внимание на массу, которая теперь находится на передних колесах, на угловых весах. Сложите две цифры вместе, чтобы получить общую переднюю массу на весах. В этом примере общая передняя масса с поднятой задней частью составила 188 кг.
Сложите две цифры вместе, чтобы получить общую переднюю массу на весах. В этом примере общая передняя масса с поднятой задней частью составила 188 кг.
Следовательно, наша передняя поднятая масса равна:
Теперь нам просто нужно вычесть это значение из нашего ранее измеренного значения общей массы передней оси, чтобы получить изменение массы передней оси:
Следовательно:
Передняя ось изменение массы оси может быть как отрицательным, так и положительным значением. Неважно, отрицательное оно или положительное, его просто нужно записать как значение.
Теперь все эти значения можно записать в предыдущую таблицу для заключительного этапа расчетов. Обновленную таблицу примеров можно увидеть ниже:
| Измеренный параметр | Вес (кг) | Длина (м) | Угол (градусы) | Процент (%) |
| Передний левый угол | 88 | ————– | ——————- | ——————- |
| Передний правый угол | 92 | ————– | ——————- | ——————- |
| Угол задний левый | 123 | ————– | ——————- | ——————- |
| Задний правый угол | 122 | ————— | ——————- | ——————- |
| Процент переднего веса | —————- | ————— | ——————- | 42,35 |
| Левый процент веса | —————- | ————— | ——————- | 49,64 |
| Колесная база | —————- | 2,65 | ——————- | ——————- |
| Ширина передней гусеницы | —————- | 1,45 | ——————- | ——————- |
| Ширина задней колеи | —————- | 1,45 | ——————- | ——————- |
| Общий вес | 425 | ————— | ——————- | ——————- |
| Передний груз поднят | 172 | ————— | ——————- | ——————- |
| Высота поднята по вертикали | —————- | 0,819 | ——————- | ——————- |
| Длина смежного этажа | —————- | ————— | ——————- | ——————- |
| Угол подъема | —————- | ————– | 18 | ——————- |
| Передняя массовая замена | 8 | ————– | ——————- | ——————- |
| Высота оси | —————- | 0,24 | ——————- | ——————- |
Теперь, когда приведенная выше таблица завершена, мы можем вставить наши цифры в одно окончательное уравнение, которое покажет нам вертикальную высоту над нашими осями положения центра тяжести. Уравнение:
Уравнение:
Следовательно:
Это значение высоты представляет собой высоту положения ЦТ над высотой оси. Чтобы получить высоту от земли, необходимо выполнить одно последнее измерение. Поставив машину на все четыре колеса, измерьте диаметр передних шин. Если у вас передние колеса или шины разного размера, возьмите среднее значение. Однако в большинстве случаев передние колеса будут иметь одинаковый диаметр. Получив диаметр, разделите его на 2, чтобы получить радиус передней шины. Это значение радиуса является высотой передней оси. В случае одноместного автомобиля радиус переднего колеса составляет 0,24 м. Это значение просто добавляется к ранее рассчитанной высоте, чтобы получить высоту положения ЦТ над уровнем земли для автомобиля.
Следовательно:
Эта высота является окончательной цифрой, необходимой для точного определения положения центра тяжести вашего автомобиля. На приведенных ниже диаграммах показано положение центра тяжести примера автомобиля при виде сверху, сбоку и спереди.
Вид спереди:
Вид сбоку:
Вид сверху:
Что дальше?
Теперь, когда вы точно определили свой центр тяжести, вы сможете приступить к регулировке вашего автомобиля, чтобы попытаться опустить его, чтобы уменьшить крены. Вы можете изменить высоту посадки или начать удалять массу из одних областей и добавлять ее в другие, чтобы сместить положение центра тяжести, чтобы сделать его как можно более центральным. Также распространена установка более легких деталей из углеродного волокна в высоких точках, таких как крыша, капот или двери. Вы можете проводить повторные измерения с помощью этого процесса после каждого изменения, чтобы увидеть, насколько эффективными были ваши изменения.
Нравится:
Нравится Загрузка…
Центр тяжести Рона Куртуса
SfC Home > Physics > Gravity >
Рон Куртус
центр тяжести (ЦТ) объекта является точкой равновесия, вокруг которой равномерно распределяется его материя. В таком случае объект может вести себя так, как если бы весь его вес был сосредоточен в ЦТ.
В таком случае объект может вести себя так, как если бы весь его вес был сосредоточен в ЦТ.
Вы можете найти центр тяжести математически, взяв среднее или среднее распределение веса объекта. Вы также можете найти центр тяжести экспериментально, используя отвес или найдя точку баланса.
Примечание : В некоторых учебниках центр тяжести путают с центром масс (ЦМ). Для нахождения центра тяжести требуется, чтобы объект находился под действием силы тяжести, а центр масс — это центр распределения масс. Хотя CG часто находится в том же месте, что и CM, это совершенно разные концепции.
( См. Гравитация и центр масс для получения дополнительной информации. )
Применение включает в себя тот факт, что свободное вращение объекта всегда происходит вокруг его центра тяжести и что объект опрокидывается, когда центр тяжести находится за пределами опорного основания объекта. Кроме того, наибольшая сила приложена через центр тяжести.
Возможные вопросы:
- Как рассчитать центр тяжести?
- Какими экспериментами можно определить центр тяжести?
- Каковы некоторые приложения CG?
Этот урок ответит на эти вопросы. Полезный инструмент: Преобразование единиц измерения
Расчет центра тяжести
Расчет центра тяжести основан на том факте, что крутящий момент, создаваемый весом системы, такой же, как если бы ее общий вес находился в центр гравитации. Эта точка является средним или средним значением распределения моментных плеч объекта.
Вычисление центра тяжести объекта включает в себя сумму весов, умноженных на их расстояние от начальной точки, деленную на общий вес объекта.
В случае очень неправильной формы груз может состоять из отдельных частиц или даже атомов. Затем исчисление используется для интегрирования произведения этих весов и дифференциального разделения.
Если объект состоит из правильных частей, таких как квадраты или круги, вы можете использовать тот факт, что у каждой из них есть центр тяжести в геометрическом центре. Это видно на иллюстрации ниже:
Это видно на иллюстрации ниже:
Вычисление центра тяжести грузов
Центр тяжести на иллюстрации находится на следующем расстоянии от произвольной нулевой точки:
CG = (aM + bN + cP)/(M + N + P)
Например, если:
- a = 1 фут
- б = 4 фута
- с = 8 футов
- М = 1 фунт
- Н = 2 фунта
- P = 4 фунта
КГ = (1*1 + 4*2 + 8*4)/(1 + 2 + 4)
КГ = 41/7
CG = 5,9 футов от нулевой точки
Приблизительный центр тяжести показан на рисунке.
Экспериментальное определение CG
Центр тяжести объектов правильной формы, таких как квадраты, кубы, круги и сферы, находится в их геометрических центрах. Для других форм или конфигураций вам нужно либо использовать эксперименты, либо расчеты. Центр тяжести многих объектов легче определить опытным путем, чем расчетным путем.
Центр тяжести многих объектов легче определить опытным путем, чем расчетным путем.
Техника отвеса
Когда объект подвешен так, чтобы он мог свободно двигаться, его центр тяжести всегда находится прямо под точкой подвеса.
Вы можете экспериментально определить центр тяжести объекта, подвесив его в нескольких точках и отметив вертикальную линию с помощью отвеса. Пересечение двух или более вертикальных линий от отвеса является центром тяжести объекта.
Измерение центра тяжести с помощью отвеса
Эта процедура относительно проста для плоского объекта. Однако это может быть сложнее, если объект имеет некоторую форму в трех измерениях.
Точка баланса
Для некоторых объектов вы можете найти точку баланса экспериментальным путем. Для объекта на иллюстрации выше можно было легко найти точку баланса. Однако было бы трудно найти точку баланса для объекта с криволинейными поверхностями.
Противовесы на острой кромке
Приложения
Низкий центр тяжести помогает предотвратить опрокидывание объекта, например автомобиля. Объекты будут вращаться вокруг своей CG. Также центр тяжести оказывает наибольшее воздействие при столкновении.
Объекты будут вращаться вокруг своей CG. Также центр тяжести оказывает наибольшее воздействие при столкновении.
Точка опрокидывания
Когда вы наклоняете объект на ребро, он опрокидывается только тогда, когда центр тяжести находится вне опорного основания объекта.
Объект опрокидывается, когда ЦТ проходит точку вращения
Объекты, которые тяжелее внизу, имеют более низкий центр тяжести, и поэтому их труднее опрокинуть. Автомобили и грузовики имеют более низкий центр тяжести для повышения их устойчивости.
ЦТ ниже точки баланса
Интересное применение, когда центр тяжести находится ниже баланса или точки поворота. Объект будет легко балансировать и может колебаться или раскачиваться взад и вперед в этом положении.
ЦТ ниже точки равновесия
Существует ряд новинок и игрушек, использующих этот принцип.
Вращается вокруг центра тяжести
Если вы подбросите объект в воздух с вращением на нем, объект будет вращаться вокруг своего центра тяжести, следуя своей траектории.
Центр тяжести мяча находится в его центре, поэтому он будет просто вращаться, когда его подбрасывают в воздух. Мяч будет двигаться по параболе, пока не упадет на землю.
Точно так же, если вы подбросите в воздух бейсбольную биту, она тоже будет вращаться вокруг своего центра оси, и эта ось пойдет по параболической траектории, аналогичной траектории мяча.
Летучая мышь движется по параболе во время вращения
Удар по бейсбольному мячу
Центр тяжести — это точка, в которой сосредоточен весь вес объекта.
CG — лучшее место для удара по мячу
Когда вы размахиваете бейсбольной битой, лучшее место для удара по мячу — центр тяжести биты. В этот момент к мячу прикладывается максимальная сила для данного удара.
Резюме
Центр тяжести (ЦТ) — это место, где кажется сосредоточенным весь вес объекта. Эта точка является средним распределением веса объекта. Центр тяжести объекта также можно найти экспериментально.
Центр тяжести объекта также можно найти экспериментально.
Свободное вращение объекта всегда происходит вокруг его центра тяжести. Объект опрокинется, когда ЦТ окажется за пределами поддержки объекта. Наибольшая сила приложена через центр тяжести.
Наблюдайте за ним, чтобы узнать больше
Ресурсы и ссылки
Рон Куртус. Условия
Веб -сайты
Центр гравита и ротационных.0129 — Wikipedia
Обнаружение Центра гравитации — НАСА
Центр гравитации Эксперимент — Exploratorium
Gravity Resources
Книги
9 9000 (Уведомление:
. )
Книги с самым высоким рейтингом по Simple Gravity Science
Книги с самым высоким рейтингом по Advanced Gravity Physics
Вопросы и комментарии
У вас есть вопросы, комментарии или мнения по этому поводу? Если это так, отправьте электронное письмо с вашим отзывом. Я постараюсь вернуться к вам как можно скорее.
Я постараюсь вернуться к вам как можно скорее.
Поделиться этой страницей
Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:
Студенты и исследователи
Веб-адрес этой страницы:
www.school-for-champions.com/science/
gravity_center.htm
Разместите его в качестве ссылки на своем веб-сайте или в качестве ссылки в своем отчете, документе или диссертации.
Copyright © Ограничения
Где ты сейчас?
Школа Чемпионов
Темы гравитации
Центр тяжести
Как определить центр тяжести любого груза
Как определить центр тяжести любого груза
Многие боятся, но немногие понимают, что центр тяжести является самым недооцененным и недооцененным свойством груза. Поскольку подавляющее большинство всех видов транспорта и подъемников включает в себя грузы с довольно централизованным центром тяжести, нет особого стимула погружаться в теории чего-то, что нельзя увидеть или измерить рулеткой.
Поскольку подавляющее большинство всех видов транспорта и подъемников включает в себя грузы с довольно централизованным центром тяжести, нет особого стимула погружаться в теории чего-то, что нельзя увидеть или измерить рулеткой.
Однако, если ЦТ не централизован или нагрузка близка к пределу возможностей транспортного или подъемного оборудования, это становится все более важным свойством, которое может обеспечить или помешать успеху проекта.
Что такое центр тяжести? Говоря математическим языком, «центр тяжести — это точка, в которой можно предположить всю массу объекта». Это может показаться немного абстрактным, но с приведенными ниже примерами это станет ясно. ЦТ определяется не формой или размером, а только весом и расположением (координатами) каждого из его отдельных компонентов.
Может быть ясно, что центр тяжести квадратной коробки находится прямо в центре этой коробки и что «манипулирование» этой коробкой, подъем, поддомкрачивание, транспортировка и т. д. не является сложной задачей с математической точки зрения. . Это меняется, когда дело доходит до объектов, состоящих из множества отдельных элементов. Рано или поздно все попадают в такую ситуацию, когда становится намного сложнее. Такими объектами могут быть салазки, содержащие компоненты от разных поставщиков, или, например, сосуды разного диаметра, масленки с сосудом высокого давления, расположенные на одной площадке, или просто деревянный ящик с неизвестным содержимым или можно ли доверять нарисованному вручную знаку CoG.
не является сложной задачей с математической точки зрения. . Это меняется, когда дело доходит до объектов, состоящих из множества отдельных элементов. Рано или поздно все попадают в такую ситуацию, когда становится намного сложнее. Такими объектами могут быть салазки, содержащие компоненты от разных поставщиков, или, например, сосуды разного диаметра, масленки с сосудом высокого давления, расположенные на одной площадке, или просто деревянный ящик с неизвестным содержимым или можно ли доверять нарисованному вручную знаку CoG.
Выяснение
Начнем с простого способа определения ЦТ. Этот метод может быть применен к каждому объекту, для которого необходимо определить CoG. Обратите внимание на рисунок 1, это двумерный объект, например, стальной лист произвольной формы, для которого необходимо определить центр тяжести. Это не может быть сделано за один шаг, а должно быть выполнено в виде серии шагов.
Примечание: расстояния даны в метрах, но это могут быть любые единицы измерения: футы, ярды и т. д. Для результатов расчета это не имеет значения.
д. Для результатов расчета это не имеет значения.
Шаг 1
Выберите положение оси X и оси Y. Их можно выбрать в любом месте, результат расчета останется прежним, если эти оси будут выбраны в другом месте. Попытайся.
В этом примере ось X выбрана в основании объекта, а ось Y выбрана таким образом, чтобы она проходила прямо вниз между треугольной и прямоугольной формой.
Шаг 2
Выберите, какая сторона оси X будет положительной, а какая отрицательной. Это необходимо, потому что расстояние в 1 метр от оси Y может быть с любой стороны, и без обозначения «+» или «-» это невозможно узнать, и, по определению, результат вычисления будет неправильным.
Шаг 3
Теперь нам нужно разделить объект на более мелкие «подобъекты», для которых мы можем легко определить ЦТ. Это показано на рис. 2 и на рис. 3. За выбором этих меньших объектов нет никакой реальной науки. Подойдет все что угодно, пока охвачен весь объект, очевидно, ничего не должно быть забыто или упущено. В этом примере мы выбрали:
В этом примере мы выбрали:
- Треугольник (квадрат 3 х 3 м, разрезанный пополам)
- Квадрат (3 х 3 м) обратите внимание, что в этом поле есть «пустота»
- Прямоугольник (1 x 2 м) представляет собой пустоту квадрата, упомянутого выше под номером 2
Шаг 4
ЦТ каждого из этих подобъектов должен быть определен и выражен в ко -ординаты. Обратите внимание на рисунки 4 и 5. Проводя вспомогательные линии (показаны красным) из одного угла в противоположный угол, можно определить положение ЦТ для квадратов и прямоугольников. Проводя (вспомогательные) линии от одного угла к центру противоположной стороны, можно найти положение ЦТ для треугольников. Этот центр тяжести находится на пересечении этих вспомогательных линий. Результат таков:
COG 1. (+1,0, +1,0)
COG 2. (-1,5, +1,5)
COG 3. (-2,5, +2,0)
Упрощение
Ранее в этом В статье я указал, что ЦТ определяется весом и расположением (координатами) каждого из отдельных компонентов. Вот подсказка, чтобы упростить расчеты. Для двумерных объектов, таких как в этом примере, площадь объекта пропорциональна весу объекта. Когда площадь в два раза больше, вес становится в два раза больше.
Вот подсказка, чтобы упростить расчеты. Для двумерных объектов, таких как в этом примере, площадь объекта пропорциональна весу объекта. Когда площадь в два раза больше, вес становится в два раза больше.
Для трехмерных объектов объем объекта пропорционален весу объекта. Эти подсказки позволяют выполнять расчеты ЦТ, не зная веса объекта или материала, из которого он сделан.
Шаг 5
Расставьте все числа, чтобы выполнить расчет ЦТ. Этап 6 расстояние на вес (площадь) и разделить на сумму всех весов (площадей).
Так как это двумерный объект, это вычисление должно выполняться как в направлении x, так и в направлении y. Для трехмерного объекта это также должно быть выполнено в направлении z.
В направлении x формулу можно переписать как CoGx = (ΣDx* W) / ΣW
Аналогично для направления y CoGy = (ΣDy* W) / ΣW
В цифрах:
CoGx = (+1,0 *4,5)+(-1,5*9)+(-2,5*-2) / (4,5+9-2) = -4 = -0,35 / 11,5
Гр = (+1,0*4,5)+(-1,5*9 )+(-2,0*-2)/(4,5+9-2) = 13 = 1,13 / 11,5
Местоположение ЦТ можно найти по координатам (-0,35, 1,13), см.


 01.01. «Устройство автомобилей»
01.01. «Устройство автомобилей»
 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления

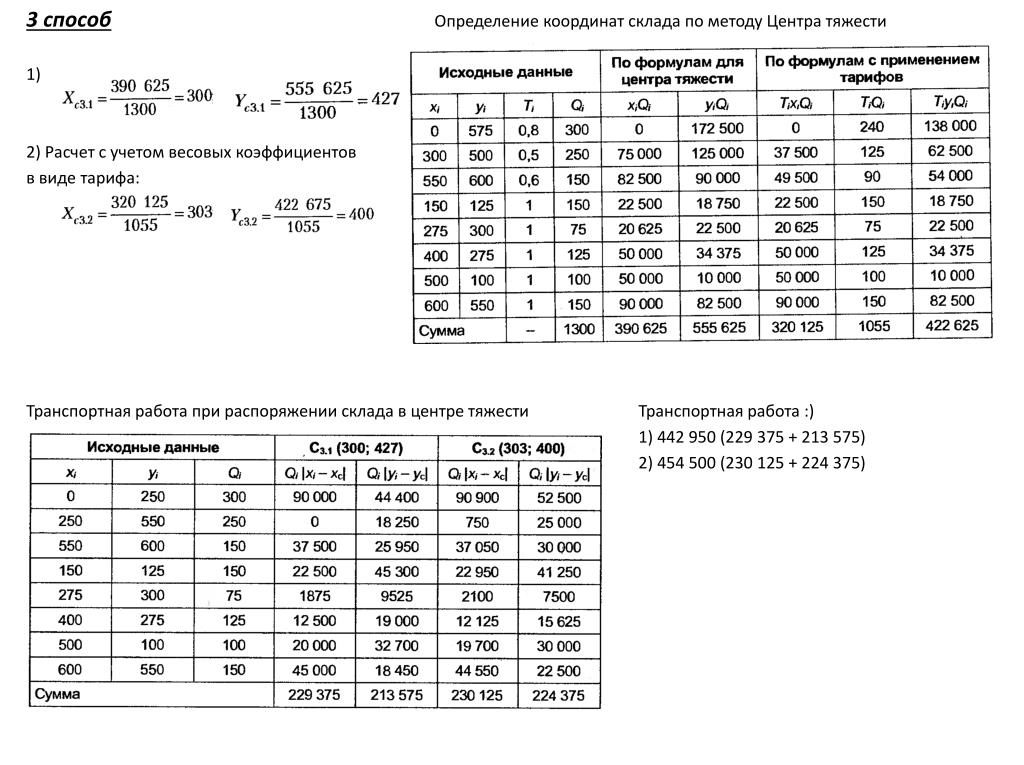

 Вид формул для определения координат центра тяжести тела при этом не меняется.
Вид формул для определения координат центра тяжести тела при этом не меняется. п., которые имеют сложную объемную форму и точечную опору на грунт.
п., которые имеют сложную объемную форму и точечную опору на грунт. 
 величины, определяемые равенствами
величины, определяемые равенствами гл. осями инерции, для к-рых Ixy = Iyz= Izx = 0. Тогда M. и. тела относительно любой оси можно определить, зная гл. оси инерции и M. и. относительно этих осей.
гл. осями инерции, для к-рых Ixy = Iyz= Izx = 0. Тогда M. и. тела относительно любой оси можно определить, зная гл. оси инерции и M. и. относительно этих осей. su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.008 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.008 с.)



 Угол β, образуемый линиями ОD и CD, и будет углом капотажа при пользовании тормозами. Угол капотажа β для случая незаторможенных колес определяется линиями OD’ и ОС. Для определения угла установки хорды обмера при стоянке самолета на земле αст нужно определить размеры h1 и h2 при этом положении самолета.
Угол β, образуемый линиями ОD и CD, и будет углом капотажа при пользовании тормозами. Угол капотажа β для случая незаторможенных колес определяется линиями OD’ и ОС. Для определения угла установки хорды обмера при стоянке самолета на земле αст нужно определить размеры h1 и h2 при этом положении самолета.
 На линиях —I, II -II и III — III откладываются от точки О размеры x1, x2 и x3 и из полученных точек 1, 2, 3 восстанавливаются перпендикуляры к линиям I — I, II— II и III — III. Точка С пересечения этих перпендикуляров-является проекцией центра тяжести самолета на плоскость симметрии.
На линиях —I, II -II и III — III откладываются от точки О размеры x1, x2 и x3 и из полученных точек 1, 2, 3 восстанавливаются перпендикуляры к линиям I — I, II— II и III — III. Точка С пересечения этих перпендикуляров-является проекцией центра тяжести самолета на плоскость симметрии.

 При этом необходимо учитывать некоторое несовпадение центра тяжести лыж с осью их вращения.
При этом необходимо учитывать некоторое несовпадение центра тяжести лыж с осью их вращения.
 Центр тяжести параллелограмма, ромба или параллелепипеда — в точке пересечения диагоналей. Центр тяжести правильного многоугольника — в центре вписанного или описанный круга.
Центр тяжести параллелограмма, ромба или параллелепипеда — в точке пересечения диагоналей. Центр тяжести правильного многоугольника — в центре вписанного или описанный круга. д.
д. Платформа имеет вытравленную сетку на поверхности для определения CG.
Платформа имеет вытравленную сетку на поверхности для определения CG.
 Для прямоугольного блока 50 х 20 х 10,
Для прямоугольного блока 50 х 20 х 10, Для шага 2 повторите процедуру с другой точки объекта.
Для шага 2 повторите процедуру с другой точки объекта. В свою очередь, масса м любого объекта равна
В свою очередь, масса м любого объекта равна Взяв сумму среднего значения веса/объема
Взяв сумму среднего значения веса/объема Они потребуются позже.
Они потребуются позже.
