Механические характеристики электродвигателей

Дата 01.06.2015 Автор Electrician2 комментарияПросмотров: 16 542

Правильный  выбор электродвигателя для производственного механизма – залог его нормальной и экономичной работы. Если электродвигатель подобран правильно, это упростит систему управления электроприводом и возможно удешевит стоимость электропривода. Как известно электропривод должен обеспечивать не только постоянство установившихся значений (скорость, момент), но и динамических (переходных процессов, таких как ускорение, тормозной момент, пусковой момент и т.д.).

Основным критерием для подбора электродвигателей используют зависимость, на которой отображают значение момента М электродвигателя и скорости вращения вала n при действии этого момента. Такая зависимость имеет название механическая характеристика n=f(M). По механическим характеристикам производят анализ электромеханических свойств двигателя, а также оценивают целесообразность применения его для различного рода механизмов и устройств. Они могут быть двух видов: естественные и искусственные.

Естественные механические характеристики: они снимаются при влиянии на двигатель номинальных параметров (номинальный ток, сопротивление обмоток, напряжение, момент сопротивления и т.д.). То есть двигатель подключается к источнику питания без каких-либо преобразовательных устройств – прямым включением.

Искусственные механические характеристики: их снимают при введении в цепь двигателя дополнительных элементов (резистор добавочный) или при пониженном напряжении питания, частоте (если двигатель переменного напряжения) и т.д. То есть на механическую характеристику двигателя производят искусственное влияние.

Также различают механические характеристики по изменению скорости вращения вала в зависимости от увеличения момента. Они оцениваются по жесткости:

и крутизне наклона:

Чтоб определить жесткость механической характеристики необходимо знать изменение скорости и момента на заданном участке зависимости n=f(M). Соответственно все расчеты жесткости ведутся либо в процентах, либо в относительных единицах.

Также механические характеристики можно отсортировать по группам:

• Абсолютно жесткая – при изменении момента нагрузки, скорость вращения вала остается неизменной. Как пример – характеристика синхронной машины.

• Жесткая – когда скорость уменьшается немного при увеличении момента нагрузки. Как пример, двигатели постоянного тока независимого возбуждения ДПТ НВ или линейная часть характеристики асинхронного двигателя.
• Мягкая – при увеличении момента нагрузки изменения в скорости вращения довольно существенные. К таким относят двигатели постоянного тока последовательного возбуждения ДПТ ПВ.

Ниже приведен график различных механических характеристик электродвигателей:

1. – это абсолютно жесткая синхронной машины
2. – жесткая ДПТ НВ
3. —  мягкая ДПТ ПВ
4. – мягкая ДПТ смешанного возбуждения
5. – асинхронного двигателя

Подбор электродвигателя определяется требованиями производственных механизмов. В таком производстве как прокатка металла, изготовление бумаги или картона, требуется четкое поддержание постоянства скорости, а такие механизмы, как подъемные и транспортные, не требуют жестких характеристик (в тяговых электроприводах используется ДПТ ПВ, также он применяется в некоторых крановых механизмах).

Posted in Электропривод

2.3. Механические характеристики исполнительных органов и электродвигателей

При рассмотрении
работы электродвигателя, приводящего
в действие исполнительный орган,
необходимо выявить соответствие
механических характеристик двигателя
характеристикам исполнительных органов.
Поэтому для правильного проектирования
и экономической эксплуатации электропривода
необходимо изучить эти характеристики.

Зависимость
между скоростью и приведенным к валу
двигателя моментом сопротивления
исполнительного органа

называют
механической характеристикой
исполнительного органа.

Эмпирическая
формула для механической характеристики
имеет вид [1]:

,
(2. 6)

где
–
момент сопротивления ИО при скорости
;

–момент сопротивления
трения в движущихся частях ИО;

–момент сопротивления
при номинальной скорости
;

–показатель
степени, характеризующий изменение
момента сопротивления при изменении
скорости.

Приведенная формула
(2.6) позволяет
классифицировать
механические
характеристики исполнительных органов
на следующие основные
категории.

1. Не
зависящая от скорости механическая
характеристика (прямая 1 на рис. 2.2.). При
этом х
= 0 и момент сопротивления не зависит от
скорости. Такой характеристикой обладают
все подъемные установки, механизмы
подач металлорежущих станков, поршневые
насосы при неизменной высоте подачи,
конвейеры с постоянной массой
передвигаемого материала и т.д., а также
все ИО, у которых основным моментом
сопротивления является момент
сопротивления трения.

2. Линейно-возрастающая
механическая
характеристика (прямая 2 на
рис. 2.2.).
В этом случае
=1
и момент сопротивления линейно зависит
от скорости
.
Такая характеристика получается,
например, в приводе генератора постоянного
тока с независимым возбуждением, если
последний будет работать на постоянный
внешний резистор.

Рис. 2.2. Механические
характеристики исполнительных органов

3. Нелинейно-возрастающая
(параболическая) механическая
характеристика (кривая 3 на рис.2.2.). Этой
характеристике соответствует
=2;
момент сопротивления здесь зависит от
квадрата скорости. По характеристике
3 работают все исполнительные органы
центробежного типа (насосы, вентиляторы,
компрессоры, дымососы, гребные винты и
т.д.).

4. Нелинейно-спадающая
(гиперболическая) механическая
характеристика (кривая 4 на рис. 2.2). При
этом х
= –1 и момент сопротивления
изменяется обратно пропорционально
скорости.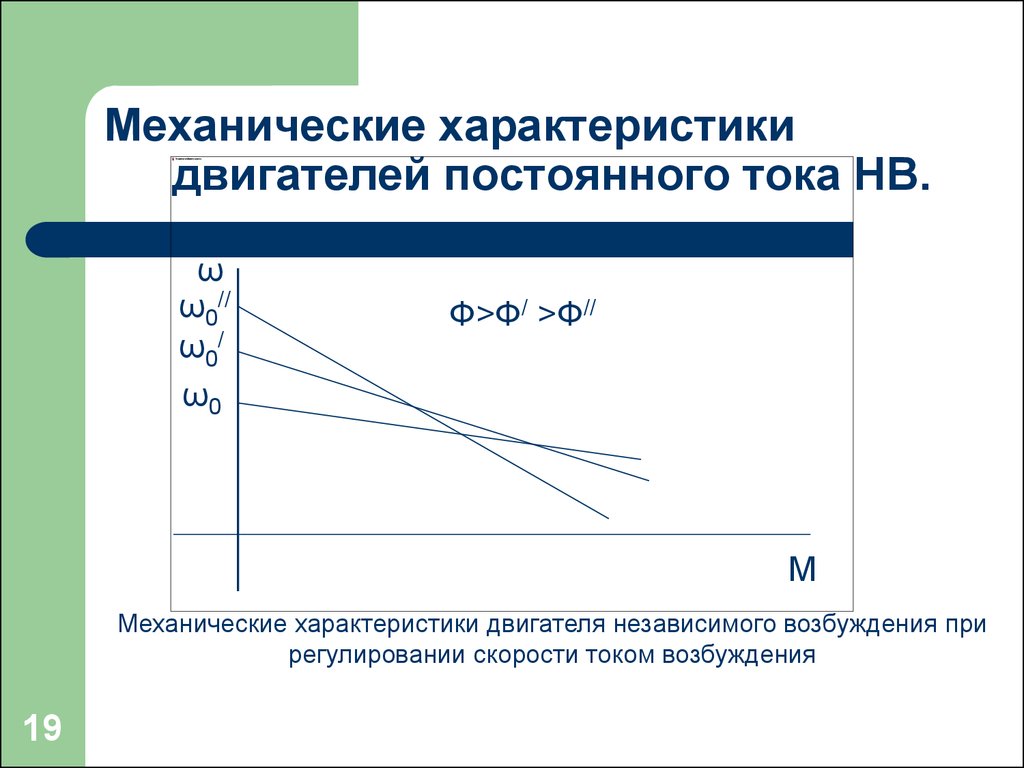

Механическую
характеристику вида 4 имеют механизмы
главного движения токарных, фрезерных
и других станков, различные наматывающие
устройства.

Механической
характеристикой
электродвигателя вращательного движения
называется зависимость его угловой
скорости от развиваемого им момента,
т.е.
.

Естественной
называется
механическая характеристика двигателя,
которая соответствует основной схеме
включения двигателя, номинальным
параметрам питающего напряжения и
отсутствию в электрических цепях
дополнительных элементов (например,
резисторов). В противном случае
электродвигатель будет иметь искусственную
(регулировочную) характеристику.
Искусственных характеристик у
электродвигателя может быть много.

На рисунке 2.3
показаны естественные характеристики
наиболее распространенных электродвигателей
вращательного движения:

1. – двигателя
   постоянного тока независимого
   возбуждения;

2. – двигателя
   постоянного тока последовательного
   возбуждения;

3. – асинхронного
   двигателя;

4 – синхронного
двигателя.

Для оценки жесткости
механической характеристики двигателя
вводится понятие
жесткости,
которое определяется как [1,4]

,
(2.7)

Используя этот
показатель, характеристику синхронного
двигателя (прямая 4 на рис. 2.3) можно
назвать абсолютно
жесткой (),
двигателя постоянного тока с независимым
возбуждением (прямая 1) –жесткой
(),
а с последовательным возбуждением
(кривая 2) –мягкой
().

Рис. 2.3. Естественные
механические характеристики
электродвигателя

Характеристика
асинхронного двигателя (кривая 3)
имеет переменную жесткость – на рабочем
участке жесткость отрицательна и
незначительна по модулю, в области
критического момента она равна нулю, а
при меньших скоростях – положительна
и невелика.

Характеристика 5
– абсолютно мягкая механическая
характеристика ().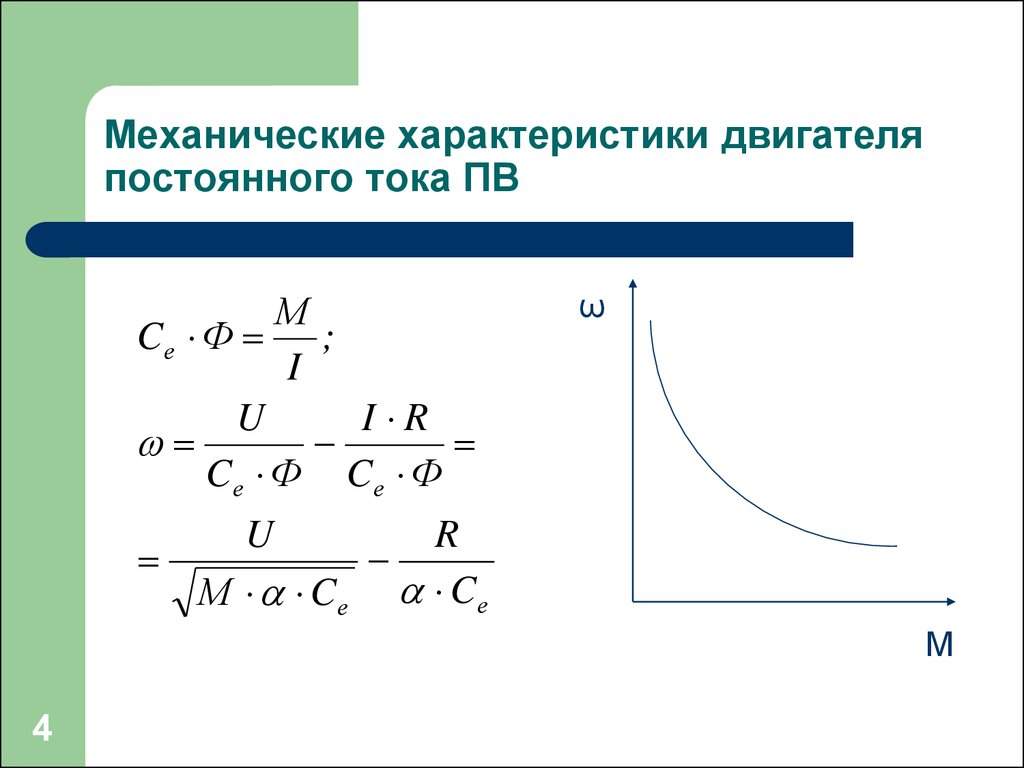
Момент двигателя с изменением угловой
скорости остается неизменным. Такой
характеристикой обладают, например,
двигатели постоянного тока независимого
возбуждения при питании их от источника
тока или при работе в замкнутых системах
электропривода в режиме стабилизации
тока якоря.

Понятие жесткости
может быть применено к механическим
характеристикам исполнительных органов.
Эти характеристики можно оценивать
жесткостью

.
(2.8)

Тогда для
характеристики 1 (рис.2.2)
,
для характеристик 2 и 3,
а для характеристики 4.

Характеристики электродвигателя — EEEGUIDE.COM

Машина и нагрузка являются двумя компонентами электромеханической системы преобразования энергии, и характеристики электродвигателя, как правило, играют преобладающую роль в рабочем поведении всей системы.

При выборе электродвигателя необходимо с достаточной степенью точности знать его характеристику скорости и крутящего момента, и, кроме того, она должна быть надлежащим образом согласована с характеристиками электродвигателя механической нагрузки.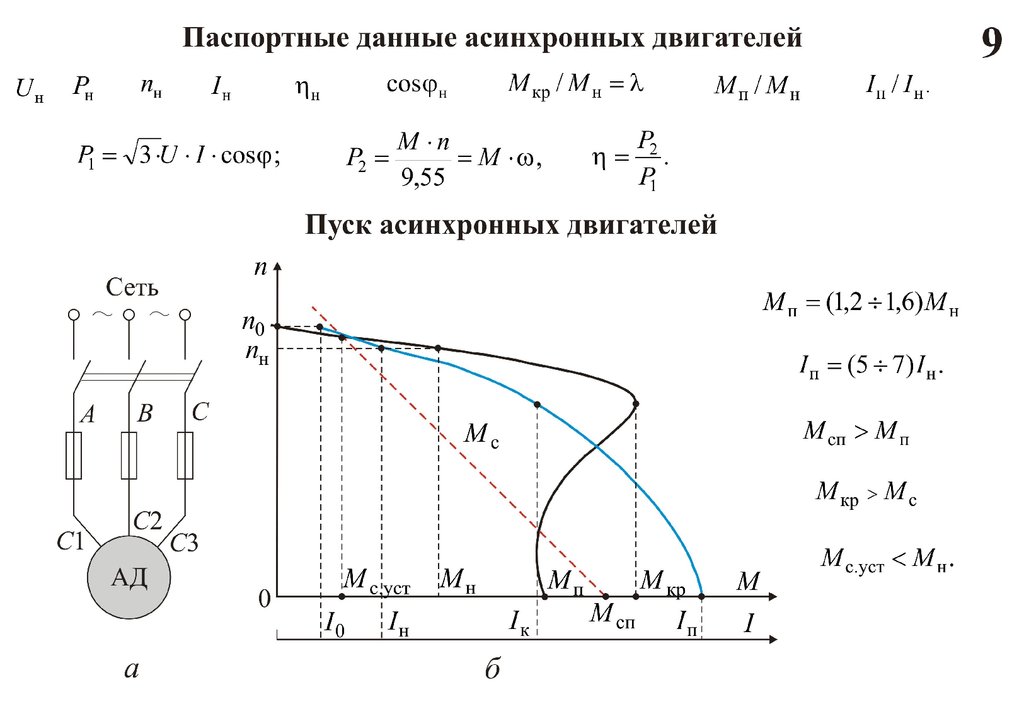 Рисунок 5.59показывает характеристику скорость-момент асинхронного двигателя с нагрузкой вентиляторного типа (момент нагрузки примерно пропорционален квадрату скорости). Установившаяся рабочая точка — это точка пересечения P двух характеристик электродвигателя. Как видно из рис. 5.59, это устойчивая рабочая точка, и система «машина-нагрузка» возвращается к ней при воздействии кратковременного возмущения.

Характеристики механической нагрузки можно классифицировать следующим образом:

1. Константа S скорость Нагрузки:

Они могут быть двух видов. Для некоторых нагрузок требуется приблизительно постоянная скорость при изменении крутящего момента нагрузки, например станки, гидравлические насосы, вентиляторы и т. д. Для некоторых специальных нагрузок, таких как приводы бумажной фабрики, требуется точно постоянная скорость, не зависящая от крутящего момента нагрузки.

2. Переменная S скорость вращения (или постоянная, кВт) Нагрузки:

Определенные нагрузки, такие как краны, подъемники и другие тяговые приводы, требуют высокого крутящего момента на низких скоростях и низкого крутящего момента на высокой скорости, так что кВт, требуемый от сети, остается практически постоянным. Эта природа сообщается нагрузке везде, где требуется ускорение тяжелой инерции.

3. Регулируемая S скорость нагрузки:

Нагрузки с постоянной регулируемой скоростью, как в некоторых станках, или с переменной регулируемой скоростью, как в кранах. Диапазон регулировки скорости в некоторых приводах может быть очень требовательным.

Характеристики электродвигателя можно классифицировать следующим образом:

1. Типы двигателей с постоянной скоростью :

Скорость остается неизменной независимо от крутящего момента, как показано на рис. 5.60(a). Этими характеристиками электродвигателя обладает синхронный двигатель.

2. Шунт Тип:

Здесь скорость двигателя падает на несколько процентов от холостого хода до полной нагрузки, как показано на рис. 5.60(b). Этой характеристикой обладают как асинхронный двигатель переменного тока (в рабочей зоне), так и шунтирующий двигатель постоянного тока.

3. Серия T тип:

Здесь скорость резко возрастает по мере уменьшения момента нагрузки, как показано на рис. 5.60(c). Этим типом характеристик электродвигателя обладает двигатель постоянного тока, идеально подходящий для нагрузок тягового типа.

Характеристики ускорения ( пуск ) и торможения ( торможение ) систем двигатель-нагрузка также имеют одинаковое значение в их промышленном применении. Система должна быть способна выйти из состояния покоя на полную скорость и быть в состоянии быть остановлена ​​за приемлемый период времени. Эти требования являются жесткими при пуске под нагрузкой и при быстром торможении и реверсе в некоторых специальных приложениях (приводы прокатных станов). Двигатель имеет три области работы — генерация , двигатель и торможение . В области генерации он возвращает тормозящую внутреннюю энергию обратно в электрическую сеть, не позволяя системе приобретать опасно высокие скорости — как при опускании подъемника или тяге вниз по уклону. В области торможения машина поглощает механическую энергию (а также некоторое количество электрической энергии) в виде потерь в ней, проявляющихся в виде тепла. Двигатель постоянного тока обладает превосходными пусковыми и тормозными характеристиками, намного превосходящими характеристики асинхронного двигателя переменного тока.

Как и в случае двигателей, рабочая точка системы генератор-нагрузка определяется характеристиками двух электродвигателей, как показано на рис. 5.61 для шунтирующего генератора постоянного тока. То же самое и с генераторами переменного тока (синхронными). В современных системах генераторы, работающие параллельно, питают нагрузки, распределенные по географически обширным территориям через линии электропередачи. Система должна удовлетворять требованиям практически постоянного напряжения, так как нагрузка изменяется в широком диапазоне. Независимый генератор, питающий один двигатель, используется в некоторых схемах управления скоростью, в которых может потребоваться, чтобы напряжение на клеммах изменялось особым образом.

Таким образом, видно, что среди особенностей, имеющих большое значение, есть характеристика скорости вращения двигателя и характеристика V-I генератора. Не менее важными могут быть пределы, в которых эти характеристики могут варьироваться.

Характеристики электродвигателей | Электротехника

ОБЪЯВЛЕНИЯ:

Для выбора надежного и экономичного двигателя необходимо хорошо знать условия эксплуатации.

Недостаточно просто указать выходную мощность в кВт и скорость, необходимо также знать следующие дополнительные данные:

(i) Крутящий момент на валу во время работы, пуска и при различных нагрузках.

РЕКЛАМА:

(ii) Ускоряющий момент и тормозной момент.

(iii) Частота переключения.

(iv) КПД двигателя при различных нагрузках.

(v) Другие рабочие требования.

РЕКЛАМА:

При изучении поведения двигателя, выбранного для конкретного приводимого агрегата, одной из первых задач является определение того, соответствует ли характеристика скорости и момента двигателя требованиям, предъявляемым характеристикой скорости и момента приводимого устройства. Поведение привода в течение переходного периода пуска, торможения или переключения скорости также зависит от того, как характеристики скорости-момента двигателя и приводимого агрегата изменяются в зависимости от скорости.

Поэтому необходимо изучить эти характеристики, чтобы иметь возможность правильно выбрать двигатель и получить экономичный привод.

1. Скоростно-моментные характеристики машин или механизмов:

Скоростно-моментная характеристика машины или механизма, определяемая соотношением ω = f(T _L ), определяется как зависимость между скоростью, с которой она работает, и развиваемым ею моментом сопротивления или нагрузки.

Разные виды механизмов и машин имеют разные скоростно-моментные характеристики. Однако можно сделать несколько общих выводов, если использовать следующее эмпирическое уравнение для скоростно-моментной характеристики некоторого ведомого узла промышленного оборудования.0003

РЕКЛАМА:

T _L =T ₀ + (T _rn -T ₀ ) (ω/ω _n ) ^x …(1. 3)

где Т _L — брутто-нагрузочный (или противодействующий) момент, развиваемый агрегатом при частоте вращения ω, к, Т ₀ — противодействующий момент, развиваемый агрегатом за счет трения в его движущихся частях, Т _рн — момент сопротивления, развиваемый агрегатом при движении с номинальной номинальной частотой вращения ω _n , а x – экспоненциальный коэффициент, характеризующий изменение момента покоя при изменении скорости.

Приведенное выше уравнение (1.3) позволяет условно разделить скоростно-моментные характеристики различных видов машин и механизмов на следующие категории:

РЕКЛАМА:

я. Нагрузки, требующие постоянного крутящего момента на всех скоростях:

Такая нагрузка создает для двигателя пассивный крутящий момент, практически не зависящий от скорости. Он также характеризуется требованием дополнительного крутящего момента при скорости, близкой к нулевой. Для этой характеристики x = 0 и момента нагрузки T _L не зависит от скорости. Скоростно-моментная характеристика для таких нагрузок показана вертикальной линией на рис. 1.4. Такими нагрузками являются сухое трение, краны при подъеме, лебедки, механизм подачи станков, поршневые насосы, работающие против постоянного напора, конвейеры, перекачивающие материал с постоянной массой в единицу времени. В силовых приложениях его обычно называют пусковым моментом, а в системах управления — трением (от трения прилипания).

Поскольку он меняет знак при изменении направления вращения, характеристика момента сухого трения является прерывистой, как показано на рис. 1.4.

ii. Нагрузки с линейно-возрастающей характеристикой:

РЕКЛАМА:

Такие характеристики скорость-момент, показанные прямой линией II на рис. 1.4, демонстрируют каландровые машины, вихретоковые тормоза, генераторы постоянного тока с независимым возбуждением, обеспечивающие фиксированные нагрузки омического сопротивления и жидкостное или вязкое трение. В этом случае x = 1 и момент нагрузки T _L повышается прямо пропорционально скорости.

III. Нагрузки с нелинейно-возрастающей (параболической) характеристикой:

Для такой характеристики x = 2 и момент нагрузки T _L пропорционален квадрату скорости. Такую характеристику иллюстрирует кривая III на рис. 1.4. Нагрузка со значительной силой ветра, предельным примером которой является вентилятор, имеет крутящий момент, который изменяется почти пропорционально квадрату скорости. Воздуходувки, центробежные насосы, гребные винты на кораблях или самолетах, водяные колеса, трение в трубах, напор насосов и т. д. также имеют тот же тип скоростно-крутящих характеристик.

iv. Нагрузки с нелинейной падающей (гиперболической) характеристикой (или нагрузкой постоянной мощности):

Для такой характеристики x = – 1 и момент нагрузки T _L обратно пропорционален скорости, а мощность, необходимая для привода данного агрегата, остается неизменной. Такую характеристику иллюстрирует кривая IV на рис. 1.4. К этой категории нагрузок относятся отдельные виды токарных, расточных, фрезерных и других видов металлорежущих станков, сталепрокатных моталок.

Перечисленные выше категории нагрузок не охватывают все случаи, с которыми можно столкнуться на практике, но дают хорошее представление о характеристиках, типичных для очень многих видов промышленного оборудования. На практике встречаются нагрузки, представляющие собой комбинацию этих основных видов нагрузок.

2. Характеристики момент-время нагрузки:

Возможно, изменение момента нагрузки во времени имеет такое же или большее значение при выборе двигателя. Это изменение в некоторых приложениях может быть периодическим и повторяющимся, один цикл изменения называется рабочим циклом.

Различные типы нагрузок с точки зрения характеристик момента нагрузки можно классифицировать следующим образом:

(i) Непрерывные, постоянные нагрузки, такие как бумагоделательные машины, центробежные насосы или вентиляторы, работающие в течение длительного времени в одних и тех же условиях.

(ii) Постоянные, переменные нагрузки, такие как подъемные лебедки, металлорежущие станки, конвейеры и т. д.

(iii) Пульсирующие нагрузки, такие как поршневые насосы и текстильные ткацкие станки и вообще все машины с коленчатым валом.

(iv) Ударная нагрузка, такая как прокатные станы, ножницы, прессы, кузнечные молоты и т. д. При таких нагрузках возникают кажущиеся, регулярные и повторяющиеся пики нагрузки или импульсы.

(v) Кратковременные нагрузки, такие как мотор-генераторы для зарядки аккумуляторов; серводвигатели, используемые для дистанционного управления зажимными штангами бурильных машин.

(vi) Кратковременные периодические нагрузки, такие как краны и подъемные механизмы, экскаваторы, роликовые поезда и т. д.

Некоторые машины (такие как шаровые мельницы) строго не относятся ни к одной из упомянутых выше категорий. Если бы такие нагрузки (шаровые мельницы, каменные дробилки и др.) характеризовались частыми ударами сравнительно небольших пиков, то правильнее было бы отнести их к разряду непрерывно-переменных нагрузок, а не к ударным нагрузкам. Иногда довольно сложно провести различие между пульсирующими нагрузками и ударными нагрузками, поскольку обе они носят периодический характер.

Один и тот же привод может быть представлен моментом нагрузки, изменяющимся либо со скоростью, либо со временем. Наиболее подходящим примером является нагрузка вентилятора, крутящий момент нагрузки которой T _L пропорционален квадрату скорости, также является постоянной постоянной нагрузкой.

3. Моменты нагрузки зависят от угла смещения вала:

Во всех машинах с коленчатым валом, таких как поршневые насосы и компрессоры, рамные пилы и т. д., момент нагрузки зависит от углового смещения вала или ротора двигателя. Для всех таких машин момент нагрузки Т _L можно разложить на две составляющие: одну постоянной величины T _av , а другую переменную T _L ‘, которая периодически изменяется по величине в зависимости от углового положения вала. Такие характеристики момента нагрузки можно для простоты представить в виде ряда Фурье в виде суммы колебаний основной и гармонической частот, т. е.

Где θ = ωt, ω — угловая скорость вала двигателя, приводящего в движение компрессор.

При изменении скорости происходят лишь небольшие отклонения от фиксированного значения скорости ω _a , поэтому перемещение можно представить как θ = (ω _a + Δω)t. Таким образом, переменная часть крутящего момента нагрузки может быть представлена ​​как:

Член r∆ωt, являющийся очень малым по величине, можно пренебречь. Таким образом, ограничиваясь малыми отклонениями по углу от положения равновесия, момент нагрузки, изменяющийся при угловом перемещении вала, может быть преобразован в момент, периодически меняющийся по отношению к валу. время.

4. Моменты нагрузки в зависимости от траектории или положения груза во время движения:

В статье 1.9.1. учитывались изменяющиеся со скоростью моменты нагрузки. Однако как в подъемных механизмах, так и в транспортных системах существуют моменты нагрузки, зависящие не только от скорости, но и от характера пути, проходимого грузом при его движении. Например, сопротивление движению поезда, движущегося вверх по уклону или совершающего поворот, зависит от величины уклона или радиуса кривизны пути соответственно.

Сила из-за градиента дается как-

F _г = 1000 Вт sin θ кг. …(1,6)

Где W — вес поезда в тоннах.

Но в железнодорожных работах уклон выражается как подъем в метрах на пути 100 м и обозначается как «уклон в процентах» (G%)

т. е. G = Sin θ x 100

или sin θ = G/100

Подставив sin θ = G/100 в уравнение (1.6), имеем-

Ф _г = 1000 Вт × G/100 = 10 WG кг. …(1,7)

Сила тяги, необходимая для преодоления сопротивления искривлению, определяется эмпирической формулой, приведенной ниже:

F _c = 700 000 Вт/Р кг …(1,8)

Где R — радиус кривизны в метрах.

В грузоподъемных механизмах, в которых не используются хвостовые канаты или уравновешивающие канаты (рис. 1.7), момент нагрузки создается не только весом ненагруженной или загруженной клети, но и грузоподъемными канатами или тросами, которые зависит от положения двух клеток.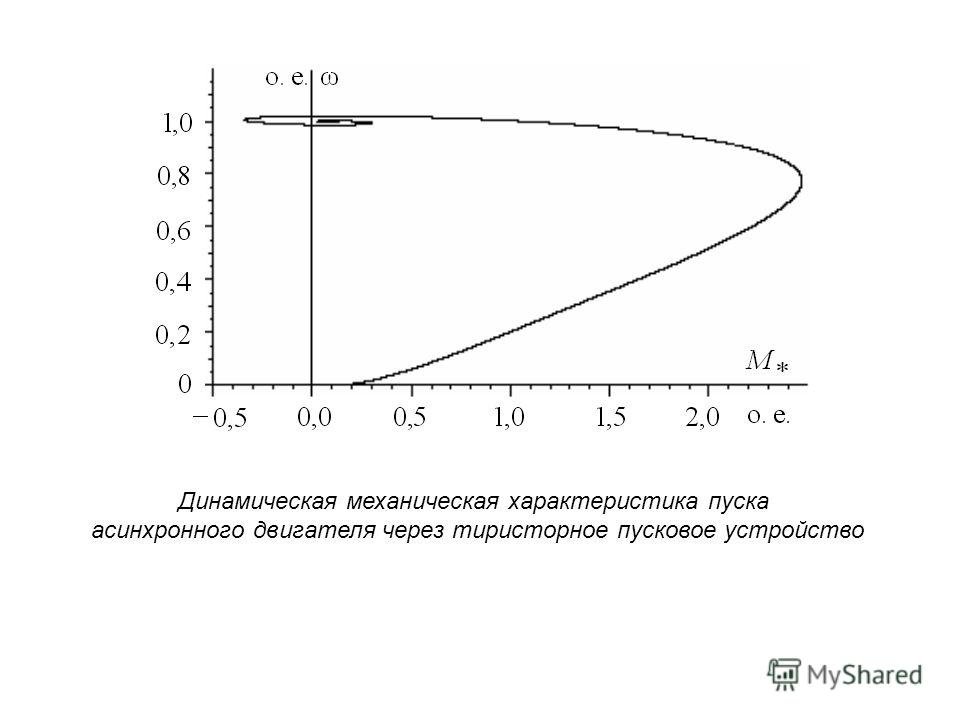 Когда клетка 1 находится в крайнем нижнем положении и должна быть поднята вверх, весь вес веревки также должен быть перемещен вверх.

Когда обе клетки находятся на одной высоте, вес поднимаемой веревки становится равным нулю, так как вес веревок с обеих сторон уравновешивает друг друга, имея одинаковую длину. Когда клетка 1 находится выше клетки 2, часть веса веревки действует таким образом, чтобы способствовать движению клетки 1 вверх. В конечном счете, когда клетка 1 достигает самого верхнего положения, весь вес веревка помогает движению вверх.

Сила сопротивления движению груза вверх, F _р в связи с различной массой каната в зависимости от положения груза принимается как-

Где, W _r — общий вес веревки в кг, h — желаемая максимальная высота, на которую клеть должна быть перемещена вверх, в метрах, а x — высота клетки в любом произвольном положении от дна наибольшая позиция в метрах.

При больших значениях h сила F _r в значительной степени влияет на работу привода, используемого в грузоподъемных механизмах, поскольку в такой ситуации вес каната может быть значительно больше веса поднимаемого груза снизу вверх. Если мы используем хвостовые канаты, как показано пунктирными линиями на рис. 1.7, вес соединительного каната может быть уравновешен, и движение клеток может быть почти плавным.

5. Скоростно-крутящие характеристики электродвигателя:

Моментно-скоростная характеристика двигателя определяется как отношение между скоростью, с которой он работает, и развиваемым им крутящим моментом, т. е. ω = f(T).

Практически все электродвигатели — параллельные, последовательные, составные двигатели постоянного тока, асинхронные двигатели с короткозамкнутым ротором и контактными кольцами, а также коллекторные двигатели переменного тока — имеют падающую скоростно-моментную характеристику, т. е. их скорость падает с увеличением момента нагрузки. Однако степень изменения скорости с изменением момента у различных типов двигателей различна, что характеризуется так называемой жесткостью их скоростно-моментной характеристики.

Скоростно-моментные характеристики электродвигателя можно разделить на три основные группы:

1. Абсолютно жесткая (плоская) характеристика скорости и крутящего момента:

Характеристика, не демонстрирующая изменения скорости при изменении момента нагрузки. С такой характеристикой работают синхронные двигатели (горизонтальная прямая I на рис. 1.8).

2. Жесткая характеристика скорости и крутящего момента:

Характеристика, показывающая скорость, которая незначительно падает с увеличением крутящего момента. Жесткую характеристику имеет двигатель постоянного тока с параллельным возбуждением, а также асинхронные двигатели в рабочей области скоростно-моментной характеристики (кривая II на рис. 1.8).

Характеристика скорость-момент асинхронного двигателя имеет «жесткость», которая различается в зависимости от того, какая точка характеристики принимается во внимание (рис. 1.9). Между точками максимального крутящего момента в режиме двигателя T _{max M} и максимального крутящего момента в режиме генератора T _{max G} асинхронная машина будет демонстрировать довольно жесткую характеристику.

3. Мягкая характеристика скорости:

Характеристика, показывающая значительное падение скорости при увеличении крутящего момента. Такой характеристикой обладает двигатель постоянного тока с последовательным возбуждением, особенно на маломоментном участке характеристики (кривая III на рис. 1.8). У таких двигателей степень жесткости характеристики меняется на всем протяжении кривой.

Двигатели постоянного тока со смешанной обмоткой, в зависимости от степени жесткости их скоростно-моментных характеристик, могут рассматриваться как двигатели с жесткими или мягкими характеристиками.

6. Совместная скоростно-моментная характеристика электродвигателя:

Совместная работа электродвигателя и приводимого им агрегата, когда скорость имеет установившееся значение, соответствует условию баланса между приводным моментом двигателя и моментом сопротивления, развиваемым приводимым агрегатом при заданной скорости. Когда сопротивление или момент нагрузки, развиваемый на валу двигателя приводным агрегатом, претерпевает некоторое изменение, скорость и крутящий момент, развиваемые двигателем, автоматически изменяются, чтобы восстановить стабильную работу при новом значении скорости и момента нагрузки.

В случае неэлектрических первичных двигателей (водяная турбина, паровая турбина или дизельный/бензиновый двигатель) баланс между моментом сопротивления и крутящим моментом достигается за счет использования регулятора соответствующего типа для управления притоком энергии к первичному двигателю путем увеличение или уменьшение расхода воды, пара или топлива. В электродвигателях роль автоматического регулятора выполняет ЭДС двигателя. Эта способность электродвигателей поддерживать равновесие системы привода при изменении момента сопротивления (нагрузки), развиваемого ведомым агрегатом, чрезвычайно ценна, поскольку этот момент очень часто в той или иной степени нестабилен.

Это можно проиллюстрировать с помощью рис. 1.10, который иллюстрирует характеристику скорость-момент (кривая III) параллельного двигателя постоянного тока и две характеристики I и II производственной единицы, приводимой в движение двигателем (например, конвейера). .

Характеристика I соответствует холостому состоянию конвейерной установки, а характеристика II соответствует более высокому уровню крутящего момента, развиваемого конвейером при обработке требуемого потока материала. Первоначально, в момент, когда конвейер работает на холостом ходу, момент двигателя Т = Т, а двигатель работает со скоростью ω ₁ . Как только конвейер начинает поддерживать поток материала, увеличение нагрузки на двигатель приводит к торможению двигателя и снижению его скорости. Это заставляет двигатель развивать меньшую ЭДС.

Следовательно, ток якоря увеличивается, и двигатель начинает развивать больший вращающий момент. Момент двигателя растет до тех пор, пока не будет достигнута точка равновесия, при которой развиваемый двигателем момент равен моменту сопротивления приводимого агрегата, т. е. T = T ₂ (где скорость ω ₂ ). Эта новая точка также является общей как для скоростной характеристики II конвейера, так и для скоростной характеристики III двигателя.

При изучении работы двигателя и агрегата, который он приводит, иногда удобно использовать так называемую совместную скоростную характеристику электропривода, представляющую собой кривую, представляющую собой алгебраическую сумму скоростно-моментной характеристики ведомого агрегата и приводного двигателя.

Скоростные характеристики вентилятора и приводного двигателя и совместная скоростная характеристика мотор-вентиляторного агрегата представлены кривыми I, II и III соответственно на рис. 1.11.

Когда агрегат достигает установившейся скорости ω _с , двигатель работает с крутящим моментом T = крутящий момент нагрузки, T _L . В этом случае крутящий момент, указанный в характеристике соединения, будет равен нулю. Работа агрегата на установившейся скорости ω _s в этом случае будет считаться устойчивой, так как любое увеличение скорости приводит к отрицательному изменению (падению) момента, а любое падение скорости – к положительному изменению (росту) в крутящем моменте.

Таким образом, кривая III

является примером совместной характеристики скорости и момента привода, который сможет работать стабильно. Если бы характеристика соединения имела форму кривой IV, работа не была бы стабильной, так как незначительное увеличение скорости приводит к ускорению, так как момент двигателя превышает момент нагрузки. С другой стороны, небольшое снижение скорости приводит к замедлению, поскольку крутящий момент двигателя становится меньше крутящего момента нагрузки.

Рассмотренные выше условия работы привода в установившемся режиме представляют собой условия, необходимые для статической устойчивости привода, и применимы только при медленном изменении скорости и крутящего момента. В периоды переходных (быстрых) изменений, связанных с динамической устойчивостью, условия устойчивости привода будут иными.

Обычно, когда электропривод проектируется под конкретный привод, заранее известна его скоростно-моментная характеристика. Таким образом, проблема достижения стабильной работы в установившемся режиме при известных скоростях и моментах нагрузки ведомого агрегата состоит в выборе двигателя, характеристика скорости и момента которого будет совместима с характеристикой ведомого агрегата.

Этого можно добиться, сначала выбрав подходящий тип двигателя, а затем соответствующим образом изменив электрические параметры его цепей. Иногда для обеспечения требуемых скоростно-моментных характеристик возникает необходимость создания специальных силовых и управляющих цепей для запутанной коммутации приводного двигателя и аппаратуры управления.

7. Динамика комбинации двигатель-нагрузка:

При поступательном движении активная или движущая сила F _d уравновешивается силой сопротивления F _r , развиваемой ведомой машиной, и силой инерции m dv/dt, возникающей из-за изменения скорости. Когда участвующее тело имеет массу m, выраженную в кг, и скорость v, выраженную в м/с, сила инерции, как и другие силы, будет выражаться в ньютонах (кг-м/с ² ).

Уравнение равновесия сил при поступательном движении тела можно соответственно записать в следующем виде:0003

Уравнение равновесия крутящего момента при поступательном движении тела можно, соответственно, записать в следующем виде:

Приведенное выше уравнение Из (1.11) видно, что развиваемый двигателем момент T _M уравновешивается противодействующим или нагрузочным моментом T _L , действующим на его вал, и инерционным или динамическим моментом J (dω/dt). В приведенных выше уравнениях. В уравнениях (1.10) и (1.11) предполагается, что масса m участвующих тел и полярный момент инерции J привода остаются постоянными, что справедливо для большого числа промышленных машин и механизмов. В некоторых приводах возникает необходимость иметь дело с переменным полярным моментом инерции, как в случае кривошипно-шатунных приводов.

Из анализа уравнения. (1.11) можно определить различные состояния, в которых может оставаться электропривод, вызывающий вращательный двигатель:

1. При T _M > T _L , dω/dt > 0, т. е. привод будет разгоняться, в частности, набирая скорость до номинальной.

2. При T _M < T _L , dω/dt < 0, т.е. привод будет тормозиться и, в частности, останавливаться. Торможение, очевидно, будет происходить и при отрицательных значениях момента двигателя. Двигатель развивает отрицательный крутящий момент, когда он переходит в режим торможения.

3. Когда T _M = T _L , dω/dt = 0, т. е. привод будет работать с установившейся скоростью.

Приведенные выше утверждения, а именно, что когда T _M > T _L привод ускоряется, а когда T _M < T _L привод замедляется, действительны только тогда, когда возникает нагрузка или сдерживающий момент T _L быть пассивным крутящим моментом. Обратное может произойти при активных нагрузках крутящего момента. Например, при включении двигателя для подъема лебедки при ее опускании под собственным весом до изменения направления вращения происходит торможение привода при Т _М > Т _Л . В случае, если T _M < T _L в описанной выше ситуации, когда двигатель был включен для подъема лебедки, нагрузка будет продолжать опускаться, и двигатель будет ускоряться, а не замедляться.

Инерция или динамический момент J (dω/dt) появляются только в переходных режимах, т. е. при изменении скорости привода. При разгоне привода момент инерции противодействует движению привода, а при торможении поддерживает движение привода. Момент инерции как по величине, так и по знаку определяется как алгебраическая сумма момента двигателя и моментов сопротивления и нагрузки.

Ввиду вышеизложенного знаки для Т _М и Т _Л в уравнении. (1.11), соответствующие двигательному режиму ведущей машины и пассивному моменту нагрузки (или активному тормозному моменту) соответственно. В общем виде уравнение крутящего момента можно записать как

Выбор знака, который будет помещен перед каждым из крутящих моментов в приведенном выше уравнении. (1.12) зависит от условий эксплуатации и характера сопротивления или момента нагрузки. Уравнение движения привода позволяет определить зависимость момента, тока, скорости и пути от времени работы в переходных режимах. Все крутящие моменты в уравнении движения должны быть отнесены к некоторому заданному элементу системы. Чаще всего к валу двигателя относят как момент нагрузки, так и динамический момент.

Пример:

Двигатель соединен с нагрузкой, имеющей следующие характеристики:

я. Двигатель: T _м = 15 – 0,5ω _м

ii. Нагрузка: Т _л = 0,5ω ² _м

Найдите стабильную рабочую точку для этой комбинации.

Решение:

Стабильная работа будет достигнута, когда-

Т _м = Т _л

или 15 – 0,5ω _м = 0,5ω _м ²

или ω _м ² + ω _м – 30 = 0

или ω _м = 5 или -6

Отбрасывая минус, имеем-

ω _м = 5 и T = 12,5

Итак, стабильная рабочая точка (12.5, 5) Ответ.

Приведенные крутящие моменты нагрузки и моменты инерции:

Двигатель обычно приводит в движение промышленную машину через некоторую систему трансмиссии, отдельные части которой работают с разными скоростями. При проведении практических расчетов возникает необходимость отнесения моментов и масс отдельных деталей к какому-либо удобному элементу, например к определенному валу.

Моменты нагрузки могут передаваться от одного вала к другому на основе баланса мощности системы. При этом учитывают потери мощности в промежуточных звеньях передачи путем введения соответствующих значений КПД.

Пусть скорость вала двигателя ω _M , а скорость вала данной промышленной машины ω _L .

На основании равенства потоков мощности имеем-

или момент нагрузки относительно вала двигателя,

, где T _L — крутящий момент нагрузки, η _T — КПД трансмиссии, а i — передаточное число, равное ω _M /ω _L .

При наличии нескольких ступеней передачи между приводным двигателем и ведомой машиной, как схематично показано на рис. 1.12, с передаточными числами i ₁ , i ₂ ,…, i _n и соответствующими коэффициентами полезного действия трансмиссии η _Т1 , η _T2 …, η _Tn , крутящий момент нагрузки относительно вала двигателя определяется как-

Моменты инерции относятся к данному валу на том основании, что общее количество кинетической энергии, запасенной в движущихся частях и относящейся к данному валу, остается неизменным.