Содержание
Основные характеристики передач
Передаточным отношением называется отношение угловой скорости ведущего звена к угловой скорости ведомого звена. Обозначается буквой i. Передаточное отношение может быть больше, меньше или равно единице.
Передаточным числом передачи называется отношение большей угловой скорости к меньшей. Обозначается буквой и.
Передаточное число не может быть меньше единицы.
В дальнейшем в целях унификации обозначений передаточные отношения и передаточные числа всех передач будем обозначать u, при необходимости с двойным индексом, соответствующим индексам звеньев передачи, т.е., передаточное отношение
.
Принято в расчетных формулах на прочность деталей машин всегда использовать передаточные числа,т. е. u ³ 1 .
Передачи, у которых угловая скорость ведомого звена меньше угловой скорости ведущего, называются понижающими или редукторами; противном случае передачи называются повышающими или мультипликаторами.
Механические передачи бывают одноступенчатыми и многоступенчатыми. Передаточное отношение ряда последовательно соединенных передач равно произведению их передаточных отношений.Например, для двухступенчатого редуктора
,
где и12 и34 – передаточные отношения соответственно первой ступени с шестерней 1 и колесом 2 и второй ступени с шестерней 3 и колесом 4.
Передачи выполняют либо с постоянным, либо с переменным передаточным отношением, причем изменение передаточного отношения может быть ступенчатым или бесступенчатым. Ступенчатое регулирование передаточного отношения осуществляется, например, коробками скоростей металлорежущих станков, автомобилей, тракторов. Механизм для плавного изменения передаточного отношения называется бесступенчатой передачей или вариатором.
2. Мощность на входе и выходе передачи
Обозначается соответственно Р1 и Р2 .
Из теоретической механики известно, что мощность Р при вращательном движении Р = Тw.
3. Частота вращения входного и выходного звеньев
Обозначается соответственно п1 и п2.
4. Коэффициент полезного действия
Отношение мощности Р2 на ведомом валу передачи к мощности Р1 на ведущем валу называется механическим коэффициентом полезного действия (КПД) и обозначается
h = Р2 / Р1.
Механический КПД характеризует механические потери в передаче; для различных передач КПД находится в пределах от 0,25 до 0,98.
В многоступенчатых передачах (при последовательном соединении ступеней) общий КПД определяется как произведение КПД каждой ступени в отдельности:
h =h1h2…hn.
Иногда КПД передачи определяют как произведение КПД отдельных элементов этой передачи. Например, для одноступенчатого зубчатого редуктора общий КПД
.
где h3 , hn , hp– коэффициенты, характеризующие потери энергии соответственно в зацеплении колес, в одной паре подшипников, на перемешивание и разбрызгивание масла в корпусе редуктора.
Наиболее часто встречающиеся расчетные зависимости:
1. Для любого звена вращающий момент и окружная сила связаны зависимостью
T = FtD/2,
откуда окружная сила:
Ft= 2T/D .
Согласно третьему закону Ньютона, окружные силы ведущего и ведомого звеньев равны (но противоположно направлены), следовательно, вращающие моменты на ведущем и ведомом валах будут различны и пропорциональны диаметрам соответствующих звеньев.
2. Из теоретической механики известно, что мощность Р при вращательном движении определяется как Р = Тw.
3. Так как Р1 = hР1,то Т2w2 = hТ1w1,
откуда
Т2 = hТ1w1/w2 = hТ1u.
Если потери в передаче невелики, то ими пренебрегают и принимают
Т2 = Т1и.
4. Вращающий момент Т (Н ∙м) на любом валу можно вычислить по мощности Р (кВт) и частоте вращения п (мин –1):
Т‘ = 9550 P/n.
Подтверждается это следующими рассуждениями. Мощность, как известно, есть работа в единицу времени. Поэтому мощность Р, кВт, при линейном перемещении (рис. 1.3, а) можно представить как произведение силы тяги F (Н) на линейную скорость v (м/с):
P = Fv/1000.
При вращательном движении мощность удобно выразить через вращающий момент Т, Н×м, и частоту вращения (мин –1).
При вращательном движении (рис. 1.3, б)
F = 1000 Т/r,
где r – радиус, мм, на котором приложена окружная сила, создающая момент, и
v = 2πrn/(60∙103).
Поэтому
Р = [1000 Т/r] ∙[2 πrп/(660∙103)]/1000 =Tn/9550,
откуда
Т‘ = 9550 P/n.
а б
Рис. 1.3. Схема движения: а – линейного; б – вращательного
Дата добавления: 2016-08-06; просмотров: 3694; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Передачи. Передачи фрикционные
|
КАТЕГОРИИ: Археология
ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы.
|
⇐ ПредыдущаяСтр 4 из 6Следующая ⇒
3 Зубчатые передачи. Геометрия и кинематика прямозубых передач
⇐ Предыдущая123456Следующая ⇒ Читайте также: Как правильно слушать собеседника Типичные ошибки при выполнении бросков в баскетболе Принятие христианства на Руси и его значение Средства массовой информации США | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 993; Нарушение авторского права страницы; Мы поможем в написании вашей работы!
infopedia.
|
8.4: Передаточное отношение
Передачи используются не только для передачи мощности, но также для обеспечения возможности настройки механического преимущества для механизма. Как обсуждалось во введении к данному блоку, в некоторых случаях электромотор сам по себе обладает достаточной мощностью для выполнения конкретной задачи, но выходные характеристики электромотора не соответствуют требованиям. Электромотор, который вращается ОЧЕНЬ быстро, но при очень малом крутящем моменте , не подходит для подъема тяжелого груза. В таких случаях возникает необходимость использования передаточного отношения для изменения выходных характеристик и создания баланса крутящего момента и скорости.
Представьте себе велосипед: велосипедист обладает ограниченной мощностью, и хочет обеспечить максимальное использование этой мощности в любой момент времени.
Путем изменения механического преимущества изменяется скорость движения. Мощность представляет собой количество проделанной работы в единицу времени. Чем больше количество работы. тем ниже скорость ее выполнения.
Пример 8.1
В примере 8.1 показано, что если на стороне входа рычаг сместится на 1 метр, на стороне выхода рычаг сместится на 4 метра. Разница пропорциональна соотношению между длинами рычагов.
Длина на выходе / Длина на входе = 8 / 2 = 4
Интересно то, что оба расстояния преодолеваются за одно и то же время. Давайте представим, что смещение рычага на входе на 1 метр происходит за 1 секунду, так что скорость движения на входе составляет 1 метр в секунду. В то же время, на выходе смещение на 4 метра также происходит за 1 секунду, так что скорость движения здесь составляет 8 метров в секунду. Скорость на выходе БОЛЬШЕ скорости на входе за счет соотношения между длинами рычагов.
Пример 8.2
В примере 8.2 представлена та же система, что и в примере 8. 1, но теперь на вход действует сила, равная 4 ньютонам. Какова равнодействующая сила на выходе?
1, но теперь на вход действует сила, равная 4 ньютонам. Какова равнодействующая сила на выходе?
Прежде всего, необходимо рассчитать приложенный момент в центре вращения, вызванный входной силой, с помощью формул из Блока 7:
Крутящий момент = Сила х Расстояние от центра гравитации = 4 Н х 2 м = 8 Н-м
Далее, необходимо рассчитать равнодействующую силу на выходе:
Сила = Крутящий момент / Расстояние = 8 Н-м / 8 м = 1 ньютон
Глядя на эти два примера, мы видим, что если система смещается на 1 метр под действием входной силы, равной 4 ньютона, то на выходе она сместится на 4 метра под действием силы, равной 1 ньютон. При меньшей силе рычаг смещается быстрее!
Мы можем видеть, как механическое преимущество (выраженное в форме рычагов) может быть использовано для управления входной силой в целях получения требуемого выхода. Передачи работают по тому же принципу.
Цилиндрическая прямозубая шестерня по сути представляет собой серию рычагов. Чем больше диаметр шестерни, тем длиннее рычаг.
Пример 8.3
Как видно из примера 8.3, результатом крутящего момента, приложенного к первой шестерне, является линейная сила, возникающая на кончиках ее зубьев. Эта же сила воздействует на кончики зубьев шестерни, с которой зацепляется первая шестерня, заставляя вторую вращаться по действием крутящего момента. Диаметры шестерен становятся длиной рычагов, при этом изменение крутящего момента равносильно соотношению диаметров. Если малые шестерни приводят в движение больше шестерни, крутящий момент увеличивается. Если большие шестерни приводят в движение малые шестерни, крутящий момент уменьшается.
Пример 8.4
В примере 8.4, если входная 36-зубая шестерня поворачивается на расстояние одного зуба (d = ширина 1 зуба), это означает, что она поворачивается на 1/36-ю своего полного оборота (а1 = 360 / 36 = 10 градусов). Поворачиваясь, она приводит в движение 60-зубую шестерню, заставляя последнюю смещаться также на 1 зуб. Тем не менее, для 60-зубой шестерни это означает смещение всего лишь на 1/60-ю полного оборота (а2 = 360 / 60 = 6 градусов).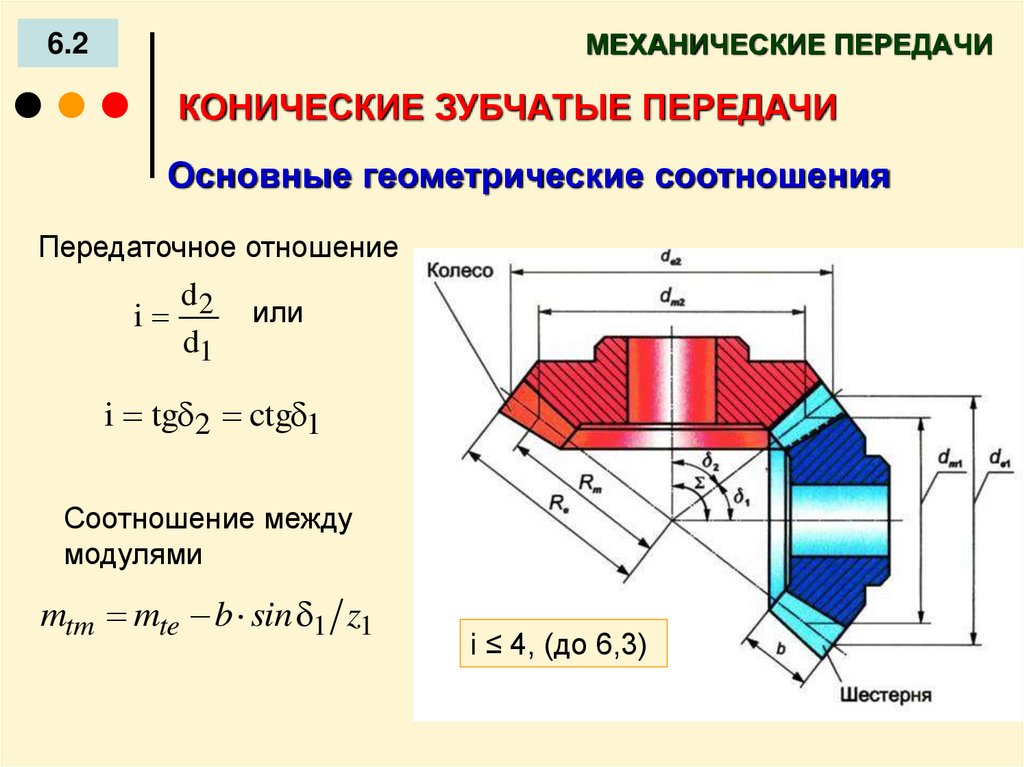
Когда малая шестерня проходит определенное расстояние в заданный интервал времени, большая шестерня при этом проходить меньшее расстояние. Это означает, что большая шестерня вращается медленнее малой. Этот принцип работает в обоих направлениях. Если малые шестерни приводят в движение больше шестерни, скорость понижается. Если большие шестерни приводят в движение малые шестерни, скорость повышается.
Из примеров 8.1 — 8.4 видно, что отношение между размерами двух зацепляющихся между собой шестерен пропорционально изменению крутящего момента и скорости между ними. Это называется передаточным числом.
Как обсуждалось выше, количество зубьев шестерни прямо пропорционально ее диаметру, поэтому для расчета передаточного отношения вместо диаметра можно просто считать зубья.
Передаточное отношение выражается как (зубья ведущей шестерни) : (зубья ведомой шестерни), поэтому представленная выше пара шестерен может быть описана как 12:60 (или 36 к 60).
Передаточное число рассчитывается по формуле (зубья ведомой шестерни) / (зубья ведущей шестерни)
Поэтому передаточное число = зубья ведомой шестерни / зубья ведущей шестерни = 60/36 = 1,67
Как обсуждалось выше, передаточное отношение выражается как (зубья ведущей шестерни) : (зубья ведомой шестерни), так что пара шестерен, представленная выше, может быть выражена как 12:60 (или 12 к 60).
Передаточное число рассчитывается по формуле (зубья ведомой шестерни) / (зубья ведущей шестерни)
Поэтому передаточное число = Зубья ведомой шестерни / Зубья ведущей шестерни = 60/12 = 5
Глядя на пример, представленный выше…
Предельный перегрузочный момент второго вала может быть рассчитан по формуле:
Выходной момент = Входной момент х Передаточное число
Выходной момент = 1,5 Н-м х 5 = 7,5 Н-м
Свободная скорость второго вала может быть рассчитана по формуле:
Выходная скорость = Входная скорость / Передаточное число = 100 об/мин / 5 = 20 об/мин
Второй вал, таким образом, вращается со свободной скоростью 20 об/мин, при этом предельный перегрузочный момент равен 7,5 Н-м. При понижении скорости крутящий момент увеличивается.
Для второго примера расчеты могут быть произведены тем же способом.
Передаточное число = Зубья ведомой шестерни / Зубья ведущей шестерни = 12/60 = 0,2
Выходной момент = Входной момент х Передаточное число = 1,5 Н-м х 0,2 = 0,3 Н-м
Выходная скорость = Входная скорость / Передаточное число = 100 об/мин / 0,2 = 500 об/мин
Второй вал, таким образом, вращается со свободной скоростью 500 об/мин, при этом предельный перегрузочный момент равен 0,3 Н-м. При повышении скорости крутящий момент уменьшается.
При повышении скорости крутящий момент уменьшается.
Шаги для расчета передаточного отношения – Блог CLR
Использование шестерен во множестве машин и устройств в настоящее время требует, чтобы они использовались с максимальной эффективностью, чтобы получить максимальную отдачу. из своих преимуществ.
Одним из ключевых понятий для их адекватного использования является передаточное число (r t ). Правильный выбор передаточного числа необходим для того, чтобы:
- Шестерня могла выдерживать больший крутящий момент , сводя к минимуму ошибки
- Движение может быть создано таким образом, что крутящий момент мотор-шестерни преодолевает инерцию шестерни.
Ниже мы познакомимся с необходимыми формулами для расчета передаточного числа , и что вы должны иметь в виду для этого расчета.
Передаточное число необходимо для того, чтобы имело место движение и чтобы шестерня могла выдерживать крутящий момент без ошибок
Что такое передача движения?
Передаточное отношение в трансмиссии — это соотношение между скоростями вращения двух зацепляющихся шестерен.
Поскольку каждая шестерня имеет разный диаметр, каждая из осей вращается с разной скоростью, когда они обе зацеплены. Изменение передаточного отношения эквивалентно изменению применяемого крутящего момента .
Передаточное число вычисляется путем деления выходной скорости на входную скорость (i= Ws/We) или путем деления числа зубьев ведущей шестерни на число зубьев ведомой шестерни (i= Ze/ Зс).
i = Ws/We
i = Ze/Zs
Преимущества зубчатых передач
Зубчатые передачи обладают рядом преимуществ по сравнению с другими трансмиссиями. Во-первых, они обеспечивают высокую производительность при передаче усилий и перемещений при длительном сроке службы и высокой надежности.
Во-первых, они обеспечивают высокую производительность при передаче усилий и перемещений при длительном сроке службы и высокой надежности.
Но что выделяет их, так это колоссальная точность передаточного отношения, а это значит, что они могут быть используется в точном машиностроении .
Передаточные числа в зубчатых передачах очень точные, что делает эти передачи идеальными для прецизионного оборудования
В отличие от других механизмов, таких как цепи или шкивы, их размер мал , а это значит, что они могут быть установлены как в обоих малые и большие машины и помещения, а также в труднодоступных местах.
Кроме того, их простота обслуживания делает редукторную трансмиссию одной из самых распространенных систем в основных отраслях промышленности, таких как автомобилестроение.
Параметры для проектирования зубчатой передачи
При проектировании зубчатой передачи необходимо иметь в виду следующие параметры:
Закон зацепления
Закон зацепления определяет положение, при котором два зубца всегда будут пересекать точку O , если это позволяет его профиль.
Эта точка O должна располагаться на линии, соединяющей центр вращения одной из шестерен и центр вращения другой .
Кроме того, радиусы шага и расстояния между точкой O и соответствующими центрами должны совпадать.
Передаточное число
Передаточное число ( r t ) — это отношение скоростей вращения двух сопряженных шестерен .
Более конкретно, это частное входной и выходной скоростей ( r t = ω s / ω e ).
Система может вызвать снижение , если передаточное число меньше 1, или умножение , если оно больше 1. о редукторах
Коэффициент контакта
Коэффициент контакта ( ε ) измеряет среднее число зубьев в контакте всегда.
Наилучшее передаточное отношение должно быть больше 1,2, чтобы обеспечить возможность передачи высоких нагрузок , обеспечить жесткость трансмиссии и обеспечить бесшумную и равномерную работу.
Как рассчитать передаточное число
Рассчитать передаточное число можно несколькими способами. Например:
Расчет передаточного числа конических зубчатых колес
При обращении к конических зубчатых колес нужно учитывать, что оно будет эквивалентно количеству зубьев ведущей шестерни, деленному на число зубьев ведомой шестерни. ( RT= Z1 / Z2 ).
Вас может заинтересовать: Расчет передач: повысьте эффективность ваших трансмиссий.
Расчет передаточного числа зубчатой передачи
В случае зубчатой передачи с двумя шестернями нам необходимо выполнить следующие шаги:
- Подсчитать количество зубьев . Сначала нам нужно будет посчитать количество зубьев ведущей шестерни и количество зубьев ведомой шестерни.

- Разделите количество зубьев ведомой шестерни на количество зубьев ведущей шестерни . Полученное число будет числом раз, которое ведомая меньшая шестерня должна повернуть, чтобы большая совершила один полный оборот.
Передаточное число будет равно количеству зубьев ведущей шестерни, деленному на количество зубьев ведомой шестерни.
В случае зубчатой передачи с более чем двумя передачами нам потребуется выполнить следующие шаги:
- Определите, какая шестерня является ведущей, а какая ведомой, и разделите количество зубьев первой и второй . Промежуточная шестерня никак не повлияет на передаточное число зубчатой передачи.
- Выполните те же шаги , что и для определения передаточного отношения двухступенчатой зубчатой передачи.
Существует множество способов расчета передаточного числа в зависимости от того, являются ли передачи коническими или зубчатыми передачами с двумя или более передачами и т.
д.
Расчет передаточного числа шестерен и цепи
Этот тип передачи образован двумя шестернями и цепью из шарнирных звеньев . В нем шестерни вращаются в одном направлении.
Используется для передачи движения между удаленными параллельными валами .
Передаточное число является результатом деления числа зубьев ведущей шестерни на число зубьев ведомой шестерни .
Вам нужна помощь в расчете передаточного числа ваших зубчатых передач? Не стесняйтесь обращаться к нам, и мы поможем вам запустить ваш проект и рассчитать ваши параметры.
Что такое передаточное число в трансмиссии?
Содержание
Введение
Мы часто слышим эти термины, когда говорим об автомобиле. Автомобиль, который должен ездить по бездорожью, то есть внедорожник 4 * 4, требует хорошего крутящего момента, а с другой стороны, автомобиль, который должен развивать высокую скорость, то есть суперкары, требует хорошей мощности или скорости. Теперь возникает вопрос, как автомобиль дает эти крутящий момент и выходную скорость? Как автомобиль получает разные крутящий момент и скорость, когда это необходимо? Разберемся, кто за них отвечает.
Теперь возникает вопрос, как автомобиль дает эти крутящий момент и выходную скорость? Как автомобиль получает разные крутящий момент и скорость, когда это необходимо? Разберемся, кто за них отвечает.
Передаточное число – это термин, относящийся к коробке передач автомобильного транспортного средства, который относится к отношению числа зубьев выбранной пары шестерен (находящихся в постоянном зацеплении) выходного вала, т. е. главного вала, к числу зубьев входной вал, т. е. промежуточный вал, который при выборе передает требуемый крутящий момент или скорость главной передаче транспортного средства.
Когда мы говорим о механической коробке передач, передаточное число первой передачи, т. е. наибольшая шестерня выходного вала и наименьшая шестерня промежуточного вала, дает высокий крутящий момент, а передаточное число высшей передачи дает высокую скорость конечному выходному валу транспортного средства.
Когда речь идет об автоматической или планетарной трансмиссии, соотношение заблокированной кольцевой шестерни к планетарной и солнечной шестерням дает высокие передаточные числа крутящего момента к главной передаче транспортного средства и передаточное отношение заблокированной солнечной шестерни к планетарной и кольцевой шестерням придает автомобилю высокие передаточные числа.
Зачем нам нужно передаточное число?
Поскольку мы знаем, что сгорание воздушно-топливной смеси вызывает движение поршня, который, в свою очередь, приводит во вращение коленчатый вал двигателя внутреннего сгорания, что является конечной мощностью двигателя, и если мы используем эту мощность непосредственно как конечную мощность для вращения колеса, чем колеса транспортного средства, вращались бы с тем же крутящим моментом и скоростью, обеспечиваемой коленчатым валом, что оказалось недостаточным для решения задач, возникающих в дорожных условиях. Цилиндровый двигатель не может обеспечить достаточный крутящий момент, который может преодолеть собственный вес автомобиля и вызвать движение автомобиля из исходного состояния.
Итак, нам нужен набор передаточных чисел, чтобы-
- Крутящий момент и скорость, обеспечиваемые двигателем, можно было умножить, чтобы автомобиль мог преодолевать дорожные трудности.
- При однократном приводе транспортного средства требуются различные соотношения крутящего момента и скорости, которые двигатель не может обеспечить, поскольку он может обеспечить ограниченный крутящий момент и скорость.

- Экономия топлива является основным фактором, поскольку, когда нагрузка на двигатель увеличивается из-за его собственного веса или других условий нагрузки, двигатель пытается сжечь все больше и больше топлива, чтобы удовлетворить потребности автомобиля.
- Для изменения направления движения автомобиля, что невозможно при прямом выходном валу двигателя?
- Для передачи мощности между двумя разными валами.
Читайте также:
- Типы зубчатых колес — Цилиндрическое, косозубое, коническое и т.д.
- Что такое порядок работы 4- и 6-цилиндрового двигателя?
- Различные типы двигателей
Расчет передаточного отношения
Передаточное отношение между двумя шестернями в зацеплении можно рассчитать, используя следующие произвольные числа шестерен в зацеплении.0005
- Число зубьев (N) – Передаточное отношение пары шестерен в зацеплении определяется отношением числа зубьев ведомой шестерни к числу зубьев ведущей шестерни или отношением числа зубьев ведущей шестерни.
 выходная передача к входной передаче.
выходная передача к входной передаче.
- Диаметр шестерен (D)- Передаточное отношение пары шестерен, находящихся в зацеплении, можно рассчитать по отношению диаметра ведомой или выходной шестерни к диаметру ведомой или входная шестерня.
- Угловая скорость ( ω ) – Передаточное отношение зубчатых колес в зацеплении может быть рассчитано отношением угловой скорости ведущей или входной шестерни к угловой скорости ведомой или выходная шестерня.
- Крутящий момент (T) – Передаточное число шестерен, находящихся в зацеплении, также можно рассчитать по отношению крутящего момента ведомой или выходной шестерни к крутящему моменту ведущей или входной шестерни
Пример –
Рассмотрим пару шестерней A и B, находящихся в зацеплении, шестерня A является ведущей, а шестерня B ведомой, и обе шестерни имеют следующие произвольные значения:
Шестерня A —
Количество зубьев- 30
Диаметр передачи- 20 см
Англосная скорость- 67 см/с
Крутящий момент- 10 кг-CM
Шехоба B-
Количество зубье шестерни- 27 см
Угловая скорость- 50 см/с
Крутящий момент- 13,5 кг-см
Тогда передаточное число G можно рассчитать, используя все произвольные значения-
(i) Количество зубьев-
Передаточное число (G) = 40/30
= 1,33 ~ 1,35
(ii) Диаметр передач-
передаточный численность (G) = 27/20
= 1,35
(III) угловая скорость-
. Г) = 67/50
Г) = 67/50
= 1,34 ~ 1,35
(iv) крутящий момент передач
Персиженное значение = 13,5/10
= 1,35
Применение
. 2 вала через шестерни, из которых одна ведущая, а другая ведомая. Размеры (количество зубьев, диаметр шестерни) шестерен выбираются в соответствии с требуемой мощностью.
Некоторые области применения передаточного числа:
- Система трансмиссии легкового автомобиля для получения требуемых соотношений крутящего момента и скорости.
- Машина для производства сока сахарного тростника для передачи высокого крутящего момента, необходимого для измельчения тростника для получения сока.
- Токарные станки для достижения разного крутящего момента и скорости, необходимых для выполнения различных работ.
- Машины, оснащенные электродвигателями в качестве источника энергии для передачи крутящего момента или скорости между различными частями.
Передаточные числа — MAE3
w3.org/1999/xhtml» cellspacing=»0″>Д-р Натан Делсон
В конструкции машин часто необходимо учитывать желаемую выходную энергию и передачу мощности. Примеры элементов силовой передачи включают в себя: шестерни, фрикционные приводы, зубчатые ремни, плоские ремни, рычаги и винтовые передачи. Силовая передача часто включает передаточное число или механическое преимущество. Передаточное число может увеличить выходной крутящий момент или выходную скорость механизма, но не то и другое одновременно. Классический пример — шестерни на велосипеде. Можно использовать пониженную передачу, которая позволяет легко крутить педали в гору, но с меньшей скоростью велосипеда. И наоборот, высокая передача обеспечивает более высокую скорость велосипеда, но для поворота кривошипа педали требуется больший крутящий момент. Этот компромисс в основном связан с законом сохранения энергии и является ключевой концепцией механического преимущества.
Механическое преимущество относится к увеличению крутящего момента или силы, достигаемой механизмом за счет элемента передачи мощности. Для вращающихся устройств термин «передаточное число» используется для определения механического преимущества. Термин «механическое преимущество» используется для описания компонентов, включающих трансляцию. Приведенный ниже анализ показывает, как можно рассчитать передаточное число и механическое преимущество компонента силовой передачи. Уравнения энергии и мощности Закон сохранения энергии гласит, что при выходном движении никогда нельзя получить больше энергии, чем обеспечивает источник энергии. Действительно, при передаче энергии всегда есть некоторая потеря энергии. Уровень потерь энергии может варьироваться от 5 % для плоскоременной передачи до 80 % для многоступенчатой зубчатой передачи (также могут встречаться более высокие и более низкие уровни).
Перед анализом сначала определим некоторые обозначения:
P => Мощность E => Энергия Вт => Работа f => Сила 04 расстояние поступательного движения θ => угол вращательного движения (в радианах) v => скорость поступательного движения ω => угловая скорость (в радианах в секунду) δ => изменение Pd => Диаметр шага n => количество зубьев на шестерне nrev => количество оборотов
Для базового анализа передаточных отношений мы сначала пренебрегаем потерями на трение, а затем учитываем их влияние отдельно. При таком предположении мы можем установить мощность на входе равной мощности на выходе.
Pin = Pout
Мощность определяется как изменение энергии, деленное на изменение во времени.
P = δE/δt
В механизме энергия передается посредством механической работы. Для поступательного движения работа определяется как:
Работа = сила X движение (где сила и движение параллельны друг другу) W = f δd
Соответствующее определение работы для вращательного движения дается формулой :
Работа = Крутящий момент X Вращательное движение Вт = τ δθ
В силовой передаче работа является источником изменения энергии, и, таким образом:
P = δE/δt = W/δt
Подставляя определение работы при вращении в приведенное выше уравнение и учитывая, что скорость вращения определяется как ω=δθ/δt, передача мощности во вращающемся устройстве равна
Аналогично, для поступательного движения передача мощности определяется по формуле: δt = f δd/δt
Ниже показана зубчатая передача с входной шестерней слева и выходной шестерней справа. Как показано, входная шестерня вращается против часовой стрелки с угловой скоростью ωin, а выходная шестерня вращается по часовой стрелке с угловой скоростью ωout. Входной крутящий момент τin прикладывается двигателем к входной шестерне, а противоположный выходной крутящий момент τout прикладывается машиной к выходной шестерне. Радиус зубчатых колес показан на делительной окружности шестерни, которая находится между верхней и нижней частью зуба шестерни и представляет собой радиус, при котором происходит контакт между двумя шестернями.
Разработка форм зубчатых колес была значительно оптимизирована для снижения потерь на трение, обеспечения плавной передачи мощности и снижения шума. Более подробное описание зубчатых колес и рекомендаций по проектированию предоставлено Boston Gear на сайте www.
Зубья шестерни имеют одинаковую форму как на входной, так и на выходной шестерне, поэтому на большей шестерне больше зубьев. Шаговое расстояние Pd — это расстояние между шестернями. Таким образом, количество зубьев на шестерне, n, умноженное на шаг, равно длине окружности шестерни. Соответственно, PD NIN = 2 π RIN PD NOUT = 2 π Route NIN/ NOUT = RIN/ RUTH ПАРЬЯ ПРОВОДА. Квазистатический анализ (предполагается, что шестерни вращаются с постоянной скоростью, поэтому моментами ускорения можно пренебречь) Потери на трение не учитываются (трение может быть значительным, и его следует учитывать отдельно!) Зубья шестерни входят в зацепление друг с другом (без перескакивания шестерен!)
Поскольку потерь на трение нет, входную и выходную мощности можно положить равными друг другу как: Pin = τin ωin Pout = τout ωout τin ωin = τout ωout • Теперь нам нужно рассмотреть относительную скорость двух шестерен, которая определяется зацеплением зубьев.
количество зубьев, входящих в зацепление = nrevin 2 π rin / Pd
Применение того же уравнения к выходной шестерне и установка количества зацепляемых зубьев равным друг другу дает:
nrevout 2 nrevout 2 / Pd = nrevin 2 π rin / Pd
Приведенное выше уравнение упрощается до:
обеих шестерен в радианах, что дает:
rin δθвх = rout δθвых • Если угол поворота разделить на время δt, то получим отношения угловых скоростей в радианах в секунду
Альтернативная интерпретация состоит в том, что угловая скорость в точке зацепления одинакова для обеих шестерен. • rin ωin = rout ωout • И мы видим, что два предыдущих уравнения идентичны.
Поскольку радиус шестерни пропорционален количеству зубьев, соотношение скоростей может быть выражено количеством зубьев на входной и выходной шестернях. Просто подставьте в вышеприведенное уравнение, что nPd=2πr для обеих шестерен, чтобы получить: ωвых / ωвх = nin / nout
Теперь мы можем объединить уравнение мощности с уравнением скорости, чтобы получить отношение входного и выходного крутящих моментов. : τin ωin = τout ωout (уравнение мощности) • τout / τin = ωin / ωout • τout / τin = rout / rin (подразделение в velocity intaintion) 905 905 905 905 905 905 905 905 905 905 905 905 905 91 9011. . 9015 901. 9015 901. 9015 905 905 905 901. Входная передача меньше, чем выходная передача: Основные уравнения для пары передач: τin ωin = τout ONUT (Power Equality) ω -ωout (Power Equality) ω -ωout (Power Equality) ω -ωout (Power Equality) ωout (Power Equality) ωout (Power Equalith rout (отношение скоростей через радиусы)
ωвых / ωвх = nin / nout (отношение скоростей в терминах количества зубьев)
τвых / τвх = rout / rin (отношение крутящего момента в терминах радиусов) / τвх = 5 9043 nin (соотношение крутящего момента с точки зрения количества зубьев)
Передаточное отношение определяется как входная скорость относительно выходной скорости.  |



 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления
 4 Что называется передаточным отношением любой передачи?
4 Что называется передаточным отношением любой передачи?
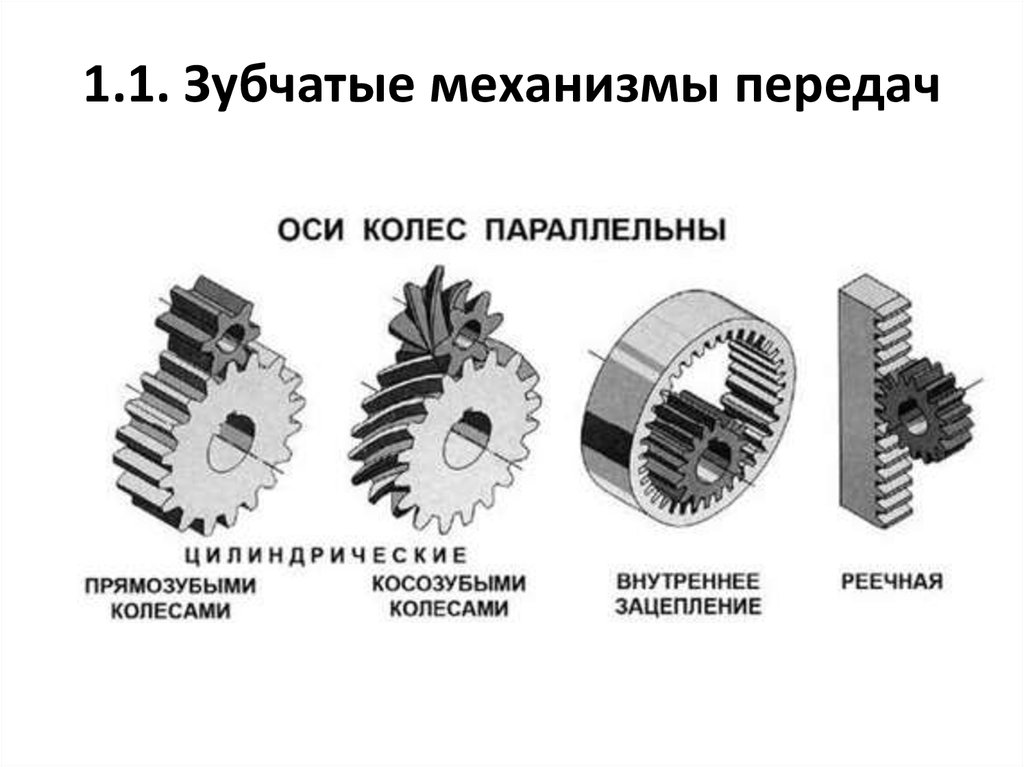 7 Каково передаточное отношение i второй цилиндрической ступени коническо-цилиндрического редуктора, если угловые скорости на входе и выходе редуктора соответственно ω1 = 155 рад/с и ω3 = =31 рад/с, а числа зубьев конической пары z1 = 20 и z2 = 50?
7 Каково передаточное отношение i второй цилиндрической ступени коническо-цилиндрического редуктора, если угловые скорости на входе и выходе редуктора соответственно ω1 = 155 рад/с и ω3 = =31 рад/с, а числа зубьев конической пары z1 = 20 и z2 = 50?
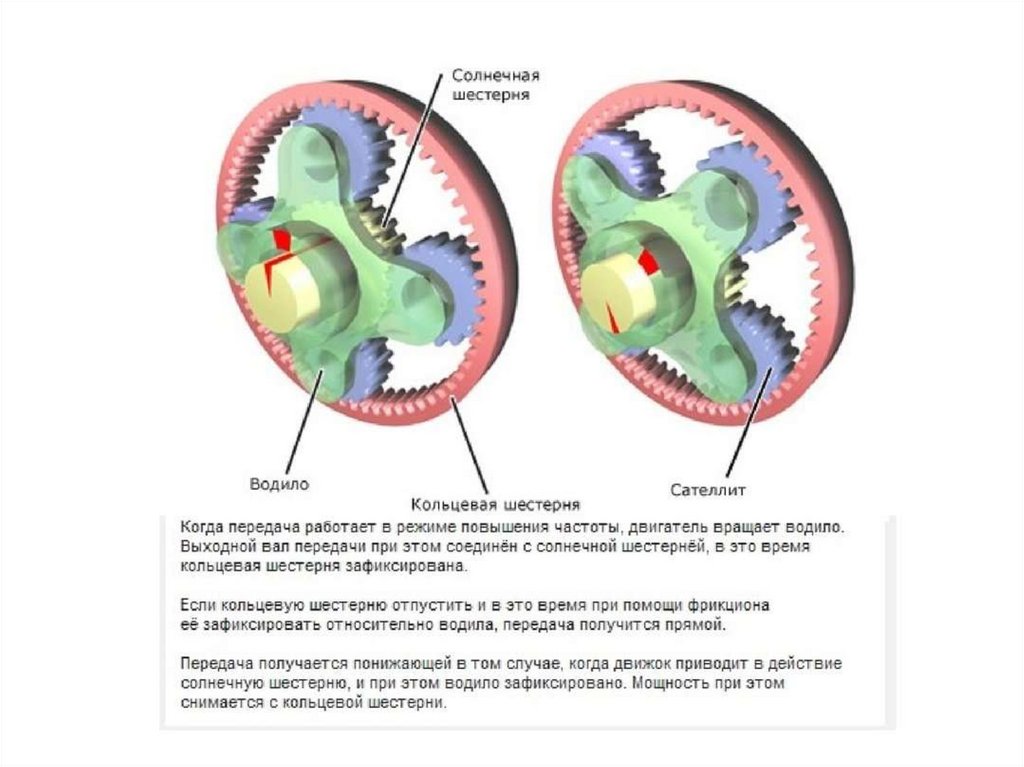 9 Как изменится мощность на выходном валу коническо-цилиндрического редуктора, если числа зубьев колёс z2 и z3 увеличить в 1.5 раза, а мощность на входе оставить без изменения?
9 Как изменится мощность на выходном валу коническо-цилиндрического редуктора, если числа зубьев колёс z2 и z3 увеличить в 1.5 раза, а мощность на входе оставить без изменения?
 12 По какой формуле вычисляется максимальная окружная сила Ftфрикционной передачи, если коэффициент трения между катками f, а пружина сжимает катки с усилением Q.?
12 По какой формуле вычисляется максимальная окружная сила Ftфрикционной передачи, если коэффициент трения между катками f, а пружина сжимает катки с усилением Q.?
 15 Укажите основную причину неконкурентоспособности фрикционных передач в сравнении с передачами зубчатыми
15 Укажите основную причину неконкурентоспособности фрикционных передач в сравнении с передачами зубчатыми
 18 Какой зависимостью выражается диапазон регулирования Д изображенного ниже дискового вариатора?
18 Какой зависимостью выражается диапазон регулирования Д изображенного ниже дискового вариатора?
 3 Что называется полюсом зацепления?
3 Что называется полюсом зацепления?
 6 Отношение какой величины к числу называют модулем m прямозубой цилиндрической передачи?
6 Отношение какой величины к числу называют модулем m прямозубой цилиндрической передачи?
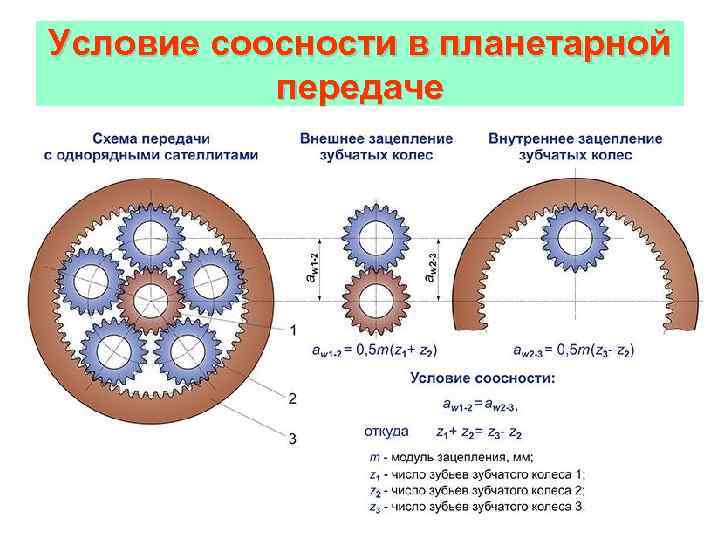 9 Каково межосевое расстояние изображённой на схеме зубчатой передачи, если числа её зубьев z1 = 30 и z2 = 60, а модуль m = = 2 мм?
9 Каково межосевое расстояние изображённой на схеме зубчатой передачи, если числа её зубьев z1 = 30 и z2 = 60, а модуль m = = 2 мм?
 12 У стандартной прямозубой передачи, представленной на нижеследующей схеме, непосредственным измерением определены межосевое расстояние aw и внешний габаритный размер А.
12 У стандартной прямозубой передачи, представленной на нижеследующей схеме, непосредственным измерением определены межосевое расстояние aw и внешний габаритный размер А.
 15 Какой формулой выражается передаточное отношение i1-2 прямозубой ортогональной конической передачи, если углы делительных конусов колеса и шестерни обозначены δ2 и δ1 остальные обозначения см. на иллюстрации?
15 Какой формулой выражается передаточное отношение i1-2 прямозубой ортогональной конической передачи, если углы делительных конусов колеса и шестерни обозначены δ2 и δ1 остальные обозначения см. на иллюстрации?
 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.006 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.006 с.)
 д.
д. 
 выходная передача к входной передаче.
выходная передача к входной передаче. С данным источником энергии вы можете достичь либо высокой скорости, либо высокой силы/крутящего момента, но не того и другого одновременно.
С данным источником энергии вы можете достичь либо высокой скорости, либо высокой силы/крутящего момента, но не того и другого одновременно.

 Для целей этого анализа мы предполагаем, что входная шестерня может быть прикреплена к двигателю, а выходная шестерня прикреплена к валу машины, которая выполняет желаемую функцию.
Для целей этого анализа мы предполагаем, что входная шестерня может быть прикреплена к двигателю, а выходная шестерня прикреплена к валу машины, которая выполняет желаемую функцию. bostongear.com. Местные копии предоставлены Boston Gear Engineering Information и Каталогом прямозубых зубчатых колес.
bostongear.com. Местные копии предоставлены Boston Gear Engineering Information и Каталогом прямозубых зубчатых колес. Поскольку зубья входят в зацепление, мы знаем, что одинаковое количество зубьев должно зацепляться с обеими шестернями. За каждый оборот ведущей шестерни через площадь зацепления проходит следующее число зубьев, где nrevin — число оборотов ведущей шестерни:
Поскольку зубья входят в зацепление, мы знаем, что одинаковое количество зубьев должно зацепляться с обеими шестернями. За каждый оборот ведущей шестерни через площадь зацепления проходит следующее число зубьев, где nrevin — число оборотов ведущей шестерни: Поскольку скорость точки на вращающемся объекте определяется как rω. Равенство скоростей в точке сетки определяется как:
Поскольку скорость точки на вращающемся объекте определяется как rω. Равенство скоростей в точке сетки определяется как: 9015 905 901. 9015 905 901. 9015
9015 905 901. 9015 905 901. 9015