Содержание
Число зубьев шестерни таблица
Модуль зубьев зубчатого колеса
Зубчатая передача впервые была освоена человеком в глубокой древности. Имя изобретателя осталось скрыто во тьме веков. Первоначально зубчатые передачи имели по шесть зубьев — отсюда и пошло название «шестерня». За многие тысячелетия технического прогресса передача многократно усовершенствовалась, и сегодня они применяются практически в любом транспортном средстве от велосипеда до космического корабля и подводной лодки. Используются они также в любом станке и механизме, больше всего шестеренок используется в механических часах.
Что такое модуль зубчатого колеса
Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров
- диаметр;
- число зубьев;
- шаг;
- высота зубца;
- и некоторые другие.

Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.
В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.
Для расчета этого параметра применяют следующие формулы:
Параметры зубчатых колес
Модуль зубчатого колеса можно рассчитать и следующим образом:
где h — высота зубца.
где De — диаметр окружности выступов,а z — число зубьев.
Что же такое модуль шестерни?
это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.
Формула расчета параметров прямозубой передачи
Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.
Длина начальной окружности равна π×D, где D — ее диаметр.
Расчет модуля зубчатого колеса
Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:
проведя преобразование, получим:
Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.
размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:
выполнив преобразование, находим:
Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов De получается равным
где h’- высота головки.
Высоту головки приравнивают к m:
Проведя математические преобразования с подстановкой, получим:
Диаметр окружности впадин Di соответствует De за вычетом двух высот основания зубца:
где h“- высота ножки зубца.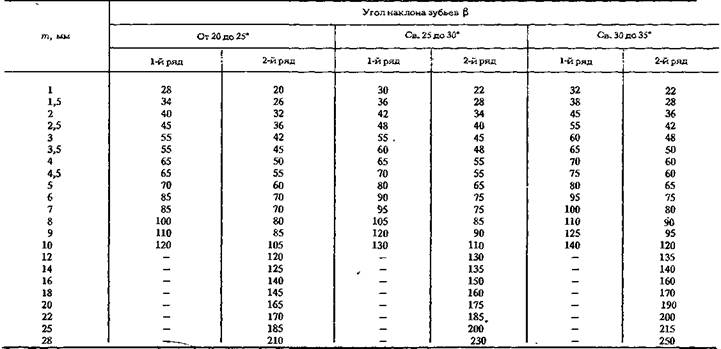
Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:
Устройство зубчатого колеса
Выполнив подстановку в правой части равенства, имеем:
что соответствует формуле:
и если выполнить подстановку, то получим:
Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.
Следующий важный размер, толщину зубца s принимают приблизительно равной:
- для отлитых зубцов: 1,53m:
- для выполненных путем фрезерования-1,57m, или 0,5×t
Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины sв, получаем формулы для ширины впадины
- для отлитых зубцов: sв=πm-1,53m=1,61m:
- для выполненных путем фрезерования- sв= πm-1,57m = 1,57m
Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:
- усилия, прикладываемые к детали при эксплуатации;
- конфигурация деталей, взаимодействующих с ней.

Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.
Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.
Исходные данные и замеры
На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.
Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.
Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.
Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.
Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.
Результаты расчетов
Для более крупных потребуются измерения и вычисления.
Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:
Последовательность действий следующая:
- измерить диаметр штангенциркулем;
- сосчитать зубцы;
- разделить диаметр на z+2;
- округлить результат до ближайшего целого числа.
Зубец колеса и его параметры
Данный метод подходит как для прямозубых колес, так и для косозубых.
Расчет параметров колеса и шестерни косозубой передачи
Расчетные формулы для важнейших характеристик шестерни косозубой передачи совпадают с формулами для прямозубой. Существенные различия возникают лишь при прочностных расчетах.
Существенные различия возникают лишь при прочностных расчетах.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Источник: stankiexpert.ru
Виды зубчатых колес, шестерен
Цилиндрические шестерни
Поперечный профиль зуба
Обычно шестерни имеют профиль зубьев с эвольвентной боковой формой. Так как эвольвентное зацепление имеет ряд преимуществ перед остальными: форма этих зубьев соответствует условиям их прочности, зубья легко изготовить и обработать, шестерни не чувствительны к точности установки. Тем не менее, существуют зубчатые передачи с циклоидальной формой профиля зубьев, а так же с шестернями с круговой формой профиля зубьев, например — передача Новикова. Помимо этого, применяется несимметричный профиль зуба, например в храповых механизмах.
Параметры эвольвентной шестерни:
Модуль шестерни (m) – это основной параметр, который определяется из прочностного расчёта зубчатых передач. Чем сильнее нагрузка на передачу, тем больше значение модуля, единица измерения модуля – миллиметры.
Чем сильнее нагрузка на передачу, тем больше значение модуля, единица измерения модуля – миллиметры.
Расчет модуля шестерни:
d — диаметр делительной окружности
z — число зубьев шестерни
da — диаметр окружности вершин темной шестерни
db — диаметр основной окружности — эвольвенты
df — диаметр окружности впадин темной шестерни
В машиностроении приняты стандартные значения модуля зубчатого колеса для удобства изготовления и замены зубчатых колёс, представляющие собой числа от 1 до 50.
Высота головки зуба — haP и высота ножки зуба — hfP в случае, так называемого, «нулевого» зубчатого колеса соотносятся с модулем m следующим образом: haP = m; hfP = 1,2 m, то есть:
Отсюда получаем, что высота зуба h = 2,2m
Так же можно практически вычислить модуль шестерни, при этом, не имея всех данных для определения модуля, по следующей формуле:
Продольная линия зуба
Прямозубые шестерни
Прямозубые шестерни — самый применяемый тип зубчатых колёс. Зубья расположены в радиальных плоскостях, линия контакта зубьев пары зубчатых колес параллельна оси вращения, как и оси обеих зубчатых колес (шестеренок) располагаются строго параллельно.
Зубья расположены в радиальных плоскостях, линия контакта зубьев пары зубчатых колес параллельна оси вращения, как и оси обеих зубчатых колес (шестеренок) располагаются строго параллельно.
Косозубые шестерни
Косозубые шестерни – это модернизированная версия прямозубых шестерен. Зубья, в таком случае, расположены под углом к оси вращения. Зацепление зубьев этих шестерен происходит тише и плавнее, чем у прямозубых. Они применяются либо в малошумных механизмах, либо в тех которые требуют передачи большого крутящего момента на больших скоростях. К недостаткам этого типа шестерен можно отнести: увеличенную площадь соприкосновения зубьев, что вызывает значительное трение и нагрев деталей, а вследствие: потеря мощности и дополнительное использование смазочных материалов; так же механическая сила, направленная вдоль оси шестеренки, вынуждает применять упорные подшипники для установки вала.
Шевронные колёса
Шевронные шестерни решают проблему механической осевой силы, которая возникает в случае применения косозубых колес, так как зубья шевронных (елочных) колёс изготавливаются в виде буквы «V» (или же они образовываются стыковкой двух косозубых колёс со встречным расположением зубьев). Осевые механические силы обеих половин шевронной шестерни взаимно компенсируются, поэтому нет нет необходимости использования упорных подшипников для установки валов. Шевронная передача является самоустанавливающейся в осевом направлении, в следствии чего, в редукторах с шевронными колесами один из валов устанавливают на подшипниках с короткими цилиндрическими роликами — плавающих опорах.
Осевые механические силы обеих половин шевронной шестерни взаимно компенсируются, поэтому нет нет необходимости использования упорных подшипников для установки валов. Шевронная передача является самоустанавливающейся в осевом направлении, в следствии чего, в редукторах с шевронными колесами один из валов устанавливают на подшипниках с короткими цилиндрическими роликами — плавающих опорах.
Шестерни с внутренним зацеплением
Шестерни такого типа имеют зубья, нарезанные с внутренней стороны. При их использовании происходит одностороннее вращение ведущей и ведомой шестерен. В данной зубчатой передаче меньше затрат на трение, а значит выше КПД. Применяются зубчатые колеса с внутренним зацеплением в ограниченных по габаритам механизмах, в планетарных передачах, в шестеренных насосах, в приводе башни танка.
Винтовые шестерни
Шестерни имеют форму цилиндра с расположенными на нем зубьями по винтовой линии. Эти шестеренки используются на непересекающихся валах, которые располагаются перпендикулярно друг друга, угол между ними 90°.
Секторные шестерни
Секторная шестерня – это часть (сектор) шестерни любого типа, она позволяет сэкономить в габаритах полноценной шестерни, так как применяется в передачах, где не требуется вращение этого зубчатого колеса (шестеренки) на полный оборот.
Шестерни с круговыми зубьями
Шестерни этого типа имеют линию зубьев в виде окружности радиуса, за счет этого контакт в передаче происходит в одной точке на линии зацепления, которая располагается параллельно осям шестерен. Передачи с круговыми зубьями «Передача Новикова» имеет лучшие ходовые качества, чем косозубые – высокую плавность хода и бесшумность, высокую нагрузочную способность зацепления, но при одинаковых условиях их ресурс работы и КПД ниже, к прочему изготовление этих шестерен значительно сложнее. Поэтому применение таких шестеренок ограниченно.
Конические шестерни
Конические шестерни имеют различные виды, отличаются они по форме линий зубьев, с прямыми, с криволинейными, с тангенциальными, с круговыми зубьями. Применяются конические зубчатые передачи в машинах для движения механизма, где требуется передать вращение с одного вала на другой, оси которых пересекаются. Например, в автомобильных дифференциалах, для передачи момента от двигателя к колесам.
Применяются конические зубчатые передачи в машинах для движения механизма, где требуется передать вращение с одного вала на другой, оси которых пересекаются. Например, в автомобильных дифференциалах, для передачи момента от двигателя к колесам.
Зубчатая рейка
Зубчатая рейка является частью зубчатого колеса с бесконечным радиусом делительной окружности. Вследствие этого ее окружности представляют собой прямые параллельные линии. Эвольвентный профиль зубчатой рейки тоже имеет прямолинейное очертание. Это свойство эвольвенты является наиболее важным при изготовлении зубчатых колёс. Передачу с применением зубчатой планки (рейки) называют — реечная передача (кремальера), она используется для преобразования вращательного движения в поступательное и наоборот. Состоит передача из зубчатой рейки и прямозубого зубчатого колеса (шестеренки). Применяется такая передача в зубчатой железной дороге.
Звездочка
Шестерня-звезда — это основная деталь цепной передачи, которая используется совместно с гибким элементом — цепью для передачи механической энергии.
Коронная шестерня
Коронная шестерня – это особый тип шестерен, их зубья находятся на боковой поверхности. Такая шестерня работает, как правило, в паре с прямозубой или с барабаном (цевочное колесо), состоящим из стержней. Такая передача используется в башенных часах.
Источник: shesterenka.com.ua
Число зубьев шестерни таблица
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
ПЕРЕДАЧИ ЗУБЧАТЫЕ КОНИЧЕСКИЕ С ПРЯМЫМИ ЗУБЬЯМИ
Straight bevel gear pairs.
Calculation of geometry
Дата введения 1975-01-01
Постановлением Государственного комитета стандартов Совета Министров СССР от 28 марта 1974 г. N 718 срок действия установлен с 01.01.75
ПЕРЕИЗДАНИЕ. Май 1990 г.
Настоящий стандарт распространяется на зубчатые конические передачи с прямыми пропорционально понижающимися зубьями внешнего зацепления с внешним окружным модулем более 1 мм, с межосевыми углами от 10 до 170° и с прямолинейным профилем исходного контура, зубчатые колеса которых нарезаются методом обкатки зубострогальными резцами и парными зуборезными головками, а также методом копирования по шаблону.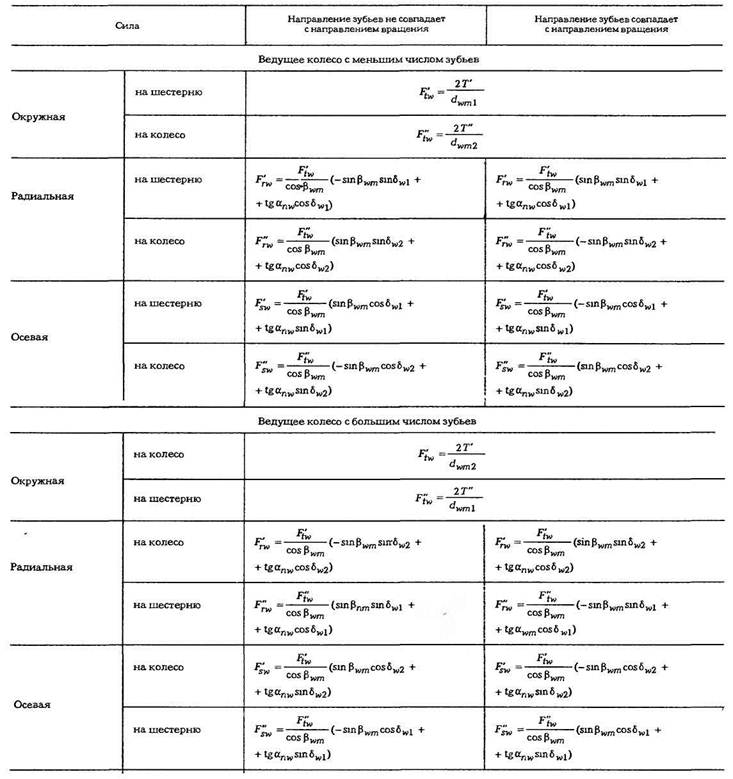
Стандарт устанавливает метод расчета геометрических параметров зубчатой передачи, а также геометрических параметров зубчатых колес, приводимых на рабочих чертежах.
Стандарт не распространяется на конические зубчатые передачи с прямыми зубьями кругового профиля.
1. ОБЩИЕ ПОЛОЖЕНИЯ
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Принципиальная схема расчета геометрии приведена на чертеже.
1.2. Термины и обозначения, примененные в настоящем стандарте, соответствуют ГОСТ 16530-83 и ГОСТ 19325-73.
1.3. Наименования параметров, приводимых на рабочих чертежах зубчатых колес, выделены в таблицах настоящего стандарта полужирным шрифтом.
1.4. При отсутствии в обозначениях параметров индексов «1» и «2», относящихся соответственно к шестерне и колесу, имеется в виду любое зубчатое колесо передачи.
1.5. При отсутствии дополнительных указаний везде, где упоминается профиль зуба, имеется в виду внешний торцовый профиль.
1.6. Расчетом определяются номинальные размеры зубчатой передачи и зубчатых колес.
1.7. Вычисления по формулам стандарта и приложений к нему, за исключением случаев специально отмеченных, должны производиться со следующей точностью:
линейные размеры — с точностью не ниже 0,0001 мм;
отвлеченные величины — с точностью не ниже 0,0001;
угловые размеры — с точностью не ниже 1′;
тригонометрические величины — с точностью не ниже 0,00001;
передаточные числа, числа зубьев эквивалентных зубчатых колес, коэффициенты смещения и коэффициенты изменения толщины зуба — с точностью не ниже 0,01.
1.8. Пример расчета приведен в справочном приложении 4.
Источник: docs.cntd.ru
Геометрический расчёт зубчатых колёс
В результате геометрического расчета прямозубых цилиндрических колес (без смещения) определим следующие их параметры (рисунок 2): межосевое расстояние , модуль зубьев m, числа зубьев шестерни z1 и колеса z2, делительные диаметры шестерни и колеса , диаметры окружности вершин и , диаметры окружности впадин и , ширина венцов колеса и шестерни .
Рисунок 2 — Параметры цилиндрических колес
1) Рассчитаем предварительно межосевое расстояние, выбрав коэффициент ширины колеса =0,4; полагая, что пара расположена симметрично опорам:
,
где Ка – коэффициент, для прямозубой передачи Ка = 495 МПа 1/3 ;
u – передаточное число редуктора, u = ……;
T2 – вращающий момент на валу колеса, T2 = …. Н·м;
[σH] — допускаемое контактное напряжение, [σH] = 491 МПа;
– коэффициент ширины венца зубчатого колеса, рекомендуемые значения = 0,4;
– коэффициент неравномерности распределения нагрузки по ширине венца зубчатого колеса, определяемый в зависимости от расположения колеса по отношению к опорам и коэффициента ширины колеса =1,3
.
2) Найдем предварительно делительный диаметр шестерни
.
3) Зададим число зубьев шестерни, учитывая, что zmin =17:
4) Подберем из стандарта величину модуля зубьев, для этого предварительно рассчитаем
Из ГОСТ 9563-60 (стандартный ряд m: 1; 1,25; 1,5; 1,75; 2; 2,25; 2,5; 2,75; 3; 3,5; 4; 4,5; 5; 5,5; 6; 7)
мм.
5) Найдем число зубьев сопряженного колеса
,
6) Рассчитаем геометрические параметры проектируемой передачи при
модуле зубьев m=2,25 мм,
числах зубьев шестерни z1=17 и колеса z2=71:
Фактическое передаточное число
Отклонение от заданного передаточного числа
Диаметры делительных окружностей
,
,
(если надо задать в п.3) большее число z1 (18, 19, 20 – 30))
Диаметры окружностей вершин
,
,
Диаметры окружностей впадин
,
,
Ширину венца шестерни назначаем больше ширины венца колеса с целью облегчения сборки механизма.
мм,
мм,
В таблице 2 приведены основные параметры передачи.
Окружная скорость вращения колёс в полюсе зацепления (на делительном диаметре)
.
По рекомендациям (табл. 2.5 в [3]) принимаем степень точности изготовления зубчатых колес 9-В (ГОСТ 1643-81), что означает 9-ю степень кинематической точности, плавности и контакта зубьев; вид сопряжения В (нормальный боковой зазор).
Таблица 2 — Основные параметры передачи
| Наименование параметра и размерность | Обозначение | Значение |
| Момент на ведомом валу, | Т2 | |
| Частота вращения вала, – ведущего – ведомого | n1 n2 | |
| Межосевое расстояние, мм | aw | |
| Число зубьев – шестерни – колеса | z1 z2 | |
| Модуль зубьев нормальный, мм | mn | |
| Передаточное число | u | |
| Материал колес, термообработка | cталь 45, улучшение | |
| Твердость рабочих поверхностей зубьев – шестерни – колеса | НВ1 HB2 | |
| Тип передачи | Прямозубая | |
| Угол наклона зуба, град, мин, с | β | |
| Диаметры делительных окружностей, мм – шестерни – колеса | d1 d2 | |
| Ширина зубчатого венца, мм – шестерни – колеса | b1 b2 |
Рисунок 3 – Геометрические параметры зубчатой пары
Источник: studopedia. ru
ru
Расчёт диаметра шестерни.
Сегодня рассмотрим как рассчитать диаметр шестерни. Сразу скажу что диаметр прямозубой шестерни имеет одну формулу, а диаметр косозубой шестерни имеет другую формулу. Хотя многие считают по одной формуле, это ошибочно. Данные расчёты нужны для других расчётах при изготовлении зубчатых колёс. Итак перейдём непосредственно к формулам (без коррекции):
Для начала значения которые надо знать при расчётах в данных формулах:
- De — диаметр окружности выступов.
- Dd — диаметр делительной окружности (непосредственно от шага которой считается модуль шестерни).
- Di — диаметр окружности впадин.
- Z — число зубьев шестерни.
- Z1 — число зубьев шестерни малого колеса.
- Z2 — число зубьев шестерни большого колеса.
- M (Mn) — модуль (модуль нормальный, по делительному диаметру).
- Ms — модуль торцевой.
- β (βd) — угол наклона шестерни (иметься ввиду угол наклона по делительному диаметру).

- Cos βd — косинус угла на делительном диаметре.
- A — межцентровое расстояние.
Формула расчёта диаметров прямозубого зубчатого колеса (шестерни):
Формула расчёта диаметров косозубого зубчатого колеса (шестерни с косым зубом):
Вроде как и на прямозубых колёсах, но на косозубых мы имеем другой делительный диаметр, следовательно диаметр окружности выступов будет другим!
То есть количество зубьев умножаем на модуль и делим на косинус угла зуба по делительному диаметру или количество зубьев умножаем на модуль торцевой.
Определяем торцевой модуль:
Ms=Mn/Cos βd =2A/Z1+Z2
То есть модуль торцевой равен — модуль нормальный делить на косинус угла зуба шестерни по делительному диаметру или два умножить на межцентровое расстояние и делить на число зубьев малого колеса плюс число зубьев большого колеса.
Для этого нам уже необходимо знать межцентровое расстояние, которое можно посчитать по формуле:
То есть число зубьев малого колеса плюс число зубьев большого колеса разделить на 2 умножить на косинус угла зуба шестерни по делительному диаметру и всё это умножить на модуль или число зубьев малого колеса плюс число зубьев большого колеса умножить (0,5 умножить на модуль торцевой).
Как видите посчитать диаметр прямозубого колеса очень просто, а вот посчитать диаметр колеса с косым зубом тут уже посложнее, так как требуется много различных составляющих. Данные составляющие не всегда есть, что усложняет расчёт. Так что для некоторых расчётов понадобится знание некоторых точных параметров, таких как точный (подчеркну точный) угол наклона зубьев шестерни на делительном диаметре или точное межцентровое расстояние! Все расчёты взаимосвязаны, всё это надо для других расчётов зубчатых передач при проектировании и в ремонтном деле.
Поделится, добавить в закладки!
Источник: zuborez.info
Что такое модуль шестерни?
Данная статья носит характер образовательный и вспомогательный для людей занимающихся моделизмом и творчеством в различных кружках или дома самостоятельно. Статья не претендует на звание научного трактата и вся предоставленная в ней информация носит лишь ознакомительный характер для понимания и определения такой важной характеристики как «модуль шестерни»
Ведущие и ведомые шестерни в коробках передач и редукторах для различных радиоуправляемых моделей имеют определенное количество зубьев с конкретным модулем и шагом (pitch).
Модуль является самым главным параметром. Через него выражаются все остальные параметры. Он стандартизирован во всем мире и определяется из прочностного расчёта зубчатых передач.
Для тех моделистов, которым покажется сложными все точные выкладки и расчеты достаточно будет в своей практике постройки различных моделей руководствоваться простыми правилами, которые будут звучать примерно так. Для любых шестеренчатых передач важно подбирать ведомые и ведущие шестерни с одинаковым модулем. При этом число зубьев в любой из подбираемых шестерен (ведомая или ведущая в шестеренчатой передаче) можно варьировать подбирая нужное соотношение мощности и оборотов, но характеристика «модуль шестерни» должна оставаться одинаковой для любых шестеренок входящих в непосредственное зацепление друг с другом. Проще говоря понятие модуль шестерни это международная стандартная характеристика обозначения формы зубца любой шестеренки (тут заложены и эвольвента и размеры по высоте и т.д.). Если модули шестерен совпадают, а количество зубьев и диаметры например различные, то можете быть уверены в том, что при правильной установке (зазоры, соосность и т. д.) эти две шестеренки будут работать правильно. Но если параметр модуля различный у шестерен участвующих в передаче, то как их не выставляй они все равно будут «выедать» одна другую и со временем шестеренчатая передача выйдет из строя.
д.) эти две шестеренки будут работать правильно. Но если параметр модуля различный у шестерен участвующих в передаче, то как их не выставляй они все равно будут «выедать» одна другую и со временем шестеренчатая передача выйдет из строя.
Производители радиоуправляемых моделей машин и бренды, выпускающие тюнинг и запчасти для автомоделей, часто (но не всегда) используют дюймовую маркировку ведущих и ведомых шестерен (32 Pitch, 48 Pitch, 64 Pitch). Это такие бренды как, LOSI, TRAXXAS, RRP, VENOM и др. В ней указывается количество зубьев на 1 дюйм диаметра.
Например: шестерня с 32 pitch будет иметь 32 зуба на 1 дюйм диаметра, а шестерня с 64 pitch будет иметь 64 зуба на 1 дюйм диаметра. То есть, чем больше значение модуля, тем ближе зубья друг к другу
Различия между модулями для визуального сравнения вы можете оценить по следующей иллюстрации:
На фото представлены ведущие шестерни с одинаковым количеством зубьев 21, но разными модулями.
Самым ходовым модулем для радиоуправляемых автомоделей является модуль 48 Pitch.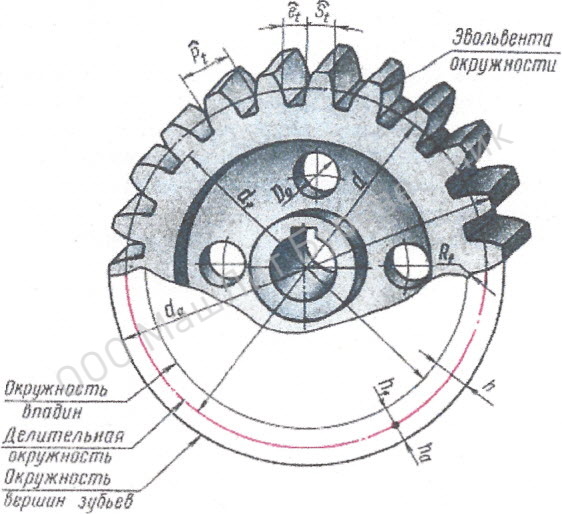
В редукторах радиоуправляемых моделей самолетов, электрических мини вертолетах и квадрокоптерах ( мультикоптерах ) обычно используют шестерни с метрической маркировкой (0.3 Module, 0.4 Module, 0.5 Module, 1.0 Module и др.).
При метрической маркировке, чем больше модуль, тем крупнее зуб. Различия между метрическими модулями для визуального сравнения вы можете оценить по следующей иллюстрации:
Поэтому покупая и заказывая запчасти в магазинах или через интернет, всегда обращайте внимание не только на количество зубьев, но и на указанные в характеристиках товара значения модуля шестерни (pitch) или (module). Эта величина модуля должна обязательно быть одинаковой у всех шестерен в зацеплении, а также обратите внимание на величину диаметра посадки шестерни на вал. При этом материалы, из которых изготовлены шестерни, могут быть абсолютно различными от пластика до высокопрочной стали.
На фото показан пример редуктора автомодели в сборе. Модуль ведущей шестерни (Pinion Gear) и ведомой шестерни (Spur Gear) – 48 Pitch.
На фото показан пример редуктора в сборе для радиоуправляемой модели самолета паркового класса. Модуль ведущей шестерни (Pinion Gear) и ведомой шестерни (Spur Gear) – 0.4 Module.
При покупке в магазинах радиоуправляемых моделей или на сайтах различных продавцов в интернете еще можно разобраться и все несколько раз перепроверить.
На фото представлены ведущие (сверху) и ведомые (ниже) шестерни разных фирм производителей в упаковках.
Буквой T обозначено общее количество зубьев на шестерне (от англ. Tooth — Зуб). Буквой P обозначено значение шага зубьев Pitch. Непосредственно значение модуля обозначено словом Module. Причем Вам при покупке пары для имеющейся у вас шестерни необходимо помнить правило: Единый Pitch для пары шестерней или единый модуль это не важно. Важно если вы подбираете пару для шестеренчатой передачи зная значение Pitch, то и продавцу задаете вопрос употребляя значение ( Pitch ), а если у вам известен модуль ( Module ), то и заказывать у продавца парную шестерню необходимо используя значение именно модуль шестерни — Module.
А вот как быть в том случае когда шестеренка уже требует замены или планового апгрейда (Upgrade) для увеличения скажем мощности. Или имеется обломок (часть шестерни) присланный, например, другом моделистом из другого региона России с просьбой достать точно такую же или «примерно такую». Для этих «сложных» случаев можно воспользоваться информацией приведенной ниже, чтобы точно определить нужный модуль шестерни перед покупкой ее в магазине или перед заказом через интернет из «забугорного» сайта. Для этой задачи необходимо вооружится необходимыми знаниями и точным измерительным инструментом (особенно если шестеренка маленькая).
Итак, начнем понемногу.
Модуль зацепления (модуль шестерни) — это отношение делительного диаметра шестерни к числу зубьев, выраженное в миллиметрах. То есть модуль шестерни равен числу миллиметров диаметра приходящееся на один зуб.
m — модуль (обозначается в англоязычных магазинах на упаковочном пакетике как module)
d — делительный диаметр (диаметр, измеренный по половине высоты зуба)
z — число зубьев (в англоязычных магазинах обозначается буквой T фрезеровкой или литьем на самой шестеренке и, как правило, на упаковочном пакетике с товаром)
p — шаг зубьев (в англоязычных магазинах обозначается как pitch иногда как P на упаковочном пакетике с товаром)
Например, если делительный диаметр d=120 мм, а число зубьев равно 60, то модуль будет равен 2 мм.
Модуль так же является и показателем высоты самого зуба — она равна 2 x m.
Например, если модуль шестерни равен 2 мм, то высота зуба будет равна 4 мм.
Надеемся эта информация поможет многим моделистам в определении, того какая именно шестеренка им необходима.
Как вычислить модуль зубчатого колеса
Цилиндрические шестерни
Поперечный профиль зуба
Обычно шестерни имеют профиль зубьев с эвольвентной боковой формой. Так как эвольвентное зацепление имеет ряд преимуществ перед остальными: форма этих зубьев соответствует условиям их прочности, зубья легко изготовить и обработать, шестерни не чувствительны к точности установки. Тем не менее, существуют зубчатые передачи с циклоидальной формой профиля зубьев, а так же с шестернями с круговой формой профиля зубьев, например – передача Новикова. Помимо этого, применяется несимметричный профиль зуба, например в храповых механизмах.
Параметры эвольвентной шестерни:
Модуль шестерни (m
) – это основной параметр, который определяется из прочностного расчёта зубчатых передач.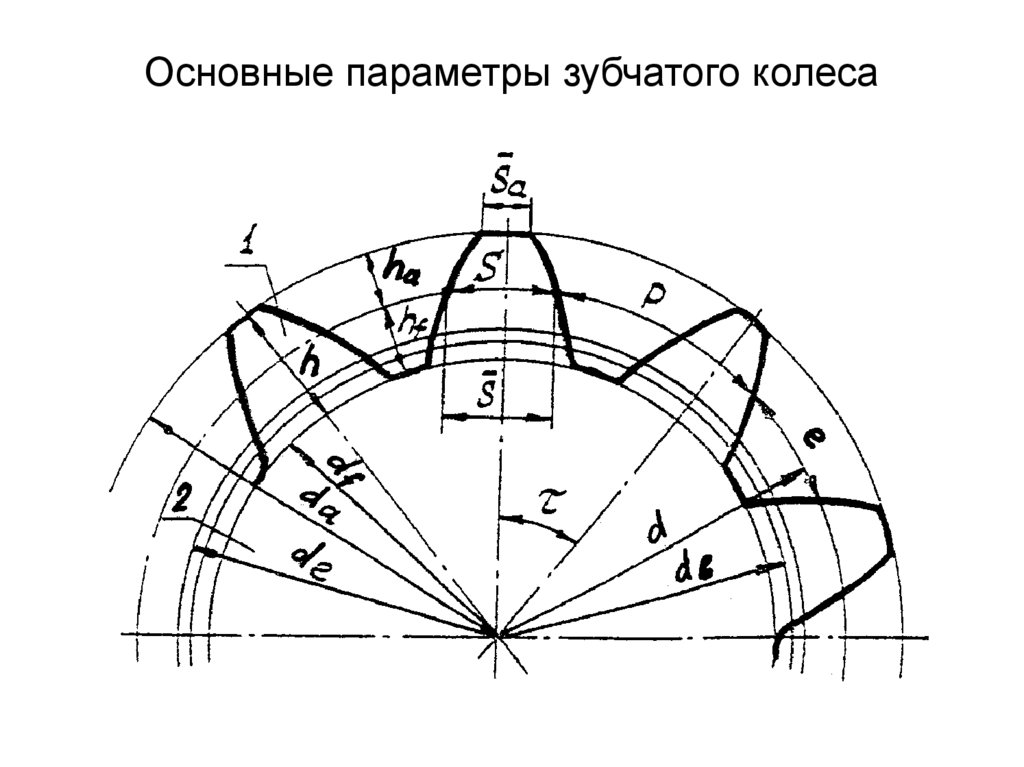 Чем сильнее нагрузка на передачу, тем больше значение модуля, единица измерения модуля – миллиметры.
Чем сильнее нагрузка на передачу, тем больше значение модуля, единица измерения модуля – миллиметры.
Расчет модуля шестерни:
d
— диаметр делительной окружности
z
— число зубьев шестерни
d
a — диаметр окружности вершин темной шестерни
d
b — диаметр основной окружности – эвольвенты
d
f — диаметр окружности впадин темной шестерни
В машиностроении приняты стандартные значения модуля зубчатого колеса для удобства изготовления и замены зубчатых колёс, представляющие собой числа от 1 до 50.
Высота головки зуба – h
aP и высота ножки зуба –
h
fP в случае, так называемого, «нулевого» зубчатого колеса соотносятся с модулем
m
следующим образом:
h
aP =
m
;
h
fP =
1,2 m
, то есть:
Отсюда получаем, что высота зуба h = 2,2m
Так же можно практически вычислить модуль шестерни, при этом, не имея всех данных для определения модуля, по следующей формуле:
Продольная линия зуба
Прямозубые шестерни
Прямозубые шестерни – самый применяемый тип зубчатых колёс. Зубья расположены в радиальных плоскостях, линия контакта зубьев пары зубчатых колес параллельна оси вращения, как и оси обеих зубчатых колес (шестеренок) располагаются строго параллельно.
Зубья расположены в радиальных плоскостях, линия контакта зубьев пары зубчатых колес параллельна оси вращения, как и оси обеих зубчатых колес (шестеренок) располагаются строго параллельно.
Косозубые шестерни
Косозубые шестерни – это модернизированная версия прямозубых шестерен. Зубья, в таком случае, расположены под углом к оси вращения. Зацепление зубьев этих шестерен происходит тише и плавнее, чем у прямозубых. Они применяются либо в малошумных механизмах, либо в тех которые требуют передачи большого крутящего момента на больших скоростях. К недостаткам этого типа шестерен можно отнести: увеличенную площадь соприкосновения зубьев, что вызывает значительное трение и нагрев деталей, а вследствие: потеря мощности и дополнительное использование смазочных материалов; так же механическая сила, направленная вдоль оси шестеренки, вынуждает применять упорные подшипники для установки вала.
Шевронные колёса
Шевронные шестерни решают проблему механической осевой силы, которая возникает в случае применения косозубых колес, так как зубья шевронных (елочных) колёс изготавливаются в виде буквы «V» (или же они образовываются стыковкой двух косозубых колёс со встречным расположением зубьев).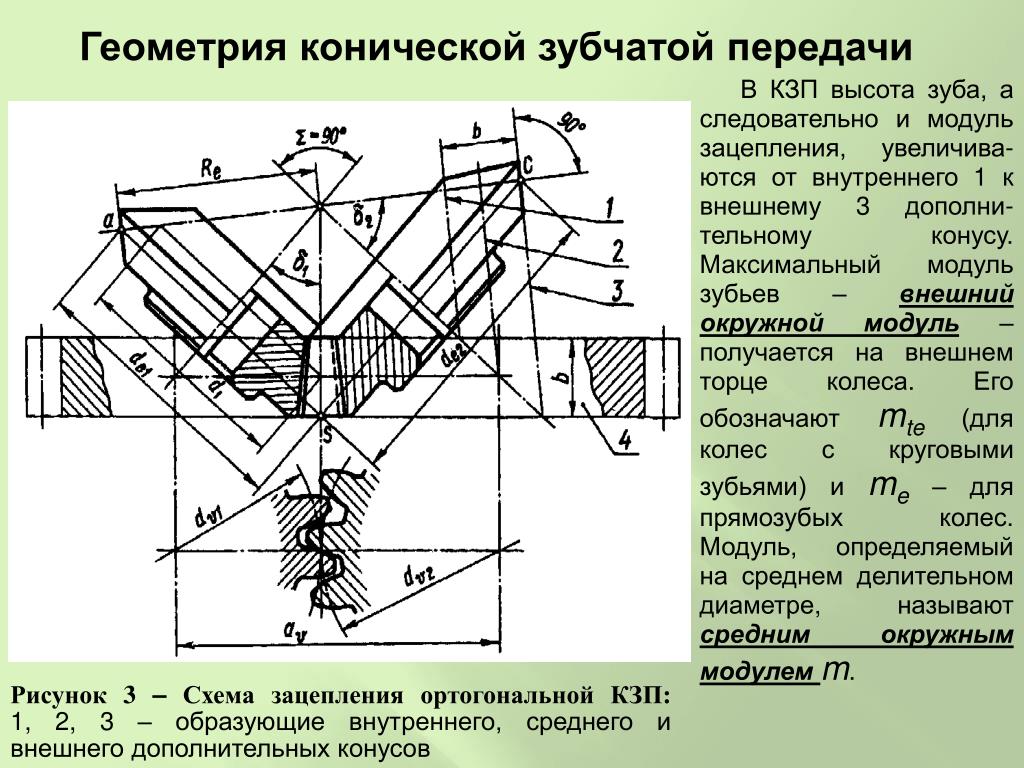 Осевые механические силы обеих половин шевронной шестерни взаимно компенсируются, поэтому нет нет необходимости использования упорных подшипников для установки валов. Шевронная передача является самоустанавливающейся в осевом направлении, в следствии чего, в редукторах с шевронными колесами один из валов устанавливают на подшипниках с короткими цилиндрическими роликами – плавающих опорах.
Осевые механические силы обеих половин шевронной шестерни взаимно компенсируются, поэтому нет нет необходимости использования упорных подшипников для установки валов. Шевронная передача является самоустанавливающейся в осевом направлении, в следствии чего, в редукторах с шевронными колесами один из валов устанавливают на подшипниках с короткими цилиндрическими роликами – плавающих опорах.
Шестерни с внутренним зацеплением
Шестерни такого типа имеют зубья, нарезанные с внутренней стороны. При их использовании происходит одностороннее вращение ведущей и ведомой шестерен. В данной зубчатой передаче меньше затрат на трение, а значит выше КПД. Применяются зубчатые колеса с внутренним зацеплением в ограниченных по габаритам механизмах, в планетарных передачах, в шестеренных насосах, в приводе башни танка.
Винтовые шестерни
Шестерни имеют форму цилиндра с расположенными на нем зубьями по винтовой линии. Эти шестеренки используются на непересекающихся валах, которые располагаются перпендикулярно друг друга, угол между ними 90°.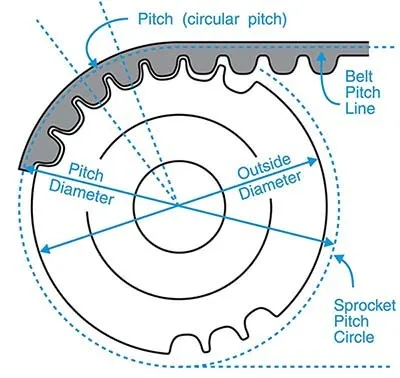
Читать также: Как сделать самодельное точило
Секторные шестерни
Секторная шестерня – это часть (сектор) шестерни любого типа, она позволяет сэкономить в габаритах полноценной шестерни, так как применяется в передачах, где не требуется вращение этого зубчатого колеса (шестеренки) на полный оборот.
Шестерни с круговыми зубьями
Шестерни этого типа имеют линию зубьев в виде окружности радиуса, за счет этого контакт в передаче происходит в одной точке на линии зацепления, которая располагается параллельно осям шестерен. Передачи с круговыми зубьями «Передача Новикова» имеет лучшие ходовые качества, чем косозубые – высокую плавность хода и бесшумность, высокую нагрузочную способность зацепления, но при одинаковых условиях их ресурс работы и КПД ниже, к прочему изготовление этих шестерен значительно сложнее. Поэтому применение таких шестеренок ограниченно.
Кинематический и силовой расчеты зубчатой передачи.
Расчетная окружная скорость v, м/с, цилиндрической передачи
конической передачи где
ω — угловая скорость зубчатого колеса, рад/с; n — частота вращения зубчатого колеса, мин-1; dw — начальный диаметр цилиндрического зубчатого колеса, м; dwm — начальный средний диаметр конического зубчатого колеса, м.
Учитывая, что скорость точек начальных окружностей, находящихся в зацеплении зубчатых колес, одинакова, имеем v=ω1dw1/2=ω2dw2/2. Выражая диаметры dw1 и dw2 через модуль и соответствующие числа зубьев, получаем v=ω1(mz1/2)=ω2(mz2/2). Отсюда передаточное отношение i пары зубчатых колес (для одноступенчатой передачи) с учетом формулы
где
ω1, n1, dw1 z1 и T1 — соответственно угловая скорость, частота вращения, начальный диаметр, число зубьев и крутящий момент ведущего зубчатого колеса; ω2, n2, dw2 z2 и T2 — то же, ведомого зубчатого колеса; η — к. п. д. передачи.
Так как для конической зубчатой передачи передаточное отношение см. предыдущую формулу
то, как следует из рис. где
δ1 — для ведущего, а δ2 — для ведомого зубчатого колеса.
Отношение числа зубьев z2 колеса к числу зубьев z1 шестерни называется передаточным числом зубчатой передачи u.
Таким образом,
Если ведущим зубчатым колесом является шестерня, то для такой передачи передаточное отношение и передаточное число представляют собой одну и ту же величину. Рекомендуемые максимальные значения передаточного числа одноступенчатой зубчатой передачи:
- Цилиндрической в закрытом корпусе: ≤12,5
- Конической в закрытом корпусе: ≤6,3
- Открытой: ≤15
Средние значения коэффициента полезного действия одноступенчатой зубчатой передачи на подшипниках качения в зависимости от конструкции и степени точности.
| Закрытая 6-6 и 7-й степеней точности с жидкой смазкой | Закрытая 8-й степени точности с жидкой смазкой | Открытая с густой смазкой | |
| Цилиндрическая | 0,98 | 0,97 | 0,96 |
| Коническая | 0,97 | 0,96 | 0,94 |
Рис. 1
Окружная сила зубчатой передачи Ft: цилиндрической (рис. 1)
конической (рис. 2)
2)
Рис. 2
Передаваемые зубчатыми колесами крутящие моменты определяют по формулам
и .
Так как силы трения между зубьями малы, то силу давления между ними F можно считать направленной по общей нормали к соприкасающимся поверхностям зубьев, т. е. по линии зацепления (см. рис. 1). Составляющие этой силы: в цилиндрических прямозубых (рис. 1) и шевронных передачах — окружная сила Ft и радиальная сила Fr; в конической прямозубой (рис. 2) и цилиндрической косозубой (рис. 3) передачах — окружная сила Ft радиальная сила Fr, и осевая сила Fa.
Рис. 3
Радиальная сила, действующая на зубчатое колесо прямозубой цилиндрической передачи (рис. 1),
косозубой (рис. 3), или шевронной, передачи конической прямозубой передачи (рис. 2)
Осевая сила, действующая на зубчатое колесо: цилиндрической косозубой передачи (рис. 3)
конической прямозубой передачи (рис.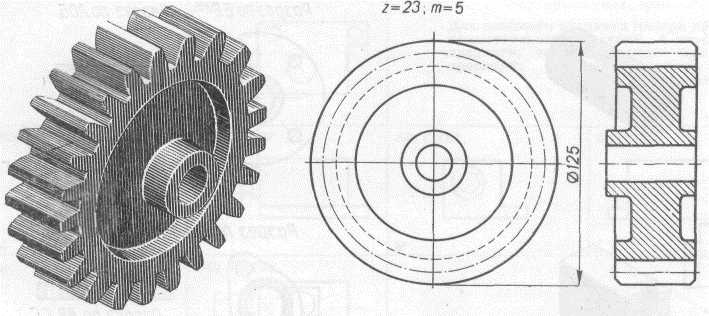 2)
2)
Сила давления между зубьями прямозубой цилиндрической передачи (рис. 1)
.
Зубчатая рейка
Зубчатая рейка является частью зубчатого колеса с бесконечным радиусом делительной окружности. Вследствие этого ее окружности представляют собой прямые параллельные линии. Эвольвентный профиль зубчатой рейки тоже имеет прямолинейное очертание. Это свойство эвольвенты является наиболее важным при изготовлении зубчатых колёс. Передачу с применением зубчатой планки (рейки) называют – реечная передача (кремальера), она используется для преобразования вращательного движения в поступательное и наоборот. Состоит передача из зубчатой рейки и прямозубого зубчатого колеса (шестеренки). Применяется такая передача в зубчатой железной дороге.
Что такое модуль зубчатого колеса
Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров
В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров
- диаметр;
- число зубьев;
- шаг;
- высота зубца;
- и некоторые другие.
Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.
В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.
Для расчета этого параметра применяют следующие формулы:
Параметры зубчатых колес
Модуль зубчатого колеса можно рассчитать и следующим образом:
где h — высота зубца.
где De — диаметр окружности выступов,а z — число зубьев.
Что же такое модуль шестерни?
это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.
Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.
Читать также: Рохля электрическая с подъемным механизмом
Основные параметры
Для обеспечения подвижности и работоспособности, конструкция отдельных деталей механической передачи должна быть согласована по размерам и геометрии. Для этого при описании подобных устройств принято использовать систему специальных параметров. В их число входят геометрические, массогабаритные и прочностные величины, закрепленные стандартами. Применение стандартных параметров позволяет сравнительно просто производить расчет унифицированных зубчатых передач и обеспечивает гарантированное сопряжение всех изделий между собой. Естественно, что для разных видов, параметры будут несколько отличаться. Далее рассматриваются термины, связанные с конструкцией эвольвентного цилиндрического колеса. Эти параметры, в своем большинстве, описывают основные характеристики и других вариантов колес.
В основе сечения зуба большинства шестерен лежит эвольвентный профиль, который получается на основе одноименной кривой. Его применение легко стандартизируется, характеризуется высокой технологичностью изготовления и низкими требованиями к качеству сборки механизма. Основными параметры эвольвентного зубчатого колеса считаются модуль зацепления и количество зубьев зубчатого колеса. При одном и том же наружном диаметре деталей значения этих величин могут существенно отличаться в разных вариантах конструкции.
Его применение легко стандартизируется, характеризуется высокой технологичностью изготовления и низкими требованиями к качеству сборки механизма. Основными параметры эвольвентного зубчатого колеса считаются модуль зацепления и количество зубьев зубчатого колеса. При одном и том же наружном диаметре деталей значения этих величин могут существенно отличаться в разных вариантах конструкции.
Число зубьев определяет коэффициент передачи и геометрические размеры зубьев. На ведущем колесе редуктора оно выполняется меньшим, чем на ведомом. В итоге один нормальный оборот ведущей шестерни приводит к повороту ведомого колеса только на определенный угол. Отношение числа зубьев двух колес дает значение передаточного коэффициента. Размеры зубьев определяются как отношение их количества к длине окружности колеса. С целью упрощения расчетов и гарантированного обеспечения зацепления между разными колесами, предусмотрен дополнительный параметр, называемый модулем зацепления. Любые шестерни с одинаковым модулем обеспечивают взаимодействие между собой и могут использоваться для построения механизмов, без дополнительной обработки.
Сумма ширины зуба и впадины совместно дают шаг зубчатого колеса. Учитывая неравномерность профиля по радиусу и зависимость длины дуги от диаметра, в каждом колесе можно определить бесконечное число значений этого параметра. С целью стандартизации принято рассматривать шаг по делительной окружности, называемый так же окружным шагом. Отношение этого шага к числу пи дает модуль зацепления. В некоторых случаях для описания шестерен используют угловой шаг, измеряемый в градусах. Стандартами предусмотрены и несколько других угловых величин. Например, для упрощения настройки оборудования при изготовлении колес рассматривают угловую ширину зуба и угловую ширину впадины. Определяются они также на основе делительной окружности.
Формула расчета параметров прямозубой передачи
Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.
Расчет модуля зубчатого колеса
Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:
Если это расстояние умножить на число зубов z, то мы должны получить ее длину:
проведя преобразование, получим:
Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.
размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:
выполнив преобразование, находим:
Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов De получается равным
где h’- высота головки.
Высоту головки приравнивают к m:
Проведя математические преобразования с подстановкой, получим:
Диаметр окружности впадин Di соответствует De за вычетом двух высот основания зубца:
где h“- высота ножки зубца.
Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:
Устройство зубчатого колеса
Выполнив подстановку в правой части равенства, имеем:
что соответствует формуле:
и если выполнить подстановку, то получим:
Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.
Следующий важный размер, толщину зубца s принимают приблизительно равной:
- для отлитых зубцов: 1,53m:
- для выполненных путем фрезерования-1,57m, или 0,5×t
Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины sв, получаем формулы для ширины впадины
- для отлитых зубцов: sв=πm-1,53m=1,61m:
- для выполненных путем фрезерования- sв= πm-1,57m = 1,57m
Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:
- усилия, прикладываемые к детали при эксплуатации;
- конфигурация деталей, взаимодействующих с ней.
Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.
Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.
Расчет параметров колеса и шестерни косозубой передачи.
Переходим к примеру с косозубой передачей и повторяем все действия, которые мы делали в предыдущем разделе.
Измерить угол наклона зубьев с необходимой точностью при помощи угломера или транспортира практически очень сложно. Я обычно прокатывал колесо и шестерню по листу бумаги и затем по отпечаткам транспортиром делительной головки кульмана производил предварительные измерения с точностью в градус или больше… В представленном ниже примере я намерил: βa1=19° и
βa2=17,5°.
Еще раз обращаю внимание, что углы наклона зубьев на цилиндре вершин
βa1иβa2– это не угол β, участвующий во всех основных расчетах передачи!!! Уголβ – это угол наклона зубьев на цилиндре делительного диаметра (для передачи без смещения).
Ввиду малости значений рассчитанных коэффициентов смещения уместно предположить, что передача была выполнена без смещения производящих контуров шестерни и зубчатого колеса.
Воспользуемся сервисом Excel «Подбор параметра». Подробно и с картинками об этом сервисе я в свое время написал здесь.
Выбираем в главном меню Excel «Сервис» — «Подбор параметра» и в выпавшем окне заполняем:
Установить в ячейке: $D$33
Значение: 0
Изменяя значение ячейки: $D$22
И нажимаем OK.
Получаем результат β=17,1462°,
xΣ(d)=0,x1=0,003≈0,x2=-0,003≈0!
Передача, скорее всего, была выполнена без смещения, модуль зубчатого колеса и шестерни, а также угол наклона зубьев мы определили, можно делать чертежи!
Исходные данные и замеры
На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.
Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.
Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.
Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.
Результаты расчетов
Для более крупных потребуются измерения и вычисления.
Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:
Последовательность действий следующая:
- измерить диаметр штангенциркулем;
- сосчитать зубцы;
- разделить диаметр на z+2;
- округлить результат до ближайшего целого числа.
Зубец колеса и его параметры
Данный метод подходит как для прямозубых колес, так и для косозубых.
Терминология зубчатых колес и формулы расчета зубьев.
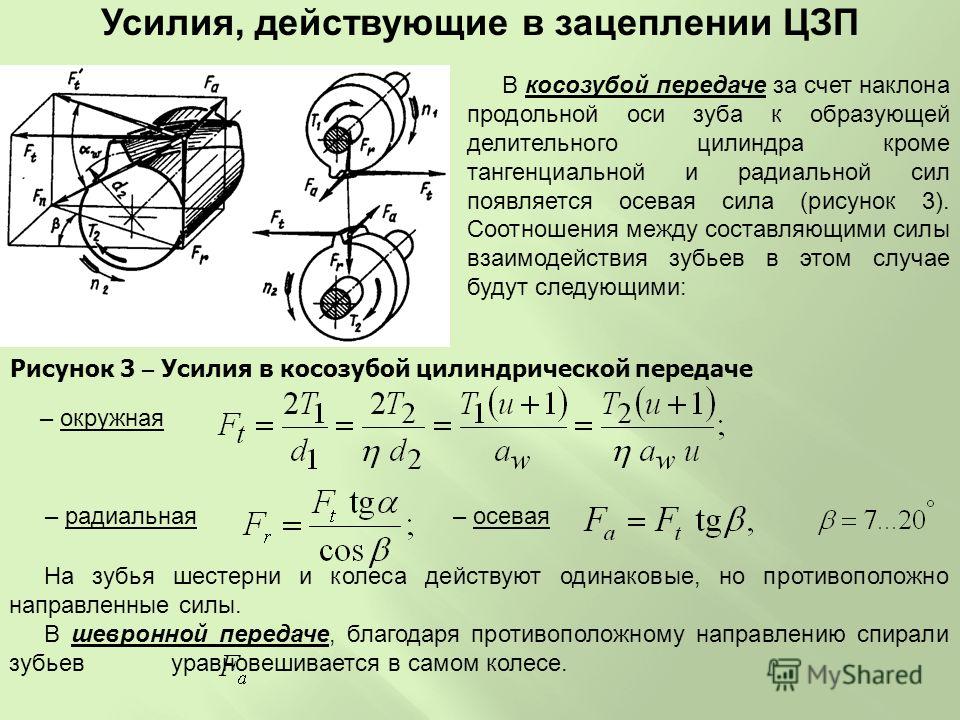 Краткое руководство
Краткое руководство
Это упрощенная версия терминологии зубчатых колес и формул расчета зубьев. кто уже давно научился переключать передачи, но хочет быстро их снова включить.
Шестерни имеют множество параметров, для полного понимания которых потребуется немного математических и геометрических знаний. Тем не менее, Вам не нужно слишком углубляться в базовые концепции знаний снаряжения, после того как вы прочтете этот пост, вы должны быть в состоянии делать предварительные проекты зубчатых колес или поддерживать эффективную связь с проектировщиками зубчатых колес .
Давайте начнем с базовой формы зубчатого колеса, цилиндрических зубчатых колес:
1. Число зубьев (z)
Это довольно просто, это количество зубьев шестерни.
2. Контрольная окружность и контрольный диаметр (d)
Диаметр вершины (da) и диаметр корня (df) соответствуют верхней и нижней части зубьев.
Эталонный диаметр используется при проектировании и расчете зубчатых колес. Он напрямую связан с другими важными параметрами зубчатого колеса, такими как модуль (m), межосевое расстояние (c) и угол давления (α).
Он напрямую связан с другими важными параметрами зубчатого колеса, такими как модуль (m), межосевое расстояние (c) и угол давления (α).
Диаметр вершины (da) и диаметр корня (df) соответствуют верхней и нижней части зуба.
Эталонный диаметр используется при проектировании и расчете зубчатых колес. Он напрямую связан с другими важными параметрами зубчатого колеса, такими как модуль (m), межосевое расстояние (c) и угол давления (α).
Поворот 2-х шестерен можно считать включенным поворотом 2-х опорных окружностей без проскальзывания. Передаточное число i=d2/d1. d1 и d2 относятся к эталонным диаметрам двух сопряженных шестерен (шестерня 1 — ведущая, шестерня 2 — ведомая).
Опорная окружность находится где-то между вершиной и низом зубьев, обычно там, где толщина зуба равна шагу, но это не всегда так (о смещении профиля мы поговорим позже в этом посте).
3. Модуль (м)
Модуль, вероятно, является самым важным параметром зубчатого колеса, и он фигурирует почти везде в формулах расчета зубьев.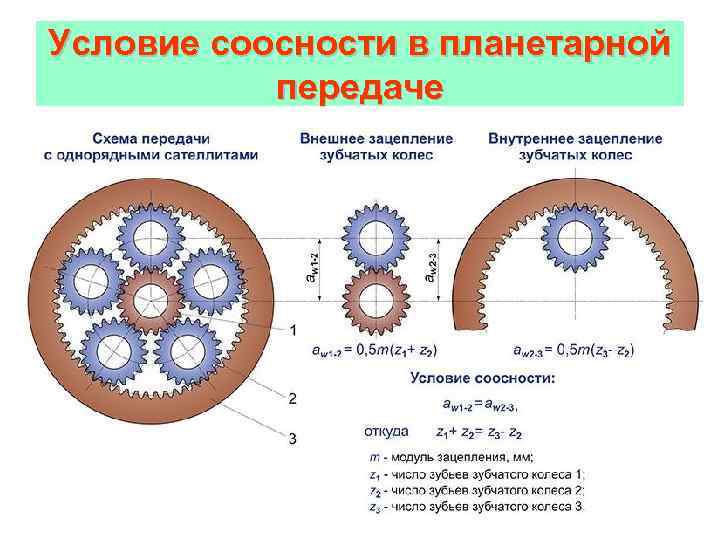 На самом деле, это не так сложно понять, как вы можете себе представить. Сначала давайте разберемся, что такое шаг. Шаг — это длина дуги между соответствующими точками на соседних зубах, обычно на эталонной окружности.
На самом деле, это не так сложно понять, как вы можете себе представить. Сначала давайте разберемся, что такое шаг. Шаг — это длина дуги между соответствующими точками на соседних зубах, обычно на эталонной окружности.
Затем у нас есть эталонный диаметр d=длина окружности/π=шаг*z/π , чтобы упростить вычисления, мы определяем шаг/π в качестве модуля, и теперь у нас есть уравнение d=m*z , это значительно упрощает вычисления, верно? Модули стандартизированы под следующими номерами (единица измерения : мм ):
Первая серия (рекомендуется): 0,1, 0,12, 0,15, 0,2, 0,25, 0,3, 0,4, 0,5, 0,6, 0,8, 1, 1,25, 1,5 , 2, 2,5, 3, 4, 5, 6, 8, 10, 12, 16, 20, 25, 32, 40, 50
Второй ряд (менее использованный): 0,35, 0,7, 0,9, 1,75, 2,25, 2,75 , 3,25, 3,5, 3,75, 4,5, 5,5, 6,5, 7, 9, 11, 14, 18, 22, 28, 30, 36, 45
Однако для литых пластмассовых шестерен нет необходимости использовать эти стандартные номера модулей, поскольку зубья не нарезаются стандартными зуборезами.
Теперь у нас есть передаточное число i=d2/d1=z2/z1 (шестерня 1 — ведущая, а шестерня 2 — ведомая).
Модуль также имеет отношение к высоте зуба, для стандартных передач высота зуба равна 2,25*м:
доп га=1*м , дедендум hf=1,25*м , высота зуба ч=2,25*м .
4. Расстояние между центрами (a)
2 зубчатых зацепления всегда имеют один и тот же модуль, в противном случае они не совпадают. Теперь можно сделать вывод, что a=(d1+d2)/z=m(z1+z2)/2 , но может немного отличаться при некоторых корректировках геометрии зубчатого колеса (смещении профиля зуба).
5. Угол давления (α)
Проще говоря, как следует из названия, это угол между направлением контактной силы в точке контакта зуба и направлением движения этой точки на профиле зуба.
В геометрии это угол между линией, нормальной к эвольвентному профилю зуба, и линией, нормальной к его радиальной линии.
Если вы хотите полностью понять угол давления, вам нужно углубиться в понимание эвольвентной линии профиля зуба. Это просто более простой способ объяснения.
Различные точки на профиле зуба имеют разные углы зацепления, но когда мы говорим об угле зацепления зубчатого колеса, это обычно относится к углу опорной окружности. Большинство зубчатых колес используют угол давления 20°, некоторые — 14,5° или 25°. 2 сопрягаемые шестерни должны иметь одинаковый модуль и угол зацепления.
6. Минимальное количество зубьев (
z min ) без подрезки в шестерне
Вы не можете иметь любое количество зубьев шестерни, какое хотите. Если зубьев слишком мало, нижняя часть зубьев будет ниже предельной точки, вследствие чего при изготовлении зубьев зуборезами будет срезана лишняя часть корня зуба.
Если зубья не обработаны зуборезами, а профили зубьев сохранились, то в трансмиссии заклинит 2 шестерни.
Формула для расчета минимального количества зубьев без подрезки: мин =17. Так, минимальное число зубьев для стандартных шестерен равно 17.
Так, минимальное число зубьев для стандартных шестерен равно 17.
7. Коэффициент смещения профиля (x)
Обычно для профиля зуба надстройка зуба ha=1*m, а нижняя часть hf=1,25*m, однако профиль зубьев можно немного сместить вверх или вниз:
Теперь у нас есть коэффициент сдвига профиля (x). При перемещении профиля вверх значение x положительное (x>0), а при перемещении профиля вниз значение x отрицательное (x<0).
С перемещением профиля зубьев теперь имеем:
- прибавление ha=(1+x)*m
- dedendum hf=(1,25-x)*m
Высота зуба h=ha+hf=2,25 * м, это все равно, что стандартные зубы.
Основными причинами смещения профиля являются:
1) При смещении профиля мы можем избежать подрезки зубьев с меньшим количеством зубьев. Формула выглядит следующим образом:
x мин =(17-z)/17
Например, если вы хотите, чтобы количество зубьев было 14, тогда X=(17-14)/17=0,176
2)Точная настройка межосевого расстояния
a=[(m+x1)z1+(m+x2)z2]/2 , поэтому межосевое расстояние не обязательно должно быть (z1+z2)*m
3) Сделайте шестерню сильнее . Обычно шестерня выходит из строя раньше, чем шестерня, за счет положительного сдвига профиля нижняя часть шестерни становится шире (в то время как кончик становится уже), что делает ее прочнее.
Обычно шестерня выходит из строя раньше, чем шестерня, за счет положительного сдвига профиля нижняя часть шестерни становится шире (в то время как кончик становится уже), что делает ее прочнее.
In summary:
| # | Item | Symbol | Formula | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | teeth number | z | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | module | m | M = шаг/π | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | Персидовая передача | I | I = D2/D1 = Z2/Z1 1: Движение вождения и 2: Driven Gear | da* | da*=1+x x=0 for standard gears | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | dedendum coefficient | df* | df*=1.25-x | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | profile shift coefficient | x | Для стандартных зубчатых колес, x=0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | угол давления | α | α=20° для большинства зубчатых колес Другими менее используемыми являются 125° и 124,5°.  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | опорный диаметр | d | d=mz | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | диаметр наконечника | da | da=d+2Ha* x m, da=(z+2ha*) m ) x m | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | диаметр хвостовика | df | df=d-2Hf* x m, df=(z-2hf*) x m 11 | дополнение | га | га=м x га* Для стандартных передач, га=м | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | dedendum | hf | hf=m x hf* For standard gears, hf=1.25m | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13 | tooth height | h | h=m x (ha*+hf*) ha*+Hf *=2,25 для большинства шестерен | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14 | межосевое расстояние | a | a=m x (z1+z2) для стандартных шестерен a=[(m+x1)z1+(m+x2)z2]/2 для профильных шестерен | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15 | Минимальное количество зубьев без поднутрения | Zmin | Zmin=2ha*/sin2α Zmin=17 при ha*=1, α=20° | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16 | Минимальное смещение профиля без подрезки 19 апреля 2019 г. В… В…boyanmfg 19 января 2020 г. Вы должны с самого начала выбрать правильного производителя пресс-формы Для любого проекта по литью пластмасс под давлением изготовление пресс-формы является самой дорогой и трудоемкой его частью. Это… Базовая терминология и расчет передач
> > > Размер шестерни, угол давления, количество зубьев… мы вводим основную терминологию, измерения и относительные выражения, необходимые для понимания основных технологий зубчатых передач. Сравнительный размер зубчатых колесВ соответствии с рекомендациями ISO (Международной организации по стандартизации) размер модуля определяется как единица, представляющая размеры зубьев зубчатого колеса. Однако используются и другие методы. Модуль (м) м = 1 (p = 3,1416) Рис. 2.1 Профили зубьев реек Если умножить модуль на Pi, можно получить шаг (p). Шаг – это расстояние между соответствующими точками на соседних зубах. p = Pi x Module = πm (2.1) Пример расчета Каков размер шага (p) шестерни с модулем m = 3? p = πm = 9,4248 CP (круговой шаг) Круговой шаг (CP) обозначает эталонный шаг (p). Преобразование CP в модуль Пример расчета CP10 преобразуется в модуль следующим образом ; м = 10 / 3,1416 = 3,1831 DP (диаметральный шаг) DP означает диаметральный шаг. Преобразование из DP в модуль Пример расчета DP 8 преобразуется в модуль следующим образом ; m = 25,4 / 8 = 3,175 Угол давления (α) Угол давления — это угол наклона зуба шестерни, элемент, определяющий профиль зуба. Рис. 2.2 Нормализованный профиль зуба по эталону (Важная терминология и номенклатура зубчатых колес на рис. 2.2)
Количество зубьев Количество зубьев обозначает количество зубьев шестерни. Рис. 2.3 Число зубьев Модуль (m), Угол давления (α) и Число зубьев, введенные здесь, являются тремя основными элементами в составе зубчатого колеса. механизм. На основе этих элементов рассчитываются размеры зубчатых колес. Глубина и толщина зуба Глубина зуба определяется размером модуля (м). Здесь представлены профили зубьев (полная глубина), указанные в стандартах ISO и JIS (японские промышленные стандарты). h = 2,25 м Рис. 2.4 Глубина и толщина зуба (Важная терминология и номенклатура зубчатых колес на рис. 2.4)
Дополнение (га) — расстояние между базовой линией и вершиной зуба. га = 1,00 м (2,5) Дедендум (hf) — расстояние между базовой линией и корнем зуба. hf = 1,25 м (2,6) Толщина зуба (s) в основном составляет половину значения шага (p). * Шаг (p) = πm s = πm / 2 (2.7) Примеры расчетов Ниже приведены расчеты глубины зуба (h)/дополнения (ha)/дедендума (hf) для зубчатого колеса с модулем 2. h = 2,25 м = 2,25 × 2 = 4,50 Диаметр шестерен (размер)Размер шестерен определяется в соответствии с эталонным диаметром (d) и определяется этими другими факторами; базовый круг, Шаг, Толщина зуба, Глубина зуба, Дополнение и Дедендум. Базовый диаметр (d) d = zm(2,8) Диаметр кончика (da) da = d + 2 м(2,9) Диаметр основания (df) df 5 м2 (1,0 d2 — 2,0 ) Рис. (Важная терминология и номенклатура шестерен на рис. 2.5)
Добавление и окружность дедендума, представленные здесь, являются эталонной окружностью, которую нельзя увидеть на шестерне, так как это виртуальная окружность, определяемая размером шестерни. Примеры расчетов Ниже приведены расчеты исходного диаметра / диаметра вершины / диаметра основания для цилиндрического зубчатого колеса с модулем (m) 2 и 20 зубьями (z). d = zm = 20 x 2 = 40
Рис. (Важная терминология и номенклатура шестерен на рис. 2.6)
Таблица 2.1 Символы и номенклатура шестерен
Расстояние между центрами и люфт Когда пара шестерен находится в зацеплении так, что их опорные окружности соприкасаются, межосевое расстояние (a) составляет половину суммы их опорных диаметров. Расстояние до центра (а) a = ( d1 + d2 ) / 2(2.11) Рис. 2.7 Расстояние между центрами Зубчатые колеса могут зацепляться, как показано на рис. может работать бесперебойно. Люфт – это люфт между поверхностями зубьев парных шестерен в зацеплении. Зазор кончика и корня (c) c = 1,25 м — 1,00 м Рис. 2.8 Зазор между вершиной и основанием (Важная терминология и номенклатура зубчатых колес на рис. 2.8)
Примеры расчетов Ниже приведены расчеты межосевого расстояния (a) и зазора между вершинами и впадинами (c), когда модуль m = 2, шестерня z1 = 20, шестерня z2 = 40 Базовый диаметр шестерни d1 = 20 × 2 = 40 Расстояние между центрами a = (40 + 80) / 2 = 60 c = 0,25 × 2 = 0,5 Примеры расчета Практика расчета размеров шестерни.
Практический тест:
Косозубая шестерня Цилиндрические шестерни с винтовыми зубьями называются косозубыми шестернями. Рис. 2.9 Правосторонняя косозубая шестерня (Важная терминология и номенклатура шестерен на рис. 2.9)
(a) Поперечная система (поперечный модуль / угол давления) * Поперечная ось обозначает центральную линию шестерни. Реляционное выражение: поперечный модуль ( mt ) и нормальный модуль ( mn ) mt = mn / cos β(2.13) Обе системы используются в KHK Stock Gears. Базовый диаметр (d) косозубой шестерни с поперечной системой можно рассчитать по уравнению (2. d = zmn / cos β(2.14) Примеры расчетов Ниже приведен расчет эталонного диаметра косозубого колеса с: 15° (П) Ниже приведен расчет эталонного диаметра косозубой шестерни с: Практический тест: Нормальный модуль ( mn ) = 4 Угол подъема винтовой линии ( β ) = 15° Поперечный модуль mt = Поиск и устранение неисправностей шестерен: объяснение терминологииТочечная коррозия Когда поверхность зубчатого колеса многократно подвергается нагрузке, а сила вблизи точки контакта превышает предел усталости материала, возникают мелкие трещины, которые в конечном итоге перерастают в разделение мелких частей, образуя ямки (кратеры). Начальная стадия Точечная коррозияПервоначальная причина связана с небольшими выпуклыми участками поверхностей зубчатых колес, контактирующими друг с другом, и локальной нагрузкой, превышающей предел усталости. По мере приведения в движение шестерен и износа поверхностей локальные выпуклости исчезают, нагрузка выравнивается, питтинг прекращается. Прогрессирующая точечная коррозия Даже после износа поверхностей зубчатых колес и выравнивания нагрузки со временем начинает появляться больше точечной коррозии, и ямки увеличиваются. Задиры Это состояние, при котором смазочное покрытие разрушается из-за перегрева локальных контактных площадок, что приводит к износу поверхности зубчатого колеса от контакта металла к металлу. Проточка В направлении скольжения шестерни появляется состояние, похожее на канавку. Это часть абразивного износа, и возможны следующие причины. Абразивный износ Износ, который выглядит как травма от истирания или имеет вид притирки. Ниже приведены некоторые из причин. Адгезионный износ Износ, обычно возникающий между металлами при скользящем контакте. Снижение износа зависит от типа, давления, скорости, расстояния и смазки. ВыкрашиваниеОтносится к симптому отпадания относительно крупной металлической стружки с поверхности зубчатого колеса из-за усталости материала под поверхностью при высокой нагрузке. Вогнутая часть поверхности зубчатого колеса большая, а форма и глубина неправильные. Поскольку приложенная сила сдвига превышает предел выносливости материала, появляются и растут усталостные трещины, что может привести к поломке зуба. Чрезмерный износ Износ от поверхности зубчатого колеса, подвергающегося интенсивному повторяющемуся контакту металла с металлом, который возникает, когда масляная пленка тонкая и смазка недостаточна по сравнению с нагрузкой и шероховатостью поверхности зубчатого колеса. Поломка из-за перегрузкиПоломка из-за неожиданно большой нагрузки в течение одного или нескольких рабочих циклов (Обычно сюда не включаются ошибки проектирования или изготовления). Поверхность излома волокнисто распространяется от начальной точки и указывает на внезапное расщепление. Причина в том, что нагрузка превышает предел прочности на растяжение материала шестерни. Это может произойти из-за первичного двигателя, ведомого механизма или поломки подшипников или других шестерен, что может вызвать заедание зубьев, внезапную остановку или концентрацию нагрузки из-за неравномерного контакта зубьев. Усталостная поломка Это случай, когда корневая часть зубчатого колеса подвергается многократной нагрузке, превышающей предел усталости материала. Трещина, которая начинается в углу корня шестерни, распространяется до тех пор, пока зуб не сломается. Поверхность излома относительно гладкая, и начальную точку часто можно распознать по береговой отметине (рисунку раковины) вокруг нее. Поломка при сдвигеЭто описывает случай, когда зуб отделяется от тела в результате сдвига из-за однократной экстремальной перегрузки. Поломка прямая в окружном направлении и выглядит плоской, как если бы она была обработана механической обработкой. В близлежащей области наблюдается пластическая деформация. Это происходит, когда приложенная сила превышает прочность материала на сдвиг. Это происходит, когда зубчатое колесо высокой жесткости и прочности входит в зацепление с зубчатым колесом, имеющим относительно низкий модуль упругости и непрочный материал. Ссылки по теме : Расчет размеров шестерни | KHK
> > > Размеры зубчатых колес определяются в соответствии с их спецификациями, такими как модуль (m), число зубьев (z), Угол давления (α) и коэффициент сдвига профиля (x). В этом разделе представлены расчеты размеров прямозубых, косозубых, зубчатых реек, конических, винтовых и червячных передач. Расчеты внешних размеров (например, диаметра наконечника) необходимы для обработки заготовок зубчатых колес. Размеры зуба, такие как диаметр корня или глубина зуба, учитываются при нарезании зубчатых колес. 4.1 Цилиндрические шестерни Цилиндрические шестерни — самый простой тип шестерен. (1) Стандартная прямозубая шестерня Рис. 4.1 Зацепление стандартных прямозубых колес Таблица 4.1 Расчеты для стандартных прямозубых колес
ПРИМЕЧАНИЕ 1. Нижние индексы 1 и 2 у z1 и z2 обозначают шестерню и шестерню. Если вместо этого заданы модуль m, межосевое расстояние а и передаточное число i, то количество зубьев z1 и z2 будет рассчитано с использованием формул, показанных в таблице 4. Таблица 4.2 Расчеты количества зубьев
Обратите внимание, что количество зубьев, вероятно, не будет целым числом при использовании формул в таблице 4. (2) Цилиндрическое зубчатое колесо со смещенным профилем В зацеплении зубчатых колес со смещенными профилями окружность рабочего шага, которая соприкасается и катится друг с другом, отражает действие зубчатого колеса. В таблице 4.3 представлены расчеты, в которых коэффициент сдвига профиля был установлен равным x1 и x2 в начале. Этот расчет основан на идее, что величина зазора между верхушкой и корнем должна быть 0,25 м. Рис. 4.2 Зацепление зубчатых колес с профильным смещением Таблица 4.
то есть х1=х2=0. Таблица 4.4 представляет собой обратную формулу пунктов с 4 по 8 таблицы 4.3. Таблица 4.4 Расчеты для прямозубых цилиндрических зубчатых колес со смещением профиля (2) Существует несколько теорий относительно распределения суммы коэффициента смещения профиля (x1 + x2) на шестерню (x1) и шестерню (x2) по отдельности. Наиболее часто используются стандарты BSS (британский) и DIN (немецкий). В приведенном выше примере 12-зубая шестерня была скорректирована для предотвращения подреза, а остаточное смещение профиля было передано сопрягаемой шестерне. (3) Реечная и цилиндрическая шестерня На рис. 4.3 (2) показано цилиндрическое зубчатое колесо со смещенным профилем, с положительной коррекцией xm, находящееся в зацеплении с зубчатой рейкой. Цилиндрическое зубчатое колесо имеет больший радиус шага, чем стандартное, на величину xm. Кроме того, делительная линия стойки сместилась наружу на величину xm. Таблица 4.5 Расчет размеров цилиндрического цилиндрического колеса со смещенным профилем и рейки Один оборот цилиндрического колеса сместит рейку l на одну длину окружности базовой окружности колеса по формуле: Перемещение рейки, l, никак не меняется при смещении профиля. Рис. 4.3 (1) Зацепление стандартной цилиндрической шестерни и рейки Рис. 4.3 (2) Зацепление профильно смещенной цилиндрической шестерни и рейки 4.2 Внутренние шестерни Внутренние шестерни состоят из шестерни цилиндрической формы с зубьями внутри круглого кольца. Зубья шестерни внутреннего зацепления входят в зацепление с пространством зубьев цилиндрической шестерни. Цилиндрические зубчатые колеса имеют профиль зуба выпуклой формы, а внутренние зубчатые колеса имеют профиль зуба вогнутой формы; эта характеристика противоположна внутренним передачам. Вот расчеты размеров внутренних шестерен и их натяга. (1) Расчет внутреннего зубчатого колеса В таблице 4.6 показаны этапы расчета. Это станет стандартным расчетом передачи, если x1=x2=0. Рис.4.4 Зацепление внутренней шестерни и внешней шестерни Таблица 4.6 Расчеты внутреннего и наружного зубчатого зацепления с профильным смещением (1) Если задано межосевое расстояние (a), x1 и x2 будут получены из обратного расчета от пунктов 4 до пунктов 8 Таблицы 4.6. Эти обратные формулы приведены в таблице 4.7. Таблица 4.7 Расчеты внутреннего зубчатого колеса и внешнего зубчатого колеса со смещенным профилем (2) Зуборезы часто используются для нарезания внутренних и внешних зубчатых колес. Фактическое значение глубины зуба и диаметра корня после обработки будет немного отличаться от расчетного. Это потому, что фреза имеет коэффициент сдвига профиля. Для получения правильного профиля зуба необходимо учитывать коэффициент смещения профиля фрезы. (2) Натяг во внутренних зубчатых колесах (a) Эвольвентная интерференция Где αa2 — угол давления на вершину внутреннего зуба шестерни. αw:угол рабочего давления Уравнение (4.5) верно, только если диаметр вершины внутреннего зубчатого колеса больше, чем окружность основания: Для стандартного внутреннего зубчатого колеса, где α=20°, уравнение ( 4.7) действителен, только если число зубьев z2 > 34. (b) Трохоидальный зацеп Здесь где αa1 угол давления вершины зуба прямозубого колеса: При зацеплении внешнего зубчатого колеса и стандартного внутреннего зубчатого колеса α=20° трохоидальное натягивание предотвращается, если разница в числе зубьев , z2 – z1, больше 9. (c) Натяг Здесь Этот тип натяга может возникнуть в процессе нарезания внутренней шестерни фрезой. В этом случае существует опасность поломки инструмента. В таблице 4.8 (1) приведен предел для зубчатой фрезы, препятствующий триммингу при нарезке стандартного внутреннего зубчатого колеса с углом зацепления α0=20° и без смещения профиля, т. Таблица 4.8 (1) Предельное значение для предотвращения натяга внутренней шестерни
There will be an involute interference between the internal gear and фрезу-шестерне, если число зубьев фрезы-шестерни находится в пределах от 15 до 22 (z0=15-22). Table 4.8 (2) The limit to prevent an internal gear from trimming interference α0=20°, x2=0
Возникнет эвольвентный натяг между внутренним зубчатым колесом и фрезой, если число зубьев фрезы находится в диапазоне от 15 до 19 (z0=15-19). Рис.4.5 Эвольвентная и трохоидальная интерференция Рис.4.6 Обрезка натяга 4.3 Косозубые шестерни Косозубая шестерня, показанная на рис. 4.7, представляет собой цилиндрическую шестерню, в которой боковые поверхности зубьев геликоидальные. Угол винтовой линии в эталонном цилиндре равен β, а смещение на один оборот — опережение, pz. Профиль зуба косозубого колеса представляет собой эвольвентную кривую в осевом виде или в плоскости, перпендикулярной оси. Косозубая передача имеет два вида профилей зубьев – один основан на нормальной системе, другой – на основе поперечной системы. Шаг, измеренный перпендикулярно зубьям, называется нормальным шагом, pn. Профиль зуба косозубого колеса с примененным нормальным модулем В осевом виде шаг на эталоне называется поперечным шагом, pt . Эти поперечный модуль mt и угол поперечного давления αt at являются базовой конфигурацией поперечной системы винтовой передачи. В поперечной системе не все так просто. Конструкцию фрезы необходимо изменить в соответствии с изменением угла наклона винтовой линии β, даже если модуль mt и угол давления at одинаковы. При зацеплении косозубых шестерен они должны иметь одинаковый угол наклона спирали, но с противоположными концами. Рис.4.7 Принципиальная взаимосвязь косозубого колеса (правостороннее) (1) Нормальная система Косозубая шестерня В таблице 4.9 показан расчет косозубых зубчатых колес со смещенным профилем в нормальной системе. Если коэффициенты смещения нормального профиля xn1, xn2 равны нулю, они становятся стандартными передачами. Таблица 4.9 Расчет косозубого колеса со смещенным профилем в нормальной системе (1) Если задано межосевое расстояние α, коэффициенты смещения нормального профиля xn1 и xn2 можно рассчитать по таблице 4.10. Это обратные уравнения с пунктов 5 по 10 таблицы 4.9. Таблица 4.10 Расчеты для косозубого колеса со смещенным профилем в нормальной системе (2) Преобразование нормальной системы в поперечную осуществляется с помощью следующих уравнений: (2) Косозубая шестерня поперечной системы Таблица 4.11 Расчеты для косозубого колеса со смещенным профилем в поперечной системе (1) В таблице 4.12 представлен расчет, обратный пунктам 5-9 таблицы 4.11. Таблица 4.12 Расчеты косозубого колеса со смещенным профилем в поперечной системе (2) Преобразование поперечной системы в нормальную описывается следующими уравнениями: (3) Винтовая рейка В поперечной плоскости зацепление косозубой рейки и зубчатого колеса такое же, как у цилиндрического зубчатого колеса и рейки. В таблице 4.13 представлены примеры расчетов сопряженной винтовой рейки с нормальным модулем и нормальным углом давления. Аналогичным образом в таблице 4.14 представлены примеры для винтовой рейки в поперечной системе (т. е. перпендикулярной оси шестерни). Таблица 4.13 Расчеты для винтовой рейки в нормальной системе Формулы для стандартной винтовой рейки аналогичны формулам из Таблицы 4.14 только с коэффициентом сдвига нормального профиля xn=0. Перемещение винтовой рейки, л, за один оборот сопряженной шестерни равно произведению поперечного шага и числа зубьев. Согласно уравнениям табл. 4.13 пусть поперечный шаг pt=8 мм и перемещение l=160 мм. Поперечный шаг и смещение можно было бы выразить в целые числа, если бы угол наклона винтовой линии был выбран правильно. Таблица 4.14 Расчеты косозубой рейки в поперечной системе В зацеплении поперечной системы косозубой рейки и косозубого колеса перемещение l за один оборот косозубого колеса равно поперечному шагу, умноженному на число зубьев. 4.4 Конические зубчатые колеса Конические зубчатые колеса, делительная поверхность которых представляет собой конус, используются для привода пересекающихся осей. Конические зубчатые колеса классифицируются в соответствии с их типом формы зуба на прямое коническое зубчатое колесо, спиральное коническое зубчатое колесо, коническое зубчатое колесо Zerol, косое коническое зубчатое колесо и т. Рис. 4.8 Контрольный угол конуса конического зубчатого колеса Как правило, наиболее часто используется угол вала Σ=90°. Иногда используются и другие углы (рис. 4.8). Тогда это называется «коническая шестерня в непрямоугольном приводе». Корпус 90° называется «коническая шестерня в прямоугольном приводе». Когда Σ=90°, уравнение (4.20) принимает вид: Угловые шестерни являются коническими шестернями с Σ=90° и z1=z2. Их передаточное отношение z2 / z1=1. На рис. 4.9 показано зацепление конических шестерен. Зацепление должно рассматриваться парами. Это связано с тем, что исходные конусы δ1 и δ2 ограничены передаточным числом z2 / z1. На лицевой стороне, которая перпендикулярна линии контакта конусов тангажа, зацепление конических шестерен кажется похожим на зацепление прямозубых шестерен. Рис. 4.9 Зацепление конических шестерен (1) Прямые конические шестерни Gleason Характеристики: ** Конструктивные шестерни со смещенным профилем Рис. 4.10 Размеры и углы конических шестерен В таблице 4.15 указано минимальное количество зубьев для предотвращения поднутрения по системе Глисона при угле наклона вала Σ=90.° поднутрение В таблице 4.16 представлены уравнения для расчета прямозубых конических зубчатых колес по системе Глисона. Значения размеров и углов показаны на рисунке 4.10 выше. Все уравнения в Таблице 4.16 также могут быть применены к коническим зубчатым колесам с любым углом наклона вала. Сказка 4.16 Расчеты прямозубых конических колес системы Глисона Первая характеристика прямозубого прямозубого зубчатого колеса Глисона — это зуб со смещенным профилем. На рисунке 4.11 мы видим профиль зуба прямой конической шестерни Глисона и стандартной прямой конической шестерни. Рис. 4.11 Профиль зубьев прямозубых конических шестерен (2) Стандартные прямозубые конические шестерни Таблица 4.17 Расчеты для стандартных прямозубых конических зубчатых колес Эти уравнения также могут быть применены к комплектам конических зубчатых колес с углами вала, отличными от 90°. (3) Спиральные конические шестерни Глисона Рис. 4.12 Спирально-коническое зубчатое колесо (левостороннее) Все уравнения в таблице 4.20 относятся к методу изготовления раздвинутого лезвия или одностороннего по Глисону. Если зубчатое колесо нарезано не по системе Глисона, уравнения будут отличаться от этих. Профиль зуба спирально-конической шестерни Глисона, показанный здесь, имеет глубину зуба h=1,888 м; просвет вершины и корня с=0,188 м; и рабочая глубина hw=1.700м. Эти спирально-конические зубчатые колеса Глисона относятся к системе коротких зубчатых колес. Это применимо к передачам с модулями m > 2,1. В таблице 4.18 показано минимальное количество зубьев, чтобы избежать поднутрения в системе Глисона с углом наклона вала Σ=90° и углом прижатия αn=20°. Таблица 4.18 Минимальное количество зубьев для предотвращения поднутрения β=35° Если количество зубьев меньше 12, для определения размеров шестерни используется Таблица 4.19. Table 4.19 Dimentions for pinions with number of teeth less than 12
ПРИМЕЧАНИЕ. Все значения в таблице основаны на m=1 В Таблице 4.20 показаны расчеты для спирально-конических колес по системе Глисона Таблица 4.20 Расчеты для спирально-конических зубчатых колес по системе Глисона Все уравнения в Таблице 4.20 также применимы к коническим зубчатым колесам Gleason с любым углом наклона вала. Набор спирально-конических зубчатых колес требует согласования рук; левый и правый в паре. (4) Конические зубчатые колеса Gleason Zerol Рис. 4.13 Левая коническая шестерня 4.5 Винтовые передачи К винтовым передачам относятся различные типы передач, используемые для привода непараллельных и непересекающихся валов, в которых зубья одного или обоих членов пары имеют винтовую форму. На рис. 4.14 показано зацепление винтовых передач. Две винтовые передачи могут зацепляться друг с другом только при условии, что нормальные модули (mn1) и (mn2) и нормальные углы давления (αn1, αn2) одинаковы. Рис.4.14 Винтовые передачи непараллельных и непересекающихся осей Пусть пара винтовых зубчатых колес имеет угол вала Σ и углы подъема винтовой линии β1 и β2 : Если бы профиль винтовых зубчатых колес был смещен, зацепление стало бы немного сложнее. В таблице 4.21 представлены уравнения для винтовой пары со смещенным профилем. При нормальных коэффициентах смещения профиля xn1=xn2=0 уравнения и расчеты такие же, как и для стандартных передач. Таблица 4.21 Уравнения для винтовой пары на непараллельных и непересекающихся осях в нормальной системе Стандартные винтовые передачи имеют следующие соотношения: dw1=d1 Приложение – Что такое винтовая передача? Эта статья воспроизводится с разрешения. Винтовая передача (или скрещенная косозубая передача) на рис. и чья делительная поверхность состоит из двух цилиндрических поверхностей, описывающих в одной точке кратчайшее расстояние между двумя осями. Винтовая передача представляет собой точечную передачу, состоящую из косо зацепленных косозубых колес, у которых сумма или разность углов закручивания дорожек зубьев равна прилежащему углу двух осей. Рис. 5.1 Винтовая передача Фон винтовой передачи На рис. 5.2 точка P в одной точке на кратчайшем расстоянии между двумя осями называется точкой тангажа , где два цилиндра с радиусом R 1 или R 2 , оси которых I и II составляют расстояние между центрами A и включают угол, описанный в точке P. район. Для того чтобы обе боковые поверхности зуба соприкасались в точке Р для передачи движения, они должны иметь общую нормаль, а составляющая скорости обоих колес в направлении нормали к боковым поверхностям зубьев должна быть одинаковой. Следовательно, в точке Р направление следов зубьев должно быть одинаковым, а составляющая скорости обоих колес под прямым углом к следам зубьев должна быть одинаковой. Более конкретно, как и на рис. 5.2, направление вертикальной линии из точки P в сторону направлений векторов скорости передачи V 1 и V 2 в точке P равны составляющей скорости обоих колес (V n ), а прямой угол (TT) к этому направлению в точке P становится направлением следа зуба в точке P. Рис 5.2 Фон винтовой передачи Предположим, что имеется косозубая рейка, которая имеет след зуба в направлении TT и ее касательная плоскость обоих делительных цилиндров в точке P является делительной плоскостью. Когда он движется со скоростью V n кривая, образованная на каждой шестерне в качестве огибающей поверхности боковой поверхности зуба рейки, становится боковой поверхностью зуба обеих шестерен. Когда боковая сторона зуба винтовой рейки плоская, боковая сторона зуба обеих шестерен становится эвольвентным геликоидом. Это эвольвентная винтовая передача, и ее нормальное сечение представляет собой эвольвентный профиль зуба. Линия одновременного контакта боковых сторон зуба каждой шестерни и рейки — след основания перпендикуляра из произвольной точки на шине каждого делительного цилиндра к поверхности зуба рейки через делительную точку Р (она становится прямой линией для эвольвентного винта механизм). След точки контакта обычно представляет собой кривую, проходящую через делительную точку P. Что касается эвольвентной винтовой передачи, то след точки контакта становится прямой линией W, которая проходит через делительную точку P, поскольку плоскость профиля зуба рейки движется параллельно. Линия называется линией действия (см. рис. 5.3), она является линией пересечения касательных плоскостей базовых цилиндров шестерен, а также является неподвижной линией контактов с обоими базовыми цилиндрами. Как и в обычных зубчатых колесах, отношение угловых скоростей равно обратному отношению числа зубьев, а модуль нормальной плоскости должен быть одинаковым для обоих зубчатых колес. Рис. 5.3 Зацепление эвольвентной винтовой передачи Предположим, что угол наклона зуба трасса – β1 и β2, модуль нормальной плоскости винтовой рейки – m n , а количество зубьев каждой шестерни z 1 и z 2 , радиусы шага цилиндров R 1 и R 2 равны: R 5 1 M N / 2COSβ1, R 2 = Z 2 M N / 2COSβ2 Затем, R 1 + R 2 = A, β1 + β2 = β , 2A / MA, 2A / MA / M. Например, когда A, β, z 1 , z 2 и m n даны, β1 и β2 определены по предыдущей формуле. Однако на предыдущем рисунке β1>0, β2>0. β1 и β2 могут быть 0 или отрицательными числами. На самом деле во многих случаях β=90°. При β=90° для минимизации межосевого расстояния установите dA / dβ1=0 и получите Применение винтовой передачи Поскольку винтовые передачи являются точечными, контактное напряжение в точке контакта велико, а смазочная пленка легко истончаются, и в результате шестерни легко изнашиваются. Поэтому винтовые передачи не подходят для передачи большой мощности. С другой стороны, шестерни зацепляются плавно и легко поддаются регулировке разреза, поэтому часто используются для трансмиссионного механизма между косыми валами, межосевое расстояние которых находится посередине. Когда одна из винтовых шестерен (ведомая шестерня) представляет собой реечную передачу, они могут иметь линейный контакт и передавать большую нагрузку. Их можно использовать для привода стола планировочной машины. Также можно использовать бритвенный станок реечного типа. Только кривая, которая проходит на каждой боковой поверхности зуба по диагонали через делительную точку, используется для зацепления боковых поверхностей зубьев винтовых передач, поэтому ширина рабочей поверхности ограничена. Однако небольшое увеличение ширины торца и возможность перемещения шестерен к оси позволит избежать чрезмерного местного износа и увеличить срок службы всей шестерни. 4.6 Цилиндрическая червячная пара Цилиндрические червяки можно рассматривать как шестерни цилиндрического типа с резьбой. В стандарте JIS B 1723-1977 есть четыре профиля червячных зубьев, как определено ниже. Стандартные червячные редукторы KHK относятся к типу III. Профили червяков (рис. Рис. 4.15 Нарезание – шлифование червяка типа III В таблице 4.22 представлены отношения между червяком и червячным колесом в отношении осевой плоскости, поперечной плоскости, нормали, модуля, угла давления, шага и шага. Рис. 4.16 Цилиндрический червяк (правосторонний) Таблица 4. Ссылка на Рисунок 4.16 может помочь понять соотношения в Таблице 4.22. Они аналогичны соотношениям в формулах (4.16) и (4.17) в том, что угол подъема спирали β заменяется на (90 град – γ). Можно считать, что червяк с углом подъема γ почти такой же, как косозубая передача с углом подъема (90 град – γ). (1) Пара червячных передач с осевым модулем Рис. 4.17 Размеры червячной цилиндрической пары Таблица 4.23 Расчеты для осевой модульной системы червячной пары ПРИМЕЧАНИЕ 1. (2) Нормальная модульная система червячной передачи Таблица 4.24 Расчеты для обычной модульной системы червячной передачи ПРИМЕЧАНИЕ: Все примечания такие же, как и в таблице 4.23. (3) Коронка зуба (a) Нарезка червячного колеса червячной фрезой с контрольным диаметром больше, чем у червяка. Это показано на рис. 4.18. Это создает контакт зубьев в центральной области с пространством для образования масляной пленки. Рис. 4.18 Способ использования фрезы большего диаметра (b) Повторная резка с регулировкой центрального положения фрезы. Рис. 4.19 Смещение вверх или вниз (c) Наклон оси фрезы Δθ от стандартного положения. Это показано на рис. 4.20. Популярен только метод (а). Методы (b) и (c) используются редко. Рис. 4.20 Наклон вправо или влево (d) Используйте червяк с большим углом давления, чем у червячного колеса. . необходимо увеличить осевой шаг pwx до нового значения px согласно уравнению (4.25). Величина выпуклости представлена как пространство между червяком и червячным колесом в точке зацепления А на рис. 4.22. Эта сумма может быть аппроксимирована следующим уравнением: Где В таблице 4.26 приведен пример расчета выпуклости червяка. Таблица 4.26 Расчеты для червячного венца (4) Самоблокировка червячных пар Самоблокировка происходит не во всех червячных сетках, так как для нее требуются особые условия, описанные здесь. В этом анализе рассматривается только движущая сила, действующая на поверхности зуба, без учета потерь из-за трения в подшипнике, перемешивания смазки и т.  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


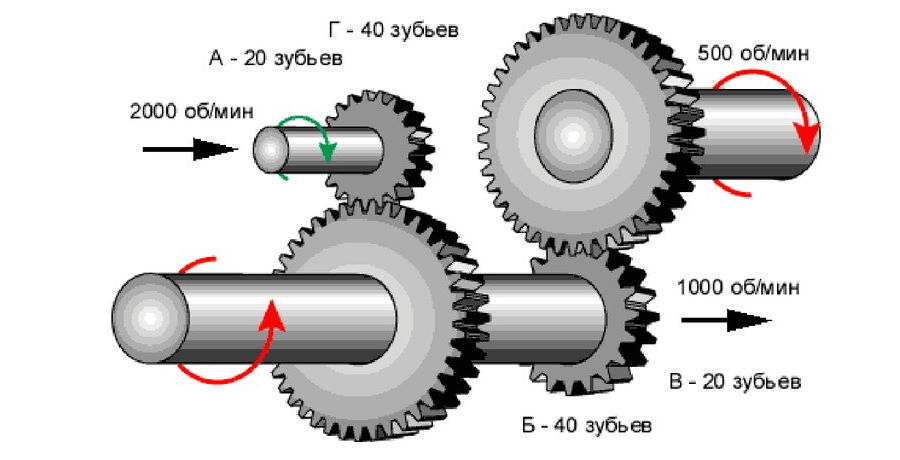





 2.5 Диаметр шестерен
2.5 Диаметр шестерен 2.6 Номенклатура рабочих шестерен
2.6 Номенклатура рабочих шестерен



 8).
8). 
 Это состояние может прогрессировать от умеренного до критического.
Это состояние может прогрессировать от умеренного до критического.
 Это состояние имеет тенденцию возникать при работе на очень низкой скорости и высокой нагрузке.
Это состояние имеет тенденцию возникать при работе на очень низкой скорости и высокой нагрузке.
 Расчеты прямозубых зубчатых колес также просты и используются в качестве основы для расчетов других типов зубчатых колес. В этом разделе представлены методы расчета стандартных цилиндрических зубчатых колес, цилиндрических зубчатых колес со смещенным профилем и линейных реек. Стандартная прямозубая шестерня представляет собой цилиндрическую шестерню без смещения профиля.
Расчеты прямозубых зубчатых колес также просты и используются в качестве основы для расчетов других типов зубчатых колес. В этом разделе представлены методы расчета стандартных цилиндрических зубчатых колес, цилиндрических зубчатых колес со смещенным профилем и линейных реек. Стандартная прямозубая шестерня представляет собой цилиндрическую шестерню без смещения профиля. 000
000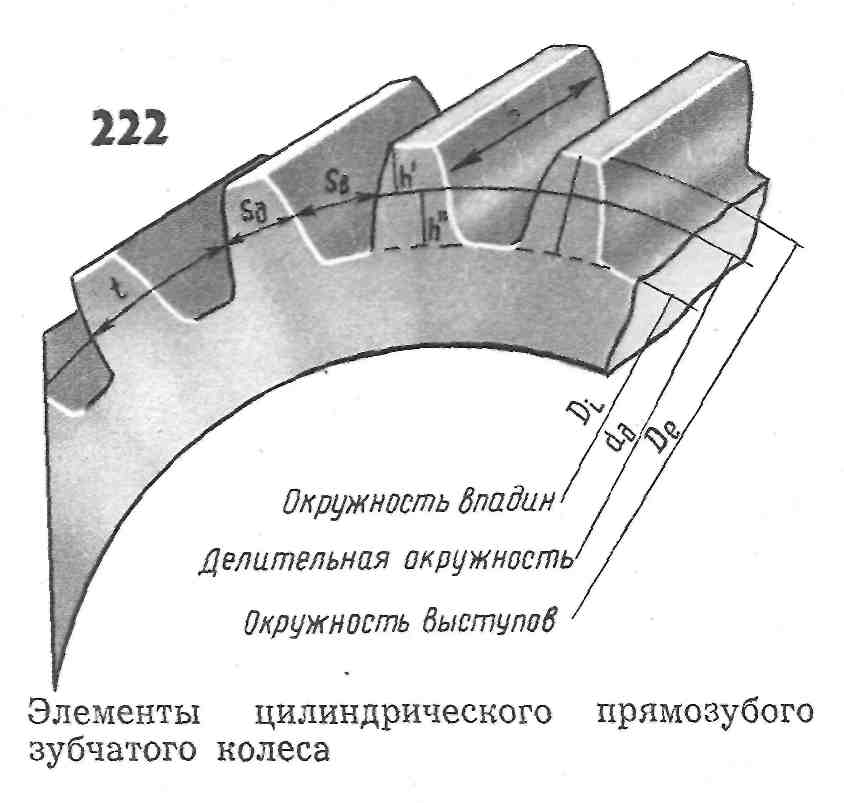 2.
2. 2. В этом случае необходимо будет прибегнуть к смещению профиля или использовать косозубые шестерни, чтобы получить как можно более близкое передаточное число.
2. В этом случае необходимо будет прибегнуть к смещению профиля или использовать косозубые шестерни, чтобы получить как можно более близкое передаточное число. 3 Расчеты для цилиндрических зубчатых колес с профильным смещением (1 )
3 Расчеты для цилиндрических зубчатых колес с профильным смещением (1 )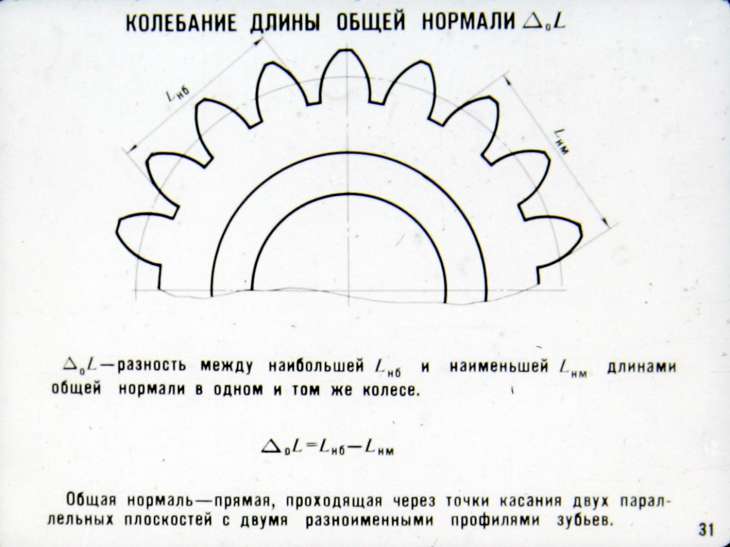 0176 αw
0176 αw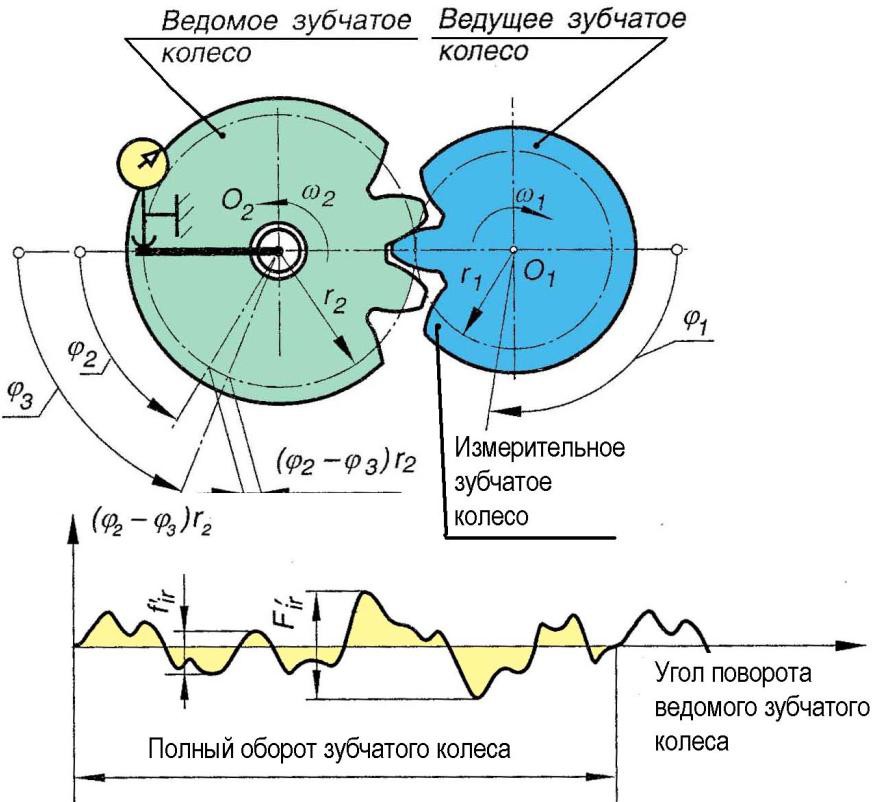 25 + y – ( x1 + x2 )}m
25 + y – ( x1 + x2 )}m 5 представлен метод расчета зацепления зубчатой рейки и цилиндрической шестерни.
5 представлен метод расчета зацепления зубчатой рейки и цилиндрической шестерни.  Уравнение (4.2) остается применимым для любого смещения профиля.
Уравнение (4.2) остается применимым для любого смещения профиля.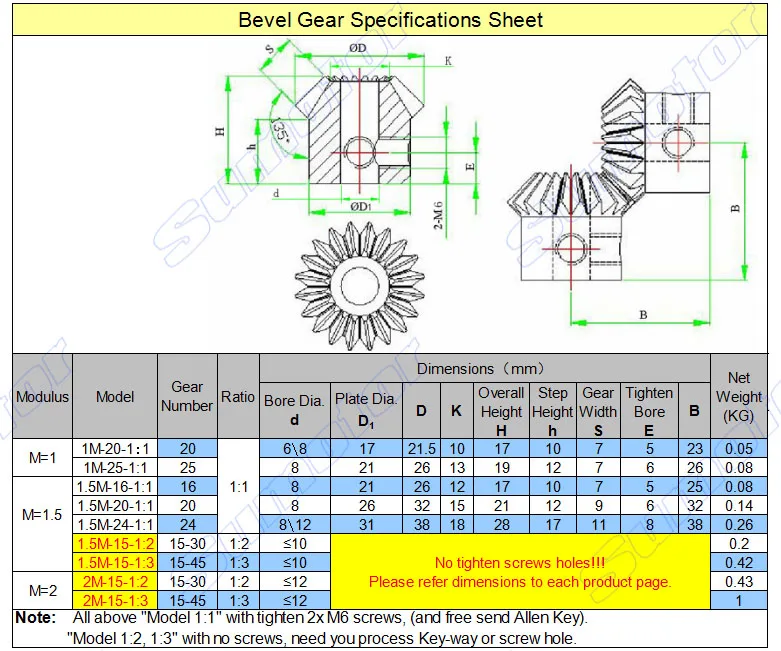 Их можно получить из межцентрового расстояния (а) и уравнений (4.3).
Их можно получить из межцентрового расстояния (а) и уравнений (4.3).
 Обычно это происходит, когда разница между числом зубьев двух шестерен невелика. Уравнение (4.8) представляет собой условие отсутствия трохоидальной интерференции.
Обычно это происходит, когда разница между числом зубьев двух шестерен невелика. Уравнение (4.8) представляет собой условие отсутствия трохоидальной интерференции. е. x0=0.
е. x0=0. В Таблице 4.8(2) показано предельное значение для фрезы со смещенным профилем для предотвращения помех при обрезке при нарезке стандартного внутреннего зубчатого колеса. Поправка (x0) представляет собой величину сдвига, которая принималась равной: x0=0,0075z0 + 0,05.
В Таблице 4.8(2) показано предельное значение для фрезы со смещенным профилем для предотвращения помех при обрезке при нарезке стандартного внутреннего зубчатого колеса. Поправка (x0) представляет собой величину сдвига, которая принималась равной: x0=0,0075z0 + 0,05. 2
2
 А pt, деленное на π, есть поперечный модуль, mt.
А pt, деленное на π, есть поперечный модуль, mt. 15). Это связано с тем, что зацепление косозубых колес в поперечной плоскости точно такое же, как и у цилиндрических зубчатых колес, и расчет аналогичен.
15). Это связано с тем, что зацепление косозубых колес в поперечной плоскости точно такое же, как и у цилиндрических зубчатых колес, и расчет аналогичен. Они становятся стандартными, если xt1=xt2=0.
Они становятся стандартными, если xt1=xt2=0.
 Д. Зацепление конических зубчатых колес означает, что конус тангажа двух зубчатых колес контактирует и катится друг с другом. Пусть z1 и z2 — числа зубьев шестерни и шестерни; угол вала Σ ; и исходные углы конусности δ1 и δ2 ; тогда:
Д. Зацепление конических зубчатых колес означает, что конус тангажа двух зубчатых колес контактирует и катится друг с другом. Пусть z1 и z2 — числа зубьев шестерни и шестерни; угол вала Σ ; и исходные углы конусности δ1 и δ2 ; тогда:



 500
500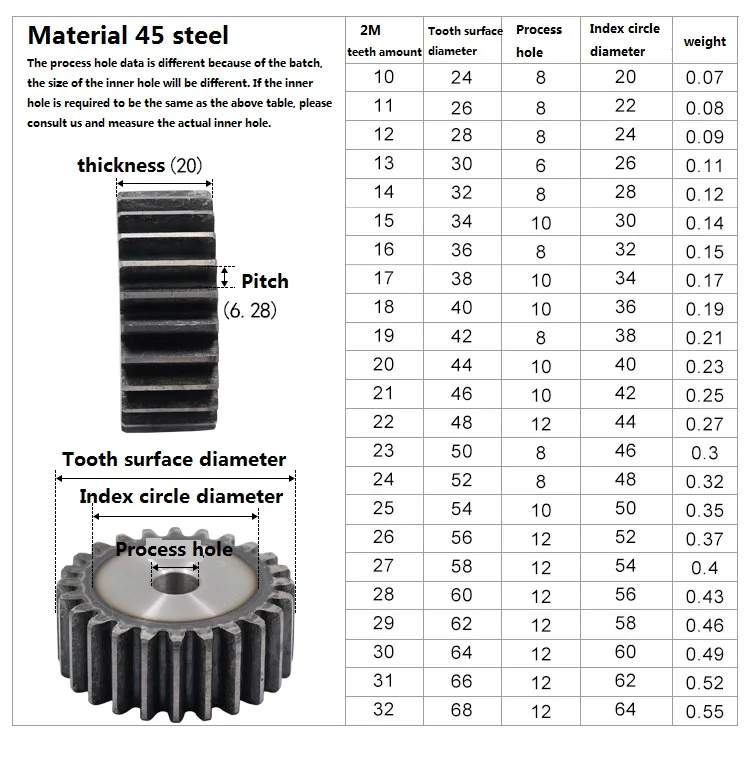 948
948
 Пусть βw1, βw2 представляют цилиндр рабочего шага;
Пусть βw1, βw2 представляют цилиндр рабочего шага;
 Компоненты скорости V 1 и V 2 не равны в направлении TT. То есть происходит скольжение в направлении следа зуба.
Компоненты скорости V 1 и V 2 не равны в направлении TT. То есть происходит скольжение в направлении следа зуба. Обе дорожки пересекаются у подножия перпендикуляра, проведенного из делительной точки Р к профилю зуба рейки. (См. рис. 5.3 (а) N A и N B ) Таким образом, оба профиля зубьев соприкасаются в этой точке.
Обе дорожки пересекаются у подножия перпендикуляра, проведенного из делительной точки Р к профилю зуба рейки. (См. рис. 5.3 (а) N A и N B ) Таким образом, оба профиля зубьев соприкасаются в этой точке. / M. / M. / M. / M. / M. / M. / M. / M. / M. / M. / M. / M. / M. / M. / M. n =z 1 / cosβ1 + z 2 / cos(β – β1)
/ M. / M. / M. / M. / M. / M. / M. / M. / M. / M. / M. / M. / M. / M. / M. n =z 1 / cosβ1 + z 2 / cos(β – β1) Кроме того, хорошо известно, что зацепление резца и обрабатываемого зубчатого колеса при зубобритье аналогично винтовым зубчатым передачам. Отношение зацепления фрезы и зубчатых колес, подлежащих нарезке, также аналогично винтовым зубчатым колесам.
Кроме того, хорошо известно, что зацепление резца и обрабатываемого зубчатого колеса при зубобритье аналогично винтовым зубчатым передачам. Отношение зацепления фрезы и зубчатых колес, подлежащих нарезке, также аналогично винтовым зубчатым колесам. Как правило, сетка имеет угол вала 90 °. Количество витков в червяке эквивалентно количеству зубьев в шестерне винтового зубчатого зацепления. Таким образом, однозаходный червяк эквивалентен однозубой шестерне; и двухзаходные, эквивалентные двум зубьям, и т. д. Ссылаясь на рисунок 4.15, для эталонного угла подъема цилиндра γ, измеренного на делительном цилиндре, каждый оборот червяка заставляет резьбу продвигаться на один шаг pz.
Как правило, сетка имеет угол вала 90 °. Количество витков в червяке эквивалентно количеству зубьев в шестерне винтового зубчатого зацепления. Таким образом, однозаходный червяк эквивалентен однозубой шестерне; и двухзаходные, эквивалентные двум зубьям, и т. д. Ссылаясь на рисунок 4.15, для эталонного угла подъема цилиндра γ, измеренного на делительном цилиндре, каждый оборот червяка заставляет резьбу продвигаться на один шаг pz. 4.15). Режущий инструмент, применяемый для обработки червячных передач, называется однолезвийным, имеющим однолезвийное лезвие. Нарезка червячных передач производится с помощью червячного отрезного станка. Поскольку зацепление червяка соединяет непараллельные и непересекающиеся оси, осевая плоскость червяка не совпадает с осевой плоскостью червячного колеса. Осевая плоскость червяка соответствует поперечной плоскости червячного колеса. Поперечная плоскость червяка соответствует осевой плоскости червячного колеса. Общая плоскость червяка и червячного колеса — нормальная плоскость. Использование обычного модуля mn наиболее популярно. Затем для нарезки червячного колеса можно использовать обычную фрезу.
4.15). Режущий инструмент, применяемый для обработки червячных передач, называется однолезвийным, имеющим однолезвийное лезвие. Нарезка червячных передач производится с помощью червячного отрезного станка. Поскольку зацепление червяка соединяет непараллельные и непересекающиеся оси, осевая плоскость червяка не совпадает с осевой плоскостью червячного колеса. Осевая плоскость червяка соответствует поперечной плоскости червячного колеса. Поперечная плоскость червяка соответствует осевой плоскости червячного колеса. Общая плоскость червяка и червячного колеса — нормальная плоскость. Использование обычного модуля mn наиболее популярно. Затем для нарезки червячного колеса можно использовать обычную фрезу. 22 Соотношения поперечных сечений червячных пар
22 Соотношения поперечных сечений червячных пар
 Это червячное колесо без короны очень сложно правильно собрать. Надлежащий контакт зубьев и полная масляная пленка обычно невозможны.
Это червячное колесо без короны очень сложно правильно собрать. Надлежащий контакт зубьев и полная масляная пленка обычно невозможны.  После этого ось фрезы немного смещают влево, а затем вправо, Δθ, в плоскости, параллельной оси червячного колеса, чтобы исключить влияние короны на зуб червячного колеса.
После этого ось фрезы немного смещают влево, а затем вправо, Δθ, в плоскости, параллельной оси червячного колеса, чтобы исключить влияние короны на зуб червячного колеса.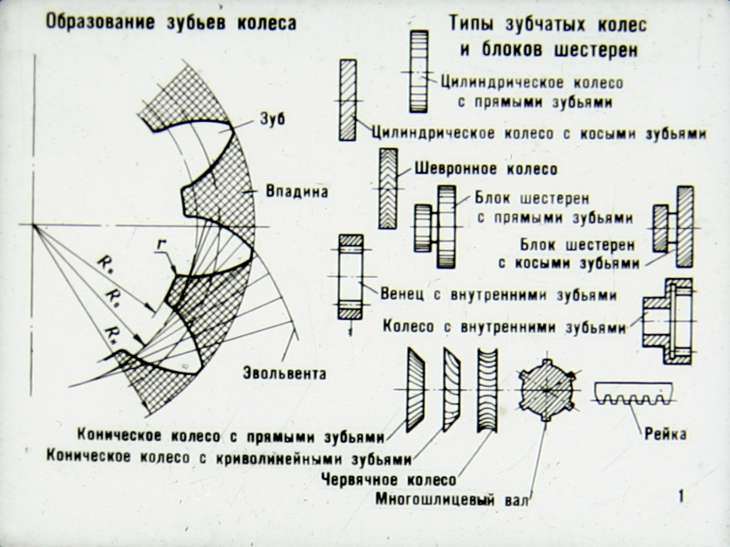 25 и рисунка 4.21
25 и рисунка 4.21