Содержание
7. Определение числа зубьев шестерни и колеса. Число зубьев шестерни определяют по формуле
.
Полученное
значение округляют до ближайшего целого.
Число
зубьев колеса определяется следующей
зависимостью: Z2=Zå-Z1.
8.
Определения
фактического передаточного числа. Его
находят по формуле: Uф=Z2/Z1
, причем на отклонение от заданного
передаточного числа наложено ограничение:
.
9.
Определение
размеров колёс. Делительные диаметры
шестерни и колеса определяют по формулам:
и
.
Далее
определяют диаметры окружностей вершин
da
и впадин df
шестерни
da1=d1+2m,
df1=d1-2,5m;
колеса
da2=d2+2m,
df2=d2-2,5m.
Ширину
шестерни принимают в зависимости от
ширины колеса.
10.
Проверка
пригодности заготовки колес. Это
необходимо, так как чтобы получить
необходимые механические характеристики
материала колес, размеры заготовки
колес не должны превышать предельно
допустимых величин. Значения Dзаг,
Cзаг,
Sзаг
(мм) вычисляют по формулам:
для шестерни
Dзаг=da+6мм;
для колеса принимают
меньшее из двух Cзаг=0,5b2;
Sзаг=8m.
Условия
пригодности заготовки колес имеют вид:
Dзаг£Dпред
, Cзаг (Sзаг)
£
Sпред.
Если
эти условия не выполняются, то необходимо
изменить материал детали или вид ее
термической обработки.
11.
Нахождение
сил в зацеплении по формулам:
окружная
;
радиальная
;
осевая
.
Подсчёты
проводятся для стандартного угла a=200.
12.
Проверка
зубьев колес по напряжениям изгиба.
Предварительно определяют степень
точности передачи в зависимости от
окружной скорости и значения коэффициентов
KFa,
Yb,
yd,
KFb,
KFV,
YV:
KFa
— по таблице, в зависимости от степени
точности передачи;
;
коэффициент
ширины ищется по формуле:
;
,
где
S — индекс схемы передачи.
Значение
коэффициента KFV
принимают в зависимости от твердости
зубьев.
Коэффициент
формы зуба
YF
принимают в зависимости от zv=z/cos3b
по таблице 2.5 [1].
Расчетное
напряжение изгиба в зубьях колеса равно:
;
Расчетное
напряжение изгиба в зубьях шестерни
равно:
;
Эти
напряжения могут отклоняться от
допускаемых не более, чем в 1,1 раза.
13.
Проверка зубьев колес по контактным
напряжениям. Для этого предварительно
определяют значения коэффициента
распределения нагрузки между зубьями
KHa.
Значение коэффициента концентрации
нагрузки подсчитывают по формуле:
,
Коэффициент
динамической нагрузки KHV
зависит
от твердости зубьев. Далее находят
расчетное контактное напряжение по
зависимости:
.
Полученное
контактное напряжение должно находиться
в интервале (0,9..1,05) [s]H.
Если это условие не выполняется, то
изменяют aw
или b2.
Варианты
N
1, 3, 4, 6, 7 ,9 не обеспечивают одинакового
погружения колёс в масляную ванну. Из
оставшихся 2, 5, 8 вариантов вариант N
2 имеет наибольшую стоимость (93.44) — это
дорого. У варианта N
8 более высокая твёрдость шестерён и
зубчатых колёс (
по 59
HRC), в то
время как у варианта N
5 твёрдость шестерён и зубчатых колёс
49
HRC и 28HRC
соответственно. Значит, выбираем вариант
Значит, выбираем вариант
N
5.
Модуль зуба шестерни. Определение, расчет, применение
Зубчатая передача представляет собой способ передачи энергии от одной детали к другой. Осуществляется данное взаимодействие с помощью таких изделий, как шестерни. Такая деталь представляет собой колесо, на поверхности которого имеются зубья. Всё разнообразие шестерней, производимых для различных механизмов или оборудования, изготавливаются с конкретным количеством зубьев, которые имеют определенные параметры модуля и шага. Модуль зуба шестерни является одним из наиболее важных параметров и используется при необходимости выбора парных шестерней, так как модуль в ведущей и ведомой шестерне должен быть одинаковым. По своей сути модуль представляет собой форму зуба шестерни, его размер и иные показатели. Для бесперебойной работы механизма значение модуля в обязательном порядке должно быть одинаковым у деталей, которые работают в зацеплении друг с другом. Параметры же диаметра или количество зубьев подбираются в зависимости от необходимой мощности.
Модуль зуба шестерни является универсальным параметром, позволяющим определить прочие необходимые показатели шестерни. Он показывает величину дуги, которая приходится на один зуб колеса. Данная величина измеряется в миллиметрах. Стандартные параметры данного показателя определяются в соответствии с нормативными актами, такими как госты. При изготовлении шестерен отталкиваются именно от параметров модуля, исходя из которых происходит расчет других величин, необходимых для производства. Величина модуля подбирается в зависимости от необходимых параметров прочности изделия, которые также зависят от требуемой мощности детали при работ механизма. После выбора нужной величины модуля и количества зубьев, необходимых для каждого конкретного случая, производятся вычисления прочих параметров, таких как диаметр впадин и вершин, длина окружного шага, толщину зубьев, а также расстояние между зубьями.
Как правило, в большинстве случае расчеты производятся для всех шестерней, входящих в состав механизма, однако, бывают случаи, требующие индивидуального расчета. В первую очередь определяется необходимое количество зубьев и параметры модуля.
В первую очередь определяется необходимое количество зубьев и параметры модуля.
- Для определения модуля требуется произвести расчеты на прочность. Они проводятся в зависимости от срока службы изделия, а также используемого материала. Также на этом этапе происходит определение расстояния между осями колес.
- По результатам полученных расчетов необходимой выносливости детали, определяют наиболее подходящую величину модуля зуба шестерни. Для этого используются данные, содержащиеся в нормативной литературе, устанавливающей минимально необходимые значения модулей для конкретных параметров выносливости.
- В зависимости от требуемых показателей мощности подбирается необходимое число зубьев будущей детали.
- На основании полученных данных относительно количества зубьев и их числа, производится расчет прочих параметров, необходимых для производства изделия.
В результате всех произведенных вычислений происходит проверка изделий на прочность. При успешной проверке рассчитанные параметры используют для производства остальных деталей механизма.
Базовая терминология и расчет передач
ВЕРШИНА
Знание передач
Азбука передач — B
Базовая терминология и расчет передач
>
>
>
Размер шестерни, угол давления, количество зубьев… мы вводим основную терминологию, измерения и относительные выражения, необходимые для понимания основных технологий зубчатых передач.
Сравнительный размер зубьев шестерни
В соответствии с рекомендациями ISO (Международной организации по стандартизации) размер модуля обозначается как единица, представляющая размеры зубьев шестерни. Однако используются и другие методы.
Модуль (м)
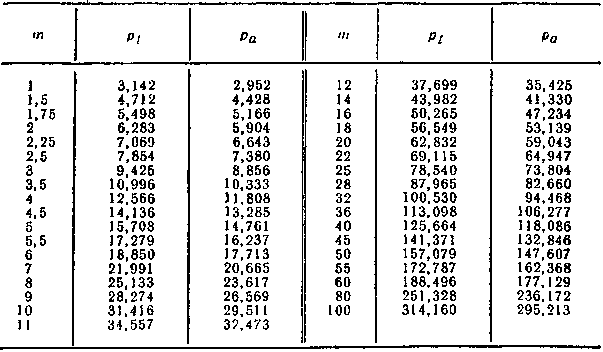
м = 1 (p = 3,1416)
м = 2 (p = 6,2832)
м = 4 (p = 12,566)
Пи, вы можете получить Шаг (p). Шаг – это расстояние между соответствующими точками на соседних зубах.
p = Pi x Module = πm (2.1)
Пример расчета
Каков размер шага (p) шестерни с модулем m = 3?
p = πm = 9,4248
CP (круговой шаг)
Круговой шаг (CP) обозначает эталонный шаг (p).
Например, вы можете производить шестерни с точным интегральным значением, например CP5/CP10/CP15/CP20.
Преобразование CP в модуль
m = CP / π (2.2)
Пример расчета
CP10 преобразуется в модуль следующим образом ;
м = 10 / 3,1416 = 3,1831
DP (диаметральный шаг)
DP означает диаметральный шаг.
По стандартам ISO единица миллиметр (мм) предназначена для выражения длины, однако в США, Великобритании и других странах используется единица измерения дюйм; Диаметральный шаг также используется в этих странах.
Преобразование DP в модуль
m = 25,4 / DP (2.3)
Пример расчета
DP 8 преобразуется в модуль следующим образом ;
м = 25,4 / 8 = 3,175
Угол давления (α)
Угол давления — это угол наклона зуба шестерни, элемент, определяющий профиль зуба.
В последнее время угол давления (α) обычно устанавливается равным 20°, однако преобладали шестерни 14,5°.
Рис. 2.2 Нормализованный профиль зуба по эталону
(Важная терминология и номенклатура зубчатых колес на рис. 2.2)
- Базовая линия
- Угол давления
- Нормальная опорная линия
- Шаг
- Поверхность зуба
- Корневая поверхность
- Верхняя земля
Количество зубьев
Количество зубьев обозначает количество зубьев шестерни.
Они подсчитываются, как показано на рисунке 2.3. Число зубьев этой шестерни равно 10.
Рис. 2.3 Число зубьев
Модуль (m), Угол давления (α) и Число зубьев, введенные здесь, являются тремя основными элементами в составе зубчатого колеса. механизм. На основе этих элементов рассчитываются размеры зубчатых колес.
механизм. На основе этих элементов рассчитываются размеры зубчатых колес.
Глубина и толщина зуба
Глубина зуба определяется размером модуля (м). Здесь представлены профили зубьев (полная глубина), указанные в стандартах ISO и JIS (японские промышленные стандарты).
Пожалуйста, см. рисунок 2.4 ниже для пояснений для Глубина зуба (h) / Дополнение (ha) / Dedendum (hf).
Глубина зуба (h) — это расстояние между вершиной зуба и корнем зуба.
h = 2,25 м
(= Дополнение + Вывод) (2.4)
Рис. 2.4 Глубина и толщина зуба
(Важная терминология и номенклатура зубчатых колес на рис. 2.4)
- Базовая линия
- Шаг
- Толщина зуба
- Приложение
- Дедендум
- Глубина зуба
- Наконечник зуба
- Корень зуба
Дополнение (га) — расстояние между базовой линией и вершиной зуба.
га = 1,00 м (2,5)
Дедендум (hf) — расстояние между базовой линией и корнем зуба.
hf = 1,25 м (2,6)
Толщина зуба (s) в основном составляет половину значения шага (p). * Шаг (p) = πm
s = πm / 2 (2.7)
Примеры расчетов
Ниже приведены расчеты глубины зуба (h)/добавления (ha)/дедендума (hf) для зубчатого колеса с модулем 2.
h = 2,25 м = 2,25 × 2 = 4,50
га = 1,00 м = 1,00 × 2 = 2,00
hf = 1,25 м = 1,25 × 2 = 2,50 Модуль», «Угол давления», «Количество зубьев» и «Глубина и толщина зуба». В этом разделе мы познакомим вас с основными частями цилиндрических зубчатых колес (цилиндрическими зубчатыми колесами) и расчетами размеров.
Диаметр шестерен (размер)
Размер шестерен определяется в соответствии с эталонным диаметром (d) и определяется этими другими факторами; базовый круг, Шаг, Толщина зуба, Глубина зуба, Дополнение и Дедендум.
Базовый диаметр (d)
d = zm(2,8)
Диаметр наконечника (da)
da = d + 2 м(2,9)
Диаметр основания (df)
df 5 м2 (1,0 d2 — 2,0 )
Рис. 2.5 Диаметр шестерен
2.5 Диаметр шестерен
(Важная терминология и номенклатура шестерен на рис. 2.5)
- Приложение
- Дедендум
- Диаметр корня
- Базовый диаметр
- Диаметр наконечника
Добавление и окружность дедендума, представленные здесь, являются эталонной окружностью, которую нельзя увидеть на шестерне, так как это виртуальная окружность, определяемая размером шестерни.
Примеры расчетов
Ниже приведены расчеты исходного диаметра / диаметра вершины / диаметра основания для цилиндрического зубчатого колеса с модулем (m) 2 и 20 зубьями (z).
d = zm = 20 x 2 = 40
da = d + 2 m = 40 + 4 = 44
df = d – 2,5 m = 40 – 5 = 35 m) = 4
Количество зубьев (z) = 40 (угол зацепления α = 20°)
| Базовый диаметр | д = | |
| Диаметр наконечника | да = | |
| Диаметр основания | дф = |
Рис. 2.6 Номенклатура рабочих шестерен
2.6 Номенклатура рабочих шестерен
(Важная терминология и номенклатура шестерен на рис. 2.6)
- Диаметр наконечника
- Базовый диаметр
- Диаметр основания
- Диаметр корня
- Ширина лица
- Толщина зуба
- Базовый шаг
- Осевая линия
- Угол давления
- Люфт
- Глубина зуба
- Приложение
- Дедендум
- Межосевое расстояние
- Наконечник и корневой зазор
Таблица 2.1 Символы и номенклатура шестерен
| Термины | Символы | Условия | Символы |
|---|---|---|---|
| Модуль | м | Толщина зуба | с |
| Угол давления | α | Базовый диаметр | д |
| Номер зуба | с | Диаметр наконечника | да |
| Шаг | р | Диаметр корня | дф |
| Глубина зуба | ч | Расстояние до центра | и |
| Приложение | га | Люфт | и |
| Дедендум | хф | Наконечник и зазор корня | в |
Расстояние между центрами и люфт
Когда пара шестерен находится в зацеплении так, что их опорные окружности соприкасаются, межосевое расстояние (a) составляет половину суммы их опорных диаметров.
Расстояние до центра (а)
a = ( d1 + d2 ) / 2(2.11)
Рис. 2.7 Расстояние между центрами
Зубчатые колеса могут зацепляться, как показано на рис. может работать бесперебойно. Люфт – это люфт между поверхностями зубьев парных шестерен в зацеплении.
Сопрягаемые шестерни также имеют зазор (люфт) по вертикали глубины зуба. Это называется зазором между вершиной и корнем (c), расстоянием между основанием зуба и вершиной зуба сопрягаемых шестерен.
Зазор кончика и корня (c)
c = 1,25 м — 1,00 м
= 0,25 м (2,12)
Рис. 2.8 Зазор между вершиной и основанием
(Важная терминология и номенклатура зубчатых колес на рис. 2.8)
- Приложение 04 круг
- Круг Дедендума
- Наконечник и корневой зазор
Примеры расчетов
Ниже приведены расчеты межцентрового расстояния (a) и зазора между вершинами и впадинами (c), когда модуль m = 2, шестерня z1 = 20, шестерня z2 = 40
Базовый диаметр шестерни d1 = 20 × 2 = 40
Базовый диаметр зубчатого колеса d2 = 40 × 2 = 80
Расстояние между центрами a = (40 + 80) / 2 = 60
c = 0,25 × 2 = 0,5
Примеры расчета
Практика расчета размеров шестерни.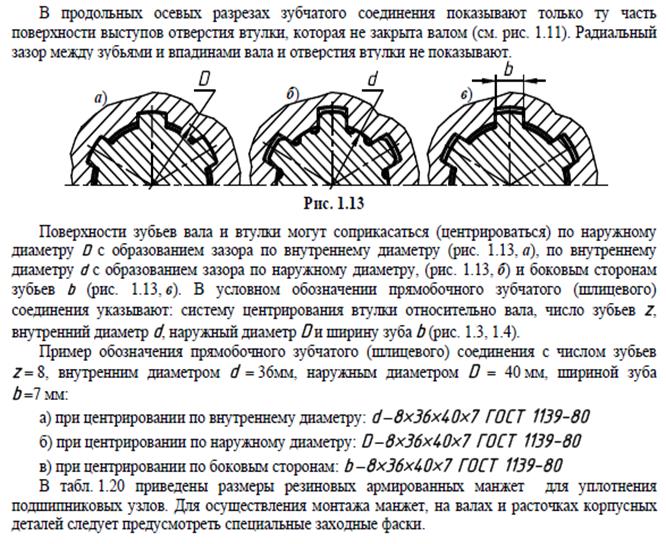
| Термины | Символы | Формула | Шестерня | Шестерня |
|---|---|---|---|---|
| Модуль | м | — | 2,5 | |
| Угол давления | α | 20° | ||
| Кол-во зубьев | с | 15 | 30 | |
| Базовый диаметр | д | с м | 37,5 | 75 |
| Приложение | га | 1,00 м | 2,5 | 2,5 |
| Дедендум | вч | 1,25 м | 3,125 | 3,125 |
| Глубина зуба | ч | 2,25 м | 5,625 | 5,625 |
| Диаметр наконечника | да | д + 2 м | 42,5 | 80 |
| Диаметр основания | дф | г — 2,5 м | 31,25 | 68,75 |
| Межцентровое расстояние | и | д1 + д2/2 | 56,25 | |
Практический тест:
Расчеты размеров зубчатых колес.
| Условия | Символы | Формула | Шестерня | Шестерня |
|---|---|---|---|---|
| Модуль | м | — | 4 | |
| Угол давления | α | 20° | ||
| Кол-во зубьев | с | 12 | 60 | |
| Базовый диаметр | д | с м | ||
| Приложение | га | 1,00 м | ||
| Дедендум | вч | 1,25 м | ||
| Глубина зуба | ч | 2,25 м | ||
| Диаметр наконечника | да | г + 2 м | ||
| Диаметр основания | дф | г — 2,5 м | ||
| Расстояние между центрами | и | д1 + д2/2 | ||
Косозубая шестерня
Цилиндрические шестерни с геликоидными зубьями называются косозубыми шестернями.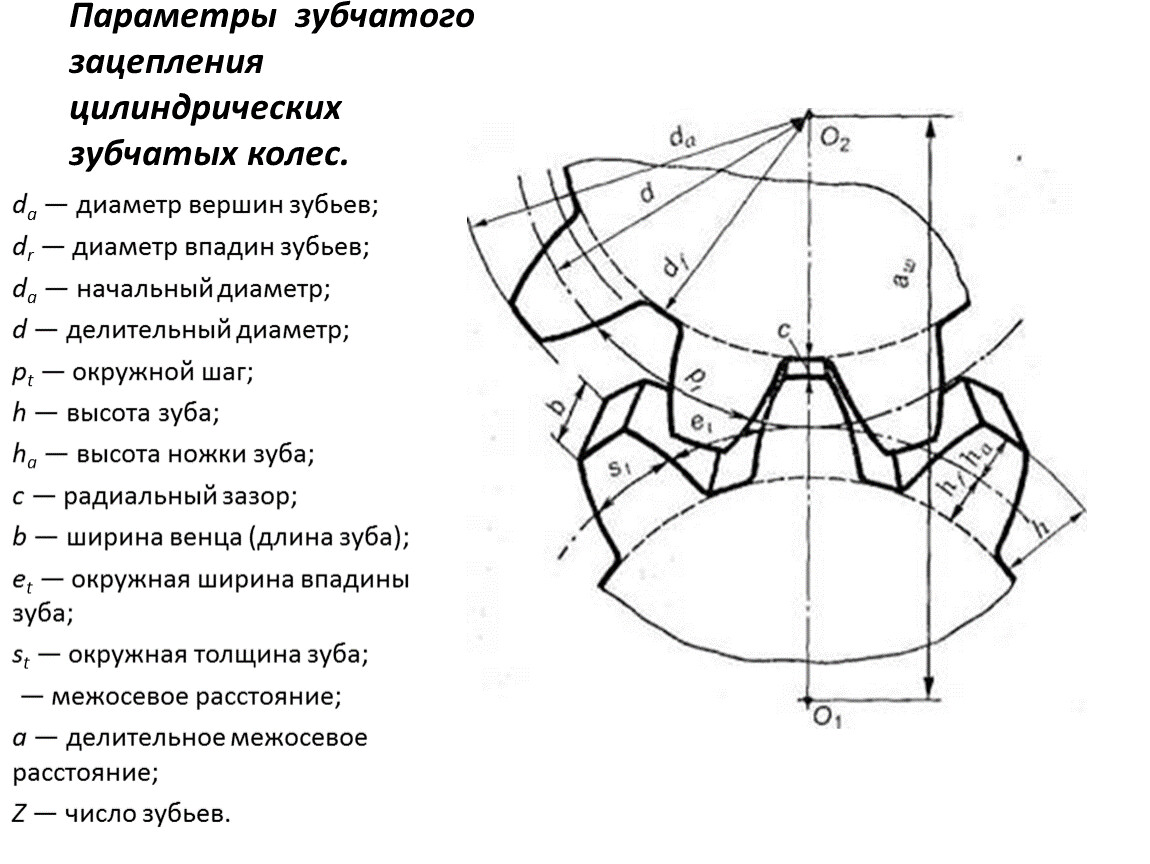
Большинство расчетов для цилиндрических зубчатых колес можно применить и к косозубым. Этот тип зубчатого колеса поставляется с двумя видами профилей зубьев в соответствии с базовой поверхностью. (Рисунок 2.9)
Рис. 2.9 Правосторонняя косозубая шестерня
(Важная терминология и номенклатура шестерен на рис. 2.9)
- Обычный модуль
- Поперечный модуль
- Угол подъема спирали β
(a) Поперечная система (поперечный модуль / угол давления) * Поперечная ось обозначает центральную линию шестерни.
(b) Стандартная система (стандартный модуль/угол давления)
Реляционное выражение: поперечный модуль ( mt ) и нормальный модуль ( mn )
mt = mn / cos β(2.13)
Обе системы используются в стандартных редукторах KHK.
Поперечная система:KHG Заземляющие косозубые шестерни
Обычная система:SH Косозубые шестерни
Базовый диаметр (d) косозубой шестерни с поперечной системой можно рассчитать по уравнению (2. 8).
8).
Базовый диаметр (d) косозубого колеса с нормальной системой можно рассчитать по уравнению (2.14).
d = zmn / cos β(2.14)
Примеры расчетов
Ниже приведен расчет эталонного диаметра косозубого колеса с:
Поперечный модуль mt = 2, число зубьев z = 30, угол подъема β = 15° (П)
Базовый диаметр d = zmt = 30 × 2 = 60
Ниже приведен расчет эталонного диаметра косозубой шестерни с:
Нормальным модулем mn = 2, числом зубьев z = 30, углом подъема винтовой линии β = 15° (R)
эталонным диаметром d = zmn / cos β = 30 × 2 / cos 15° = 62,117
Практический тест:
Технические характеристики косозубого колеса
Нормальный модуль (mn) = 4 Угол подъема винтовой линии (β) = 15°
Поперечный модуль mt =
Поиск и устранение неисправностей шестерен: объяснение терминологии
Точечная коррозия
Когда поверхность зубчатого колеса постоянно подвергается нагрузке, а усилие вблизи точки контакта превышает предел усталости материала, возникают мелкие трещины, которые в конечном итоге перерастают в разделение мелких частей, образуя ямки (кратеры).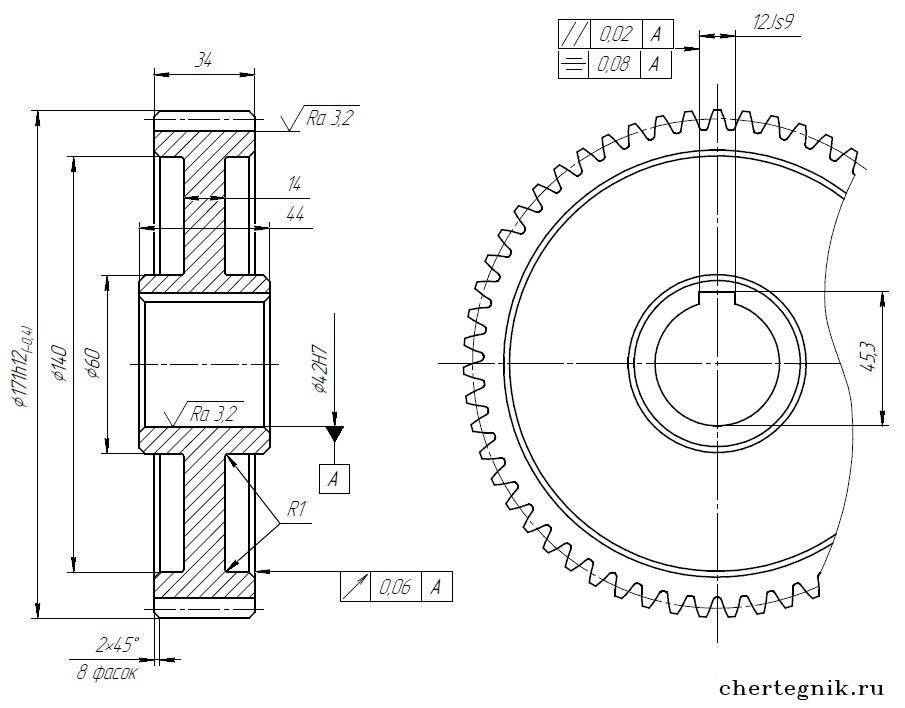
Начальная стадия Точечная коррозия
Первоначальная причина связана с небольшими выпуклыми участками поверхностей зубчатых колес, контактирующими друг с другом, и локальной нагрузкой, превышающей предел усталости. По мере приведения в движение шестерен и износа поверхностей локальные выпуклости исчезают, нагрузка выравнивается, питтинг прекращается.
Прогрессирующая точечная коррозия
Даже после износа поверхностей зубчатых колес и выравнивания нагрузки со временем начинает появляться больше точечной коррозии, и ямки увеличиваются.
(1) Когда существует состояние перегрузки и нагрузка на поверхность зубчатого колеса превышает предел усталости материала.
(2) Во время движения распределение нагрузки по поверхности зубчатого колеса может стать неравномерным из-за прогиба различных частей, что приведет к превышению предела усталости.
Вот некоторые из возможных причин прогрессирующей точечной коррозии.
Задиры
Это состояние, при котором смазочное покрытие разрушается из-за перегрева локальных контактных площадок, что приводит к износу поверхности зубчатого колеса от контакта металла к металлу. Это состояние может прогрессировать от умеренного до критического.
Это состояние может прогрессировать от умеренного до критического.
Проточка
В направлении скольжения шестерни появляются канавки. Это часть абразивного износа, и возможны следующие причины.
(1) Износ из-за попадания твердого постороннего предмета, превышающего толщину масляной пленки, в зацепление шестерни.
(2) Износ из-за твердого постороннего предмета, по какой-то причине застрявшего в зубе противоположной шестерни.
(3) Износ от твердой выпуклой части зуба противоположной шестерни, врезающейся в зацепляющую шестерню.
Абразивный износ
Износ, который выглядит как травма от истирания или имеет вид притирки. Ниже приведены некоторые из причин.
(1) Возможен износ из-за попадания в смазку твердых посторонних предметов (таких как металлические частицы износа, заусенцы, окалина, песок и т. д.).
(2) Износ из-за разницы в твердости двух зацепляющихся шестерен, в которых твердая выпуклая часть впивается в более мягкую поверхность шестерни.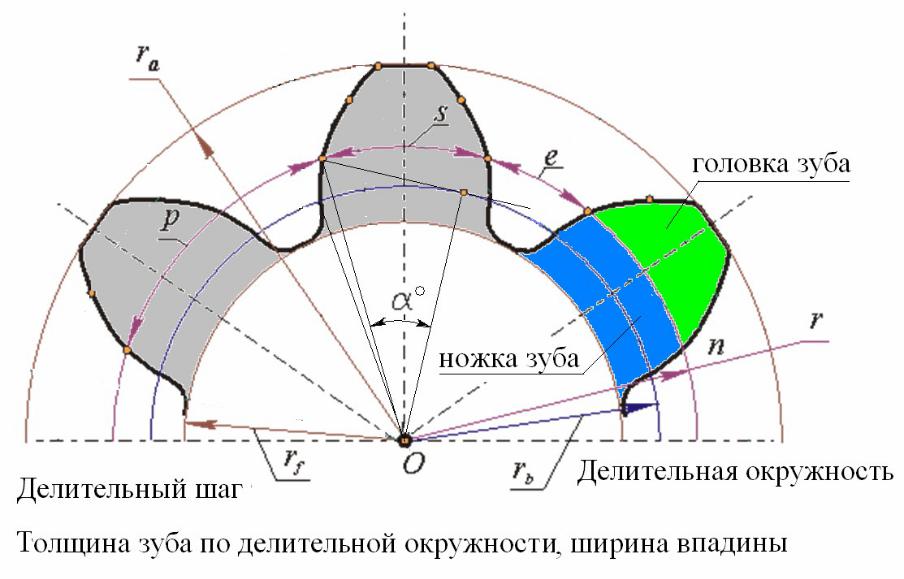
Адгезионный износ
Износ, обычно возникающий между металлами при скользящем контакте. Снижение износа зависит от типа, давления, скорости, расстояния и смазки.
Незначительная часть материала в контактных сварных швах (прилипаниях) и механизм износа возникает в результате их отслоения под действием силы сдвига.
Выкрашивание
Относится к симптому отпадания относительно крупной металлической стружки с поверхности зубчатого колеса из-за усталости материала под поверхностью при высокой нагрузке. Вогнутая часть поверхности зубчатого колеса большая, а форма и глубина неправильные. Поскольку приложенная сила сдвига превышает предел выносливости материала, появляются и растут усталостные трещины, что может привести к поломке зуба.
Чрезмерный износ
Износ от поверхности зубчатого колеса, подвергающегося интенсивному повторяющемуся контакту металла с металлом, который возникает, когда масляная пленка тонкая и смазка недостаточна по сравнению с нагрузкой и шероховатостью поверхности зубчатого колеса. Это состояние имеет тенденцию возникать при работе на очень низкой скорости и высокой нагрузке.
Это состояние имеет тенденцию возникать при работе на очень низкой скорости и высокой нагрузке.
Поломка из-за перегрузки
Поломка из-за неожиданно большой нагрузки в течение одного или нескольких рабочих циклов (Обычно сюда не включаются ошибки проектирования или изготовления). Поверхность излома волокнисто распространяется от начальной точки и указывает на внезапное расщепление. Причина в том, что нагрузка превышает предел прочности на растяжение материала шестерни. Это может произойти из-за первичного двигателя, ведомого механизма или поломки подшипников или других шестерен, что может вызвать заедание зубьев, внезапную остановку или концентрацию нагрузки из-за неравномерного контакта зубьев.
Усталостная поломка
Это случай, когда корневая часть зубчатого колеса подвергается многократной нагрузке, превышающей предел усталости материала. Трещина, которая начинается в углу корня шестерни, распространяется до тех пор, пока зуб не сломается. Поверхность излома относительно гладкая, и начальную точку часто можно распознать по береговой отметине (рисунку раковины) вокруг нее.
Поломка при сдвиге
Описывает случай, когда зуб отделяется от тела в результате сдвига из-за однократной экстремальной перегрузки. Поломка прямая в окружном направлении и выглядит плоской, как если бы она была обработана механической обработкой. В близлежащей области наблюдается пластическая деформация. Это происходит, когда приложенная сила превышает прочность материала на сдвиг. Это происходит, когда зубчатое колесо высокой жесткости и прочности входит в зацепление с зубчатым колесом, имеющим относительно низкий модуль упругости и непрочный материал.
Ссылки по теме :
Шестерни для робототехники
Бесплатный калькулятор шестерен
Терминология шестерен
Типы шестерен и терминология
Расчет размеров шестерен
齿轮的基本用语和尺寸计算 — 中文鵗
Упрощенное руководство по терминологии и формулам для расчета зубчатых колес
Это упрощенная версия терминологии для зубчатых колес и формул для расчета зубьев тем, кто давно выучил передачи, но хочет быстро их снова включить.
Шестерни имеют множество параметров, для полного понимания которых потребуется немного математических и геометрических знаний. Тем не менее, вам не нужно слишком углубляться в базовые знания о зубчатых колесах, после того, как вы прочитаете этот пост, вы сможете сделать предварительные проекты зубчатых колес или эффективно общаться с конструкторами зубчатых колес .
Давайте начнем с базовой формы шестерни, прямозубые шестерни:
1. Число зубьев (z)
Это довольно просто, это количество зубьев шестерни.
2. Контрольная окружность и контрольный диаметр (d)
Диаметр вершины (da) и диаметр корня (df) соответствуют верхней и нижней части зубьев.
Эталонный диаметр используется при проектировании и расчете зубчатых колес. Он напрямую связан с другими важными параметрами зубчатого колеса, такими как модуль (m), межосевое расстояние (c) и угол давления (α).
Диаметр вершины (da) и диаметр корня (df) соответствуют верхней и нижней части зуба.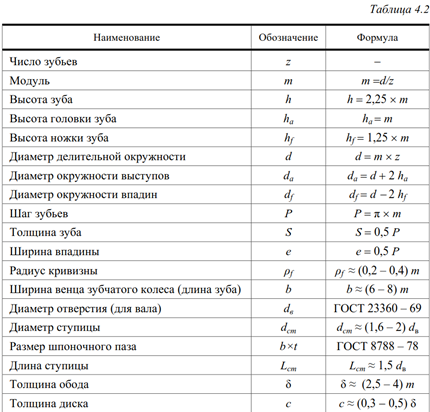
Эталонный диаметр используется при проектировании и расчете зубчатых колес. Он напрямую связан с другими важными параметрами зубчатого колеса, такими как модуль (m), межосевое расстояние (c) и угол давления (α).
Поворот 2-х шестерен можно считать включенным поворотом 2-х опорных окружностей без проскальзывания. Передаточное число i=d2/d1. d1 и d2 относятся к эталонным диаметрам двух сопряженных шестерен (шестерня 1 — ведущая, шестерня 2 — ведомая).
Опорная окружность находится где-то между вершиной и низом зубьев, обычно там, где толщина зуба равна шагу, но это не всегда так (о смещении профиля мы поговорим позже в этом посте).
3. Модуль (m)
Модуль, вероятно, является самым важным параметром зубчатого колеса, и он появляется почти везде в формулах расчета зубьев. На самом деле, это не так сложно понять, как вы можете себе представить. Сначала давайте разберемся, что такое шаг. Шаг — это длина дуги между соответствующими точками на соседних зубах, обычно на эталонной окружности.
Затем у нас есть эталонный диаметр d=длина окружности/π=шаг*z/π , чтобы упростить вычисления, мы определяем шаг/π в качестве модуля, и теперь у нас есть уравнение d=m*z , это значительно упрощает вычисления, верно? Модули стандартизированы под следующими номерами (единица измерения : мм ):
Первая серия (рекомендуется): 0,1, 0,12, 0,15, 0,2, 0,25, 0,3, 0,4, 0,5, 0,6, 0,8, 1, 1,25, 1,5 , 2, 2,5, 3, 4, 5, 6, 8, 10, 12, 16, 20, 25, 32, 40, 50
Второй ряд (менее использованный): 0,35, 0,7, 0,9, 1,75, 2,25, 2,75 , 3,25, 3,5, 3,75, 4,5, 5,5, 6,5, 7, 9, 11, 14, 18, 22, 28, 30, 36, 45
Однако для литых пластмассовых шестерен нет необходимости использовать эти стандартные номера модулей, поскольку зубья не нарезаются стандартными зуборезами.
Теперь у нас есть передаточное отношение i=d2/d1=z2/z1 (шестерня 1 — ведущая, а шестерня 2 — ведомая).
Модуль также имеет отношение к высоте зуба, для стандартных передач высота зуба равна 2,25*м:
доп га=1*м , дедендум hf=1,25*м , высота зуба ч=2,25*м .
4. Расстояние между центрами (a)
2 зубчатых зацепления всегда имеют один и тот же модуль, в противном случае они не совпадают. Теперь можно прийти к выводу, что a=(d1+d2)/2=m(z1+z2)/2 , но может немного отличаться при некоторых корректировках геометрии зубчатого колеса (смещении профиля зуба).
5. Угол давления (α)
Проще говоря, как следует из названия, это угол между направлением контактной силы в точке контакта зуба и направлением движения этой точки на профиле зуба.
В геометрии это угол между линией, нормальной к эвольвентному профилю зуба, и линией, нормальной к его радиальной линии.
Если вы хотите полностью понять угол давления, вам нужно углубиться, чтобы понять эвольвентную линию профиля зуба. Это просто более простой способ объяснения.
Различные точки на профиле зуба имеют разные углы зацепления, но когда мы говорим об угле зацепления зубчатого колеса, это обычно относится к углу опорной окружности. Большинство зубчатых колес используют угол давления 20°, некоторые — 14,5° или 25°. 2 сопрягаемые шестерни должны иметь одинаковый модуль и угол зацепления.
Большинство зубчатых колес используют угол давления 20°, некоторые — 14,5° или 25°. 2 сопрягаемые шестерни должны иметь одинаковый модуль и угол зацепления.
6. Минимальное количество зубьев (
z min ) без подрезки в шестерне
Вы не можете иметь любое количество зубьев шестерни, как хотите. Если зубьев слишком мало, нижняя часть зубьев будет ниже предельной точки, вследствие чего при изготовлении зубьев зуборезами будет срезана лишняя часть корня зуба.
Если зубья не обработаны зуборезами, а профили зубьев сохранились, то в трансмиссии заклинит 2 шестерни.
Формула для расчета минимального количества зубьев без подрезки: мин =17. Так, минимальное количество зубьев для стандартных шестерен равно 17.
7. Коэффициент смещения профиля (x)
Обычно для профиля зуба надстройка зуба ha=1*m, а нижняя часть hf=1,25*m, однако профиль зубьев можно немного сдвинуть вверх или вниз:
Теперь у нас есть коэффициент сдвига профиля (x).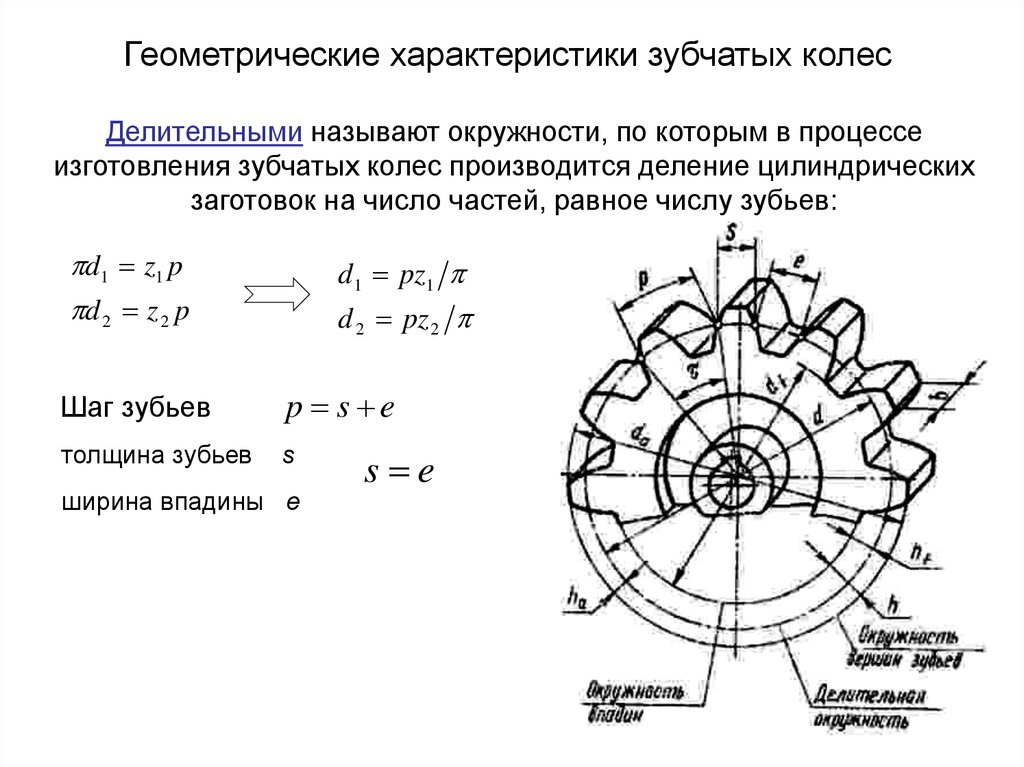 При перемещении профиля вверх значение x положительное (x>0), а при перемещении профиля вниз значение x отрицательное (x<0).
При перемещении профиля вверх значение x положительное (x>0), а при перемещении профиля вниз значение x отрицательное (x<0).
С перемещением профиля зубьев теперь имеем:
- дополнение ha=(1+x)*m
- dedendum hf=(1,25-x)*m
Высота зуба h=ha+hf=2,25 * м, это все равно, что стандартные зубы.
Основными причинами смещения профиля являются:
1) При смещении профиля мы можем избежать подрезки зубьев с меньшим количеством зубьев. Формула выглядит следующим образом:
x мин =(17-z)/17
Например, если вы хотите, чтобы число зубьев было 14, тогда X=(17-14)/17=0,176
2)Точная настройка межосевого расстояния
a=[(m+x1)z1+(m+x2)z2]/2 , поэтому межосевое расстояние не обязательно должно быть (z1+z2)*m
3) Сделайте шестерню сильнее . Обычно шестерня выходит из строя раньше, чем шестерня, за счет положительного сдвига профиля нижняя часть шестерни становится шире (в то время как кончик становится уже), что делает ее прочнее.
In summary:
| # | Item | Symbol | Formula |
|---|---|---|---|
| 1 | teeth number | z | |
| 2 | module | m | M = шаг/π |
| 3 | передаточное взаимодействие | I | I = D2/D1 = Z2/Z1 1: Griving Gear и 2: Driven Gear |
| 4 | DA* | DA* = 1+x x = 0 для стандартных передач | |
| 5 | Коэффициент DEDENDUM | DF* | DF* = 1,25-X | . | x | Для стандартных шестерен, x=0 |
| 7 | Угол давления | α | α=20° для большинства шестерен Другие менее используемые 125° и 124,5°.   |

