Содержание
Белорусский государственный университет транспорта — БелГУТ (БИИЖТ)
Регистрация на конференцию «Проблемы безопасности на транспорте»
Регистрация на конференцию «Тихомировские чтения»
Как поступить в БелГУТ:
дневное, заочное полное,
заочное сокращенное
Как получить место
в общежитии БелГУТа
Как поступить иностранному гражданину
События
Все события
| Пн | Вт | Ср | Чт | Пт | Сб | Вс |
|---|---|---|---|---|---|---|
1 Дата : 2022-09-01 | 2 | 3 | 4 | |||
5 Дата : 2022-09-05 | 6 Дата : 2022-09-06 | 7 Дата : 2022-09-07 | 8 Дата : 2022-09-08 | 9 Дата : 2022-09-09 | 10 Дата : 2022-09-10 | 11 Дата : 2022-09-11 |
12 | 13 | 14 | 15 Дата : 2022-09-15 | 16 Дата : 2022-09-16 | 17 Дата : 2022-09-17 | 18 |
19 | 20 | 21 Дата : 2022-09-21 | 22 Дата : 2022-09-22 | 23 | 24 | 25 |
26 | 27 | 28 | 29 | 30 | ||
Все анонсы
- Экспозиции, посвященные Грунтову П.
 С. и Белому В.А…
С. и Белому В.А… - Турнир на джойстиках по игре в MORTAL COMBAT IX…
- С Днем народного единства!
- Студсовет поздравляет с Днем народного единства…
- Заседание совета университета…
- Молодёжный сентябрь
- Конкурс кандидатов в перспективный кадровый резерв…
- Велопробег «В единстве — сила»…
- Логистика. Обучение для студентов выпускных курсов…
- Акция «Мы едины» — поем гимн вместе…
Анонсы
Университет
Абитуриентам
Студентам
Конференции
Приглашения
Экспозиции, посвященные Грунтову П.С. и Белому В.А…
Турнир на джойстиках по игре в MORTAL COMBAT IX…
С Днем народного единства!
Студсовет поздравляет с Днем народного единства…
Новости
Университет
Международные связи
Спорт
Воспитательная работа
Жизнь студентов
Новости подразделений
Университет
Заседание Совета ветеранов, актива БРСМ и Студсовета. ..
..
20 сентября 2022
Спорт
Победа в соревнованиях по пляжному волейболу…
20 сентября 2022
Воспитательная работа
Лекция по профилактике суицида и пропаганде ценности жизни…
19 сентября 2022
Воспитательная работа
Патриотический форум «Это НАША история!»…
19 сентября 2022
Университет
Челлендж «Рукопожатие» в День народного единства…
19 сентября 2022
Университет
Студенческий совет на праздничном концерте…
18 сентября 2022
Спорт
В единстве — сила! Велопробег
17 сентября 2022
Студенческая жизнь
Белорусский Студенческий патриотический форум, приуроченный ко Дню нар. ..
..
17 сентября 2022
Студенческая жизнь
Выставка военной атрибутики
16 сентября 2022
Другие новости
- Матч по мини-футболу между БелГУТом и ГГТУ…
- Исполняем гимн вместе
- Диалоговая площадка «Беларусь адзіная»…
- Мероприятие «День народного единства — праздник всей страны» в студенч…
- Квиз «Гісторыя майго жыцця»
- Флэшмоб «Мы едины»
- Встреча секретаря БРСМ БелГУТа со студентами…
- Встреча ректора со студентами в студенческом городке…
- Проект студента востребован в городе
- Будущее Беларуси — в единстве
- Видео-репортаж Дня рождения Гомеля
КУДА ПОСТУПАТЬ
Все факультеты
БелГУТ на Доске почета
Достижения университета
Предложения
Все предложения
Видеотека
Все видео
Фотогалерея
Все фото
ПДД РФ, 8.
 Начало движения, маневрирование \ КонсультантПлюс
Начало движения, маневрирование \ КонсультантПлюс
Данный документ включен в перечень НПА, на которые не распространяется требование об отмене с 01.01.2021, установленное ФЗ от 31.07.2020 N 247-ФЗ.
ПДД РФ, 8. Начало движения, маневрирование
8.1. Перед началом движения, перестроением, поворотом (разворотом) и остановкой водитель обязан подавать сигналы световыми указателями поворота соответствующего направления, а если они отсутствуют или неисправны — рукой. При выполнении маневра не должны создаваться опасность для движения, а также помехи другим участникам дорожного движения.
(в ред. Постановления Правительства РФ от 10.05.2010 N 316)
(см. текст в предыдущей редакции)
Сигналу левого поворота (разворота) соответствует вытянутая в сторону левая рука либо правая, вытянутая в сторону и согнутая в локте под прямым углом вверх. Сигналу правого поворота соответствует вытянутая в сторону правая рука либо левая, вытянутая в сторону и согнутая в локте под прямым углом вверх. Сигнал торможения подается поднятой вверх левой или правой рукой.
Сигнал торможения подается поднятой вверх левой или правой рукой.
8.2. Подача сигнала указателями поворота или рукой должна производиться заблаговременно до начала выполнения маневра и прекращаться немедленно после его завершения (подача сигнала рукой может быть закончена непосредственно перед выполнением маневра). При этом сигнал не должен вводить в заблуждение других участников движения.
Подача сигнала не дает водителю преимущества и не освобождает его от принятия мер предосторожности.
8.3. При выезде на дорогу с прилегающей территории водитель должен уступить дорогу транспортным средствам и пешеходам, движущимся по ней, а при съезде с дороги — пешеходам и велосипедистам, путь движения которых он пересекает.
8.4. При перестроении водитель должен уступить дорогу транспортным средствам, движущимся попутно без изменения направления движения. При одновременном перестроении транспортных средств, движущихся попутно, водитель должен уступить дорогу транспортному средству, находящемуся справа.
8.5. Перед поворотом направо, налево или разворотом водитель обязан заблаговременно занять соответствующее крайнее положение на проезжей части, предназначенной для движения в данном направлении, кроме случаев, когда совершается поворот при въезде на перекресток, где организовано круговое движение.
При наличии слева трамвайных путей попутного направления, расположенных на одном уровне с проезжей частью, поворот налево и разворот должны выполняться с них, если знаками 5.15.1 или 5.15.2 либо разметкой 1.18 не предписан иной порядок движения. При этом не должно создаваться помех трамваю.
(в ред. Постановлений Правительства РФ от 24.01.2001 N 67, от 14.12.2005 N 767)
(см. текст в предыдущей редакции)
8.6. Поворот должен осуществляться таким образом, чтобы при выезде с пересечения проезжих частей транспортное средство не оказалось на стороне встречного движения.
При повороте направо транспортное средство должно двигаться по возможности ближе к правому краю проезжей части.
8.7. Если транспортное средство из-за своих габаритов или по другим причинам не может выполнить поворот с соблюдением требований пункта 8.5 Правил, допускается отступать от них при условии обеспечения безопасности движения и если это не создаст помех другим транспортным средствам.
8.8. При повороте налево или развороте вне перекрестка водитель безрельсового транспортного средства обязан уступить дорогу встречным транспортным средствам и трамваю попутного направления.
Если при развороте вне перекрестка ширина проезжей части недостаточна для выполнения маневра из крайнего левого положения, его допускается производить от правого края проезжей части (с правой обочины). При этом водитель должен уступить дорогу попутным и встречным транспортным средствам.
8.9. В случаях, когда траектории движения транспортных средств пересекаются, а очередность проезда не оговорена Правилами, дорогу должен уступить водитель, к которому транспортное средство приближается справа.
8. 10. При наличии полосы торможения водитель, намеревающийся повернуть, должен своевременно перестроиться на эту полосу и снижать скорость только на ней.
10. При наличии полосы торможения водитель, намеревающийся повернуть, должен своевременно перестроиться на эту полосу и снижать скорость только на ней.
При наличии в месте въезда на дорогу полосы разгона водитель должен двигаться по ней и перестраиваться на соседнюю полосу, уступая дорогу транспортным средствам, движущимся по этой дороге.
8.11. Разворот запрещается:
на пешеходных переходах;
в тоннелях;
на мостах, путепроводах, эстакадах и под ними;
на железнодорожных переездах;
в местах с видимостью дороги хотя бы в одном направлении менее 100 м;
в местах остановок маршрутных транспортных средств.
(в ред. Постановления Правительства РФ от 25.09.2003 N 595)
(см. текст в предыдущей редакции)
8.12. Движение транспортного средства задним ходом разрешается при условии, что этот маневр будет безопасен и не создаст помех другим участникам движения. При необходимости водитель должен прибегнуть к помощи других лиц.
Движение задним ходом запрещается на перекрестках и в местах, где запрещен разворот согласно пункту 8. 11 Правил.
11 Правил.
Понравилась статья? Вы можете поделиться с друзьями через соц. |
Разбор задач тренировочных заданий по кинематике
В большинстве компьютерных вариантов заданий для каждого
участника генерируются свои наборы данных
Задание
1 «С какой скоростью движется вторая машина относительно первой (4
балла)».
Две машины приближаются к перекрестку, двигаясь под прямым углом друг к другу со скоростями 54 км/ч и 72 км/ч. С какой
скоростью движется вторая машина относительно первой?
|
Дано:
|
Перевод единиц:
|
|
v1 = 54 км/ч
|
15 м/с
|
|
v2 = 72 км/ч
|
20 м/с
|
|
= ?
|
|
Решение.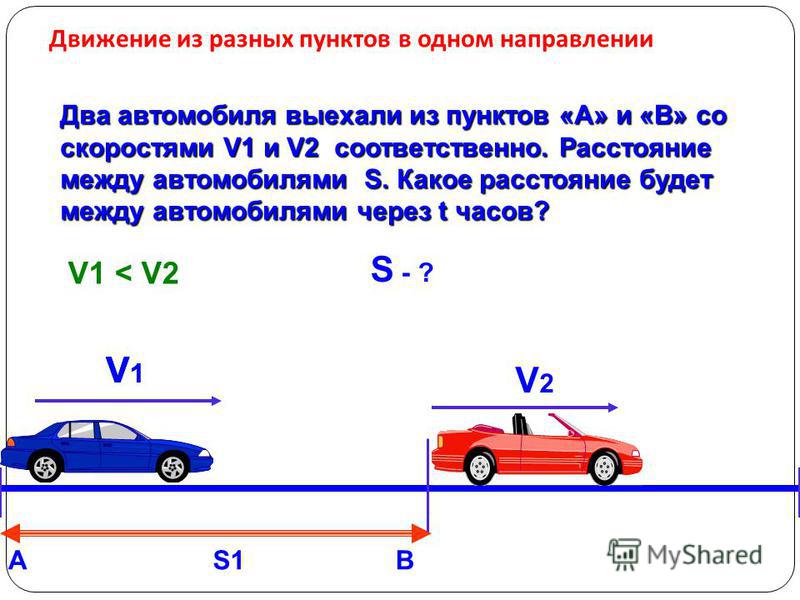 Скорости, заданные в условии,
Скорости, заданные в условии,
измерены относительно системы отсчета, связанной с землей. Уточним обозначение
этих скоростей:
, .
Скорость второй машины относительно первой — это
скорость второй машины измеренная в системе отсчета,
связанной с первой машиной (например, водителем первой машины). Если первая
машина двигается относительно земли со скоростью , то в системе отсчета первой машины земля двигается с такой
же по величине скоростью, но в обратном направлении:
.
Для водителя первой машины
скорость второй машины будет складываться из ее скорости относительно земли и
скорости земли в системе отсчета первой машины:
.
Величина относительной
скорости второй машины v21
равна гипотенузе прямоугольного треугольника, образованного скоростями машин
относительно земли. По теореме Пифагора находим:
По теореме Пифагора находим:
.
Заметим, если относительная
скорость окажется направленной по линии, соединяющей машины, то продолжая
двигаться с такими скоростями, они неминуемо столкнутся!
Ответ: 25 м/с.
Задание 2 «Вычислите среднюю скорость движения
человека (8 баллов)»
Вычислите среднюю скорость
движения человека, если первую треть пути он шел со скоростью 1,5 м/с, а
оставшуюся часть пути со скоростью 1,0 м/с.
|
Дано:
|
|
v1 = 1,5 м/с
|
|
v2 = 1,0 м/с
|
|
= ?
|
Решение. Согласно общему определению средней скорости:
,
где S — весь пройденный путь, а t —
все время движения.
Времена t1 и t2 прохождения первой трети
пути и остальных двух третей равны, соответственно
, .
Учитывая, что t = t1 + t2 находим
.
Ответ: 1,125
м/с.
Задание 3 «Найдите ускорение и путь автомобиля (8
баллов)»
Автомобиль, движущийся со
скоростью 36 км/ч,
разгоняется в течение десяти секунд до 108 км/ч и затем за полминуты сбрасывает
скорость до нуля. Считая движение при разгоне и торможении равнопеременным,
найдите ускорение и путь для каждого из промежутков
времени.
|
Дано:
|
Перевод единиц:
|
|
v1 = 36 км/ч
|
10 м/с
|
|
t1 = 10 c
|
|
|
v2 = 108 км/ч
|
30 м/с
|
|
t2 = 0,5 мин
|
30 c
|
|
a1, S1, a2, S2 = ?
|
|
Решение. Применяя формулу скорости для равноускоренного движения в течение
Применяя формулу скорости для равноускоренного движения в течение
времени t1,
получим
,
откуда
.
Находим путь, пройденный на
участке разгона:
.
Скорость
при торможении машины меняется по формуле
v = v2 – a2t, (1)
убывая за время t2 до v = 0.
Подставляя нуль в правую часть уравнения (1), и выражая величину ускорения,
получаем
.
Отметим, что в данном случае
проекция ускорения на ось OX
отрицательна: a2x = —a2 = –1 м/с2.
Соответствующий
путь составляет
.
Ответ: a1 = 2 м/с2, S1 = 200 м, a2 = 1 м/с2 (a2x = –1 м/с2), S2 = 450 м.
Задание 4 «Вычислите максимальную высоту подъема
тела, брошенного под углом к горизонту (8 баллов)»
Вычислите максимальную высоту
подъема тела, брошенного под углом 30 к горизонту со
скоростью 20 м/с. Сопротивлением
воздуха пренебрегите.
|
Дано:
|
|
= 30
|
|
v0 = 20 м/с
|
|
hmax = ?
|
Решение. Проанализируем, как изменяется со временем
проекция скорости на ось OY. Cуществует такой момент
времени t1 = v0y/g, при котором проекция vy
обращается в нуль. До этого момента времени vy
положительна, то есть тело движется вверх. После момента времени проекция vy
становится отрицательной, то есть тело движется вниз.
Очевидно, что в этот момент
времени достигается максимальная высота hmax.:
.
Используя численные данные,
находим:
.
Ответ: 5 м.
Задание 5 «Модель: Измерьте скорость тележки (8
баллов)»
Задание: Измерьте с помощью оптических
датчиков скорость тележки. Занесите результаты в отчёт (меню в верхней части
программы) и отошлите отчёт на сервер.
Стойки с датчиками расположите так, чтобы они фиксировали моменты прохождения
тележки. Позицию датчиков можно менять мышью или с помощью пункта ввода.
Конечный результат округляйте до сотых. Пример округления: 0,605 можно
округлять до 0,60 или до 0,61.
Рис.1 Начальное состояние системы
Для измерения скорости
следует установить стойки с датчиками, например, на позиции с координатами x1=0. 2 м и x2=0.8 м и
2 м и x2=0.8 м и
нажать кнопку “Пуск”. Тележка доедет до противоположной стенки и остановится, а
на датчиках появятся показания (рис.2).
Рис.2 Конечное состояние системы
Скорость находим как
отношение пути между x2 и x1 к затраченному времени t2-t1:
v=(x2-x1)/(t2-t1)
При этом пусть мы сначала
ошибемся и напишем v= (0.8-0.2)/(2.5-0.278) м/с
= 0.6/2.222 м/с = 0.270027 … м/с
(вместо x2=0.9 м написали x2=0.8 м). Округляем до сотых: v=0.27 м/с
Открываем пункт меню “Отчёт…”
в верхней части программы, и в появившемся окне вводим это значение (рис.3):
Рис.3 Отсылка отчёта
Нажимаем кнопку “Отправить
результаты на сервер” и получаем отзыв с сервера с информацией о неправильном
решении:
Рис.4 Результат проверки со стороны
сервера
При нажатии кнопки “Закрыть”
любая информация в окне отчета сохраняется и показывается вновь при открытии
отчета. При нажатии кнопки “Очистить” восстанавливается первоначальное
При нажатии кнопки “Очистить” восстанавливается первоначальное
состояние окна отчета с пустыми пунктами ввода.
Мы можем нажать кнопку “Очистить”,
затем кнопку “Закрыть”, проверить правильность наших действий и вычислений.
Например, заново проделать
измерения при тех же или других расстояниях между датчиками. Обнаруживаем
ошибку и исправляем ее:
v=(x2-x1)/(t2-t1) = (0.9-0.2)/(2.5-0.278) м/с = 0.7/2.222 м/с = 0.360036 … м/с
Округляем до сотых: v=0.36 м/с.
Открываем отчет, вводим
ответ, отсылаем отчет на сервер и получаем:
Рис.5 Результат проверки нового
результата
Итоговый балл за выполнение
задания получился 7 из 8 возможных, так как имелась одна дополнительная попытка
отсылки результатов на сервер.
Задание 6 «Тест: Кинематика (16 вопросов, 25
баллов)»
Тест будет разбираться в
отдельном документе.
Задание 7 «Модель: Измерьте среднюю и мгновенную
скорость тележки (12 баллов)»
Задание: По наклонному рельсу из точки с
координатой х=0 из состояния покоя начинает равноускоренно двигаться тележка.
Определите время движения тележки до её удара о стенку, а также её среднюю и
конечную скорость на отрезке от x=0 до x=0.5
Время
определите с точностью до тысячных, а остальные величины до сотых, и отошлите
результаты на сервер. В промежуточных вычислениях сохраняйте не менее 4
значащих цифр.
Оптические
датчики срабатывают при пересечении светового луча датчика флажком тележки.
Положение ворот с оптическими датчиками можно изменять при помощи мыши или
задавая значения их координат х1 и х2 при помощи
клавиатуры.
На рис.6 показано начальное
состояние системы.
Рис.6 Начальное состояние системы
Первую стойку передвигаем в
позицию x1=0.5 м, вторую (с помощью пункта ввода для x2) — в позицию x2=0.99999 м (если x2=1 м тележка не пересекает луч, поэтому ставим стойку
очень близко к x=1 м). Нажимаем кнопку “Пуск” и
получаем, например, t1=1.443 с, t2=2. 041 с (рис.7).
041 с (рис.7).
Рис.7 Конечное состояние системы
Полное время движения равно t2. Средняя скорость vср
движения на отрезке от x=0 м до x=0.5 м равна x1/t1. Конечная скорость v1 движения на этом отрезке в два раза больше, так как
при равноускоренном движении vср=(v0+v1)/2, а v0=0. То есть v1 проще вычислить чем измерить с достаточной точностью.
Трогание автомобиля
Трогание автомобиля
В движении автомобиль преодолевает ряд сил, создающих сопротивление его движению. Это сила сопротивления качению колес, сила сопротивления воздуха, сила инерции и сила сопротивления подъему (скатывающая сила). Сумму этих сил называют силой сопротивления движению. Для обеспечения равномерного движения автомобиля на его ведущих колесах двигателем создается сила тяги, по величине равная силе сопротивления движению. Если сила тяги больше силы сопротивления, то автомобиль получает ускорение, т. е. разгоняется, если она меньше — движение замедляется.
е. разгоняется, если она меньше — движение замедляется.
Сила тяги на ведущих колесах реализуется через соответствующую силу сцепления, создаваемую при взаимодействии колес с дорогой. Движение автомобиля обеспечивается лишь тогда, когда сила сцепления по величине равна силе тяги или больше ее. Когда это условие не выдержано и сила тяги превышает силу сцепления, ведущие колеса начинают буксовать и движение становится невозможным.
Сила сцепления зависит в основном от массы автомобиля, приходящейся на ведущие колеса (термин «сцепной вес») и от состояния дороги или грунта. Состояние дороги (грунта) характеризуется коэффициентом спепления шин с дорогой.
Рекламные предложения на основе ваших интересов:
Дополнительные материалы по теме:
Таким образом, сила сцепления может быть выражена как произведение сцепного веса на коэффициент сцепления.
При трогании с места на ровном участке дороги в безветренную погоду необходимо преодолеть лишь силу сопротивления качению колес и силу инерции. Сила сопротивления качению колес равна произведению общей силы тяжести автомобиля на соответствующий коэффициент, характеризующий состояние дорожного покрытия или грунта.
Сила сопротивления качению колес равна произведению общей силы тяжести автомобиля на соответствующий коэффициент, характеризующий состояние дорожного покрытия или грунта.
Сила инерции зависит от общей массы автомобиля и придаваемых ему ускорений.
Трогание автомобиля начинают, как правило, на первой передаче в КП, создающей наибольшую тягу на ведущих колесах. Трогание в местах с большим сопротивлением качению колес (на мягком грунте, в песке, в снегу) требует большей силы тяги и поэтому производится при частоте вращения коленчатого вала, увеличенной пропорционально силам сопротивления.
Резкое трогание отрицательно отражается на состоянии ходовой части, особенно шин. Иные водители считают, что если при трогании ведущие колеса не пробуксовывают, то и износа шин не будет. Это ошибочное мнение: износ при резком трогании всегда повышенный. Особенно сильно изнашиваются шины при пробуксовке на сухом асфальте или бетоне.
Примечания:
1. Коэффициент возрастает с увеличением скорости движения автомобиля, на плохих дорогах с неровностями, в дождь.
2. Коэффициент у радиальных шин иа 5—7% ниже указанных значений.
3. С понижением давления воздуха в шинах коэффициент возрастает (рис. 1).
Рис. 2. Коэффициент сопротивления качению колес на дороге с асфальтобетонным покрытием увеличивается с возрастанием скорости движения и с уменьшением давления в шинах
Бывает, что перед троганием непрогретого автомобиля при выключенном полностью сцеплении передача в КП не включается и рычаг КП упирается во что-то. Чаще это наблюдается при попытке включения задней передачи. Причиной невключения передачи обычно является случайное совпадение зубьев шестерен коробки передач. В этом случае надо вернуть рычаг КП в нейтральное положение, отпустить педаль сцепления и, вновь выжав ее, включить передачу. Но бывает и хуже.
После длительной стоянки автомобиля на открытой площадке или под навесом (обычно зимой) водитель может столкнуться с очень неприятным явлением, когда передача в КП при работающем двигателе не включается и после неоднократного выключения сцепления. Несмотря на то что на длительную стоянку автомобиль был поставлен совершенно исправным и теперь водитель при попытке включить передачу выжимает полностью педаль сцепления, в коробке передач слышен скрежет шестерен, но они в зацепление не входят. Причина здесь очевидна: диск сцепления прилип к маховику коленчатого вала и сцепление не выключается. Для отсоединения диска от маховика существует несколько способов, которые ниже излагаются в последовательности, предусматривающей нарастание трудностей работы и соответствующее возрастание напряжений, возникающих при этом в сцеплении и в трансмиссии в целом. Каждый из последующих способов применяется лишь тогда, когда предыдущий не дал желаемого результата.
Несмотря на то что на длительную стоянку автомобиль был поставлен совершенно исправным и теперь водитель при попытке включить передачу выжимает полностью педаль сцепления, в коробке передач слышен скрежет шестерен, но они в зацепление не входят. Причина здесь очевидна: диск сцепления прилип к маховику коленчатого вала и сцепление не выключается. Для отсоединения диска от маховика существует несколько способов, которые ниже излагаются в последовательности, предусматривающей нарастание трудностей работы и соответствующее возрастание напряжений, возникающих при этом в сцеплении и в трансмиссии в целом. Каждый из последующих способов применяется лишь тогда, когда предыдущий не дал желаемого результата.
Способ 1. Автомобиль затормаживается стояночным тормозом. При неработающем двигателе включается первая передача в КП, педаль сцепления выжимается полностью и удерживается в этом положении помощником или какой-либо распоркой (доской, палкой). Сильным рывком пусковой рукоятки делают попытку провернуть коленчатый вал двигателя. Попытки повторяют до характерного щелчка в сцеплении. Щелчок и свободная в дальнейшем прокрутка коленчатого вала свидетельствуют о том, что диск освободился.
Попытки повторяют до характерного щелчка в сцеплении. Щелчок и свободная в дальнейшем прокрутка коленчатого вала свидетельствуют о том, что диск освободился.
Способ 2. Вывешиваются задние (ведущие) колеса. Под передние колеса обязательно подкладывают упоры. Двигатель пускается при нейтральном положении рычага КП, прогревается и останавливается. Водитель садится на свое рабочее место, включает первую передачу в КП и вновь пускает двигатель, Увеличив частоту вращения коленчатого вала, водитель выжимает педаль сцепления и нажимает на педаль рабочего тормоза. При этом частота вращения коленчатого вала обычно будет резко уменьшаться. Не дав двигателю остановиться, водитель отпускает педаль рабочего тормоза, затем вновь (порезче) нажимает на нее. Так повторяется до щелчка в сцеплении. После щелчка задние колеса при нажатии на педаль тормоза будут останавливаться, а частота вращения коленчатого вала при выжатой педали сцепления не будет изменяться. Это и есть свидетельство восстановления нормальной работы сцепления.
Способ 3. Выбирается свободный участок дороги или площадка длиной 100—200 м и туда вручную выкатывается автомобиль. При нейтральном положении рычага КП двигатель пускается, прогревается и останавливается. Находясь за рулем автомобиля, водитель включает первую передачу в КП и пускает двигатель стартером. Автомобиль начинает движение. Установив повышенную частоту вращения коленчатого вала, водитель выжимает педаль сцепления и легким рывком нажимает на педаль тормоза. При этом автомобиль замедлит движение и частота вращения коленчатого вала уменьшится. Но до полной остановки автомобиля и двигателя допускать нельзя, для чего следует прекратить нажимать на педаль тормоза. Затем нажать на педаль тормоза резче. Так повторяется до появления щелчка в сцеплении, после чего при нажатии на педаль тормоза (и при выключенном сцеплении) автомобиль будет останавливаться без уменьшения частоты вращения коленчатого вала.
При трогании обычно допускаются две характерные ошибки: сильный рывок и глушение двигателя. Причинами первой ошибки могут быть резкое включение сцепления или большая частота вращения коленчатого вала, а чаще всего — то и другое вместе. Вторая ошибка допускается при очень малой частоте вращения коленчатого вала, не соответствующей силе сопротивления качению колес, при резком отпускании педали сцепления, при неотпущенном стояночном тормозе, при включении по ошибке высшей передачи в КП.
Причинами первой ошибки могут быть резкое включение сцепления или большая частота вращения коленчатого вала, а чаще всего — то и другое вместе. Вторая ошибка допускается при очень малой частоте вращения коленчатого вала, не соответствующей силе сопротивления качению колес, при резком отпускании педали сцепления, при неотпущенном стояночном тормозе, при включении по ошибке высшей передачи в КП.
От указанных ошибок можно избавиться с помощью специальных тренировок в трогании на ровной площадке по рекомендуемой методике. Для этого на полностью прогретом двигателе рукояткой управления воздушной заслонкой устанавливается несколько повышенная частота вращения коленчатого вала, включается первая передача в КП и затем очень медленно отпускается педаль сцепления. Отпуская педаль сцепления, водитель улавливает момент, когда автомобиль начинает трогаться, и фиксирует это положение. Затем он снова выжимает педаль сцепления и вновь отпускает ее, добиваясь плавного трогания автомобиля. Так он повторяет это упражнение, каждый раз побыстрее отпуская педаль сцепления.
Когда водитель добьется плавного, устойчивого трогания автомобиля с места, он открывает полностью воздушную заслонку карбюратора и проделывает это же упражнение, регулируя частоту вращения коленчатого вала нажатием на педаль управления дроссельной заслонкой. Усложняя упражнение, в дальнейшем целесообразно такие тренировки проводить при трогании из небольшой канавки, при нахождении колес в песке.
В силу того, что каждый автомобиль имеет свои особенности трогания, тренировки по этой методике рекомендуются всем водителям при освоении вновь приобретенного автомобиля, «характер» которого еще недостаточно изучен.
При трогании на подъеме, кроме двух уже упомянутых сил сопротивления движению, преодолевается дополнительно сила сопротивления подъему. Поэтому частота вращения коленчатого вала здесь должна быть большей. Трогаться на подъеме нужно без скатывания автомобиля назад, которое грозит наездом на другие транспортные средства или пешеходов. Перед троганием автомобиль обязательно затормаживают стояночным тормозом. Техника трогания такова: выжимают педаль сцепления и включают первую передачу, медленно отпускают педаль сцепления и одновременно увеличивают частоту вращения коленчатого вала (чем круче подъем, тем большей должна быть частота вращения). В момент, когда сцепление должно включаться (примерно на половине хода педали), отпускают стояночный тормоз, еще больше увеличивают нажим на педаль управления дроссельной заслонкой, полностью отпускают педаль сцепления. Автомобиль плавно трогается без скатывания назад.
Техника трогания такова: выжимают педаль сцепления и включают первую передачу, медленно отпускают педаль сцепления и одновременно увеличивают частоту вращения коленчатого вала (чем круче подъем, тем большей должна быть частота вращения). В момент, когда сцепление должно включаться (примерно на половине хода педали), отпускают стояночный тормоз, еще больше увеличивают нажим на педаль управления дроссельной заслонкой, полностью отпускают педаль сцепления. Автомобиль плавно трогается без скатывания назад.
При скатывании автомобиля назад водитель обычно теряется, резко нажимает на педаль управления дроссельной заслонкой, двигатель «ревет», а скатывание продолжается. Надо принять за правило: если на подъеме началось скатывание автомобиля назад, немедленно остановить автомобиль любым тормозом, затем затянуть стояночный тормоз (если он не был затянут) и начать трогание заново. Недопустимо при начавшемся скатывании пытаться все же выехать на подъем: это только усугубит положение.
Кроме скатывания, при трогании на подъеме может остановиться двигатель (заглохнуть). Это происходит при резком отпускании педали сцепления, при недостаточной частоте вращения коленчатого вала, при задержке момента выключения стояночного тормоза. При остановке двигателя автомобиль также затормаживается стояночным тормозом, а затем, после пуска двигателя, повторяется попытка тронуться вновь.
Это происходит при резком отпускании педали сцепления, при недостаточной частоте вращения коленчатого вала, при задержке момента выключения стояночного тормоза. При остановке двигателя автомобиль также затормаживается стояночным тормозом, а затем, после пуска двигателя, повторяется попытка тронуться вновь.
Формулы прямолинейного равноускоренного движения
☰
При прямолинейном равноускоренном движении тело
- двигается вдоль условной прямой линии,
- его скорость постепенно увеличивается или уменьшается,
- за равные промежутки времени скорость меняется на равную величину.
Например, автомобиль из состояния покоя начинает двигаться по прямой дороге, и до скорости, скажем, в 72 км/ч он двигается равноускоренно. Когда заданная скорость достигнута, то авто движется без изменения скорости, т. е. равномерно. При равноускоренном движении его скорость возрастала от 0 до 72 км/ч. И пусть за каждую секунду движения скорость увеличивалась на 3,6 км/ч. Тогда время равноускоренного движения авто будет равно 20 секундам. Поскольку ускорение в СИ измеряется в метрах на секунду в квадрате, то надо ускорение 3,6 км/ч за секунду перевести в соответствующие единицы измерения. Оно будет равно (3,6 * 1000 м) / (3600 с * 1 с) = 1 м/с2.
Тогда время равноускоренного движения авто будет равно 20 секундам. Поскольку ускорение в СИ измеряется в метрах на секунду в квадрате, то надо ускорение 3,6 км/ч за секунду перевести в соответствующие единицы измерения. Оно будет равно (3,6 * 1000 м) / (3600 с * 1 с) = 1 м/с2.
Допустим, через какое-то время езды с постоянной скоростью автомобиль начал тормозить, чтобы остановиться. Движение при торможении тоже было равноускоренным (за равные промежутки времени скорость уменьшалась на одинаковую величину). В данном случае вектор ускорения будет противоположен вектору скорости. Можно сказать, что ускорение отрицательно.
Итак, если начальная скорость тела нулевая, то его скорость через время в t секунд будет равно произведению ускорения на это время:
v = at
При падении тела «работает» ускорение свободного падения, и скорость тела у самой поверхности земли будет определяться по формуле:
v = gt
Если известна текущая скорость тела и время, которое понадобилось, чтобы развить такую скорость из состояния покоя, то можно определить ускорение (т. е. как быстро менялась скорость), разделив скорость на время:
е. как быстро менялась скорость), разделив скорость на время:
a = v/t
Однако тело могло начать равноускоренное движение не из состояния покоя, а уже обладая какой-то скоростью (или ему придали начальную скорость). Допустим, вы бросаете камень с башни вертикально вниз с приложением силы. На такое тело действует ускорение свободного падения, равное 9,8 м/с2. Однако ваша сила придала камню еще скорости. Таким образом, конечная скорость (в момент касания земли) будет складываться из скорости, развившийся в результате ускорения и начальной скорости. Таким образом, конечная скорость будет находиться по формуле:
v = v0 + at
Однако, если камень бросали вверх. То начальная его скорость направлена вверх, а ускорение свободного падения вниз. То есть вектора скоростей направлены в противоположные стороны. В этом случае (а также при торможении) произведение ускорения на время надо вычитать из начальной скорости:
v = v0 – at
Получим из этих формул формулы ускорения. В случае ускорения:
В случае ускорения:
at = v – v0
a = (v – v0)/t
В случае торможения:
at = v0 – v
a = (v0 – v)/t
В случае, когда тело равноускоренно останавливается, то в момент остановки его скорость равна 0. Тогда формула сокращается до такого вида:
a = v0/t
Зная начальную скорость тела и ускорение торможения, определяется время, через которое тело остановится:
t = v0/a
Теперь выведем формулы для пути, которое тело проходит при прямолинейном равноускоренном движении. Графиком зависимость скорости от времени при прямолинейном равномерном движении является отрезок, параллельный оси времени (обычно берется ось x). Путь при этом вычисляется как площадь прямоугольника под отрезком. То есть умножением скорости на время (s = vt). При прямолинейном равноускоренном движении графиком является прямая, но не параллельная оси времени. Эта прямая либо возрастает в случае ускорения, либо убывает в случае торможения. Однако путь также определяется как площадь фигуры под графиком.
Эта прямая либо возрастает в случае ускорения, либо убывает в случае торможения. Однако путь также определяется как площадь фигуры под графиком.
При прямолинейном равноускоренном движении эта фигура представляет собой трапецию. Ее основаниями являются отрезок на оси y (скорость) и отрезок, соединяющий точку конца графика с ее проекцией на ось x. Боковыми сторонами являются сам график зависимости скорости от времени и его проекция на ось x (ось времени). Проекция на ось x — это не только боковая сторона, но еще и высота трапеции, т. к. перпендикулярна его основаниям.
Как известно, площадь трапеции равна полусумме оснований на высоту. Длина первого основания равна начальной скорости (v0), длина второго основания равна конечной скорости (v), высота равна времени. Таким образом получаем:
s = ½ * (v0 + v) * t
Выше была дана формула зависимости конечной скорости от начальной и ускорения (v = v0 + at). Поэтому в формуле пути мы можем заменить v:
s = ½ * (v0 + v0 + at) * t = ½ * (2v0 + at) * t = ½ * t * 2v0 + ½ * t * at = v0t + 1/2at2
Итак, пройденный путь определяется по формуле:
s = v0t + at2/2
(К данной формуле можно прийти, рассматривая не площадь трапеции, а суммируя площади прямоугольника и прямоугольного треугольника, на которые разбивается трапеция. )
)
Если тело начало двигаться равноускоренно из состояния покоя (v0 = 0), то формула пути упрощается до s = at2/2.
Если вектор ускорения был противоположен скорости, то произведение at2/2 надо вычитать. Понятно, что при этом разность v0t и at2/2 не должна стать отрицательной. Когда она станет равной нулю, тело остановится. Будет найден путь торможения. Выше была приведена формула времени до полной остановки (t = v0/a). Если подставить в формулу пути значение t, то путь торможения приводится к такой формуле:
s = v02/(2a)
Вопрос Видео: Расчет средней скорости автомобиля, движущегося по прямой
Стенограмма видео
Рассчитайте среднюю скорость автомобиля, который проехал по прямой расстояние 120 метров со скоростью восемь метров в секунду, а затем двигался в том же направлении по той же линии на расстояние 180 метров со скоростью шесть метров в секунду. Это (а) семь метров в секунду, (б) 6,7 метра в секунду, (в) 6,3 метра в секунду или (г) 7,2 метра в секунду?
Это (а) семь метров в секунду, (б) 6,7 метра в секунду, (в) 6,3 метра в секунду или (г) 7,2 метра в секунду?
Итак, этот вопрос относится к машине, движущейся по прямой. Вопрос не говорит нам, в каком направлении движется автомобиль. Предположим, что он движется слева направо. Этот выбор направления не влияет на ответ, который мы получим, но помогает нам нарисовать то, что происходит. Предположим, что наша машина стартует в этом месте. И вопрос говорит нам о том, что сначала автомобиль движется 120 метров вправо к этой точке со скоростью восемь метров в секунду. Затем нам говорят, что автомобиль движется еще 180 метров в том же направлении по той же линии, на этот раз со скоростью шесть метров в секунду. Итак, в целом наша машина переместилась из исходной позиции здесь в конечную позицию вправо вот сюда.
Поскольку вопрос просил нас найти среднюю скорость автомобиля, мы должны начать с того, что напомним, что средняя скорость объекта определяется как полное перемещение объекта, деленное на общее время всего пути. Здесь давайте вычислим две величины в правой части этого уравнения по отдельности; т. е. сначала вычислим полное водоизмещение автомобиля, а затем вычислим общее время пути.
Здесь давайте вычислим две величины в правой части этого уравнения по отдельности; т. е. сначала вычислим полное водоизмещение автомобиля, а затем вычислим общее время пути.
Начнем с вычисления полного смещения автомобиля, где мы напомним, что смещение определяется как кратчайшее расстояние от начальной точки объекта до конечной точки объекта. Помните, что смещение является векторной величиной, поэтому оно не только имеет числовое значение, но и имеет положительный или отрицательный знак, который говорит нам, в каком направлении движется автомобиль. Здесь мы можем предположить, что вправо является положительным направлением. . Таким образом, любое положительное смещение означает, что объект движется вправо. Для нашего автомобиля смещение — это просто расстояние по прямой линии от начальной до конечной точки.
Если обозначить полный водоизмещение автомобиля 𝑑, то мы можем вычислить 𝑑, просто прибавив расстояние, пройденное автомобилем за первую часть пути, к расстоянию, пройденному автомобилем за вторую часть пути. Это означает, что 𝑑 равно 120 метрам — столько автомобиль проедет за первую часть пути, плюс 180 метров — сколько проедет автомобиль за вторую часть пути. Теперь, если бы вторая часть пути не проходила точно в том же прямолинейном направлении, что и первая часть пути, вычислить это смещение было бы сложнее. Но так как они находятся в одном направлении, мы можем просто сложить два расстояния вместе.
Это означает, что 𝑑 равно 120 метрам — столько автомобиль проедет за первую часть пути, плюс 180 метров — сколько проедет автомобиль за вторую часть пути. Теперь, если бы вторая часть пути не проходила точно в том же прямолинейном направлении, что и первая часть пути, вычислить это смещение было бы сложнее. Но так как они находятся в одном направлении, мы можем просто сложить два расстояния вместе.
Итак, делая это сложение, мы видим, что полное водоизмещение автомобиля составляет 300 метров. И помните, что это перемещение является векторной величиной. Таким образом, тот факт, что она положительна, говорит нам о том, что в целом автомобиль движется вправо. Это означает, что мы выполнили первую часть нашего вопроса, потому что рассчитали полный водоизмещение автомобиля. Итак, давайте запишем это смещение здесь, чтобы не забыть его, пока мы продолжаем работать над остальной частью вопроса.
Второе, что нам нужно выяснить, это общее время всего пути автомобиля. Вопрос не говорит нам, как долго машина едет, поэтому нам нужно вычислить его на основе имеющейся информации. Уравнение, которое нам нужно, чтобы вычислить время пути, состоит в том, что скорость равна расстоянию во времени. Мы можем перестроить это уравнение, чтобы сделать его предметом время, сначала умножив обе части уравнения на время, что фактически приведет время к левой части этого уравнения. Затем мы можем разделить обе части на скорость, что фактически сведет скорость к нижней части правой части этого уравнения. Это означает, что наше уравнение для времени становится временем, равным расстоянию, деленному на скорость.
Уравнение, которое нам нужно, чтобы вычислить время пути, состоит в том, что скорость равна расстоянию во времени. Мы можем перестроить это уравнение, чтобы сделать его предметом время, сначала умножив обе части уравнения на время, что фактически приведет время к левой части этого уравнения. Затем мы можем разделить обе части на скорость, что фактически сведет скорость к нижней части правой части этого уравнения. Это означает, что наше уравнение для времени становится временем, равным расстоянию, деленному на скорость.
Поскольку автомобиль двигался с двумя разными скоростями, нам нужно вычислить время, затрачиваемое на каждую часть пути отдельно, потому что уравнение, которое мы только что записали, предполагает, что все числа, с которыми мы работаем, постоянны. Итак, обозначим время, затрачиваемое автомобилем на прохождение первой части пути, через 𝑡 единицу. Тогда из уравнения, которое мы только что записали, 𝑡 единица равна расстоянию, пройденному в первой части пути, что составляет 120 метров, деленному на скорость, с которой автомобиль двигался в течение первой части пути, которая составлял восемь метров в секунду.
Мы можем вычислить числовую часть этой дроби, которая равна 120, разделенному на восемь, равной 15. А единицы, метры, деленные на метры в секунду, просто дают нам секунды. Итак, 𝑡 первое, время, за которое автомобиль проходит первую часть пути, составляет 15 секунд.
Теперь обозначим время, за которое автомобиль проедет вторую часть пути, 𝑡 два. И мы можем вычислить 𝑡 два так же, как вычислили 𝑡 один. То есть 𝑡 два равно расстоянию, пройденному на второй части пути, что составляет 180 метров, деленному на скорость автомобиля на этом участке пути, которая составляет шесть метров в секунду. И если мы это проработаем, то увидим, что 𝑡 два равно 30 секундам.
Теперь нам просто нужно рассчитать общее время в пути. Итак, если мы назовем это общее время 𝑡 без нижнего индекса, то 𝑡 будет просто равно сумме всех времен всех частей пути. Это означает, что здесь 𝑡 просто равно 𝑡 один плюс 𝑡 два. Итак, если мы подставим только что найденные числа для 𝑡 один и 𝑡 два, мы увидим, что общее время 𝑡 равно 15 секундам плюс 30 секунд. Таким образом, это равно 45 секундам. Давайте запишем это сбоку, чтобы не забыть, пока будем вычислять среднюю скорость.
Таким образом, это равно 45 секундам. Давайте запишем это сбоку, чтобы не забыть, пока будем вычислять среднюю скорость.
Теперь у нас есть все необходимое для определения средней скорости автомобиля, потому что мы вычислили полное перемещение автомобиля и общее время всего пути. Итак, если мы назовем среднюю скорость 𝑣 индексом avg, то из нашего определения средней скорости 𝑣 avg равно полному перемещению автомобиля, деленному на общее время всего пути, которое мы можем записать как 𝑣 avg равно 𝑑 разделить на 𝑡. Затем нам просто нужно подставить значения, которые мы нашли для 𝑑 и 𝑡. Мы обнаружили, что 𝑑 равно 300 метрам, а 𝑡 равно 45 секундам. Итак, давайте запишем, что 𝑣 avg равно 300 метрам, разделенным на 45 секунд.
Если мы это проработаем, то числовая часть скорости даст нам 6,6 повторений, а наши единицы — метры в секунду. Эта штриховая нотация — это то, как мы пишем повторяющиеся десятичные дроби, что означает, что шестерка после запятой повторяется вечно.
Это близко к нашему окончательному ответу. Но если мы посмотрим на все предложенные нам варианты множественного выбора, мы увидим, что все они даны с точностью до одного десятичного знака. Таким образом, мы также должны округлить наш ответ до одного десятичного знака. Если мы округлим 6,6 до одного десятичного знака, то получим 6,7. Таким образом, мы находим, что средняя скорость автомобиля равна 𝑣 avg равна 6,7 метра в секунду. Помните, что, как и смещение, скорость является векторной величиной. Таким образом, тот факт, что эта скорость положительна, говорит нам о том, что в данном случае автомобиль движется вправо. Снова сравнивая с нашими вариантами множественного выбора, мы находим совпадение, в данном случае (b). И, следовательно, мы можем дать это как наш окончательный ответ, что средняя скорость автомобиля равна 6,7 метра в секунду вправо.
Но если мы посмотрим на все предложенные нам варианты множественного выбора, мы увидим, что все они даны с точностью до одного десятичного знака. Таким образом, мы также должны округлить наш ответ до одного десятичного знака. Если мы округлим 6,6 до одного десятичного знака, то получим 6,7. Таким образом, мы находим, что средняя скорость автомобиля равна 𝑣 avg равна 6,7 метра в секунду. Помните, что, как и смещение, скорость является векторной величиной. Таким образом, тот факт, что эта скорость положительна, говорит нам о том, что в данном случае автомобиль движется вправо. Снова сравнивая с нашими вариантами множественного выбора, мы находим совпадение, в данном случае (b). И, следовательно, мы можем дать это как наш окончательный ответ, что средняя скорость автомобиля равна 6,7 метра в секунду вправо.
Университет Акрона, Огайо
Вернуться к указателю планов уроков
Версия для печати
Классы: 6–8
Автор: Сэнди Ван Натта
Источник: Powered of a The Motion из материалов OSCI 7-10 Physical Science Materials, разработанных в 2005 г.
Abstract
Учащиеся используют переменные времени и пройденного расстояния, чтобы наблюдать характеристики графиков зависимости расстояния от времени для движения автомобиля с батарейным питанием, работающего от одной батареи, а затем снова с двумя батареями. Это позволяет учащимся изучить, как количество аккумуляторов, используемых для питания автомобиля, влияет на характеристики графиков зависимости расстояния от времени. Затем учащиеся используют данные о времени и расстоянии, собранные для движения автомобилей в двух испытаниях, для расчета средней скорости автомобиля в каждом случае. Затем средние скорости будут сравниваться с наклонами соответствующих графиков зависимости расстояния от времени.
Цели
Что должны знать учащиеся в результате этого урока?
- Учащиеся узнают, что скорость или скорость определяется расстоянием, пройденным объектом за заданный промежуток времени.
- Учащиеся узнают, что контрольная точка необходима для измерения расстояний и направлений, пройденных движущимся объектом.

- Студент будет знать, что автомобиль, работающий от аккумуляторной батареи, движется с постоянной скоростью, однако общая средняя скорость автомобиля будет зависеть от количества аккумуляторов, используемых для питания автомобиля.
- Учащиеся смогут связать наклон линии на графике расстояние/время со средней скоростью своего автомобиля.
Что учащиеся должны уметь делать в результате этого урока?
- Учащийся будет собирать данные о расстоянии и времени для автомобиля с аккумуляторным приводом.
- Учащиеся будут строить графики на основе своих данных.
- Учащийся нарисует прямую линию, наиболее соответствующую точкам, нанесенным на их графики.
- Учащиеся смогут описать движение своего автомобиля с батарейным питанием.
Материалы
Для подготовки:
- Одна машинка на аккумуляторе на группу — недорогие машинки продаются в магазинах игрушек. Автомобили также доступны через каталоги научных товаров.

- 2 батарейки — нужного размера для автомобиля
- Провод
- Кусачки и инструменты для зачистки проводов (только для учителей)
- Опционально – металлический стержень, отрезанный по длине, соответствующей размеру батареи
Для помолвки:
- Маленькая заводная игрушка
Для процедуры:
- Малярная лента
- Измерительная линейка
- Автомобиль на аккумуляторе — подготовлен в процессе подготовки
- 6 секундомеров
- Миллиметровая бумага
- Линейка
Подготовка:
- Для части A подготовьте провод для каждого автомобиля, который немного длиннее, чем длина аккумулятора, необходимая для автомобиля. Если провод изолирован, удалите около 1 см изоляции с каждого конца.
- Поместите один аккумулятор и один провод в аккумуляторный отсек каждой машины. Убедитесь, что провод соприкасается с металлическими контактами держателя аккумулятора, чтобы автомобиль «работал» на одном аккумуляторе.
 (Вместо провода можно использовать металлический стержень длиной с батарею.
(Вместо провода можно использовать металлический стержень длиной с батарею. - Для части B установите по две батареи в каждую машину
Процедуры
Занятие
Установите маленькую заводную игрушку в центральном месте, где ее могут видеть ученики. Сверните игрушку и дайте ей двигаться по гладкой ровной поверхности. Поднимите игрушку с поверхности, прежде чем она начнет замедляться до полной остановки. Попросите учащихся описать движение игрушки. Большинство учеников скажут, что игрушка движется с постоянной скоростью на протяжении большей части своего «бега». (Игрушка действительно «ускоряется», когда начинает движение, но большая часть ее движения будет казаться постоянной.) Спросите учащихся, как они могли бы доказать, что игрушка двигалась с постоянной скоростью. Помогите своим учащимся понять, что им нужно будет знать, какое расстояние игрушка прошла за заданный промежуток времени, а затем сравнить равные периоды времени, чтобы точно описать движение игрушки.
Оценка: Постарайтесь вовлечь в обсуждение всех учащихся. Попросите учащихся привести примеры наблюдаемых ими в повседневной жизни объектов, которые могут двигаться с постоянной скоростью.
Исследование
Часть A: Автомобиль с одной аккумуляторной батареей
- Объедините 7 учащихся в группу.
- Наклейте на пол кусок малярной ленты длиной 10 см. Отметьте эту ленту как стартовую линию или d = 0,
- От линии старта отмерьте 100 см и приложите вторую 10-сантиметровую ленту. Обозначьте эту ленту 100 см.
- Отмерьте еще 100 см и приклейте третий отрезок ленты длиной 10 см. Обозначьте эту ленту 200 см.
- Продолжайте размещать и маркировать ленту через каждые 100 см, пока последняя лента не будет равна 600 см.
- Поставьте одного ученика, держащего машину, на стартовой линии. Расположите остальных 6 учеников, у каждого с секундомером, на каждой из 100-сантиметровых отметок. Убедитесь, что все секундомеры установлены на 0,00 с
- Не включая секундомер, попросите ученика, держащего автомобиль, запустить его электродвигатель и отпустить его со стартовой линии.
 Попросите учащихся следить за тем, как машина проезжает над каждым отмеченным кусочком ленты. Попросите их описать движение автомобиля и сказать, движется ли автомобиль быстро или медленно.
Попросите учащихся следить за тем, как машина проезжает над каждым отмеченным кусочком ленты. Попросите их описать движение автомобиля и сказать, движется ли автомобиль быстро или медленно. - Вернуть машину в исходное положение. На этот раз попросите учащихся засекать время движения машины по своему пути. Попросите ученика с «работающей» машиной держать передние колеса примерно на 3 см выше линии старта и кричать «Готово, поехали». На старте машина должна быть поставлена и отпущена на стартовую линию, а все остальные учащиеся должны включить свои секундомеры.
- Когда автомобиль проходит каждую отметку расстояния, учащийся на этой отметке должен остановить свой секундомер.
- Запишите время в столбце 1 таблицы данных (в Испытании 1).
- Сбросить все секундомеры на 0,00 сек. Верните автомобиль на стартовую линию и повторите шаги 8 и 9. Запишите время в столбце 2 таблицы данных (в испытании 2).
- Повторите шаг 11 для испытания 3 и запишите данные в столбце 3.

- Рассчитайте среднее время трех попыток для каждой дистанции. Запишите средние значения в столбце 4 таблицы данных.
- Рассчитайте время, за которое автомобиль проезжает каждые 100 см пути. Запишите время на каждые 100 см расстояния в столбце 5 таблицы данных.
- На листе миллиметровой бумаги начертите зависимость общего расстояния (см) от среднего времени (сек).
- Используя линейку, проведите наиболее подходящую прямую линию через ваши точки. Не волнуйтесь, если линия не касается всех точек.
.
Часть B: Автомобиль с двумя аккумуляторами
- Поместите второй аккумулятор в аккумуляторный отсек автомобиля.
- Повторите шаги с 8 по 14 из части A, записывая все данные во вторую таблицу данных.
- На том же листе миллиметровой бумаги, на котором есть график данных из части A, нанесите данные общего расстояния и среднего времени для части B. Используйте другой цвет для построения этих точек. Нарисуйте линию «наилучшего соответствия», чтобы соответствовать второму набору точек данных.

Часть C: Средняя скорость
- Следующие расчеты должны быть выполнены для таблиц данных частей A и B. Используя формулу средняя скорость = расстояние/время (ср = d/t), рассчитайте среднюю скорость на каждые 100 см расстояния. Это можно сделать, разделив 100 см на каждое время в столбце 5. Это дает среднюю скорость автомобиля на каждые 100 см расстояния. Запишите средние скорости в столбец 6 таблиц.
- Рассчитайте среднюю скорость всего пробега как в части A, так и в части B. Снова используйте формулу vavg = d/t, но на этот раз разделите 600 см на время, необходимое автомобилю для достижения 600-сантиметровой ленты.
- Рассчитать наклон каждой линии на графике. Выберите две точки, которые находятся на прямой и как можно дальше друг от друга. Обведите выбранные точки. Запишите координаты каждой точки рядом с кругом. Время должно быть указано первым в упорядоченной паре. Используйте формулу наклона = (d2 — d1)/(t2 — t1) для каждой линии.

Оценка: Следите за тем, чтобы учащиеся соблюдали надлежащие лабораторные процедуры. Убедитесь, что каждая группа записывает все свои данные и строит графики.
Объяснение
Обсудите наблюдения и графики учащегося. Помогите учащимся получить следующее понимание. «Как далеко?», «Как долго?» и «Как быстро?» — вопросы, которые задаются при изучении движения. Например, если наблюдатель наблюдает за бегом на 100 м в легкой атлетике, наблюдатель хочет знать, как долго пробег был? — 100 м; сколько времени ушло на то, чтобы пробежать дистанцию? — около 9,8 секунд; и какова была средняя скорость бегуна? — 10,2 м/сек. Движение автомобиля можно описать, измерив расстояние и время для расчета скорости
Как далеко? — Расстояние
Чтобы определить расстояние, пройденное объектом, сначала необходимо установить местоположение (положение) автомобиля, а также его направление. Должна быть выбрана опорная точка, от которой можно измерять расстояния. В этом упражнении первой контрольной точкой является исходное положение, обозначенное как d=0. Это положение вместе с другими отметками, сделанными с интервалом 100 см по прямой линии, обеспечивает систему отсчета, которую можно использовать для определения местоположения автомобиля. Пройденное расстояние — это переход от одного положения к другому относительно нашей системы отсчета. Это изменение положения также называется смещением. Смещение — это расстояние и направление изменения положения объекта.
В этом упражнении первой контрольной точкой является исходное положение, обозначенное как d=0. Это положение вместе с другими отметками, сделанными с интервалом 100 см по прямой линии, обеспечивает систему отсчета, которую можно использовать для определения местоположения автомобиля. Пройденное расстояние — это переход от одного положения к другому относительно нашей системы отсчета. Это изменение положения также называется смещением. Смещение — это расстояние и направление изменения положения объекта.
Как долго? — Время
Когда автомобиль находится в исходной позиции d=0, время также равно 0. Автомобиль и секундомер были запущены одновременно. Каждый раз, когда автомобиль проходит одну из контрольных отметок через каждые 100 см, фиксируется время на секундомере. Время прохождения определенного расстояния — это время, записанное для этой контрольной отметки на этом расстоянии от d=0. Чтобы найти интервал времени между любыми двумя референтными отметками (например, от отметки 100 см до отметки 200 см), вычтите время, записанное на отметке 100 см, из времени, записанного на отметке 200 см. Это будет время, необходимое для прохождения 100 см от отметки 100 см до отметки 200 см.
Это будет время, необходимое для прохождения 100 см от отметки 100 см до отметки 200 см.
Как быстро? — Скорость или скорость
Когда наблюдатель наблюдает за движением автомобиля в системе отсчета, он/она может качественно определить, движется ли автомобиль быстро или медленно. Вычисление числового значения скорости автомобиля дает более точное значение терминам «быстрый» или «медленный». Среднюю скорость автомобиля можно найти, разделив пройденное расстояние на время, необходимое для преодоления этого расстояния.
ср = d/t
ср означает среднюю скорость или скорость. Скорость на самом деле является скалярной величиной, которая говорит только о том, как быстро движется объект. Скорость — это векторная величина, которая говорит не только о том, насколько быстро движется объект, но и о том, в каком направлении он движется. После того, как значения vag были рассчитаны, легко определить, какой автомобиль движется быстрее или медленнее. Автомобиль с большим числовым значением vavg движется быстрее, чем автомобиль с меньшим значением.
При построении графиков движения автомобилей точки данных образуют почти прямую линию. Это указывает на то, что и время, и расстояние изменяются с постоянной скоростью. Автомобиль движется с постоянной скоростью. Линия с самым крутым уклоном представляет автомобиль, движущийся с более высокой скоростью. Числовое значение уклона равно средней скорости автомобиля.
Оценка: Соберите и оцените таблицы данных и графики учащихся.
Разработка
Предложите учащимся разработать эксперимент для определения скорости другого объекта, движущегося с постоянной скоростью, например заводной игрушки, которую можно использовать в разделе «Помолвка». Или учащиеся могут захотеть предсказать, что произойдет со скоростью автомобиля с аккумулятором, если он будет двигаться вверх по наклонной плоскости. Если используются наклонные плоскости, их длина должна быть не менее 1–2 метров, чтобы учащиеся могли записать как можно больше точек данных. Однако используемые расстояния необходимо будет измерять с гораздо меньшим шагом, чем 100 см. Это будет зависеть от скорости автомобиля и длины на наклонной плоскости. Можно попробовать расстояние 25 см. Примечание: автомобиль по-прежнему будет двигаться вверх по наклонной плоскости с постоянной скоростью. Однако общая средняя скорость будет меньше, чем у автомобиля, движущегося по ровной поверхности.
Это будет зависеть от скорости автомобиля и длины на наклонной плоскости. Можно попробовать расстояние 25 см. Примечание: автомобиль по-прежнему будет двигаться вверх по наклонной плоскости с постоянной скоростью. Однако общая средняя скорость будет меньше, чем у автомобиля, движущегося по ровной поверхности.
Оценка: Учащиеся должны записать процедуры, таблицы данных и данные, относящиеся к их эксперименту. Они должны построить графики для представления своих результатов. Используя свои данные и графики в качестве доказательства, учащиеся должны написать вывод, касающийся движения их машины или игрушки в изучаемых обстоятельствах.
Предпосылки
Учащиеся должны уметь производить измерения с помощью линейки и секундомера. Учащиеся должны уметь строить графики, используя координаты x и y, и находить наклоны линий.
Передовой опыт преподавания
- Цикл обучения
- Практическое/интеллектуальное обучение
- Запрос
Согласование со стандартами
Стандарты NGSS:
- MS-PS2-2 Спланируйте исследование, чтобы получить доказательства того, что изменение движения объекта зависит от суммы сил, действующих на объект, и массы объекта .

- MS-PS3-1 Создание и интерпретация графических отображений данных для описания отношений кинетической энергии с массой объекта и со скоростью объекта.
Общие базовые стандарты:
- RST.6-8.1 Приведите конкретные текстовые доказательства для поддержки анализа научных и технических текстов.
- RST.6-8.3 При проведении экспериментов, проведении измерений или выполнении технических задач строго следуйте многоступенчатой процедуре.
Национальные стандарты:
- Стандарт содержания A: 5-8 Наука как исследование
- Содержание Стандарт B: 5-8 Физические науки
Стандарты штата Огайо:
- Физические науки для 6-8 классов Benchmark B
- Научные исследования 6–8 классов, контрольный показатель A
- Уровень научных исследований 6-8 классов B
Content Knowledge
Если время и расстояние изменяются с постоянной скоростью, объект движется с постоянной скоростью. Такое движение можно изобразить на графике (время по оси X и расстояние по оси Y) и получить прямую линию с положительным наклоном. Наклон линии представляет собой числовое значение средней скорости объекта. Чем круче склон, тем больше общая средняя скорость объекта.
Такое движение можно изобразить на графике (время по оси X и расстояние по оси Y) и получить прямую линию с положительным наклоном. Наклон линии представляет собой числовое значение средней скорости объекта. Чем круче склон, тем больше общая средняя скорость объекта.
Безопасность
Никаких специальных процедур безопасности или утилизации не требуется.
Приложения
Всякий раз, когда объект движется с постоянной скоростью в заданном направлении, он имеет постоянную скорость. Автомобиль с круиз-контролем, движущийся по автостраде, или пешеход, движущийся с постоянной равномерной скоростью, преодолевают равные расстояния за сравнительное время. Это примеры объектов, движущихся с постоянной скоростью.
Оценка
Дайте учащемуся ряд графиков зависимости расстояния от времени, представляющих движение движущихся объектов. На некоторых графиках должны быть прямые линии с положительным наклоном. Другие могут иметь изогнутые линии или горизонтальные линии. Попросите учащихся выбрать объекты, движущиеся с постоянными скоростями (графики, изображающие прямые линии с положительным наклоном), и определить средние скорости каждого объекта по представленным данным.
Попросите учащихся выбрать объекты, движущиеся с постоянными скоростями (графики, изображающие прямые линии с положительным наклоном), и определить средние скорости каждого объекта по представленным данным.
Другие соображения
Предложения по группированию Постарайтесь разместить в каждой группе учащихся с разным уровнем подготовки и способностями. Наличие в каждой группе учащегося с сильными математическими способностями поможет в групповых расчетах.
Шаг/Рекомендуемое время: Подготовка Getty займет около 15 минут. Оставшееся действие должно занять около 90 минут.
Рабочие листы в формате PDF для печати
Аккумулятор автомобиля Рабочий лист
3.4 Движение с постоянным ускорением
Цели обучения
К концу этого раздела вы сможете:
- Определить, какие уравнения движения следует использовать для решения неизвестных.
- Используйте соответствующие уравнения движения для решения задачи преследования двух тел.

Можно догадаться, что чем больше ускорение, скажем, автомобиля, удаляющегося от знака остановки, тем больше перемещение автомобиля за заданное время. Но мы не разработали конкретное уравнение, связывающее ускорение и перемещение. В этом разделе мы рассмотрим некоторые удобные уравнения для кинематических взаимосвязей, начиная с определений перемещения, скорости и ускорения. Сначала мы исследуем один объект в движении, называемое движением одного тела. Затем мы исследуем движение двух объектов, называемых задачи преследования двух тел .
Обозначение
Сначала давайте сделаем некоторые упрощения в обозначениях. Принятие начального времени равным нулю, как если бы время измерялось секундомером, является большим упрощением. Поскольку прошедшее время равно [латекс] \text{Δ}t={t}_{\text{f}}-{t}_{0} [/latex], принимая [латекс] {t}_{0}= 0 [/latex] означает, что [latex] \text{Δ}t={t}_{\text{f}} [/latex], последнее время на секундомере. Когда начальное время принимается равным нулю, мы используем нижний индекс 0 для обозначения начальных значений положения и скорости. То есть [латекс] {x}_{0} [/латекс] — начальная позиция , а [latex] {v}_{0} [/latex] — начальная скорость . Мы не помещаем нижние индексы в окончательные значения. То есть t — конечное время , x — конечное положение , а v — конечная скорость . Это дает более простое выражение для прошедшего времени: [латекс] \текст{Δ}t=t[/латекс]. Это также упрощает выражение для смещения x , которое теперь равно [латекс] \текст{Δ}х=х-{х}_{0} [/латекс]. Кроме того, это упрощает выражение для изменения скорости, которое теперь равно [латекс] \текст{Δ}v=v-{v}_{0} [/латекс]. Подводя итог, используя упрощенную запись, с начальным временем, принятым равным нулю,
То есть [латекс] {x}_{0} [/латекс] — начальная позиция , а [latex] {v}_{0} [/latex] — начальная скорость . Мы не помещаем нижние индексы в окончательные значения. То есть t — конечное время , x — конечное положение , а v — конечная скорость . Это дает более простое выражение для прошедшего времени: [латекс] \текст{Δ}t=t[/латекс]. Это также упрощает выражение для смещения x , которое теперь равно [латекс] \текст{Δ}х=х-{х}_{0} [/латекс]. Кроме того, это упрощает выражение для изменения скорости, которое теперь равно [латекс] \текст{Δ}v=v-{v}_{0} [/латекс]. Подводя итог, используя упрощенную запись, с начальным временем, принятым равным нулю,
[латекс] \begin{array}{c}\text{Δ}t=t\hfill \\ \text{Δ}x=x-{x}_{0}\hfill \\ \text{Δ} v=v-{v}_{0},\hfill \end{array} [/latex]
, где нижний индекс 0 обозначает начальное значение, а отсутствие нижнего индекса обозначает конечное значение в любом рассматриваемом движении.
Теперь мы делаем важное предположение, что ускорение является постоянным . Это предположение позволяет нам избежать использования исчисления для нахождения мгновенного ускорения. Поскольку ускорение постоянно, среднее и мгновенное ускорения равны, т. е.
Это предположение позволяет нам избежать использования исчисления для нахождения мгновенного ускорения. Поскольку ускорение постоянно, среднее и мгновенное ускорения равны, т. е.
[латекс] \overset{\text{–}}{a}=a=\text{константа}\текст{.} [/latex]
Таким образом, мы можем использовать символ a для ускорения вообще раз. Предположение, что ускорение является постоянным, серьезно не ограничивает ситуации, которые мы можем изучать, и не снижает точность нашего лечения. Во-первых, ускорение 90 378 – постоянное 90 379 в большом количестве ситуаций. Кроме того, во многих других ситуациях мы можем точно описать движение, предполагая постоянное ускорение, равное среднему ускорению для этого движения. Наконец, для движения, при котором ускорение резко меняется, например, когда автомобиль разгоняется до максимальной скорости, а затем тормозит до полной остановки, движение можно рассматривать в отдельных частях, каждая из которых имеет свое постоянное ускорение.
Смещение и положение по скорости
Чтобы получить наши первые два уравнения, мы начнем с определения средней скорости:
[латекс] \overset{\text{–}}{v}=\frac{\text{Δ }x}{\text{Δ}t}. [/latex]
[/latex]
Подстановка упрощенных обозначений для [латекс] \text{Δ}x [/latex] и [латекс] \text{Δ}t [/latex] дает
[латекс] \overset{\text{ –}}{v}=\frac{x-{x}_{0}}{t}. [/latex]
Решение для x дает нам
[latex] x={x}_{0}+\overset{\text{–}}{v}t, [/latex]
, где средняя скорость равна
[латекс] \overset{\text{–}}{v}=\frac{{v}_{0}+v}{2}. [/latex]
Уравнение [latex] \overset{\text{–}}{v}=\frac{{v}_{0}+v}{2} [/latex] отражает тот факт, что при ускорении постоянна, v — это просто среднее арифметическое начальной и конечной скоростей. (Рисунок) иллюстрирует эту концепцию графически. В части (а) рисунка ускорение постоянно, а скорость увеличивается с постоянной скоростью. Средняя скорость на часовом интервале от 40 км/ч до 80 км/ч составляет 60 км/ч:
[латекс] \overset{\text{–}}{v}=\frac{{v}_{0}+v}{2}=\frac{40\,\text{км/ч}+80 \,\text{км/ч}}{2}=60\,\text{км/ч}\text{.} [/latex]
В части (b) ускорение непостоянно. В течение 1-часового интервала скорость ближе к 80 км/ч, чем к 40 км/ч. Таким образом, средняя скорость больше, чем в части (а).
В течение 1-часового интервала скорость ближе к 80 км/ч, чем к 40 км/ч. Таким образом, средняя скорость больше, чем в части (а).
Рисунок 3.18 (a) График зависимости скорости от времени с постоянным ускорением, показывающий начальную и конечную скорости [латекс] {v}_{0}\,\text{and}\,v [/latex]. Средняя скорость равна [латекс] \frac{1}{2}({v}_{0}+v)=60\,\text{км}\text{/}\text{ч} [/latex]. (b) График зависимости скорости от времени с ускорением, изменяющимся со временем. Средняя скорость не определяется как [latex] \frac{1}{2}({v}_{0}+v) [/latex], но превышает 60 км/ч.
Нахождение конечной скорости по ускорению и времени
Мы можем вывести еще одно полезное уравнение, манипулируя определением ускорения:
[латекс] a=\frac{\text{Δ}v}{\text{Δ}t} . [/latex]
Замена [латекс] \text{Δ}v [/latex] и [латекс] \text{Δ}t [/latex] упрощенными обозначениями дает нам
[латекс] a=\frac{ v-{v}_{0}}{t}\enspace(\text{константа}\,a). [/latex]
Решение для v дает
[latex] v={v}_{0}+at\enspace(\text{constant}\,a). [/латекс] 9{2},t=40\,\text{s} [/latex].
[/латекс] 9{2},t=40\,\text{s} [/latex].
Во-вторых, мы идентифицируем неизвестное; в данном случае это конечная скорость [латекс] {v}_{\text{f}} [/латекс].
Наконец, мы определяем, какое уравнение использовать. Для этого выясняем, какое кинематическое уравнение дает неизвестное через известные. Мы рассчитываем конечную скорость, используя (Рисунок), [латекс] v={v}_{0}+at [/латекс].
Решение
Показать ответ
Рисунок 3.19 Самолет приземляется с начальной скоростью 70,0 м/с и замедляется до конечной скорости 10,0 м/с, прежде чем взять курс на аэродром. Обратите внимание, что ускорение отрицательно, потому что его направление противоположно его скорости, которая положительна.
Значимость
Конечная скорость намного меньше начальной скорости, как и требуется при замедлении, но все же положительна (см. рисунок). С реактивными двигателями реверсивная тяга может поддерживаться достаточно долго, чтобы остановить самолет и начать движение его назад, на что указывает отрицательная конечная скорость, но здесь это не так.
Уравнение [латекс] v={v}_{0}+at [/латекс] не только полезно при решении задач, но и дает нам представление о взаимосвязях между скоростью, ускорением и временем. Мы видим, например, что
- Конечная скорость зависит от того, насколько велико ускорение и как долго оно длится
- Если ускорение равно нулю, то конечная скорость равна начальной скорости ( v = v 0 ), как и ожидалось (другими словами, скорость постоянна)
- Если a отрицательно, то конечная скорость меньше начальной скорости
Все эти наблюдения соответствуют нашей интуиции. Обратите внимание, что всегда полезно исследовать основные уравнения в свете нашей интуиции и опыта, чтобы убедиться, что они действительно точно описывают природу.
Решение конечного положения с постоянным ускорением
Мы можем объединить предыдущие уравнения, чтобы найти третье уравнение, которое позволит нам вычислить конечное положение объекта, испытывающего постоянное ускорение. Начнем с
Начнем с
[латекс] v={v}_{0}+at. [/latex]
Добавление [latex] {v}_{0} [/latex] к каждой стороне этого уравнения и деление на 2 дает
[latex] \frac{{v}_{0}+v} {2}={v}_{0}+\frac{1}{2}at. [/latex]
Так как [latex] \frac{{v}_{0}+v}{2}=\overset{\text{–}}{v} [/latex] для постоянного ускорения, мы имеем 9{2}\enspace(\text{константа}\,а). [/latex]
Пример
Расчет смещения ускоряющегося объекта
Драгстеры могут развивать среднее ускорение 26,0 м/с 2 . Предположим, драгстер разгоняется с такой скоростью за 5,56 с (рисунок). Какое расстояние он проходит за это время?
Рис. 3.20 Пилот Top Fuel в армии США Тони «Сержант» Шумахер начинает гонку с контролируемым выгоранием. (Источник: подполковник Уильям Турмонд. Фото предоставлено армией США.) 9{2} [/latex], когда мы идентифицируем [латекс] {v}_{0} [/латекс], [латекс] а [/латекс] и т из условия задачи.
Рисунок 3.21 Эскиз разгоняющегося драгстера.
Решение
Показать ответ
Значение
Если мы преобразуем 402 м в мили, мы обнаружим, что пройденное расстояние очень близко к четверти мили, стандартной дистанции для дрэг-рейсинга. Итак, наш ответ разумен. Это впечатляющее смещение, которое можно преодолеть всего за 5,56 с, но первоклассные драгстеры могут проехать четверть мили за еще меньшее время. Если бы драгстеру была задана начальная скорость, это добавило бы еще один член в уравнение расстояния. Если в уравнении используются те же ускорение и время, то пройденное расстояние будет намного больше. 9{2}\,\text{становится}\,x={x}_{0}+{v}_{0}t. [/латекс]
Решение конечной скорости по расстоянию и ускорению
Четвертое полезное уравнение может быть получено путем другой алгебраической обработки предыдущих уравнений. Если мы решим [латекс] v={v}_{0}+at [/латекс] для t , мы получим
[латекс] t=\frac{v-{v}_{0}}{a }. [/latex]
Подставив это и [latex] \overset{\text{–}}{v}=\frac{{v}_{0}+v}{2} [/latex] в [latex] x ={x}_{0}+\overset{\text{–}}{v}t [/latex], получаем 9{2}+2a(x-{x}_{0}) [/latex] идеально подходит для этой задачи, поскольку связывает скорости, ускорения и перемещения, а информация о времени не требуется.
Решение
Показать ответ
Значение
Скорость 145 м/с составляет около 522 км/ч или около 324 миль/ч, но даже эта головокружительная скорость не соответствует рекорду на четверть мили. Также обратите внимание, что квадратный корень имеет два значения; мы взяли положительное значение, чтобы указать скорость в том же направлении, что и ускорение. 9{2}+2a(x-{x}_{0}) [/latex] может дать дополнительные сведения об общих соотношениях между физическими величинами:
- Конечная скорость зависит от того, насколько велико ускорение и расстояние, на котором это действует.
- При фиксированном ускорении автомобиль, который едет в два раза быстрее, не просто останавливается на удвоенном расстоянии. Чтобы остановиться, нужно гораздо больше. (Поэтому у нас есть зоны пониженной скорости возле школ.)
Составление уравнений
В следующих примерах мы продолжаем исследовать одномерное движение, но в ситуациях, требующих более сложных алгебраических операций. Примеры также дают представление о методах решения проблем. Следующее примечание предназначено для удобства обращения к необходимым уравнениям. Имейте в виду, что эти уравнения не являются независимыми. Во многих ситуациях у нас есть два неизвестных и нужно два уравнения из набора для решения неизвестных. Нам нужно столько уравнений, сколько неизвестных, чтобы решить данную ситуацию. 9{2}+2a(x-{x}_{0}) [/latex]
Примеры также дают представление о методах решения проблем. Следующее примечание предназначено для удобства обращения к необходимым уравнениям. Имейте в виду, что эти уравнения не являются независимыми. Во многих ситуациях у нас есть два неизвестных и нужно два уравнения из набора для решения неизвестных. Нам нужно столько уравнений, сколько неизвестных, чтобы решить данную ситуацию. 9{2}+2a(x-{x}_{0}) [/latex]
Прежде чем перейти к примерам, давайте более внимательно рассмотрим некоторые уравнения, чтобы увидеть поведение ускорения при экстремальных значениях. Переставляя (рисунок), мы имеем
[латекс] a=\frac{v-{v}_{0}}{t}. [/latex]
Отсюда мы видим, что за конечное время, если разница между начальной и конечной скоростями мала, ускорение мало, приближаясь к нулю в пределе, когда начальная и конечная скорости равны. Наоборот, в пределе [латекс] t\to 0 [/латекс] при конечной разности между начальной и конечной скоростями ускорение становится бесконечным. 9{2}}{2(х-{х}_{0})}. [/latex]
[/latex]
Таким образом, при конечной разнице между начальной и конечной скоростями ускорение становится бесконечным, в пределе перемещения приближаются к нулю. Ускорение стремится к нулю в пределе, когда разность начальной и конечной скоростей стремится к нулю при конечном перемещении.
Пример
Как далеко едет машина?
На сухом бетоне автомобиль может замедляться со скоростью 7,00 м/с 2 , тогда как на мокром бетоне он может замедляться только со скоростью 5,00 м/с 2 . Найдите расстояние, необходимое для остановки автомобиля, движущегося со скоростью 30,0 м/с (около 110 км/ч) по (а) сухому бетону и (б) мокрому бетону. (c) Повторите оба вычисления и найдите перемещение от точки, в которой водитель видит красный сигнал светофора, учитывая время его реакции 0,500 с, чтобы нажать на педаль тормоза.
Стратегия
Сначала нам нужно нарисовать эскиз (Рисунок). Чтобы определить, какие уравнения лучше всего использовать, нам нужно перечислить все известные значения и точно определить, что нам нужно решить.
Рисунок 3.22 Пример эскиза для визуализации замедления и тормозного пути автомобиля.
Решение
- Во-первых, нам нужно определить известные и то, что мы хотим решить. Мы знаем, что v 0 = 30,0 м/с, v = 0 и a = −7,00 м/с 2 ( a отрицательно, потому что оно находится в направлении, противоположном скорости) . Мы принимаем x 0 за ноль. Ищем смещение [латекс] \текст{Δ}х[/латекс], или 9{2}+2а(х-{х}_{0}). [/латекс]
Это уравнение лучше всего, потому что оно включает только одно неизвестное, x . Мы знаем значения всех остальных переменных в этом уравнении. (Другие уравнения позволили бы нам решить для x , но они требуют, чтобы мы знали время остановки, t , которого мы не знаем. Мы могли бы использовать их, но это потребовало бы дополнительных вычислений.)
В-третьих, мы перестраиваем уравнение для решения x :
.
 {2}}{2a} [/latex] 9{2})}. [/латекс]
{2}}{2a} [/latex] 9{2})}. [/латекс]Таким образом,
[латекс] x=64,3\,\text{м на сухом бетоне}\text{.} [/латекс]
- Эту часть можно решить точно так же, как (а). Единственное отличие состоит в том, что ускорение равно −5,00 м/с 2 . Результат
[латекс] {x}_{\text{мокрый}}=90,0\,\text{м на мокром бетоне.} [/латекс]
Показать ответ
Рисунок 3.23 Расстояние, необходимое для остановки автомобиля, сильно различается в зависимости от дорожных условий и времени реакции водителя. Здесь показаны тормозные пути для сухого и мокрого покрытия, рассчитанные в этом примере для автомобиля, движущегося изначально со скоростью 30,0 м/с. Также показано общее расстояние, пройденное от точки, когда водитель впервые видит красный свет, при условии времени реакции 0,500 с.
Значение
Перемещения, найденные в этом примере, кажутся подходящими для остановки быстро движущегося автомобиля. На мокром асфальте машина останавливается дольше, чем на сухом. Интересно, что к перемещениям существенно добавляет время реакции, но важнее общий подход к решению задач. Мы идентифицируем известные и определяемые величины, затем находим соответствующее уравнение. Если имеется более одного неизвестного, нам нужно столько независимых уравнений, сколько неизвестных для решения. Часто существует более одного способа решения проблемы. Различные части этого примера на самом деле могут быть решены другими методами, но представленные здесь решения являются самыми короткими.
На мокром асфальте машина останавливается дольше, чем на сухом. Интересно, что к перемещениям существенно добавляет время реакции, но важнее общий подход к решению задач. Мы идентифицируем известные и определяемые величины, затем находим соответствующее уравнение. Если имеется более одного неизвестного, нам нужно столько независимых уравнений, сколько неизвестных для решения. Часто существует более одного способа решения проблемы. Различные части этого примера на самом деле могут быть решены другими методами, но представленные здесь решения являются самыми короткими.
Пример
Расчет времени
Предположим, что автомобиль въезжает в полосу движения на 200-метровом съезде. Если его начальная скорость равна 10,0 м/с, а ускорение составляет 2,00 м/с 2 , за какое время автомобиль проедет 200 м вверх по пандусу? (Эта информация может пригодиться инженеру по транспорту.)
Стратегия
Сначала рисуем эскиз (рисунок). Нас просят решить за время t . Как и раньше, мы отождествляем известные величины, чтобы выбрать удобное физическое соотношение (то есть уравнение с одним неизвестным, t .)
Как и раньше, мы отождествляем известные величины, чтобы выбрать удобное физическое соотношение (то есть уравнение с одним неизвестным, t .)
Рисунок 3.24 Эскиз автомобиля, разгоняющегося на съезде автострады.
Решение
Показать ответ
Значение
Всякий раз, когда уравнение содержит неизвестное в квадрате, есть два решения. В некоторых задачах оба решения имеют смысл; в других разумно только одно решение. Ответ 10,0 с кажется разумным для типичного съезда с автострады.
Проверьте свои знания
Пилотируемая ракета разгоняется со скоростью 20 м/с 2 во время запуска. За какое время ракета достигнет скорости 400 м/с?
Показать решение
Пример
Разгон космического корабля
Космический корабль покинул орбиту Земли и направляется к Луне. Он разгоняется со скоростью 20 м/с 2 за 2 мин и преодолевает расстояние 1000 км. Каковы начальная и конечная скорости космического корабля?
Каковы начальная и конечная скорости космического корабля?
Стратегия
Нас просят найти начальную и конечную скорости космического корабля. Глядя на кинематические уравнения, мы видим, что одно уравнение не даст ответа. Мы должны использовать одно кинематическое уравнение, чтобы найти одну из скоростей, и подставить его в другое кинематическое уравнение, чтобы получить вторую скорость. Таким образом, мы решаем два кинематических уравнения одновременно.
Решение
Показать ответ
Значение
В смещении, времени, скорости и ускорении есть шесть переменных, описывающих движение в одном измерении. Начальными условиями данной задачи может быть множество комбинаций этих переменных. Из-за этого разнообразия решения могут быть не такими простыми, как простые подстановки в одно из уравнений. Этот пример показывает, что для решения кинематики может потребоваться решение двух одновременных кинематических уравнений.
Познакомившись с основами кинематики, мы можем перейти ко многим другим интересным примерам и приложениям. В процессе разработки кинематики мы также заметили общий подход к решению задач, который дает как правильные ответы, так и понимание физических взаимосвязей. Следующий уровень сложности наших задач кинематики связан с движением двух взаимосвязанных тел, называемых задачами преследования двух тел .
Задачи преследования двух тел
До этого момента мы рассматривали примеры движения одного тела. Даже для задачи с двумя автомобилями и тормозным путем на мокрой и сухой дороге мы разделили эту задачу на две отдельные задачи, чтобы найти ответы. В задача преследования двух тел , движения объектов связаны — это означает, что искомое неизвестное зависит от движения обоих объектов. Чтобы решить эти задачи, мы пишем уравнения движения для каждого объекта, а затем решаем их одновременно, чтобы найти неизвестное. Это показано на (рис.).
Рисунок 3. 25 Сценарий преследования двух тел, в котором автомобиль 2 движется с постоянной скоростью, а автомобиль 1 отстает с постоянным ускорением. Автомобиль 1 догоняет автомобиль 2 позже.
25 Сценарий преследования двух тел, в котором автомобиль 2 движется с постоянной скоростью, а автомобиль 1 отстает с постоянным ускорением. Автомобиль 1 догоняет автомобиль 2 позже.
Время и расстояние, необходимые для того, чтобы автомобиль 1 догнал автомобиль 2, зависят от начального расстояния между автомобилем 1 и автомобилем 2, а также от скоростей обоих автомобилей и ускорения автомобиля 1. Кинематические уравнения, описывающие движение обоих автомобилей, должны решить, чтобы найти эти неизвестные.
Рассмотрим следующий пример.
Пример
Гепард ловит газель
Гепард ждет, прячась за кустом. Гепард замечает газель, пробегающую мимо со скоростью 10 м/с. В момент, когда газель проходит мимо гепарда, гепард ускоряется из состояния покоя со скоростью 4 м/с 2 поймать газель. а) Сколько времени потребуется гепарду, чтобы поймать газель? б) Каково водоизмещение газели и гепарда?
Стратегия
Для решения этой задачи мы используем систему уравнений для постоянного ускорения. Поскольку движутся два объекта, у нас есть отдельные уравнения движения, описывающие каждое животное. Но что связывает уравнения, так это общий параметр, который имеет одинаковое значение для каждого животного. Если мы внимательно посмотрим на проблему, то станет ясно, что общим параметром для каждого животного является их позиция 9.0378 x позже t . Поскольку они оба начинаются с [latex] {x}_{0}=0 [/latex], их смещения одинаковы в более позднее время t , когда гепард догоняет газель. Если мы выберем уравнение движения, которое определяет смещение для каждого животного, мы можем тогда установить уравнения равными друг другу и найти неизвестное, то есть время.
Поскольку движутся два объекта, у нас есть отдельные уравнения движения, описывающие каждое животное. Но что связывает уравнения, так это общий параметр, который имеет одинаковое значение для каждого животного. Если мы внимательно посмотрим на проблему, то станет ясно, что общим параметром для каждого животного является их позиция 9.0378 x позже t . Поскольку они оба начинаются с [latex] {x}_{0}=0 [/latex], их смещения одинаковы в более позднее время t , когда гепард догоняет газель. Если мы выберем уравнение движения, которое определяет смещение для каждого животного, мы можем тогда установить уравнения равными друг другу и найти неизвестное, то есть время.
Решение
Показать ответ
Показать ответ
Значение
Важно анализировать движение каждого объекта и использовать соответствующие кинематические уравнения для описания движения каждого отдельного объекта. Также важно иметь хорошее визуальное представление о задаче преследования двух тел, чтобы увидеть общий параметр, который связывает движение обоих объектов.
Также важно иметь хорошее визуальное представление о задаче преследования двух тел, чтобы увидеть общий параметр, который связывает движение обоих объектов.
Проверьте свои знания
Велосипед движется с постоянной скоростью 10 м/с. Человек стартует с места и бежит, чтобы догнать велосипед за 30 с. Каково ускорение человека?
Показать решение
Резюме
- При анализе одномерного движения с постоянным ускорением определите известные величины и выберите соответствующие уравнения для решения неизвестных. Для решения неизвестных необходимо одно или два кинематических уравнения, в зависимости от известных и неизвестных величин.
- Задачи преследования двух тел всегда требуют одновременного решения двух уравнений для неизвестных.
Концептуальные вопросы
При анализе движения отдельного объекта, какое количество известных физических переменных требуется для решения неизвестных величин с помощью кинематических уравнений?
Приведите два сценария кинематики одиночного объекта, в которых три известных величины требуют решения двух кинематических уравнений для неизвестных.
Показать решение
Задачи
Частица движется прямолинейно с постоянной скоростью 30 м/с. Каково его перемещение между t = 0 и t = 5,0 с?
Показать решение
Частица движется прямолинейно с начальной скоростью 30 м/с и постоянным ускорением 30 м/с 2 . Если в [латекс] t=0,x=0 [/латекс] и [латекс] v=0 [/латекс], какова позиция частицы в t = 5 с?
Частица движется прямолинейно с начальной скоростью 30 м/с и постоянным ускорением 30 м/с 2 . а) Чему равно его водоизмещение при т = 5 с? б) Какова его скорость в это же время?
Показать решение
(a) Нарисуйте график зависимости скорости от времени, соответствующий графику зависимости смещения от времени, представленному на следующем рисунке. б) Определите время или моменты времени ( t a , t b , t c и т. д.), в которые мгновенная скорость имеет наибольшее положительное значение. в) В какие моменты времени он равен нулю? г) В какие моменты он отрицательный?
д.), в которые мгновенная скорость имеет наибольшее положительное значение. в) В какие моменты времени он равен нулю? г) В какие моменты он отрицательный?
Показать ответ
(a) Нарисуйте график зависимости ускорения от времени, соответствующий графику зависимости скорости от времени, представленному на следующем рисунке. (b) Определите время или времена ( t a , t b , t c и т. д.), при которых ускорение имеет наибольшее положительное значение. в) В какие моменты времени он равен нулю? г) В какие моменты он отрицательный?
Показать ответ
Частица имеет постоянное ускорение 6,0 м/с 2 . а) Если его начальная скорость равна 2,0 м/с, то в какой момент времени его перемещение составит 5,0 м? б) Какова его скорость в этот момент?
При t = 10 с частица движется слева направо со скоростью 5,0 м/с. В 9{\ text {−} 4} \, \ text {s} [/ латекс]. Какова его начальная скорость (то есть конечная скорость)?
В 9{\ text {−} 4} \, \ text {s} [/ латекс]. Какова его начальная скорость (то есть конечная скорость)?
Показать решение
(a) Легкий пригородный поезд движется со скоростью 1,35 м/с 2 . Сколько времени требуется, чтобы достичь максимальной скорости 80,0 км/ч, начиная с состояния покоя? (b) Тот же поезд обычно замедляется со скоростью 1,65 м/с 2 . Сколько времени требуется, чтобы остановиться на максимальной скорости? (c) В аварийных ситуациях поезд может замедляться быстрее, останавливаясь со скорости 80,0 км/ч за 8,30 с. Каково его аварийное ускорение в метрах в секунду в квадрате?
При выезде на автостраду автомобиль разгоняется из состояния покоя со скоростью 2,04 м/с 2 за 12,0 с. а) Нарисуйте схему ситуации. б) Перечислите известные в этой задаче. в) Какой путь проедет автомобиль за эти 12,0 с? Чтобы решить эту часть, сначала определите неизвестное, а затем укажите, как вы выбрали подходящее уравнение для его решения. После выбора уравнения покажите, как вы решаете неизвестное, проверьте свои единицы измерения и обсудите, разумен ли ответ. г) Чему равна конечная скорость автомобиля? Решите для этого неизвестного так же, как в (c), явно показывая все шаги.
После выбора уравнения покажите, как вы решаете неизвестное, проверьте свои единицы измерения и обсудите, разумен ли ответ. г) Чему равна конечная скорость автомобиля? Решите для этого неизвестного так же, как в (c), явно показывая все шаги.
Показать решение
Необоснованные результаты В конце забега бегун замедляется со скорости 9,00 м/с до скорости 2,00 м/с 2 . а) Какое расстояние она пройдет за следующие 5,00 с? б) Какова его конечная скорость? в) Оцените результат. Имеет ли это смысл?
Кровь ускоряется из покоя до 30,0 см/с на расстоянии 1,80 см левым желудочком сердца. а) Составьте схему ситуации. б) Перечислите известные в этой задаче. в) Сколько времени занимает ускорение? Чтобы решить эту часть, сначала определите неизвестное, а затем обсудите, как вы выбрали подходящее уравнение для его решения. Выбрав уравнение, покажите свои шаги в решении неизвестного, проверив свои единицы измерения. (d) Является ли ответ разумным по сравнению со временем сердцебиения? 9{2} [/latex], сколько времени потребуется, чтобы остановиться с такой скоростью? в) Какое расстояние он пройдет в каждом случае?
Снаряд фейерверка разгоняется из состояния покоя до скорости 65,0 м/с на расстоянии 0,250 м. {2} [/латекс ], какое расстояние он пролетит, прежде чем поднимется в воздух? б) Сколько времени это занимает?
{2} [/латекс ], какое расстояние он пролетит, прежде чем поднимется в воздух? б) Сколько времени это занимает?
Мозг дятла специально защищен от больших ускорений сухожилиями внутри черепа. Клевая дерево, голова дятла останавливается с начальной скоростью 0,600 м/с на расстоянии всего 2,00 мм. а) Найдите ускорение в метрах в секунду в квадрате и в единицах, кратных g , где g = 9,80 м/с 2 . б) Рассчитайте время остановки. (c) Сухожилия, удерживающие мозг, растягиваются, делая его тормозной путь равным 4,50 мм (больше, чем у головы, и, следовательно, меньшее ускорение мозга). Чему равно ускорение мозга, выраженное в кратном г ?
Показать решение
Неосторожный футболист сталкивается с обивкой стойки ворот во время бега со скоростью 7,50 м/с и полностью останавливается после сжатия обивки и своего тела на 0,350 м. а) Чему равно его ускорение? б) Как долго длится столкновение?
Посылка выпадает из грузового самолета и приземляется в лесу. Если предположить, что скорость пакета помощи при ударе составляет 54 м/с (123 мили в час), то каково его ускорение? Предположим, что деревья и снег останавливают его на расстоянии 3,0 м. 9{2} [/latex] по мере прохождения. Длина станции 210,0 м. а) С какой скоростью он движется, когда нос покидает станцию? б) Какова длина носа поезда на станции? в) Если поезд имеет длину 130 м, какова скорость конца поезда при выходе из него? г) Когда поезд отходит от станции?
Если предположить, что скорость пакета помощи при ударе составляет 54 м/с (123 мили в час), то каково его ускорение? Предположим, что деревья и снег останавливают его на расстоянии 3,0 м. 9{2} [/latex] по мере прохождения. Длина станции 210,0 м. а) С какой скоростью он движется, когда нос покидает станцию? б) Какова длина носа поезда на станции? в) Если поезд имеет длину 130 м, какова скорость конца поезда при выходе из него? г) Когда поезд отходит от станции?
Необоснованные результаты Дрэгстеры могут достичь максимальной скорости 145,0 м/с всего за 4,45 с. а) Рассчитайте среднее ускорение такого драгстера. (b) Найдите конечную скорость этого драгстера, начиная с состояния покоя и ускоряясь со скоростью, указанной в (а), на протяжении 402,0 м (четверть мили) без использования какой-либо информации о времени. в) Почему конечная скорость больше той, которая использовалась для нахождения среднего ускорения? ( Подсказка : Проверьте, справедливо ли предположение о постоянном ускорении для драгстера. Если нет, обсудите, будет ли ускорение больше в начале или в конце пробега и как это повлияет на конечную скорость.)
Если нет, обсудите, будет ли ускорение больше в начале или в конце пробега и как это повлияет на конечную скорость.)
Показать решение
Глоссарий
- задача преследования двух тел
- задача кинематики, в которой неизвестные вычисляются путем одновременного решения кинематических уравнений для двух движущихся объектов
2. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
2. ПРЯМОЛИнейНОЕ ДВИЖЕНИЕ
- ДВИЖЕНИЕ ПО ПРЯМОЙ ЛИНИИ
- 2.1. Должность
- 2.2. Скорость
- 2.3. Ускорение
- 2.4. Постоянное ускорение
- 2.5. Гравитационное ускорение
В механике нас интересует попытка понять движение объектов.
В этой главе будет обсуждаться движение объектов в 1 измерении.
Движение в 1 измерении — это движение по прямой линии.
Положение объекта на прямой линии можно однозначно определить по
его расстояние от (выбранного пользователем) источника. (см. рис. 2.1). Примечание :
(см. рис. 2.1). Примечание :
позиция полностью определяется 1 координатой (поэтому это 1-мерное
проблема).
Рисунок 2.1. Одномерное положение.
Рисунок 2.2. графики зависимости x от t для различных скоростей.
Для данной задачи начало может быть выбрано в любой точке.
удобный. Например, положение объекта в момент времени t = 0 часто
выбран в качестве источника. Положение объекта в общем случае будет функцией
времени: x(t). Рисунок 2.2. показывает положение в зависимости от времени для
объект в состоянии покоя, а также для объектов, движущихся влево и вправо.
Наклон кривой на графике зависимости положения от времени зависит от
скорость объекта. См., например, рисунок 2.3. Через 10 секунд
гепард преодолел расстояние 310 метров, человек 100 метров, а свинья
50 метров. Очевидно, что гепард имеет наибольшую скорость. Похожий
вывод получается, когда мы рассматриваем время, необходимое для покрытия фиксированного
расстояние. Гепард преодолевает 300 метров за 10 с, человек за 30 с, а свинья
Гепард преодолевает 300 метров за 10 с, человек за 30 с, а свинья
требуется 60 с. Ясно, что более крутой наклон кривой зависимости x от t
график соответствует более высокой скорости.
Рисунок 2.3. графики x и t для различных существ.
Объект, который меняет свое положение, имеет ненулевую скорость. В среднем
скорость
объекта в течение заданного интервала времени определяется как:
Если объект движется вправо, средняя скорость положительна. Ан
объект, движущийся влево, имеет отрицательную среднюю скорость. Это ясно из
определение средней скорости, которая
зависит только от положения объекта в момент времени t = t 1 и по адресу
время t = t 2 . Это хорошо показано в задаче 2-1 из примера .
и 2-2 .
Пример задачи 2-1
Вы едете на потрепанном пикапе по прямой дороге 5,2 мили со скоростью 43 мили в час,
в этот момент у вас закончилось топливо. Вы идете на 2 мили дальше, до ближайшего
Вы идете на 2 мили дальше, до ближайшего
АЗС, за 27 мин (= 0,450 ч). Какова ваша средняя скорость от
время, когда вы завели свой грузовик, до того, как вы прибыли на станцию?
Пикап первоначально преодолевает расстояние 5,2 мили со скоростью
43 мили/час. Это занимает 7,3 минуты. После того, как у пикапа закончился
газа, вам потребуется 27 минут, чтобы дойти до ближайшей заправки, что составляет 1,2
миль вниз по дороге. Когда вы приедете на заправку, вы покрыли (5.2
+ 1,2) = 6,4 мили за период (7,3 + 27) = 34,3 минуты. Ваш средний
скорость до этой точки:
Пример задачи 2-2
Предположим, вы затем везете топливо обратно в грузовик, делая
туда и обратно за 35 мин. Какова ваша средняя скорость на всем пути от
начало вашего движения к вам возвращение к грузовику с топливом ?
Вам потребуется еще 35 минут, чтобы вернуться к своей машине. Когда вы достигнете своего
грузовик, вы снова находитесь в 5,2 милях от исходной точки и путешествовали уже
(34,4 + 35) = 69,4 минуты. В этот момент ваша средняя скорость равна:
В этот момент ваша средняя скорость равна:
После этого эпизода вы возвращаетесь домой. Вы преодолеваете 5,2 мили
снова за 7,3 минуты (скорость 43 мили/час). Когда ты приедешь домой,
вы находитесь в 0 милях от исходной точки, и, очевидно, ваша средняя скорость:
Средняя скорость пикапа, оставленного в гараже
также 0 миль/час. Поскольку средняя скорость тела зависит только от
его начальное и конечное положение и время, а не движение объекта в
между, это вообще не полезный параметр. Более полезное количество
мгновенная скорость объекта при данной
мгновенный. Мгновенная скорость – это значение, при котором средняя скорость
приближается по мере того, как интервал времени, в течение которого он измеряется, приближается к нулю:
Например: см. пример задачи 2-5 .
Теперь можно рассчитать скорость объекта при t = 3,5 с:
Скорость объекта определяется с точки зрения изменения
положение этого объекта во времени. Величина, используемая для описания изменения
Величина, используемая для описания изменения
скорость тела во времени есть ускорение а.
среднее ускорение за интервал времени между
t 1 и t 2 определяется как:
Обратите внимание на сходство между определением средней скорости и
определение среднего ускорения. мгновенный
ускорение а определяется как:
Из определения ускорения видно, что
ускорение имеет следующие единицы измерения:
Положительное ускорение обычно интерпретируется как означающее
увеличение скорости. Однако это неверно. Из определения
ускорение, можно сделать вывод, что ускорение положительное, если
Это, очевидно, верно, если скорости положительны, а скорость
увеличивается со временем. Однако это верно и для отрицательных скоростей, если
скорость становится менее отрицательной с течением времени.
Объекты, падающие под действием силы тяжести, являются одним из примеров объектов
движется с постоянным ускорением. Постоянное ускорение означает, что
ускорение не зависит от времени:
Интегрируя это уравнение, скорость объекта может быть
получено:
где v 0 — скорость объекта в момент времени t = 0. Из
скорость, положение объекта как функцию времени можно
рассчитано:
где x 0 — положение объекта в момент времени t = 0,
Примечание 1 : проверьте эти отношения, интегрируя формулы для
положение и скорость.
Примечание 2 : уравнения движения лежат в основе большинства задач (см.
пример задачи 7).
Пример задачи 2-8
Заметив полицейскую машину, вы тормозите Porsche с 75 км/ч до 45 км/ч.
на дистанции 88 м. а) Чему равно ускорение, если считать его постоянным?
б) Сколько времени прошло? c) Если вы продолжаете замедляться с
ускорение, рассчитанное в (а) выше, сколько времени пройдет, чтобы привести
машина отдыхает с 75 км/ч? d) В (c) выше, какое расстояние будет
покрытый ? д) Предположим, что при втором испытании с рассчитанным ускорением
в (а) выше и с другой начальной скоростью, вы останавливаете свой автомобиль после
прохождение 200 м. Каково было общее время торможения?
Каково было общее время торможения?
а) Нашими отправными точками являются уравнения движения:
(1)
(2)
Предоставляется следующая информация:
* v(t = 0) = v 0 = 75 км/ч = 20,8 м/с
* v(t 1 ) = 45 км/ч = 12,5 м/с
* x(t = 0) = x 0 = 0 м (Примечание: начало координат определяется как положение Porsche
при t = 0 с)
* х(т 1 ) = 88 м
* а = константа
Из уравнения (1) получаем:
(3)
Замените (3) в (2):
(4)
Из уравнения (4) мы можем получить ускорение a:
(5)
б) Подставьте уравнение (5) в уравнение (3):
(6)
в) Автомобиль находится в состоянии покоя в момент времени t 2 :
(7)
Подставив ускорение, рассчитанное с использованием уравнения (5), в уравнение (3):
(8)
d) Подставьте t 2 (из уравнения (8)) и a (из уравнения (5)) в уравнение (2):
(9)
д) Предоставляется следующая информация:
* v(t 3 ) = 0 м/с (Примечание: Porsche в состоянии покоя при t = t 3 )
* x(t = 0) = x 0 = 0 м (Примечание: начало координат определяется как положение Porsche
при t = 0)
* х(т 3 ) = 200 м
* a = постоянная = — 1,6 м/с 2
Уравнение (1) говорит нам:
(10)
Подставьте уравнение (10) в уравнение (2):
(11)
Время t 3 теперь можно легко вычислить:
(12)
Частным случаем постоянного ускорения является свободное падение (падение в
вакуум). В задачах о свободном падении направление свободного падения
В задачах о свободном падении направление свободного падения
определяется вдоль оси Y, и положительное положение вдоль оси Y
соответствует восходящему движению. Ускорение свободного падения (g) равно 9,8.
м/с 2 (по отрицательной оси ординат). Уравнения движения на свободе
fall очень похожи на рассмотренные ранее для постоянных
ускорение:
где y 0 и v 0 — положение и скорость
объекта в момент времени t = 0,
Пример
Питчер подбрасывает бейсбольный мяч вертикально вверх с начальной скоростью 25 м/с. (а)
Сколько времени нужно, чтобы достичь высшей точки? б) на какой высоте находится мяч
подняться выше точки его выброса? в) Через какое время мяч достигнет
точка на 25 м выше точки его выброса.
Рисунок 2.4. Вертикальное положение бейсбольного мяча как функция времени.
а) Нашими отправными точками являются уравнения движения:
Начальные условия:
* v(t = 0) = v 0 = 25 м/с (движение вверх)
* y(t = 0) = y 0 = 0 м (Примечание: начало координат определяется как положение мяча в
т = 0)
* г = 90,8 м/с 2
Высшая точка получена в момент времени t = t 1 . В этот момент
скорость равна нулю:
Мяч достигает высшей точки через 2,6 с (см. рис. 2.4).
б) Положение шара в момент t 1 = 2,6 с легко определить.
рассчитано:
c) Уравнение для y(t) можно легко переписать как:
где у — высота мяча в момент времени t. Это уравнение может быть
легко решается для t:
Используя начальные условия, указанные в (а), это уравнение можно использовать
для расчета времени достижения мячом высоты 25 м (y = 25 м):
t = 1,4 с
t = 3,7 с
Рис. 2.5. Скорость бейсбольного мяча как функция времени.
2.5. Скорость бейсбольного мяча как функция времени.
Скорости мяча в эти моменты времени равны (см. также рис. 2.5):
v(t = 1,4 с) = + 11,3 м/с
v(t = 3,7 с) = — 11,3 м/с
В момент времени t = 1,4 с мяч находится на высоте y = 25 м с положительной скоростью (вверх
движение). В момент времени t = 2,6 с мяч достигает высшей точки (v = 0). После т =
2,6 с, мяч начинает падать (отрицательная скорость). В t= 3,7 с мяч
снова находится на y = 25 м, но теперь движется вниз.
Присылайте комментарии, вопросы и/или предложения по электронной почте [email protected] и/или
посетите домашнюю страницу Фрэнка
Волки.
Требование центростремительной силы
Как упоминалось ранее в этом уроке, объект, движущийся по кругу, испытывает ускорение. Даже если двигаться по периметру круга с постоянной скоростью, все равно происходит изменение скорости и, следовательно, ускорение. Это ускорение направлено к центру окружности. А согласно второму закону движения Ньютона, объект, испытывающий ускорение, также должен испытывать результирующую силу. Направление чистой силы совпадает с направлением ускорения. Таким образом, для объекта, движущегося по кругу, должна быть внутренняя сила, действующая на него, чтобы вызвать его внутреннее ускорение. Иногда его называют 9.0372 требование центростремительной силы . Слово центростремительный (не путать с F-словом центробежный ) означает поиск центра. Для объекта, движущегося по кругу, есть результирующая сила, действующая к центру, которая заставляет объект искать центр.
А согласно второму закону движения Ньютона, объект, испытывающий ускорение, также должен испытывать результирующую силу. Направление чистой силы совпадает с направлением ускорения. Таким образом, для объекта, движущегося по кругу, должна быть внутренняя сила, действующая на него, чтобы вызвать его внутреннее ускорение. Иногда его называют 9.0372 требование центростремительной силы . Слово центростремительный (не путать с F-словом центробежный ) означает поиск центра. Для объекта, движущегося по кругу, есть результирующая сила, действующая к центру, которая заставляет объект искать центр.
Чтобы понять важность центростремительной силы, важно хорошо понимать первый закон движения Ньютона — закон инерции . Закон инерции гласит, что…
… движущиеся объекты имеют тенденцию оставаться в движении с той же скоростью и в том же направлении, если на них не действует неуравновешенная сила.
Согласно первому закону движения Ньютона, естественной тенденцией всех движущихся объектов является продолжать движение в том же направлении, в котором они движутся… движение от своего прямолинейного пути. Движущиеся объекты имеют тенденцию естественным образом двигаться по прямым линиям; неуравновешенная сила требуется только для того, чтобы заставить его вращаться. Таким образом, для движения объектов по кругу требуется наличие неуравновешенной силы.
Инерция, сила и ускорение для пассажира автомобиля
Идея, выраженная законом инерции Ньютона, не должна нас удивлять. Мы сталкиваемся с этим явлением инерции почти каждый день, когда ведем машину. Например, представьте, что вы — пассажир автомобиля на светофоре. Свет загорается зеленым, и водитель ускоряется из состояния покоя. Автомобиль начинает разгоняться вперед, но относительно сиденья, на котором вы находитесь, ваше тело начинает отклоняться назад. Ваше тело, находящееся в состоянии покоя, имеет тенденцию оставаться в покое. Это один из аспектов закона инерции: «объекты в состоянии покоя стремятся оставаться в покое». Когда колеса автомобиля вращаются, создавая движущую силу, действующую на автомобиль и вызывающую ускорение вперед, ваше тело старается оставаться на месте. Вам, конечно, может показаться, что ваше тело испытывает обратную силу, заставляющую его ускоряться назад. Тем не менее, вам было бы трудно идентифицировать такую обратную силу, действующую на ваше тело. Действительно нет ни одного. Ощущение отбрасывания назад — это просто тенденция вашего тела сопротивляться ускорению и оставаться в состоянии покоя. Автомобиль ускоряется из-под вашего тела, оставляя вас с ложным ощущением того, что вас толкают назад.
Ваше тело, находящееся в состоянии покоя, имеет тенденцию оставаться в покое. Это один из аспектов закона инерции: «объекты в состоянии покоя стремятся оставаться в покое». Когда колеса автомобиля вращаются, создавая движущую силу, действующую на автомобиль и вызывающую ускорение вперед, ваше тело старается оставаться на месте. Вам, конечно, может показаться, что ваше тело испытывает обратную силу, заставляющую его ускоряться назад. Тем не менее, вам было бы трудно идентифицировать такую обратную силу, действующую на ваше тело. Действительно нет ни одного. Ощущение отбрасывания назад — это просто тенденция вашего тела сопротивляться ускорению и оставаться в состоянии покоя. Автомобиль ускоряется из-под вашего тела, оставляя вас с ложным ощущением того, что вас толкают назад.
Теперь представьте, что вы находитесь в той же машине, которая движется с постоянной скоростью и приближается к светофору. Водитель нажимает на тормоза, колеса автомобиля блокируются, и автомобиль начинает буксовать до полной остановки. На движущуюся вперед машину действует сила, направленная назад, а затем на машину действует обратное ускорение. Однако ваше тело, находясь в движении, имеет тенденцию продолжать движение, пока автомобиль буксует до полной остановки. Вам, конечно, может показаться, что ваше тело подвергается действию направленной вперед силы, заставляющей его двигаться вперед с ускорением. И все же вам снова будет трудно идентифицировать такую поступательную силу, действующую на ваше тело. Действительно, нет никакого физического объекта, ускоряющего вас вперед. Ощущение того, что вас бросает вперед, — это просто тенденция вашего тела сопротивляться замедлению и оставаться в состоянии движения вперед. Это второй аспект закона инерции Ньютона: «тело в движении имеет тенденцию оставаться в движении с той же скоростью и в том же направлении…». Неуравновешенная сила, действующая на автомобиль, заставляет его замедляться, в то время как ваше тело продолжает движение вперед. Вы снова остаетесь с ложным ощущением того, что вас толкают в направлении, противоположном вашему ускорению.
На движущуюся вперед машину действует сила, направленная назад, а затем на машину действует обратное ускорение. Однако ваше тело, находясь в движении, имеет тенденцию продолжать движение, пока автомобиль буксует до полной остановки. Вам, конечно, может показаться, что ваше тело подвергается действию направленной вперед силы, заставляющей его двигаться вперед с ускорением. И все же вам снова будет трудно идентифицировать такую поступательную силу, действующую на ваше тело. Действительно, нет никакого физического объекта, ускоряющего вас вперед. Ощущение того, что вас бросает вперед, — это просто тенденция вашего тела сопротивляться замедлению и оставаться в состоянии движения вперед. Это второй аспект закона инерции Ньютона: «тело в движении имеет тенденцию оставаться в движении с той же скоростью и в том же направлении…». Неуравновешенная сила, действующая на автомобиль, заставляет его замедляться, в то время как ваше тело продолжает движение вперед. Вы снова остаетесь с ложным ощущением того, что вас толкают в направлении, противоположном вашему ускорению.
Эти два сценария вождения показаны на следующем рисунке.
В каждом случае — при трогании автомобиля с места и при торможении движущегося автомобиля до остановки — направление, в котором наклоняются пассажиры, противоположно направлению ускорения. Это всего лишь результат инертности пассажира — склонности сопротивляться ускорению. Наклон пассажира — это не ускорение само по себе, а тенденция сохранять состояние движения, пока автомобиль совершает ускорение. Тенденция тела пассажира сохранять свое состояние покоя или движения, в то время как окружающая среда (автомобиль) ускоряется, часто неверно истолковывается как ускорение. Это становится особенно проблематичным, когда мы рассматриваем третий возможный опыт инерции пассажира в движущемся автомобиле — левый поворот.
Предположим, что на следующем участке пути водитель автомобиля делает резкий поворот налево с постоянной скоростью. Во время поворота автомобиль движется по круговой траектории. То есть машина проезжает четверть круга. Сила трения, действующая на вращающиеся колеса автомобиля, вызывает неуравновешенную силу на автомобиль и последующее ускорение. Неуравновешенная сила и ускорение направлены к центру окружности, вокруг которой вращается автомобиль. Ваше тело, однако, находится в движении и имеет тенденцию оставаться в движении. Именно инерция вашего тела — склонность сопротивляться ускорению — заставляет его продолжать движение вперед. Пока автомобиль ускоряется внутрь, вы продолжаете движение по прямой. Если вы сидите с пассажирской стороны автомобиля, то в конечном итоге внешняя дверь автомобиля ударит вас, когда машина повернется внутрь. Это явление может заставить вас думать, что вы получаете ускорение от центра круга. На самом деле вы продолжаете свой прямолинейный инерционный путь по касательной к окружности, в то время как автомобиль ускоряется из-под вас. Ощущение внешней силы и внешнего ускорения есть ложное ощущение. Нет физического объекта, способного вытолкнуть вас наружу. Вы просто испытываете тенденцию вашего тела продолжать движение по касательной к круговой траектории, по которой поворачивает машина.
Сила трения, действующая на вращающиеся колеса автомобиля, вызывает неуравновешенную силу на автомобиль и последующее ускорение. Неуравновешенная сила и ускорение направлены к центру окружности, вокруг которой вращается автомобиль. Ваше тело, однако, находится в движении и имеет тенденцию оставаться в движении. Именно инерция вашего тела — склонность сопротивляться ускорению — заставляет его продолжать движение вперед. Пока автомобиль ускоряется внутрь, вы продолжаете движение по прямой. Если вы сидите с пассажирской стороны автомобиля, то в конечном итоге внешняя дверь автомобиля ударит вас, когда машина повернется внутрь. Это явление может заставить вас думать, что вы получаете ускорение от центра круга. На самом деле вы продолжаете свой прямолинейный инерционный путь по касательной к окружности, в то время как автомобиль ускоряется из-под вас. Ощущение внешней силы и внешнего ускорения есть ложное ощущение. Нет физического объекта, способного вытолкнуть вас наружу. Вы просто испытываете тенденцию вашего тела продолжать движение по касательной к круговой траектории, по которой поворачивает машина. Вы снова остаетесь с ложным ощущением того, что вас толкают в направлении, противоположном вашему ускорению.
Вы снова остаетесь с ложным ощущением того, что вас толкают в направлении, противоположном вашему ускорению.
Центростремительная сила и изменение направления
На любой объект, движущийся по кругу (или по круговой траектории), действует центростремительная сила . То есть есть какая-то физическая сила, толкающая или притягивающая объект к центру круга. Это требование центростремительной силы. Слово центростремительный — это просто прилагательное, используемое для описания направления силы. Мы не представляем новый тип силы, а скорее описывает направление чистой силы, действующей на объект, который движется по кругу. Каким бы ни был объект, если он движется по кругу, на него действует некоторая сила, заставляющая его отклоняться от своего прямолинейного пути, ускоряться внутрь и двигаться по круговому пути. Три таких примера центростремительной силы показаны ниже.
Когда автомобиль совершает поворот, сила трения, действующая на повернутые колеса автомобиля, создает центростремительную силу, необходимую для кругового движения. | Поскольку ведро с водой привязано к веревке и вращается по кругу, сила натяжения, действующая на ведро, создает центростремительную силу, необходимую для кругового движения. | Когда Луна вращается вокруг Земли, сила тяжести, действующая на Луну, создает центростремительную силу, необходимую для кругового движения. |
Центростремительная сила для равномерного кругового движения изменяет направление объекта без изменения его скорости. Идея о том, что неуравновешенная сила может изменить направление вектора скорости, но не его величину, может показаться немного странной. Как это могло быть? Есть несколько подходов к этому вопросу. Один из подходов предполагает анализ движения с точки зрения работы и энергии. Вспомним из Раздела 5 Учебного класса физики, что работа на 9 баллов.0372 сила , действующая на объект, вызывающая смещение . Количество работы, проделанной над объектом, определяется с помощью уравнения
Как это могло быть? Есть несколько подходов к этому вопросу. Один из подходов предполагает анализ движения с точки зрения работы и энергии. Вспомним из Раздела 5 Учебного класса физики, что работа на 9 баллов.0372 сила , действующая на объект, вызывающая смещение . Количество работы, проделанной над объектом, определяется с помощью уравнения
, где тета в уравнении представляет собой угол между силой и смещением. Поскольку центростремительная сила действует на объект, движущийся по окружности с постоянной скоростью, сила всегда действует внутрь, поскольку скорость объекта направлена по касательной к окружности. Это означало бы, что сила всегда направлена перпендикулярно направлению смещения объекта. Угол Theta в приведенном выше уравнении равен 90 градусов, а косинус 90 градусов равен 0. Таким образом, работа центростремительной силы при равномерном круговом движении равна 0 Дж. Вспомните также из Раздела 5 Учебного класса физики, что, когда внешние силы не совершают никакой работы над объектом, полная механическая энергия (потенциальная энергия плюс кинетическая энергия) объекта остается постоянной. Таким образом, если объект движется по горизонтальному кругу с постоянной скоростью, центростремительная сила не совершает работы и не может изменить полную механическую энергию объекта. По этой причине кинетическая энергия и, следовательно, скорость объекта останутся постоянными. Сила действительно может ускорить объект, изменив его направление, но не может изменить его скорость. Фактически, всякий раз, когда неуравновешенная центростремительная сила действует перпендикулярно направлению движения, скорость объекта остается постоянной. Чтобы неуравновешенная сила изменила скорость объекта, должна быть составляющая силы в направлении (или в противоположном направлении) движения объекта.
Вспомните также из Раздела 5 Учебного класса физики, что, когда внешние силы не совершают никакой работы над объектом, полная механическая энергия (потенциальная энергия плюс кинетическая энергия) объекта остается постоянной. Таким образом, если объект движется по горизонтальному кругу с постоянной скоростью, центростремительная сила не совершает работы и не может изменить полную механическую энергию объекта. По этой причине кинетическая энергия и, следовательно, скорость объекта останутся постоянными. Сила действительно может ускорить объект, изменив его направление, но не может изменить его скорость. Фактически, всякий раз, когда неуравновешенная центростремительная сила действует перпендикулярно направлению движения, скорость объекта остается постоянной. Чтобы неуравновешенная сила изменила скорость объекта, должна быть составляющая силы в направлении (или в противоположном направлении) движения объекта.
Применение компонент вектора и второго закона Ньютона
Второй подход к этому вопросу о том, почему центростремительная сила вызывает изменение направления, а не изменение скорости, включает компоненты вектора и второй закон Ньютона. Следующий воображаемый сценарий будет использован, чтобы помочь проиллюстрировать это.
Следующий воображаемый сценарий будет использован, чтобы помочь проиллюстрировать это.
Предположим, что на местной фабрике по производству льда кусок льда выскальзывает из морозильной камеры, и механическая рука прикладывает силу, чтобы ускорить его движение по ледяной поверхности без трения. На прошлой неделе механическая рука работала со сбоями и толкала беспорядочно. Различные направления сил, приложенных к движущейся глыбе льда, показаны ниже. В каждом случае наблюдайте за силой по сравнению с направлением движения ледяного блока и предскажите, будет ли сила ускоряться, замедляться или не будет влиять на скорость блока. Используйте векторные компоненты, чтобы делать прогнозы. Затем проверьте свои ответы, нажав на кнопку.
а. | |||
б. | |||
в. | |||
д. |
| ||
эл. |
|
Приведенные выше примеры показывают, что сила способна замедлять или ускорять объект только тогда, когда есть составляющая, направленная в том же или противоположном направлении, что и движение объекта. В случае e вертикальная сила не изменяет горизонтального движения. Иногда говорят, что перпендикулярные компоненты движения не зависят друг от друга. Вертикальная сила не может повлиять на горизонтальное движение.
Иногда говорят, что перпендикулярные компоненты движения не зависят друг от друга. Вертикальная сила не может повлиять на горизонтальное движение.
Подводя итог, можно сказать, что на объект, совершающий равномерное круговое движение, действует направленная внутрь результирующая сила. Эту внутреннюю силу иногда называют центростремительной силой, где центростремительный описывает ее направление. Без этой центростремительной силы объект никогда не мог бы изменить свое направление. Тот факт, что центростремительная сила направлена перпендикулярно касательной скорости, означает, что сила может изменить направление вектора скорости объекта без изменения его величины.
Мы хотели бы предложить …
Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего Интерактивного приложения Uniform Circular Motion и/или нашего интерактивного режима Race Track. Вы можете найти их в разделе Physics Interactives на нашем сайте. Оба интерактива позволяют учащемуся в интерактивном режиме исследовать результирующую силу для объекта, движущегося по кругу.
Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего Интерактивного приложения Uniform Circular Motion и/или нашего интерактивного режима Race Track. Вы можете найти их в разделе Physics Interactives на нашем сайте. Оба интерактива позволяют учащемуся в интерактивном режиме исследовать результирующую силу для объекта, движущегося по кругу.
Посетите: Равномерное круговое движение | Гоночная трасса
Проверьте свое понимание
Для вопросов №1–№5: Объект движется в по часовой направлении по окружности с постоянной скоростью. Используйте свое понимание понятий скорости, ускорения и силы, чтобы ответить на следующие пять вопросов. Используйте схему, показанную справа. Нажмите кнопку, чтобы проверить свои ответы.
1. Какой из приведенных ниже векторов представляет направление вектора силы, когда объект находится в точке А на окружности?
2. Какой из приведенных ниже векторов представляет направление вектора силы, когда объект находится в точке C на окружности?
Какой из приведенных ниже векторов представляет направление вектора силы, когда объект находится в точке C на окружности?
3. Какой из приведенных ниже векторов представляет направление вектора скорости, когда объект находится в точке B на окружности?
4. Какой из приведенных ниже векторов представляет направление вектора скорости, когда объект находится в точке C на окружности?
5. Какой из приведенных ниже векторов представляет направление вектора ускорения, когда объект находится в точке B на окружности?
6. Рекс Вещи и Дорис Локед идут на свидание. Рекс делает быстрый правый поворот. Дорис начинает скользить по виниловому сиденью (которое Рекс предварительно натер воском и полировал) и сталкивается с Рексом. Чтобы сломать неловкость ситуации, Рекс и Дорис начинают обсуждать физику только что испытанного движения. Рекс предполагает, что объекты, которые движутся по кругу, испытывают внешнюю силу. Таким образом, когда поворот был сделан, Дорис испытала внешнюю силу, которая подтолкнула ее к Рексу. Дорис не соглашается, утверждая, что объекты, которые движутся по кругу, испытывают внутреннюю силу. В этом случае, по словам Дорис, Рекс двигался по кругу из-за того, что дверь толкала его внутрь. Дорис не двигалась по кругу, так как не было никакой силы, толкающей ее внутрь; она просто продолжала двигаться по прямой, пока не столкнулась с Рексом. Кто прав? Аргументируйте одну из этих двух позиций.
Рекс предполагает, что объекты, которые движутся по кругу, испытывают внешнюю силу. Таким образом, когда поворот был сделан, Дорис испытала внешнюю силу, которая подтолкнула ее к Рексу. Дорис не соглашается, утверждая, что объекты, которые движутся по кругу, испытывают внутреннюю силу. В этом случае, по словам Дорис, Рекс двигался по кругу из-за того, что дверь толкала его внутрь. Дорис не двигалась по кругу, так как не было никакой силы, толкающей ее внутрь; она просто продолжала двигаться по прямой, пока не столкнулась с Рексом. Кто прав? Аргументируйте одну из этих двух позиций.
7. Кара Лотт занимается зимним вождением на стоянке GBS. Кара поворачивает руль, чтобы повернуть налево, но ее машина продолжает двигаться по прямой по льду. Учитель А и Учитель Б наблюдали за явлением. Учитель А утверждает, что отсутствие силы трения между шинами и льдом приводит к балансу сил, благодаря которому автомобиль движется прямолинейно. Учитель Б утверждает, что лед воздействовал на шину силой, направленной наружу, чтобы уравновесить силу поворота и, таким образом, удерживать машину на прямолинейном движении. Какой учитель (А или Б) является учителем физики? ______ Объясните ошибочность аргумента другого учителя.
Какой учитель (А или Б) является учителем физики? ______ Объясните ошибочность аргумента другого учителя.
Следующий раздел:
Перейти к следующему уроку:
Типы ускорения, единицы измерения, важность и графическое представление движения по прямой
Когда водитель движущегося автомобиля использует тормоза, мы описываем движение автомобиля как движение с замедлением потому что скорость автомобиля уменьшается со временем проходит. Отношение d/t остается постоянным в случае тела, движущегося с постоянной скоростью , потому что это тело преодолевает равные расстояния за равные промежутки времени. Тело, движущееся с ускорением, не может двигаться с постоянной скоростью, потому что его скорость меняется с течением времени.
Графическое представление движения по прямой линии
Графики и таблицы важны для физиков, Физические явления могут быть описаны и поняты многими способами, Физики используют математические отношения между переменными для описания определенных явлений . Физики используют другие математические отношения, такие как графики и таблицы, чтобы:
Физики используют другие математические отношения, такие как графики и таблицы, чтобы:
- предсказать связь между определенными физическими величинами.
- понять практические результаты.
- описывают физические явления более простым способом.
Графическое изображение штатной (равномерной) скорости
Данные о штатной скорости по прямой:
- График (расстояние – время) регулярного движения с постоянной (равномерной) скоростью представлен прямой линией, проходящей через начальную точку, поскольку расстояние прямо пропорционально времени, когда объект движется с постоянной скоростью.
- График (скорость – время) закономерного движения с постоянной (равномерной) скоростью изображается прямой линией, параллельной оси времени.
График (расстояние-время) объекта в состоянии покоя представлен прямой линией, параллельной оси времени. График отношения (расстояние-время) для объекта, движущегося с неравномерной скоростью, представлен в виде кривой линии, проходящей через исходную точку.
График отношения (расстояние-время) для объекта, движущегося с неравномерной скоростью, представлен в виде кривой линии, проходящей через исходную точку.
Ускорение
Ускорение
Когда вы сидите в машине рядом с водителем, и машина начинает движение из состояния покоя по прямой, вы замечаете, что скорость автомобиля постепенно увеличивается с течением времени. Когда скорость автомобиля в 1 секунду становится 5 м/сек, в 2 секунды становится 10 м/сек, в 3 секунды становится 15 м/сек. и так далее.
Для описания изменения скорости автомобиля за одну секунду в этом случае мы используем физическую величину, называемую «ускорение». Ускорение — это изменение скорости объекта за одну секунду в определенном направлении или скорость изменения скорости.
Ускорение (a) = изменение скорости (ΔV)/время, в течение которого происходит изменение (Δt) 1 )]/ Время (Δt)
Дельта (Δ) означает скорость изменения любой физической величины.
To calculate V 1 or V₂: V 1 = V 2 − (a × t) , V 2 = V 1 + (a × t)
Единицы измерения ускорения
Единица измерения ускорения = метр/секунда². Мы используем единицу ускорения (м/сек²), когда скорость измеряется в метрах в секунду, а время измеряется в секундах, или (км/ч²), когда скорость измеряется в километрах в час, а время измеряется в час.
Руководство по решению задач на ускорение:
- Для расчета: ускорения, изменения скорости и времени, a = ΔV/ Δt
- Если тело движется с постоянной скоростью, то его ускорение равно нулю, потому что его скорость не меняется с течением времени [когда (AV) = ноль, тогда (a) = ноль].
- Если тело начинает движение из состояния покоя, то его начальная скорость (V₁) равна нулю.

- Когда тело перестает двигаться, его конечная скорость (V₂) равна нулю.
- Когда автомобиль движется, то через некоторое время включается тормоз, чтобы остановить автомобиль, поэтому его конечная скорость равна нулю.
Равномерное ускорение
Когда автомобиль преодолевает равные расстояния за равные промежутки времени, говорят, что автомобиль движется с равномерной (равномерной) скоростью. Но если его скорость изменяется (уменьшается или увеличивается) на равные величины в равные промежутки времени, говорится, что автомобиль движется с равномерным (равномерным) ускорением.
При t скорость автомобиля увеличивается на 10 м/с каждые 2 с, поэтому ускорение (а) = (20-10)/10 = 5 м/с². Равномерное ускорение — это ускорение, с которым объект движется по прямой, когда его скорость изменяется на равные величины через равные промежутки времени.
Когда автомобиль движется с равномерным ускорением, равным 5 м/с². Это означает, что автомобиль движется прямолинейно и его скорость изменяется с 5 м/с. каждую секунду.
Виды равномерного ускорения
- Положительное ускорение.
- Отрицательное ускорение.
Положительное ускорение
Объект движется с равномерным положительным ускорением (ускоряющее движение), когда [Его начальная скорость < Его конечная скорость]. Положительное ускорение — это ускорение, с которым объект движется по прямой, когда его скорость увеличивается на равные значения через равные промежутки времени.
Когда объект n движется с положительным ускорением, равным 2 м/с². Это означает, что объект движется прямолинейно и его скорость увеличивается на 2 м/сек каждую секунду. Знак (+) означает, что скорость объекта регулярно увеличивается на 2 м/сек. каждую секунду.
Знак (+) означает, что скорость объекта регулярно увеличивается на 2 м/сек. каждую секунду.
Отрицательное ускорение
Объект движется с равномерным отрицательным ускорением (замедление движения). [Его начальная скорость> Его конечная скорость]. Отрицательное ускорение есть ускорение, при котором объект движется по прямой, когда его скорость уменьшается на равные величины через равные промежутки времени
Когда n объект движется с отрицательным ускорением, равным -2 м/сек². Это означает, что объект движется прямолинейно и его скорость уменьшается на 2 м/сек каждую секунду. Знак (-) указывает на то, что скорость объекта регулярно уменьшается на 2 м/сек. каждую секунду.
Таким образом, мы можем вывести тип ускорения из формы графика:
- Положительное ускорение: когда t объект движется с (неравномерной скоростью), V (начальная) < V (финал), Значит, он движется с ускорением.

- Отрицательное ускорение: Объект движется с (неравномерной скоростью), V (начальная) > V (конечная), Таким образом, он движется с замедлением.
- Нулевое ускорение: Объект движется с (равномерной скоростью), V (начальная) = V (конечная).
Ускорение положительное, когда его значение увеличивается, и отрицательное, когда его значение уменьшается b потому что при движении с положительным ускорением конечная скорость больше начальной скорости, а при движении с отрицательным ускорением, конечная скорость меньше начальной.
Объект, который движется с постоянной скоростью, его ускорение равно нулю. Тело движется с нулевым ускорением, потому что его скорость не меняется с течением времени (ΔV = ноль).
Проблемы
• Объект движется из состояния покоя и его скорость достигает 20 м/сек. за 5 секунд. Вычислите ускорение движущегося тела? Что такое тип ускорения?
за 5 секунд. Вычислите ускорение движущегося тела? Что такое тип ускорения?
Раствор
V₁ = 0 , V₂ = 20 м/с. , Δt = 5 сек.
а = V₂ – V₁ /Δt
a = (20- 0)/5= 4 м/с², Положительное ускорение.
• Поезд движется с постоянной скоростью 20 м/сек. Когда машинист нажимает на тормоз, поезд останавливается через 4 с. Вычислите ускорение, с которым движется поезд, и укажите тип ускорения.
Раствор
V₁ = 20 м/сек. V2 = 00373 Торможение
• Водитель автомобиля движется со скоростью 80 м/сек. использовали тормоза, чтобы заставить автомобиль двигаться с равномерным убывающим ускорением 2 м/с? Найдите скорость автомобиля через 12 секунд после начала торможения.
Solution
V₁ = 80 m/sec , V₂=56 m/sec , a = – 2 m/sec , Δt = 12 sec
V 2 = V 1 + (а × т)
V₂ = 80 + ( – 2 × 12) = 56 м/с
Рекомендации по решению задач
При движении с постоянной скоростью через промежуток времени (АВ) и затем движение с равноускорением через другой промежуток времени (ВС). Итак, равномерная скорость за период времени (AB) = начальная скорость за период времени (BC). [V₁ в точке (B)].
Итак, равномерная скорость за период времени (AB) = начальная скорость за период времени (BC). [V₁ в точке (B)].
• Объект движется по прямой с постоянной скоростью. Если время, затраченное на объект перемещается из (А) в (В) 4 секунды, затем он движется с равномерным ускорением из точки (В) до остановки в точке (С) за 20 секунд. Рассчитайте каждое из следующих значений:
- Обычная скорость объекта для преодоления расстояния (AB).
- Равномерное ускорение, с которым объект перемещается из точки (В) в точку (С).
Решение
1. Обычная скорость в (AB) = Расстояние/Время = 40/4= 10 м/сек.
2. Начальная скорость при (BC) = равномерная скорость при (AB) = 10 м/с
Равномерное ускорение при (BC) (a) = (V₂ – V₁)/At = (0 – 10) /20 = – 0,5 м/сек²
• Автомобиль движется со скоростью 60 м/сек, если водитель притормозил, чтобы снизить скорость на 3 м/сек.




 Необходимо поставить автомобиль на уклоне (положение 1), не пересекая линию «Старт».
Необходимо поставить автомобиль на уклоне (положение 1), не пересекая линию «Старт».

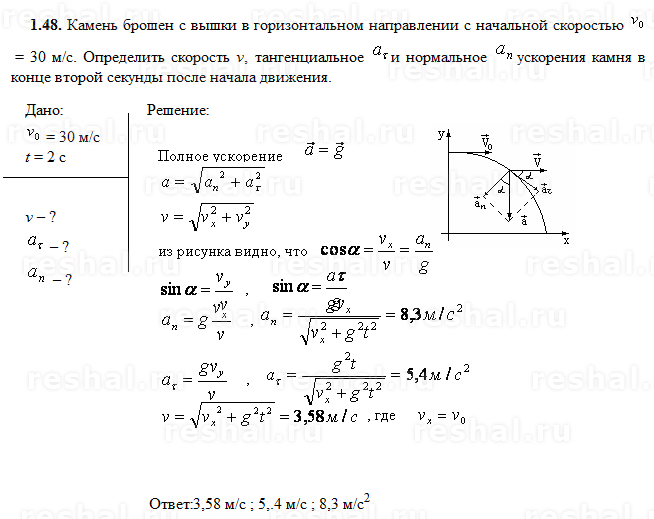




 Включаем первую передачу, снимаем с «ручника».
Включаем первую передачу, снимаем с «ручника».



 сети, отправить по почте, добавить в закладки или распечатать.
сети, отправить по почте, добавить в закладки или распечатать.