Противораскачивание груза — Крановые панели и системы управления кранами

Не секрет, что каждое движение крана с подвешенным грузом приводит к его колебаниям, поэтому оператор крана должен постоянно корректировать свои действия с учетом этого раскачивания. Опытный и внимательный оператор может достаточно быстро уменьшить колебания груза путем принятия соответствующих контрмер. Если же оператор не обладает большим опытом управления краном или оператор потерял внимание по причине утомления, то даже самые простые операции могут привести к огромной потере времени или к возникновению рисков коллизий и/или аварийных ситуаций.

Системы уменьшения колебаний груза (системы противораскачивания), такие как CeSAR, снимают с оператора задачи по уменьшению раскачивания груза, как следствие он может сосредоточиться на управлении краном, сконцентрироваться на подъеме груза, его перемещении, позиционировании и опускании в нужную точку.

Область применения

Системы противораскачивания служат для уменьшения колебаний груза, вызванных ускорениями механизмов в процессе эксплуатации крана. Успокоение достигается за счет точного воздействия на процессы разгона и торможения. Системы противораскачивания могут применяться как в составе систем управления для новых кранов, так и в качестве дополнения к уже существующим системам управления. Уменьшение колебаний позволяет снизить риск возникновения коллизий и аварийных ситуаций в сочетании с одновременной быстротой и точностью позиционирования груза. Такие системы могут применяться как для ручного режима работы крана (кран управляется оператором), так и для автоматических крановых систем. Система противораскачивания CeSAR позволяет уменьшить колебания при перемещении моста, тележки и поворота крана одновременно. CeSAR не предполагает использования механических демпфирующих (амортизационных) элементов. 

Существует два основных вида электронных систем противораскачивания: системы с прямой обратной связью, имеющие в своем составе камеру и рефлектор (отражатель), которые обеспечивают получение оперативной достоверной информации об отклонении груза, и системы, работающие на основе математической модели, описывающей колебания груза при движении механизмов крана, то есть угол отклонения груза в той или иной плоскости вычисляется исходя из физических и математических законов.

В системах с обратной связью камера с высоким разрешением используется для измерения отклонения крюка или другого типа грузозахватного органа от своей оси. Для того, что бы сделать это возможным, на грузозахватный механизм устанавливается специальный отражатель. В самом простом случае отражатель представляет собой плоскость квадратной формы с расположенными на ней в шахматном порядке двумя белыми квадратами. Данный тип рефлектора называется пассивным. В случае, когда на него могут воздействовать чрезмерное освещение или тени, которые влияют на точность системы измерения, рекомендуется использовать активный рефлектор, снабженный LED-матрицей, а также обогревом, способствующим таянию снега, если кран используется на открытом воздухе. Самым лучшим же выходом в случае использования системы «камера-рефлектор» является применения инфракрасного рефлектора и оснащение камеры инфракрасным фильтром. Точность определения колебаний составляет 5 мм на расстоянии от камеры до рефлектора 10м, точность определения расстояния между камерой и рефлектором составляет 1%. Такие системы способны также исключать колебания груза при наличии сильного бокового ветра. 

«Слепые» системы противораскачивания (CeSAR blind) разработаны для кранов, работающих в закрытых помещениях и не подверженных влиянию внешних возмущений, например, ветру.

Какой бы вид системы противораскачивания груза ни был установлен на кране, ее применение ведет к снижению времени выполнения операций, повышению точности позиционирования груза, уменьшению утомляемости операторов во время работы, а также снижает риск возникновения аварийных ситуаций. 

Автоматическая система компенсации раскачки груза (антираскачки) на оборудовании Schneider Electric.

Проблемы:

Сильная раскачка груза при его перемещении несмотря на уменьшение скорости крана почти в два раза. Постоянная опасность повреждения цехового оборудования. Очень низкая производительность.

В обычном режиме работы раскачка груза обусловлена законами физики и ее последствия исключаются вручную опытом крановщика. При этом следует отметить, что при наличии частотно-регулируемого привода крановщику почти невозможно справиться с раскачкой груза, так как разгон и торможение крана и тележки происходит постепенно за фиксированное в настройках ПЧ время (в среднем 4-6 секунд). Также отсутствуeт режим «противотоков», к которому крановщики привыкли при работе на кранах с контакторными системами управления. Нужны время и опыт работы для точного позиционирования груза с одного захода, без «додергивания» крана и тележки. И все вышеперечисленнное только усиливается, практикуемой многими предприятиями, ротацией крановщиков между кранами.

Решение:

Установка программируемого логического контроллера (ПЛК) Шнейдер Электрик со специальным заводским программным обеспечением для автоматической компенсации раскачки груза.

Уникальность этого решения заключается в том, что оно экономичное и в тоже время технически несложное, так как нет необходимости устанавливать дополнительные датчики. При этом ничего из существующего электрооборудования на кране не выкидывается и всегда есть возможность переключить кран в обычный режим^[1]. Так как раскачка груза зависит только от длины каната на котором подвешен груз, то наша задача ее определить и передать в ПЛК. В настройках ПЛК предусмотрено автоматическое задание длины каната с помощью командоаппарата или энкодера, установленного на механизме подъема, а также ручное задание длины каната с помощью 3-х позиционного переключателя. ПЛК Шнейдер Электрик представлены несколькими сериями, в том числе в виде карты расширения, устанавливаемой внутрь преобразователей частоты (ПЧ) серии Altivar71, что также упрощает монтаж.

Решение антираскачки груза позволяет уменьшить требование к квалификации оператора крана и одновременно с этим увеличить производительность крана и точность позиционирования, а также снизить степень опасности в цеху исходящей от использования грузоподъемного оборудования.

ПЛК при активированном режиме автоматической компенсации раскачки груза обеспечивает:

— гашение колебание груза за счет встроенного запатентованного алгоритма разгона и торможения крана и грузовой тележки, раскачка груза компенсируется по двум осям одновременно, в том числе при одновременном перемещении моста и тележки крана, скорости перемещения крана и тележки могут быть абсолютно любыми – от минимальной до максимальной;

— несколько алгоритмов измерения длины каната до крюка с грузом, в том числе не требующий применения специальных датчиков обеспечивает в большинстве случаев бюджетное решение;

— управление краном по шине CANopen^[2]. Соединение по шине позволяет не переделывая схему крана, а только дополняя ее, соединить между собой ПЛК с преобразователями частоты ATV71 и/или ATV31/32 электроприводов перемещения крана и тележки, используя уже имеющиеся на ПЧ интерфейсы CANopen и независимо от наличия свободных дискретных сигналов на ПЧ.

Монтаж системы на кране:

В нашем случае, мозг решения автоматической компенсации раскачки груза представляет собой карту встроенного ПЛК (Controller Inside Card) VW3A3501 для преобразователя частоты Altivar71. Карта установлена непосредственно внутрь преобразователя частоты Altivar71. Для определения длины каната рекомендуется использование датчиков (энкодеров) на приводе подъема, но так как решение бюджетное, то было решено установить 3-х позиционный переключатель выбора длины каната. ПЛК и преобразователи частоты соединили по шине CANopen. Далее поднастроены параметры ПЧ и карты ПЛК при помощи дисплеев, установленных на ПЧ. Также возможна настройка параметров ПЧ с ноутбука кабелем или по Bluetooth через программное обеспечение SoMove Light.

Установка крановой карты позволила полностью исключить раскачку груза при его перемещении краном. Отсутствие раскачки при разгоне и торможении крана позволяет увеличить скорости передвижения крана и тележки, тем самым увеличить производительность. В нашем примере в процессе повышения скорости владелец крана дал команду остановиться на 70% (было 50%) от номинальной скорости крана.

Результат:

• При перемещении груза раскачка практически отсутствует.
• Нет необходимости придерживать груз, в том числе руками, что снижает риск травматизма и положительное влияет на безопасность работ.
• Груз точнее и быстрее подводится к месту назначения.
• Отсутствует время ожидания перед опусканием груза.
• Скорости передвижения крана и тележки увеличены на 15-20%.
• Интуитивная комфортность управления краном и снижение требований к квалификации персонала.

[1] Так как алгоритм разгона и торможения механизмов крана нелинеен, то при нахождении оператора крана в кабине его может «укачивать». Для кранов на радиоуправлении или с подвесным пультом это не существенно.

[2] Шина CANopen за скорость и надежность передачи данных активно используется в автомобильной промышленности для связи автомобильных датчиков с бортовым ПЛК (компьютером).

Five Star Model (CN)

Информация о бренде

Название:

Пятизвездочная модель »Модель». Домашняя страница

Страна:

Действие:

2011

Продукты:

Aftermarket (625) | Наборы (64)|Инструменты (22)|Фигурки (19)|Дополнительно (2)

Посмотреть все продукты

Все наборы » Все принадлежности »

Новинки

Китайский десантный корабль НОАК Тип 271II (2 корабля) Модель из смолы

Пятизвездочная модель 1:700

FS720035 2022 Новый инструмент

Второй мировой войны Королевский тайский флот

Тонбури-класс прибрежный корабль (смола)

Пять звезд модель 1: 350

FS360004 2021 Новый инструмент

WWI. Five Star Model 1:700

FS720044 2021 New tool

WWII IJN 150t Type Minelayer Early Type (with board shield)

Five Star Model 1:700

FS720043 2021 New tool

WWII IJN (Manchukuo) Destroyer Kashi ( Хайвэй)

Five Star Model 1:700

FS720039 2021 Новый инструмент

Подробнее »

Горячие наборы

Современный атомный крейсер ВМФ России

Петр Великий `2017` (Тип 1144) — Полный набор 9 9 9 0 9 звёзд для Trumpeter Модель 1: 350

FS350087 2021*

WWII USS Tennessee BB-43 1945 Набор обновления

Пятизвездочная модель 1: 700

FS700106 2017 Новый инструмент

USS SAN FRANCISCO CA-38 SOTER SOTERSETER SOTERSETER SATETER CA-3880028

Пятизвездочная модель 1: 700

FS700036

WWII USN FLECHER Class Class Set Essumper Set (Bridge Late Type) для Tamiya 31907

Набор обновлений

Five Star Model 1:350

FS350035 2017 New tool

WWII USS California BB-44 1945 Upgrade Set (для Trumpeter 05784)

Five Star Model 1:700

7 инструмент FS700270028

Второй мировой войны Немецкий ВМС. Масштаб 1:350

FS360004 2021 Новый инструмент

Вторая мировая война USN

USS Texas BB-35 1945 — Upgrade Set

Five Star Model 1:700

Modern FS7000129

29 20280 20280 Русский0027 Ракетный крейсер класса «Слава» «Варяг» (Тип 1164) — полный набор улучшений 32 шт.)

Пятизвездочная модель 1: 700

FS710358

WWII IJN E-27 Радар 3D Print для 3D-печати сосудов — (12 шт.)

Пятизвездочная модель 1: 700

FS710354

WWII

IJN Тип 89 12,7 см. Двойной AA Gun с Shield 3D Print 89 12,7 см Двойной зенитный пистолет без щита (поздний тип) 3D-печать (8 комплектов)

Модель Five Star 1:700

FS710351

Подробнее »Кристиан Абрахам на Modellmarine

Japanische Hilfsminenrämer Wa-1 и Wa-2

Five Star Model 1:700

by Christian Abraham на Modellmarine

Japanischer Minenleger Toshima

Five Star Model 1:700 9009 на Abraham 900 Modellmarine

Japanisches Kranschiff Seishu Maru

Five Star Model 1:700

Кристиан Абрахам на Modellmarine

Подробнее »

История выпуска

Гистограмма, показывающая количество и распространение выпусков:

2012

2022

Согласно нашим записям, первый выпуск Five Star Model был примерно 11 лет назад в 2012 году.

289 продуктов Five Star Model не имеют четкого года выпуска и не показаны в выше статистика

86.000+ пластиковых моделистов используют нас

Регистрация Войти

Новые выпуски (Пулеметы в масштабе 1:700)

Подробнее »

Горячие наборы (Пулеметы в масштабе 1:700)

Подробнее »

Anti-Sway and Positioning Adaptive Управление крановой системой с двойным маятниковым эффектом с компенсацией нейронной сети

Введение

Краны обычно используются для подъема или перемещения грузов в сфере строительства, логистики, обрабатывающей промышленности и т. д. Краны бывают различных форм, и большинство кранов работают с использованием проволочных канатов для подвешивания груза. При движении крана или внешних возмущениях груз будет раскачиваться из-за гибкости тросов, и для перемещения груза в нужное положение используются активные и пассивные методы. Раскачивание груза — это своего рода простая гармоническая вибрация. Когда груз, перевозимый кранами, начинает раскачиваться, требуется несколько периодов для его подавления, что отнимает много времени и даже приводит к проблемам с эффективностью работы. Поэтому проблема раскачивания стала актуальной темой, особенно для портовой отрасли. Более того, проблема раскачивания вызовет проблемы с безопасностью при перевозке грузов большой массы и может даже сильно повлиять на конструкцию конструкции крана.

Технология предотвращения раскачивания кранов изучалась в течение последних 20 лет. Внимание было уделено кранам как с одинарным маятником, так и с двойным маятниковым эффектом с использованием механической и автоматической технологии предотвращения раскачивания. Когда масса спредера для крана достаточно велика, нельзя пренебрегать эффектом двойного маятника кранов. Чтобы устранить этот эффект двойного маятника, который вносит в систему более сильную нелинейность, вызванную взаимодействием между разбрасывателем и полезной нагрузкой, контроллеры спроектированы так, чтобы справляться с раскачиванием. Было проведено множество исследований по разработке таких контроллеров для решения проблемы эффекта двойного маятника. Камаль (Мустафа и Эбейд, 19 лет)88) и др. вывела нелинейную динамическую модель кранов, а в 1988 году также был представлен метод управления с обратной связью для устранения раскачивания груза. М. Гутьеррес и соавт. (Gutierrez and Solo, 1998) предложили контроллер на основе нечеткой логики для модели прототипа мостового крана, который показал отличные характеристики управления в ходе моделирования и экспериментов. Z Nowacki и соавт. (Nowacki et al., 1996) представили ПД-контроллер с двумя контурами обратной связи для мостового крана, а также был предложен анализ надежности системы. Чва и др. (Dongkyoung, 2017) представили метод управления слежением, основанный на методе управления скользящим режимом для трехмерной системы мостового крана, чтобы подавить углы раскачивания тележки, и эффективность управления оказалась превосходной. Х. Х. Ли и соавт. (Чо и Ли, 2002) представили новую схему нечеткого управления против раскачивания в сочетании с сервоуправлением положением и нечетким логическим управлением для прототипа мостового крана, и эффективность предложенной стратегии управления доказана экспериментами.

Благодаря превосходной аппроксимационной способности метода нейронной сети исследователи представили несколько исследований для решения проблемы раскачивания кранов. Chunshien Li и Chun-yi Lee et al. (Li and Lee, 2001a; Li and Lee, 2001b) предложили составной метод в сочетании с методом адаптивного управления нейронной сетью с нечетким управлением для мостового крана с высокой способностью противостоять возмущениям. Парк и др. (Park and Le, 2012) предложили совместное моделирование виртуального прототипа с помощью MATLAB и ADAMS для изучения плавучего контейнерного крана. Чжан и др. (Zhang et al., 2016) предложили адаптивный контроллер слежения на основе двухмаятниковых мостовых кранов с неопределенностями и возмущениями путем построения новой функции скольжения в качестве желаемой траектории. Оуян и др. (Оуян и др., 2019 г.) представил новый адаптивный иерархический контроллер режима скольжения для мостовых кранов с эффектом двойного маятника, который может ускорить переход состояний системы на желаемую поверхность скольжения и даже улучшить точность отслеживания тележки. Нин Сун и др. (Sun et al., 2020a) создали динамическую модель кооперативной системы сдвоенных поворотных кранов на основе метода Лагранжа. Учитывая ограничения привода, также был представлен метод управления выходной обратной связью, который помогает повысить точность позиционирования двойной стрелы. Кроме того, метод управления, упомянутый в (Sun et al., 2020a), был распространен на управление позиционированием и отслеживанием пневматической искусственной мышечной системы (Sun et al., 2020b). Чен Х и др. представили новую стратегию управления своего рода системой с недостаточным приводом, рассматривая различные ограничения, и предложенный метод был применен к крановой системе с двойным маятником с превосходными характеристиками (Chen et al., 2019).; Чен и Сун, 2020 г.). Ян Т и др. (Yang et al., 2020) разработали метод адаптивного управления на основе нейронной сети для решения задач позиционирования судовых кранов.

Исходя из предыдущего анализа, устранение двойного маятникового эффекта кранов играет важную роль для обеспечения безопасности и эффективности кранов при эксплуатации. Основной вклад этой работы заключается в следующем:

1. Предлагаемый контроллер может реализовать функцию быстрого позиционирования и антираскачивания для крановой системы с эффектом двойного поворота.

2. Адаптивный контроллер на основе нейросетевой компенсации RBF имеет функцию онлайн-обучения и не чувствителен к изменению параметров. Даже если в контроллере отсутствуют некоторые элементы, он все равно может получить лучший эффект контроля за счет компенсации онлайн-обучения.

3. Результаты эксперимента показывают, что точность позиционирования и скорость отклика лучше, чем у традиционного контроллера скользящего режима.

В данной работе в качестве объекта исследования выбран мостовой кран с двойным маятниковым эффектом. Во-первых, создается математическая модель крана с двойным маятниковым эффектом. На основе математической модели разработан адаптивный регулятор, основанный на методе компенсации нейронной сети радиальной базисной функции, где ядром регулятора является робастный регулятор, а нейронная сеть работает как дополнительная система для вывода силы компенсации. Затем проводится анализ устойчивости по Ляпунову для подтверждения устойчивости крановой системы с нейросетевым контроллером. Наконец, для проверки предлагаемого контроллера используется аппаратное обеспечение на экспериментальной платформе с контуром. Также представлено сравнение между контроллером скользящего режима и контроллером нейронной сети для проверки эффективности и осуществимости стратегии управления.

Моделирование кранов с двойным маятниковым эффектом

Конструкция мостового крана с двойным маятниковым эффектом состоит из тележки, спредера большой массы (полезная нагрузка первого порядка) и полезной нагрузки (полезная нагрузка второго порядка). ). Соединения между разбрасывателем, тележкой и грузом выполнены из стальных тросов, как показано на рис. 1.

РИСУНОК 1 . Двухмаятниковый кран.

Предполагается, что тележка, разбрасыватель и полезная нагрузка крана работают в двухмерной плоскости, а траектория тележки горизонтальна. Он рассматривает распорку и полезную нагрузку как частицы, а точка соединения троса находится в центре тяжести распорки и полезной нагрузки. Кратковременные возмущения ветра и трение между тележкой, спредером и точкой соединения полезной нагрузки не учитываются. Упрощенная модель показана на рис. 2.

РИСУНОК 2 . Упрощенная модель крана с двойным маятником.

На рис. 2 положительное направление оси x указывает вправо; F обозначает движущую силу тележки; f представляет силу трения между тележкой и рельсом; М обозначает массу тележки; м ₁ и м ₂ представляют собой массу разбрасывателя и полезной нагрузки соответственно; l ₁ и l ₂ обозначают длину стального троса между центроидами распределителя, тележки и полезной нагрузки соответственно; x представляет перемещение тележки; θ ₁ и θ ₂ обозначают угол поворота разбрасывателя и полезную нагрузку соответственно.

По уравнению Лагранжа второго рода можно получить систему уравнений динамики крана с двойным маятником:

{(M+m1+m2)x¨+(m1+m2)l1(θ¨1⁡cos⁡θ1−θ˙12⁡sin⁡θ1)+m2l2(θ¨2⁡cos⁡θ2−θ˙22 ⁡sin⁡θ2)+bx˙=Fm1l1(x¨cos⁡θ1+g⁡sin⁡θ1+l1θ¨1)+m2l1[l1θ¨1+l2θ¨2⁡cos(θ1−θ2)+l2θ˙22⁡sin (θ1−θ2)+x¨cos⁡θ1+g⁡sin⁡θ1]=0m2l22θ¨2+m2l1l2θ¨1⁡cos(θ1−θ2)−m2l1l2θ˙12⁡sin(θ1−θ2)+m2l2x¨cos⁡θ2 +m2l2g⁡sin⁡θ2=0(1)

, где b обозначает коэффициент демпфирования; x˙ представляет собой скорость тележки; x¨ обозначает ускорение тележки; θ˙1 и θ¨1 представляют собой угловую скорость и ускорение угла поворота 1 соответственно; θ˙2 и θ¨2 обозначают угловую скорость и ускорение угла поворота 2 соответственно.

Адаптивный контроллер, основанный на методе компенсации нейронной сети RBF

Благодаря развитию технологии нейронных сетей (Hunt et al., 1992; Feng, 1995) был достигнут большой прогресс в области автоматического управления, обработки сигналов, и распознавание образов. В этом случае в систему крана был введен метод нейронной сети, и модель двойного маятникового крана соответствует уравнению. 2:

M(q)q¨+C(q,q˙)q˙+G(q)=τ+d(2)

, где q=[xθ1θ2]T; q˙=[x˙θ˙1θ˙2]T; q¨=[x¨θ¨1θ¨2]T; т=[F00]Т;

Задача управления двухмаятникового крана состоит в том, чтобы помочь тележке остановиться в нужном положении, в то время как первый и второй грузы, установленные под тележкой, остаются неподвижными. Сигнал отслеживания определяется как qd=[xdθ1dθ2d]; q˙d=[x˙dθ˙1dθ˙2d]; q¨d=[x¨dθ¨1dθ¨2d].

Расчетная тяга используется для управления двухмаятниковой крановой системой. Контроллер состоит из метода расчета тяги и метода компенсации нейронной сети. Контроллер коррекции нейронной сети RBF определен как дополнительный для распознавания ошибки онлайн-модели крана. Как показано на рисунке 3.

РИСУНОК 3 . Адаптивное управление на основе нейросетевой компенсации.

Расчетный контроллер тяги

Расчетный метод управления тягой определяется как разновидность надежного контроллера (Weiping et al. , 2004). Согласно динамическому уравнению 2 крана закон управления можно записать следующим образом:

τ=M0(q)(q¨d−kve˙−kpe)+C0(q,q˙)q˙+G0(q)(3)

, где kp=[α1000α2000α3]; kv=[β1000β2000β3], α > 0, β > 0.

Систематическая ошибка определяется следующим образом:

e¨+kve˙+kpe=0(4)

где e=q−qd; e˙=q˙−q˙d; q _d представляет собой идеальный сигнал слежения.

Контроллер нейронной сети RBF и анализ устойчивости

Метод нейронной сети RBF используется для аппроксимации f(·), а сетевой алгоритм RBF может быть определен следующим образом:

hi=exp(‖x−ci‖22bi2),i= 1,2,…,n(5)

f=wTh(x)(6)

где вход сети определяется как x=[e,e˙]T; с _i обозначает вектор координат центральной точки базисной функции Гаусса i -го нейрона в скрытом слое сети; b _i представляет собой ширину функции Гаусса i -го нейрона в скрытом слое; h=[h2,h3,…,hn]T обозначает вычисленный выход функции Гаусса; w представляет вес сети; f обозначает вывод силы компенсации из сети. 9˙=γhxTPB(7)

, где γ > 0; A=(0I-kp-kv); B=[0M0−1(q)].

Функция Ляпунова устроена следующим образом:

V=12xTPx+12γ‖w˜‖2(8)

где γ > 0,

Матрица P является симметричной и положительно определенной. Кроме того, P должны удовлетворять уравнению Ляпунова следующим образом: |2=tr(RRT)=tr(RTR)(10)

, где tr(·) обозначает след матрицы. Мы можем получить следующее:

‖w˜‖2=tr(w˜Tw˜)(11)

V выводится по времени, и мы можем получить следующее:

V˙= 12[xTPx˙+x˙TPx]+1γtr(w˜˙Tw˜)=12{xTP[Ax+B(η−w˜Th)]+[xTAT+(η−w˜Th)TBT]Px}+1γtr (w˜˙Tw˜)=12[xT(PA+ATP)x+(xTPBη−xTPBw˜Th+ηTBTPx−hTw˜BTPx)]+1γtr(w˜˙Tw˜)=12xTQx+ηTBTPx−hTw˜BTPx+1γtr (w˜˙Tw˜)

, где xTPBw˜Th=hTw˜BTPx; xTPBη=ηTBTPx.

Из-за

hTw˜BTPx=tr[BTPxhTw˜](12)

V˙ можно переписать следующим образом:

V˙=−12xTQx+1γtr(−γBTPxhTw˜+w˜˙Tw˜)+ηTBTPx=−12xTQx+ηTBTPx(13)

По известным условиям можно можно сделать вывод, что (P)‖x‖=−12‖x‖[λmin(Q)‖x‖−2‖η0‖‖M0−1(q)‖λmin(P)](14)

где λ _макс ( P ) обозначает максимальное собственное значение матрицы P , λ _min ( Q ) обозначает минимальное собственное значение матрицы Q .

В этом случае, пока λmin(Q)≥2‖M0−1(q)‖λmax(P)‖x‖‖η0‖, тогда: V˙≤0.

В этот момент система удовлетворяет устойчивости по Ляпунову.

Согласно критериям анализа устойчивости, если матрица P является симметричной и положительно определенной, то для сохранения устойчивости системы уравнение Ляпунова PA + 9(·)(15)

MATLAB используется для установки крановой системы и системы управления. Подходящие параметры управления настраиваются, и результаты адаптивной системы управления на основе компенсации нейронной сети показаны на рис. 4 и рис. 5.

РИСУНОК 4 . Реакция управления нейронной сетью системы управления.

РИСУНОК 5 . Реакция нейросетевой системы управления компенсацией на фазовую траекторию.

Из рисунка 4 видно, что компенсация нейронной сети может точно отслеживать положение и очень хорошо подавлять угол поворота. На рисунке 5 также показано, что конечное состояние контроллера нейросети сходится к нулю, что подтверждает эффективность контроллера.

Эксперименты

Аппаратное моделирование в контуре (HIL) введено в эксперимент, который известен как передовой метод научных исследований. В этом эксперименте HIL в основном состоит из ПК, контроллера и механической конструкции. На ПК уже было установлено программное обеспечение MATLAB/Simulink, и он использовался в качестве главного компьютера. Плата управления движением управляется и обменивается данными с ПК. Механическая конструкция управляется картой движения, а параметры движения механической конструкции собираются картой управления движением и передаются на ПК. Экспериментальный физический прототип показан на рис. 6.9.0028

РИСУНОК 6 . Экспериментальный физический прототип.

Чтобы подтвердить производительность представленного контроллера на основе нейронной сети, хорошо работающий контроллер скользящего режима в (Tuan and Lee, 2013) также представлен в качестве группы сравнения. Вход регулятора скользящего режима определяется следующим образом:

u=−(m1+m2)l1θ¨1⁡cos⁡θ1−m2l2θ¨2⁡cos⁡θ2+bx˙+(m1+m2)l1θ˙12⁡ sin⁡θ1+m2l2θ˙22⁡sin⁡θ2−(M+m1+m2)(λx˙+αθ˙1+βθ˙2)−Ksgn(s)(16)

, где K обозначает амплитуду усиление переключателя управления; λ , α , β представляют расчетные параметры; sign( · ) обозначает функцию знака.

Эксперименты по управлению позиционированием контроллера и предотвращению раскачивания

Контроллер скользящего режима устанавливается в MATLAB/Simulink, а параметры управления настраиваются для адаптации к экспериментальным установкам. Экспериментальная установка в исходной точке статична. Под управлением контроллера движение тележки следует целевому положению, и получаются результаты отклика.

На Рисунке 7 показано, что метод, основанный на управлении скользящим режимом, может очень быстро устранить угловую скорость поворота в широком диапазоне, а амплитуда угла поворота довольно мала. Однако характер переключения угла поворота с высокой частотой, особенно для углов поворота около 0°, приведет к колебаниям.

РИСУНОК 7 . Реакция позиционирующей противораскачивающей системы на основе метода скользящего режима.

При том же объекте управления результаты нейросетевого компенсационного контроллера RBF отображаются следующим образом:

Из рисунка 8 видно, что адаптивный контроллер, основанный на компенсации нейронной сети RBF, не имеет проблем с вибрацией контроллера скользящего режима, и процесс более плавный, чем у контроллера скользящего режима.

РИСУНОК 8 . Реакция системы с использованием адаптивного контроллера компенсации нейронной сети.

Эксперимент по контролю помех

Этот эксперимент начинается со статической тележки, а полезная нагрузка не имеет угла поворота. После этого полезной нагрузке придается сила, которая заставляет полезную нагрузку раскачиваться, и эксперимент используется для оценки характеристик защиты от помех представленного контроллера.

На рисунке 9 показано, что после внешнего возбуждения спредер или полезная нагрузка могут очень быстро вернуться в исходное положение с помощью контроллера скользящего режима; эффект противодействия колебаниям значителен, а конечное состояние представляет собой состояние высокочастотного колебания. Когда угол поворота достаточно велик, эффект управления лучше.

РИСУНОК 9 . Реакция противоаварийной системы на основе метода скользящего режима.

Производительность контроллера на основе нейронной сети показана на рис. 10. По сравнению с контроллером на основе скользящего режима контроллер на основе нейронной сети может управлять большим углом поворота. Кроме того, при большем возбуждении максимальный угол поворота может достигать 30°. Доказано, что предлагаемый контроллер на основе нейронной сети может управлять большим углом поворота, что позволит быстрее реагировать на те же возмущения, а рабочие характеристики выше в суровых условиях.

РИСУНОК 10 . Реакция системы защиты от помех на основе контроллера компенсации на основе нейронной сети.

Заключение

В качестве объекта исследования выбран мостовой кран с эффектом двойного маятника. Сначала была создана динамическая модель крана. Затем предлагается адаптивный контроллер компенсации нейронной сети на основе RBF, а также выполняется моделирование с помощью MATLAB для проверки стабильности системы. Наконец, представлены эксперименты с HIL для тестирования представленного контроллера, где также представлено сравнение с контроллером на основе скользящего режима. Экспериментальные результаты показывают, что по сравнению с традиционным контроллером на основе скользящего режима контроллер на основе нейронной сети имеет превосходную производительность и лучшую способность к подавлению помех и без колебаний. Кроме того, экспериментальные результаты показали, что предложенный контроллер также адекватен для управления в реальном времени.

Заявление о доступности данных

Первоначальные материалы, представленные в исследовании, включены в статью/дополнительный материал. Дальнейшие запросы можно направлять соответствующему автору.

Вклад авторов

Компания H-YQ разработала контроллер и подготовила документ. Y-gS выполнил моделирование. J-cL и D-sD помогают анализу стабильности и проведенным экспериментам. Все авторы прочитали и согласились с опубликованной версией рукописи.

Конфликт интересов

Авторы заявляют, что исследование проводилось в отсутствие каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.

Ссылки

Чен Х. и Сун Н. (2020). Нелинейное управление недоприведенными в действие системами с учетом ограничений как при активированном, так и при неактивированном состоянии с экспериментальной проверкой. IEEE Trans. Инд. Электрон. 67 (9), 7702–7714. doi:10.1109/tie.2019.2946541

Полнотекстовая перекрестная ссылка | Google Scholar

Чен Х., Сюань Б. и Ян П. (2019). Новый метод экстренного торможения мостового крана с теоретическим анализом и экспериментальной проверкой. Нелинейный динам. 98 (3), 2211–2225. doi:10.1007/s11071-019-05318-6

CrossRef Full Text | Google Scholar

Чо С.-К. и Ли Х.-Х. (2002). Противораскачивающий контроллер с нечеткой логикой для трехмерных мостовых кранов. ИСА транс. 41 (2), 235–243. дои: 10.1016/s0019-0578(07)60083-4

Реферат PubMed | Полный текст перекрестной ссылки | Google Scholar

Dongkyoung, C. (2017). Надежное управление трехмерным мостовым краном, основанное на скользящем режиме управления, с конечным временем и защитой от раскачивания.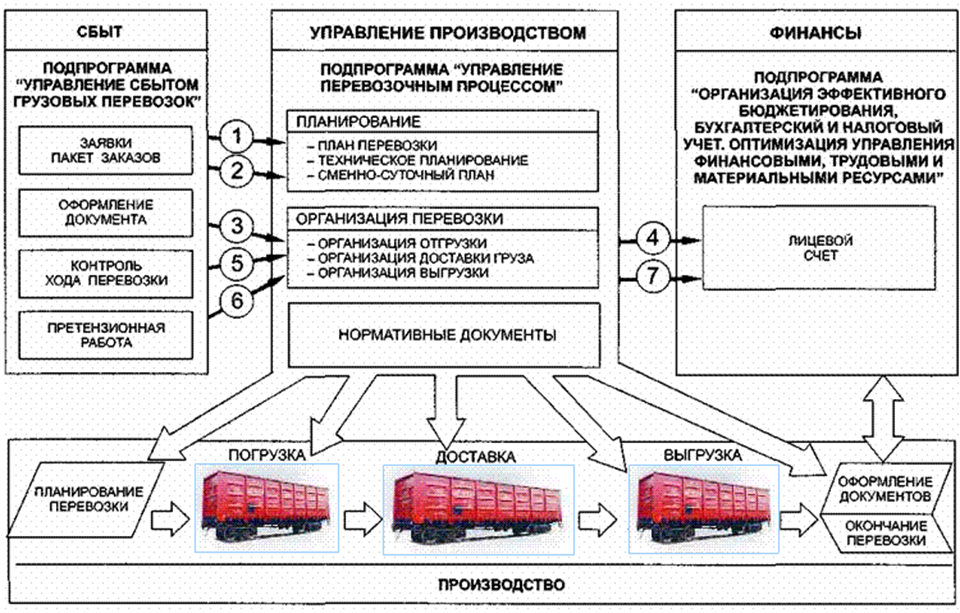 IEEE Trans. Инд. Электрон. 64, 6775–6784. doi:10.1109/TIE.2017.2701760

CrossRef Полный текст | Google Scholar

Фэн Г. (1995). Компенсационная схема слежения за роботом на основе нейронных сетей. Робот. Автон. Сист. 15 (3), 199–206. дои: 10.1016/0921-8890(95)00023-9

Полный текст CrossRef | Google Scholar

Гутьеррес М. и Соло Р. (1998). «Нечеткое управление масштабным прототипом мостового крана», в материалах 37-й конференции IEEE по решениям и управлению, Тампа, Флорида, 18–18 декабря 1998 г., Нью-Йорк, штат Нью-Йорк: IEEE, 18.

Google Scholar

Hunt , К.Дж., Сбарбаро, Д., Жбиковски, Р., и Гаутроп, П.Дж. (1992). Нейронные сети для систем управления — обзор. Автоматика 28 (6), 1083–1112. дои: 10.1016/0005-1098(92)

-I

CrossRef Полный текст | Google Scholar

Li, C., and Lee, CY (2001a). Нечеткое управление движением автоскладской крановой системы. IEEE Trans. Инд. Электрон. 48 (5), 983–994. doi:10.1109/41.954563

CrossRef Полный текст | Google Scholar

Li, C., and Lee, CY (2001b). «Мягкая вычислительная система для управления движением», в 2001 г. IEEE Intelligent Transportation Systems, Окленд, Калифорния, 25–29 августа 2001 г.

Google Scholar

Мустафа, К.А.Ф., и Эбейд, А.М. (1988). Нелинейное моделирование и контроль раскачивания груза мостового крана. J. Динамическая система. Изм. Контроль 110 (3), 266–271. doi:10.1115/1.3152680

CrossRef Полный текст | Google Scholar

Nowacki, Z., Owczarz, D., and Wozniak, P. (1996). «Об устойчивости нечеткого управления мостовым краном», на Международном симпозиуме IEEE по промышленной электронике, Варшава, Польша, 17 июня 1996 г., Нью-Йорк, штат Нью-Йорк: IEEE.

Академия Google

Оуян Х., Ван Дж., Чжан Г., Мэй Л. и Дэн Х. (2019). Новое адаптивное иерархическое управление режимом скольжения для отслеживания траектории и подавления раскачивания груза в мостовых кранах с двойным маятником. IEEE Access 7 , 1. doi:10.1109/ACCESS.2019.2891793

CrossRef Full Text | Google Scholar

Парк, Х.-С., и Ле, Н.-Т. (2012). Моделирование и управление мобильной портовой крановой системой с помощью технологии виртуального прототипирования. Междунар. J. Управление автоматом. Сист. 10 (6), 1204–1214. doi:10.1007/s12555-012-0615-y

CrossRef Full Text | Google Scholar

Сунь Н., Лян Д., Ву Ю., Чен Ю., Цинь Ю. и Фанг Ю. (2020a). Адаптивное управление пневматическими искусственными мышцами с параметрическими неопределенностями и однонаправленными входными ограничениями. IEEE Trans. Инд Инф. 16(2):969–979. doi:10.1109/tii.2019.2923715

Полный текст CrossRef | Google Scholar

Сунь, Н., Фу, Ю., Ян, Т., Чжан, Дж., Фан, Ю. и Синь, X. (2020b). Нелинейное управление движением сложных двухповоротных крановых систем без обратной связи по скорости: проектирование, анализ и аппаратные эксперименты. IEEE Trans. автомат. науч. англ. 17 (2), 1017–1029. doi:10.1109/tase.2019.2961258

Полный текст CrossRef | Google Scholar

Туан, Л. А., и Ли, С.-Г. (2013). Скользящее управление двухмаятниковыми крановыми системами. Дж. Мех. науч. Технол. 27 (6), 1863–1873. doi:10.1007/s12206-013-0437-8

CrossRef Full Text | Google Scholar

Weiping, G., Diantong, L., Jianqiang, Y., and Dongbin, Z. (2004). Пассивное управление мостовыми кранами с двойным маятником[C]//2004 IEEE Region 10 Conference TENCON 2004. IEEE 500, 546–549.

Google Scholar

Ян Т., Сун Н., Чен Х. и Фанф Ю. (2020). Нейросетевое адаптивное противораскачивающее управление маломощным корабельным краном с креновыми движениями и входными мертвыми зонами. IEEE Trans. Нейронная сеть. Учиться. Сист. 31 (3), 901–914. doi:10.1109/tnnls.2019.2910580

PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

Чжан М., Ма Х., Ронг Х., Тайн Х. и Ли Ю. (2016). Адаптивное управление слежением за двухмаятниковыми мостовыми кранами с учетом ограничения погрешности слежения, параметрических неопределенностей и внешних возмущений.