Содержание
Модуль зубьев зубчатого колеса: расчет, стандартные, определение
Зубчатая передача впервые была освоена человеком в глубокой древности. Имя изобретателя осталось скрыто во тьме веков. Первоначально зубчатые передачи имели по шесть зубьев — отсюда и пошло название «шестерня». За многие тысячелетия технического прогресса передача многократно усовершенствовалась, и сегодня они применяются практически в любом транспортном средстве от велосипеда до космического корабля и подводной лодки. Используются они также в любом станке и механизме, больше всего шестеренок используется в механических часах.
Зубчатое колесо
Содержание
Что такое модуль зубчатого колеса
Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров
Каждую шестеренку характеризует несколько основных параметров
- диаметр;
- число зубьев;
- шаг;
- высота зубца;
- и некоторые другие.
Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.
Скачать ГОСТ 9563-60
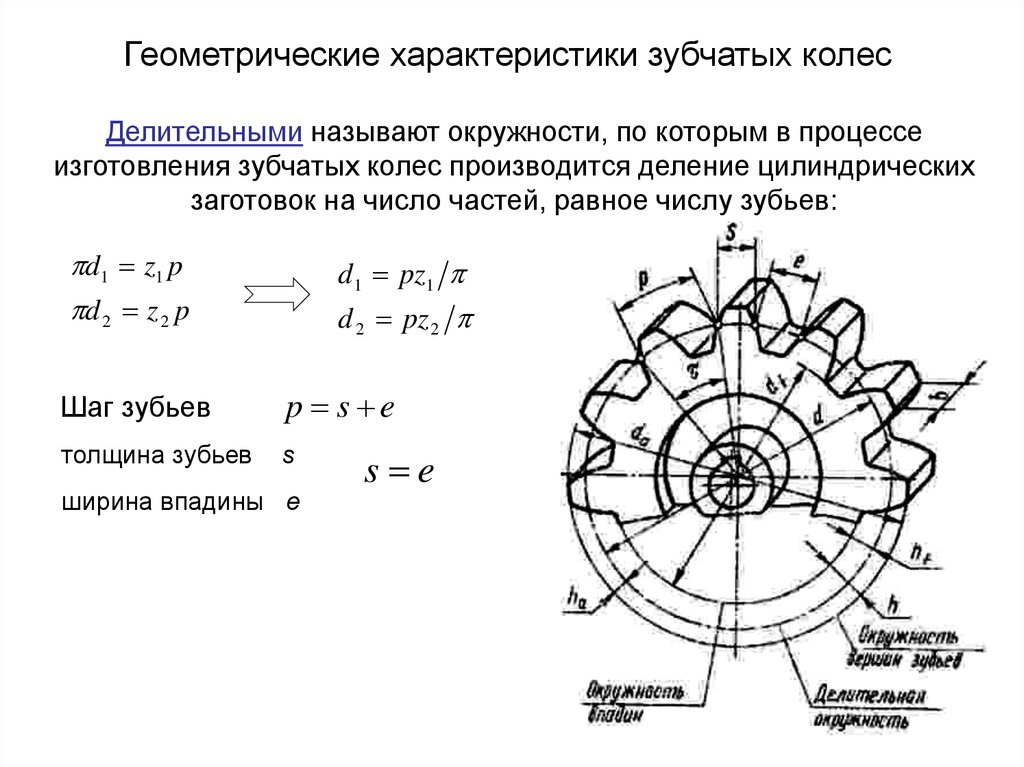
В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.
Для расчета этого параметра применяют следующие формулы:
m=t/π,
где t — шаг.
Параметры зубчатых колес
Модуль зубчатого колеса можно рассчитать и следующим образом:
m=h/2,25,
где h — высота зубца.
И, наконец,
m=De/(z+2),
где De — диаметр окружности выступов,а z — число зубьев.
Что же такое модуль шестерни?
это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.
Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.
Формула расчета параметров прямозубой передачи
Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.
Расчет модуля зубчатого колеса
Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:
π×D=t×z,
проведя преобразование, получим:
D=(t /π)×z
Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.
t/π=m,
размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:
В=m×z;
выполнив преобразование, находим:
m=D / z.
Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов De получается равным
Диаметр окружности выступов De получается равным
De=d+2× h’,
где h’- высота головки.
Высоту головки приравнивают к m:
h’=m.
Проведя математические преобразования с подстановкой, получим:
De=m×z+2m = m(z+2),
откуда вытекает:
m=De/(z+2).
Диаметр окружности впадин Di соответствует De за вычетом двух высот основания зубца:
Di=D-2h“,
где h“- высота ножки зубца.
Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:
h’ = 1,25m.
Устройство зубчатого колеса
Выполнив подстановку в правой части равенства, имеем:
Di = m×z-2×1,25m = m×z-2,5m;
что соответствует формуле:
Di = m(z-2,5m).
Полная высота:
h = h’+h“,
и если выполнить подстановку, то получим:
h = 1m+1,25m=2,25m.
Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.
Следующий важный размер, толщину зубца s принимают приблизительно равной:
- для отлитых зубцов: 1,53m:
- для выполненных путем фрезерования-1,57m, или 0,5×t
Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины sв, получаем формулы для ширины впадины
- для отлитых зубцов: sв=πm-1,53m=1,61m:
- для выполненных путем фрезерования- sв= πm-1,57m = 1,57m
Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:
- усилия, прикладываемые к детали при эксплуатации;
- конфигурация деталей, взаимодействующих с ней.

Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.
Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.
Исходные данные и замеры
На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.
Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны.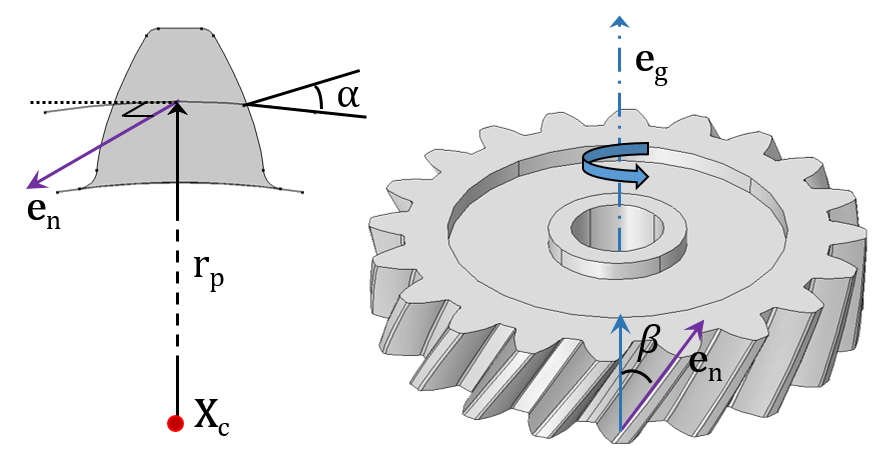 Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.
Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.
Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.
Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.
Результаты расчетов
Для более крупных потребуются измерения и вычисления.
Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:
m=De/(z+2)
Последовательность действий следующая:
- измерить диаметр штангенциркулем;
- сосчитать зубцы;
- разделить диаметр на z+2;
- округлить результат до ближайшего целого числа.

Зубец колеса и его параметры
Данный метод подходит как для прямозубых колес, так и для косозубых.
Расчет параметров колеса и шестерни косозубой передачи
Расчетные формулы для важнейших характеристик шестерни косозубой передачи совпадают с формулами для прямозубой. Существенные различия возникают лишь при прочностных расчетах.
Что такое модуль зубчатого колеса? Как вычислить модуль зубчатого колеса
Содержание
- История
- Модуль зубьев зубчатого колеса
- Что такое модуль зубчатого колеса
- Чему равен модуль зубчатого колеса?
- Для чего нужен модуль зубчатого колеса?
- Как определить параметры шестерни?
- Как найти модуль шестерни?
- Как найти делительный диаметр шестерни?
- Как найти модуль зуба?
- Какие бывают модули зубчатых колес?
- Цилиндрические зубчатые колёса
- Продольная линия зуба
- Прямозубые колёса
- Косозубые колёса
- Шевронные колеса
- Колёса с круговыми зубьями
- Винтовые шестерни
- Секторные колёса
- Зубчатые колёса с внешним и внутренним зацеплением
- Звездочка
- Реечная передача (кремальера)
- Коронные колёса
- Конические зубчатые колёса
- Зубчатые передачи
- Типы зубчатых передач
- Эвольвентное зацепление
- Форма зубьев
- Коррегирование зубчатого зацепления
- Зубчатые передачи с точно заданным межосевым расстоянием
- Зубчатые передачи с изменяемым межосевым расстоянием
- Расчетные формулы для зубчатых передач
- Основные параметры зубчатых цилиндрических передач
- Межосевые расстояния
- Межосевые расстояния для двухступенчатых несоосных редукторов общего назначения
- Коэффициент запаса прочности при работе зуба двумя сторонами
- Межосевые расстояния для трехступенчатых несоосных редукторов общего назначения
- Номинальные передаточные числа
- Почему шестерни часто выполняют заодно с валом?
История
Сама по себе идея механической передачи восходит к идее колеса. Применяя систему из двух колёс разного диаметра, можно не только передавать, но и преобразовывать движение. Если ведомым будет большее колесо, то на выходе мы потеряем в скорости, но зато крутящий момент этой передачи увеличится. Эта передача удобна там, где требуется «усилить движение», например, при подъеме тяжестей. Но сцепление между передаточными колесами с гладким ободом недостаточно жесткое, колёса проскальзывают. Поэтому вместо гладких колес начали использовать зубчатые.
Применяя систему из двух колёс разного диаметра, можно не только передавать, но и преобразовывать движение. Если ведомым будет большее колесо, то на выходе мы потеряем в скорости, но зато крутящий момент этой передачи увеличится. Эта передача удобна там, где требуется «усилить движение», например, при подъеме тяжестей. Но сцепление между передаточными колесами с гладким ободом недостаточно жесткое, колёса проскальзывают. Поэтому вместо гладких колес начали использовать зубчатые.
В Древнем Египте для орошения земель уже использовались приводимые в действие быками устройства, состоявшие из деревянной зубчатой передачи и колеса с большим числом ковшей.
Вместо зубьев первоначально использовали деревянные цилиндрические или прямоугольные пальцы, которые устанавливали по краю деревянных ободьев.
Изготовленный в I веке до н.э. Антикитерский механизм состоял из десятков металлических зубчатых колес [4] .
Модуль зубьев зубчатого колеса
Зубчатая передача впервые была освоена человеком в глубокой древности. Имя изобретателя осталось скрыто во тьме веков. Первоначально зубчатые передачи имели по шесть зубьев — отсюда и пошло название «шестерня». За многие тысячелетия технического прогресса передача многократно усовершенствовалась, и сегодня они применяются практически в любом транспортном средстве от велосипеда до космического корабля и подводной лодки. Используются они также в любом станке и механизме, больше всего шестеренок используется в механических часах.
Имя изобретателя осталось скрыто во тьме веков. Первоначально зубчатые передачи имели по шесть зубьев — отсюда и пошло название «шестерня». За многие тысячелетия технического прогресса передача многократно усовершенствовалась, и сегодня они применяются практически в любом транспортном средстве от велосипеда до космического корабля и подводной лодки. Используются они также в любом станке и механизме, больше всего шестеренок используется в механических часах.
Что такое модуль зубчатого колеса
Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров
- диаметр;
- число зубьев;
- шаг;
- высота зубца;
- и некоторые другие.

Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.
В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.
Для расчета этого параметра применяют следующие формулы:
Параметры зубчатых колес
Модуль зубчатого колеса можно рассчитать и следующим образом:
где h — высота зубца.
где De — диаметр окружности выступов,а z — число зубьев.
Чему равен модуль зубчатого колеса?
Модуль зубчатого колеса Модуль зубчатого колеса, геометрический параметр зубчатых колёс. Для прямозубых цилиндрических зубчатых колёс модуль m равен отношению диаметра делительной окружности dд к числу зубьев z или отношению шага t по делительной окружности к числу: m = dд/z = ts/p.
Для чего нужен модуль зубчатого колеса?
Что же такое модуль шестерни? это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.
Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.
Как определить параметры шестерни?
Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр. Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.
Как найти модуль шестерни?
Как определить модуль косозубой шестерни.
Измеряем диаметр:
- Диаметр окружности выступов (De) равен 28,6 мм.
- Считаем количество зубьев. Z=25.
- Делительный диаметр (De) делим на количество зубьев 25 +2. Равно 28,6 разделить на 27=1,05925925925926.
- Округляем до ближнего модуля. Получается модуль 1.
Как найти делительный диаметр шестерни?
Диаметр делительной окружности d является одним из основных параметров, по которому производят расчет зубчатого колеса: d = m × z, где z – число зубьев; m – модуль.
Как найти модуль зуба?
Модуль = De/Z+2. То есть диаметр окружности выступов разделить на количество зубьев плюс 2. Измеряем диаметр: Диаметр окружности выступов (De) равен 28,6 мм.
Какие бывают модули зубчатых колес?
Модуль — это линейная величина, в π раз меньшая шага зубьев p (окружного pt, осевого рx, нормального рn и других шагов) эвольвентного зубчатого колеса m = р/π. Соответственно различают модули: окружной mt, осевой mx, нормальный mn и др.
Цилиндрические зубчатые колёса
Параметры зубчатого колеса
Профиль зубьев колёс как правило имеет эвольвентную боковую форму. Однако существуют передачи с круговой формой профиля зубьев (передача Новикова с одной и двумя линиями зацепления) и с циклоидальной. Кроме того, в храповых механизмах применяются зубчатые колёса с несимметричным профилем зуба.
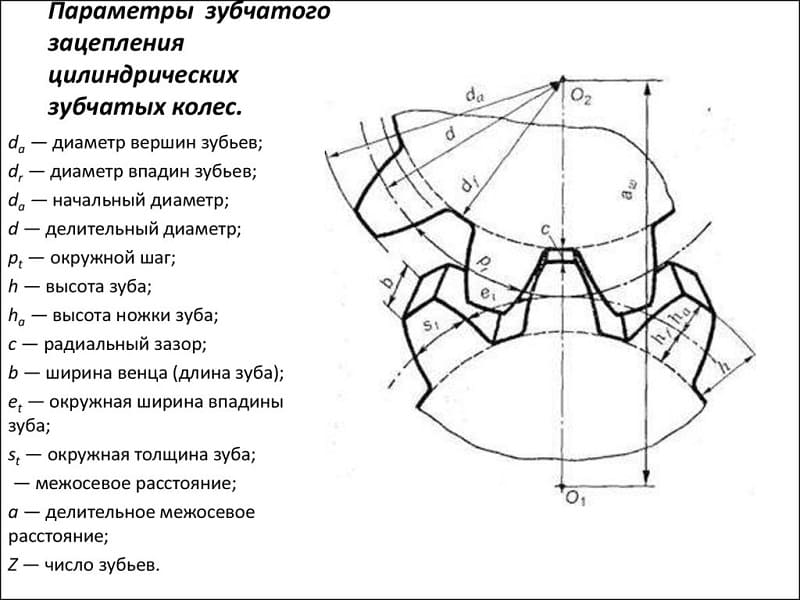
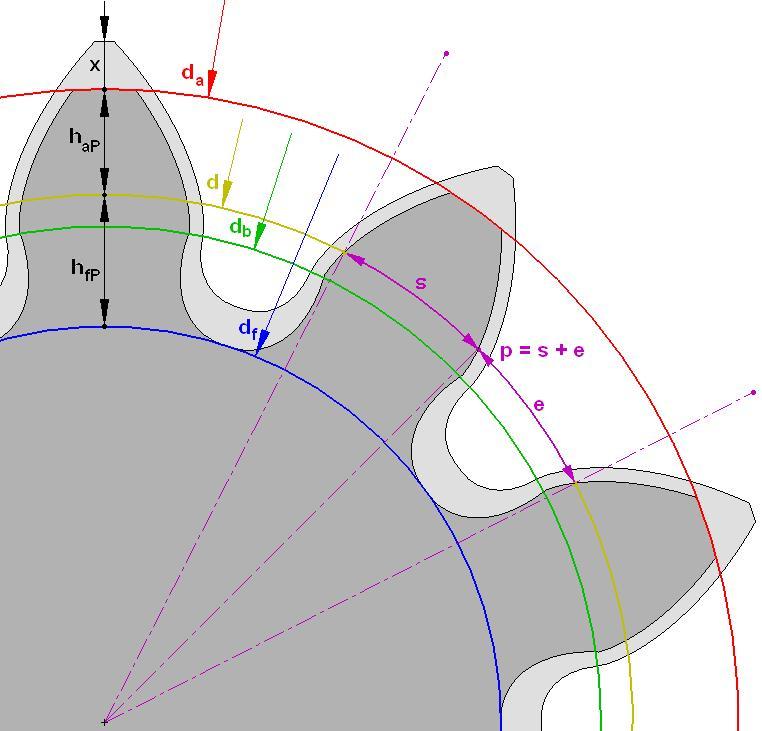
Параметры эвольвентного зубчатого колеса:
- m — модуль колеса. Модулем зацепления называется линейная величина в π раз меньшая окружного шага P или отношение шага по любой концентрической окружности зубчатого колеса к π, то есть модуль — число миллиметров диаметра делительной окружности приходящееся на один зуб.
 Тёмное и светлое колёсо имеют одинаковый модуль. Самый главный параметр, стандартизирован, определяется из прочностного расчёта зубчатых передач. Чем больше нагружена передача, тем выше значение модуля. Через него выражаются все остальные параметры. Модуль измеряется в миллиметрах, вычисляется по формуле:
Тёмное и светлое колёсо имеют одинаковый модуль. Самый главный параметр, стандартизирован, определяется из прочностного расчёта зубчатых передач. Чем больше нагружена передача, тем выше значение модуля. Через него выражаются все остальные параметры. Модуль измеряется в миллиметрах, вычисляется по формуле:
- z — число зубьев колеса
- p — шаг зубьев (отмечен сиреневым цветом)
- d — диаметр делительной окружности (отмечена жёлтым цветом)
- da — диаметр окружности вершин тёмного колеса (отмечена красным цветом)
- db — диаметр основной окружности — эвольвенты (отмечена зелёным цветом)
- df — диаметр окружности впадин тёмного колеса (отмечена синим цветом)
- haP+hfP — высота зуба тёмного колеса, x+haP+hfP — высота зуба светлого колеса
Для целей стандартизации, удобства изготовления и замены зубчатых колёс в машиностроении приняты определённые значения модуля зубчатого колеса m, представляющие собой ряд из чисел на выбор: 0,05; 0,06; 0,08; 0,1; 0,12; 0,15; 0,2; 0,25; 0,3; 0,4; 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 25; 32; 40; 50; 60; 80; 100.

Зубчатые колеса могут быть изготовлены с различным смещением режущей рейки: без смещения (нулевое зубчатое колесо или «с нулевыми зубцами»), с положительным смещением (смещение в сторону увеличения материала), с отрицательным смещением (смещение в сторону уменьшения материала).
Высота головки зуба — haP и высота ножки зуба — hfP — в случае нулевого зубчатого колеса соотносятся с модулем m следующим образом: haP = m; hfP = 1,25 m, то есть:
Отсюда получаем, что высота зуба h (на рисунке не обозначена):
Вообще из рисунка ясно, что диаметр окружности вершин da больше диаметра окружности впадин df на двойную высоту зуба h. Исходя из всего этого, если требуется практически определить модуль m зубчатого колеса, не имея нужных данных для вычислений (кроме числа зубьев z), то необходимо точно измерить его наружный диаметр da и результат разделить на число зубьев z плюс 2:
Продольная линия зуба
Цилиндрические зубчатые колеса классифицируются в зависимости от формы продольной линии зуба на:
| ПРЯМОЗУБЫЕ | КОСОЗУБЫЕ | ШЕВРОННЫЕ | ЗУБЬЯ НОВИКОВА |
Прямозубые колёса
Зубья расположены в радиальных плоскостях, а линия контакта зубьев обеих шестерён параллельна оси вращения.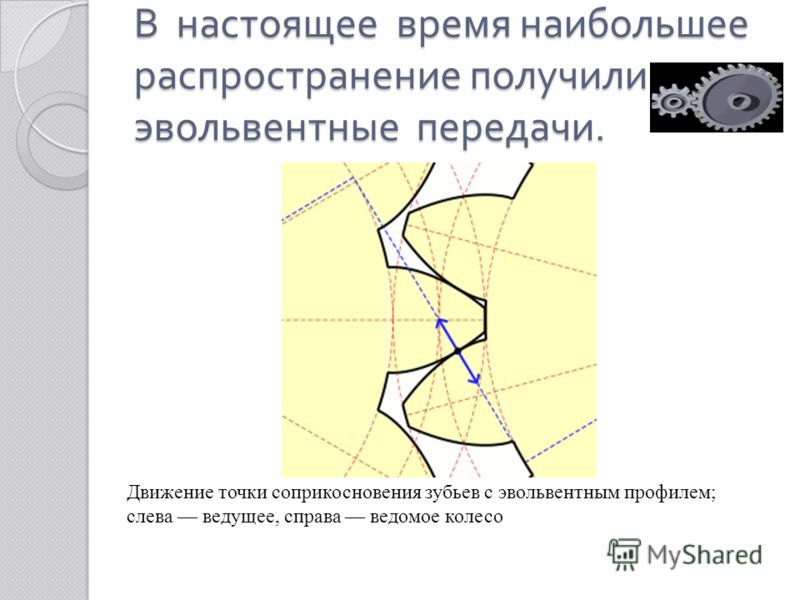 При этом оси обеих шестерён также должны располагаться строго параллельно. Прямозубые колеса имеют наименьшую стоимость, их работа имеет наивысший КПД, но, в то же время, предельный передаваемый крутящий момент таких колес ниже, чем косозубых и шевронных.
При этом оси обеих шестерён также должны располагаться строго параллельно. Прямозубые колеса имеют наименьшую стоимость, их работа имеет наивысший КПД, но, в то же время, предельный передаваемый крутящий момент таких колес ниже, чем косозубых и шевронных.
Косозубые колёса
Зубья располагаются под углом к оси вращения, а по форме образуют часть винтовой линии. Зацепление таких колёс происходит плавнее, чем у прямозубых, и с меньшим шумом. Также увеличена площадь контакта, что при тех же размерах с прямозубыми позволяет передавать больший крутящий момент. При работе косозубой пары зацепления возникает механическая осевая сила, направленная вдоль оси вращения каждого колеса и стремящаяся раздвинуть оба колеса в противоположные стороны от плоскости контакта, что обязательно требует применения упорных подшипников. Увеличенная площадь трения зубьев косозубого зацепления вызывает дополнительные потери мощности на нагрев. В целом, косозубые колёса применяются в механизмах, требующих передачи большого крутящего момента на высоких скоростях, либо имеющих жёсткие ограничения по шумности.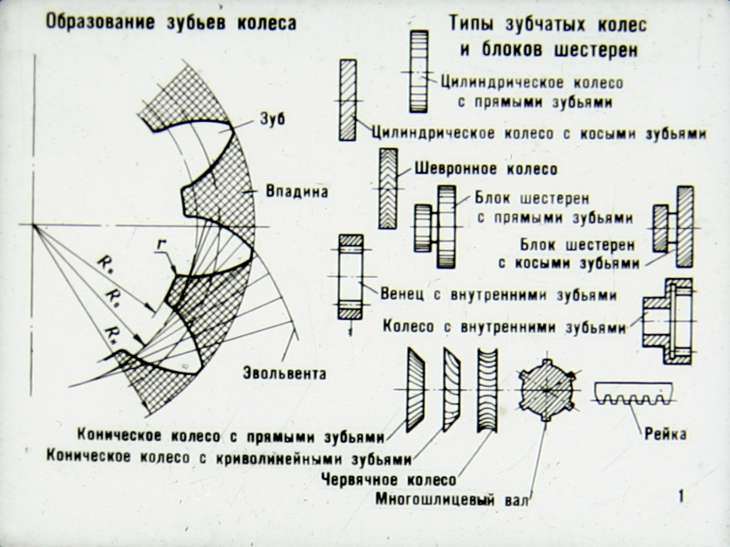
Шевронные колеса
Изобретение шевронного профиля зуба часто приписывают Андре Ситроену, однако на самом деле он лишь выкупил патент на более совершенную схему, которую придумал польский механик-самоучка [6] . Зубья таких колёс изготавливаются в виде буквы «V» (либо они получаются стыковкой двух косозубых колёс со встречным расположением зубьев). Шевронные колёса решают проблему осевой силы. Осевые силы обеих половин такого колеса взаимно компенсируются, поэтому отпадает необходимость в установке валов на упорные подшипники. При этом передача является самоустанавливающейся в осевом направлении, по причине чего в редукторах с шевронными колесами один из валов устанавливают на плавающих опорах (как правило — на подшипниках с короткими цилиндрическими роликами).
Колёса с круговыми зубьями
Передача на основе колёс с круговыми зубьями (Передача Новикова) имеет ещё более высокие ходовые качества, чем косозубые — высокую нагрузочную способность зацепления, высокую плавность и бесшумность работы. Однако они ограничены в применении сниженными, при тех же условиях, КПД и ресурсом работы, такие колёса заметно сложнее в производстве. Линия зубьев у них представляет собой окружность радиуса, подбираемого под определённые требования. Контакт поверхностей зубьев происходит в одной точке на линии зацепления, расположенной параллельно осям колёс.
Однако они ограничены в применении сниженными, при тех же условиях, КПД и ресурсом работы, такие колёса заметно сложнее в производстве. Линия зубьев у них представляет собой окружность радиуса, подбираемого под определённые требования. Контакт поверхностей зубьев происходит в одной точке на линии зацепления, расположенной параллельно осям колёс.
Винтовые шестерни
Шестерни имеют форму цилиндра с расположенными на нем зубьями по винтовой линии. Эти шестеренки используются на непересекающихся валах, которые располагаются перпендикулярно друг друга, угол между ними 90°.
Секторные колёса
Секторное колесо представляет собой часть обычного цилиндрического колеса с зубьями любого типа. Такие колёса применяются в тех случаях, когда не требуется вращение звена на полный оборот, и поэтому можно сэкономить на его габаритах.
Зубчатые колёса с внешним и внутренним зацеплением
Пара зубчатых колёс с ВНЕШНИМ зацеплением. Передаточное число — 3 (42/14). Вращение колёс происходит противонаправлено. | Пара зубчатых колёс с ВНУТРЕННИМ зацеплением. Передаточное число — 3 (42/14). Вращение колёс происходит сонаправленно. |
Звездочка
Шестерня-звезда – это основная деталь цепной передачи, которая используется совместно с гибким элементом – цепью для передачи механической энергии.
Реечная передача (кремальера)
Реечная передача (кремальера)
Реечная передача (кремальера) применяется в тех случаях, когда необходимо преобразовать вращательное движение в поступательное и обратно. Состоит из обычной прямозубой шестерни и зубчатой планки (рейки). Работа такого механизма показана на рисунке.
Зубчатая рейка представляет собой часть колеса с бесконечным радиусом делительной окружности. Поэтому делительная окружность, а также окружности вершин и впадин превращаются в параллельные прямые линии. Эвольвентный профиль рейки также принимает прямолинейное очертание. Такое свойство эвольвенты оказалось наиболее ценным при изготовлении зубчатых колёс.
Такое свойство эвольвенты оказалось наиболее ценным при изготовлении зубчатых колёс.
Также реечная передача применяется в зубчатой железной дороге.
Цевочная передачаКоронная шестерня
Коронные колёса
Коронное колесо — особый вид колёс, зубья которых располагаются на боковой поверхности. Такое колесо, как правило, стыкуется с обычным прямозубым, либо с барабаном из стержней (цевочное колесо), как в башенных часах. Передачи с цевочным колесом — одни из самых ранних и просты в изготовлении, но характеризуются очень большими потерями на трение.
Конические зубчатые колёса
Главная передача в заднеприводном автомобиле
Во многих машинах осуществление требуемых движений механизма связано с необходимостью передать вращение с одного вала на другой при условии, что оси этих валов пересекаются. В таких случаях применяют коническую зубчатую передачу. Различают виды конических колёс, отличающихся по форме линий зубьев: с прямыми, тангенциальными, круговыми и криволинейными зубьями. Конические колёса с круговым зубом, например, применяются в автомобильных главных передачах коробки передач.
Конические колёса с круговым зубом, например, применяются в автомобильных главных передачах коробки передач.
Зубчатые передачи
Зубчатые передачи — это механизм или часть механизма механической передачи, в состав которого входят зубчатые колёса. Зубчатые передачи служат для того, чтобы непрерывно передавать силу и крутящий момент двух валов, расположение которых определяет тип имеющейся зубчатой передачи. Вот о том, что представляют зубчатые передачи, мы и поговорим в этой статье.
Типы зубчатых передач
Эвольвентное зацепление
Все прямозубые цилиндрические передачи с одинаковым модулем зацепления могут изготавливаться на одном оборудовании, независимо от количества зубьев и размеров головки.
Модули зацепления цилиндрических и конических зубчатых колес стандартизированы по DIN 780; модули зацепления червячных передач по DIN 780; модули шлицевых соединений по DIN 5480; модули зубчатого зацепления нормального профиля для шестерен со спиральными зубьями по DIN 780.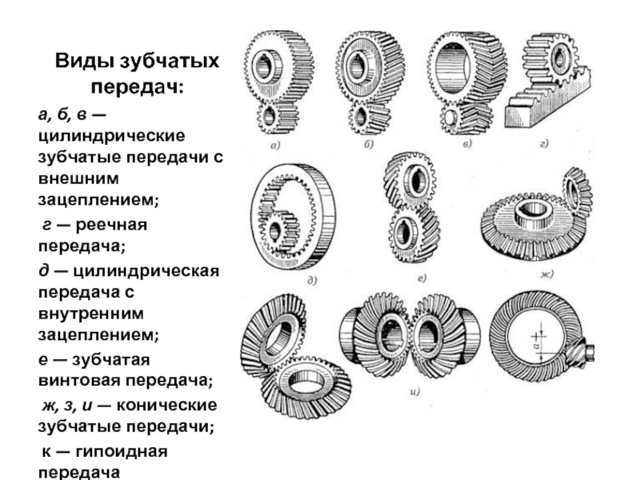
Форма зубьев
Для прямозубых цилиндрических передач форма зубьев определяется DIN 867, DIN 58400; конических передач — DIN 3971; червячных передач — DIN 3975; шлицевых соединений — DIN 5480 (см. рис. «Прямые и косые зубья (наружное зацепление)» ).
Форма зубьев гипоидных передач регламентируется стандартом DIN 867. В дополнение к стандартным углам зацепления (20° для зубчатых передач и 30° для шлицевых соединений) применяются также и углы зацепления 12°, 14°30 15°, 17°30′| 22°30′ и 25°.
Коррегирование зубчатого зацепления
Коррегирование зубчатого зацепления (изменение высоты головки зуба (см. рис. «Коррегирование зубчатого зацепления прямозубой цилиндрической передачи (циклоидное зацепление)» ) применяется для предотвращения подрезания у шестерен с малым количеством зубьев. Оно позволяет увеличить прочность ножки зуба и точно обеспечить межосевое расстояние.
Зубчатые передачи с точно заданным межосевым расстоянием
У зубчатых пар с точно заданным межосевым расстоянием изменение высоты головки зуба для шестерни и зубчатого колеса производится на одинаковую величину, но в противоположных направлениях, что позволяет сохранить межосевое расстояние неизменным. Такое решение применяется в гипоидных и косозубых передачах.
Такое решение применяется в гипоидных и косозубых передачах.
Зубчатые передачи с изменяемым межосевым расстоянием
Изменение высоты головки зуба для шестерни и зубчатого колеса производится независимо друг от друга, поэтому межосевое расстояние передачи может изменяться. Допускаемые отклонения линейных размеров зубчатых передач регламентированы. Для прямозубых цилиндрических передач — DIN 3960, DIN 58405; для конических передач — DIN 3971; червячных передач — DIN 3975.
Подставляя jη = 0 в приведенные ниже формулы, рассчитывают параметры зацепления без зазора между зубьями. Для определения зазора между зубьями допускаемые отклонения толщины зубьев и зоны их зацепления принимают в соответствии со стандартами DIN 3967 и DIN 58405 в зависимости от требуемой степени точности зубчатой передачи.
Следует отметить, что не обязательно стремиться к нулевому зазору между зубьями. Для компенсации имеющихся отклонений размеров зубьев и сборки шестерен достаточно иметь минимальный зазор, который, кроме того, предотвращает возможность заклинивания зубчатых колес.
Допускаемые отклонения других расчетных параметров (зазор между ножками двух смежных зубьев, межцентровое расстояние) приведены в стандартах DIN 3963, DIN 58405, DIN 3962 Т2, DIN 3967, DIN 3964.
Расчетные формулы для зубчатых передач
Основные параметры зубчатых цилиндрических передач
Стандарт распространяется на цилиндрические передачи внешнего зацепления для редукторов и ускорителей, в том числе и комбинированных (коническо-цилиндрических, цилиндро-червячных и др.), выполняемых в виде самостоятельных агрегатов. Стандарт не распространяется на передачи редукторов специального назначения и специальной конструкции Для встроенных передач стандарт является рекомендуемым
Межосевые расстояния
| 1 ряд | 40 | 50 | 63 | 80 | 100 | 125 | — | 160 | — | 200 | — | 250 | — | 315 | — | 400 |
| 2 ряд | — | — | — | — | — | — | 140 | — | 180 | — | 225 | — | 280 | — | 355 | — |
| 1 ряд | — | 500 | — | 630 | — | 800 | — | 1000 | — | 1250 | — | 1600 | — | 2000 | — | 2500 |
| 2 ряд | 450 | — | 560 | — | 710 | — | 900 | — | 1120 | — | 1400 | — | 1800 | — | 2240 | — |
1-й ряд следует предпочитать 2-му
Межосевые расстояния для двухступенчатых несоосных редукторов общего назначения
| Быстроходная ступень | 40 | 50 | 63 | 80 | 100 | 125 | 140 | 160 | 180 | 200 | 225 | 250 | 280 | 315 |
| Тихоходная ступень | 63 | 80 | 100 | 125 | 160 | 200 | 225 | 250 | 280 | 315 | 355 | 400 | 450 | 500 |
| Быстроходная ступень | 355 | 400 | 450 | 500 | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 |
| Тихоходная ступень | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 | 1800 | 2000 | 2240 | 2500 |
Коэффициент запаса прочности при работе зуба двумя сторонами
Например: зубья реверсивных передач или зубья сателлитов в планетарных передачах
| Материал колес и термо- обработка | Отливки стальные и чугунные без термо- обработки | Отливки стальные и чугунные с термо- обработкой | Поковки стальные нормали- зованные или улучшенные | Поковки и отливки стальные с поверх- ностной закалкой (сердцевина вязкая) | Стальные, нормали- зованные или улучшенные, а также с поверх- ностной закалкой | Стальные с объемной закалкой | Стальные, подверг- нутые цементации, азоти- рованию, циани- рованию и др.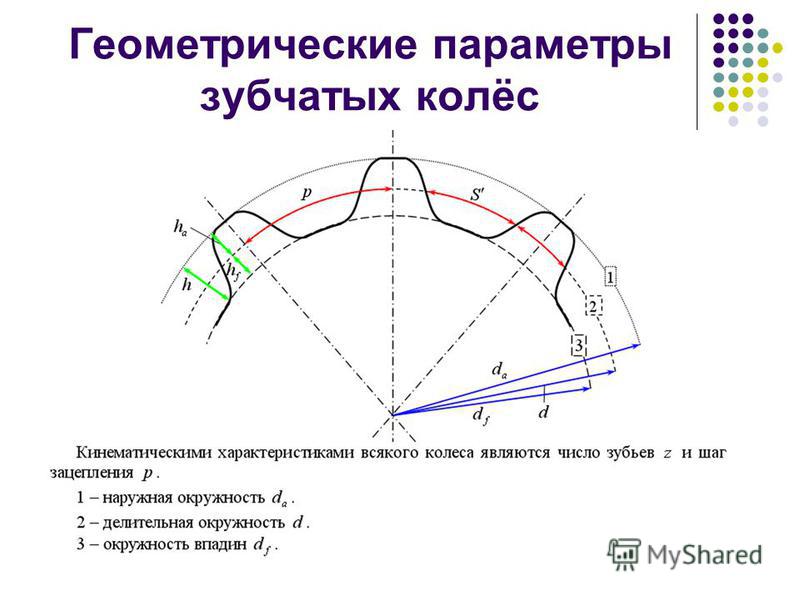 | Чугунные и пласт- массовые колеса |
| Коэфф. | 1,9 | 1,7 | 1,5 | 2,2 | 1,4 — 1,6 | 1,8 | 1,2 | 1 — 1,2 |
Межосевые расстояния для трехступенчатых несоосных редукторов общего назначения
| Быстроходная ступень | 40 | 50 | 63 | 80 | 100 | 125 | 140 | 160 | 180 | 200 |
| Промежуточная ступень | 63 | 80 | 100 | 125 | 160 | 200 | 225 | 250 | 280 | 315 |
| Тихоходная ступень | 100 | 125 | 160 | 200 | 250 | 315 | 355 | 400 | 450 | 500 |
| Быстроходная ступень | 225 | 250 | 280 | 315 | 355 | 400 | 450 | 500 | 560 | 630 |
| Промежуточная ступень | 355 | 400 | 450 | 500 | 560 | 630 | 710 | 800 | 900 | 1000 |
| Тихоходная ступень | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 |
Номинальные передаточные числа
| 1 ряд | 1,0 | — | 1,25 | — | 1,6 | — | 2,0 | — | 2,5 | — | 3,15 | |
| 2 ряд | — | 1,12 | — | 1,4 | — | 1,8 | — | 2,24 | — | 2,8 | — | |
| 1 ряд | — | 4,0 | — | 5,0 | — | 6,3 | — | 8,0 | — | 10 | — | 12,5 |
| 2 ряд | 3,55 | — | 4,5 | — | 5,6 | — | 7,1 | — | 9,0 | — | 11,2 | — |
1-й ряд следует предпочитать 2-му Фактические значения передаточных чисел не должны отличаться от номинальных более чем на 2,5% при номинальном меньше 4,5 и на 4% при номинальном больше 4,5
Коэффициент ширины зубчатых колес (отношение ширины зубчатого колеса к межосевому расстоянию) должен соответствовать: 0,100; 0,125; 0,160; 0,200; 0,315; 0,400; 0,500; 0,630; 0,800; 1,0; 1,25
Численные значения ширины зубчатых колес округляются до ближайшего числа из ряда Ra20 по ГОСТу 6636.
При различной ширине сопряженных зубчатых колес значение коэффициента ширины зубчатых колес относится к более узкому из них.
Почему шестерни часто выполняют заодно с валом?
Несмотря на это, в редукторах шестерню часто выполняют заодно с валом и даже при толщине, значительно превышающей указанные нормы. Это объясняется большей жесткостью и прочностью, а также технологичностью вала-шестерни, что в конечном итоге оправдывает ее стоимость.
Источники
- https://ru.wikipedia.org/wiki/%D0%97%D1%83%D0%B1%D1%87%D0%B0%D1%82%D0%BE%D0%B5_%D0%BA%D0%BE%D0%BB%D0%B5%D1%81%D0%BE
- https://doctordent.su/pulpit/kak-opredelit-modul-zuba-shesterni-po-diametru.html
- https://novoe-info.ru/chto-takoe-modul-zubchatogo-kolesa/
- https://novoe-info.ru/kak-nayti-modul-zubchatogo-kolesa/
- https://morflot.su/kak-vychislit-modul-zubchatogo-kolesa/
- https://wiki2.org/ru/%D0%97%D1%83%D0%B1%D1%87%D0%B0%D1%82%D0%BE%D0%B5_%D0%BA%D0%BE%D0%BB%D0%B5%D1%81%D0%BE
- https://nzmetallspb.
 ru/prochee/modul-zubev-zubchatogo-kolesa-raschet-standartnye-opredelenie.html
ru/prochee/modul-zubev-zubchatogo-kolesa-raschet-standartnye-opredelenie.html - https://armatool.ru/modul-zubev-zubcatogo-kolesa-rascet-standartnye-opredelenie/
Модуль шестерни.Что это такое? — Справочная информация
Основные сведения об эвольвентном зацеплении
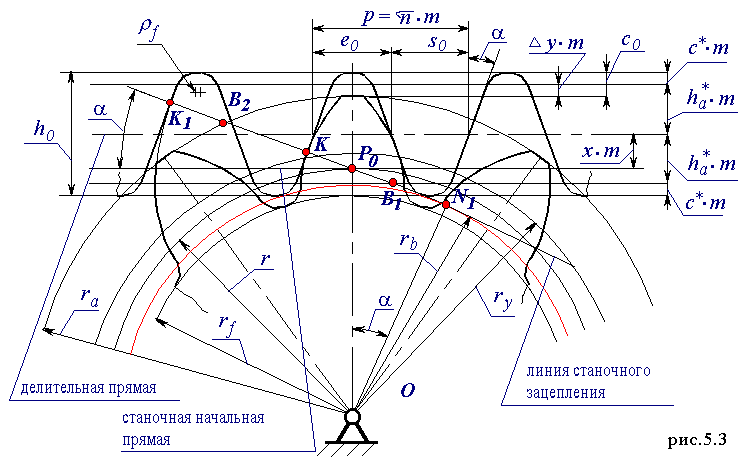
Профиль боковых сторон зубьев зубчатых колес с эвольвентным зацеплением представляет собой две симметрично расположенные эвольвенты.
Эвольвента — это плоская кривая с переменным радиусом кривизны, образованная некоторой точкой на прямой, обкатывающейся без скольжения по окружности, диаметром (радиусом) db(rb) называемой основной окружностью.
Основные параметры эвольвентного зацепления. На рис. 1.1 показано зацепление двух зубчатых колес с эвольвентным профилем. Рассмотрим основные параметры зацепления, их определения и стандартные обозначения.
В отличие от принятого ранее, обозначение всех параметров производится строчными, а не заглавными буквами с индексами, указывающими их принадлежность колесу, инструменту, типу окружности и виду сечения.
Стандартом предусмотрены три группы индексов:
- первая группа: n, t, x — означает вид сечения, соответственно нормальный, торцовый (окружной), осевой;
- вторая группа: a,f,b,w,y- означает, что параметр относится соответственно к окружностям выступов, впадин, основной, начальной и любой концентричной окружности. Для делительной окружности индекс не указывается;
- третья группа: 1, 2, 0 — означает, что параметр относится соответственно к шестерне, колесу, зуборезному инструменту.
Порядок использования индексов определяется номером группы, т.е. вначале предпочтение отдается индексам первой группы, затем второй и т.д.
Некоторые индексы разрешается опускать в случаях, исключающих возникновение недоразумений или не имеющих применения по определению. Например, у прямозубых цилиндрических колес не используются индексы первой группы. В ряде случаев некоторые индексы с целью сокращения записи также опускаются.
Некоторые индексы разрешается опускать в случаях, исключающих возникновение недоразумений или не имеющих применения по определению. Например, у прямозубых цилиндрических колес не используются индексы первой группы. В ряде случаев некоторые индексы с целью сокращения записи также опускаются.
Например, у прямозубых цилиндрических колес не используются индексы первой группы. В ряде случаев некоторые индексы с целью сокращения записи также опускаются.
Рассмотрим зацепление двух прямозубых цилиндрических (рис. 1.1) колес: с меньшим числом зубьев (z1), называемого шестерней, и с большим числом зубьев (z2), называемого колесом; соответственно с центрами колес в точках О1 и О2. В процессе обката шестерни с колесом происходит качение без скольжения двух центроид — окружностей, соприкасающихся в полюсе зацепления — Р. Эти окружности называются начальными, а их диаметры (радиусы) обозначаются с индексом w: dwl (rwl), dw2 (rw2). Для некорригированных колес эти окружности совпадают с делительными окружностями, обозначение диаметров (радиусов) которых дается без индексов первой и второй групп, т.е. для шестерни — d1(r1), для колеса — d2(r2).
Рис. 1.1. Эвольвентное зацепление зубчатых колес
1.1. Эвольвентное зацепление зубчатых колес
Делительная окружность — окружность, на которой шаг между зубьями и угол профиля равны им же на делительной прямой зубчатой рейки, сцепленной с колесом. При этом шаг (Р = π · m) — расстояние между двумя соседними одноименными сторонами профиля. Отсюда диаметр делительной окружности колеса d = P · Z / π = m · Z
Модуль зуба (m = P / π) — величина условная, имеющая размерность в миллиметрах (мм) и используемая как масштаб для выражения многих параметров зубчатых колес. В зарубежной практике в этом качестве используется питч — величина, обратная модулю.
Основная окружность — это окружность, от которой образуется эвольвента. Все параметры, относящиеся к ней, обозначаются с индексом b например, диаметры (радиусы) колес в зацеплении: db1 (rbl), db2 (rb).
Касательно к основным окружностям через полюс зацепления Р проходит прямая N-N, а ее участок N1-N2 называется линией зацепления, по которой в процессе обката перемещается точка контакта сопрягаемых профилей колес.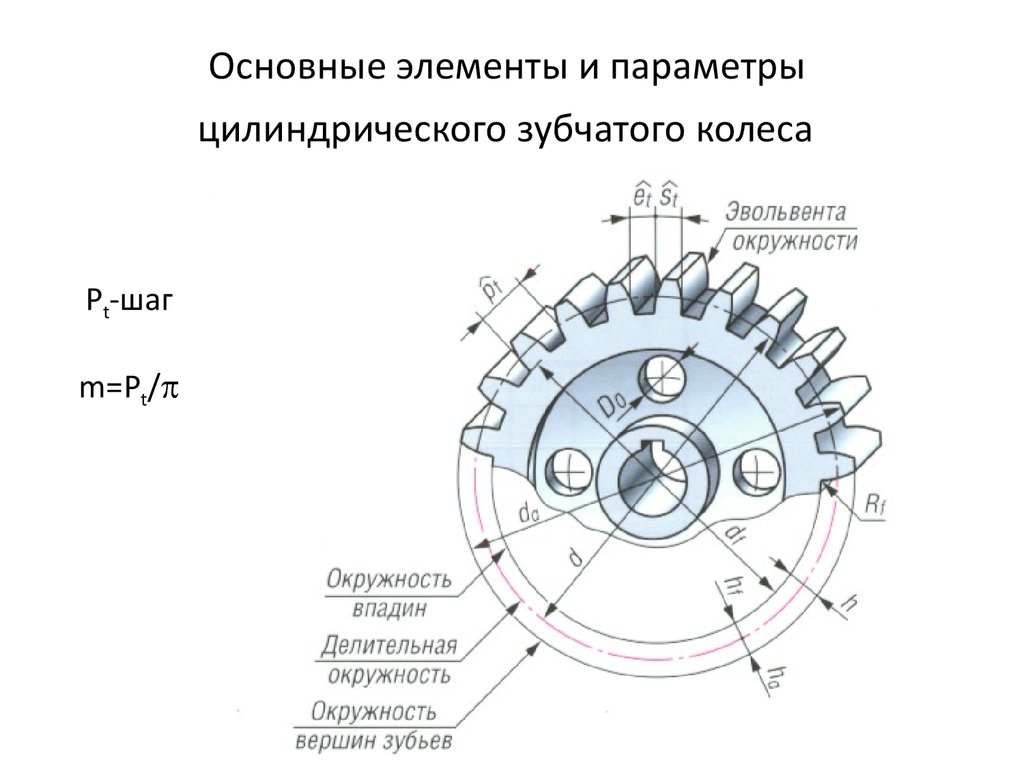 N1-N2 называется номинальной (теоретической) линией зацепления, обозначаемой буквой g. Расстояние между точками пересечения ее с окружностями выступов колес называется рабочим участком линии зацепления и обозначается ga.
N1-N2 называется номинальной (теоретической) линией зацепления, обозначаемой буквой g. Расстояние между точками пересечения ее с окружностями выступов колес называется рабочим участком линии зацепления и обозначается ga.
В процессе обката зубчатых колес точка контакта профилей перемещается в пределах активного (рабочего) участка линии зацепления ga, которая является нормалью к профилям обоих колес в этих точках и одновременно общей касательной к обеим основным окружностям.
Угол между линией зацепления и перпендикуляром к линии, соединяющей центры сопрягаемых колес, называется углом зацепления. У корригированных колес этот угол обозначается αw12; для некорригированных колес αw12 = α0.
Межцентровое расстояние некорригированных колес
aW12 = rW1 + rW2 = r1 + r2 = m ·( Z1 + Z2 ) / 2
Окружности выступов и впадин — окружности, проходящие соответственно через вершины и впадины зубьев колес.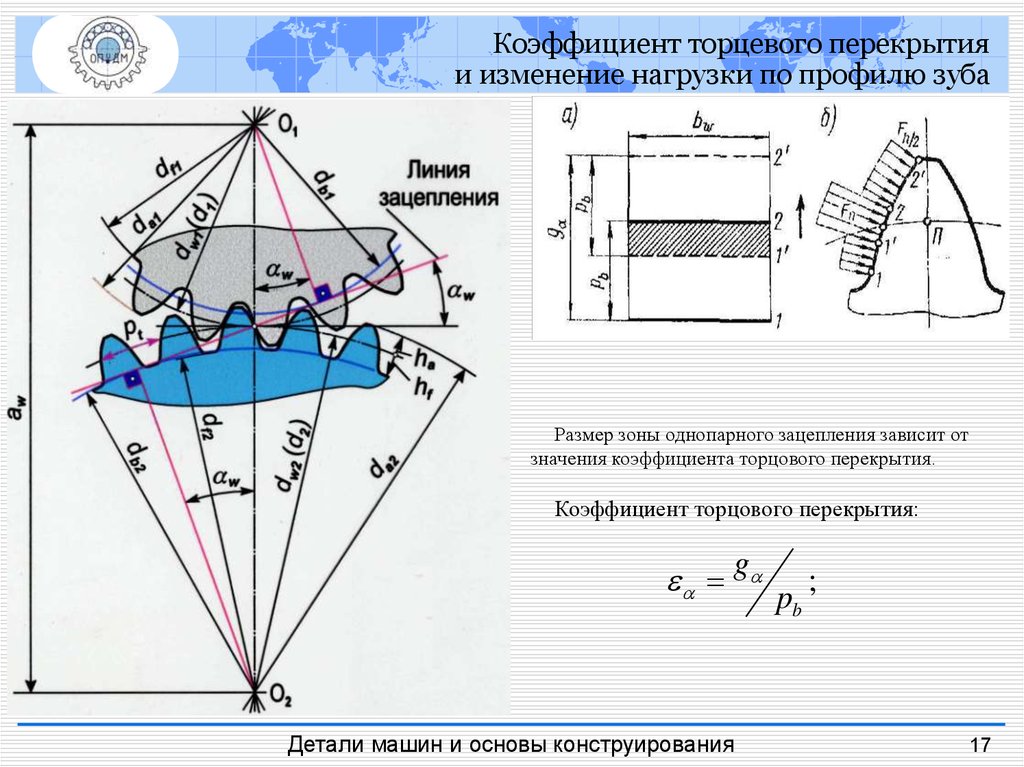 Их диаметры (радиусы) обозначаются: da1 ( ra1 ), df1 ( rf1 ), da2 ( ra2 ), df2( rf2 ).
Их диаметры (радиусы) обозначаются: da1 ( ra1 ), df1 ( rf1 ), da2 ( ra2 ), df2( rf2 ).
Шаги зубьев колес — Pt Рb, Рn, Рх — это расстояния между одноименными сторонами профиля, замеренные:
- по дуге делительной окружности в торцовом сечении — окружной (торцевый) шаг Pt = d / Z;
- по дуге основной окружности — основной шаг Pb = db / Z;
- по контактной нормали (линии зацепления) — основной нормальный шаг Рbn;
- по нормали к направлению зубьев и по оси (у винтовых передач) — нормальный шаг Рn и осевой шаг Рх.
Коэффициент перекрытия, ε — отношение активной (рабочей) части линии зацепления к основному нормальному шагу:
ε = ga / Pbn
Окружная (торцовая) толщина зуба, St — длина дуги делительной окружности, заключенная между двумя сторонами зуба.
Окружная ширина впадины между зубьями, е — расстояние между разноименными сторонами профиля по дуге делительной окружности.
Высота головки зуба, ha — расстояние между окружностями выступов и делительной:
ha = ra — r
Высота ножки зуба hf — расстояние между окружностями делительной и впадин:
hf = r — rf
Высота зуба:
h = ha + hf
Рабочий участок профиля зуба — геометрическое место точек контакта профилей сопрягаемых колес, определяется как расстояние от вершины зуба до точки начала эвольвенты. Ниже последней следует переходная кривая.
Переходная кривая профиля зуба — часть профиля от начала эвольвенты, т.е. от основной окружности до окружности впадин. При методе копирования соответствует форме головки зуба инструмента, а при методе обкатки образуется вершинной кромкой режущего инструмента и имеет форму удлиненной эвольвенты (для инструментов реечного типа) или эпициклоиды (для инструментов типа колеса).
Рис. 1.2. Зацепление зубчатой рейки с колесом
Понятие об исходном контуре рейки
Как было показано выше, частным случаем эвольвенты при z = (бесконечность) является прямая линия. Это дает основание использовать в эвольвентном зацеплении рейку с прямобочными зубьями. При этом любое зубчатое колесо данного модуля независимо от числа зубьев может быть сцеплено с рейкой того же модуля. Отсюда возникла идея обработки колес методом обкатки. В зацеплении колеса с рейкой (рис. 1.2) радиус начальной окружности последней равен бесконечности, а сама окружность превращается в начальную прямую рейки. Линия зацепления N1N2Так как профиль зубьев рейки — прямая линия, это в значительной мере упрощает контроль линейных параметров зубьев и угла профиля. С этой целью стандартами установлено понятие исходного контура зубчатой рейки (рис. 1.4, а) проходит через полюс Р касательно к основной окружности колеса и перпендикулярно к боковой стороне профиля зуба рейки.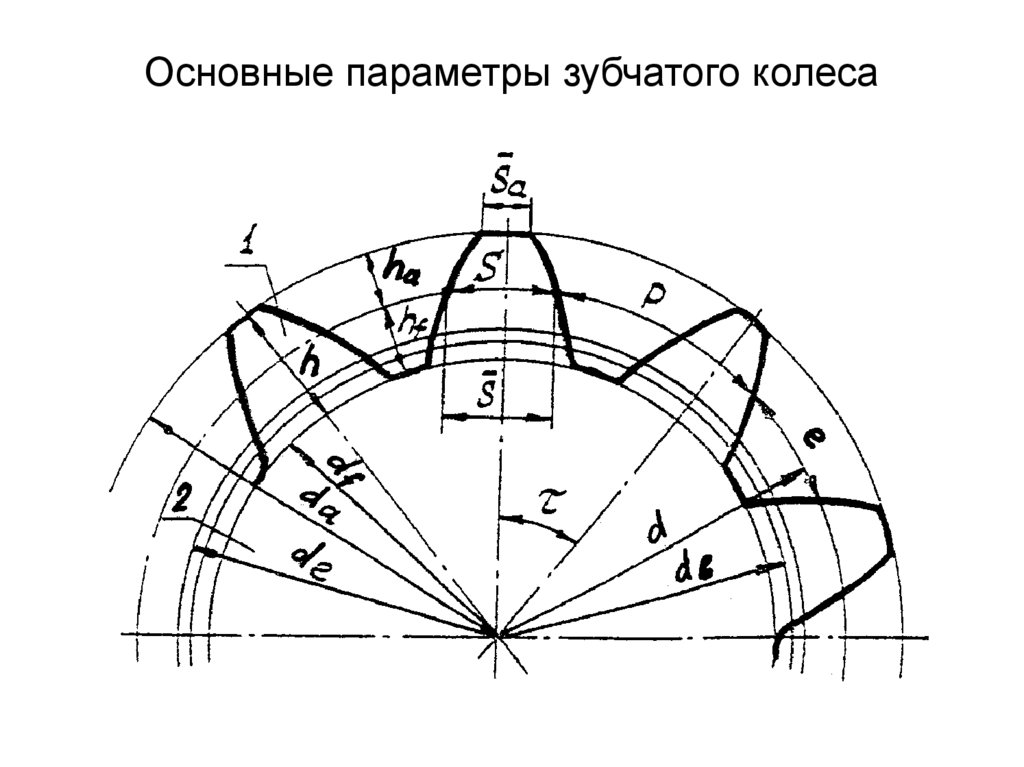 В процессе зацепления начальная окружность колеса обкатывается по начальной прямой рейки, а угол зацепления становится равным углу профиля зуба рейки α .
В процессе зацепления начальная окружность колеса обкатывается по начальной прямой рейки, а угол зацепления становится равным углу профиля зуба рейки α .
Так как профиль зубьев рейки — прямая линия, это в значительной мере упрощает контроль линейных параметров зубьев и угла профиля. С этой целью стандартами установлено понятие исходного контура зубчатой рейки (рис. 1.3, а)
В соответствии со стандартами, принятыми в нашей стране для эвольвентного зацепления, исходный контур имеет следующие параметры зубьев в зависимости от модуля:
- угол профиля α = 20°;
- коэффициент высоты головки h*a = 1;
- коэффициент высоты ножки h*f = 1,25;
- коэффициент радиального зазора с* = 0,25 или 0,3;
- коэффициент граничной (рабочей) высоты зуба h*L = 2;
- шаг зубьев Р = π · m;
- толщина зуба S и ширина впадины е: S = е = 0,5Р = π · m / 2.

Делительная прямая рейки проходит по середине рабочей высоты зуба hL.
Для зуборезных инструментов основные параметры зубьев по аналогии с изложенным выше задаются параметрами исходной инструментальной рейки (рис. 1.3, б). Так как зубья режущего инструмента обрабатывают впадину между зубьями колеса и могут нарезать колеса с модифицированным (фланкированным) профилем, между названными исходными контурами имеются существенные различия:
- Высота головки зуба исходной инструментальной рейки ha0 = (h*f0 + с0 )m = 1,25 m, т.е. коэффициент высоты головки й h*a0 =1,25. Высота ножки зуба hf0 = 1,25 m, а полная высота зуба h0 = ha0 + hf0 = 2,5 m.
- Если нарезаемое колесо имеет срез у головки (модифицированный профиль), то ножка зуба инструментальной рейки должна иметь утолщение с параметрами h ф 0 , α ф 0 , n ф 0.

- Толщина зуба у зубчатой рейки S = π · m / 2 ,
а у инструментальной рейки при нарезании колес с модифицированным профилем зубьев S0 = π · m / 2 ± ΔS0Рис. 1.3. Исходные контуры:
а — зубчатой рейки; б — инструментальной рейки
Поправка ΔS 0 берется из справочников [23, 24] в зависимости от величины модуля зуба. Знак «+» берется для чистовых, а знак «-« — для черновых инструментов. В первом случае происходит утонение зубьев нарезаемого колеса с целью создания бокового зазора между зубьями сцепляемых колес, во втором случае утолщение, в результате чего нарезаемые зубья получают припуск на чистовую обработку.
У колес с обычным (модифицированным) профилем зубьев изменение толщины нарезаемых зубьев можно получить путем смещения инструментальной рейки относительно центра колеса и утолщение ее зубьев у ножки не требуется.
Параметры зацепления корригированных зубчатых колес.
 Корригирование (исправление) колес дает возможность улучшить зубчатое зацепление по сравнению с нормальным зацеплением в отношении трения, износа и прочности зубьев, уменьшить вероятность подреза ножки зубьев при малом их числе и др.
Корригирование (исправление) колес дает возможность улучшить зубчатое зацепление по сравнению с нормальным зацеплением в отношении трения, износа и прочности зубьев, уменьшить вероятность подреза ножки зубьев при малом их числе и др.Применительно к долбякам корригирование дает возможность получения задних углов на режущих кромках (см. ниже).
Из известных методов корригирования на практике наибольшее применение нашло высотное корригирование, которое осуществляется путем смещения профиля исходной инструментальной рейки относительно центра нарезаемого колеса. Такое смещение принято считать положительным, если рейка отводится от центра колеса, и отрицательным, когда она приближается к его центру (рис. 1.4).
Рис. 1.4. Схема высотного корригирования зубчатого колеса:
1 — положительное смещение; 2 — нулевое смещение; 3 — отрицательное смещение
Величина смещения оценивается произведением хо · m, где х0 — коэффициент смещения
При положительном смещении высота головки зуба нарезаемого колеса h‘a1 увеличивается на величину хот, а высота ножки h‘f1 уменьшается на ту же величину.
 При отрицательном смещении, наоборот, высота головки зуба уменьшается, а высота ножки увеличивается. Полная высота зуба колеса в обоих случаях остается неизменной.
При отрицательном смещении, наоборот, высота головки зуба уменьшается, а высота ножки увеличивается. Полная высота зуба колеса в обоих случаях остается неизменной.Так как при этом положение делительной и основной окружностей колеса постоянно и не зависит от величины смещения, то неизбежно изменение толщины зуба нарезаемого колеса по делительной окружности из-за смещения делительной прямой рейки относительно начального положения на величину ± хо · m. Как видно из рис. 1.5, толщина зуба по делительной окружности у корригированного колеса при смещении рейки инструмента
S‘1, 3 = π · m / 2 ± 2 · x0 · m · tg α0
где ΔS = x0 · m · tg α 0.
Знак «+» берется при положительном, а знак «-« — при отрицательном смещении.
При расчетах зуборезных инструментов, например долбяков, зубья которых корригированы, возникает необходимость определения толщины зуба на окружности любого радиуса — rу, концентричной с делительной окружностью радиусом r.

Рис. 1.5. Изменение толщины зуба на делительной окружности при положительном смещении инструментальной рейки.
http://texinfo.inf.u…zuboobr_c1.html
Выбор зубчатых колес, наиболее подходящих для вашего применения
Вопросы и ответы с Рональдом Валенсуэла, техническим руководителем, KHK Gears: По мере развития технологий мы стали свидетелями перехода к использованию зубчатых колес с гораздо меньшим шагом. Мы, конечно, сталкивались с более экзотическими конструкциями зубчатых колес в области мехатроники, которые требуют гораздо меньшего размера.
Выбор редукторов, наиболее подходящих для вашего применения
Вопросы и ответы с Рональдом Валенсуэла, техническим менеджером | КХК Шестерни
18.09.19, 08:00
| Цепочка поставок, инжиниринг
| Отдел запчастей
Расскажите нам о KHK Gears и вашей роли в компании.

Мы (KHK-USA Inc.) являемся стопроцентной дочерней компанией Kohara Gear Industry (KHK), производителя зубчатых колес мирового класса, расположенного в Кавагути, Япония. KHK — многонациональная корпорация с международными каналами сбыта, которые распространяются по всей Азии, Европе, Северной Америке и Латинской Америке. Под торговой маркой KHK компания Kohara Gear стала лидером в производстве серийного снаряжения в Японии, занимая 80% рынка. В настоящее время в KHK работает более 200 человек в 2 офисах в Японии. Главный офис находится в Кавагути и занимается в основном заказными продуктами, а производство серийных шестерен находится в Ноде. Все производственные предприятия Kohara Gear имеют сертификат ISO 9Сертификаты 001 и ISO 14001. Мы представляем Kohara Gear на рынке Северной Америки, и, поскольку мы не являемся независимым дистрибьютором, мы предоставляем нашим клиентам заводские цены на все их потребности в зубчатых передачах.
Моя роль здесь, в KHK-USA Inc., заключается в том, что я являюсь менеджером по проектированию, и я контролирую всю деятельность, связанную с проектированием, на территориях Северной Америки, Канады и Мексики.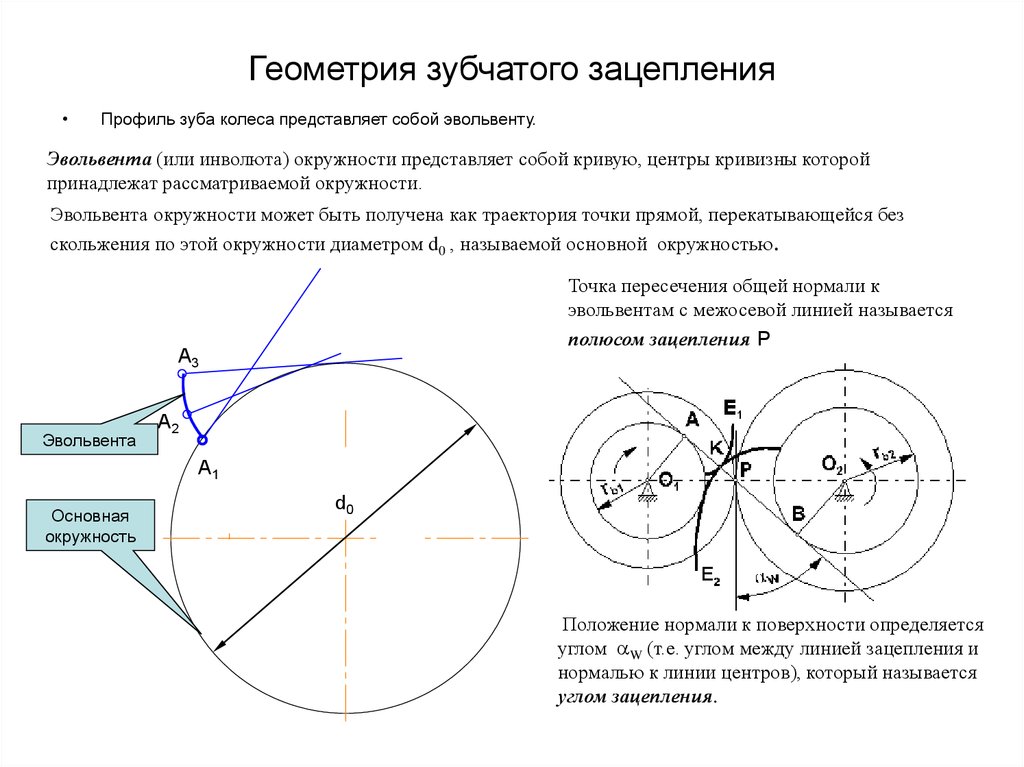 Передо мной и моей командой ежедневно стоит задача предлагать индивидуальные инженерные решения для различных приложений, а также оказывать дизайнерскую и техническую помощь по всей нашей линейке продуктов для всех наших клиентов. Наша основная деятельность связана с передачей электроэнергии, упаковкой и промышленной автоматизацией. Мы тщательно анализируем заявку и требования клиента, чтобы разработать правильное решение для зубчатой передачи. Даже если у клиента уже есть проект, наша работа заключается в рассмотрении и предложении индивидуального решения для его запроса на основе предоставленной информации и всегда с учетом производственных возможностей, масштабируемости и, что более важно, стоимости.
Передо мной и моей командой ежедневно стоит задача предлагать индивидуальные инженерные решения для различных приложений, а также оказывать дизайнерскую и техническую помощь по всей нашей линейке продуктов для всех наших клиентов. Наша основная деятельность связана с передачей электроэнергии, упаковкой и промышленной автоматизацией. Мы тщательно анализируем заявку и требования клиента, чтобы разработать правильное решение для зубчатой передачи. Даже если у клиента уже есть проект, наша работа заключается в рассмотрении и предложении индивидуального решения для его запроса на основе предоставленной информации и всегда с учетом производственных возможностей, масштабируемости и, что более важно, стоимости.
Что такое модуль и чем он отличается от диаметрального шага?
Наиболее популярным обозначением шага за пределами США является то, что известно как модуль. Чтобы определить значение модуля для данной передачи, вы измеряете длину шага в миллиметрах и делите это значение на π. Например, если длина шага составляет 9,425 мм, это будет шестерня модуля 3. Включив π в значение шага, метрические размеры цилиндрического зубчатого колеса рассчитать очень просто. Делительный диаметр цилиндрической шестерни модуля 3 с 25 зубьями равен модулю (3), умноженному на число зубьев (25), или 75 мм. Это также упрощает расчет для добавления, удаления и полной глубины. Для шестерни DP сложение равно 1/DP, сложение равно всей глубине за вычетом сложения, а вся глубина равна 2,157/DP. При работе с модулем дополнение равно модулю, дедендум равен 1,25-кратному модулю, а вся глубина равна 2,25-кратному модулю.
Например, если длина шага составляет 9,425 мм, это будет шестерня модуля 3. Включив π в значение шага, метрические размеры цилиндрического зубчатого колеса рассчитать очень просто. Делительный диаметр цилиндрической шестерни модуля 3 с 25 зубьями равен модулю (3), умноженному на число зубьев (25), или 75 мм. Это также упрощает расчет для добавления, удаления и полной глубины. Для шестерни DP сложение равно 1/DP, сложение равно всей глубине за вычетом сложения, а вся глубина равна 2,157/DP. При работе с модулем дополнение равно модулю, дедендум равен 1,25-кратному модулю, а вся глубина равна 2,25-кратному модулю.
Аналогично передаче DP, установлены стандартные значения модуля. Для зубчатых передач с линейным шагом типичные значения модуля составляют 10, 8, 6, 5, 4 и 3. Для передаточного механизма с дробным шагом среднего шага значения модуля составляют 2,5, 2, 1,5 и 1,25. Для зубчатой передачи с мелким шагом типичные значения составляют 1, 0,8, 0,7, 0,5, 0,4, 0,3 и 0,2. В метрических передачах также существует понятие кругового шага (CP). Вычитая значение π, значения CP 2,5 мм, 5 мм, 10 мм, 15 мм и 20 мм являются обычными.
Вычитая значение π, значения CP 2,5 мм, 5 мм, 10 мм, 15 мм и 20 мм являются обычными.
Не могли бы вы дать нам несколько советов о том, как выбрать лучший тип редуктора для различных применений?
Это распространенный вопрос, с которым мы с моей командой сталкиваемся каждый день. Реальный ответ заключается в том, что каждый тип зубчатого колеса предлагает уникальные преимущества, основанные на геометрии зубчатого колеса и характеристиках зацепления.
Чтобы найти правильный тип шестерни для приложения, в первую очередь необходимо определить, какой тип шестерни будет соответствовать ориентации вала системы. Возможности:
- Параллельные оси
- Пересекающиеся оси
- Непараллельные и непересекающиеся оси
Поскольку каждое решение всегда зависит от приложения, необходимо установить следующую информацию:
- Число оборотов в минуту / Передаточное число
- Требования к нагрузке/крутящему моменту/рабочему циклу
- Окружающая среда, в которой он будет работать
- Жилищные ограничения
- Целевая цена
Когда у нас будет полное понимание того, что требуется, мы сможем предложить подходящее решение, основанное на конкретных параметрах приложения. Важно отметить, что прямозубые / косозубые шестерни используются чаще всего из-за широкого диапазона доступных конфигураций зубьев и их гибкости для применения во многих механизмах. Например, два цилиндрических зубчатых колеса могут зацепляться в механизме с параллельным валом, что позволяет передавать движение и изменять направление, или шестерня может соединяться с зубчатой рейкой, тем самым преобразовывая вращательное движение в линейное перемещение, и, наконец, цилиндрическое зубчатое колесо может быть частью механизма. планетарный зубчатый механизм, в котором он будет сопрягаться с внутренней шестерней и использоваться в качестве повышающего или редуктора скорости.
Важно отметить, что прямозубые / косозубые шестерни используются чаще всего из-за широкого диапазона доступных конфигураций зубьев и их гибкости для применения во многих механизмах. Например, два цилиндрических зубчатых колеса могут зацепляться в механизме с параллельным валом, что позволяет передавать движение и изменять направление, или шестерня может соединяться с зубчатой рейкой, тем самым преобразовывая вращательное движение в линейное перемещение, и, наконец, цилиндрическое зубчатое колесо может быть частью механизма. планетарный зубчатый механизм, в котором он будет сопрягаться с внутренней шестерней и использоваться в качестве повышающего или редуктора скорости.
Как качество шестерни влияет на общую производительность механизма?
Точность является ключевым фактором, когда речь идет о создании эффективного редуктора. Качественно изготовленная шестерня снизит уровень шума, люфта, вибрации и позволит уменьшить габариты конструкции. Все эти преимущества значительно повышают эффективность механизма и гарантируют получение хорошо спроектированного продукта после его сборки.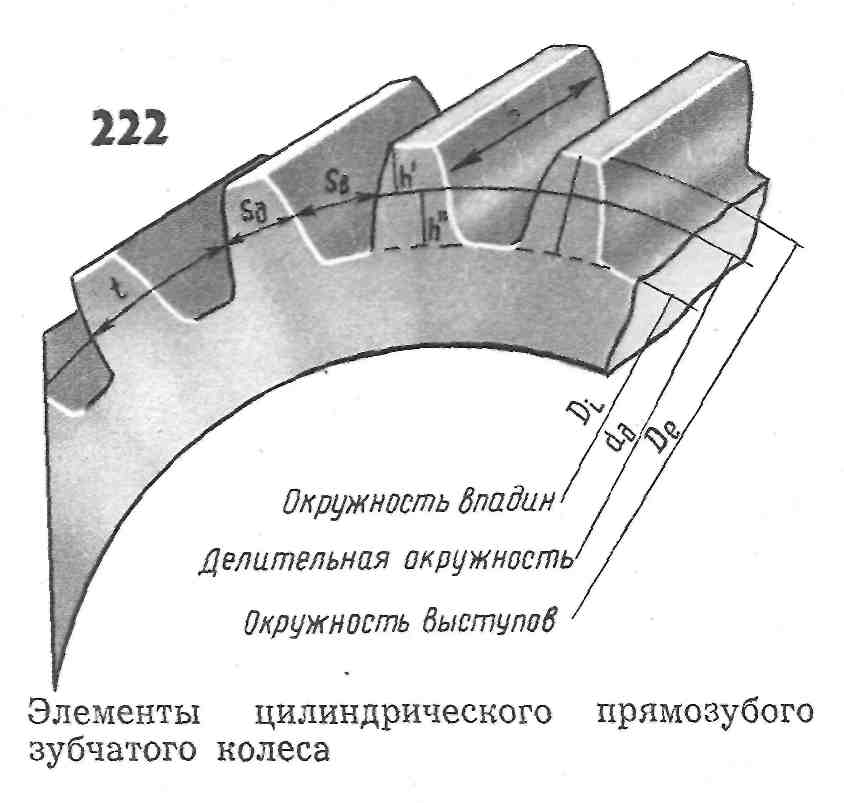
Мы получаем много запросов от многочисленных клиентов, которые ранее приобретали некачественные шестерни от разных поставщиков, и выражают свое недовольство, когда их отдел контроля качества должен отказаться от продукта, потому что шестерни не прошли проверку или шестерни вышли из строя на этапе прототипа. Мы гордимся тем, что предлагаем высококачественные зубчатые передачи, и у нас есть необходимые процессы, установленные во время производства, чтобы свести к минимуму дефекты.
Со всеми новыми типами волокнистых пластиков на рынке сталь по-прежнему остается лучшим вариантом? Когда волокнистый пластик может быть лучшим вариантом?
Есть много новых пластиков, которые наводняют промышленность, однако они имеют высокую цену. Это действительно зависит от типа проекта, масштаба и финансирования, доступного для каждого приложения. Сталь всегда будет лучшим вариантом для приложений, требующих высокой прочности, точности и доступности. Кроме того, из-за свойств обрабатываемости стоимость производства некоторых стальных компонентов может быть значительно ниже по сравнению с некоторыми пластиковыми материалами.
Кроме того, из-за свойств обрабатываемости стоимость производства некоторых стальных компонентов может быть значительно ниже по сравнению с некоторыми пластиковыми материалами.
Пластмассы, индуцированные волокном, идеально подходят для приложений, которые имеют ограничения по весу, но требуют передачи приличного крутящего момента. Эти материалы могут подвергаться воздействию агрессивных сред или иметь агрессивные химические вещества, вводимые во время работы, и не имеют отрицательных побочных эффектов. Благодаря их способности поглощать удары или вибрацию, а также низкому коэффициенту трения они настоятельно рекомендуются для применений, требующих самосмазывания зубчатой передачи или в случаях, когда уровень шума вызывает беспокойство. Некоторые материалы, такие как PEEK, обеспечивают высокое соотношение прочности к весу, и мы заметили значительное увеличение их использования за последнее десятилетие.
Пластиковые шестерни также могут использоваться в качестве отказоустойчивых в сложной трансмиссии. При использовании в качестве отказоустойчивого разработчик признает, что система может потерпеть катастрофический отказ, и, включив в систему расходуемую нейлоновую шестерню, они могут предотвратить повреждение остальной части привода. Когда система испытывает пиковую нагрузку, превышающую проектную, первым из компонентов, который выйдет из строя, будет пластмассовая шестерня.
При использовании в качестве отказоустойчивого разработчик признает, что система может потерпеть катастрофический отказ, и, включив в систему расходуемую нейлоновую шестерню, они могут предотвратить повреждение остальной части привода. Когда система испытывает пиковую нагрузку, превышающую проектную, первым из компонентов, который выйдет из строя, будет пластмассовая шестерня.
Каковы преимущества прямого и спирального зубьев?
Конструкция с прямыми зубьями обеспечивает самый простой тип зубчатого зацепления, что делает его идеальным для приложений, требующих зубчатого механизма по самой доступной цене. Наиболее благоприятным преимуществом выбора конструкции с прямыми зубьями должно быть большое разнообразие шагов и конфигураций зубьев, которые легко доступны на рынке. Кроме того, прямозубые зубчатые колеса обеспечивают гораздо более короткие сроки производства и более низкие производственные затраты.
Ниже перечислены некоторые недостатки, связанные с выбором конструкции с прямыми зубьями:
- Ограниченный крутящий момент
- Повышенный уровень шума во время работы
- Нижняя контактная поверхность
Спиральная конструкция зуба имеет угол наклона спирали, который усиливает многие основные преимущества конструкции с прямым зубом. Угол наклона спирали увеличивает площадь контактной поверхности зубчатого колеса, что позволяет передавать более высокий крутящий момент. Как правило, спиральные зубчатые колеса обеспечивают гораздо более прочное, тихое и плавное зацепление.
Угол наклона спирали увеличивает площадь контактной поверхности зубчатого колеса, что позволяет передавать более высокий крутящий момент. Как правило, спиральные зубчатые колеса обеспечивают гораздо более прочное, тихое и плавное зацепление.
Ниже перечислены некоторые из недостатков, связанных с выбором конструкции спирального зуба:
- Создает или усиливает осевое осевое усилие
- Требуются левосторонняя и правосторонняя версии
- Более высокая стоимость производства
- Более длительное время выполнения заказа
В связи с тем, что производство быстро меняется, какие изменения вы заметили в типах востребованных зубчатых колес?
По мере развития технологий мы стали свидетелями перехода к использованию зубчатых передач с более мелким шагом. Мы, безусловно, сталкивались с более экзотическими конструкциями зубчатых передач в области мехатроники, которые требуют гораздо меньших размеров, чем когда-либо прежде. Конструкции становятся все более компактными и весовыми, а механизм имеет гораздо более жесткие ограничения, чем то, что мы привыкли видеть. Наконец, наблюдается заметный всплеск использования всех новых различных типов пластиковых материалов с добавлением волокон, которые становятся доступными.
Конструкции становятся все более компактными и весовыми, а механизм имеет гораздо более жесткие ограничения, чем то, что мы привыкли видеть. Наконец, наблюдается заметный всплеск использования всех новых различных типов пластиковых материалов с добавлением волокон, которые становятся доступными.
Как компания KHK Gears адаптируется к постоянно меняющимся требованиям клиентов и остается актуальной?
Мы способны адаптироваться, потому что постоянно инвестируем в нашу рабочую силу и должным образом обучаем ее проектированию, изготовлению и контролю качества зубчатых колес. Разносторонний сотрудник всегда даст компании конкурентное преимущество перед конкурентами и предложит потребителю приятный опыт.
Мы слушаем и обращаем внимание на наших клиентов и актуальные темы в отрасли. Наши клиенты являются основным источником информации о тенденциях и возможностях отрасли, они могут пролить свет на многие вопросы, которые мы могли упустить из виду. Мы также посещаем множество торговых выставок и съездов в течение года, межличностное общение, которое мы получаем как с лидерами отрасли, так и с потенциальными клиентами, дает нам прямой взгляд на актуальные темы или достижения в отраслях, в которых мы работаем.
Содержание и мнения в этой статье принадлежат автору и не обязательно отражают точку зрения ManufacturingTomorrow
18.09.19, 08:00
| Цепочка поставок, инжиниринг
| Отдел запчастей
Другие технические статьи | Истории | Новости
Эта запись не имеет комментариев. Будьте первым, кто оставит комментарий ниже.
Опубликовать комментарий
Прежде чем оставлять комментарии, вы должны войти в систему. Войти сейчас.
Рекомендуемый продукт
Панели ResinDek®, напольное покрытие для антресолей
Напольные панели ResinDek
предназначены для приподнятых платформ, таких как антресоли, модули выбора и рабочие платформы. Они обладают проверенной структурной целостностью, позволяющей выдерживать динамические и статические пределы качения от 2000 до 8000 фунтов. Напольные панели ResinDek доступны во множестве вариантов, которые настраиваются в зависимости от грузоподъемности, требуемого типа отделки, объема и типа движения, включая тяжелые грузы с тележкой для поддонов и роботизированное движение с помощью AGV и AMR.
Напольные панели ResinDek доступны во множестве вариантов, которые настраиваются в зависимости от грузоподъемности, требуемого типа отделки, объема и типа движения, включая тяжелые грузы с тележкой для поддонов и роботизированное движение с помощью AGV и AMR.
Модуль 1 Конические шестерни | TYMA CZ
Мы используем файлы cookie
Этот веб-сайт использует файлы cookie. Некоторые из них необходимы для работы веб-сайта, другие вы можете выбрать сами.
Вы можете изменить свои настройки в любое время с помощью ссылки «Cookies» в нижнем колонтитуле веб-сайта.
Ваши настройки
Технические файлы cookie
Мы используем их, например, для функции корзины, переключения валюты интернет-магазина или администрирования этих согласий. Но это также файл cookie Диспетчера тегов Google.
Интернет не работает должным образом без них. Поэтому их нельзя отключить в настройках
Поэтому их нельзя отключить в настройках
Статистические файлы cookie
Файлы cookie Google Analytics, а иногда также файлы cookie Microsoft Clarity
Они помогают нам с веб-разработкой и отладкой, спасибо! 🙂
Маркетинговые файлы cookie
Файлы cookie рекламной системы Google и файлы cookie Seznam Sklik
Повышают релевантность рекламных кампаний
TYMA CZSearchEshop Дерево категорий
Модуль 1 Конические шестерни — это детали машин, используемые для передачи крутящего момента между двумя валами с разными осями.
Поставляются модулями M1 — M5 . Конические шестерни чаще всего поставляются в виде зубчатой передачи (пары шестерен) с передаточным числом 1:1, 1:1,5, 1:2, 1:2,5, 1:3, 1:3,5 и 1:4. Они также могут быть поставлены как отдельные колеса.
Они также могут быть поставлены как отдельные колеса.
Конические зубчатые колеса с прямыми зубьями делятся по типу на тип А по DIN 3967 по UNI 6588, или тип В – Gleason System .
Предлагаемые нами конические шестерни имеют прямые зубья и угол зацепления 20° .
Осторожно
Конические шестерни в зубчатой передаче должны иметь один и тот же модуль и один и тот же тип (A или B).
Для более сложных и точных требований необходимо использовать специальные конические шестерни, разработанные и изготовленные специализированными поставщиками непосредственно для применения.
подробнее
показать фильтр продукта
Коническая шестерня
Нет в наличии
В течение 2 недель Обычно этот продукт готов к отправке. Фактическая доступность может отличаться из-за непредвиденных обстоятельств в исключительных случаях.
28,71€ без учета НДС
34,74€ вкл. НДС
Коническая шестерня
Нет в наличии
В течение 2 недель Обычно этот продукт готов к отправке. Фактическая доступность может отличаться из-за непредвиденных обстоятельств в исключительных случаях.
38,14€ без учета НДС
46.15€ вкл. НДС
Коническая шестерня
Нет в наличии
В течение 2 недель Обычно этот продукт готов к отправке. Фактическая доступность может отличаться из-за непредвиденных обстоятельств в исключительных случаях.
48,24€ без учета НДС
58. 38€ вкл. НДС
38€ вкл. НДС
Коническая шестерня
Нет в наличии
В течение 2 недель Обычно этот продукт готов к отправке. Фактическая доступность может отличаться из-за непредвиденных обстоятельств в исключительных случаях.
21,68€ без учета НДС
26.23€ вкл. НДС
Коническая шестерня
Нет в наличии
В течение 2 недель Обычно этот продукт готов к отправке. Фактическая доступность может отличаться из-за непредвиденных обстоятельств в исключительных случаях.
25,77€ без учета НДС
31.18€ вкл. НДС
Коническая шестерня
Нет в наличии
В течение 2 недель Обычно этот продукт готов к отправке. Фактическая доступность может отличаться из-за непредвиденных обстоятельств в исключительных случаях.
Фактическая доступность может отличаться из-за непредвиденных обстоятельств в исключительных случаях.
35,20€ без НДС НДС
42,60€ вкл. НДС
Коническая шестерня
Нет в наличии
В течение 2 недель Обычно этот продукт готов к отправке. Фактическая доступность может отличаться из-за непредвиденных обстоятельств в исключительных случаях.
25,19€ без учета НДС
30.48€ вкл. НДС
Коническая шестерня
Нет в наличии
В течение 2 недель Обычно этот продукт готов к отправке. Фактическая доступность может отличаться из-за непредвиденных обстоятельств в исключительных случаях.
27,43€ без учета НДС
33. 19€ вкл. НДС
19€ вкл. НДС
Коническая шестерня
Нет в наличии
В течение 2 недель Обычно этот продукт готов к отправке. Фактическая доступность может отличаться из-за непредвиденных обстоятельств в исключительных случаях.
31,65€ без учета НДС
38.30€ вкл. НДС
Коническая шестерня
Нет в наличии
В течение 2 недель Обычно этот продукт готов к отправке. Фактическая доступность может отличаться из-за непредвиденных обстоятельств в исключительных случаях.
37,06€ без учета НДС
44,84€ вкл. НДС
Коническая шестерня
Нет в наличии
В течение 2 недель Обычно этот продукт готов к отправке. Фактическая доступность может отличаться из-за непредвиденных обстоятельств в исключительных случаях.
Фактическая доступность может отличаться из-за непредвиденных обстоятельств в исключительных случаях.
22,96€ без учета НДС
27,78€ вкл. НДС
Коническая шестерня
Нет в наличии
В течение 2 недель Обычно этот продукт готов к отправке. Фактическая доступность может отличаться из-за непредвиденных обстоятельств в исключительных случаях.
22,96€ без учета НДС
27,78€ вкл. НДС
Шестерни конические предназначены для общего применения в машиностроении .
Поставляемые нами стандартные конические зубчатые колеса предназначены в первую очередь для базовых, более простых конструкций и технических решений для конвейеров , прессов, редукторов, деревообрабатывающих станков, сельскохозяйственных машин, но, конечно же, и для многих других применений.
Сталь C45 (ČSN 12050), шестерни незакаленные.
Пример:
OKS M1 Z30/30 B (сталь)
| Код Деталь | Описание |
|---|---|
| ОКС | Коническая шестерня |
| М1 | Модуль |
| Z30/30 | Количество зубьев (передаточное отношение 1:1) |
| Б | Тип зубчатой передачи |
| Сталь | Материал зубчатой передачи |
Размеры и параметры конических зубчатых колес
TYMA CZ Спецификации
Чешский и английский языки (PDF 1,09 МБ) Журнал Gear Solutions Ваш ресурс для производителей зубчатых передач
Шаг шестерни определяется как расстояние между двумя одинаковыми точками на двух соседних зубьях шестерни. В идеале она измеряется на линии основного тона, обозначенной на рисунке 1 как опорная линия.
В зубчатых передачах есть три обозначения шага: шестерни могут быть изготовлены с диаметральным шагом (DP), круговым шагом (CP) или модулем, также известным как метрический шаг. Наиболее часто используемым обозначением шага в Соединенных Штатах является диаметральный шаг. Этот метод определения размера зуба шестерни основан на единичной окружности. Если вы нарисуете круг диаметром один дюйм и равномерно разместите 16 зубьев вокруг этого круга, при этом диаметр шага перекрывает круг диаметром один дюйм, то вы создали форму зуба шестерни 16DP. Если бы вы продолжали рисовать зубы того же размера на двухдюймовом круге, то у вас было бы 32 зуба, а шаг был бы 32/2, или 16DP.
Диапазон возможных значений для передачи DP может быть бесконечным, поэтому размеры некоторых наборов эволюционировали. Для зубчатой передачи с прямым шагом и передачей мощности типичными значениями для зубчатой передачи с диаметральным шагом являются 2DP, 4DP, 5DP, 6DP и 8DP. В редукторе со средним шагом дробной мощности обычно используются 10DP, 12DP, 16DP и 20DP. Для зубчатой передачи инструмента с мелким шагом типичные значения составляют 24 DP, 32 DP, 48 DP, 64 DP, 96 DP и 120 DP. Преимущество этих значений в том, что каждое из них сильно делится на множество факторов. Шестерня 48DP имеет коэффициенты 2, 3, 4, 6, 8, 12, 16 и 24. Это позволяет использовать несколько передаточных чисел с использованием общего количества зубьев.
Для зубчатой передачи инструмента с мелким шагом типичные значения составляют 24 DP, 32 DP, 48 DP, 64 DP, 96 DP и 120 DP. Преимущество этих значений в том, что каждое из них сильно делится на множество факторов. Шестерня 48DP имеет коэффициенты 2, 3, 4, 6, 8, 12, 16 и 24. Это позволяет использовать несколько передаточных чисел с использованием общего количества зубьев.
Рисунок 1
Одним из недостатков DP-передачи является то, что, когда угловое движение цилиндрической шестерни преобразуется в прямолинейное движение вдоль зубчатой рейки, сдвиг вдоль рейки является дробным числом. Например, если мы работаем с 25-зубчатой шестерней 5DP, перемещающейся вдоль зубчатой рейки 5DP, шестерня будет перемещаться (5 x π) 15,708 дюйма за оборот. Если конструкция требует, чтобы шестерня перемещалась на 45 дюймов, а затем реверсировала, разработчику пришлось бы настроить механизм так, чтобы он не совершал третий оборот, иначе шестерня переместилась бы слишком далеко. Так родилась концепция кругового шага, или КП. Это обозначение шага допускает линейный перевод, приравнивающий обороты шестерни к целым числам. В семействе круговых шагов есть как дюймовые CP, так и метрические CP. Если бы мы выбрали значение CP 5/8 дюйма для той же шестерни с 25 зубьями, но уменьшили количество зубьев до 24, каждый оборот результирующей шестерни перемещал бы 15 дюймов линейно вдоль зубчатой рейки. Зубчатые передачи CP обычно используются в приложениях «взять и поместить» или в портальных системах, где требуется частое реверсирование и точное позиционирование.
Это обозначение шага допускает линейный перевод, приравнивающий обороты шестерни к целым числам. В семействе круговых шагов есть как дюймовые CP, так и метрические CP. Если бы мы выбрали значение CP 5/8 дюйма для той же шестерни с 25 зубьями, но уменьшили количество зубьев до 24, каждый оборот результирующей шестерни перемещал бы 15 дюймов линейно вдоль зубчатой рейки. Зубчатые передачи CP обычно используются в приложениях «взять и поместить» или в портальных системах, где требуется частое реверсирование и точное позиционирование.
Третьим и самым популярным обозначением высоты тона за пределами США является модуль. Чтобы определить значение модуля для данной передачи, вы измеряете длину шага в миллиметрах и делите это значение на π. Например, если длина шага составляет 9,425 мм, это будет шестерня модуля 3. Включив π в значение шага, метрические размеры цилиндрического зубчатого колеса рассчитать очень просто. Делительный диаметр цилиндрической шестерни модуля 3 с 25 зубьями равен модулю (3), умноженному на число зубьев (25), 75 мм. Это также упрощает расчет для добавления, удаления и полной глубины. Для шестерни DP сложение равно 1/DP, сложение равно всей глубине за вычетом сложения, а вся глубина равна 2,157/DP. При работе с модулем дополнение равно модулю, дедендум равен 1,25-кратному модулю, а вся глубина равна 2,25-кратному модулю.
Это также упрощает расчет для добавления, удаления и полной глубины. Для шестерни DP сложение равно 1/DP, сложение равно всей глубине за вычетом сложения, а вся глубина равна 2,157/DP. При работе с модулем дополнение равно модулю, дедендум равен 1,25-кратному модулю, а вся глубина равна 2,25-кратному модулю.
Аналогично передаче DP, установлены стандартные значения модуля. Для зубчатой передачи с прямым шагом типичные значения модуля составляют 10, 8, 6, 5, 4 и 3. Для зубчатой передачи с дробной мощностью среднего шага значения модуля составляют 2,5, 2, 1,5 и 1,25. Для зубчатой передачи привода инструмента с мелким шагом типичные значения составляют 1, 0,8, 0,7, 0,5, 0,4, 0,3 и 0,2. В рамках метрической передачи также существует понятие CP. Вычитая значение π, значения CP 2,5 мм, 5 мм, 10 мм, 15 мм и 20 мм являются обычными.
Также распространено неправильное представление о том, что две шестерни с одинаковым шагом «найдут» свою золотую середину, если их сцепить вместе.




 Тёмное и светлое колёсо имеют одинаковый модуль. Самый главный параметр, стандартизирован, определяется из прочностного расчёта зубчатых передач. Чем больше нагружена передача, тем выше значение модуля. Через него выражаются все остальные параметры. Модуль измеряется в миллиметрах, вычисляется по формуле:
Тёмное и светлое колёсо имеют одинаковый модуль. Самый главный параметр, стандартизирован, определяется из прочностного расчёта зубчатых передач. Чем больше нагружена передача, тем выше значение модуля. Через него выражаются все остальные параметры. Модуль измеряется в миллиметрах, вычисляется по формуле:
 ru/prochee/modul-zubev-zubchatogo-kolesa-raschet-standartnye-opredelenie.html
ru/prochee/modul-zubev-zubchatogo-kolesa-raschet-standartnye-opredelenie.html
 Корригирование (исправление) колес дает возможность улучшить зубчатое зацепление по сравнению с нормальным зацеплением в отношении трения, износа и прочности зубьев, уменьшить вероятность подреза ножки зубьев при малом их числе и др.
Корригирование (исправление) колес дает возможность улучшить зубчатое зацепление по сравнению с нормальным зацеплением в отношении трения, износа и прочности зубьев, уменьшить вероятность подреза ножки зубьев при малом их числе и др. При отрицательном смещении, наоборот, высота головки зуба уменьшается, а высота ножки увеличивается. Полная высота зуба колеса в обоих случаях остается неизменной.
При отрицательном смещении, наоборот, высота головки зуба уменьшается, а высота ножки увеличивается. Полная высота зуба колеса в обоих случаях остается неизменной.
